A Double-Sampling Extension of the German National Forest Inventory for Design-Based Small Area Estimation on Forest District Levels
Abstract
1. Introduction
2. Terrestrial Sampling Design of the German NFI
3. Double Sampling in the Infinite Population Approach
4. Estimators
4.1. Design-Based One-Phase Estimator for Cluster Sampling (SRS)
4.2. Design-Based Small Area Regression Estimators for Cluster Sampling
4.2.1. Pseudo Small Area Estimator (PSMALL)
4.2.2. Pseudo Synthetic Estimator (PSYNTH)
4.2.3. Extended Pseudo Synthetic Estimator (EXTPSYNTH)
4.3. Measures of Estimation Accuracy
5. Case Study
5.1. Study Area and Small Area Units
5.2. Terrestrial Sample
5.3. Extension to Double-Sampling Design
5.4. Auxiliary Data
5.4.1. LiDAR Canopy Height Model
5.4.2. Tree Species Classification Map
5.5. Calculation of the Explanatory Variables
5.5.1. Canopy Height Model
5.5.2. Tree Species Classification Map
5.6. Regression Model
6. Results
6.1. General Estimation Results
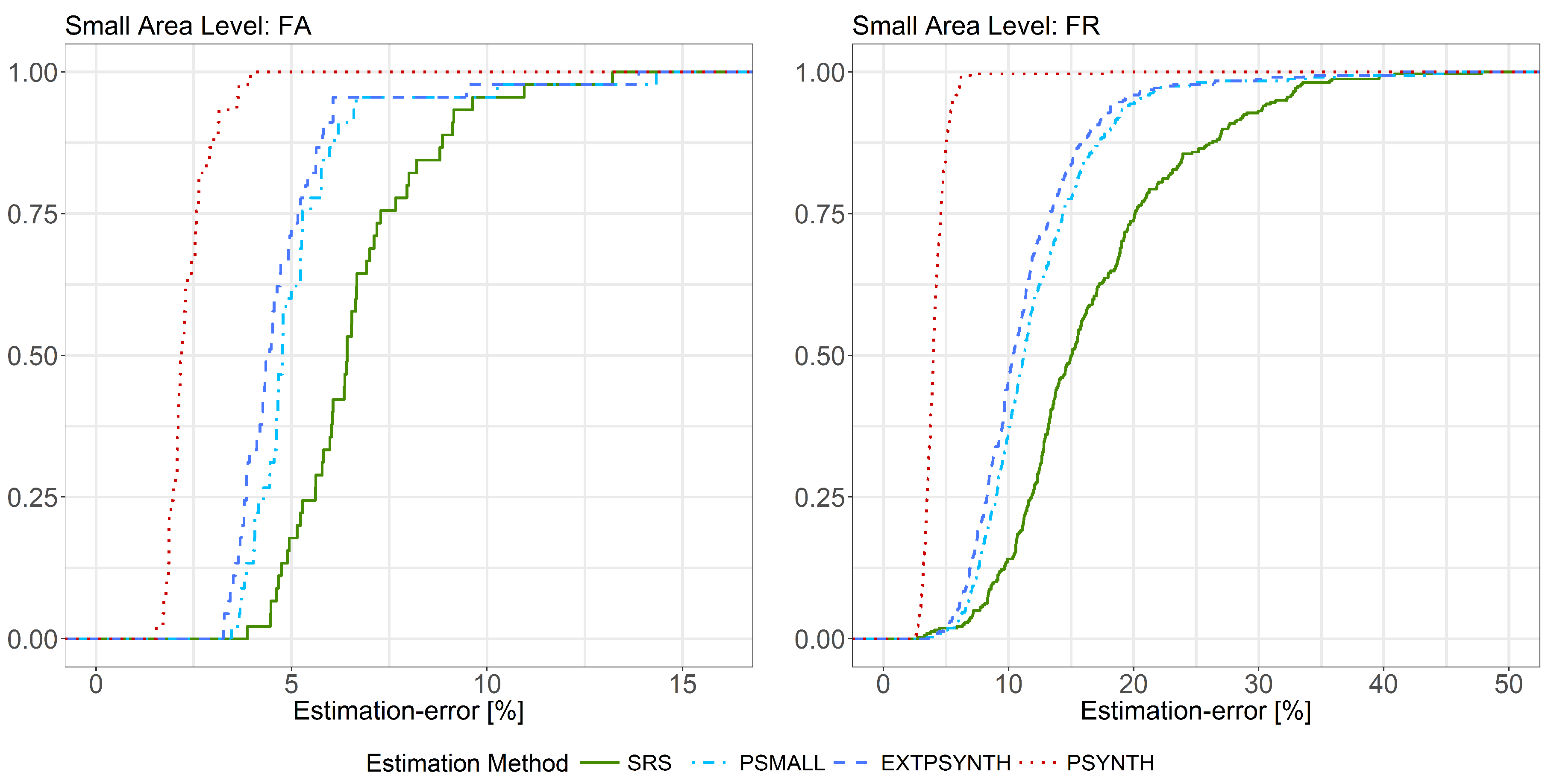
6.2. Estimation Errors
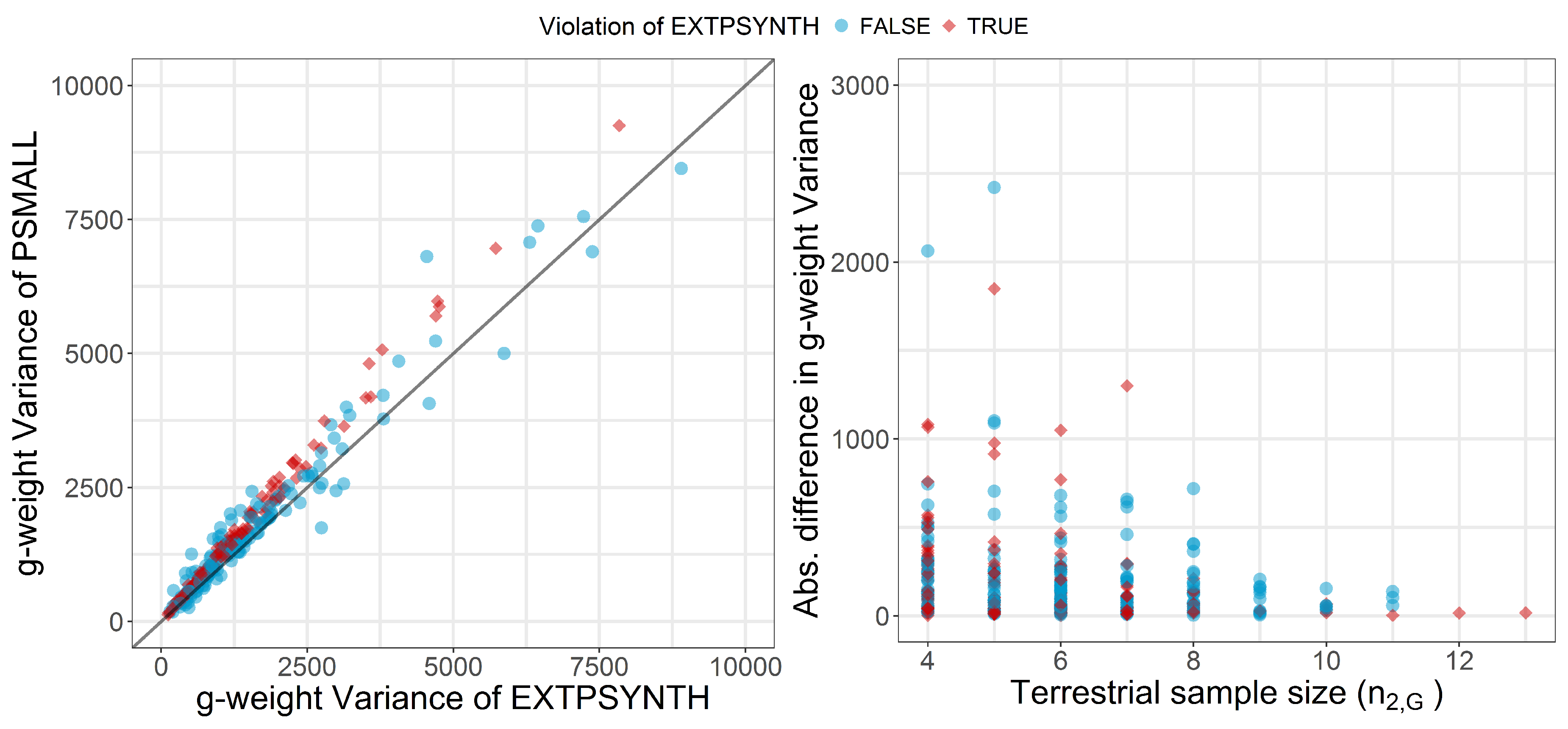
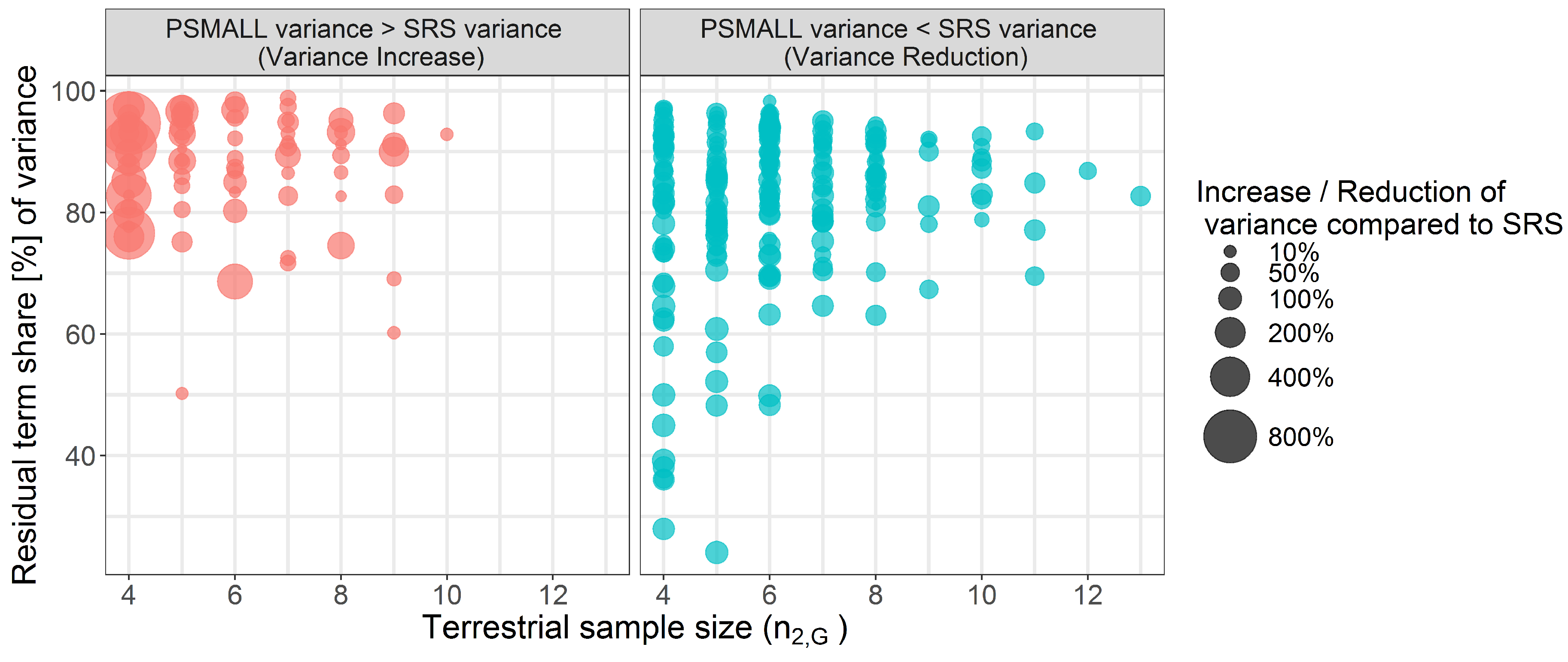
6.3. Comparison of PSMALL and EXTPSYNTH
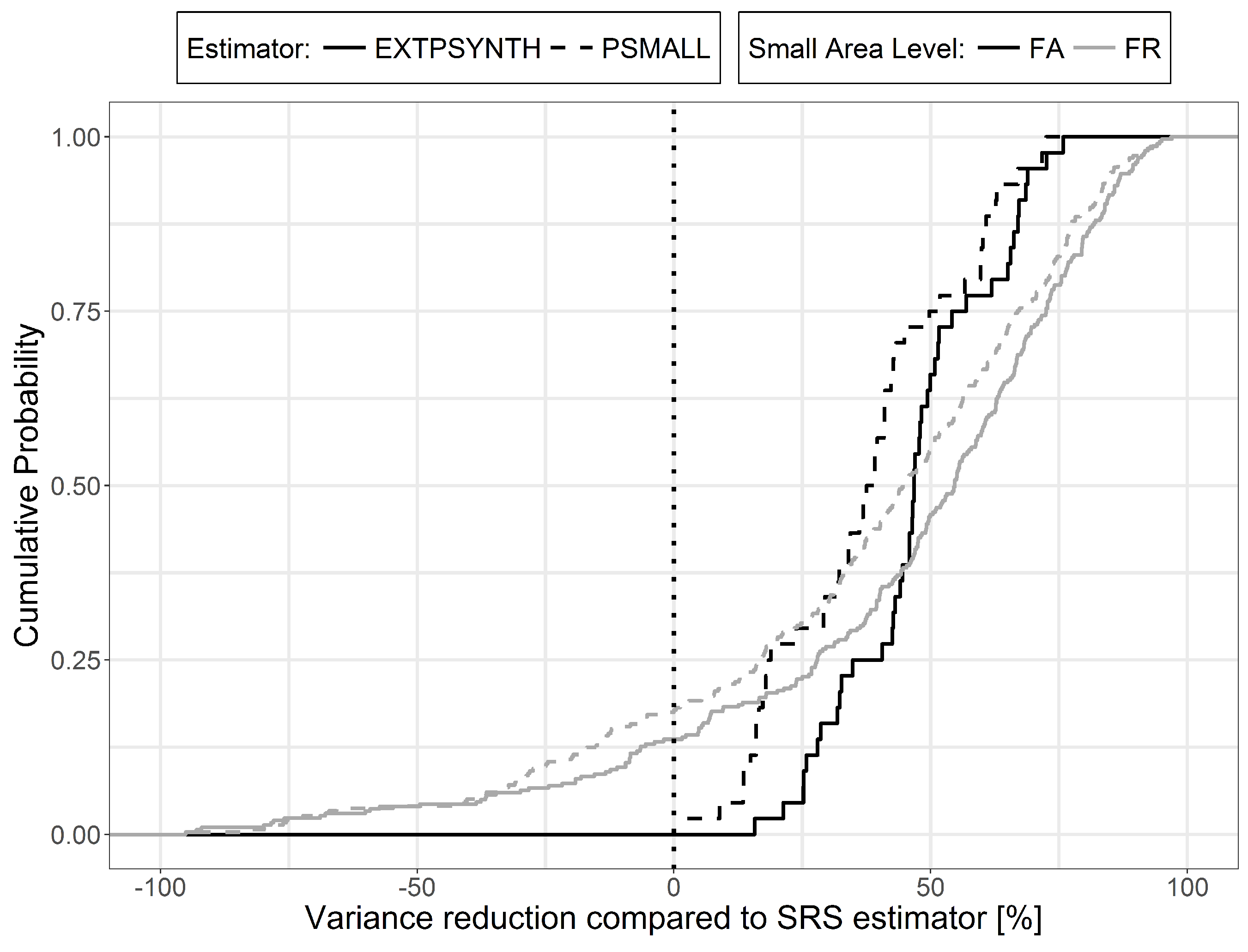
6.4. Variance Reduction Compared to SRS
7. Discussion
7.1. Performance of Estimators
7.2. Auxiliary Data
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. R-Squared on Cluster Level
Appendix A.2. RMSE on Cluster Level
References
- Polley, H.; Schmitz, F.; Hennig, P.; Kroiher, F. National Forest Inventories—Pathways for Common Reporting; Springer: Heidelberg/Berlin, Germany, 2010; Chapter 13; pp. 223–243. [Google Scholar]
- Thünen-Institut. Dritte Bundeswaldinventur 2012, 2014. Available online: https://bwi.info (accessed on 3 February 2012).
- Kuliešis, A.; Tomter, S.M.; Vidal, C.; Lanz, A. Estimates of stem wood increments in forest resources: comparison of different approaches in forest inventory: Consequences for international reporting: case studyof European forests. Ann. For. Sci. 2016, 73, 857–869. [Google Scholar] [CrossRef]
- Böckmann, T.; Saborowski, J.; Dahm, S.; Nagel, J.; Spellmann, H. Neukonzeption und Weiterentwicklung der Forsteinrichtung in Niedersachsen. Forst und Holz (Germany) 1998, 53, 298–302. [Google Scholar]
- Von Lüpke, N.; Hansen, J.; Saborowski, J. A Three-Phase Sampling Procedure for Continuous Forest Inventory with Partial Re-measurement and Updating of Terrestrial Sample Plots. Eur. J. For. Res. 2012, 131, 1979–1990. [Google Scholar] [CrossRef]
- Von Lüpke, N. Approaches for the Optimisation of Double Sampling for Stratification in Repeated Forest Inventories. Ph.D. Thesis, University of Göttingen, Göttingen, Germany, 2013. [Google Scholar]
- De Vries, P.G. Sampling Theory for Forest Inventory: A Teach-Yourself Course; Springer: Heidelberg/Berlin, Germany, 1986. [Google Scholar]
- Cochran, W.G. Sampling Techniques; Wiley Series in Probability and Mathematical Statistics; Wiley: Hoboken, NJ, USA, 1977. [Google Scholar]
- Särndal, C.E.; Swensson, B.; Wretman, J. Model Assisted Survey Sampling; Springer Science & Business Media: Heidelberg/Berlin, Germany, 2003. [Google Scholar]
- Gregoire, T.G.; Valentine, H.T. Sampling Strategies for Natural Resources and the Environment; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Köhl, M.; Magnussen, S.S.; Marchetti, M. Sampling Methods, Remote Sensing and GIS Multiresource Forest Inventory; Springer Science & Business Media: Heidelberg/Berlin, Germany, 2006. [Google Scholar]
- Mandallaz, D. Sampling Techniques for Forest Inventories; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Gillis, M.; Boudewyn, P.; Power, K.; Russo, G. Canada. In National Forest Inventories—Pathways for Common Reporting; Springer: Heidelberg/Berlin, Germany, 2010; Chapter 4; pp. 97–111. [Google Scholar]
- Chojnacky, D.C. Double Sampling for Stratification: A Forest Inventory Application in the Interior West; Technical Report; US Department of Agriculture, Forest Service, Rocky Mountain Research Station Ogden: Washington, DC, USA, 1998. [Google Scholar]
- Lanz, A.; Brändli, U.B.; Brassel, P.; Ginzler, C.; Kaufmann, E.; Thürig, E. Switzerland. In National Forest Inventories–Pathways for Common Reporting; Springer: Heidelberg/Berlin, Germany, 2010; Chapter 36; pp. 555–565. [Google Scholar]
- Gasparini, P.; Tosi, V.; DiCosmo, L. Italy. In National Forest Inventories—Pathways for Common Reporting; Springer: Heidelberg/Berlin, Germany, 2010; Chapter 19; pp. 311–331. [Google Scholar]
- Saborowski, J.; Marx, A.; Nagel, J.; Böckmann, T. Double sampling for stratification in periodic inventories—Infinite population approach. For. Ecol. Manag. 2010, 260, 1886–1895. [Google Scholar] [CrossRef]
- Grafström, A.; Schnell, S.; Saarela, S.; Hubbell, S.; Condit, R. The continuous population approach to forest inventories and use of information in the design. Environmetrics 2017, 28. [Google Scholar] [CrossRef]
- Massey, A.; Mandallaz, D.; Lanz, A. Integrating remote sensing and past inventory data under the new annual design of the Swiss National Forest Inventory using three-phase design-based regression estimation. Can. J. For. Res. 2014, 44, 1177–1186. [Google Scholar] [CrossRef]
- Mandallaz, D. A three-phase sampling extension of the generalized regression estimator with partially exhaustive information. Can. J. For. Res. 2013, 44, 383–388. [Google Scholar] [CrossRef]
- Rao, J.N. Small-Area Estimation; Wiley Online Library: Hoboken, NJ, USA, 2015. [Google Scholar]
- Breidenbach, J.; Astrup, R. Small area estimation of forest attributes in the Norwegian National Forest Inventory. Eur. J. For. Res. 2012, 131, 1255–1267. [Google Scholar] [CrossRef]
- Goerndt, M.E.; Monleon, V.J.; Temesgen, H. A comparison of small-area estimation techniques to estimate selected stand attributes using LiDAR-derived auxiliary variables. Can. J. For. Res. 2011, 41, 1189–1201. [Google Scholar] [CrossRef]
- Steinmann, K.; Mandallaz, D.; Ginzler, C.; Lanz, A. Small area estimations of proportion of forest and timber volume combining Lidar data and stereo aerial images with terrestrial data. Can. J. For. Res. 2013, 28, 373–385. [Google Scholar] [CrossRef]
- Mandallaz, D.; Breschan, J.; Hill, A. New regression estimators in forest inventories with two-phase sampling and partially exhaustive information: A design-based monte carlo approach with applications to small-area estimation. Can. J. For. Res. 2013, 43, 1023–1031. [Google Scholar] [CrossRef]
- Koch, B. Status and future of laser scanning, synthetic aperture radar and hyperspectral remote sensing data for forest biomass assessment. ISPRS J. Photogramm. Remote Sens. 2010, 65, 581–590. [Google Scholar] [CrossRef]
- Naesset, E. Area-Based Inventory in Norway—From Innovation to an Operational Reality. In Forest Applications of Airborne Laser Scanning—Concepts and Case Studies; Springer: Heidelberg/Berlin, Germany, 2014; Chapter 11; pp. 216–240. [Google Scholar]
- Magnussen, S.; Mauro, F.; Breidenbach, J.; Lanz, A.; Kändler, G. Area-level analysis of forest inventory variables. Eur. J. For. Res. 2017, 136, 839–855. [Google Scholar] [CrossRef]
- Magnussen, S.; Mandallaz, D.; Breidenbach, J.; Lanz, A.; Ginzler, C. National forest inventories in the service of small area estimation of stem volume. Can. J. For. Res. 2014, 44, 1079–1090. [Google Scholar] [CrossRef]
- Mandallaz, D. Design-based properties of some small-area estimators in forest inventory with two-phase sampling. Can. J. For. Res. 2013, 43, 441–449. [Google Scholar] [CrossRef]
- Bundesministerium für Ernährung, L.u.V. Aufnahmeanweisung für die Dritte Bundeswaldinventur BWI3 (2011–2012); BMELV: Berlin, Germany, 2011. [Google Scholar]
- Bitterlich, W. The Relascope Idea. Relative Measurements in Forestry; Commonwealth Agricultural Bureaux: Wallingford, UK, 1984. [Google Scholar]
- Kublin, E.; Breidenbach, J.; Kändler, G. A flexible stem taper and volume prediction method based on mixed-effects B-spline regression. Eur. J. For. Res. 2013, 132, 983–997. [Google Scholar] [CrossRef]
- Schmitz, F.; Polley, H.; Hennig, P.; Dunger, K.; Schwitzgebel, F. Die Zweite Bundeswaldinventur-BWI2: Inventur- und Auswertmethoden, Bundesministerium fur Ernahrung, Land-Wirtschaft und Verbraucherschutz (Hrsg); BMELV: Berlin, Germany, 2008. [Google Scholar]
- Mandallaz, D.; Hill, A.; Massey, A. Design-Based Properties of Some Small-Area Estimators in Forest Inventory with Two-Phase Sampling—Revised Version; Technical Report; Department of Environmental Systems Science, ETH Zurich: Zürich, Switzerland, 2016. [Google Scholar]
- Hill, A.; Massey, A. Forestinventory: Design-Based Global and Small-Area Estimations for Multiphase Forest Inventories. 2017. Available online: https://cran.r-project.org/web/packages/forestinventory/forestinventory.pdf (accessed on 16 October 2017).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- Gauer, J.; Aldinger, E. Waldökologische Naturräume Deutschlands-Wuchsgebiete. Mitt. Ver. Forstliche Standortskunde Forstpflanzenzüchtung 2005, 43, 281–288. [Google Scholar]
- LWaldG. Landeswaldgesetz Rheinland-Pfalz (Forest Act Rhineland-Palatinate); Rhineland: Palatinate, Germany, 2000. [Google Scholar]
- Lamprecht, S.; Hill, A.; Stoffels, J.; Udelhoven, T. A Machine Learning Method for Co-Registration and Individual Tree Matching of Forest Inventory and Airborne Laser Scanning Data. Remote Sens. 2017, 9. [Google Scholar] [CrossRef]
- Hill, A.; Buddenbaum, H.; Mandallaz, D. Combining canopy height and tree species map information for large-scale timber volume estimations under strong heterogeneity of auxiliary data and variable sample plot sizes. Eur. J. For. Res. 2018. [Google Scholar] [CrossRef]
- Stoffels, J.; Hill, J.; Sachtleber, T.; Mader, S.; Buddenbaum, H.; Stern, O.; Langshausen, J.; Dietz, J.; Ontrup, G. Satellite-Based Derivation of High-Resolution Forest Information Layers for Operational Forest Management. Forests 2015, 6, 1982–2013. [Google Scholar] [CrossRef]
- Stoffels, J.; Mader, S.; Hill, J.; Werner, W.; Ontrup, G. Satellite-based stand-wise forest cover type mapping using a spatially adaptive classification approach. Eur. J. For. Res. 2012, 131, 1071–1089. [Google Scholar] [CrossRef]
- White, J.C.; Coops, N.C.; Wulder, M.A.; Vastaranta, M.; Hilker, T.; Tompalski, P. Remote sensing technologies for enhancing forest inventories: A review. Can. J. Remote Sens. 2016, 42, 619–641. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Congalton, R.G.; Green, K. Assessing the Accuracy of Remotely Sensed Data: Principles and Practices; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Fahrmeir, L.; Kneib, T.; Lang, S.; Marx, B. Regression: Models, Methods and Applications; Springer Science & Business Media: Heidelberg/Berlin, Germany, 2013. [Google Scholar]
- Wilcoxon, F.; Katti, S.; Wilcox, R.A. Critical values and probability levels for the Wilcoxon rank sum test and the Wilcoxon signed rank test. Sel. Tables Math. Stat. 1970, 1, 171–259. [Google Scholar]
- Kirchhoefer, M.; Schumacher, J.; Adler, P.; Kändler, G. Considerations towards a Novel Approach for Integrating Angle-Count Sampling Data in Remote Sensing Based Forest Inventories. Forests 2017, 8, 239. [Google Scholar] [CrossRef]
- ESA. Sentinel-2 Earth Observation Mission, 2017. Available online: https://sentinel.esa.int/web/sentinel/missions/sentinel-2 (accessed on 29 March 2017).
- Massey, A.; Mandallaz, D. Design-based regression estimation of net change for forest inventories. Can. J. For. Res. 2015, 45, 1775–1784. [Google Scholar] [CrossRef]
| Variable | Mean | SD | Maximum |
|---|---|---|---|
| Timber Volume (m/ha) | 300.9 | 195.6 | 1375.3 |
| Mean DBH (mm) | 354.9 | 137.2 | 1123.2 |
| Mean height (dm) | 239.6 | 72.4 | 497.4 |
| Mean stem density per hectare | 101 | 114 | 1010 |
| Sampling Frame | ||||
|---|---|---|---|---|
| municipal and state forest | 96,854 | 33,365 | 5791 | 2055 |
| missing CHM | 18 | 10 | 0 | 0 |
| missing TSPEC | 7060 | 3587 | 414 | 385 |
| missing CHM and TSPEC | 3 | 2 | 0 | 0 |
| missing CHM or TSPEC | 7075 | 3595 | 414 | 385 |
| Main Plot Species | Producer’s Accuracy [%] | User’s Accuracy [%] | ||
|---|---|---|---|---|
| Beech | 22.3 | 47.0 | 883 | 419 |
| Douglas Fir | 24.8 | 48.7 | 230 | 117 |
| Oak | 11.1 | 48.5 | 289 | 66 |
| Spruce | 53.2 | 61.1 | 651 | 566 |
| Scots Pine | 22.9 | 46.1 | 179 | 89 |
| Mixed | 84.5 | 64.5 | 3152 | 4127 |
| Overall accuracy: 62.0% | 5384 | 5384 | ||
| Model Terms | Model | RMSE | RMSE% | |
|---|---|---|---|---|
| meanheight + stddev + meanheight + | full model | 0.58 | 90.11 | 29.76 |
| treespecies + ALSyear + | (0.48) | (139.22) | (45.98) | |
| meanheight:treespecies + | ||||
| meanheight:ALSyear + meanheight:stddev + | ||||
| stddev:ALSyear | ||||
| meanheight + stddev + meanheight + | reduced model | 0.55 | 95.23 | 31.65 |
| ALSyear + meanheight:ALSyear + | (0.45) | (144.13) | (47.60) | |
| meanheight:stddev + stddev:ALSyear |
| ALSyear | RMSE | RMSE% | n | ||
|---|---|---|---|---|---|
| 2012 | 2807 | 0.65 | 98.52 | 29.62 | 156 |
| (0.61) | (135.84) | (44.87) | (408) | ||
| 2011 | 4361 | 0.60 | 96.89 | 29.66 | 354 |
| (0.57) | (146.21) | (48.29) | (883) | ||
| 2010 | 4182 | 0.64 | 76.38 | 27.57 | 420 |
| (0.51) | (120.90) | (39.93) | (1171) | ||
| 2009 | 2100 | 0.53 | 92.22 | 33.31 | 218 |
| (0.42) | (133.42) | (44.07) | (559) | ||
| 2008 | 2968 | 0.61 | 87.10 | 32.20 | 247 |
| (0.48) | (130.38) | (43.06) | (701) | ||
| 2008_1 | 2116 | 0.43 | 117.99 | 33.64 | 157 |
| (0.33) | (175.43) | (57.94) | (394) | ||
| 2007 | 3498 | 0.56 | 82.43 | 26.57 | 135 |
| (0.46) | (136.47) | (45.08) | (418) | ||
| 2003 | 602 | 0.34 | 85.92 | 27.31 | 145 |
| (0.27) | (154.48) | (51.02) | (529) | ||
| 2002 | 775 | 0.52 | 87.25 | 27.22 | 97 |
| (0.44) | (141.55) | (46.75) | (314) |
| District Level | Estimator | Point Estimates | Error | |||||
|---|---|---|---|---|---|---|---|---|
| Mean | Min | Max | Mean | Min | Max | |||
| FA | SRS | ( = 45) | 300.16 | 215.91 | 392.84 | 6.69 | 3.87 | 13.21 |
| PSMALL | ( = 45) | 307.29 | 209.26 | 417.10 | 5.16 | 3.46 | 14.33 | |
| EXTPSYNTH | ( = 45) | 307.27 | 209.01 | 415.02 | 4.78 | 3.25 | 13.88 | |
| PSYNTH | ( = 45) | 306.90 | 223.51 | 409.92 | 2.34 | 1.54 | 3.95 | |
| FR | SRS | ( = 321) | 302.77 | 99.89 | 552.87 | 16.94 | 2.76 | 55.51 |
| PSMALL | ( = 321) | 308.15 | 159.64 | 568.67 | 12.24 | 3.48 | 44.94 | |
| EXTPSYNTH | ( = 321) | 308.38 | 154.07 | 544.34 | 11.34 | 3.60 | 40.91 | |
| PSYNTH | ( = 321) | 305.56 | 197.47 | 444.29 | 4.13 | 2.56 | 18.07 | |
| District Level | Estimator | Variance Reduction [%] | Relative Efficiency | |||||
|---|---|---|---|---|---|---|---|---|
| Mean | Min | Max | Mean | Min | Max | |||
| FA | PSMALL | ( = 45) | 33.51 | 2.6 | 72.5 | 1.74 | 1.03 | 3.64 |
| EXTPSYNTH | ( = 45) | 43.30 | 15.7 | 75.8 | 2.03 | 1.18 | 4.13 | |
| FR | PSMALL | ( = 321) | 12.48 | 96.8 | 2.54 | 0.08 | 31.61 | |
| EXTPSYNTH | ( = 321) | 24.75 | 97.0 | 2.95 | 0.10 | 33.70 | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hill, A.; Mandallaz, D.; Langshausen, J. A Double-Sampling Extension of the German National Forest Inventory for Design-Based Small Area Estimation on Forest District Levels. Remote Sens. 2018, 10, 1052. https://doi.org/10.3390/rs10071052
Hill A, Mandallaz D, Langshausen J. A Double-Sampling Extension of the German National Forest Inventory for Design-Based Small Area Estimation on Forest District Levels. Remote Sensing. 2018; 10(7):1052. https://doi.org/10.3390/rs10071052
Chicago/Turabian StyleHill, Andreas, Daniel Mandallaz, and Joachim Langshausen. 2018. "A Double-Sampling Extension of the German National Forest Inventory for Design-Based Small Area Estimation on Forest District Levels" Remote Sensing 10, no. 7: 1052. https://doi.org/10.3390/rs10071052
APA StyleHill, A., Mandallaz, D., & Langshausen, J. (2018). A Double-Sampling Extension of the German National Forest Inventory for Design-Based Small Area Estimation on Forest District Levels. Remote Sensing, 10(7), 1052. https://doi.org/10.3390/rs10071052





