The Use of Massive Deformation Datasets for the Analysis of Spatial and Temporal Evolution of Mauna Loa Volcano (Hawai’i)
Abstract
1. Introduction
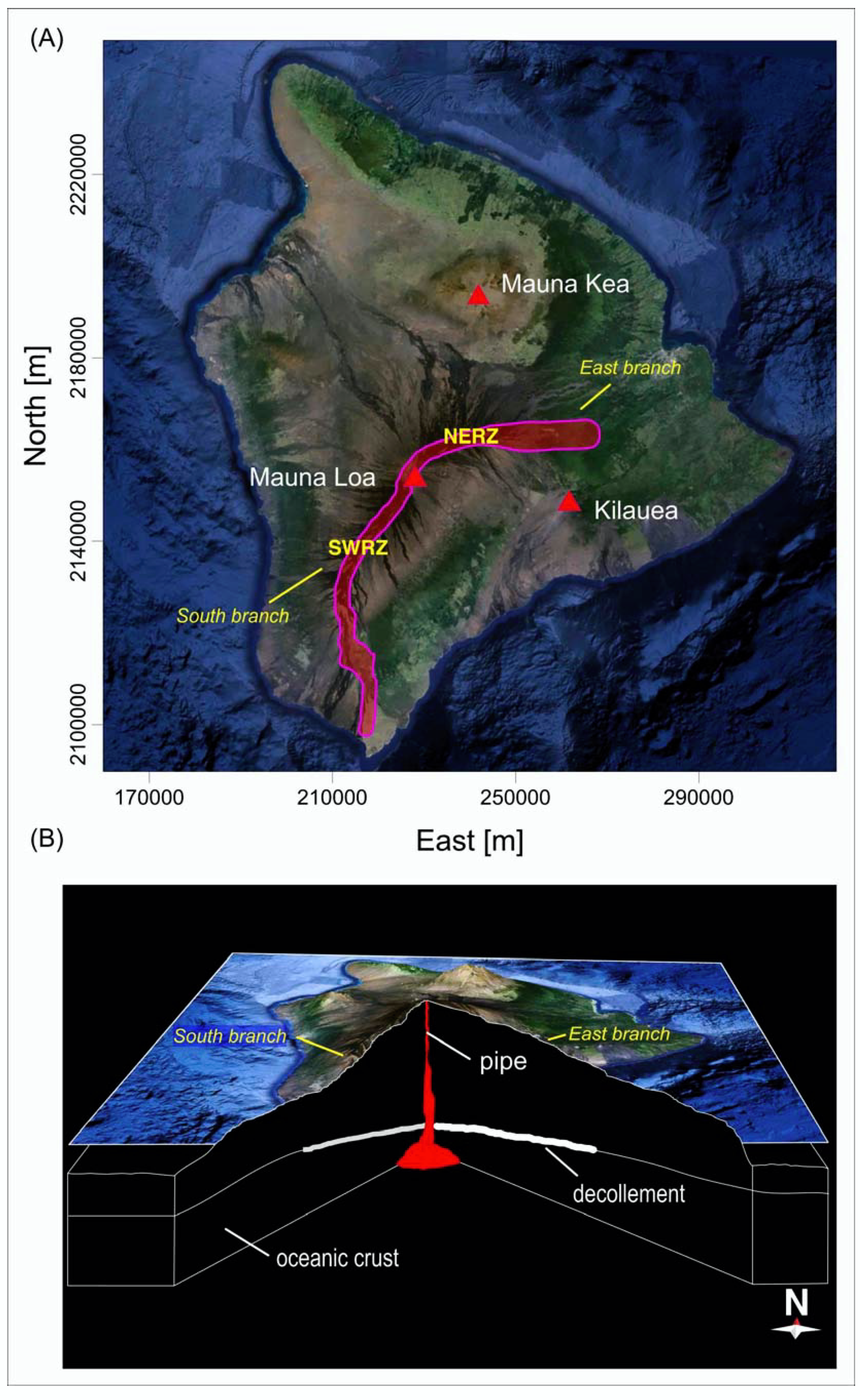
2. Geological Background
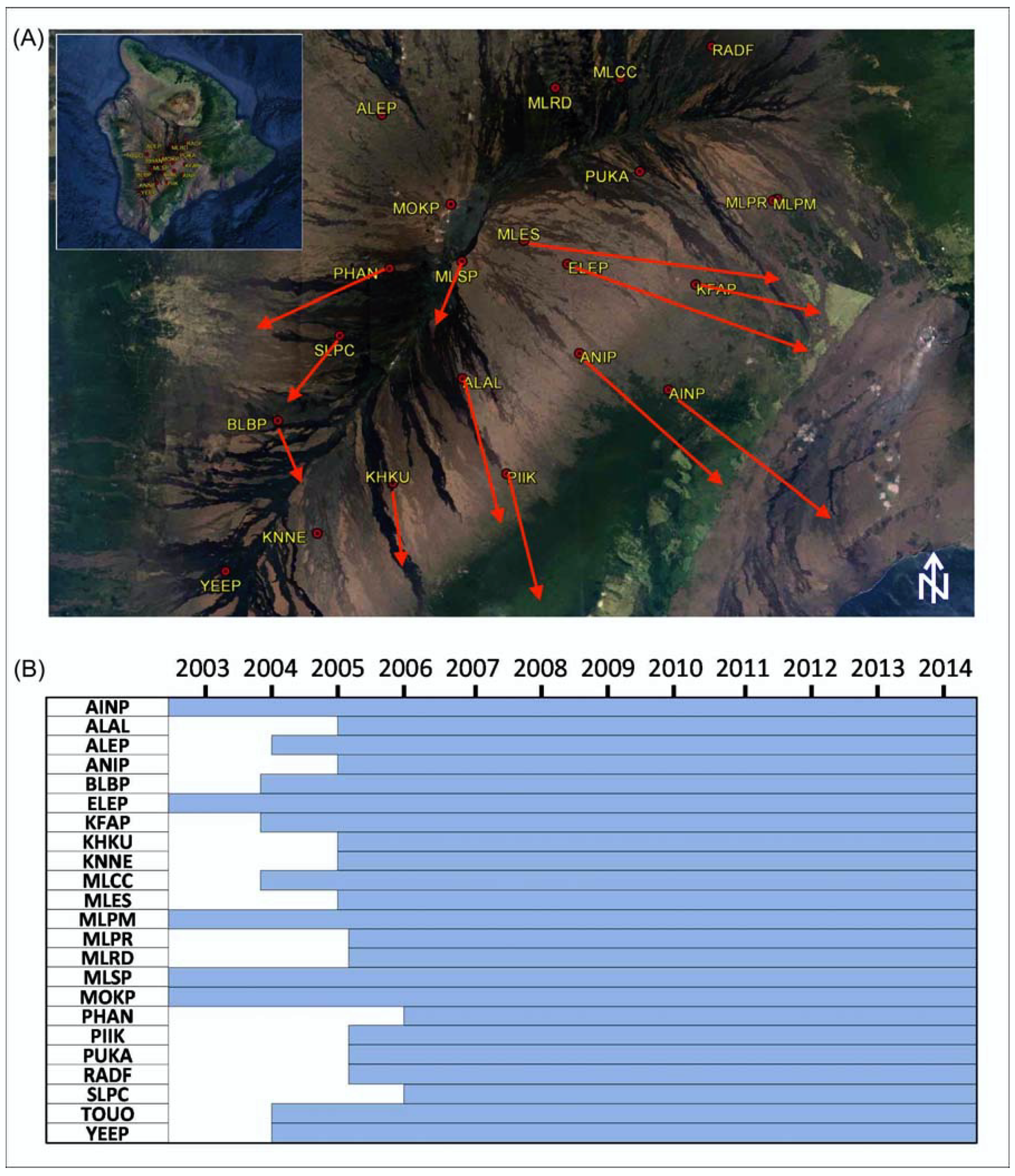
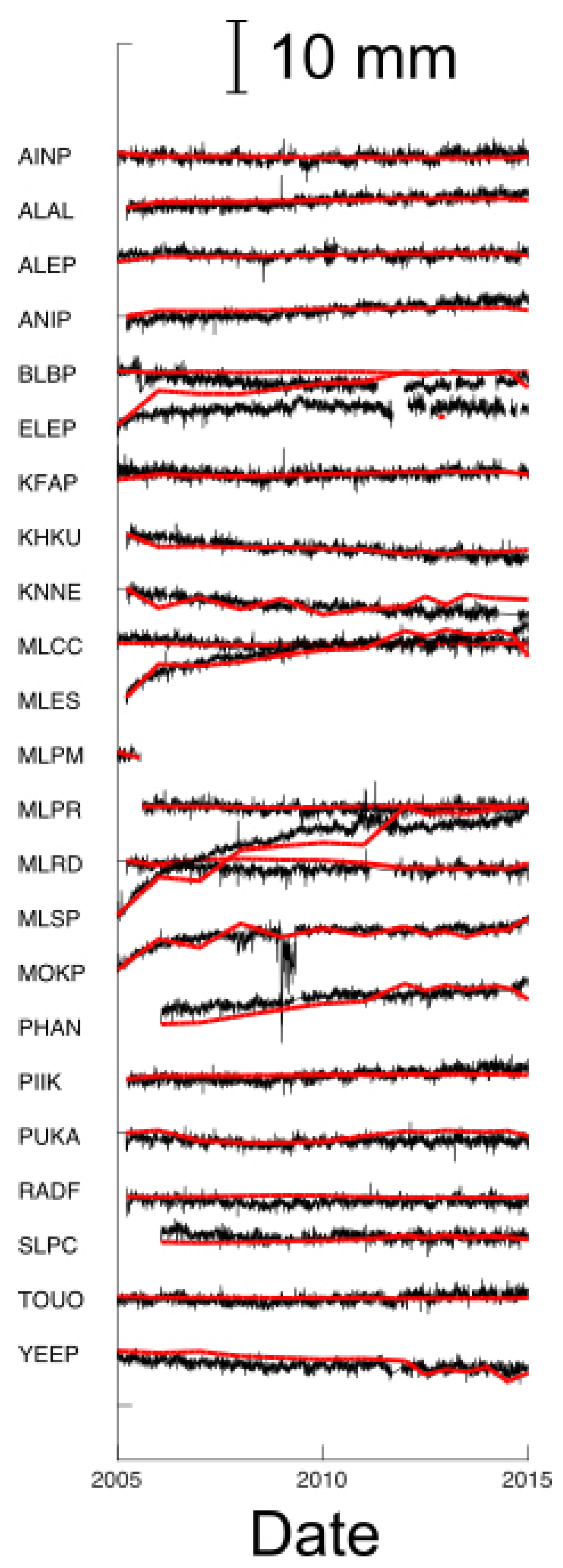
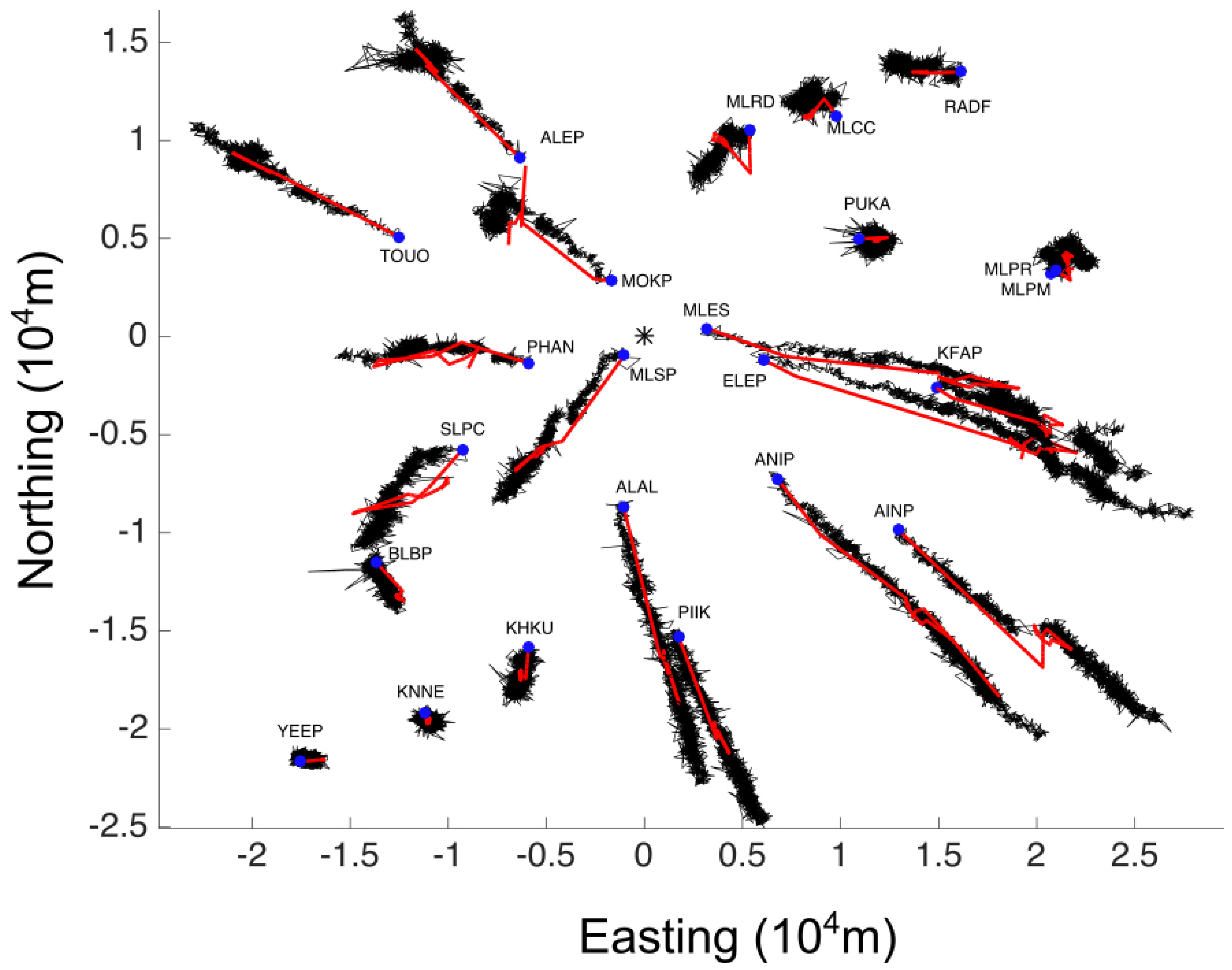
3. Data Analysis
4. Inverse Modeling
4.1. Methods
4.2. Source Geometry
- the shallow magma chamber, modeled as a point source [52].
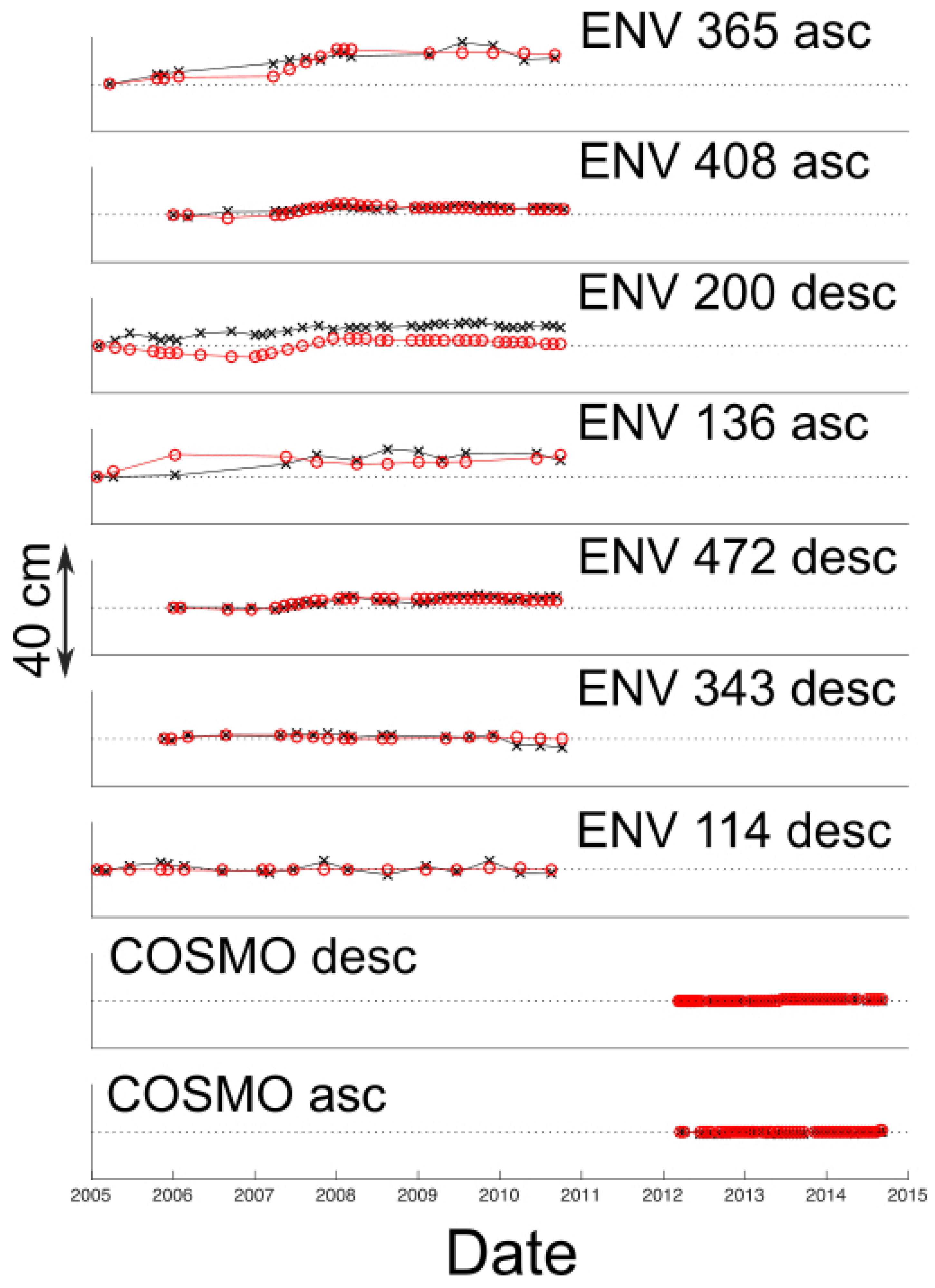
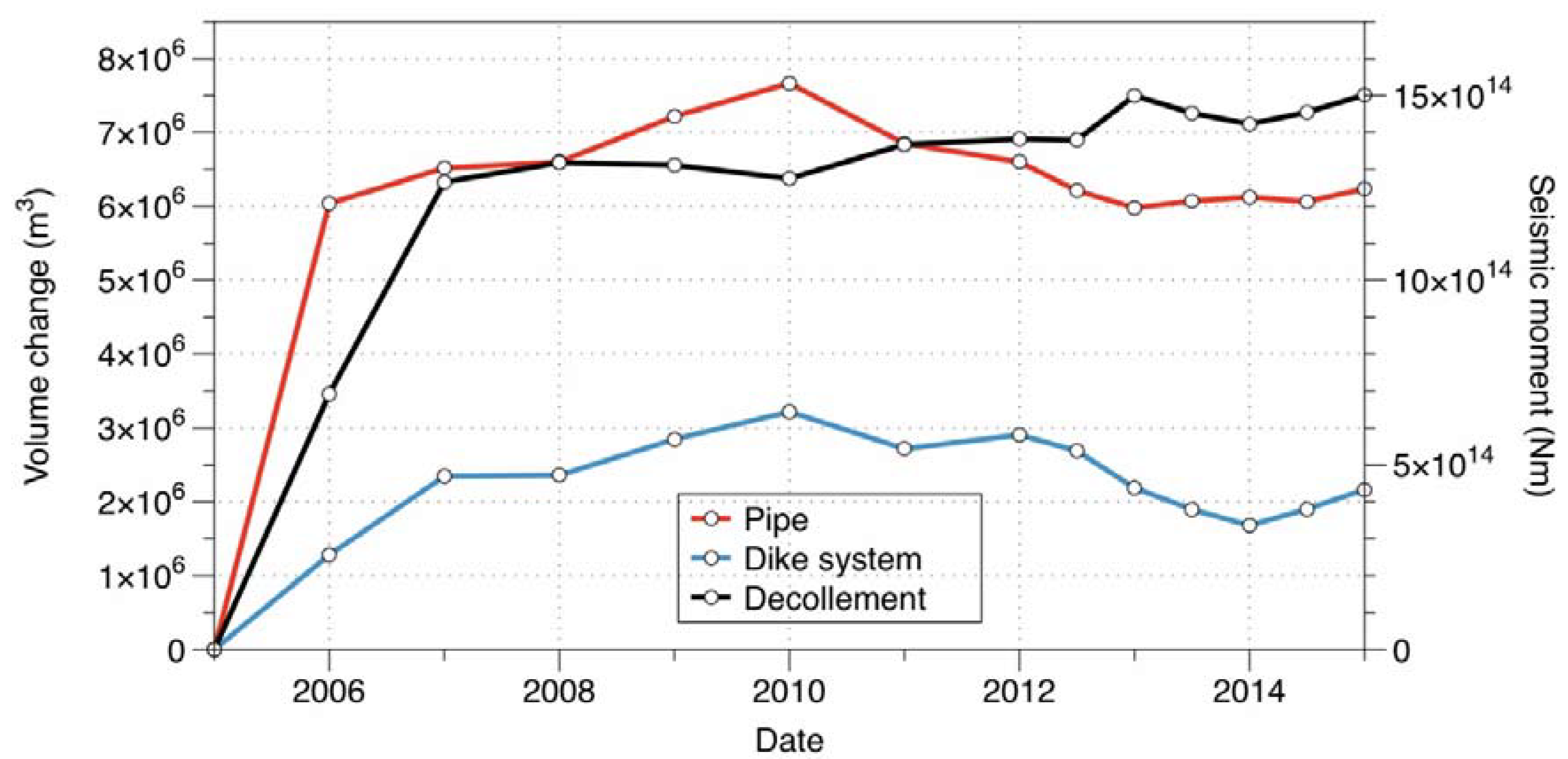
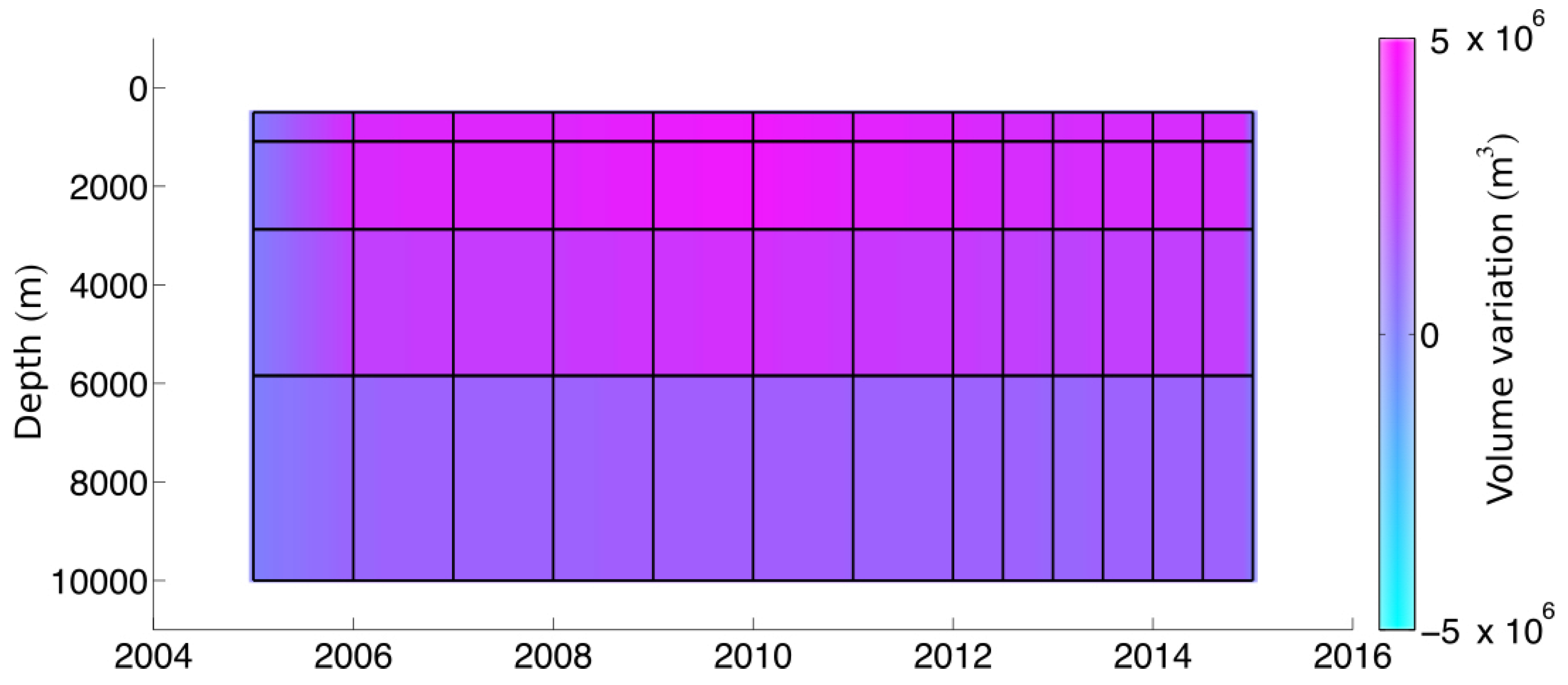
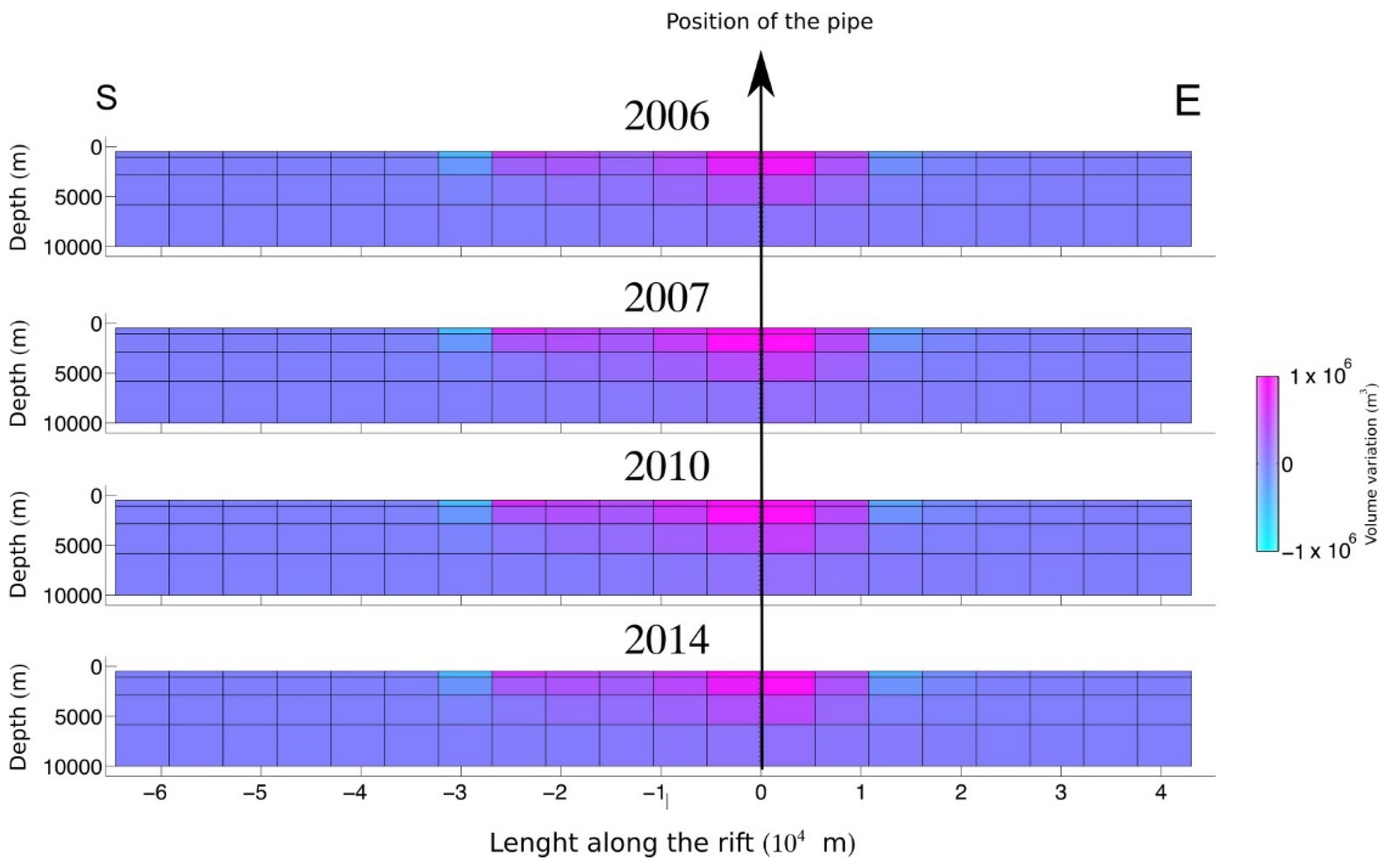
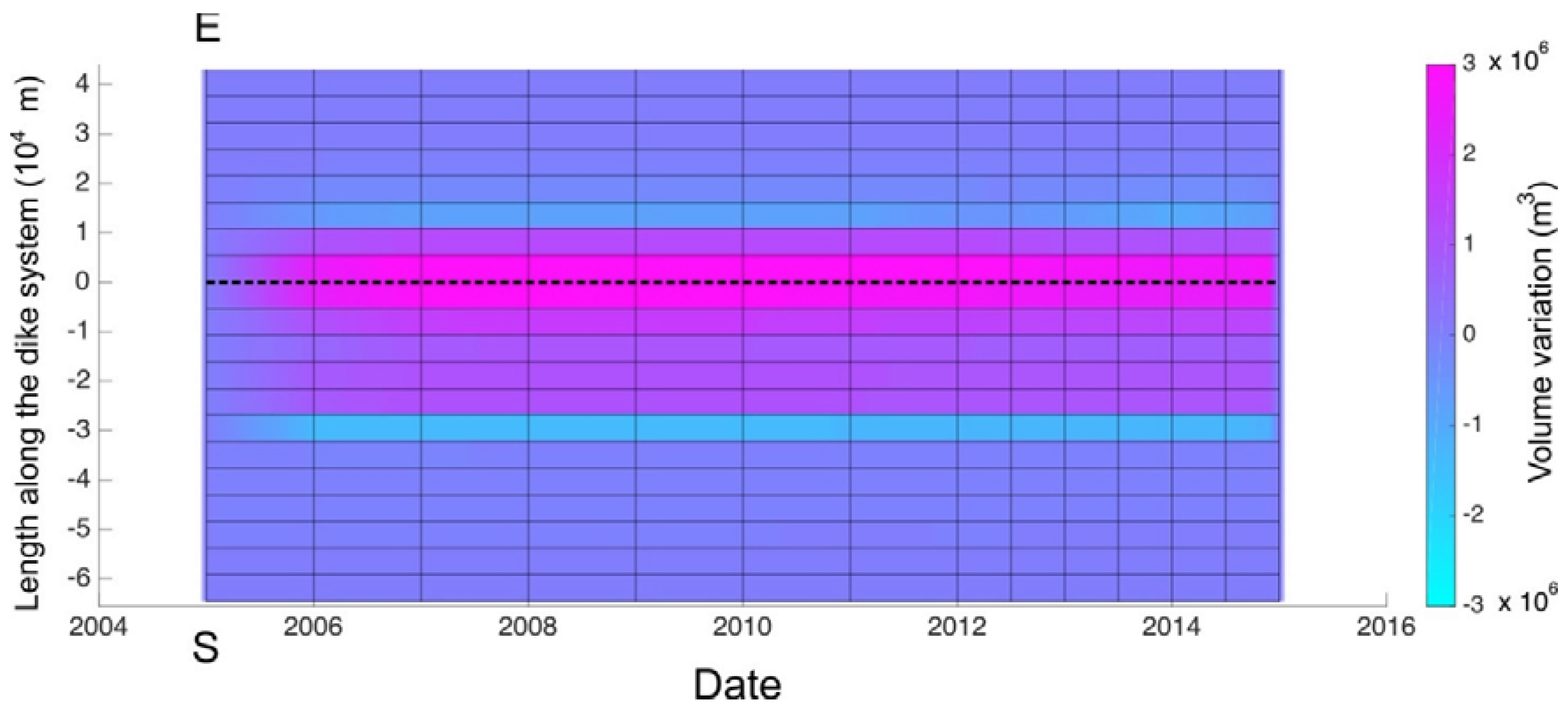
4.3. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Raspini, F.; Bianchini, S.; Ciampalini, A.; Del Soldato, M.; Solari, L.; Novali, F.; Del Conte, S.; Rucci, A.; Ferretti, A.; Casagli, N. Continuous, semi-automatic monitoring of ground deformation using Sentinel-1 satellites. Sci. Rep. 2018, 8, 7253. [Google Scholar] [CrossRef] [PubMed]
- Casu, F.; Poland, M.; Solaro, G.; Tizzani, P.; Miklius, A.; Sansosti, E.; Lanari, R. Surface deformation analysis of the Mauna Loa and Kilauea volcanoes, Hawaii, revealed by InSAR measurements. Geophys. Res. Abstr. 2009, 11, 4454. [Google Scholar]
- Pagli, C.; Wang, H.; Wright, T.J.; Calais, E.; Lewi, E. Current plate boundary deformation of the Afar rift from a 3-D velocity field inversion of InSAR and GPS. J. Geophys. Res. Solid Earth 2014, 119, 8562–8575. [Google Scholar] [CrossRef]
- Sigmundsson, F.; Hooper, A.; Hreinsdóttir, S.; Vogfjörd, K.S.; Ófeigsson, B.G.; Heimisson, E.R.; Dumont, S.; Parks, M.; Spaans, K.; Gudmundsson, G.B.; et al. Segmented lateral dyke growth in a rifting event at Bardarbunga volcanic system, Iceland. Nature 2015, 517, 191–195. [Google Scholar] [CrossRef] [PubMed]
- Samsonov, S.V.; Tiampo, K.F.; Camacho, A.G.; Fernández, J.; González, P.J. Spatiotemporal analysis and interpretation of 1993–2013 ground deformation at Campi Flegrei, Italy, observed by advanced DInSAR. Geophys. Res. Lett. 2014, 41, 6101–6108. [Google Scholar] [CrossRef]
- Tizzani, P.; Battaglia, M.; Zeni, G.; Atzori, S.; Berardino, P.; Lanari, R. Uplift and magma intrusion at Long Valley caldera from InSAR and gravity measurements. Geology 2009, 37, 63–66. [Google Scholar] [CrossRef]
- D’Auria, L.; Pepe, S.; Castaldo, R.; Giudicepietro, F.; Macedonio, G.; Ricciolino, P.; Tizzani, P.; Casu, F.; Lanari, R.; Manzo, M.; et al. Magma injection beneath the urban area of Naples: A new mechanism for the 2012–2013 volcanic unrest at Campi Flegrei caldera. Sci. Rep. 2015, 5, 13100. [Google Scholar] [CrossRef] [PubMed]
- Swanson, D.A.; Duffield, W.A.; Fiske, R.S. Displacement of the south flank of Kilauea Volcano: The result of forceful intrusion of magma into the rift zones: U. S. Geol. Surv. Prof. Pap. 1976, 963, 1–37. [Google Scholar]
- Borgia, A. Dynamic basis of volcanic spreading. J. Geophys. Res. Solid Earth 1994, 99, 17791–17804. [Google Scholar] [CrossRef]
- Lockwood, J.P. Mauna Loa eruptive history—The preliminary radiocarbon record. In Mauna Loa Revealed: Structure, Composition, History, and Hazards; Rhodes, J.M., Lockwood, J.P., Eds.; American Geophysical Union Monograph: Washington, DC, USA, 1995; Volume 92, pp. 81–94. [Google Scholar]
- Decker, R.W.; Koyanagi, R.Y.; Dvorak, J.J.; Lockwood, J.P.; Okamura, A.T.; Yamashita, K.M.; Tanigawa, W.R. Seismicity and surface deformation of Mauna Loa Volcano, Hawaii. Eos, Trans. Am. Geophys. Union 1983, 64, 545–547. [Google Scholar] [CrossRef]
- Lipman, P.W.; Lockwood, J.P.; Okamura, R.T.; Swanson, D.A.; Yamashita, K.M. Ground Deformation Associated with the 1975 Magnitude-7.2 Earthquake and Resulting Changes in Activity of Kilauea Volcano, Hawaii; US Geological Survey professional paper 1276; US Geological Survey: Tacoma, WA, USA, 1985; p. 45.
- Morgan, J.K.; Clague, D.A. Volcanic spreading on Mauna Loa volcano, HI: Evidence from accretion, alteration, and exhumation of volcaniclastic sediments. Geology 2003, 30, 411–414. [Google Scholar] [CrossRef]
- Morgan, J.K.; Clague, D.A.; Borchers, D.C.; Davis, A.S.; Milliken, K.L. Mauna Loa’s submarine western flank: Evidence for deep volcanic spreading and hydrothermal alteration. Geochem. Geophys. Geosyst. 2007, 8, Q05002. [Google Scholar] [CrossRef]
- Amelung, F.; Yun, S.H.; Walter, T.R.; Segall, P.; Kim, S.W. Stress control of deep rift intrusion at Mauna Loa Volcano, Hawaii. Science 2007, 316, 1026–1030. [Google Scholar] [CrossRef] [PubMed]
- Casu, F.; Elefante, S.; Imperatore, P.; Zinno, I.; Manunta, M.; De Luca, C.; Lanari, R. SBAS-DInSAR Parallel Processing for Deformation Time-Series Computation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3285–3296. [Google Scholar] [CrossRef]
- De Luca, C.; Cuccu, R.; Elefante, S.; Zinno, I.; Manunta, M.; Casola, V.; Rivolta, G.; Lanari, R.; Casu, F. An On-Demand Web Tool for the Unsupervised Retrieval of Earth’s Surface Deformation from SAR Data: The P-SBAS Service within the ESA G-POD Environment. Remote Sens. 2015, 7, 15630–15650. [Google Scholar] [CrossRef]
- Biggs, J.; Lu, Z.; Fournier, T.; Freymueller, J.T. Magma flux at Okmok Volcano, Alaska, from a joint inversion of continuous GPS, campaign GPS, and interferometric synthetic aperture radar. J. Geophys. Res. 2010, 115, B12401. [Google Scholar] [CrossRef]
- Parks, M.M.; Moore, J.D.; Papanikolaou, X.; Biggs, J.; Mather, T.A.; Pyle, D.M.; Raptakis, C.; Paradissis, D.; Hooper, A.; Parsons, B.; et al. From quiescence to unrest: 20 years of satellite geodetic measurements at Santorini volcano, Greece. J. Geophys. Res. Solid Earth 2015, 120, 1309–1328. [Google Scholar] [CrossRef]
- Di Traglia, F.; Battaglia, M.; Nolesini, T.; Lagomarsino, D.; Casagli, N. Shifts in the eruptive styles at Stromboli in 2010–2014 revealed by ground-based InSAR data. Sci. Rep. 2015, 5, 13569. [Google Scholar] [CrossRef] [PubMed]
- Walter, T.R.; Amelung, F. Volcano-earthquake interaction at Mauna Loa volcano, Hawaii. J. Geophys. Res. Solid Earth 2006, 111, B05204. [Google Scholar] [CrossRef]
- Nakamura, K. Why do long rift zones develop in Hawaiian volcanoes: A possible role of thick oceanic sediments. Bull. Geol. Soc. Jpn. 1980, 25, 255–269. [Google Scholar]
- Ando, M. The Hawaii earthquake of November 29, 1975: Low dip angle faulting due to forceful injection of magma. J. Geophys. Res. Solid Earth 1979, 84, 7616–7626. [Google Scholar] [CrossRef]
- Borgia, A.; Delaney, P.T.; Denlinger, R.P. Spreading volcanoes. Annu. Rev. Earth Planet. Sci. 2000, 28, 539–570. [Google Scholar] [CrossRef]
- Swanson, D.A.; Jackson, D.B.; Koyanagi, R.Y.; Wright, T.L. The February 1969 East Rift Eruption of Kilauea Volcano, Hawaii; U.S. Geological Survey Professional Paper 891; US Geological Survey: Tacoma, WA, USA, 1976; pp. 1–30.
- Wyss, M.; Klein, F.; Nagamine, K.; Wiemer, S. Anomalously high b-values in the south flank of Kilauea volcano, Hawaii; evidence for the distribution of magma below Kilauea’s east rift zone. J. Volcanol. Geotherm. Res. 2001, 106, 23–37. [Google Scholar] [CrossRef]
- Cayol, V.; Dieterich, J.H.; Okamura, A.T.; Miklius, A. High magma storage rates before the 1983 eruption of Kilauea, Hawaii. Science 2000, 288, 2343–2346. [Google Scholar] [CrossRef] [PubMed]
- Poland, M.P.; Miklius, A.; Montgomery-Brown, E.K. Magma supply, storage, and transport at shield-stage Hawaiian volcanoes. In Characteristics of Hawaiian Volcanoes; Poland, M.P., Landowski, C.M., Takahashi, T.J., Eds.; U.S. Geological Survey Professional Paper 1801; US Geological Survey: Tacoma, WA, USA, 2014; pp. 179–234. [Google Scholar]
- Rubin, A.M. Propagation of magma-filled cracks. Annu. Rev. Earth Planet. Sci. 1995, 23, 287–336. [Google Scholar] [CrossRef]
- Taisne, B.; Jaupart, C. Dike propagation through layered rocks. J. Geophys. Res. Solid Earth 2009, 114, 18. [Google Scholar] [CrossRef]
- Traversa, P.; Pinel, V.; Grasso, J.-R. A constant influx model for dike propagation; implications for magma reservoir dynamics. J. Geophys. Res. Solid Earth 2010, 115, 18. [Google Scholar] [CrossRef]
- Gudmundsson, A.; Marinoni, L.B.; Marti, J. Injection and arrest of dykes; implications for volcanic hazards. J. Volcanol. Geotherm. Res. 1999, 88, 1–13. [Google Scholar] [CrossRef]
- Gudmundsson, A. Emplacement and arrest of sheets and dykes in central volcanoes. J. Volcanol. Geotherm. Res. 2002, 116, 279–298. [Google Scholar] [CrossRef]
- Rivalta, E.; Böttinger, M.; Dahm, T. Buoyancy-driven fracture ascent; experiments in layered gelatin. J. Volcanol. Geotherm. Res. 2005, 144, 273–285. [Google Scholar] [CrossRef]
- Taisne, B.; Tait, S. Eruption versus intrusion? Arrest of propagation of constant volume, buoyant, liquid-filled cracks in an elastic, brittle host. J. Geophys. Res. Solid Earth 2009, 114, 7. [Google Scholar] [CrossRef]
- Taisne, B.; Tait, S.; Jaupart, C. Conditions for the arrest of a vertical propagating dyke. Bull. Volcanol. 2011, 73, 191–204. [Google Scholar] [CrossRef]
- Geshi, N.; Kusumoto, S.; Gudmundsson, A. Effects of mechanical layering of host rocks on dike growth and arrest. J. Volcanol. Geotherm. Res. 2012, 223–224, 74–82. [Google Scholar] [CrossRef]
- Miklius, A.; Lisowski, M.; Delaney, P.T.; Denlinger, R.P.; Dvorak, J.J.; Okamura, A.T.; Sakol, M.K. Recent Inflation and Flank Movement of Mauna Loa Volcano. In Mauna Loa Revealed: Structure, Composition, History, and Hazards; Rhodes, J., Lockwood, J., Eds.; American Geophysical Union: Washington, DC, USA, 2013. [Google Scholar] [CrossRef]
- De Luca, C.; Zinno, I.; Manunta, M.; Lanari, R.; Casu, F. Large areas surface deformation analysis through a cloud computing P-SBAS approach for massive processing of DInSAR time of DInSAR time series. Remote Sens. Environ. 2017, 202, 3–17. [Google Scholar] [CrossRef]
- Fialko, Y.; Simons, M.; Agnew, D. The complete (3-D) surface displacement field in the epicentral area of the 1999 Mw7.1 Hector Mine earthquake, California, from space geodetic observations. Geophys. Res. Lett. 2001, 28, 3063–3066. [Google Scholar] [CrossRef]
- Hanssen, R.F. Radar Interferometry: Data Interpretation and Error Analysis; Kluwer: Dordrecht, The Netherlands, 2001; p. 308. [Google Scholar]
- Wright, T.J.; Parsons, B.E.; Lu, Z. Toward mapping surface deformation in three dimensions using InSAR. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Guzzetti, F.; Manunta, M.; Ardizzone, F.; Pepe, A.; Cardinali, M.; Zeni, G.; Reichenbach, P.; Lanari, R. Analysis of ground deformation detected using the SBAS-DInSAR technique in Umbria, central Italy. Pure Appl. Geophy. 2009, 166, 1425–1459. [Google Scholar] [CrossRef]
- Casu, F.; Manconi, A. Four-dimensional surface evolution of active rifting from spaceborne SAR data. Geosphere 2016, 12, 697–705. [Google Scholar] [CrossRef]
- Dzurusin, D. Volcano Deformation: Geodetic Monitoring Techniques; Springer-Praxis Books in Geophysical Sciences; Springer: Berlin, Germany, 2006; 441p. [Google Scholar]
- Casu, F.; Manzo, M.; Lanari, R. A quantitative assessment of the SBAS algorithm performance for surface deformation retrieval from DInSAR data. Remote Sens. Environ. 2006, 102, 195–210. [Google Scholar] [CrossRef]
- Akaike, H. On the statistical estimation of the frequency response function of a system having multiple input. Ann. Inst. Stat. Math. 1965, 17, 185–210. [Google Scholar] [CrossRef]
- Bonaccorso, A.; Davis, P.M. Models of ground deformation from vertical volcanic conduits with application to eruptions of Mount St. J. Geophys. Res. Solid Earth 1999, 104, 10531–10542. [Google Scholar] [CrossRef]
- Fialko, Y.; Khazan, Y.; Simons, M. Deformation due to a pressurized horizontal circular crack in an elastic half-space, with applications to volcano geodesy. Geophys. J. Int. 2001, 146, 181–190. [Google Scholar] [CrossRef]
- Okada, Y. Surface deformation due to shear and tensile faults in a half-space. Bull. Seism. Soc. Am. 1985, 75, 1135–1154. [Google Scholar]
- Hansen, P.C. Analysis of discrete ill-posed problems by means of the L-curve. SIAM Rev. 1992, 34, 561–580. [Google Scholar] [CrossRef]
- Battaglia, M.; Cervelli, P.F.; Murray, J.R. dMODELS: A MATLAB software package for modeling crustal deformation near activefaults and volcanic centers. J. Volcanol. Geotherm. Res. 2013, 254, 1–4. [Google Scholar] [CrossRef]
- Lin, G.; Shearer, P.M.; Matoza, R.S.; Okubo, P.G.; Amelung, F. Three-dimensional seismic velocity structure of Mauna Loa and Kilauea volcanoes in Hawaii from local seismic tomography. J. Geophys. Res. Solid Earth 2014, 119, 4377–4392. [Google Scholar] [CrossRef]
- Okubo, P.G.; Benz, H.M.; Chouet, B.A. Imaging the crustal magma sources beneath Mauna Loa and Kilauea volcanoes, Hawaii. Geology 1997, 25, 867–870. [Google Scholar] [CrossRef]
- Bagnardi, M.; Poland, M.P.; Carbone, D.; Baker, S.; Battaglia, M.; Amelung, F. Gravity changes and deformation at Kīlauea Volcano, Hawaii, associated with summit eruptive activity, 2009–2012. J. Geophys. Res. Solid Earth 2014, 119, 7288–7305. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R.A. Simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Mogi, K. Relations between the eruptions of various volcanoes and the deformations of the ground surfaces around them. Bull. Earthq. Res. Inst. 1985, 36, 99–134. [Google Scholar]
- Parker, R.L. Geophysical Inverse Theory, Princeton series in Geophysics; Princeton University Press: Princeton, NJ, USA, 1994. [Google Scholar]
- Lockwood, J.P.; Lipman, P.W. Holocene Eruptive History of Mauna Loa Volcano; US Geological Survey professional paper 1350; US Geological Survey: Tacoma, WA, USA, 1987; pp. 509–535.
- Lipman, P.W. The Southwestern Rift Zone of Mauna Kea: Implications for Structural Evolution of Hawaiian Volcanoes. Am. J. Sci. 1980, 280, 752–776. [Google Scholar]
- Lipman, P.W.; Calvert, A.T. Modeling volcano growth on the Island of Hawaii: Deep-water perspectives. Geol. Soc. Am. 2013. Published on August 2013, First Published on 14 August 2013. [Google Scholar] [CrossRef]
- Tizzani, P.; Battaglia, M.; Castaldo, R.; Pepe, A.; Zeni, G.; Lanari, R. Magma and fluid migration at Yellowstone Caldera in the last three decades inferred from InSAR, leveling, and gravity measurements. J. Geophys. Res. Solid Earth 2015, 120, 2627–2647. [Google Scholar] [CrossRef]
- González, P.J.; Samsonov, S.V.; Pepe, S.; Tiampo, K.F.; Tizzani, P.; Casu, F.; Fernández, J.; Camacho, A.G. Magma storage and migration associated with the 2011–2012 El Hierro eruption: Implications for crustal magmatic systems at oceanic island volcanoes. J. Geophys. Res. Solid Earth 2013, 118, 4361–4377. [Google Scholar] [CrossRef]
- Wang, H.; Wright, T.J. Satellite geodetic imaging reveals internal deformation of western Tibet. Geophys. Res. Lett. 2012, 39, L07303. [Google Scholar] [CrossRef]
- Samsonov, S.; d’Oreye, N. Multidimensional time-series analysis of ground deformation from multiple InSAR data sets applied to Virunga Volcanic Province. Geophys. J. Int. 2012, 191, 1095–1108. [Google Scholar]
- Guglielmino, F.; Bignami, C.; Bonforte, A.; Briole, P.; Obrizzo, F.; Puglisi, G.; Stramondo, S.; Wegmüller, U. Analysis of satellite and in situ ground deformation data integrated by the SISTEM approach: The April 3, 2010 earthquake along the Pernicana fault (Mt. Etna—Italy) case study. J. Geophys. Res. 2011, 114, B09301. [Google Scholar] [CrossRef]
- Shirzaei, M.; Walter, T.R. Time-dependent volcano source monitoring using interferometric synthetic aperture radar time series: A combined genetic algorithm and Kalman filter approach. J. Geophys. Res. 2010, 115, B10421. [Google Scholar] [CrossRef]
- Aster, R.C.; Borchers, B.; Thurber, C.H. Parameter Estimation and Inverse Problems; Elsevier Academic: Cambridge, MA, USA, 2005. [Google Scholar]
- Dietrich, J.H.; Decker, R.W. Finite element modeling of surface deformation associated with volcanism. J. Geophy. Res. 1975, 29, 4094–4106. [Google Scholar] [CrossRef]
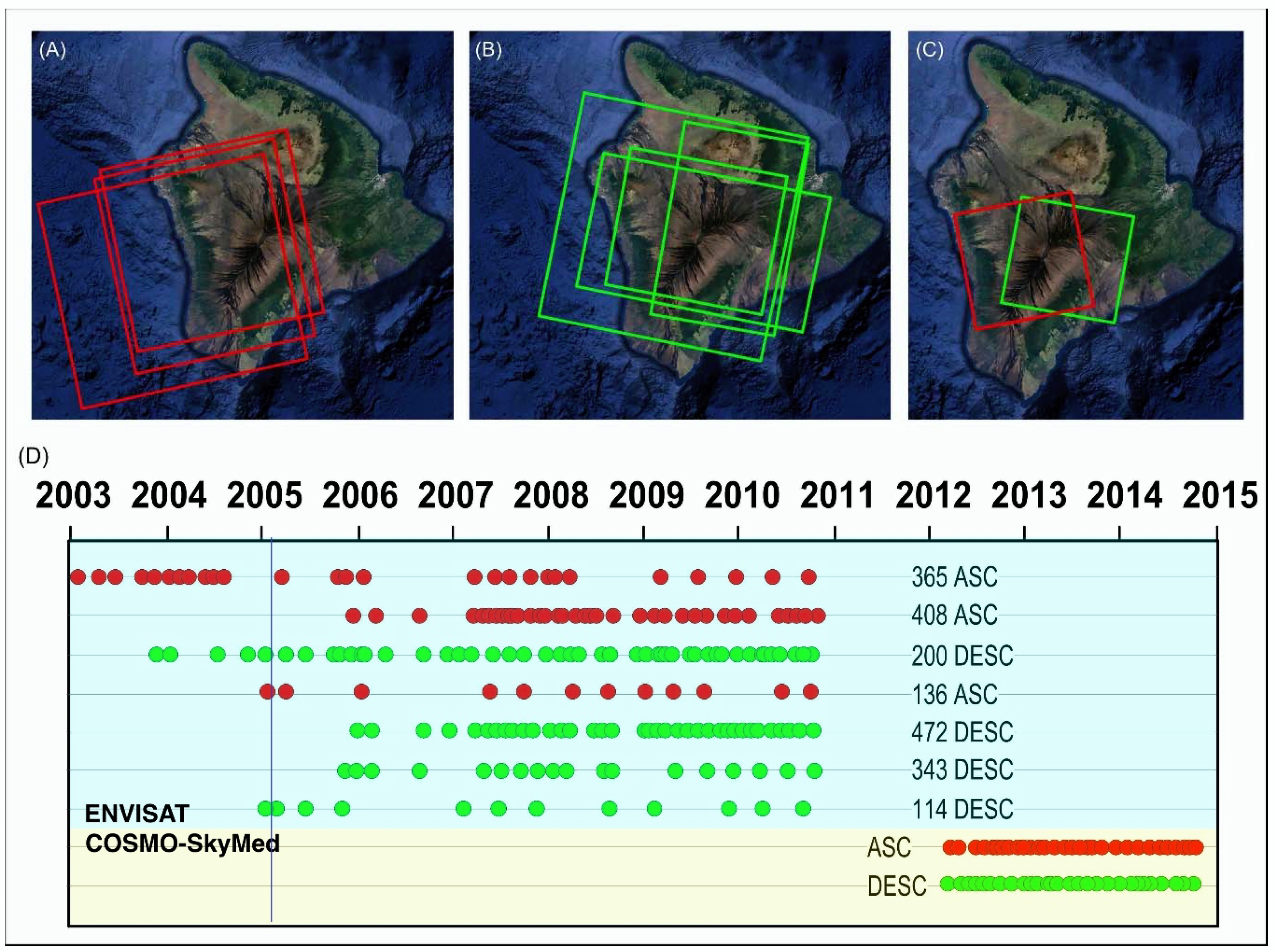
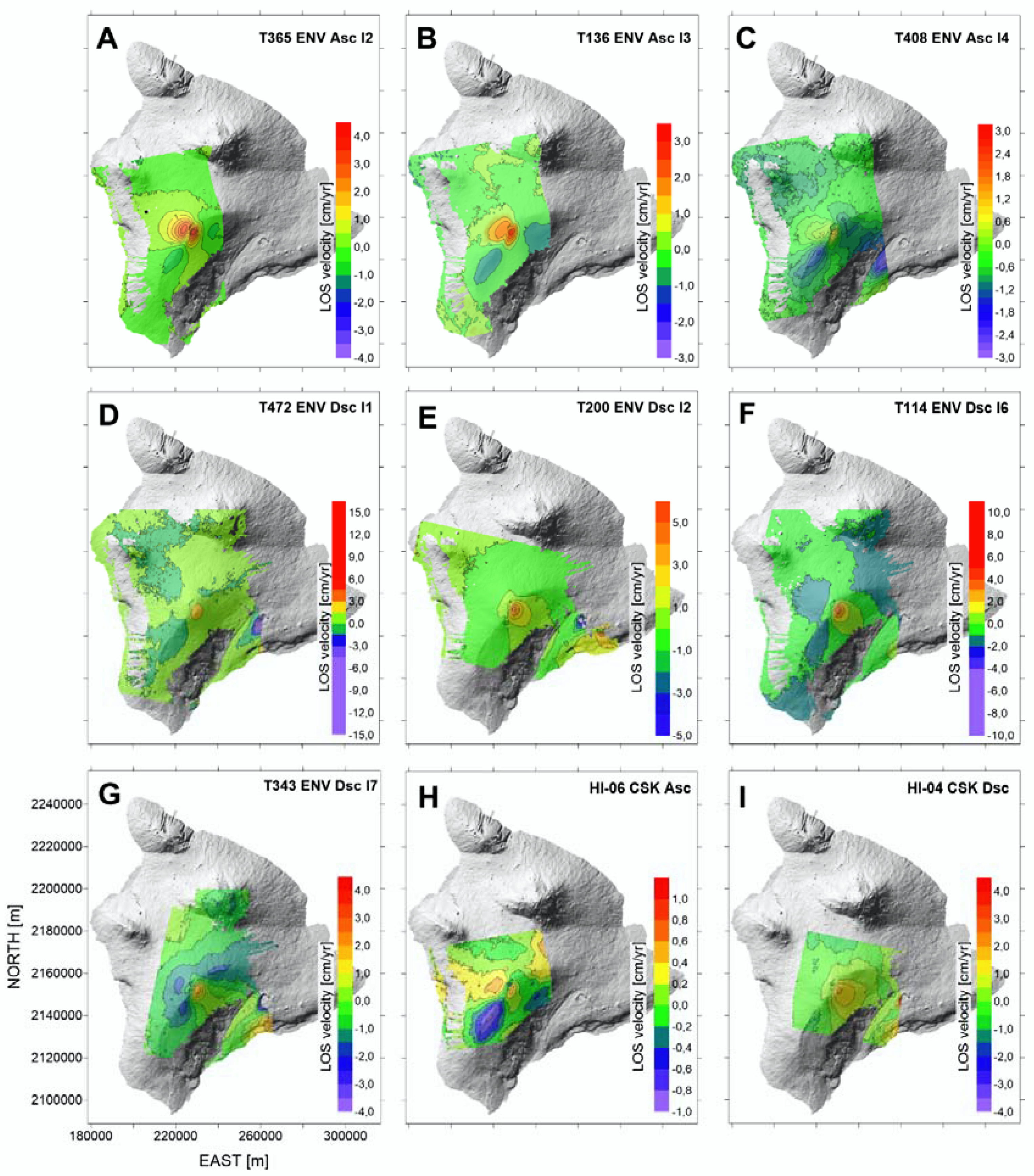
| Sensor | Mode | Track | Image Swath | Number of SLC | Number of Interferograms | Time Interval * |
|---|---|---|---|---|---|---|
| ENVISAT | Descending | 472 | I1 | 36 | 106 | 31122005–11092010 |
| ENVISAT | Ascending | 136 | I3 | 12 | 34 | 27012005–23092010 |
| ENVISAT | Descending | 343 | I7 | 18 | 50 | 17112005–07102010 |
| ENVISAT | Descending | 200 | I2 | 42 | 123 | 08122003–27092010 |
| ENVISAT | Ascending | 408 | I4 | 36 | 105 | 27122005–12102010 |
| ENVISAT | Descending | 114 | I6 | 12 | 48 | 25012005–17082010 |
| ENVISAT | Ascending | 365 | I2 | 27 | 76 | 08022003–04092010 |
| CSK | Ascending | ------ | HI_06 | 51 | 154 | 13032012–07092014 |
| CSK | Descending | ------ | HI_04 | 67 | 200 | 03032012–05092014 |
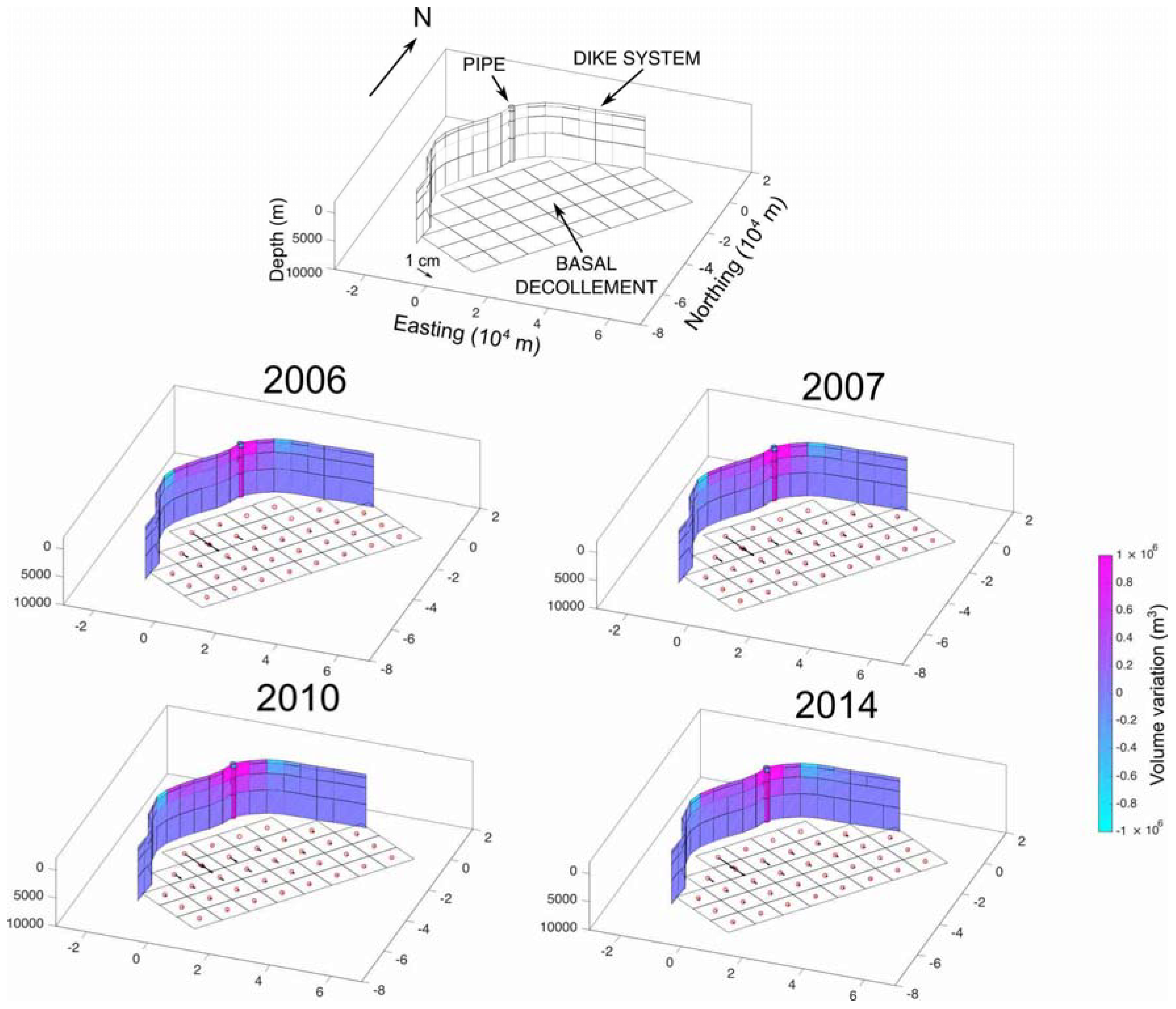
| Model | Mogi | Pipe | Dike | Decoll. | # eig. | RSS | AIC |
|---|---|---|---|---|---|---|---|
| 1 | N | Y | Y | Y | 127 | 22,99275438 | 0 |
| 2 | Y | N | Y | Y | 124 | 26,27011658 | 17355.3 |
| 3 | Y | Y | N | Y | 133 | 24,57768648 | 8697 |
| 4 | Y | Y | Y | N | 132 | 23,11053503 | 675,7 |
| 5 | Y | Y | Y | Y | 131 | 22,99243673 | 6,2 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pepe, S.; D’Auria, L.; Castaldo, R.; Casu, F.; De Luca, C.; De Novellis, V.; Sansosti, E.; Solaro, G.; Tizzani, P. The Use of Massive Deformation Datasets for the Analysis of Spatial and Temporal Evolution of Mauna Loa Volcano (Hawai’i). Remote Sens. 2018, 10, 968. https://doi.org/10.3390/rs10060968
Pepe S, D’Auria L, Castaldo R, Casu F, De Luca C, De Novellis V, Sansosti E, Solaro G, Tizzani P. The Use of Massive Deformation Datasets for the Analysis of Spatial and Temporal Evolution of Mauna Loa Volcano (Hawai’i). Remote Sensing. 2018; 10(6):968. https://doi.org/10.3390/rs10060968
Chicago/Turabian StylePepe, Susi, Luca D’Auria, Raffaele Castaldo, Francesco Casu, Claudio De Luca, Vincenzo De Novellis, Eugenio Sansosti, Giuseppe Solaro, and Pietro Tizzani. 2018. "The Use of Massive Deformation Datasets for the Analysis of Spatial and Temporal Evolution of Mauna Loa Volcano (Hawai’i)" Remote Sensing 10, no. 6: 968. https://doi.org/10.3390/rs10060968
APA StylePepe, S., D’Auria, L., Castaldo, R., Casu, F., De Luca, C., De Novellis, V., Sansosti, E., Solaro, G., & Tizzani, P. (2018). The Use of Massive Deformation Datasets for the Analysis of Spatial and Temporal Evolution of Mauna Loa Volcano (Hawai’i). Remote Sensing, 10(6), 968. https://doi.org/10.3390/rs10060968