1. Introduction
Catastrophic landslides are responsible for about 1000 fatalities per year [
1,
2], while causing total financial costs for direct infrastructure restoration and remedial, as well as indirect economic productivity losses in the order of billions of US dollars [
3,
4]. In general, slope instabilities are geomorphological processes that involve the movement of soil or rock driven by gravity [
3]. Predisposing factors for slope instabilities include e.g., the topography of the slope, the type of the rock or soil and its structure and lateral constraints [
5]. Slope failures are finally triggered by heavy rainfall events, snowmelt, earthquakes, or human activity [
6]. Prior to failure, the deformation of a slope’s surface is one of the main parameters that allow for describing and observing the temporal evolution of slope instabilities, to understand their behavior, and to predict their potential failure [
5,
7,
8]. The slow and continuous displacement of slopes over long periods of time can also be utilized to detect previously unknown instabilities and assess their hazard potential.
In this scenario, ground-based monitoring instruments may provide important information on displacements; however, these methods are often impractical for this purpose. For example, access to failure-prone slopes can be hazardous, thus, the installation of in situ monitoring equipment can be dangerous [
9]. Moreover, regional scale analyses or even at the scale of a single slope implies high costs. The application of remote sensing techniques enables also the extraction of information about the evolution of the slope instability. Within the last decade, air- and spaceborne remote sensing methods using active sensors, such as differential synthetic aperture radar (SAR) interferometry (DInSAR) [
5,
10,
11], or methods using input from passive sensors, such as digital image correlation (DIC) [
12,
13,
14,
15,
16], have been established to detect and monitor surface displacements at regional scales.
DIC, also known as feature-tracking or subpixel offset [
15], is an image processing technique that identifies and quantifies ground displacement occurring orthogonal to the line-of-sight (LOS) of the camera [
17]. Amongst others, DIC has been applied to monitor the glacier velocities [
18,
19], the ground displacement caused by earthquakes or tectonic activity [
17,
20], and the deformations at volcanoes [
21]. A selection of application examples for DIC is listed in
Table 1. While DIC can be applied on various types of input data from different platforms, its primary potential for slope instability detection and monitoring lies in the utilization of high-resolution optical imagery, acquired by satellites [
22] and manned or unmanned aerial vehicles (UAVs) [
23]. The exploitation of such data enables a detailed investigation and observation of slope instabilities on a local and on a regional scale, in any terrain. DIC analysis can provide key information on the spatial and temporal evolution of surface displacements at large slope instabilities; however, its potential and accuracy has not been thoroughly evaluated yet.
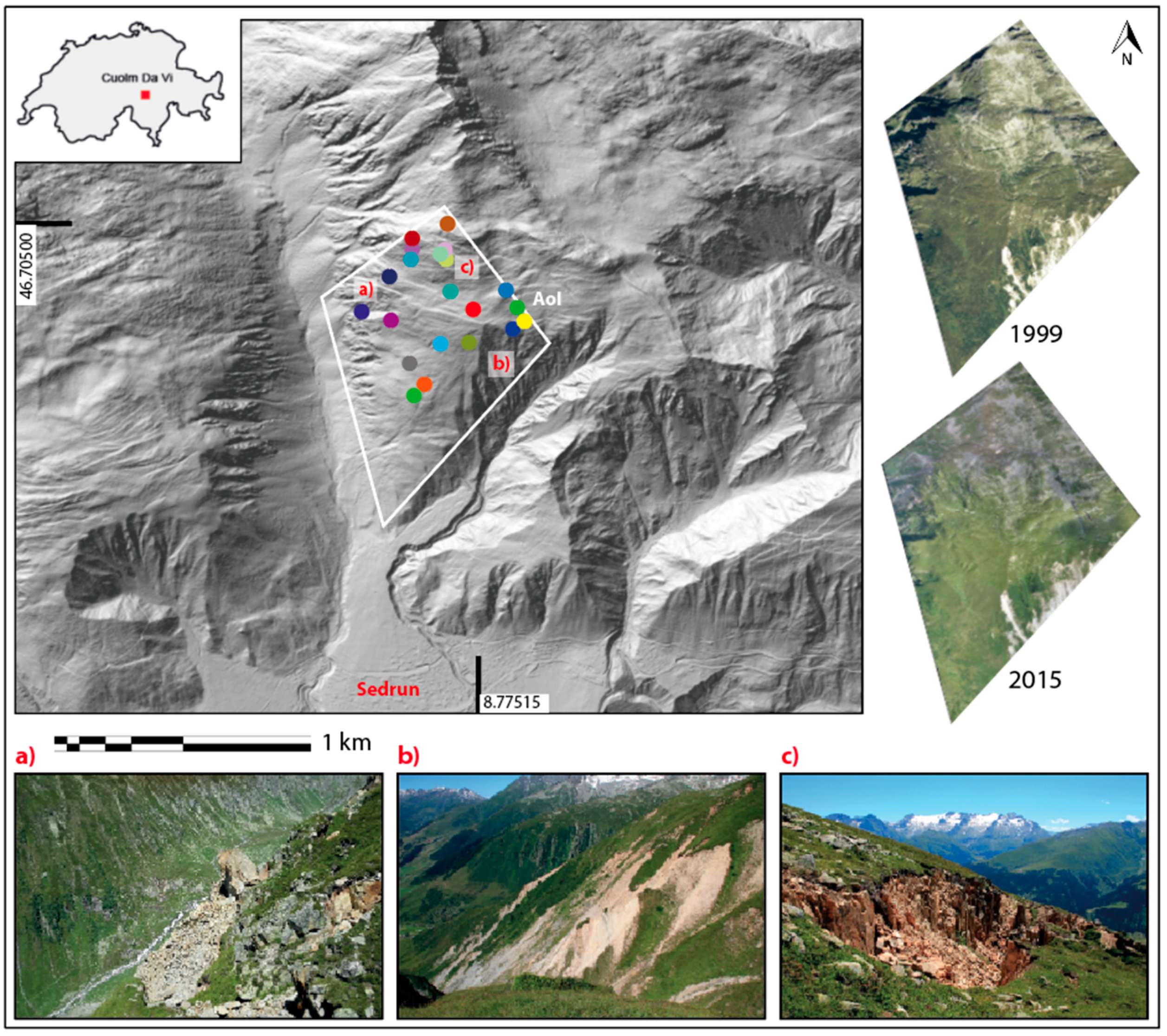
In order to provide new insights in this context, here, we investigate the qualitative and quantitative ability of three commonly used DIC algorithms to measure the deformation of a deep-seated gravitational slope deformation (DSGSD) located in the Swiss Alps. Two high-resolution optical images taken from airborne sensors optical images spanning 16 years were used as input for the DIC analyses. The results were compared to 23 points across the DSGSD, monitored via global navigation satellite system (GNSS) in the same time period.
In the following sections, we introduce the study site, followed by a short description of the DIC approach. Subsequently, we present the data used and the workflow. Next, we describe the derived results and discuss their implications. In the appendices, we provide detailed information on technical aspects of this study.
4. Results
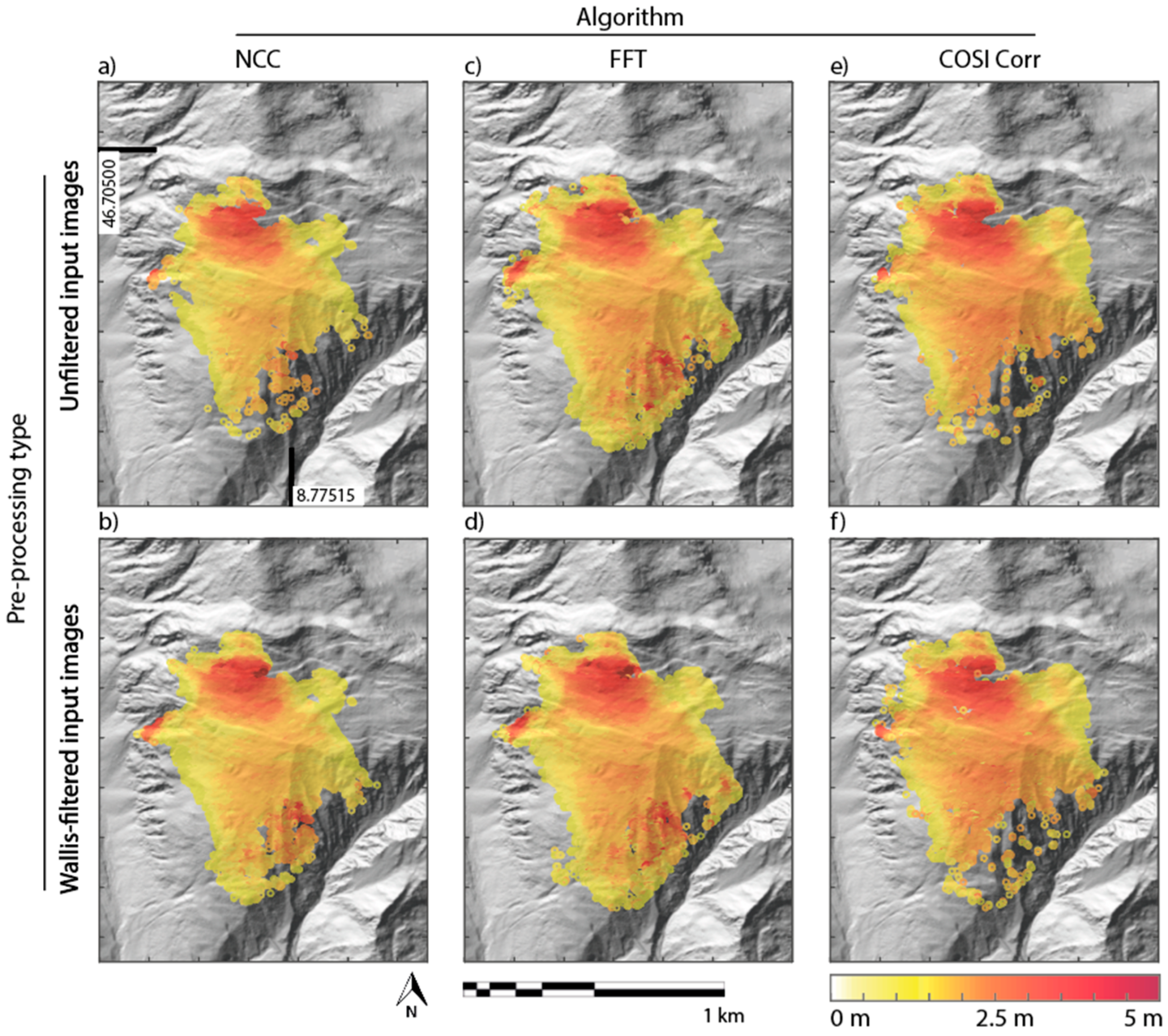
According to the DIC measurements, the major peak of the CdV deformation is situated in the North portions of the slope, with fringes extending towards the SE, W, and SW. The results show that data preprocessing has a significant impact on the correlation quality, and that all used algorithms have different abilities to represent the occurred displacement in the AoI over 16 years. The accumulated displacement measured by DIC over 16 years reaches up to 5 m. One example for the returned spatial coverage of the deformation field magnitude by each DIC algorithm is displayed in
Figure 3), using original and preprocessed input image pairs as input. The used template size was 64 × 64 pixels, and all results have been filtered using the spatial vector operator. A zoom on details of the slope area towards the west is shown in
Figure S3 in the Supplementary Material, which underlines quality differences in the returned displacement field, depending on the used code and the preprocessing.
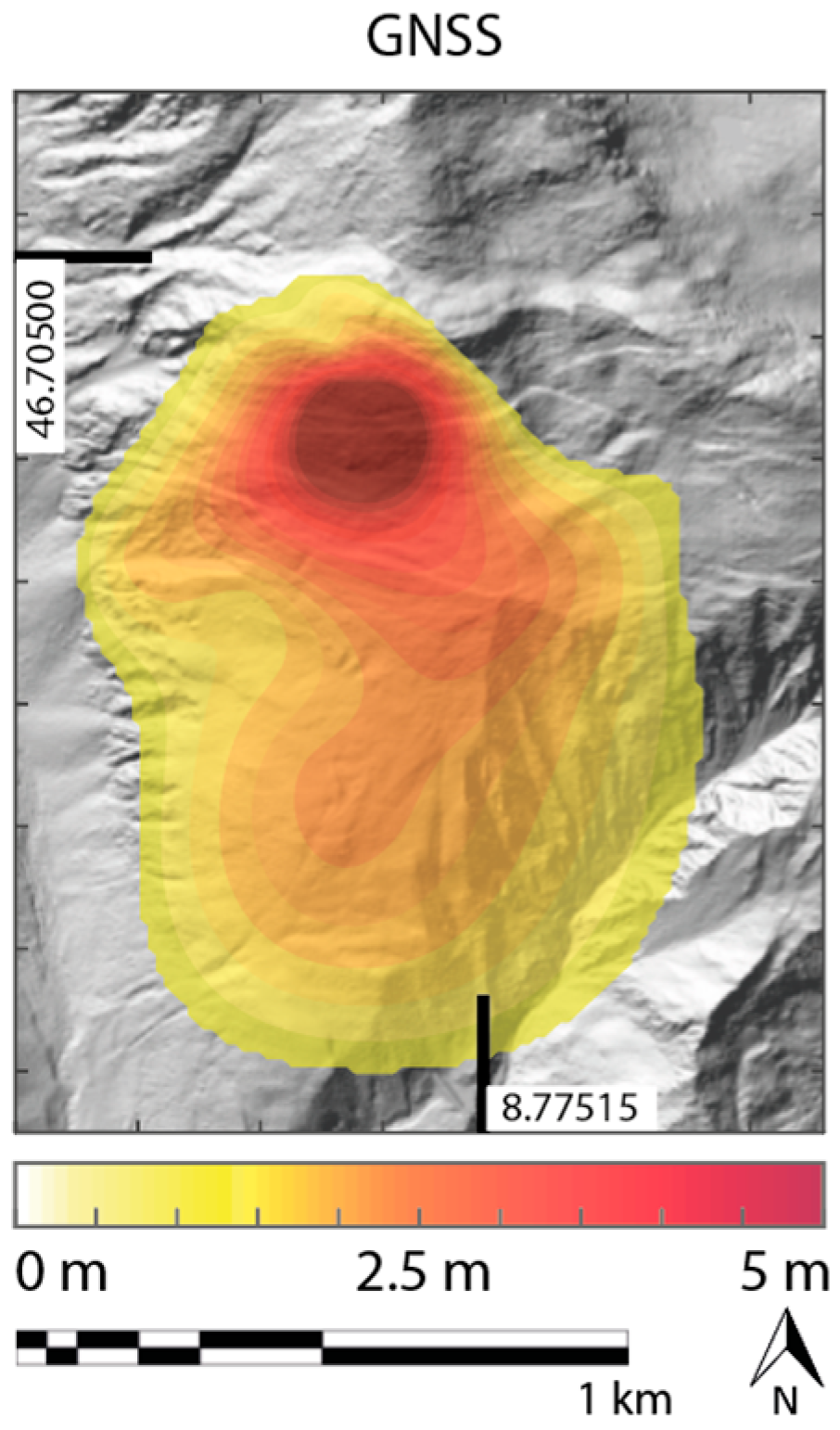
An interpolation of the derived GNSS displacement data from 23 measurement points across the AoI generally indicates a similar spatial deformation field and similar quantities as derived using DIC, while locally, the accumulated deformation exceeds 5 m. The resulting displacement field is illustrated in
Figure 4.
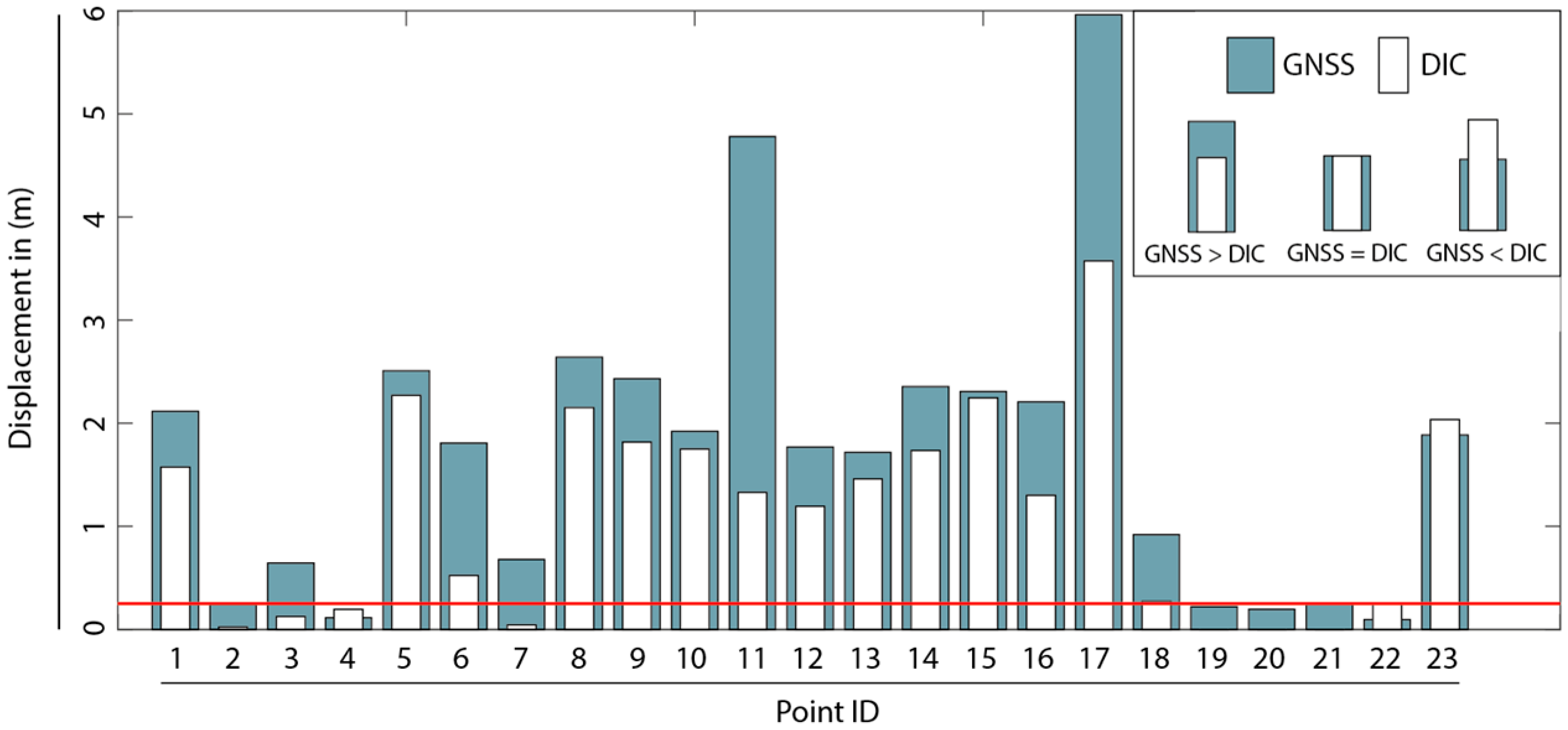
A direct quantitative comparison of the displacement at each measurement point as derived by DIC and GNSS shows good agreement. However, DIC measurements generally appear to slightly underestimate the true displacement throughout the AoI. In addition, for two measurement points (IDs 11 and 17) a substantial difference between DIC and GNSS of 3.5 and 2.5 m was identified (i.e., 14 and 10 pixels). The analysis of aerial imagery from the AoI suggests that there are no geomorphological features in the AoI that could explain the significantly different (i.e., larger) displacement values at these two monitoring points. Further, the patches of the DIC-derived displacement field in close vicinity to points 11 and 17 are not affected by noise. Although the discrepancy between the GNSS and DIC measurement has no obvious explanation, we considered these two GNSS measurement points as outliers, and discarded them from our further analysis.
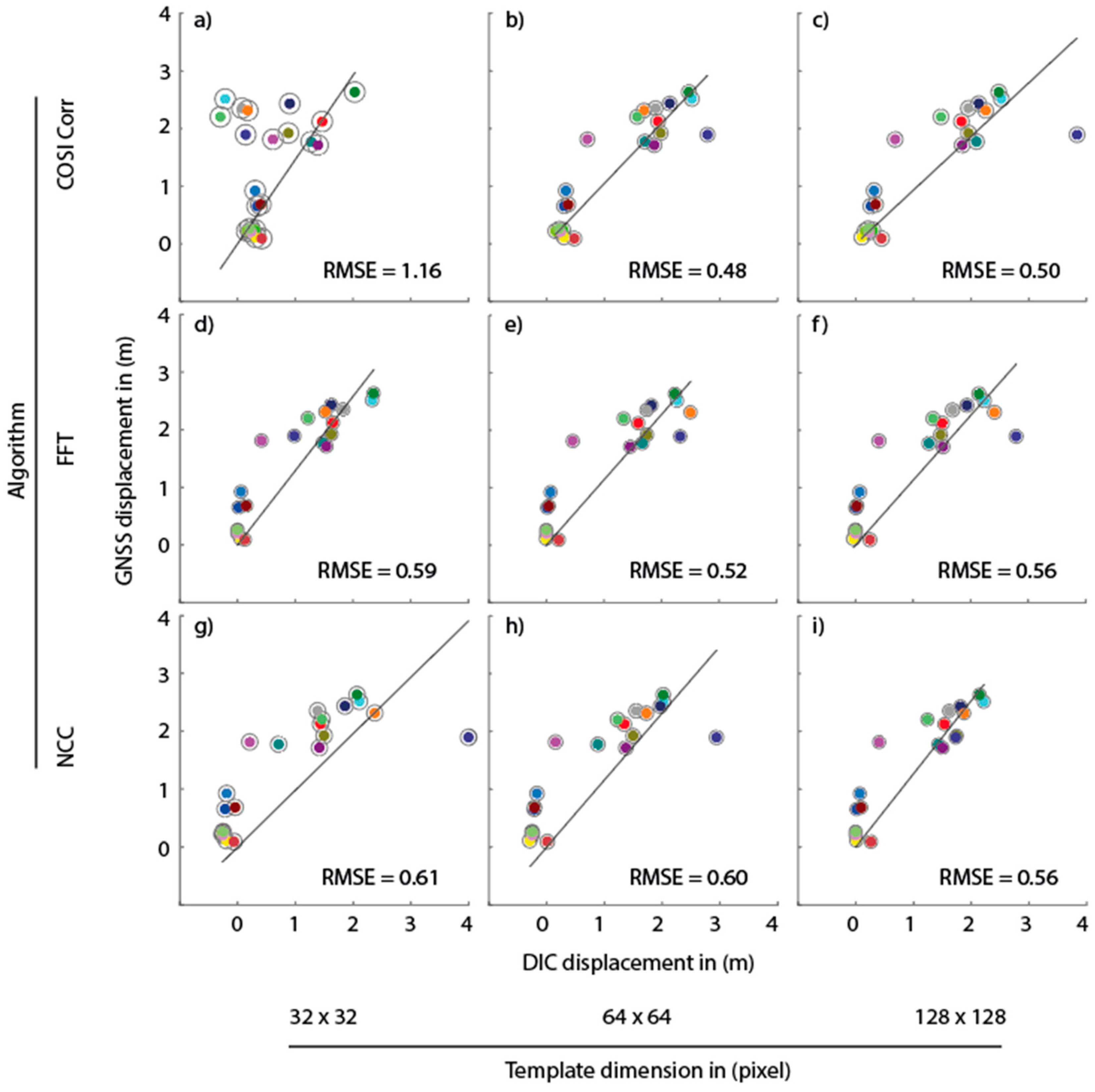
Figure 5 illustrates the comparison for a representative DIC run using a FFT-based correlator and a template size of 64 × 64 pixels, as well as a spatial vector operator. The GNSS-derived data has been plotted in grey color and in the background, while the DIC-derived data has been placed in the foreground and in white. Due to the similar quantitative performance of all assessed DIC codes,
Figure 5 can be accounted as being representative for all conducted runs. The data further suggests that the minimum sensitivity of the applied algorithms is in the range of 25 cm or 1 pixel.
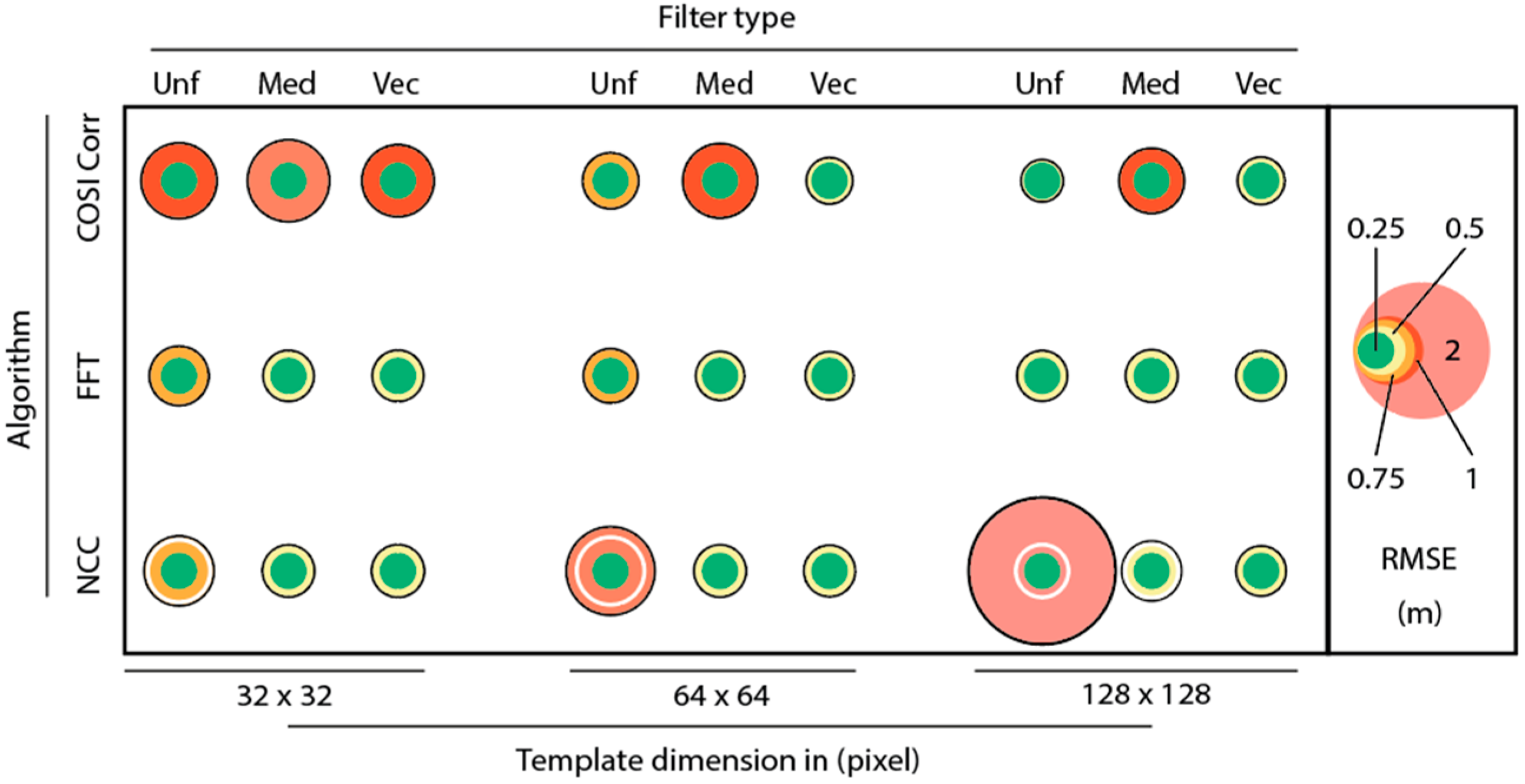
The quantitative analysis of 54 conducted DIC runs shows that the accuracy depends on the used algorithm, the input parameters, and the pre- and postprocessing procedures. The optimal performance is almost identical for all validated codes and is in the range of 0.5 m or 2 pixels. The results indicate that COSI Corr performs not as good as with small template sizes, while the other codes are relatively independent, particularly the FFT-based approach. An application of a Wallis filter does only have a relevant influence of the matching accuracy of the spatial-domain correlation code, but not on the frequency-domain codes. Postprocessing however, enhances the accuracy of all algorithms and template sizes, particularly if using a spatial vector operator. The overall accuracy of the assessed algorithms and setups ranges from 0.5 to more than 1 m, i.e., from 2 pixels to more than 4 pixels, depending on preprocessing treatment and on DIC processing parameters.
Figure 6 illustrates the quantitative comparison, using the size of the respective circle as an indicator for the achieved RMSE. The matrix represents runs with different template window sizes, ranging from 32 × 32 over 64 × 64 to 128 × 128 pixels, and using original as well as Wallis-filtered input imagery. In addition, the effect of no postprocessing, median filtering, and spatial vector filtering is displayed.
A comparison of the correlation error on a per-point-basis suggests that the inaccuracy of the displacement measurement with DIC is mainly caused by a general trend, rather than by isolated extreme mismatches. Further, the results of the analysis reveal differing capabilities of the used algorithms to match the image patches of master and slave around the GNSS measurement points. The velocity of the observed displacement does not seem to have an influence on the correlation accuracy, independent from the used DIC code.
Figure 7 illustrates this analysis for selected runs. The horizontal rows represent the different algorithms, while the vertical rows represent template window sizes, ranging from 32 × 32 over 64 × 64 to 128 × 128 pixels.
5. Discussion
All three algorithms produce consistent results in terms of the spatial distribution of the displacement field. The DIC code based on a FFT approach returns the best spatial representation of the deformation field with the lowest contribution of noise, almost reaching a full coverage of the DSGSD (
Figure 3c,d). The detection of displacements by DIC, in general, seems to be facilitated by applying an appropriate preprocessing to the input data. The contrast-enhanced images deliver results with less noise, less mismatches, and therefore, a better spatial coverage of the deformation field, particularly for NCC-based DIC algorithms (cf.
Figure S3). Contrast enhancement improves the matching quality even in areas with different shadow extents caused by different lighting conditions, as encountered in the NW of the CdV area. Parts of the slope in the northern peak area, as well as in the western displacement zone and in the southwestern ravine area show patches without data, as well as sharp contrasts in displacement; these regions are affected by noise, and were removed by the applied postprocessing filters. After field visits for ground-truthing, the most probable reasons for the noise level with respect to the extreme values at these locations, are correlator mismatches caused by illumination differences, changes in vegetation cover over the years, or the occurrence of failure-related rapid and non-linear surface changes, such as by erosion or shallow instabilities in the SE (cf. to
Figure 1a–c) and
Figures S1 and S2 in the Supplementary Material section for details).
The interpolated GNSS displacement map shows a similar deformation trend and spatial distribution of the displacement field as indicated by all DIC codes (
Figure 4), and confirms the accumulated slope displacement of more than 5 m. The GNSS data reveals a single area with significantly larger displacements in the upper part of the slope towards the North. This is in contrast to the results derived with DIC, which indicate three hotspots: (1) in the area of the ravine in the SE; (2) in the northern part of the landslide (i.e., consistent with the area of larger displacements identified with GNSS); and (3) in the western part of the landslide on a slope towards the Val Strem. In the latter area, a major rock fall event occurred on 14 March 2016—roughly one year after the acquisition of the 2015 image used for this study—with an estimated volume of 2 × 10
5 cubic meters [
45]. The event caused damage to a small power plant within the valley and led authorities to restrict access to Val Strem until present. This illustrates a main advantage of the DIC technique, as displacements are measured over large areas and with quasi-full coverage, avoiding biases introduced by the selective placement of instrumentation or measurement points. If images are acquired regularly, DIC can be used to identify spatial and temporal variations of the deformation field, enabling the targeted application of countermeasures. An additional benefit is that the second hotspot area is located on a steep slope, which is difficult to access with GNSS. A remote measurement taken, e.g., by a UAV, is a much quicker and safer option, than, e.g., performing in situ GNSS measurements. A comparison of
Figure 3 and
Figure 4 also illustrates the finer spatial resolution of the DIC-derived deformation, which could be relevant for a precise assessment of the hazard potential of close-by infrastructures, in this case, the Parlet cable car station in the very East of the AoI.
For the quantitative assessment of the applied DIC methods, the twelve nearest-neighbors of each GNSS measurement point were extracted from the DIC derived deformation matrix (cf.
Figure S4). Due to the relatively large spatial footprint of these twelve points, depending on the used scan window size and the search window movement pattern, the derived average of the deformation field might be biased, as the DIC codes sample the displacement over a larger area than is measured with the GNSS antenna, potentially considering areas with lower or higher deformation. In addition, the footprint might contain pixels, which are noise. Thus, in both cases, the accuracy of the respective extraction, and therefore, the accuracy of the entire assessment would be reduced. However, a trial and error approach has shown that this number of points delivers the best compromise between susceptibility to noise and accuracy, in direct comparison to an extraction of the single, four, or twenty-four closest points from the respective DIC deformation matrix. Still, the used extraction technique introduces a certain bias, which will generally lead to a slight underestimation of the actual accuracy of all applied DIC algorithms.
The quantitative assessment (
Figure 6) shows that all applied algorithms predominantly achieve accuracies of around 50 cm (e.g., two pixels considering source imagery GSD), with significant differences in the quality of the spatial coverage, however. COSI Corr tends to achieve higher accuracies when using large search windows, opposite to the NCC-based algorithm. The FFT-based code performs with a constantly high accuracy over a broad range of template sizes (the code for the FFT-based routine is available on GitHub and MathWorks File Exchange, see Acknowledgements). Remarkably, the accuracy of COSI Corr drops significantly for smaller template dimensions, i.e., 32 pixels, confirming similar findings by [
17,
22]. A similar behavior cannot be observed for the other frequency domain based code using a FFT-correlator, however.
Ref. [
33] proposed that DIC is capable to achieve subpixel accuracies for slope instability monitoring, but these results were not confirmed by an external source of displacement information, such as a GNSS dataset. Ref. [
13] reports correlation accuracies within the range of 2 to 3 or more pixels for aerial e.g., [
46], and roughly 0.2 to 1 pixels for satellite optical imagery e.g., [
22]. In addition, Ref. [
16] describes RMSEs of around 0.26 to 0.36 m using satellite optical imagery with a GSD of 0.5 m/pixel, validated against a small number of GNSS points. The results of our study therefore fit well into the findings of previous work, although different source data, as well as processing routines, have been applied. As generally discussed by [
33], quantitative errors in DIC application could be caused by several factors, such as misfits in master and slave co-registration, the usage of different optical instruments and platforms (plane—UAV), platform attitude, orthorectification errors, inaccurate resampling, and the applied DIC technique, with respect to the input parameters. In addition, long temporal baselines (in our specific case 16 years) might negatively influence the correlation of the input images, thus affecting the DIC accuracy as well.
As indicated in
Figure 6, a Wallis preprocessing does not have a significant influence on the accuracy of DIC, apart from the spatial domain algorithm that significantly benefits from the radiometric correction, as long as no postprocessing is applied. Generally, the application of postprocessing filters increases the performance of all tested DIC codes, particularly by using the spatial vector filter. If the applied template size is very large or if the used imagery has a very poor GSD, the vector filter routine could erroneously remove true surface displacements as noise, if the moving area is only represented by one or a couple of cells, and therefore, underrepresented within the local pixel neighborhood. In such a specific case, the application of no postprocessing filter is recommended to retain all information for interpretations.
The comparison of the DIC- and GNSS-derived displacement at each measurement point (
Figure 7) indicates that the discrepancy of the measured deformation is not caused by isolated extreme values, but rather by general mismatching trends. The used algorithms appear to have correlation difficulties with different GNSS points, probably indicating a varying degree of susceptibility to radiometric differences by each code, depending on the method and domain of operation.
Figure 7 further proposes that the accuracy of all DIC codes is independent of the magnitude of the observed displacement, i.e., slow movements are measured with the same accuracy as fast movements.
Some authors mention oversampling as a possibility to enhance the accuracy of the matching procedure [
24,
25]. For this study, three different methods of oversampling have been applied for the FFT-based and the NCC-based DIC algorithms. An increase of oversampling factor of both correlators has negligible effects. When oversampling the displacement field by using a template shift smaller than the Nyquist sample ratio, in this case, a quarter and an eighth instead of half of the applied template size, the RMSE remains at an equal level as well. It seems that the modified scan window sampling pattern, although producing a denser spatial representation of the deformation field, is not able to reduce the influence of noisy pixels or of true but non-representative displacements values of the surroundings. By applying DIC codes to up- or downsampled input images, i.e., over- or undersampled images using a factor of two, their accuracy reduces, particularly for the downsampled image. Probably the resampling and the associated blurring, with respect to averaging of the images, has a negative influence on the correlator, which also decreases the sensitivity of the algorithm. Generally, it has been found that oversampling has no influence on the quality of the returned displacement field, i.e., on the matching quality, nor has the noise level been increased. Still, oversampling has not been capable of enhancing the accuracy of DIC codes for the CdV case study, while increasing computational cost.
Besides the oversampling and the image pre- respectively post-processing, the search window size is a decisive parameter for DIC, as found during this study (cf.
Figure 6), and as discussed by several authors [
17,
22]. Ref. [
13,
28] state that the dimensions of the template are a compromise between the desired accuracy of the displacement measurement and the spatial resolution of the displacement field. A larger template will facilitate the identification of matches while assuring a good signal-to-noise ratio (SNR), but the accuracy on the displacement estimates decreases because they are averaged over a larger correlation window. Therefore, the template size is a decisive parameter for DIC application, which is connected to the spatial resolution of the used input imagery, as well as to the magnitude of the expected deformation. The dimensions of the search window are normally related to the spatial extent of the template. A larger search window will slow down the correlation speed, as more matches have to be calculated, but enables the detection of larger displacements, in turn.
The optimal dimensions of the template window are tied to the GSD of the applied input imagery and to the magnitude of the observed deformation. Generally, as a theoretical initial guess, Ref. [
47] recommend for COSI Corr to choose a template with a size of at least twice the expected deformation magnitude. In practice, they suggest the usage of a larger template however, within 8 to 17 times the expected deformation in pixels [
47]. Using the results of this work with peak displacements of about 2.5 m, i.e., equal to 10 pixels, and with best results derived with templates of 64 × 64 and 128 × 128 pixels in size, the initial guess should be within 6 to 12 times the expected deformation. In addition, this study showed that this assumption is equally valid not only for COSI Corr, but also for the other two assessed DIC-algorithms, operating in the spatial as well as in the frequency domain. In consensus with [
47], this study’s results suggests that the initial template size should be selected according to this formula
with
as the expected deformation,
as the scan window size, both in pixels, and coefficient K varying between 6 and 17.
The findings suggest that sensors with a poorer spatial resolution cannot resolve slow landslide displacements, and that they need a larger temporal baseline to detect a slow displacement, assuming constant deformation over time. Cameras with a smaller GSD would be more efficient in the detection of similar displacements considering smaller temporal baselines. It is important to note that, in theory, sensors with large GSDs are capable of detecting the same surface deformations as cameras with small GSDs, if the temporal baseline is sufficiently long, or if the deformation rate of the observed instability is high enough. Yet, cameras with a large GSD will fail to identify displacements with a spatial footprint smaller than their spatial resolution, independent of the magnitude of the deformation. The recommendation for window size by [
47], as well as the modification on behalf of the authors, still requires at least an estimate of the scale and magnitude of the expected slope instability deformation, which might be difficult or impossible to assume before. As observed surface displacements might be nonlinear, or only active under certain conditions, an application of DIC for instability monitoring can be further exacerbated, because the used input imagery must have a sufficient temporal baseline, which covers actual deformation with, at the same time, a potentially detectable speed of displacement. Therefore, the use of imagery with varying GSDs, e.g., images taken by a UAV from different altitudes above the slope instability, as well as the application of input data with varying temporal baselines in combination with differing template sizes, starting from the recommendations given by the discussed Formula (1), is proposed for a comprehensive detection and monitoring of slope instabilities.
Other limitations of DIC for slope monitoring are environmental conditions that impede the acquisition of optical imagery, such as fog, low clouds, or strong winds. As heavy rainfalls, and water, in general, have been identified as a main trigger of landslides [
6], monitoring capabilities of DIC can be restricted by poor weather conditions, and the impossibility to fly UAVs. Further, using only nadir looking imagery from off-ground platforms, the monitoring of vertical displacements is not possible, significantly limiting the ability of DIC to directly monitor, e.g., the rotational component of slope instability. This limitation can be overcome using, e.g., UAVs and oblique acquisitions. In addition, advanced DIC approaches combining multiple viewing geometries could be used to retrieve 3D displacements of an active slope instability.
However, DIC in combination with off-ground sensors offers the possibility to derive fairly accurate and unbiased displacement measurements over large areas for comparably low costs. As the accuracy is dependent on the GSD, the application of UAVs flying repeatedly at low altitudes enables monitoring with very high accuracy and temporal resolution. In addition, observations in remote areas are possible, where direct access is denied by rough terrain or steep slopes.
6. Conclusions
This study showed that DIC applied to high-resolution optical imagery from an airborne sensor allows the detection and accurate monitoring of slow and fast coherent displacements of the CdV DSGSD over 16 years. All DIC codes have achieved peak accuracies and precisions around 50 cm or 2 pixels, while the FFT-based algorithm provided a significantly better spatial coverage of the instability, in combination with a particularly constant level of performance, independent of template size or pre- and postprocessing. Dynamic range enhancement and radiometric preprocessing significantly improves the deformation field coverage by DIC, even in regions with extremely different illumination, especially for codes operating in the spatial domain, while reducing the general noise level. Still, the accuracy of matching is only improved for spatial correlators without any applied postprocessing. Appropriate removal of noise by postprocessing filters, particularly by a newly developed spatial vector filter, proved to be capable of further improving the accuracy of all algorithms and in any situation. Still, DIC appeared to slightly underestimate the occurred true displacement, in a general trend. An oversampling during DIC or as preparation prior to DIC has not been found to improve the accuracy of spatial and frequency domain DIC codes in any way, nor has it been found to affect the noise level or the quality of the spatial coverage of the displacement field. By contrast, the over- or downsampling of the used input imagery resulted in worse results, probably caused by a blurring of the images, causing a systematic underestimation of the displacement field by spatial and frequency domain DIC codes.
The findings of this study confirm assertions from the literature that the used template window size is the decisive parameter for the effectiveness of DIC, and that it has to be carefully determined and altered. An initial guess can be based on the presented Equation (1). In general, the application of imagery with different spatial resolutions, as well as data with varying temporal baselines in combination with the application of varying template window sizes is recommended to optimize detection and monitoring of slope instabilities with DIC. In addition, the utilization of input image preprocessing involving a radiometric correction, e.g., a Wallis filter, as well as the application of postprocessing filters, e.g., using a spatial vector filter, is suggested to further enhance the accuracy and quality of the correlation.
The CdV case study has shown that DIC codes used on airborne optical imagery are reliable and capable of reaching high accuracies, while being able to monitor displacements on large or even regional scales, and over long timescales. At the same time, the derived deformation enables not only the monitoring of slope instabilities, but also the detection of yet unknown features, as demonstrated by the recognition of the significant displacement of CdV West, prior to failure on 14 March 2016. This information allows an adaptation or even the deployment of a respectively traditional in situ on-ground monitoring system, in order to maximize the capabilities to monitor a particular slope instability. Further, DIC, in combination with off-ground platforms, can facilitate the access to remote or dangerous areas, while providing an excellent cost/benefit ratio per measurement. These properties promote the utility of DIC in combination with off-ground optical high-resolution data for numerous applications, including landslide hazard observation.