Abstract
A model based on the known high correlation between photosynthetically active radiation (PAR) and global horizontal irradiance (GHI) was implemented to estimate PAR from GHI measurements in this present study. The model has been developed using satellite-derived GHI and PAR estimations. Both variables can be estimated using Kato bands, provided by Satellite Application Facility on Climate Monitoring (CM-SAF), and its ratio may be used as the variable of interest in order to obtain the model. The study area, which was located in mainland Spain, has been split by cluster analysis into regions with similar behavior, according to this ratio. In each of these regions, a regression model estimating PAR from GHI has been developed. According to the analysis, two regions are distinguished in the study area. These regions belong to the two climates dominating the territory: an Oceanic climate on the northern edge; and a Mediterranean climate with hot summer in the rest of the study area. The models obtained for each region have been checked against the ground measurements, providing correlograms with determination coefficients higher than 0.99.
1. Introduction
Photosynthetically active radiation (PAR) is radiation with wavelengths of 400–700 nm in the solar spectrum. Biomass and algae production, plant physiology, energy balance in ecosystems, natural illumination of greenhouses, etc., require knowledge of this part of the solar spectrum. Despite its importance, PAR measurement stations are very scarce and, thus, usually it is estimated from empirical expressions relating it to solar global irradiance [1,2,3,4,5,6,7], which is measured more frequently. PAR estimations can also be obtained from satellites. Liang et al. [8] developed a method based on the look-up table approach for estimating PAR from Moderate-Resolution Imaging Spectrometer (MODIS) data. Similarly, other authors [9] have derived PAR using Geostationary Operational Environmental Satellite (GOES) data. On the other hand, Rubio et al. [10] estimated global horizontal irradiance (GHI) from a satellite, before PAR was obtained using an empirical model proposed by Alados-Arboledas et al. [11], which was developed from a database located at Almería. Wandji et al. [12] described a technique for an accurate assessment of PAR under clear-sky conditions using Kato bands [13] from libRadtran simulations. Kato bands are 32 bands of different widths which the solar spectrum can be divided into. In each of those bands, the absorption coefficient of different gases is almost constant.
The width of Kato bands depends on the distribution and structure of the absorption bands. These bands are also provided for the Satellite Application Facility on Climate Monitoring (CM-SAF), which belongs to the European Organization for the Exploitation of Meteorological Satellites (EUMETSAT); thus, PAR can be obtained, in a first approximation, using the bands included in the part of the spectrum from 400 up to 700 nm. Indeed, of the 32 Kato bands available in the entire solar spectrum, the interval of bands 7–16 includes the region corresponding to PAR (Table 1).

Table 1.
Kato bands in the photosynthetically active radiation (PAR) region.
Therefore, GHI and PAR can be estimated in a first approximation from satellite-derived Kato bands. On the other hand, the linear relationship between both variables is usually the basis of the empirical models used to obtain the PAR value [14] and, thus, PAR can be approximated from the knowledge of the ratio between both variables and the GHI value. According to these considerations, this ratio was the variable used for the analysis performed in this work. The spatial and temporal variability of solar radiation advises a clustering analysis [15,16,17,18], which provides the groups within which the variable of interest, namely, the ratio between both radiations, is coherent. Once the regions with similar behavior in terms of the PAR/GHI ratio have been obtained by clustering analysis, a linear regression model in each of these regions is developed. The performance of this model from satellite-derived PAR and GHI estimations is the main novelty of this work. Thus, this model allows for the estimation of PAR in any part of this region from GHI measurements carried out at this location.
2. Data
The spectral-resolved irradiance [19] containing the Kato bands was the product required from CM-SAF for this work. The CM-SAF includes the following atmospheric input information to retrieve the surface incoming solar radiation: effective cloud albedo and clear sky index, aerosol, water vapor, ozone, and surface albedo.
Solar surface irradiance on a horizontal plane is supplied by the MAGICSOL (Magic Solar Irradiance) method, which only needs the satellite information from the broadband visible channel. Thus, it can be implemented in different satellite generations [20]. On the other hand, MAGICSOL’s method for clouds is based on the Heliosat algorithm [21], which determines the cloud index (n) using reflection measurements given as normalized digital counts. This index measures the reflectance detected on the sensor that is normalized by the dynamic range [22,23]. The following expression provides this index:
where ρ is the instantaneous planetary albedo, which is estimated from the digital count of the satellite sensor; is the cloud albedo estimated from the brightest pixel; and is the ground albedo, estimated from the darkest pixel.
However, the spectral-resolved irradiance requires modifications of the original method [24,25]. Indeed, the spectral effect of clouds is treated using the spectral corrections of the broadband effective cloud albedo, which is carried out by the application of the radiative transfer model.
The CM-SAF surface solar radiation datasets, which have a native spatial resolution of 0.05° × 0.05°, have been already validated in previous studies [26,27]. Besides this, a spatial distribution of the errors for these datasets was found in a previous study [28], where the surface solar radiation estimates derived from SAFs were compared with gridded daily solar radiation estimates obtained from station measurements of Joint Research Centre Monitoring Agricultural ResourceS (JRC-MARS) database.
The area requested for this work covers from 44°N to 35.3°N latitude and 9.5°W to 3.5°E longitude, where the study region (mainland Spain) is included. The spatial resolution was 0.1° × 0.1° and the mean daily data during 1991–2011 (21 years) were used. After this, for the clustering analysis, the data were grouped in months in order to reduce the high temporal resolution. This restricts the computational complexity and avoids fluctuations that can introduce noise into a climatological study.
On the other hand, PAR and GHI daily ground measurements were taken in order to validate the model obtained at three sites: Plataforma Solar de Almería (PSA-CIEMAT), from 24 February 2016 to 22 June 2017; Centro de Desarrollo de Energías Renovables (CEDER-CIEMAT), from 26 January 2016 to 20 August 2017; and Santiago de Compostela (Santiago-EOAS, [29]), from 1 January 2016 to 31 December 2017.
Regarding the two first stations, the PAR sensor, an Eko ML-020P model, was installed over a horizontal plane on the top of a weather house at 3 agl m of altitude. There were also other sensors installed for the characterization of solar radiation (global, direct, and diffuse). The placement of instruments was free of obstacles, such as mountains, buildings, and trees. Therefore, any radiation measurement at these sites can represent the conditions above the canopy layer. GHI was recorded using a CM21 (Kipp & Zonen) pyranometer at the first two stations. Data from those stations were monitored and collected continuously every 1 min (on average).
Regarding the Santiago-EOAS station, the PAR at ground level was measured at this meteorological site over a horizontal plane at 1.5 agl m by using a multiband GUV-2511 radiometer. This site is located at the top of a hill in a flat grassland terrain without any obstacle in the surrounding area. Therefore, any radiation measurement at this site can represent the conditions above the canopy layer. The 10 min average PAR solar radiation data were collected. On the other hand, GHI data from MeteoGalicia were measured using a pyrradiometer PH.SCHENK Type 8111.
For this work, all data were transformed into daily data.
3. Methodology
The methodology applied is based on the clustering analysis performed on the PAR/GHI ratio estimations. The role of clustering is to identify regions with different cloud patterns throughout the year and, thus, to develop specific models for each region that can be sensitive to the different cloud dynamics of each region.
The clustering technique used for this study was k-means, which is one of the most widely used methods. The k-means algorithm [30,31,32] is based on the minimization of the sum of squared distances between the centroid of the group and each object of this group. k-means is implemented as follows: (a) initial clusters are randomly selected; (b) distances between data and centroids of each cluster are determined; (c) data are assigned to clusters so that their centroids are the nearest; (d) according to the new data, new centroids are obtained for each cluster; and (e) the process is repeated until the sum of distances between the data and centroids of clusters converges.
On the other hand, the optimal number of clusters for the clustering must be determined. Indeed, the optimal number of clusters allows for identification of the most significant clusters. If a smaller number of clusters was considered, certain zones with differing behavior would not be taken into account. In contrast, considering too many clusters would make similarly behaving regions appear different. In this work, the optimal number was determined using the so-called silhouette method [33], which validates the consistency within clusters.
After this, a linear regression model to obtain PAR from GHI, trained with satellite data, was produced for each cluster. Finally, this model was validated with the available ground measurements from three stations.
Next, the steps followed in the methodology, as well as the justification and limitations of the applied method, are shown.
3.1. Steps Followed
The methodology includes the following steps:
- Step 1: Obtaining GHI and PAR Estimations
GHI and PAR estimations were obtained by summing the satellite-derived Kato bands. In the case of PAR, the interval of bands is {7–16}. In the case of GHI, all bands provided for CM-SAF were used, which had the interval {4–27}. The percentage of the radiation included in the three first bands, which are not included in CM-SAF, can be considered to be negligible [34]. Regarding the five last bands that were not included {28–32}, although the percentage included in this interval must be small, an approximation was conducted considering a triangle whose base was the width of the interval and height the radiation corresponding to Band 27. From these estimations, the PAR/GHI ratio is available for the following analysis.
- Step 2: Clustering Analysis
The k-means algorithm was applied to the clustering analysis. As mentioned, the silhouette method [33] was used in order to determine the optimal number of clusters. For each individual object i of the cluster, the silhouette width value, s(i), is defined as
where a(i) is the average dissimilarity of the object i regarding all other data within the same cluster; b(i) is the lowest average dissimilarity of i regarding any neighbor cluster; and s(i) is in the interval range of [−1,1]. If s(i) ≈ +1, then i is well matched within the group, as a(i) << b(i). In contrast, if s(i) ≈ −1, then i is mislabeled as a(i) >> b(i).When s(i) ≈ 0, i is between two groups because a(i) = b(i). The quality of the whole structure of the cluster is measured by the average silhouette width (ASW), which is defined as
Thus, the silhouette plots may be used to determine the natural number of clusters for a certain dataset so the highest ASW shows the optimal number of clusters.
As indicated, the variable of interest for the analysis was the PAR/GHI ratio, which uses 12 features (12 months) at each grid point, so the distances between pairs of data were calculated considering these 12 features.
- Step 3: Obtaining Regression Models
A regression linear model trained with only the satellite data within each region was produced. The satellite-derived PAR and GHI values corresponding to the same grid point and same day were the pairs of points used for the regression. Due to the temporal variability affecting the solar radiation, a different model for each month (12 models for each region) was obtained.
- Step 4: Validation
The regression models were validated with the ground measurements obtained for two years (2016 and 2017) in the three sites previously indicated (PSA-CIEMAT, CEDER-CIEMAT, and Santiago-EOAS). As mentioned, the linear relationship between PAR and GHI is usually the basis of the empirical models used to obtain the PAR values. Thus, the coherence between both variables was analyzed by checking this linear relationship and removing the data corresponding to extreme outliers. These outliers are the points that are very far off from the regression line and the process to obtain them was the following:
- (a)
- Obtaining the regression line between PAR measured versus GHI measured;
- (b)
- Obtaining the distances between the PAR measured values and PAR values obtained by the regression line;
- (c)
- Obtaining the interquartile range and the 25th and 75th percentiles of these distances; and
- (d)
- Determining the points with a PAR measured that is either higher than the 75th percentile plus three times the interquartile range or lower than the 25th percentile minus three times this interquartile range. These points are the extreme values [35].
Once the data were filtered according to the former process, the GHI ground measurements were introduced in the models obtained in Step 3 (Obtaining Regression Models) using the satellite-derived estimates. After this, the obtained PAR values were compared with the measured PAR values at these three stations.
3.2. Justification of Method
Satellite-derived irradiances (broadband and spectral) have uncertainties as a result of several factors of different natures (systematic errors, approximations made in the model, etc.). In fact, CM-SAF provides, apart from Kato bands, the global irradiance for the overall spectrum and this value is not fully consistent with the approximation from the sum of Kato bands. Thus, it is very common to correct and improve these retrievals by identifying bias and errors with the help of ground data. The motivation to develop a PAR model from the satellite-derived data in which the more accurate GHI ground measurements are used for its application is twofold: on the one hand, the improvement of the retrieval provided by the satellite and on the other hand, the fact that Kato bands are not available in the whole dataset of the CM-SAF product (CM-SAF only provides the Spectral-Resolved Irradiance, containing the Kato bands, until 31 December 2011). Thus, this model will help to extend the usability, allowing PAR computation from the whole period of global irradiance data in the CM-SAF database.
3.3. Limitations of Method
Two limitations can be found:
- The lack of more ground measurements prevents correcting the model using such measurements. In fact, this work is supported by the Spanish Ministry of Economy, Industry and Competitiveness (Project CGL2016-79284-P AEI/FEDER/UE), which is devoted to reducing this lack of measurements via the installation of a network of stations.
- The assumption of the PAR/GHI ratio estimation provided by the satellite is accurate enough and, thus, a model based on this ratio can be used to obtain PAR from ground GHI values. This assumption is based on the fact that both satellite-derived radiation types are obtained by the same method (summing Kato bands). However, there are no simultaneous ground and satellite data that can be used to assess this accuracy.
4. Results and Discussion
4.1. Determination of the Optimal Number of Clusters According to the Silhouette Method
The silhouette width according to the number of clusters is shown in Figure 1.
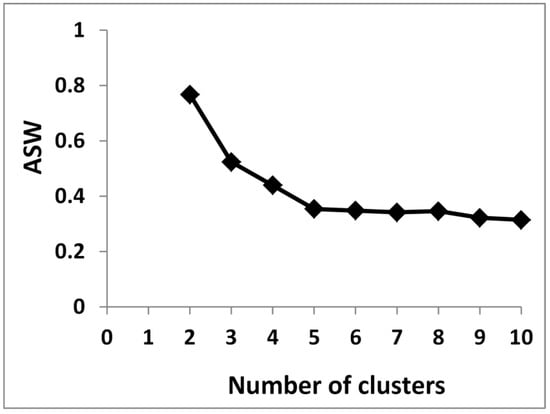
Figure 1.
Average silhouette width versus number of clusters (from k-means).
The highest value of silhouette is obtained for two clusters and, thus, according to the (previously mentioned) silhouette method, this value is the optimum number of clusters.
4.2. Clustering Analysis
Figure 2 shows the two regions based on the k-means algorithm, which uses the PAR/GHI ratio as variable of interest.
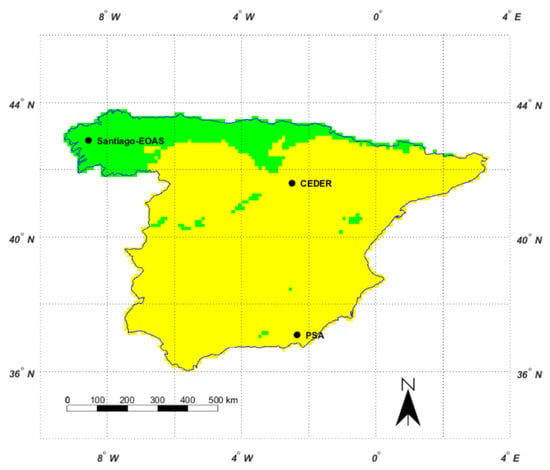
Figure 2.
Clusters by the k-means algorithm (2 clusters).
The two regions are clearly different. One of them extends along the north of the Iberian Peninsula, which also includes other punctual zones. The other region covers most of the territory.
In order to see the difference between both regions more clearly, complementary information about the annual variability of the radiation was calculated. Table 2 shows the size and the mean PAR/GHI values during different months for each cluster.

Table 2.
Number of points for the two clusters and mean PAR/global horizontal irradiance (GHI) values for the different months (N: Number of points).
The mean values of the small region (green) are slightly higher. In addition, the values corresponding to winter months are also slightly higher than the values of other months.
The division obtained has also physical meaning since it is consistent with the global climatology of Spain [27,36,37]. Indeed, in the northern edge of the territory, the climate is Oceanic, with continuous clouds and precipitation over the year. However, in the rest of the territory, the Mediterranean climate with hot summer is dominant. The climate of a region is obviously related to the solar radiation reaching Earth’s surface and, thus, the clustering achieved must agree with these climatological features. The north edge in Figure 2 is clearly associated with the Oceanic climate where abundant clouds decrease the solar activity [38]. This activity increases in the rest of the territory, which is characterized by a Mediterranean climate. However, we must recall that the variable used for the study was the PAR/GHI ratio, and not the solar radiation. This ratio depends on the attenuation, which affects the different bands of the solar spectrum. Regarding the spectral attenuation caused by clouds, the scattering is nonselective [39] and, thus, there are no important differences between the behavior of this ratio in cloudy and noncloudy zones. The case of absorption is different as water has absorption mainly in the infrared region [40], which affects the attenuation of the global radiation, but not the attenuation in the PAR band. Thus, in cloudy zones, an increase in the PAR/GHI ratio can be expected.
Regarding the punctual zones of the green region, they belong to important mountain ranges where cloudiness is abundant, which is the same as in the zone associated with the Oceanic climate.
4.3. Regression Model
The model obtained according to Step 3 (Obtaining Regression Models) of the methodology from the satellite-derived PAR and GHI values is the following:
where a and b take the values shown in Table 3.

Table 3.
Values of slope and intercept for the model.
4.4. Validation
The former regression model was validated with ground measurements obtained at three stations. Two of these stations are included within the larger cluster (yellow): PSA-CIEMAT and CEDER-CIEMAT. The other station, Santiago-EOAS, belongs to the small cluster. Once the lags were deducted, the numbers of points (days) for the study were: 483 from PSA-CIEMAT, 549 from CEDER-CIEMAT, and 368 from Santiago-EOAS. These stations are also shown in Figure 2. These ground measurements were filtered according to Step 4 (Validation) of the methodology. At this end, the regression lines between PAR ground measurements and GHI ground measurements were obtained (Figure 3).
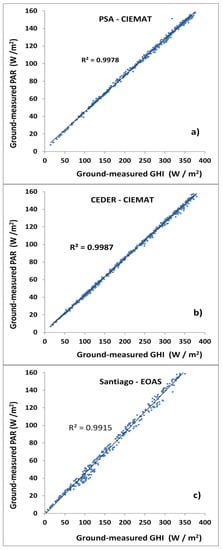
Figure 3.
PAR measured versus GHI measured for validation stations: (a–c) correspond to PSA-CIEMAT, CEDER-CIEMAT, and Santiago-EOAS stations, respectively.
Figure 3 clearly shows the good linear relationship between both variables. Only one data point of PSA-CIEMAT had to be removed according to the coherence filter applied due to some punctual incidence on the ground sensors. The ground-measured and filtered GHI values at these places were introduced in Equation (4) and the obtained PAR values were compared with the ground-measured PAR values. This comparison can be appreciated in the corresponding correlograms (Figure 4).
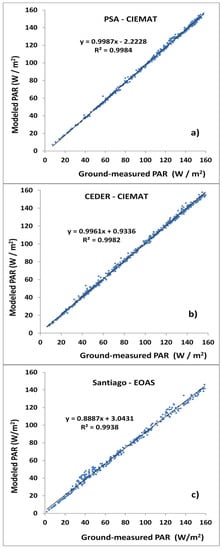
Figure 4.
Correlograms for validation stations: (a–c) correspond to PSA-CIEMAT, CEDER-CIEMAT, and Santiago-EOAS stations, respectively.
The statistics obtained from the correlograms: determination coefficients (R2), slopes, and intercepts, as well as the mean bias errors (MBE) and the root mean square errors (RMSE) have been included in Table 4, in order to assess the goodness degree of the model at the places with ground measurements.

Table 4.
Statistics of validation.
In all cases, the correlation is very high (determination coefficients are higher than 0.99). However, the stations of the center and south zone (PSA-CIEMAT and CEDER-CIEMAT) show better behavior compared to the station of the north zone (Santiago de Compostela), especially in the case of CEDER-CIEMAT. According to the results of Santiago-EOAS (MBE = −4.741 and slope = 0.889), the model slightly underestimates the PAR in the north region. This underestimation could be due to a low estimation of the satellite-derived PAR/GHI relation. However, since there are no simultaneous ground and satellite data to assess the accuracy in the estimation of this relation, the mean value of the PAR/GHI ratio has been obtained from the ground measurements and compared with the mean values corresponding to the north zone (Table 2). The relation from the ground measurements (0.46) is slightly higher than these means, which are in the range of 0.43–0.44, and this helps to understand the underestimation observed. On the other hand, the errors shown in Table 4 can also be due to the satellite-derived GHI error itself. Indeed, according to a previous study [28], higher errors in GHI are appreciated in the northern zone of Spain, which is consistent with the findings of another study [27], in which a similar behavior to those shown in Table 4 was observed. Indeed, in that study, the satellite-derived GHI estimates were compared with the ground measurements at three stations of Spain (sited at north zone, center, and Mediterranean coast) and according to the results, the highest errors were located at the northern station and the lowest at the center station.
5. Conclusions
A model based on the known linear relationship between GHI and PAR was implemented to estimate PAR from GHI measurements in this present study. The model has been developed using satellite-derived GHI and PAR estimations, which is the main novelty of this work. These estimations were achieved using the Kato bands provided for CM-SAF. The ratio between both variables was considered as the variable of interest in order to split the study area into regions within which the relation between PAR and GHI was similar. This consideration seems suitable since the division obtained provided two regions in accordance with the climatological features of mainland Spain. Indeed, the different regimes of clouds and precipitation characteristics of each climate affect the ratio of PAR/GHI in a different way. On the one hand, the northern area, along with some small and punctual zones, is associated with the Oceanic climate. On the other hand, the rest of the territory has a dominant Mediterranean climate. In addition, a separation across different months was included in order to consider the different seasonal behavior. In fact, according to Table 2, in both zones, the values corresponding to the winter months are slightly higher than the values of other months.
The validation of the model carried out with the three stations (two included within the south in the yellow zone) show correlograms with very high determination coefficients (higher than 0.99), as well as slopes that are practically equal to 1 for the largest region. According to all statistics of validation, the behavior of the model is better in this region, as the model slightly underestimates the PAR in the north region. This underestimation could be due to a previous underestimation of the relation of PAR/GHI from the satellite. Indeed, according to Table 2, the monthly mean values of the north region (green) fluctuate between 0.43 and 0.44, while this relation measured at the station has a mean value of 0.46. On the other hand, the errors in the spatial distribution shown in this table can also be due to the satellite-derived GHI error distribution itself as the highest errors are located in the northern zone and the lowest are in the center zone of the country.
On the other hand, the proposed method could be used for obtaining PAR historical values from the satellite-derived GHI estimates. The model coefficients have been derived using a long series of daily data (21 years) and, thus, they should show high temporal stability, at least, for periods with available satellite data.
Finally, according to the results of the work, there is the need for a PAR station network in order to allow for the usual correction of the satellite-derived solar radiation estimations.
Author Contributions
J.M.V. conceived the proposed model, which was designed with the rest of co-authors; J.M.V., R.X.V., A.A.N., L.F.Z. and A.P.-G. processed satellite data, and they processed and validated PSA-CIEMAT and CEDER-CIEMAT data; J.A.S., R.M.-G., D.C., and J.J.C., processed and validated Santiago–EOAS data.
Acknowledgments
This work was supported by the Spanish Ministry of Economy, Industry and Competitiveness (MINECO) [Project CGL2016-79284-P AEI/FEDER/UE]. Authors also acknowledge the data provided by EUMETSAT for the SRI product, MeteoGalicia (Consellería de Medio Ambiente e Ordenación do Territorio, Xunta de Galicia) for global irradiance data at Santiago-EOAS station, and University of Santiago de Compostela for the PAR data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Akitsu, T.; Kume, A.; Hirose, Y.; Ijima, O.; Nasahara, K.N. On the stability of radiometric ratios of photosynthetically active radiation to global solar radiation in Tsukuba, Japan. Agric. For. Meteorol. 2015, 209, 59–68. [Google Scholar] [CrossRef]
- Alados, I.; Foyo-Moreno, I.; Alados-Arboledas, L. Photosynthetically active radiation: Measurements and modelling. Agric. For. Meteorol. 1996, 78, 121–131. [Google Scholar] [CrossRef]
- Escobedo, J.F.; Gomes, E.N.; Oliveira, A.P.; Soares, J. Modeling hourly and daily fractions of UV, PAR and NIR to global solar radiation under various sky conditions at Botucatu, Brazil. Appl. Energy 2009, 86, 299–309. [Google Scholar] [CrossRef]
- Hu, B.; Wang, Y.; Liu, G. Measurements and estimations of photosynthetically active radiation in Beijing. Atmos. Res. 2007, 85, 361–371. [Google Scholar] [CrossRef]
- Jacovides, C.P.; Tymvios, F.S.; Boland, J.; Tsitouri, M. Artificial Neural Network models for estimating daily solar global UV, PAR and broadband radiant fluxes in an eastern Mediterranean site. Atmos. Res. 2015, 152, 138–145. [Google Scholar] [CrossRef]
- Sudhakar, K.; Srivastava, T.; Satpathy, G.; Premalatha, M. Modelling and estimation of photosynthetically active incident radiation based on global irradiance in Indian latitudes. Int. IJEEE 2013, 4, 21. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, Y.; Zhoub, Y. Measuring and modelling photosynthetically active radiation in Tibet Plateau during April-October. Agric. For. Meteorol. 2000, 102, 207–212. [Google Scholar] [CrossRef]
- Liang, S.; Zheng, T.; Liu, R.; Fang, H.; Tsay, S.-C.; Running, S. Estimation of incident photosynthetically active radiation from Moderate Resolution Imaging Spectrometer data. J. Geophys. Res. Atmos. 2006, 111, D15208. [Google Scholar] [CrossRef]
- Zheng, T.; Liang, S.; Wang, K. Estimation of incident photosynthetically active radiation from GOES visible imagery. J. Appl. Meteorol. Climatol. 2008, 47, 853–868. [Google Scholar] [CrossRef]
- Rubio, M.A.; López, G.; Tovar, J.; Pozo, D.; Batlles, F.J. The use of satellite measurements to estimate photosynthetically active radiation. Phys. Chem. Earth Parts A/B/C 2005, 30, 159–164. [Google Scholar] [CrossRef]
- Alados-Arboledas, L.; Olmo, F.J.; Alados, I.; Perez, M. Parametric models to estimate photosynthetically active radiation in Spain. Agric. For. Meteorol. 2000, 101, 187–201. [Google Scholar] [CrossRef]
- Wandji, W.; Espinar, B.; Blanc, P.; Wald, L. Estimating the photosynthetically active radiation under clear skies by means of a new approach. Adv. Sci. Res. 2015, 12, 5–10. [Google Scholar] [CrossRef]
- Seiji, K.; Ackerman, Y.P.; Mather, J.H.; Clothiaux, E.E. The k-distribution method and correlated-k approximation for a shortwave radiative transfer model. J. Quant. Spectrosc. Radiat. Transf. 1999, 62, 109–121. [Google Scholar]
- López, G.; Rubio, M.A.; Martínez, M.; Batlles, F.J. Estimation of hourly global photosynthetically active radiation using artificial neural network models. Agric. For. Meteorol. 2001, 107, 279–291. [Google Scholar] [CrossRef]
- Gastón-Romeo, M.; Leon, T.; Mallor, F.; Ramírez-Santigosa, L. A Morphological Clustering Method for daily solar radiation curves. Sol. Energy 2011, 85, 1824–1836. [Google Scholar] [CrossRef]
- Ghayekhloo, M.; Ghofrani, M.; Menhaj, M.B.; Azimi, R. A novel clustering approach for short-term solar radiation forecasting. Sol. Energy 2015, 122, 1371–1383. [Google Scholar] [CrossRef]
- Jiménez-Pérez, P.F.; Mora-López, L. Modeling and forecasting hourly global solar radiation using clustering and classification techniques. Sol. Energy 2016, 135, 682–691. [Google Scholar] [CrossRef]
- Polo, J.; Gastón, M.; Vindel, J.M.; Pagola, I. Spatial variability and clustering of global solar irradiation in Vietnam from sunshine duration measurements. Renew. Sustain. Energy Rev. 2015, 42, 1326–1334. [Google Scholar] [CrossRef]
- Stengel, M.; Kniffka, A.; Meirink, J.F.; Lockhoff, M.; Tan, J.; Hollmann, R. Claas: The CM SAF cloud property dataset using SEVIRI. Atmos. Chem. Phys. Discuss. 2013, 13, 26451–26487. [Google Scholar] [CrossRef]
- Posselt, R.; Mueller, R.; Stöckli, R.; Trentmann, J. Spatial and Temporal Homogeneity of Solar Surface Irradiance across Satellite Generations. Remote Sens. 2011, 3, 1029–1046. [Google Scholar] [CrossRef]
- Müller, R.; Pfeifroth, U.; Träger-Chatterjee, C.; Cremer, R.; Trentmann, J.; Hollmann, R. Surface Solar Radiation Data Set—Heliosat (SARAH)—Edition 1; EUMETSAT: Darmstadt, Germany, 2015. [Google Scholar]
- Perez, R.; Ineichen, P.; Moore, K.; Kmiecik, M.; Chain, C.; George, R.; Vignola, F. A new operational model for satellite-derived irradiances: Description and validation. Sol. Energy 2002, 73, 307–317. [Google Scholar] [CrossRef]
- Zelenka, A.; Perez, R.; Seals, R.; Renné, D. Effective accuracy of satellite-derived hourly irradiances. Theor. Appl. Climatol. 1999, 62, 199–207. [Google Scholar] [CrossRef]
- Mueller, R.; Behrendt, T.; Hammer, A.; Kemper, A. A New Algorithm for the Satellite-Based Retrieval of Solar Surface Irradiance in Spectral Bands. Remote Sens. 2012, 4, 622–647. [Google Scholar] [CrossRef]
- Mueller, R.; Behrendt, T. Algorithm Theoretical Baseline Document: Spectrally Resolved Solar Surface Irradiance SRI. 2013. Available online: http://www.cmsaf.eu/EN/Documentation/Documentation/ATBD/pdf/SAF_CM_DWD_ATBD_SRI_1.pdf?__blob=publicationFile&v=4 (accessed on 4 April 2018). [CrossRef]
- Riihelä, A.; Carlund, T.; Trentmann, J.; Müller, R.; Lindfors, A.V. Validation of CM SAF Surface Solar Radiation Datasets over Finland and Sweden. Remote Sens. 2015, 7, 6663–6682. [Google Scholar] [CrossRef]
- Vindel, J.M.; Navarro, A.A.; Valenzuela, R.X.; Ramírez, L. Temporal scaling analysis of irradiance estimated from daily satellite data and numerical modelling. Atmos. Res. 2016, 181, 154–162. [Google Scholar] [CrossRef]
- Bojanowski, J.S.; Vrieling, A.; Skidmore, A.K. A comparison of data sources for creating a long-term time series of daily gridded solar radiation for Europe. Sol. Energy 2014, 99, 152–171. [Google Scholar] [CrossRef]
- Pettazzi, A.; Souto, J.A.; Salsón, S.; Pérez Muñuzuri, V. EOAS, a shared joint atmospheric observation site of MeteoGalicia. In Proceedings of the 4th International Conference on Experiences with Automatic Weather Stations, Lisboa, Portugal, 24–26 May 2006. [Google Scholar]
- Andenberg, M.R. Cluster Analysis for Applications; Academic: New York, NY, USA, 1973. [Google Scholar]
- Adam, F.; Celebi, M.E. An Accelerated Nearest Neighbor Search Method for the K-Means Clustering Algorithm. In Proceedings of the Twenty-Sixth International Florida Artificial Intelligence Research Society Conference, St. Pete Beach, FL, USA, 22–24 May 2013; AAAI Press: Palo Alto, CA, USA, 2013. [Google Scholar]
- Macqueen, J. Some methods for classification and analysis of multivariate observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 7 January 1966; Le, L.M., Neyman, J., Eds.; University of California Press: Berkeley, CA, USA, 1967; pp. 281–297. [Google Scholar]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Wandji, W.; Espinar, B.; Blanc, P.; Wald, L. How close to detailed spectral calculations is the k-distribution method and correlated-k approximation of Kato et al. (1999) in each spectral interval? Meteorol. Z. 2014, 23, 547–556. [Google Scholar] [CrossRef]
- He, X. Quartiles and Boxplots (Modified). Normal Quantile Plots (QQ-Plot). 2012. Available online: http://www.stat.purdue.edu/~xuanyaoh/stat350/xyJan27Lec6.pdf (accessed on 4 April 2018).
- Peña-Angulo, D.; Trigo, R.M.; Cortesi, N.; González-Hidalgo, J.C. The influence of weather types on the monthly average maximum and minimum temperatures in the Iberian Peninsula. Atmos. Res. 2016, 178–179, 217–230. [Google Scholar]
- Agencia Estatal de Meteorología (AEMET); Instituto de Meteorología de Portugal (IM). Iberian Climate Atlas; AEMET-Ministerio de Medio Ambiente y Medio Rural y Marino & IM: Madrid, Spain, 2011; ISBN 978-84-7837-079-5. [Google Scholar]
- Mueller, R.; Trentmann, J.; Träger-Chatterjee, C.; Posselt, R.; Stöckli, R. The Role of the Effective Cloud Albedo for Climate Monitoring and Analysis. Remote Sens. 2011, 3, 2305–2320. [Google Scholar] [CrossRef]
- Woodhous, I.H. Introduction to Microwave Remote Sensing; Taylor & Francis Group: Boca Raton, FL, USA, 2006. [Google Scholar]
- Hill, C.; Jones, R.L. Absorption of solar radiation by water vapor in clear and cloudy skies: Implications for anomalous absorption. J. Geophys. Res. 2000, 105, 9421–9428. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).