Deep Cube-Pair Network for Hyperspectral Imagery Classification
Abstract
1. Introduction
- (1)
- Cube-pair is used when modeling CNN classification architecture. The advantage of using cube-pair is that it can not only generate more samples for training but can also utilize the local 3D structure directly.
- (2)
- A 3D FCN is modeled within a cube-pair-based HSI classification architecture, which is a deep end-to-end 3D network pertinent for the 3D structure of HSI. In addition, it has fewer parameters than the traditional CNN. Provided the same amount of training samples, the modeled network can go deeper than traditional CNN and thus has superior generalization ability.
- (3)
- The proposed method obtains the best classification results, compared with the pixel-pair CNN and other deep-learning-based methods.
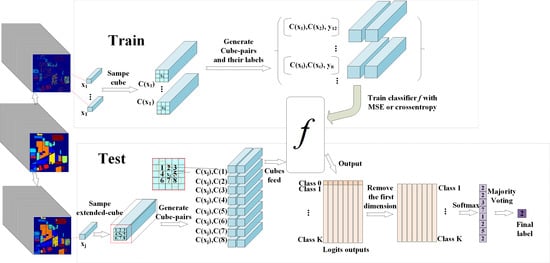
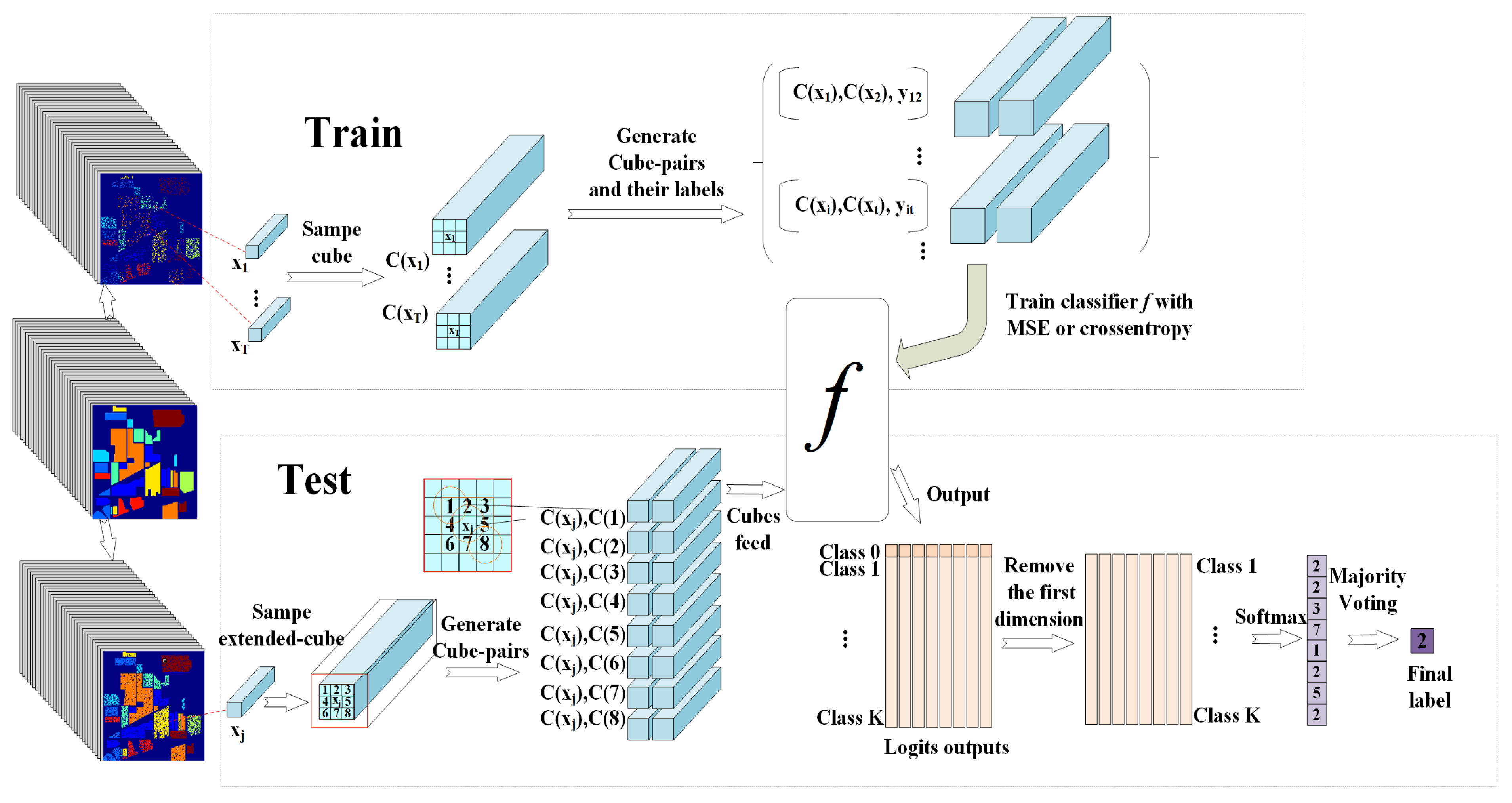
2. The Deep Cube-Pair Network for HSI Classification
2.1. Mathematical Formulation of Commonly Used CNN-Based HSI Classification Architecture
2.2. The Cube-Pair-Based CNN Classification Architecture
2.2.1. The Proposed Architecture
2.2.2. Training and Test Procedures of the Proposed Architecture
2.3. The Proposed Deep Cube-Pair Network
2.3.1. The Structure of the DCPN
2.3.2. Training and Test Schemes of DCPN
3. Experimental Results and Discussion
3.1. Dataset Description
3.2. Experimental Setup
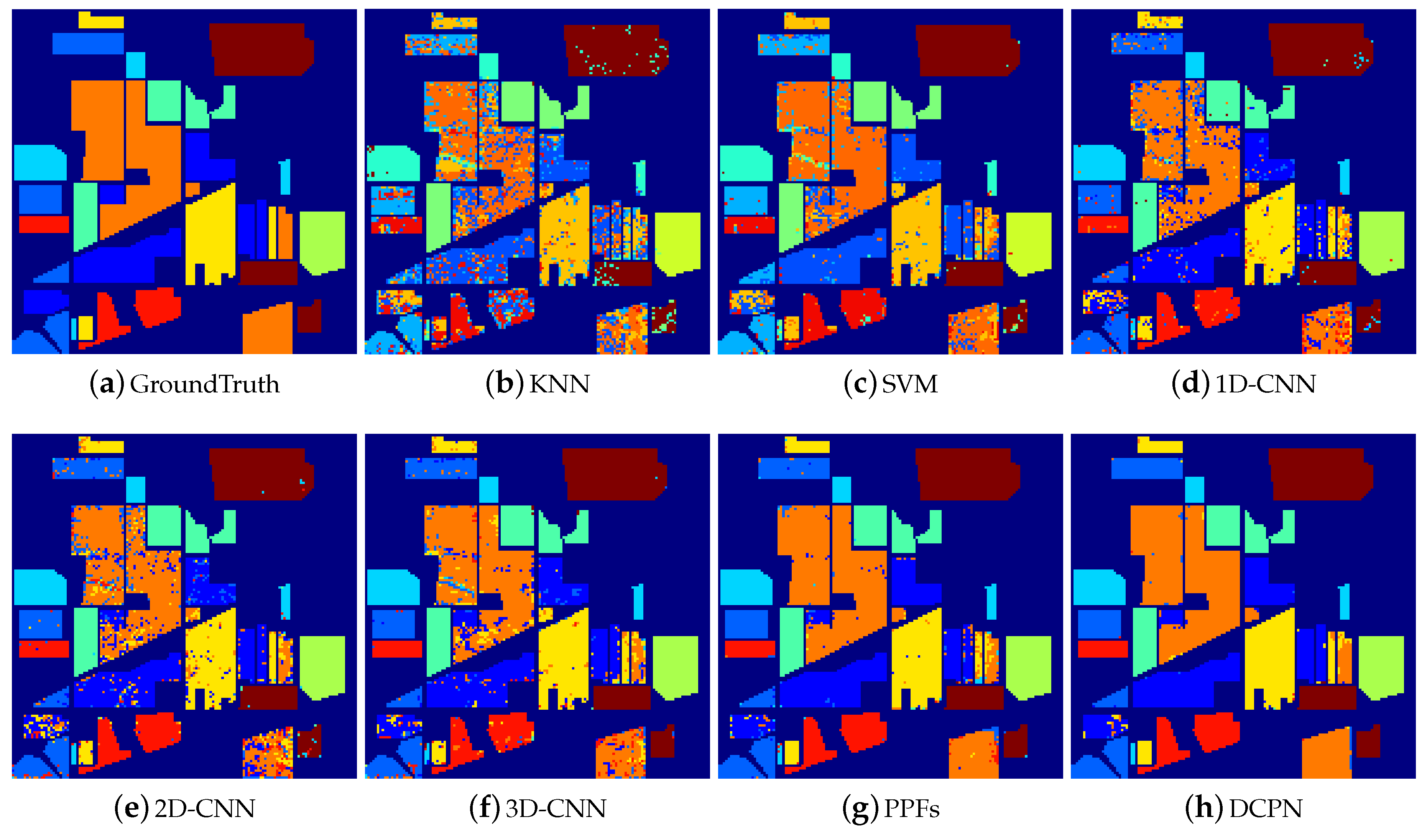
3.3. Comparison with Other Methods
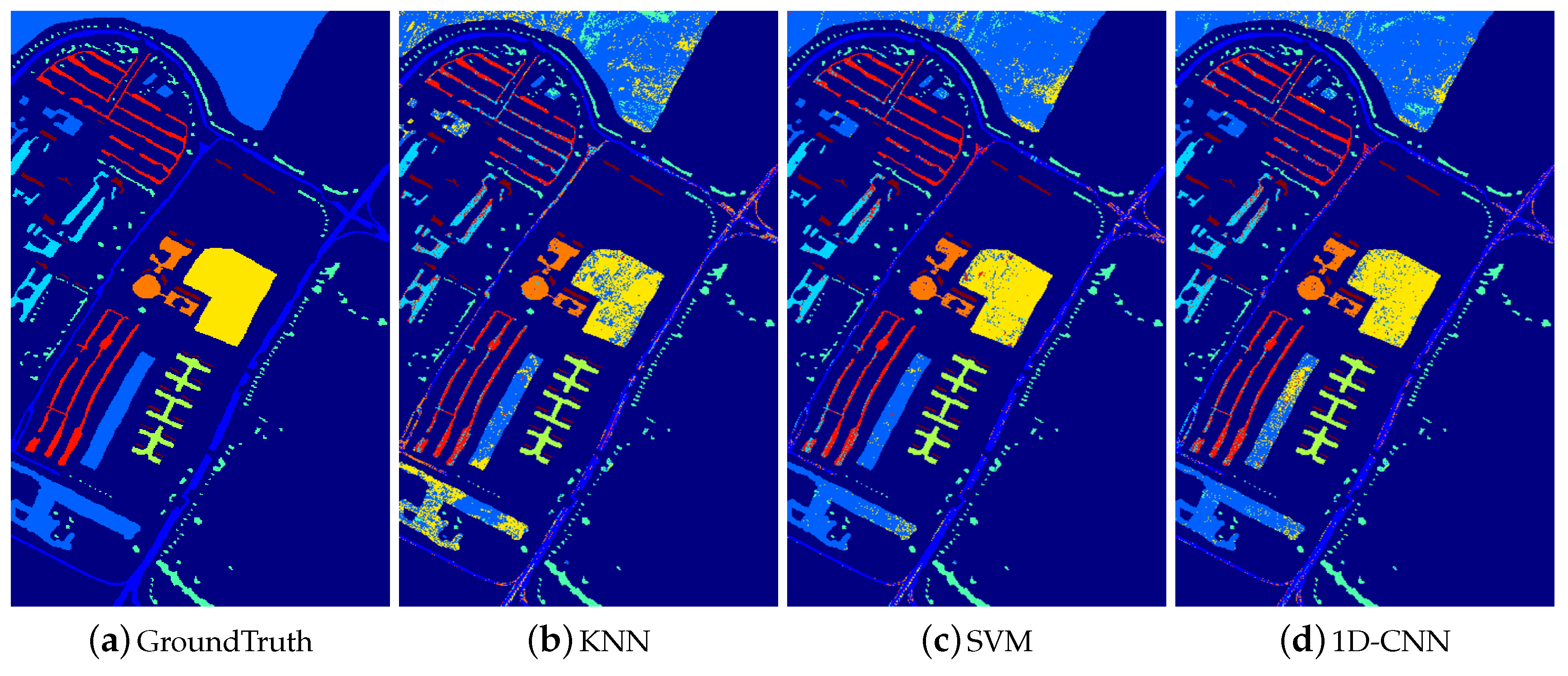
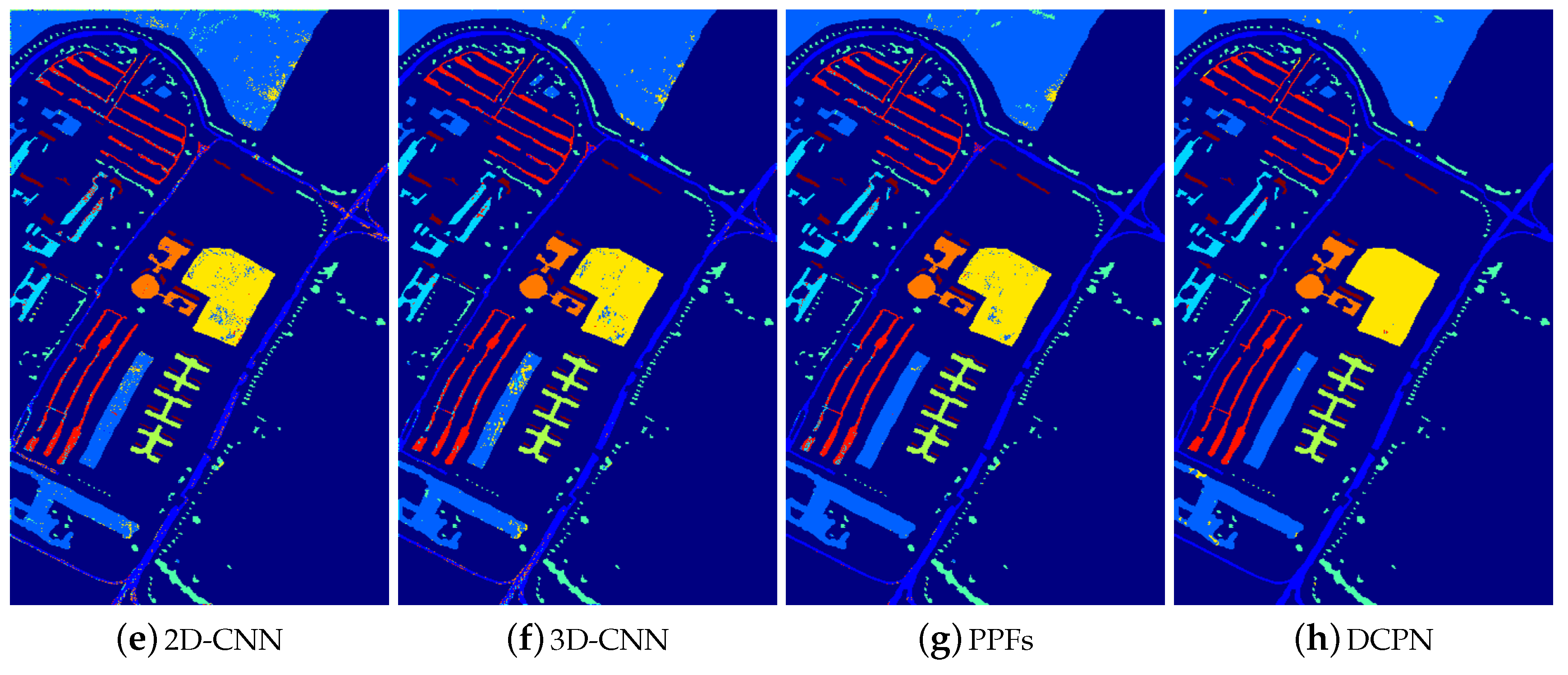
3.3.1. Experimental Results with 200 Training Samples
- (1)
- The majority of deep-learning-based methods have superior performance than the non-deep-learning-based HSI classification methods. Specifically, 2D-CNN, 3D-CNN, PPFs, and DCPN have superior performance than KNN and SVM. These experimental results verify the powerful capability of CNN-based methods for HSI classification.
- (2)
- Compared with the pixel-level-based CNN method, i.e., 1D-CNN, the proposed method improves the overall accuracy dramatically, e.g., 17.42% for the Indiana Pine dataset. Considering the difference between the proposed CNN architecture and pixel-level-based CNN architecture, we attribute the improvement mainly from the integration of 3D local structure and the cube-pair strategy.
- (3)
- It can be seen that pixel-pair-based method (i.e., PPFs) also improves the classification performance of HSI significantly, compared with the pixel-level-based method. This reflects the effectiveness of the pair-based strategy. However, the performance of PPFs inferiors to the proposed method, e.g., nearly 3% for the Indiana Pine dataset, which demonstrates that the local 3D structure is helpful to improve the HSI classification accuracy.
- (4)
- Though cube-based methods including 3D-CNN and 2D-CNN have superior performance than pixel-level-based methods, these methods are inferior to both the proposed method and the pixel-pair-based method. This phenomenon is caused by limited training samples, which makes 3D-CNN and 2D-CNN not well trained. Thus, it generalizes poorly on the test data. On the contrary, both cube-pair and pixel-pair strategies increase the training samples effectively, which guarantee that the network can be well trained.
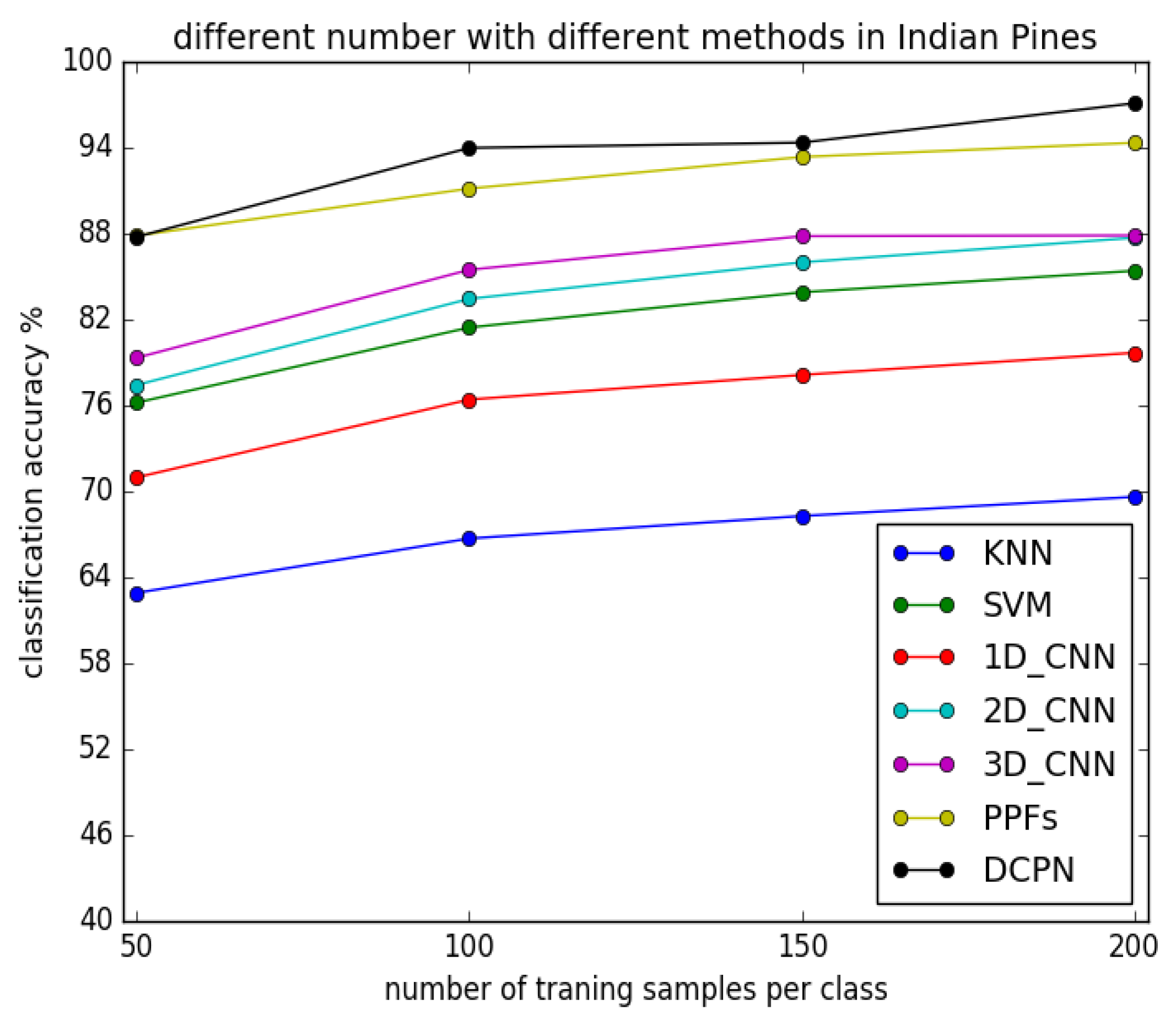
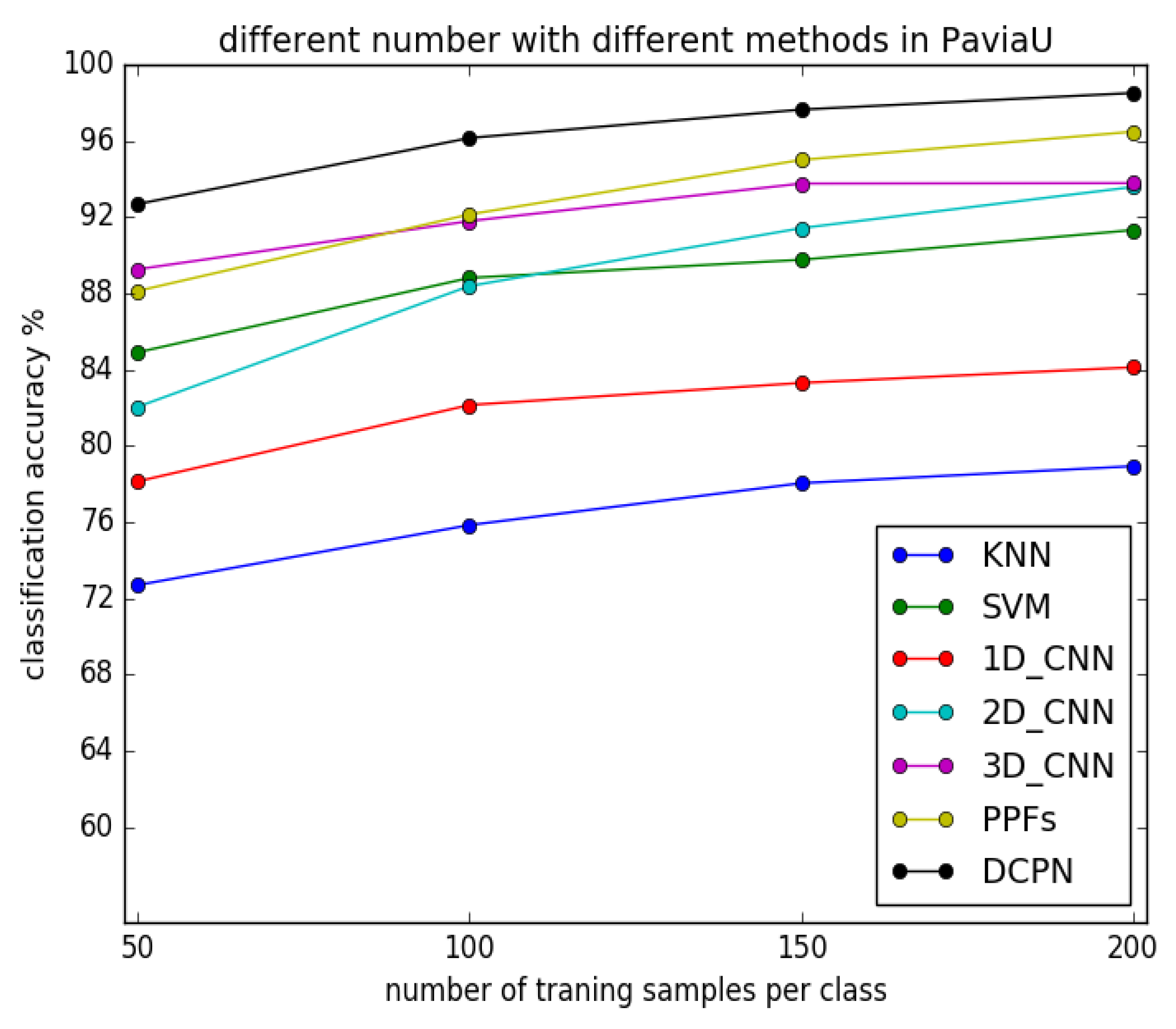
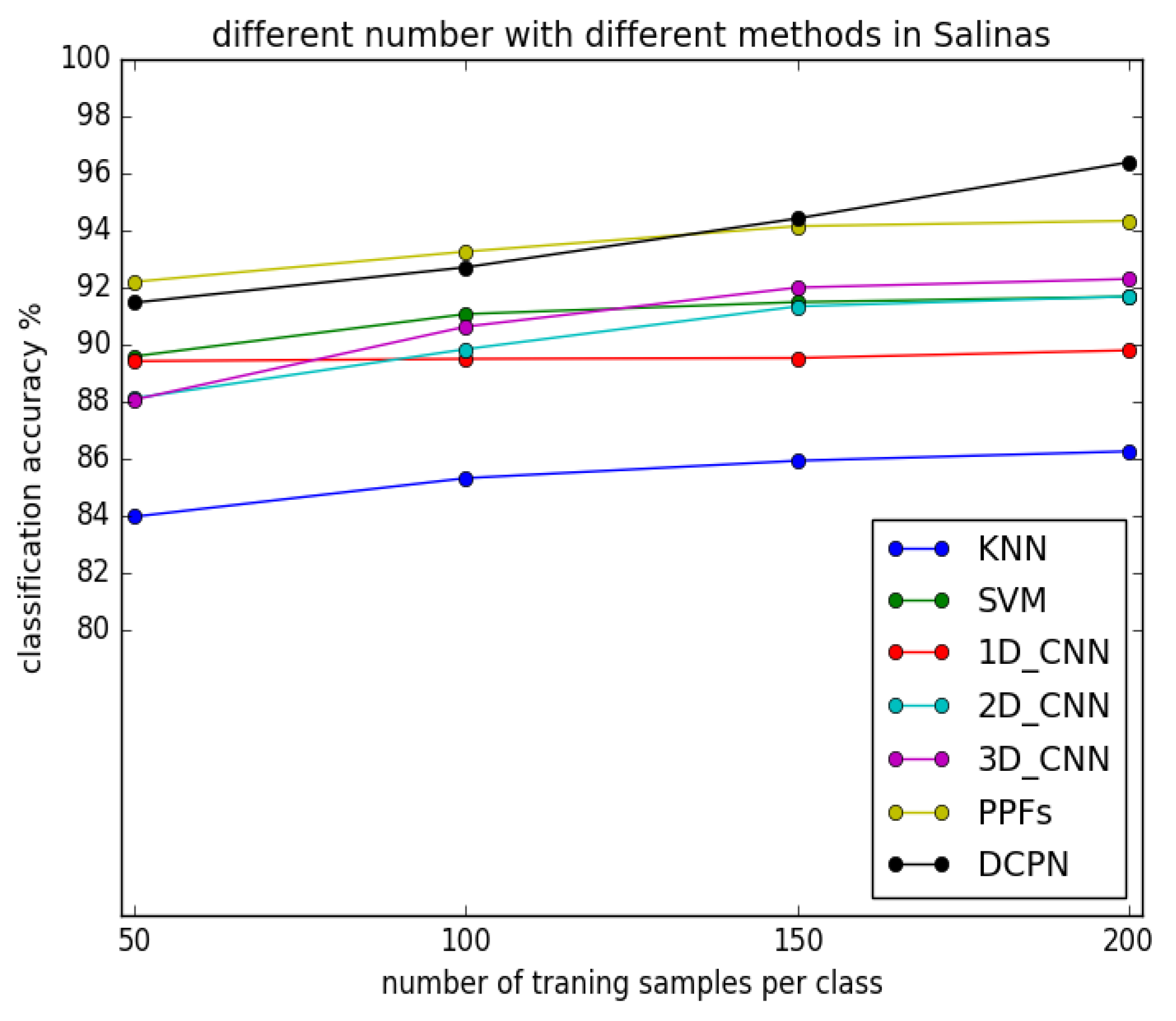
3.3.2. Experimental Results with Different Number of Training Samples
3.4. Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ghamisi, P.; Yokoya, N.; Li, J.; Liao, W.; Liu, S.; Plaza, J.; Rasti, B.; Plaza, A. Advances in Hyperspectral Image and Signal Processing: A Comprehensive Overview of the State of the Art. IEEE Geosci. Remote Sens. Mag. 2018, 5, 37–78. [Google Scholar] [CrossRef]
- Wei, W.; Zhang, L.; Tian, C.; Plaza, A.; Zhang, Y. Structured Sparse Coding-Based Hyperspectral Imagery Denoising With Intracluster Filtering. IEEE Trans. Geosc. Remote Sens. 2017, 55, 6860–6876. [Google Scholar] [CrossRef]
- He, L.; Li, J.; Liu, C.; Li, S. Recent Advances on Spectral-Spatial Hyperspectral Image Classification: An Overview and New Guidelines. IEEE Trans. Geosci. Remote Sens. 2017, 56, 1579–1597. [Google Scholar] [CrossRef]
- Guerra, R.; Barrios, Y.; Díaz, M.; Santos, L.; López, S.; Sarmiento, R. A New Algorithm for the On-Board Compression of Hyperspectral Images. Remote Sens. 2018, 10, 428. [Google Scholar] [CrossRef]
- Fauvel, M.; Tarabalka, Y.; Benediktsson, J.A.; Chanussot, J.; Tilton, J.C. Advances in Spectral-Spatial Classification of Hyperspectral Images. Proc. IEEE 2013, 101, 652–675. [Google Scholar] [CrossRef]
- Zhang, L.; Wei, W.; Shi, Q.; Shen, C.; Hengel, A.v.d.; Zhang, Y. Beyond Low Rank: A Data-Adaptive Tensor Completion Method. arXiv, 2017; arXiv:1708.01008. [Google Scholar]
- Rasti, B.; Ghamisi, P.; Plaza, J.; Plaza, A. Fusion of Hyperspectral and LiDAR Data Using Sparse and Low-Rank Component Analysis. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6354–6365. [Google Scholar] [CrossRef]
- Zhang, L.; Wei, W.; Zhang, Y.; Shen, C.; van den Hengel, A.; Shi, Q. Cluster Sparsity Field: An Internal Hyperspectral Imagery Prior for Reconstruction. Int. J. Comput. Vis. 2018, 1–25. [Google Scholar] [CrossRef]
- Lanaras, C.; Baltsavias, E.; Schindler, K. Hyperspectral Super-Resolution with Spectral Unmixing Constraints. Remote Sens. 2017, 9, 1196. [Google Scholar] [CrossRef]
- Yang, J.; Zhao, Y.; Yi, C.; Chan, C.W. No-Reference Hyperspectral Image Quality Assessment via Quality-Sensitive Features Learning. Remote Sens. 2017, 9, 305. [Google Scholar] [CrossRef]
- Transon, J.; d’Andrimont, R.; Maugnard, A.; Defourny, P. Survey of Hyperspectral Earth Observation Applications from Space in the Sentinel-2 Context. Remote Sens. 2018, 10, 157. [Google Scholar] [CrossRef]
- Zhang, L.; Wei, W.; Zhang, Y.; Shen, C.; Hengel, A.V.D.; Shi, Q. Dictionary Learning for Promoting Structured Sparsity in Hyperspectral Compressive Sensing. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7223–7235. [Google Scholar] [CrossRef]
- Li, J.; Bioucas-Dias, J.M.; Plaza, A.; Liu, L. Robust Collaborative Nonnegative Matrix Factorization for Hyperspectral Unmixing. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6076–6090. [Google Scholar] [CrossRef]
- Zhang, L.; Wei, W.; Tian, C.; Li, F.; Zhang, Y. Exploring structured sparsity by a reweighted laplace prior for hyperspectral compressive sensing. IEEE Trans. Image Process. 2016, 25, 4974–4988. [Google Scholar] [CrossRef]
- Ertürk, A.; Plaza, A. Informative Change Detection by Unmixing for Hyperspectral Images. IEEE Geosci. Remote Sens. Lett. 2017, 12, 1252–1256. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, Y.; Yan, H.; Gao, Y.; Wei, W. Salient Object Detection in Hyperspectral Imagery using Multi-scale Spectral-Spatial Gradient. Neurocomputing 2018, 291, 215–225. [Google Scholar] [CrossRef]
- Xue, J.; Zhao, Y.; Liao, W.; Kong, S.G. Joint Spatial and Spectral Low-Rank Regularization for Hyperspectral Image Denoising. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1940–1958. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Bruzzone, L. Kernel-based methods for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1351–1362. [Google Scholar] [CrossRef]
- Wang, Q.; Lin, J.; Yuan, Y. Salient Band Selection for Hyperspectral Image Classification via Manifold Ranking. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 1279. [Google Scholar] [CrossRef] [PubMed]
- Rajadell, O.; García-Sevilla, P.; Pla, F. Spectral–Spatial Pixel Characterization Using Gabor Filters for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2013, 10, 860–864. [Google Scholar] [CrossRef]
- Wang, Q.; Meng, Z.; Li, X. Locality Adaptive Discriminant Analysis for Spectral–Spatial Classification of Hyperspectral Images. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2077–2081. [Google Scholar] [CrossRef]
- Ahmad, M.; Khan, A.M.; Hussain, R. Graph-based spatial–spectral feature learning for hyperspectral image classification. IET Image Process. 2017, 11, 1310–1316. [Google Scholar] [CrossRef]
- Majdar, R.S.; Ghassemian, H. A probabilistic SVM approach for hyperspectral image classification using spectral and texture features. Int. J. Remote Sens. 2017, 38, 4265–4284. [Google Scholar] [CrossRef]
- Samat, A.; Li, J.; Liu, S.; Du, P.; Miao, Z.; Luo, J. Improved hyperspectral image classification by active learning using pre-designed mixed pixels. Pattern Recognit. 2016, 51, 43–58. [Google Scholar] [CrossRef]
- Medjahed, S.A.; Saadi, T.A.; Benyettou, A.; Ouali, M. Gray Wolf Optimizer for hyperspectral band selection. Appl. Soft Comput. 2016, 40, 178–186. [Google Scholar] [CrossRef]
- Wang, Q.; Wan, J.; Yuan, Y. Locality Constraint Distance Metric Learning for Traffic Congestion Detection. Pattern Recognit. 2017, 75. [Google Scholar] [CrossRef]
- Liu, L.; Wang, P.; Shen, C.; Wang, L.; Van Den Hengel, A.; Wang, C.; Shen, H.T. Compositional model based fisher vector coding for image classification. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2335–2348. [Google Scholar] [CrossRef] [PubMed]
- Blanzieri, E.; Melgani, F. Nearest Neighbor Classification of Remote Sensing Images With the Maximal Margin Principle. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1804–1811. [Google Scholar] [CrossRef]
- Ricardo, D.D.S.; Pedrini, H. Hyperspectral data classification improved by minimum spanning forests. J. Appl. Remote Sens. 2016, 10, 025007. [Google Scholar]
- Guccione, P.; Mascolo, L.; Appice, A. Iterative Hyperspectral Image Classification Using Spectral–Spatial Relational Features. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3615–3627. [Google Scholar] [CrossRef]
- Li, J.; Bioucas-Dias, J.M.; Plaza, A. Spectral–Spatial Hyperspectral Image Segmentation Using Subspace Multinomial Logistic Regression and Markov Random Fields. IEEE Trans. Geosci. Remote Sens. 2012, 50, 809–823. [Google Scholar] [CrossRef]
- Appice, A.; Guccione, P.; Malerba, D. Transductive hyperspectral image classification: toward integrating spectral and relational features via an iterative ensemble system. Mach. Learn. 2016, 103, 343–375. [Google Scholar] [CrossRef]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef]
- Sharma, S.; Buddhiraju, K.M. Spatial–spectral ant colony optimization for hyperspectral image classification. Int. J. Remote Sens. 2018, 39, 2702–2717. [Google Scholar] [CrossRef]
- Lopatin, J.; Fassnacht, F.E.; Kattenborn, T.; Schmidtlein, S. Mapping plant species in mixed grassland communities using close range imaging spectroscopy. Remote Sens. Environ. 2017, 201, 12–23. [Google Scholar] [CrossRef]
- Xue, Z.; Du, P.; Su, H. Harmonic Analysis for Hyperspectral Image Classification Integrated With PSO Optimized SVM. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2131–2146. [Google Scholar] [CrossRef]
- Zabalza, J.; Ren, J.; Yang, M.; Zhang, Y.; Wang, J.; Marshall, S.; Han, J. Novel Folded-PCA for improved feature extraction and data reduction with hyperspectral imaging and SAR in remote sensing. ISPRS J. Photogramm. Remote Sens. 2014, 93, 112–122. [Google Scholar] [CrossRef]
- Mura, M.D.; Villa, A.; Benediktsson, J.A.; Chanussot, J.; Bruzzone, L. Classification of Hyperspectral Images by Using Extended Morphological Attribute Profiles and Independent Component Analysis. IEEE Geosci. Remote Sens. Lett. 2011, 8, 542–546. [Google Scholar] [CrossRef]
- Nielsen, A.A. Kernel Maximum Autocorrelation Factor and Minimum Noise Fraction Transformations. IEEE Trans. Image Process. 2011, 20, 612. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Wu, G.; Zhang, F.; Du, Q. Hyperspectral Image Classification Using Deep Pixel-Pair Features. IEEE Trans. Geosci. Remote Sens. 2016, 55, 844–853. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Y.; Zhang, Y.; Shen, Q. Spectral-spatial classification of hyperspectral imagery using a dual-channel convolutional neural network. Remote Sens. Lett. 2017, 8, 438–447. [Google Scholar] [CrossRef]
- Hu, W.; Huang, Y.; Wei, L.; Zhang, F.; Li, H. Deep Convolutional Neural Networks for Hyperspectral Image Classification. J. Sens. 2015, 2015, 258619. [Google Scholar] [CrossRef]
- Wang, P.; Wu, Q.; Shen, C.; Dick, A.; Hengel, A.V.D. FVQA: Fact-based Visual Question Answering. IEEE Trans. Pattern Anal. Mach. Intell. 2017. [Google Scholar] [CrossRef] [PubMed]
- Othman, E.; Bazi, Y.; Alajlan, N.; Alhichri, H.; Melgani, F. Using convolutional features and a sparse autoencoder for land-use scene classification. Int. J. Remote Sens. 2016, 37, 2149–2167. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Shen, Q. Spectral-Spatial Classification of Hyperspectral Imagery with 3D Convolutional Neural Network. Remote Sens. 2017, 9, 67. [Google Scholar] [CrossRef]
- Slavkovikj, V.; Verstockt, S.; Neve, W.D.; Hoecke, S.V.; Walle, R.V.D. Hyperspectral Image Classification with Convolutional Neural Networks. In Proceedings of the Acm International Conference on Multimedia, Brisbane, Australia, 26–30 October 2015; pp. 1159–1162. [Google Scholar]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep Feature Extraction and Classification of Hyperspectral Images Based on Convolutional Neural Networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep Learning-Based Classification of Hyperspectral Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 7, 2094–2107. [Google Scholar] [CrossRef]
- Wang, P.; Cao, Y.; Shen, C.; Liu, L.; Shen, H.T. Temporal Pyramid Pooling-Based Convolutional Neural Network for Action Recognition. IEEE Trans. Circuits Syst. Video Technol. 2017, 27, 2613–2622. [Google Scholar] [CrossRef]
- Zhang, X.; Liang, Y.; Li, C.; Ning, H.; Jiao, L.; Zhou, H. Recursive Autoencoders-Based Unsupervised Feature Learning for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1928–1932. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, L.; Wei, W.; Zhang, Y. When Low Rank Representation Based Hyperspectral Imagery Classification Meets Segmented Stacked Denoising Auto-Encoder Based Spatial-Spectral Feature. Remote Sens. 2018, 10, 284. [Google Scholar] [CrossRef]
- Wang, Q.; Gao, J.; Yuan, Y. Embedding Structured Contour and Location Prior in Siamesed Fully Convolutional Networks for Road Detection. IEEE Trans. Intell. Transp. Syst. 2018, 19, 230–241. [Google Scholar] [CrossRef]
- Zhong, P.; Gong, Z.; Li, S.; Schönlieb, C.B. Learning to Diversify Deep Belief Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, PP, 1–15. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, X.; Jia, X. Spectral–Spatial Classification of Hyperspectral Data Based on Deep Belief Network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2381–2392. [Google Scholar] [CrossRef]
- Lin, M.; Chen, Q.; Yan, S. Network In Network. arXiv, 2013; arXiv:1312.4400. [Google Scholar]
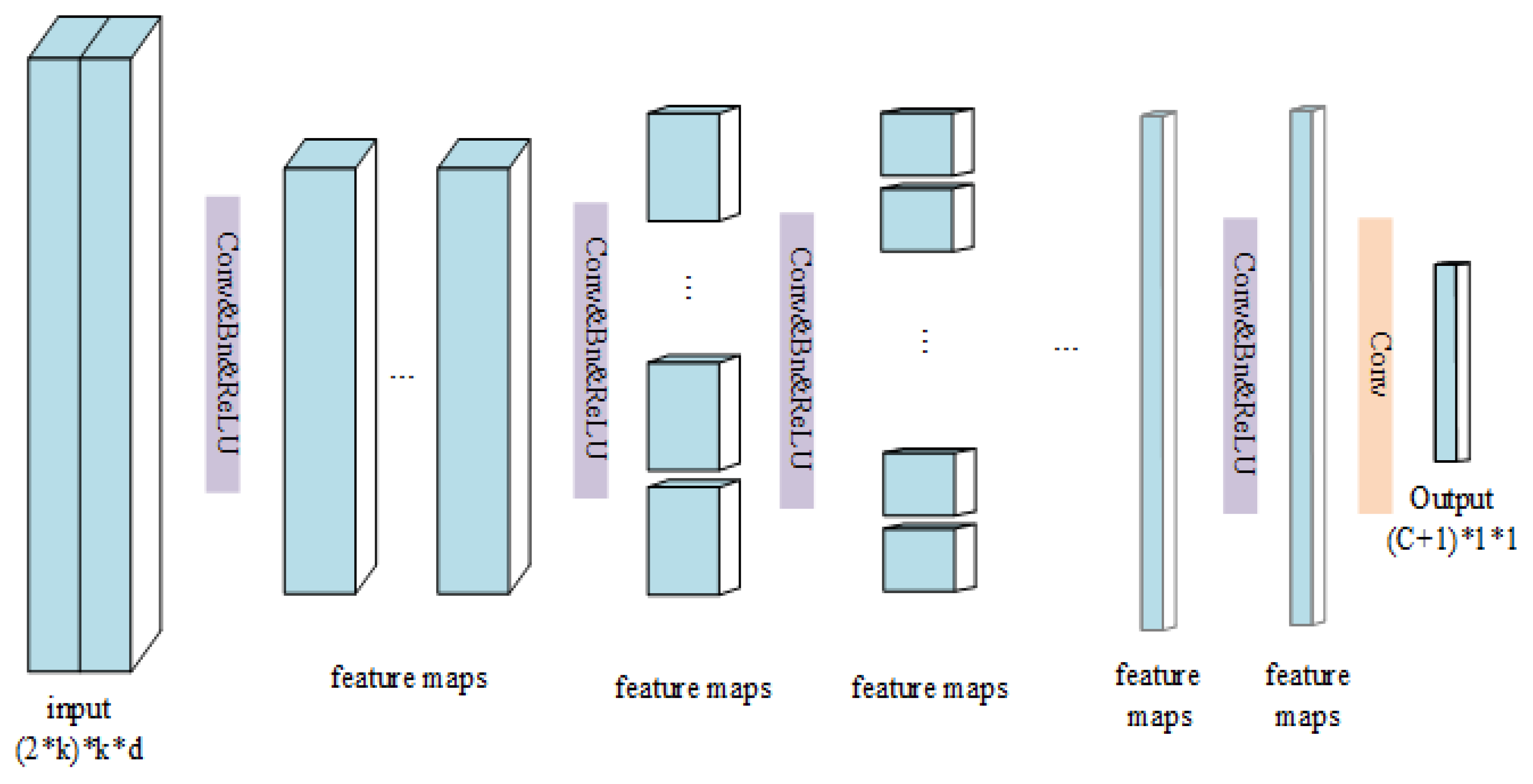


| Layer ID. | Input Size | Kernel Size | Stride | Output Size | Convolution Kernel Num |
|---|---|---|---|---|---|
| 1 | 6 | ||||
| 2 | 6 | ||||
| 3 | 12 | ||||
| 4 | 24 | ||||
| 5 | 48 | ||||
| 6 | 48 | ||||
| 7 | 96 | ||||
| 8 | 96 | ||||
| 9 | 10 |
| No. | Indiana Pines | PaviaU | Salinas | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Class Name | Train | Test | Class Name | Train | Test | Class Name | Train | Test | |
| 1 | Corn-notill | 200 | 1228 | Asphalt | 200 | 6431 | Brocoli_1 | 200 | 1809 |
| 2 | Corn-mintill | 200 | 630 | Meadows | 200 | 18,449 | Brocoli_2 | 200 | 3526 |
| 3 | Grass-pasture | 200 | 283 | Gravel | 200 | 1899 | Fallow | 200 | 1776 |
| 4 | Grass-trees | 200 | 530 | Trees | 200 | 2864 | Fallow_plow | 200 | 1194 |
| 5 | Hay-win. | 200 | 278 | Sheets | 200 | 1145 | Fallow_smooth | 200 | 2478 |
| 6 | Soy.-notill | 200 | 772 | Bare Soil | 200 | 4829 | Stubble | 200 | 3759 |
| 7 | Soy.-mintill | 200 | 2255 | Bitumen | 200 | 1130 | Celery | 200 | 3379 |
| 8 | Soy.-clean | 200 | 393 | Bricks | 200 | 3482 | Grapes | 200 | 11,071 |
| 9 | Woods | 200 | 1065 | Shadows | 200 | 747 | Soil_vinyard | 200 | 6003 |
| 10 | Corn_weeds | 200 | 3078 | ||||||
| 11 | Lettuce_4wk | 200 | 868 | ||||||
| 12 | Lettuce_5wk | 200 | 1727 | ||||||
| 13 | Lettuce_6wk | 200 | 716 | ||||||
| 14 | Lettuce_7wk | 200 | 870 | ||||||
| 15 | Vinyard_un. | 200 | 7068 | ||||||
| 16 | Vinyard_ve. | 200 | 1607 | ||||||
| Sum | 1800 | 7434 | 1800 | 40,976 | 3200 | 50,929 | |||
| No. | KNN | SVM | 1D-CNN | 2D-CNN | 3D-CNN | PPFs | DCPN |
|---|---|---|---|---|---|---|---|
| 1 | 63.07 | 80.92 | 74.56 | 84.53 | 83.70 | 92.99 | 95.32 |
| 2 | 61.38 | 85.10 | 59.34 | 74.70 | 73.06 | 96.66 | 98.55 |
| 3 | 91.52 | 96.61 | 84.21 | 89.42 | 93.01 | 98.58 | 99.68 |
| 4 | 98.81 | 99.06 | 95.07 | 98.44 | 98.82 | 100 | 99.87 |
| 5 | 99.46 | 99.68 | 98.58 | 99.89 | 99.75 | 100 | 100 |
| 6 | 74.70 | 86.76 | 65.06 | 74.15 | 76.49 | 96.26 | 97.91 |
| 7 | 51.74 | 74.17 | 84.66 | 92.33 | 93.92 | 87.80 | 94.42 |
| 8 | 57.18 | 89.24 | 66.27 | 78.99 | 76.19 | 98.98 | 98.93 |
| 9 | 92.66 | 98.62 | 98.77 | 99.56 | 99.33 | 99.81 | 99.86 |
| OA | 69.62 | 85.40 | 79.68 | 87.71 | 87.87 | 94.34 | 97.10 |
| No. | KNN | SVM | 1D-CNN | 2D-CNN | 3D-CNN | PPFs | DCPN |
|---|---|---|---|---|---|---|---|
| 1 | 75.45 | 86.35 | 94.32 | 97.84 | 97.80 | 97.42 | 98.95 |
| 2 | 76.51 | 92.38 | 95.38 | 96.71 | 98.06 | 95.76 | 98.24 |
| 3 | 76.94 | 86.08 | 60.14 | 84.68 | 82.01 | 94.05 | 97.19 |
| 4 | 92.21 | 96.76 | 74.96 | 91.68 | 91.49 | 97.52 | 97.81 |
| 5 | 99.38 | 99.65 | 99.07 | 98.57 | 99.77 | 100 | 100 |
| 6 | 76.54 | 92.35 | 68.66 | 83.82 | 85.02 | 99.13 | 98.94 |
| 7 | 92.12 | 93.95 | 56.51 | 91.02 | 82.12 | 96.19 | 98.99 |
| 8 | 76.12 | 86.44 | 75.05 | 90.71 | 90.03 | 93.62 | 98.87 |
| 9 | 99.95 | 99.99 | 99.01 | 99.27 | 99.92 | 99.60 | 99.75 |
| OA | 78.93 | 91.32 | 84.12 | 93.58 | 93.76 | 96.48 | 98.51 |
| No. | KNN | SVM | 1D-CNN | 2D-CNN | 3D-CNN | PPFs | DCPN |
|---|---|---|---|---|---|---|---|
| 1 | 98.10 | 99.57 | 99.93 | 98.06 | 99.81 | 100 | 99.86 |
| 2 | 99.38 | 99.78 | 99.27 | 99.42 | 99.91 | 99.88 | 99.79 |
| 3 | 99.32 | 99.66 | 98.69 | 97.71 | 98.36 | 99.60 | 99.66 |
| 4 | 99.66 | 99.56 | 97.26 | 99.53 | 99.37 | 99.49 | 99.71 |
| 5 | 99.26 | 97.69 | 97.85 | 97.75 | 98.13 | 98.34 | 99.65 |
| 6 | 99.51 | 99.78 | 99.76 | 99.49 | 99.87 | 99.97 | 99.97 |
| 7 | 99.08 | 99.54 | 98.82 | 99.29 | 98.13 | 100 | 99.91 |
| 8 | 64.69 | 83.79 | 81.30 | 91.42 | 85.09 | 88.68 | 89.89 |
| 9 | 96.91 | 99.34 | 99.32 | 99.06 | 99.32 | 98.33 | 99.92 |
| 10 | 90.21 | 94.49 | 95.66 | 90.29 | 91.89 | 98.60 | 98.42 |
| 11 | 97.43 | 98.29 | 98.73 | 89.82 | 93.85 | 99.54 | 99.48 |
| 12 | 99.92 | 99.92 | 98.81 | 96.24 | 97.99 | 100 | 99.91 |
| 13 | 98.32 | 99.37 | 99.20 | 91.24 | 98.04 | 99.44 | 100 |
| 14 | 94.21 | 98.77 | 93.76 | 90.91 | 95.07 | 98.96 | 99.71 |
| 15 | 67.82 | 70.60 | 66.47 | 72.84 | 77.08 | 83.53 | 91.41 |
| 16 | 98.48 | 99.04 | 98.80 | 91.58 | 97.52 | 99.31 | 99.28 |
| OA | 86.26 | 91.68 | 89.80 | 91.69 | 92.30 | 94.80 | 96.39 |
| k | 1 | 3 | 5 | |
|---|---|---|---|---|
| ecs | ||||
| 3 | 94.45 | / | / | |
| 5 | 94.71 | 96.18 | / | |
| 7 | 95.57 | 97.10 | 96.16 | |
| 9 | / | 97.04 | 96.88 | |
| 11 | / | / | 97.21 | |
| Layers | 3 | 5 | 7 | 10 |
|---|---|---|---|---|
| 3D-CNN | 87.87 | 83.61 | 77.79 | 75.86 |
| DCPN | 93.40 | 96.22 | 97.09 | 97.10 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, W.; Zhang, J.; Zhang, L.; Tian, C.; Zhang, Y. Deep Cube-Pair Network for Hyperspectral Imagery Classification. Remote Sens. 2018, 10, 783. https://doi.org/10.3390/rs10050783
Wei W, Zhang J, Zhang L, Tian C, Zhang Y. Deep Cube-Pair Network for Hyperspectral Imagery Classification. Remote Sensing. 2018; 10(5):783. https://doi.org/10.3390/rs10050783
Chicago/Turabian StyleWei, Wei, Jinyang Zhang, Lei Zhang, Chunna Tian, and Yanning Zhang. 2018. "Deep Cube-Pair Network for Hyperspectral Imagery Classification" Remote Sensing 10, no. 5: 783. https://doi.org/10.3390/rs10050783
APA StyleWei, W., Zhang, J., Zhang, L., Tian, C., & Zhang, Y. (2018). Deep Cube-Pair Network for Hyperspectral Imagery Classification. Remote Sensing, 10(5), 783. https://doi.org/10.3390/rs10050783