Machine Learning Automatic Model Selection Algorithm for Oceanic Chlorophyll-a Content Retrieval
Abstract
1. Introduction
2. Materials and Methods
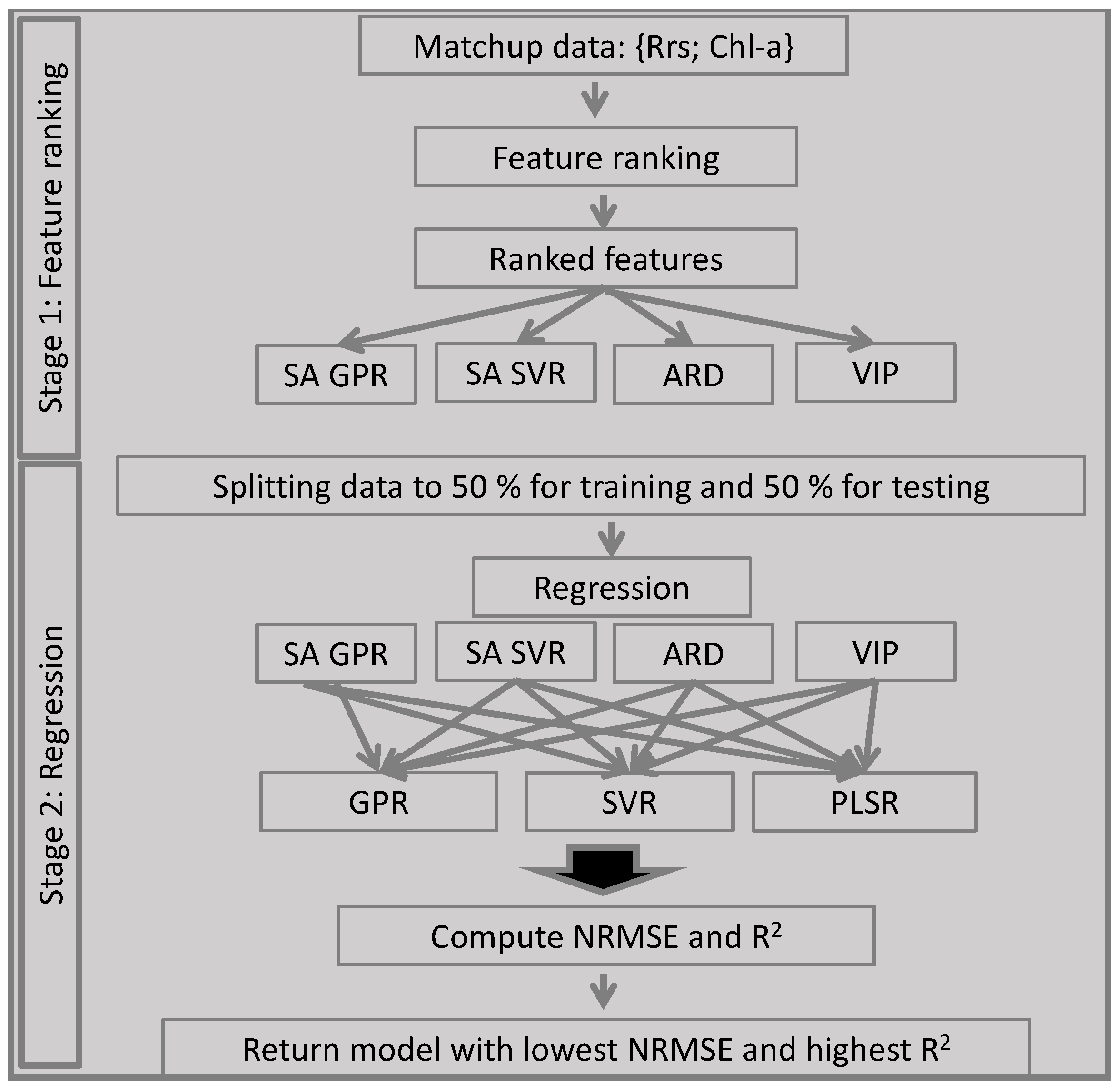
2.1. The Automatic Model Selection Algorithm
2.1.1. The Concept of the AMSA
2.2. Demonstration of an AMSA Implementation
2.2.1. The Matchup Data
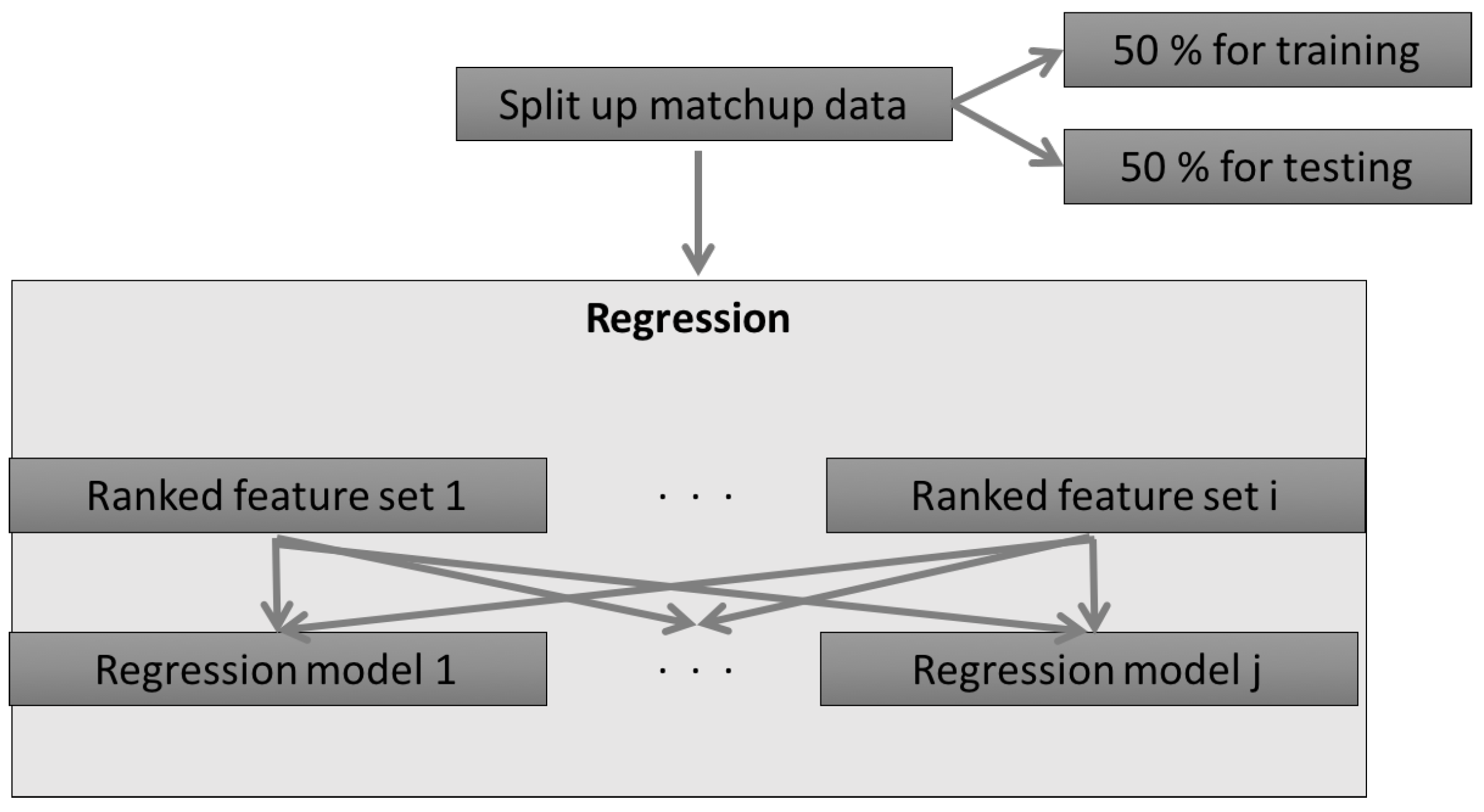
2.2.2. Regression Models
2.2.3. Feature Ranking Methods
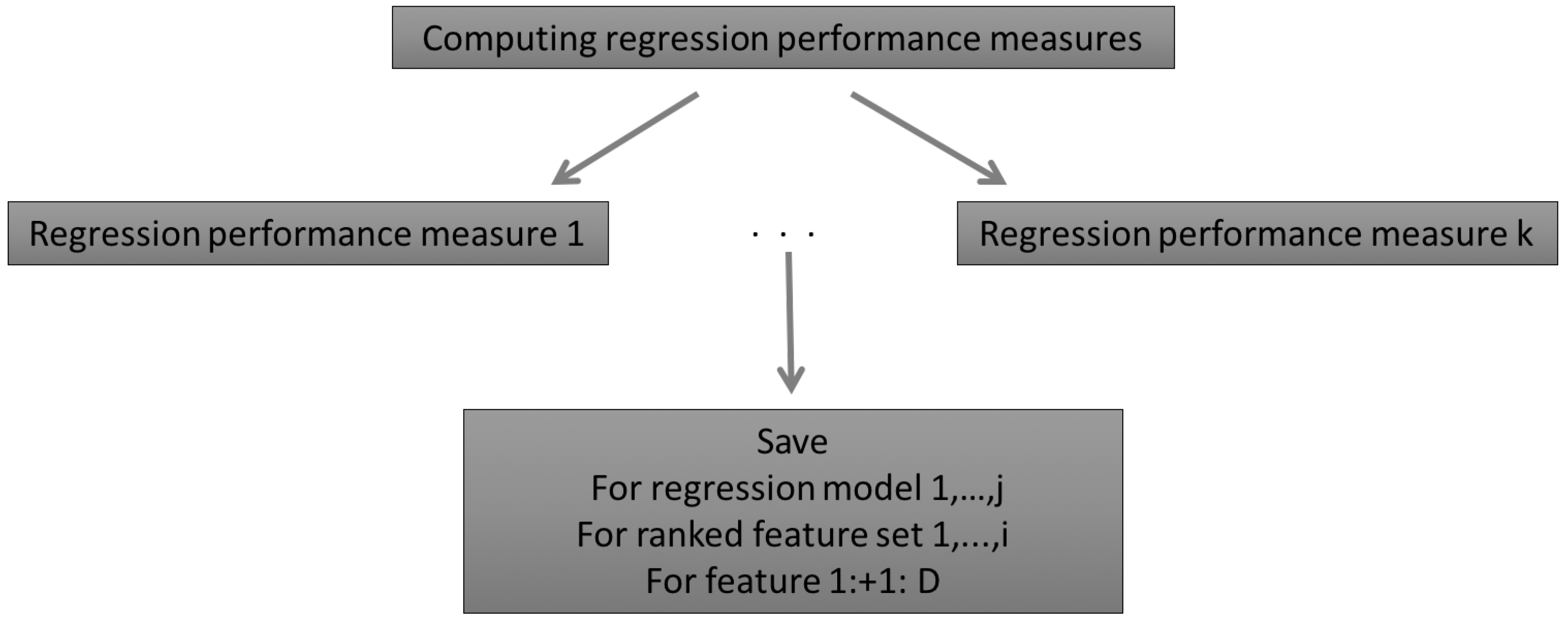
2.2.4. Regression Performance Measures
2.2.5. Summary of the AMSA Approach
2.3. Data
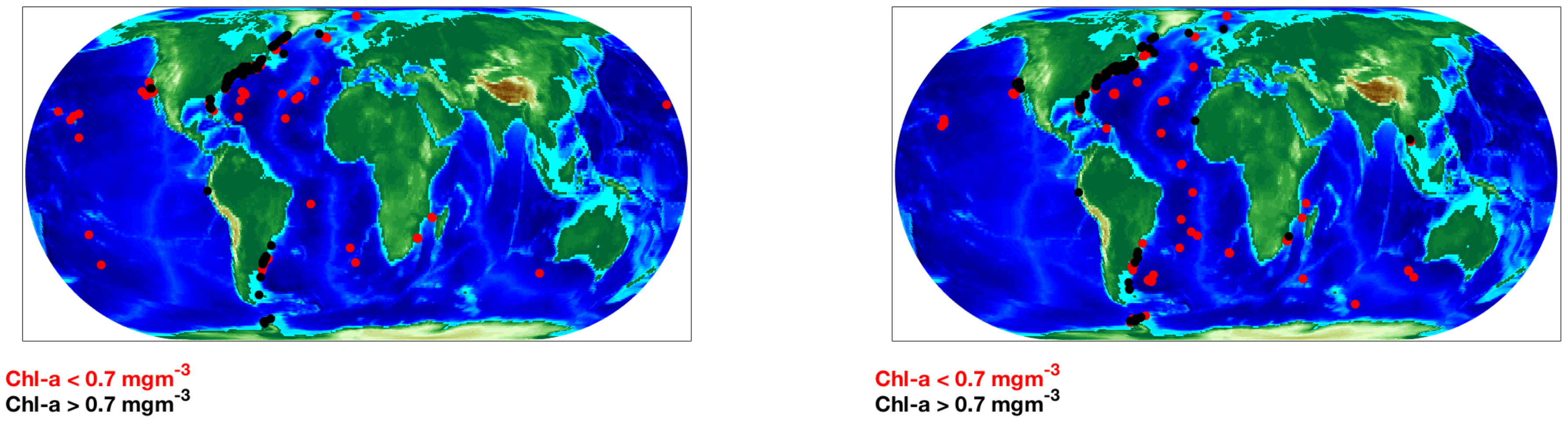
2.3.1. Training Data
2.3.2. Test Data
3. Results
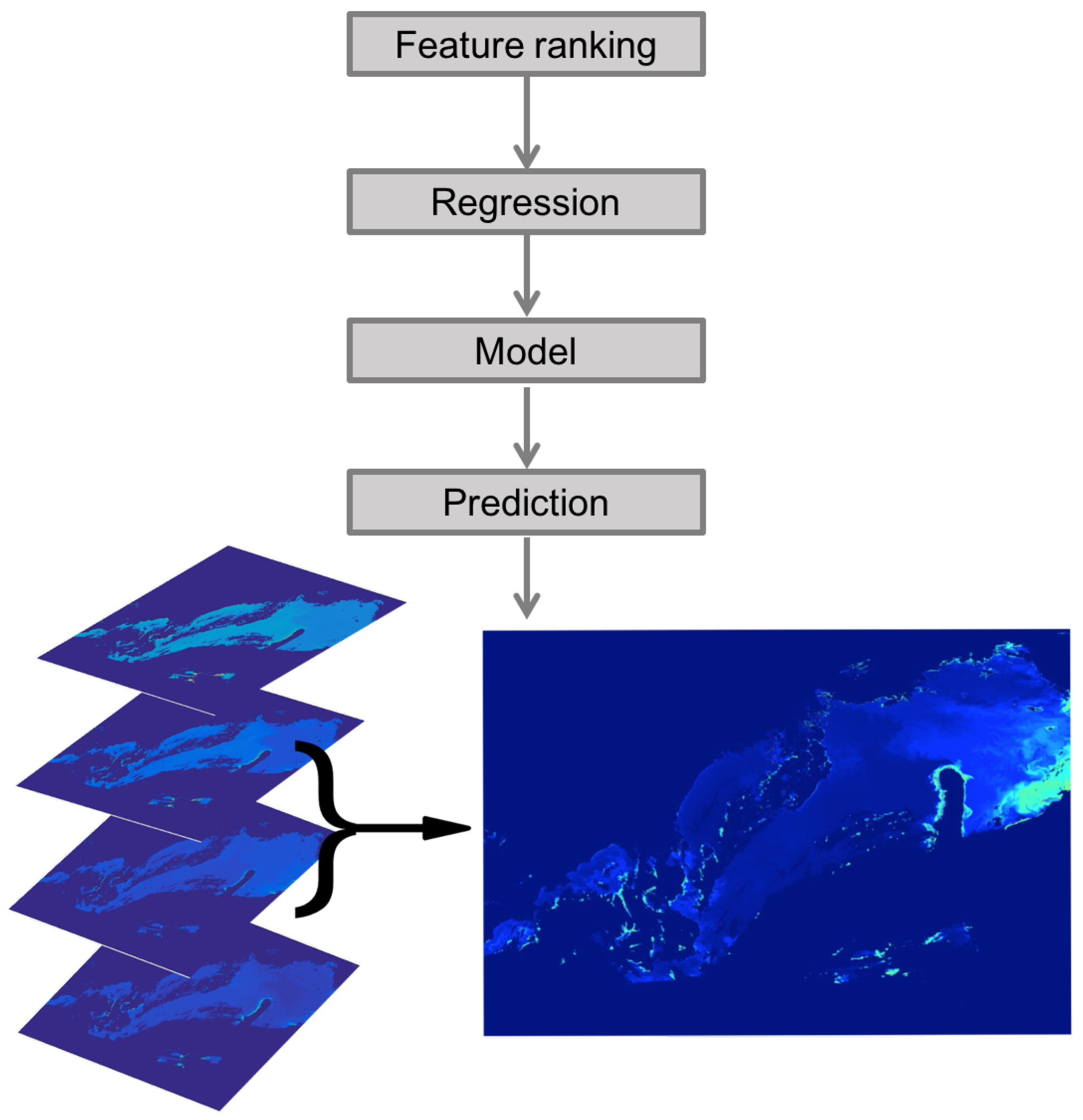
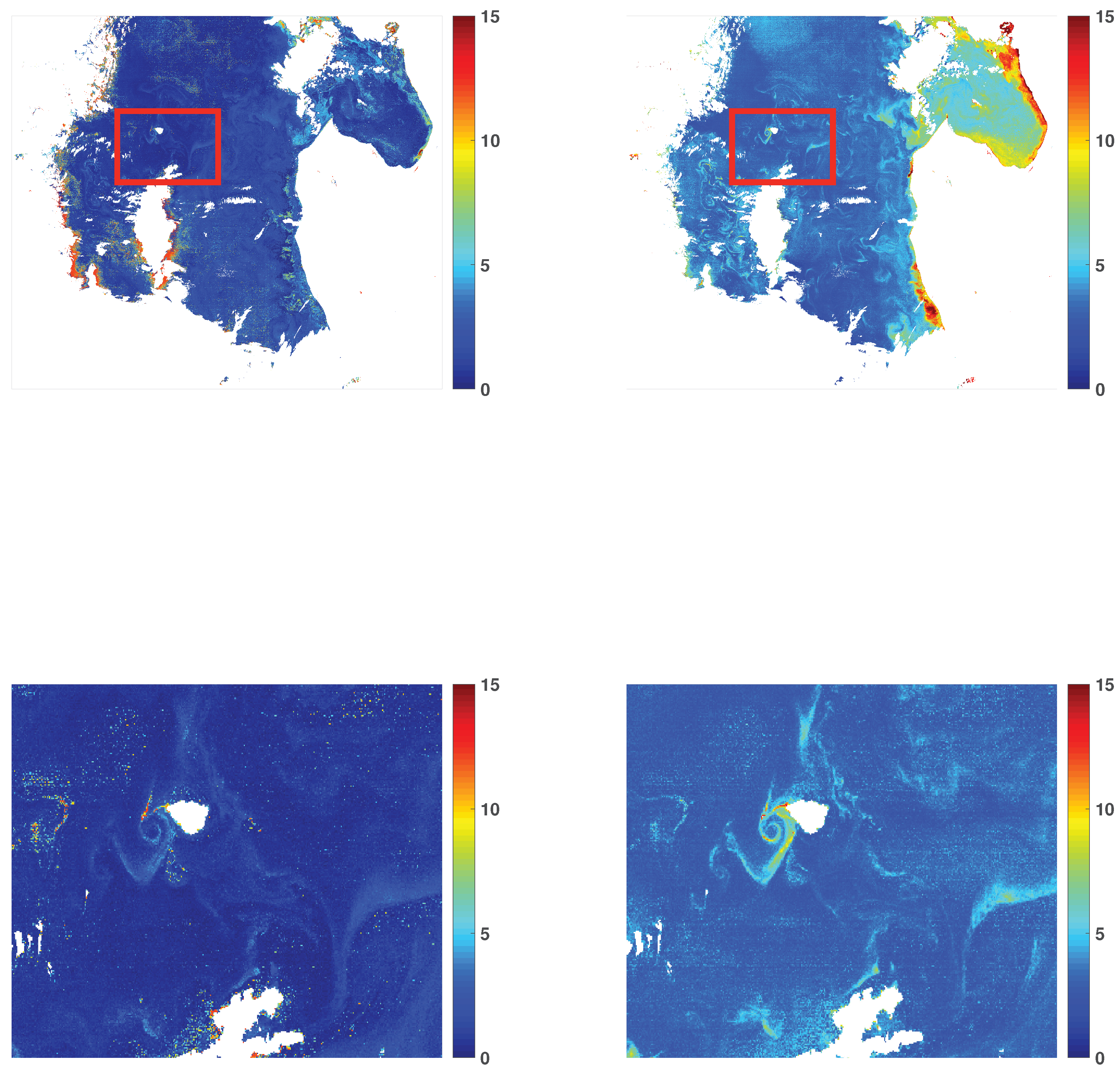
3.1. Chlorophyll-a Maps
3.2. Cross Validation
3.3. Visual Illustrations
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kahru, M.; Mitchell, B.G. Ocean Color Reveals Increased Blooms in Various Parts of the World. Eos Trans. Am. Geophys. Union 2008, 89, 170. [Google Scholar] [CrossRef]
- McClain, C.R. A Decade of Satellite Ocean Color Observations. Ann. Rev. Mar. Sci. 2009, 1, 19–42. [Google Scholar] [CrossRef] [PubMed]
- Gholizadeh, M.H.; Melesse, A.M.; Reddi, L. A Comprehensive Review on Water Quality Parameters Estimation Using Remote Sensing Techniques. Sensors 2016, 16, 1298. [Google Scholar] [CrossRef] [PubMed]
- Wilson, C. The rocky road from research to operations for satellite ocean-colour data in fishery management. ICES J. Mar. Sci. 2011, 68, 677–686. [Google Scholar] [CrossRef]
- Ha, N.T.T.; Koike, K.; Nhuan, M.T. Improved Accuracy of Chlorophyll-a Concentration Estimates from MODIS Imagery Using a Two-Band Ratio Algorithm and Geostatistics: As Applied to the Monitoring of Eutrophication Processes over Tien Yen Bay (Northern Vietnam). Remote Sens. 2014, 6, 421–442. [Google Scholar] [CrossRef]
- Yang, X.E.; Wu, X.; Hao, H.L.; He, Z.L. Mechanisms and assessment of water eutrophication. J. Zhejiang Univ. Sci. B 2008, 9, 197–209. [Google Scholar] [CrossRef] [PubMed]
- Behrenfeld, M.J.; O’Malley, R.T.; Siegel, D.A.; McClain, C.R.; Sarmiento, J.L.; Feldman, G.C.; Milligan, A.J.; Falkowski, P.G.; Letelier, R.M.; Boss, E.S. Climate-driven trends in contemporary ocean productivity. Nature 2006, 444, 752–755. [Google Scholar] [CrossRef] [PubMed]
- Ritchie, J.C.; Zimba, P.V.; Everitt, J.H. Remote Sensing Techniques to Assess Water Quality. Photogramm. Eng. Remote Sens. 2003, 69, 695–704. [Google Scholar] [CrossRef]
- Govindjee. Bioenergetics of Photosynthesis; Academic Press: Cambridge, MA, USA, 1975. [Google Scholar]
- Volk, T.; Hoffert, M.I. Ocean Carbon Pumps: Analysis of Relative Strengths and Efficiencies in Ocean-Driven Atmospheric CO2 Changes; American Geophysical Union: Washington, DC, USA, 2013; pp. 99–110. [Google Scholar]
- Arrigo, K.R.; Robinson, D.H.; Worthen, D.L.; Dunbar, R.B.; DiTullio, G.R.; VanWoert, M.; Lizotte, M.P. Phytoplankton Community Structure and the Drawdown of Nutrients and CO2 in the Southern Ocean. Science 1999, 283, 365–367. [Google Scholar] [CrossRef] [PubMed]
- Hein, M.; Sand-Jensen, K. CO2 increases oceanic primary production. Nature 1997, 388, 526–527. [Google Scholar] [CrossRef]
- Hofmann, M.; Worm, B.; Rahmstorf, S.; Schellnhuber, H.J. Declining ocean chlorophyll under unabated anthropogenic CO2 emissions. Environ. Res. Lett. 2011, 6, 34–35. [Google Scholar] [CrossRef]
- Hu, C.; Lee, Z.; Franz, B. Chlorophyll a algoritms for oligotrophic oceans: A novel approach based on three-band reflectance difference. J. Geophys. Res. 2012, 117. [Google Scholar] [CrossRef]
- Morel, A.; Maritorena, S. Bio-optical properties of oceanic waters: A reappraisal. J. Geophys. Res. Ocean. 2001, 106, 7163–7180. [Google Scholar] [CrossRef]
- O’Reilly, J.E.; Maritirena, S.; Mitchell, B.G.; Siegel, D.A.; Carder, K.L.; Garver, S.A.; Kahru, M.; McClain, C. Ocean color chlorophyll algorithms for SeaWiFS. J. Geophys. Res. 1998, 103, 24937–24953. [Google Scholar] [CrossRef]
- O’Reilly, J.E.; Maritorena, S.; O’Brien, M.C.; Siegel, D.A.; Toole, D.; Menzies, D.; Smith, R.C.; Mueller, J.L.; Mitchell, B.G.; Kahru, M.; et al. SeaWiFS Postlaunch Calibration and Validation Analyses, Part 3. Nasa Tech. Memo. 2000, 11, 3–8. [Google Scholar]
- Werdell, P.J.; Bailey, S.W. An improved bio-optical data set for ocean color algorithm development and satellite data product validation. Remote Sens. Environ. 2005, 98, 122–140. [Google Scholar] [CrossRef]
- Blondeau-Patissier, D.; Gower, J.F.; Dekker, A.G.; Phinn, S.R.; Brando, V.E. A review of ocean color remote sensing methods and statistical techniques for the detection, mapping and analysis of phytoplankton blooms in coastal and open oceans. Prog. Oceanogr. 2014, 123, 123–144. [Google Scholar] [CrossRef]
- Matthews, M.W. A current review of empirical procedures of remote sensing in inland and near-coastal transitional waters. Int. J. Remote Sens. 2011, 32, 6855–6899. [Google Scholar] [CrossRef]
- Odermatt, D.; Gitelson, A.; Brando, V.E.; Schaepman, M. Review of constituent retrieval in optically deep and complex waters from satellite imagery. Remote Sens. Environ. 2012, 118, 116–126. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Schalles, J.F.; Hladik, C.M. Remote chlorophyll-a retrieval in turbid, productive estuaries: Chesapeake Bay case study. Remote Sens. Environ. 2007, 109, 464–472. [Google Scholar] [CrossRef]
- Wang, T.S.; Tan, C.H.; Chen, L.; Tsai, Y.C. Applying Artificial Neural Networks and Remote Sensing to Estimate Chlorophyll-a Concentration in Water Body. Int. Symp. Intell. Inf. Technol. Appl. 2008, 1, 540–544. [Google Scholar]
- Canziani, G.; Ferrati, R.; Marinelli, C.; Dukatz, F. Artificial neural networks and remote sensing in the analysis of the highly variable Pampean shallow lakes. Math. Biosci. Eng. 2008, 5, 691–711. [Google Scholar] [CrossRef] [PubMed]
- Gross, L.; Thiria, S.; Frouin, R. Applying artificial neural network methodology to ocean color remote sensing. Ecol. Modell. 1999, 120, 237–246. [Google Scholar] [CrossRef]
- Nabavi-Pelesaraei, A.; Bayat, R.; Hosseinzadeh-Bandbafha, H.; Afrasyabi, H.; Chau, K.-W. Modeling of energy consumption and environmental life cycle assessment for incineration and landfill systems of municipal solid waste management—A case study in Tehran Metropolis of Iran. J. Clean. Prod. 2017, 148, 427–440. [Google Scholar] [CrossRef]
- Chen, X.Y.; Chau, K.W. A Hybrid Double Feedforward Neural Network for Suspended Sediment Load Estimation. Water Resour. Manag. 2016, 30, 2179–2194. [Google Scholar] [CrossRef]
- Alizadeh, M.J.; Kavianpour, M.R.; Kisi, O.; Nourani, V. A new approach for simulating and forecasting the rainfall-runoff process within the next two months. J. Hydrol. 2017, 548, 588–597. [Google Scholar] [CrossRef]
- Zhan, H.; Shi, P.; Chen, C. Retrieval of Oceanic Chlorophyll Concentration Using Support Vector Machines. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2947–2951. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Gómez-Chova, L.; Muñoz-Marí, J.; Vila-Francés, J.; Amorós-López, J.; Calpe-Maravilla, J. Retrieval of oceanic chlorophyll concentration with relevance vector machines. Remote Sens. Environ. 2006, 105, 23–33. [Google Scholar] [CrossRef]
- Blix, K.; Camps-Valls, G.; Jenssen, R. Gaussian Process Sensitivity Analysis for Oceanic Chlorophyll Estimation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 1265–1277. [Google Scholar] [CrossRef]
- Blix, K.; Eltoft, T. Evaluation of Feature Ranking and Regression Methods for Oceanic Chlorophyll-a Estimation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1403–1418. [Google Scholar] [CrossRef]
- Sawaya, K.E.; Olmanson, L.G.; Heinert, N.J.; Brezonik, P.L.; Bauer, M.E. Extending satellite remote sensing to local scales: Land and water resource monitoring using high-resolution imagery. Remote Sens. Environ. 2003, 88, 144–156. [Google Scholar] [CrossRef]
- Brando, V.E.; Dekker, A.G. Satellite hyperspectral remote sensing for estimating estuarine and coastal water quality. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1378–1387. [Google Scholar] [CrossRef]
- Vargas, M.; Brown, C.W.; Sapiano, M.R.P. Phenology of marine phytoplankton from satellite ocean color measurements. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- D’Alimonte, D.; Melin, F.; Zibordi, G.; Berthon, J.F. Use of the novelty detection technique to identify the range of applicability of empirical ocean color algorithms. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2833–2843. [Google Scholar] [CrossRef]
- Fukushima, H.; Higurashi, A.; Mitomi, Y.; Nakajima, T.; Noguchi, T.; Tanaka, T.; Toratani, M. Correction of atmospheric effect on ADEOS/OCTS ocean color data: Algorithm description and evaluation of its performance. J. Oceanogr. 1998, 54, 417–430. [Google Scholar] [CrossRef]
- Guyon, I.; Elisseeff, A. An Introduction to Feature Extraction. In Feature Extraction: Foundations and Applications; Springer: Berlin/Heidelberg, Germany, 2006; pp. 1–25. [Google Scholar]
- Ferreira, E. Model Selection in Time Series Machine Learning Applications. Ph.D. Thesis, University of Oulu, Oulu, Finland, 2015. [Google Scholar]
- Verrelst, J.; Alonso, L.; Camps-Valls, G.; Delegido, J.; Moreno, J. Retrieval of Vegetation Biophysical Parameters Using Gaussian Process Techniques. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1832–1843. [Google Scholar] [CrossRef]
- Verrelst, J.; Muñoz, J.; Alonso, L.; Rivera, J.P.; Camps-Valls, G.; Moreno, J. Machine learning regression algorithms for biophysical parameter retrieval: Opportunities for Sentinel-2 and -3. Remote Sens. Environ. 2012, 118, 127–139. [Google Scholar] [CrossRef]
- Verrelst, J.; Rivera, J.P.; Gitelson, A.; Delegido, J.; Moreno, J.; Camps-Valls, G. Spectral band selection for vegetation properties retrieval using Gaussian processes regression. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 554–567. [Google Scholar] [CrossRef]
- Kwiatkowska, E.J.; Fargion, G.S. Application of Machine-Learning Techniques Toward the Creation of a Consistent and Calibrated Global Chlorophyll Concentration Baseline Dataset Using Remotely Sensed Ocean Color Data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2844–2860. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Muñoz-Marí, J.; Gómez-Chova, L.; Richter, K.; Calpe-Maravilla, J. Biophysical Parameter Estimation With a Semisupervised Support Vector Machine. IEEE Geosci. Remote Sens. Lett. 2009, 6, 248–252. [Google Scholar] [CrossRef]
- Rasmussen, P.M.; Madsen, K.H.; Lund, T.E.; Hansen, L.K. Visualization of nonlinear kernel models in neuroimaging by sensitivity maps. NeuroImage 2011, 55, 1120–1131. [Google Scholar] [CrossRef] [PubMed]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: a basic tool of chemometrics. Chem. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Ryan, K.; Ali, K. Application of a partial least-squares regression model to retrieve chlorophyll-a concentrations in coastal waters using hyper-spectral data. Ocean Sci. J. 2016, 51, 209–221. [Google Scholar] [CrossRef]
- Lee, Z.P. Remote Sensing of Inherent Optical Properties: Fundamentals, Test of Algorithms, and Applications; Technical Report; International Ocean-Colour Coordinating Group, IOCCG: Busan, Korea, 2006. [Google Scholar]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Process for Machine Learning; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Schölkopf, B.; Smola, A. Learning with Kernels-Support Vector Machines, Regularization, Optimization and Beyond; MIT Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Murphy, K.P. Machine Learning A probabilistic Perspective; MIT Press: Cambridge, MA, USA, 2012; pp. 496–498. [Google Scholar]
- Kung, S.Y. Kernel Methods and Machine Learning; Cambridge University Press: Cambridge, UK, 2014; pp. 381–383. [Google Scholar]
- Gosselin, R.; Rodrigue, D.; Duchesne, C. A Bootstrap-VIP approach for selecting wavelength intervals in spectral imaging applications. Chem. Intell. Lab. Syst. 2010, 100, 12–21. [Google Scholar] [CrossRef]
- Afanador, N.L. Important Variable Selection in Partial Least Squares for Industrial Process Understanding and Control. Ph.D. Thesis, Radboud University Nijmegen, Nijmegen, The Netherlands, 2014. [Google Scholar]
- Abdi, H. Partial least squares regression and projection on latent structure regression (PLS Regression). Wiley Int. Rev. Comput. Stat. 2010, 2, 97–106. [Google Scholar] [CrossRef]
- Rännar, S.; Lindgren, F.; Geladi, P.; Wold, S. A PLS kernel algorithm for data sets with many variables and fewer objects. Part 1: Theory and algorithm. J. Chem. 1994, 8, 111–125. [Google Scholar] [CrossRef]
- De Jong, S. SIMPLS: An alternative approach to partial least squares regression. Chem. Intell. Lab. Syst. 1993, 18, 251–263. [Google Scholar] [CrossRef]
- Dayal, B.S.; MacGregor, J.F. Improved PLS algorithms. J. Chem. 1997, 11, 73–85. [Google Scholar] [CrossRef]
- Song, K.; Lu, D.; Li, L.; Li, S.; Wang, Z.; Du, J. Remote sensing of chlorophyll-a concentration for drinking water source using genetic algorithms (GA)-partial least square (PLS) modeling. Ecol. Inf. 2012, 10, 25–36. [Google Scholar] [CrossRef]
- Blix, K.; Camps-Valls, G.; Jenssen, R. Sensitivity Analysis of Gaussian Processes for Oceanic Chlorophyll Prediction. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, IGARSS, Milan, Italy, 26–31 July 2015; pp. 996–999. [Google Scholar]
- Micchelli, C.A.; Xu, Y.; Zhang, H. Universal Kernels. J. Mach. Learn. Res. 2006, 7, 2651–2667. [Google Scholar]
- Eriksson, L.; Johansson, E.; Kettaneh-Wold, N.; Wold, S. Multi- and Megavariate Data Analysis. Principles and Applications. J. Chem. 2001, 16, 261–262. [Google Scholar]
- Jonsson, P. Surface Status Classification, Utilizing Image Sensor Technology and Computer Models. Ph.D. Thesis, Mid Sweden University, Sundsvall, Sweden, 2015. [Google Scholar]
- Mehmood, T.; Liland, K.H.; Snipen, L.; Sæbø, S. A review of variable selection methods on Partial Least Squares Regression. Chem. Intell. Lab. Syst. 2012, 118, 62–69. [Google Scholar] [CrossRef]
- Liang, L.; Qin, Z.; Zhao, S.; Di, L.; Zhang, C.; Deng, M.; Lin, H.; Zhang, L.; Wang, L.; Liu, Z. Estimating crop chlorophyll content with hyperspectral vegetation indices and the hybrid inversion method. Int. J. Remote Sens. 2016, 37, 2923–2949. [Google Scholar] [CrossRef]
- Sayuri, F.; Watanabe, F.; Alcantara, E.; Walesza, T.; Rodrigues, T.; Imai, N.; Clemente, C.; Barbosa, C.; Luiz, H.; Da, S.; et al. Estimation of Chlorophyll-a Concentration and the Trophic State of the Barra Bonita Hydroelectric Reservoir Using OLI/Landsat-8 Images. Int. J. Environ. Res. Public Health 2015, 12, 10391–10417. [Google Scholar]
- Werdell, P.J.; Bailey, S.W. The SeaWIFS Bio-optical Archive and Storage System (SeaBASS): Current architeture and implementation. In NASA Technical Memoranda 2002-211617; Fargion, G.S., McClain, C.R., Eds.; NASA Goddard Space Flight Center: Greenbelt, MD, USA, 2002; p. 45. [Google Scholar]
- Werdell, P.J.; Bailey, S.W.; Fargion, G.S.; Pietras, C.; Knobelspiesse, K.D.; Feldman, G.C.; McClain, C.R. Unique data repository facilitates ocean color satellite validation. EOS Trans. AGU 2003, 84, 387. [Google Scholar] [CrossRef]
- Cannizzaro, J.P.; Carder, K.L. Estimating chlorophyll a concentrations from remote-sensing reflectance in optically shallow waters. Remote Sens. Environ. 2006, 101, 13–24. [Google Scholar] [CrossRef]
- Wei, J.; Lee, Z. Retrieval of phytoplankton and colored detrital matter absorption coefficients with remote sensing reflectance in an ultraviolet band. Appl. Opt. 2015, 54, 636–649. [Google Scholar] [CrossRef] [PubMed]


| Regression model | Feature ranking method | The features | # of features | Value of the regression performance measures |
| Synthetic resampled MERIS global (MS 1a) | |
| Bands ( (nm)) | 413 443 490 510 560 620 665 681 |
| Band width | 10 nm and 7.5 nm |
| Spatial resolution | 300 m |
| Chl-a range (mgm) | 0.03–30 |
| (m) | 0.0025–2.3677 |
| Nr. of samples | 478 |
| Synthetic resampled MERIS eutrophic (MS 1b) | |
| Chl-a range (mgm) | 0.7–30 |
| (m) | 0.06–2.3677 |
| Nr. of samples | 300 |
| MERIS global (MS 2a) | |
| Chl-a range (mgm) | 0.017–40.23 |
| Nr. of samples | 557 |
| MERIS eutrophic (MS 2b) | |
| Chl-a range (mgm) | 0.7076–40.23 |
| Nr. of samples | 247 |
| Synthetic resampled MODIS-Aqua global (MS 3a) | |
| Bands ( (nm)) | 412 443 488 531 551 667 678 |
| Band width | 10 nm, 15 nm |
| Spatial resolution | 1000 m |
| Chl-a range (mgm) | 0.03–30 |
| (m) | 0.0025–2.3677 |
| Nr. of samples | 478 |
| Synthetic resampled MODIS-Aqua eutrophic (MS 3b) | |
| Chl-a range (mgm) | 0.03–30 |
| (m) | 0.06–2.3677 |
| Nr. of samples | 300 |
| MODIS-Aqua global (MS 4a) | |
| Bands ( (nm)) | 412 443 488 531 551 667 678 |
| Band width | 10 nm, 15 nm |
| Spatial resolution | 1000 m |
| Chl-a range (mgm) | 0.0153–25.4985 |
| Nr. of samples | 579 |
| MODIS-Aqua eutrophic (MS 4b) | |
| Chl-a range (mgm) | 0.703–25.4985 |
| Nr. of samples | 392 |
| Data Label | Model | Spectral Bands | # of Bands | NRMSE | R |
|---|---|---|---|---|---|
| MS 1a | GPR by VIP | 1,…,7 | 7 | 0.0983 | 0.9463 |
| MS 1b | GPR by VIP | 4, 5 and 6 | 3 | 0.1363 | 0.9157 |
| MS 2a | GPR by SA GP | 1, 2, 5, 6 and 7 | 5 | 0.0764 | 0.9159 |
| MS 2b | SVR by VIP | 4, 5 and 6 | 3 | 0.1305 | 0.8332 |
| MS 3a | GPR by ARD | 1, 3 and 7 | 3 | 0.1082 | 0.9353 |
| MS 3b | GPR by ARD | 1, 3, 5 and 7 | 4 | 0.144 | 0.9068 |
| MS 4a | SVR by VIP | 1, 2, 3, 4, 5 and 7 | 6 | 0.1094 | 0.8402 |
| MS 4b | SVR by ARD | 1, 2, 3 and 7 | 4 | 0.1180 | 0.7540 |
| MS1b | ||
|---|---|---|
| NRMSE | R | |
| GPR | 0.1497 | 0.8973 |
| SVR | 0.1527 | 0.836 |
| MS2b | ||
| NRMSE | R | |
| GPR | 0.1464 | 0.824 |
| SVR | 0.1438 | 0.831 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blix, K.; Eltoft, T. Machine Learning Automatic Model Selection Algorithm for Oceanic Chlorophyll-a Content Retrieval. Remote Sens. 2018, 10, 775. https://doi.org/10.3390/rs10050775
Blix K, Eltoft T. Machine Learning Automatic Model Selection Algorithm for Oceanic Chlorophyll-a Content Retrieval. Remote Sensing. 2018; 10(5):775. https://doi.org/10.3390/rs10050775
Chicago/Turabian StyleBlix, Katalin, and Torbjørn Eltoft. 2018. "Machine Learning Automatic Model Selection Algorithm for Oceanic Chlorophyll-a Content Retrieval" Remote Sensing 10, no. 5: 775. https://doi.org/10.3390/rs10050775
APA StyleBlix, K., & Eltoft, T. (2018). Machine Learning Automatic Model Selection Algorithm for Oceanic Chlorophyll-a Content Retrieval. Remote Sensing, 10(5), 775. https://doi.org/10.3390/rs10050775






