Training Small Networks for Scene Classification of Remote Sensing Images via Knowledge Distillation
Abstract
:1. Introduction
2. Method
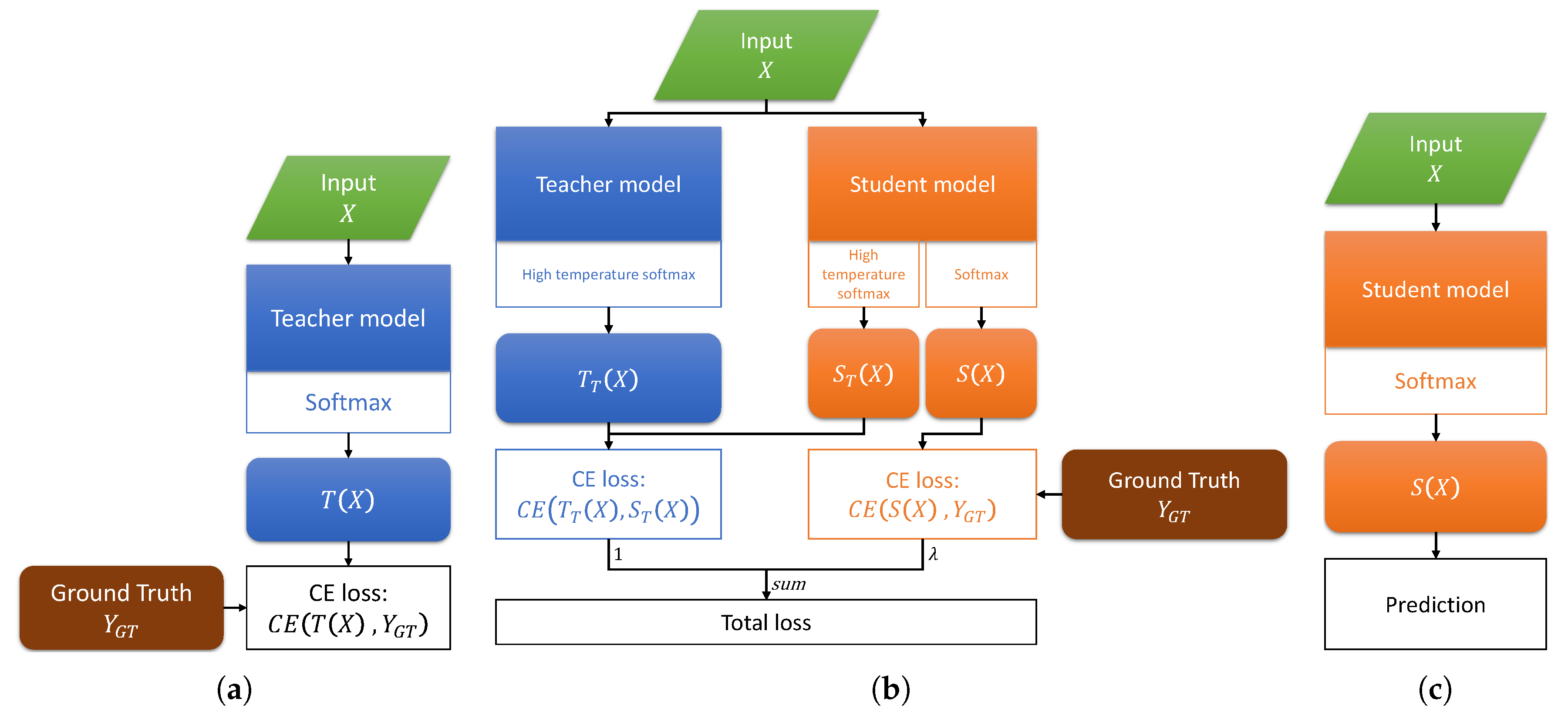
2.1. Teacher-Student Training
2.2. Knowledge Distillation Framework
2.2.1. Knowledge from Probability Distribution
2.2.2. KD Training Process
3. Experimental Results and Analysis
3.1. Experiments on AID Dataset
3.1.1. Dataset Description
3.1.2. Structure of Networks and Direct Training
- random scaling in the range [0.8, 1.2];
- random rotation by [−30, 30] degrees;
- random vertically and horizontally flipping.
3.1.3. KD Training and Results
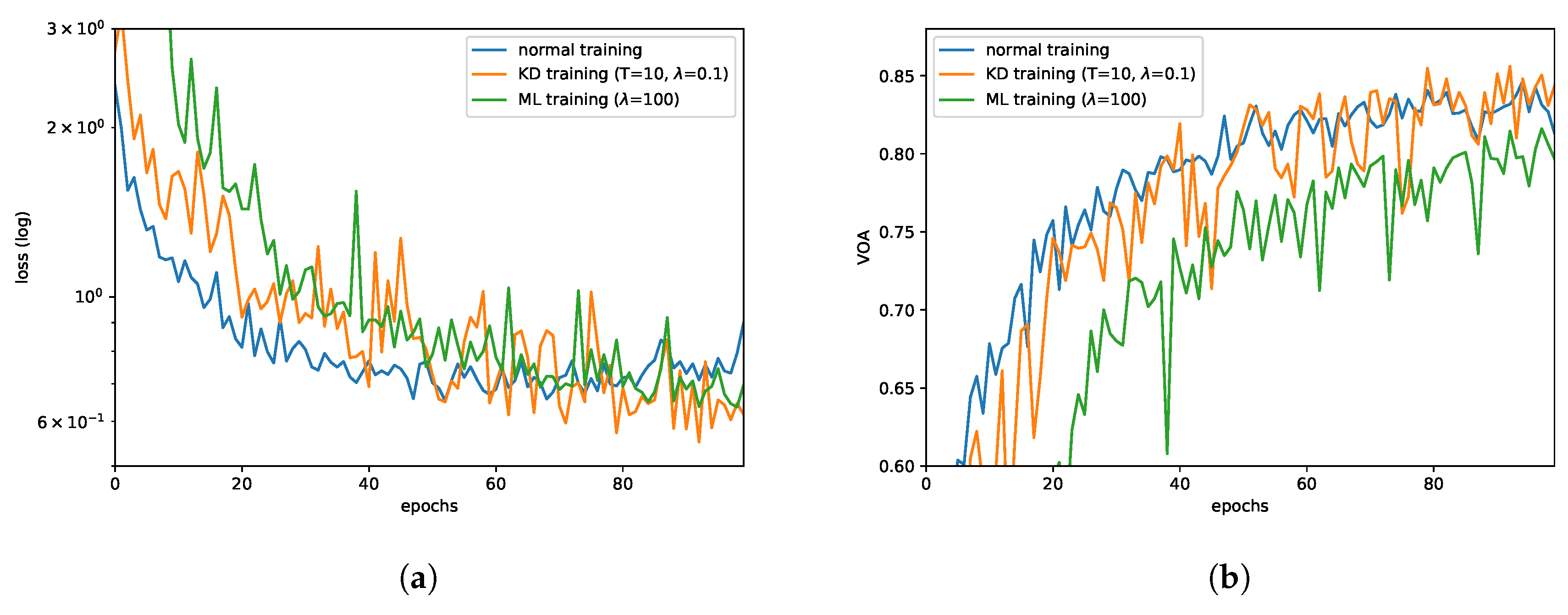
- KD training is effective. It could increase OA by approximately 3%, compared to the direct training way. However, ML training did not seem to work or even reduce the OA. For further analysis, we draw the validation loss curves and VOA curves of these three types of training methods, which are shown in Figure 4a,b. From training curves, we could find that direct training leads to faster convergence (50 epochs) but falls into local optima while KD training could always reduce the loss.
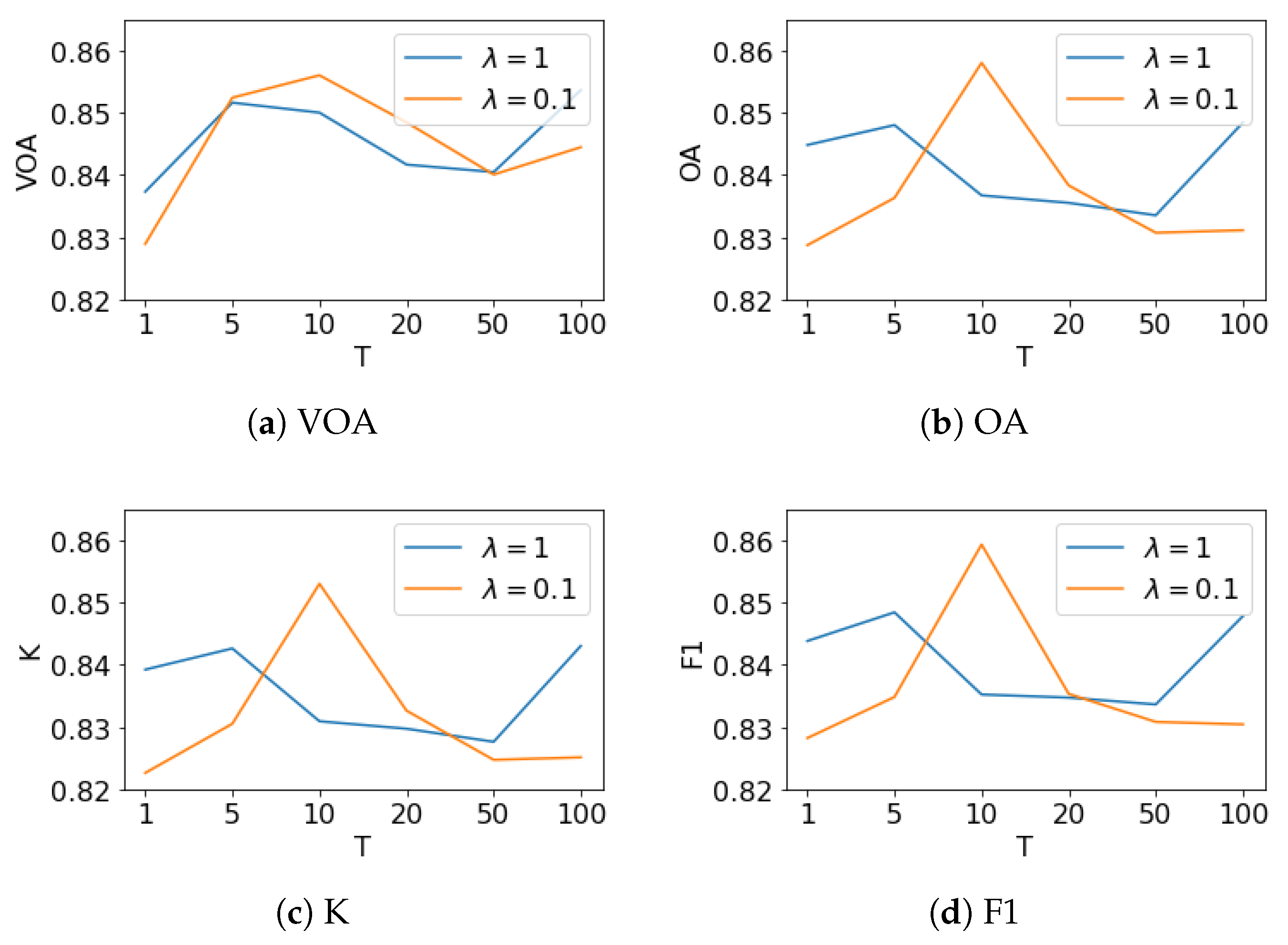
- The student model learned more knowledge from the teacher model via higher temperature softmax output. Different from T, the effect of parameter is not clear. When T is 1, 5, 50, or 100, the bigger the better OA achieved. However, if T is set to 10 or 20, the smaller value performed better. To further analyze , we drew four subfigures in Figure 5 to demonstrate the relationship between our four metrics and the temperature T. The curves shows that the trend of VOA are similar to other metrics whether or on AID dataset.
- From a macro point of view, KD training methods could improve the performance of a network model, in terms of OA, K or F1. In test data evaluation, it even surpassed the deep teacher model by 60% higher speed and using only 2.4% model parameters.
3.1.4. KD Training on Small Dataset
3.1.5. Remove One Category
3.1.6. The Relationship between the Optimal Temperature and the Number of Categories
3.1.7. Evaluating Our Proposed KD Method on AID Dataset
3.2. Additional Experiments
3.2.1. Experiments on UCMerced Dataset
3.2.2. Experiments on NWPU-RESISC Dataset
3.2.3. Experiments on EuroSAT Dataset
3.2.4. Discussions
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A. The Model Structures Used in This Paper
Appendix A.1. The Student Models in Experiments on AID, NWPU-RESISC, and EuroSAT Datasets
| Layer type | Attributes | Output Size | Parameters |
|---|---|---|---|
| Input | 224, 224, 3 | 0 | |
| Conv2D | filters: 64, kernel size: (3, 3), activation: ReLU | 224, 224, 64 | 1792 |
| MaxPooling2D | pool size: (2, 2) | 112, 112, 64 | 0 |
| Conv2D | filters: 64, kernel size: (3, 3), activation: ReLU | 112, 112, 64 | 36,928 |
| MaxPooling2D | pool size: (2, 2) | 56, 56, 64 | 0 |
| Conv2D | filters: 128, kernel size: (3, 3), activation: ReLU | 56, 56, 128 | 73,856 |
| MaxPooling2D | pool size: (2, 2) | 28, 28, 128 | 0 |
| Conv2D | filters: 128, kernel size: (3, 3), activation: ReLU | 28, 28, 128 | 147,584 |
| MaxPooling2D | pool size: (2, 2) | 14, 14, 128 | 0 |
| Flatten | 25,088 | 0 | |
| Dropout | drop rate: 0.3 | 25,088 | 0 |
| Dense | units: 30 | 30 | 752,670 |
| Softmax | 30 | 0 | |
| Total | 1,012,830 |
Appendix A.2. The Teacher Model and the Student Model in Experiments on UCMerced Dataset
| Layer Type | Attributes | Output Size | Parameters |
|---|---|---|---|
| Input | 224, 224, 3 | 0 | |
| Conv2D | filters: 64, kernel size: (3, 3), activation: ReLU | 224, 224, 64 | 1792 |
| MaxPooling2D | pool size: (2, 2) | 112, 112, 64 | 0 |
| Conv2D | filters: 128, kernel size: (3, 3), activation: ReLU | 112, 112, 128 | 73,856 |
| MaxPooling2D | pool size: (2, 2) | 56, 56, 128 | 0 |
| Conv2D | filters: 256, kernel size: (3, 3), activation: ReLU | 56, 56, 256 | 295,168 |
| MaxPooling2D | pool size: (2, 2) | 28, 28, 256 | 0 |
| Conv2D | filters: 512, kernel size: (3, 3), activation: ReLU | 28, 28, 512 | 1,180,160 |
| MaxPooling2D | pool size: (2, 2) | 14, 14, 512 | 0 |
| Flatten | 100,352 | 0 | |
| Dropout | drop rate: 0.3 | 100,352 | 0 |
| Dense | units: 21 | 21 | 2,107,413 |
| Softmax | 21 | 0 | |
| Total | 3,658,389 |
| Layer Type | Attributes | Output Size | Parameters |
|---|---|---|---|
| Input | 224, 224, 3 | 0 | |
| Conv2D | filters: 32, kernel size: (3, 3), activation: ReLU | 224, 224, 32 | 896 |
| MaxPooling2D | pool size: (2, 2) | 112, 112, 32 | 0 |
| Conv2D | filters: 32, kernel size: (3, 3), activation: ReLU | 112, 112, 32 | 9248 |
| MaxPooling2D | pool size: (2, 2) | 56, 56, 32 | 0 |
| Conv2D | filters: 64, kernel size: (3, 3), activation: ReLU | 56, 56, 64 | 18,496 |
| MaxPooling2D | pool size: (2, 2) | 28, 28, 64 | 0 |
| Conv2D | filters: 64, kernel size: (3, 3), activation: ReLU | 28, 28, 64 | 36,928 |
| MaxPooling2D | pool size: (2, 2) | 14, 14, 64 | 0 |
| Dropout | drop rate: 0.3 | 14, 14, 64 | 0 |
| Conv2D | filters: 21, kernel size: (1, 1) | 14, 14, 21 | 0 |
| GlobalAveragePooling2D | 21 | 1365 | |
| Softmax | 21 | 0 | |
| Total | 66,933 |
References
- Estoque, R.C.; Murayama, Y.; Akiyama, C.M. Pixel-based and object-based classifications using high- and medium-spatial-resolution imageries in the urban and suburban landscapes. Geocarto Int. 2015, 30, 1113–1129. [Google Scholar] [CrossRef]
- Helber, P.; Bischke, B.; Dengel, A.; Borth, D. Eurosat: A novel dataset and deep learning benchmark for land use and land cover classification. arXiv, 2017; arXiv:1709.00029. [Google Scholar]
- Zhang, X.; Wang, Q.; Chen, G.; Dai, F.; Zhu, K.; Gong, Y.; Xie, Y. An object-based supervised classification framework for very-high-resolution remote sensing images using convolutional neural networks. Remote Sens. Lett. 2018, 9, 373–382. [Google Scholar] [CrossRef]
- Chen, G.; Zhang, X.; Wang, Q.; Dai, F.; Gong, Y.; Zhu, K. Symmetrical Dense-Shortcut Deep Fully Convolutional Networks for Semantic Segmentation of Very-High-Resolution Remote Sensing Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1633–1644. [Google Scholar] [CrossRef]
- Gualtieri, J.A.; Cromp, R.F. Support vector machines for hyperspectral remote sensing classification. In Proceedings of the 27th AIPR Workshop: Advances in Computer-Assisted Recognition, Washington, DC, USA, 14–16 October 1998; International Society for Optics and Photonics: Bellingham, WA, USA, 1999; Volume 3584, pp. 221–233. [Google Scholar]
- Duro, D.C.; Franklin, S.E.; Dubé, M.G. A comparison of pixel-based and object-based image analysis with selected machine learning algorithms for the classification of agricultural landscapes using SPOT-5 HRG imagery. Remote Sens. Environ. 2012, 118, 259–272. [Google Scholar] [CrossRef]
- Cheriyadat, A.M. Unsupervised Feature Learning for Aerial Scene Classification. IEEE Trans. Geosci. Remote Sens. 2014, 52, 439–451. [Google Scholar] [CrossRef]
- Peña, J.; Gutiérrez, P.; Hervás-Martínez, C.; Six, J.; Plant, R.; López-Granados, F. Object-Based Image Classification of Summer Crops with Machine Learning Methods. Remote Sens. 2014, 6, 5019–5041. [Google Scholar] [CrossRef]
- Lu, D.; Li, G.; Moran, E.; Kuang, W. A comparative analysis of approaches for successional vegetation classification in the Brazilian Amazon. GISci. Remote Sens. 2014, 51, 695–709. [Google Scholar] [CrossRef]
- De Chant, T.; Kelly, M. Individual object change detection for monitoring the impact of a forest pathogen on a hardwood forest. Photogramm. Eng. Remote Sens. 2009, 75, 1005–1013. [Google Scholar] [CrossRef]
- Dribault, Y.; Chokmani, K.; Bernier, M. Monitoring Seasonal Hydrological Dynamics of Minerotrophic Peatlands Using Multi-Date GeoEye-1 Very High Resolution Imagery and Object-Based Classification. Remote Sens. 2012, 4, 1887–1912. [Google Scholar] [CrossRef]
- Hu, F.; Xia, G.S.; Hu, J.; Zhang, L. Transferring Deep Convolutional Neural Networks for the Scene Classification of High-Resolution Remote Sensing Imagery. Remote Sens. 2015, 7, 14680–14707. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Yang, Y.; Newsam, S. Comparing SIFT descriptors and Gabor texture features for classification of remote sensed imagery. In Proceedings of the 15th IEEE International Conference on Image Processing (ICIP 2008), San Diego, CA, USA, 12–15 October 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 1852–1855. [Google Scholar]
- Dalal, N.; Triggs, B. Histograms of oriented gradients for human detection. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; IEEE: Piscataway, NJ, USA, 2005; Volume 1, pp. 886–893. [Google Scholar]
- Risojević, V.; Babić, Z. Aerial image classification using structural texture similarity. In Proceedings of the 2011 IEEE International Symposium on Signal Processing and Information Technology (ISSPIT), Bilbao, Spain, 14–17 December 2011; pp. 190–195. [Google Scholar]
- Ojala, T.; Pietikainen, M.; Maenpaa, T. Multiresolution gray-scale and rotation invariant texture classification with local binary patterns. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 971–987. [Google Scholar] [CrossRef]
- Risojević, V.; Momić, S.; Babić, Z. Gabor descriptors for aerial image classification. In International Conference on Adaptive and Natural Computing Algorithms; Springer: Berlin, Germany, 2011; pp. 51–60. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Altman, N.S. An introduction to kernel and nearest-neighbor nonparametric regression. Am. Stat. 1992, 46, 175–185. [Google Scholar]
- Yang, Y.; Newsam, S. Geographic image retrieval using local invariant features. IEEE Trans. Geosci. Remote Sens. 2013, 51, 818–832. [Google Scholar] [CrossRef]
- Yang, Y.; Newsam, S. Bag-of-visual-words and Spatial Extensions for Land-use Classification. In Proceedings of the 18th SIGSPATIAL International Conference on Advances in Geographic Information Systems (GIS ’10), San Jose, CA, USA, 2–5 November 2010; ACM: New York, NY, USA, 2010; pp. 270–279. [Google Scholar]
- Chen, L.; Yang, W.; Xu, K.; Xu, T. Evaluation of local features for scene classification using VHR satellite images. In Proceedings of the 2011 Joint Urban Remote Sensing Event (JURSE), Munich, Germany, 11–13 April 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 385–388. [Google Scholar]
- Perronnin, F.; Dance, C. Fisher kernels on visual vocabularies for image categorization. In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition (CVPR’07), Minneapolis, MN, USA, 17–22 June 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 1–8. [Google Scholar]
- Yang, Y.; Newsam, S. Spatial pyramid co-occurrence for image classification. In Proceedings of the 2011 IEEE International Conference on Computer Vision (ICCV), Barcelona, Spain, 6–13 November 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 1465–1472. [Google Scholar]
- Lazebnik, S.; Schmid, C.; Ponce, J. Beyond bags of features: Spatial pyramid matching for recognizing natural scene categories. In Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, New York, NY, USA, 17–22 June 2006; IEEE: Piscataway, NJ, USA, 2006; Volume 2, pp. 2169–2178. [Google Scholar]
- Chen, Y.; Zhao, X.; Jia, X. Spectral-Spatial Classification of Hyperspectral Data Based on Deep Belief Network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2381–2392. [Google Scholar] [CrossRef]
- Bosch, A.; Zisserman, A.; Muñoz, X. Scene classification via pLSA. In Proceedings of the 9th European Conference on Computer Vision—ECCV 2006, Graz, Austria, 7–13 May 2006; pp. 517–530. [Google Scholar]
- Lienou, M.; Maitre, H.; Datcu, M. Semantic annotation of satellite images using latent Dirichlet allocation. IEEE Geosci. Remote Sens. Lett. 2010, 7, 28–32. [Google Scholar] [CrossRef]
- Kusumaningrum, R.; Wei, H.; Manurung, R.; Murni, A. Integrated visual vocabulary in latent Dirichlet allocation–based scene classification for IKONOS image. J. Appl. Remote Sens. 2014, 8, 083690. [Google Scholar] [CrossRef]
- Zhong, Y.; Cui, M.; Zhu, Q.; Zhang, L. Scene classification based on multifeature probabilistic latent semantic analysis for high spatial resolution remote sensing images. J. Appl. Remote Sens. 2015, 9, 095064. [Google Scholar] [CrossRef]
- Zhong, Y.; Zhu, Q.; Zhang, L. Scene classification based on the multifeature fusion probabilistic topic model for high spatial resolution remote sensing imagery. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6207–6222. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Bengio, I.G.Y.; Courville, A. Deep Learning; Book in preparation for MIT Press.
- Gu, J.; Wang, Z.; Kuen, J.; Ma, L.; Shahroudy, A.; Shuai, B.; Liu, T.; Wang, X.; Wang, G.; Cai, J.; et al. Recent advances in convolutional neural networks. Pattern Recognit. 2017, 77, 354–377. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [PubMed]
- Mnih, V. Machine Learning for Aerial Image Labeling. Ph.D. Thesis, University of Toronto, Toronto, ON, Canada, 2013. [Google Scholar]
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep Learning-Based Classification of Hyperspectral Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Marmanis, D.; Wegner, J.D.; Galliani, S.; Schindler, K.; Datcu, M.; Stilla, U. Semantic segmentation of aerial images with an ensemble of CNSS. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 3, 473–480. [Google Scholar] [CrossRef]
- Nogueira, K.; Penatti, O.A.B.; Santos, J.A.D. Towards better exploiting convolutional neural networks for remote sensing scene classification. Pattern Recognit. 2017, 61, 539–556. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, G.; Wang, W.; Wang, Q.; Dai, F. Object-Based Land-Cover Supervised Classification for Very-High-Resolution UAV Images Using Stacked Denoising Autoencoders. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3373–3385. [Google Scholar] [CrossRef]
- Liu, Y.; Huang, C. Scene classification via triplet networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 11, 220–237. [Google Scholar] [CrossRef]
- Li, W.; Fu, H.; Yu, L.; Gong, P.; Feng, D.; Li, C.; Clinton, N. Stacked Autoencoder-based deep learning for remote-sensing image classification: a case study of African land-cover mapping. Int. J. Remote Sens. 2016, 37, 5632–5646. [Google Scholar] [CrossRef]
- Zhang, M.; Hu, X.; Zhao, L.; Lv, Y.; Luo, M.; Pang, S. Learning Dual Multi-Scale Manifold Ranking for Semantic Segmentation of High-Resolution Images. Remote Sens. 2017, 9, 500. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Advances in Neural Information Processing Systems; MIT Press Ltd.: Cambridge, MA, USA, 2012; pp. 1097–1105. [Google Scholar]
- Jia, Y.; Shelhamer, E.; Donahue, J.; Karayev, S.; Long, J.; Girshick, R.; Guadarrama, S.; Darrell, T. Caffe: Convolutional architecture for fast feature embedding. In Proceedings of the 22nd ACM international conference on Multimedia, Orlando, FL, USA, 3–7 November 2014; ACM: New York, NY, USA, 2014; pp. 675–678. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv, 2014; arXiv:1409.1556. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas Valley, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Huang, G.; Liu, Z.; Weinberger, K.Q.; van der Maaten, L. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; Volume 1, p. 3. [Google Scholar]
- Zhang, L.; Zhang, L.; Du, B. Deep Learning for Remote Sensing Data: A Technical Tutorial on the State of the Art. IEEE Geosci. Remote Sens. Mag. 2016, 4, 22–40. [Google Scholar] [CrossRef]
- Xia, G.S.; Hu, J.; Hu, F.; Shi, B.; Bai, X.; Zhong, Y.; Zhang, L.; Lu, X. AID: A benchmark data set for performance evaluation of aerial scene classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3965–3981. [Google Scholar] [CrossRef]
- Chen, W.; Wilson, J.; Tyree, S.; Weinberger, K.; Chen, Y. Compressing neural networks with the hashing trick. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 2285–2294. [Google Scholar]
- Zhao, W.; Fu, H.; Luk, W.; Yu, T.; Wang, S.; Feng, B.; Ma, Y.; Yang, G. F-CNN: An FPGA-based framework for training Convolutional Neural Networks. In Proceedings of the 2016 IEEE 27th International Conference on Application-specific Systems, Architectures and Processors (ASAP), London, UK, 6–8 July 2016; pp. 107–114. [Google Scholar] [CrossRef]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. Mobilenets: Efficient convolutional neural networks for mobile vision applications. arXiv, 2017; arXiv:1704.04861. [Google Scholar]
- Cao, C.; De Luccia, F.J.; Xiong, X.; Wolfe, R.; Weng, F. Early on-orbit performance of the visible infrared imaging radiometer suite onboard the Suomi National Polar-Orbiting Partnership (S-NPP) satellite. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1142–1156. [Google Scholar] [CrossRef]
- He, Y.; Zhang, X.; Sun, J. Channel Pruning for Accelerating Very Deep Neural Networks. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017. [Google Scholar]
- Molchanov, P.; Tyree, S.; Karras, T.; Aila, T.; Kautz, J. Pruning convolutional neural networks for resource efficient transfer learning. arXiv, 2016; arXiv:1611.06440. [Google Scholar]
- Han, S.; Mao, H.; Dally, W.J. Deep compression: Compressing deep neural networks with pruning, trained quantization and huffman coding. arXiv, 2015; arXiv:1510.00149. [Google Scholar]
- Zhou, S.; Wu, Y.; Ni, Z.; Zhou, X.; Wen, H.; Zou, Y. DoReFa-Net: Training low bitwidth convolutional neural networks with low bitwidth gradients. arXiv, 2016; arXiv:1606.06160. [Google Scholar]
- Courbariaux, M.; Hubara, I.; Soudry, D.; El-Yaniv, R.; Bengio, Y. Binarized neural networks: Training deep neural networks with weights and activations constrained to +1 or −1. arXiv, 2016; arXiv:1602.02830. [Google Scholar]
- Rastegari, M.; Ordonez, V.; Redmon, J.; Farhadi, A. XNOR-Net: ImageNet classification using binary convolutional neural networks. In Proceedings of the European Conference on Computer Vision (ECCV’16), Amsterdam, The Netherlands, 8–16 October 2016; Springer: Berlin, Germany, 2016; pp. 525–542. [Google Scholar]
- Bucilua, C.; Caruana, R.; Niculescu-Mizil, A. Model compression. In Proceedings of the 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD ’06), Philadelphia, PA, USA, 20–23 August 2006; ACM: New York, NY, USA, 2006; pp. 535–541. [Google Scholar] [CrossRef]
- Hinton, G.; Vinyals, O.; Dean, J. Distilling the knowledge in a neural network. arXiv, 2015; arXiv:1503.02531. [Google Scholar]
- Chen, T.; Goodfellow, I.; Shlens, J. Net2net: Accelerating learning via knowledge transfer. arXiv, 2015; arXiv:1511.05641. [Google Scholar]
- Ba, J.; Caruana, R. Do Deep Nets Really Need to be Deep? In Advances in Neural Information Processing Systems 27; Ghahramani, Z., Welling, M., Cortes, C., Lawrence, N.D., Weinberger, K.Q., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2014; pp. 2654–2662. [Google Scholar]
- Lopez-Paz, D.; Bottou, L.; Schölkopf, B.; Vapnik, V. Unifying distillation and privileged information. arXiv, 2015; arXiv:1511.03643. [Google Scholar]
- Hu, Z.; Ma, X.; Liu, Z.; Hovy, E.; Xing, E. Harnessing deep neural networks with logic rules. arXiv, 2016; arXiv:1603.06318. [Google Scholar]
- Yim, J.; Joo, D.; Bae, J.; Kim, J. A Gift from Knowledge Distillation: Fast Optimization, Network Minimization and Transfer Learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4133–4141. [Google Scholar]
- Huang, Z.; Wang, N. Like What You Like: Knowledge Distill via Neuron Selectivity Transfer. arXiv, 2017; arXiv:1707.01219. [Google Scholar]
- Romero, A.; Ballas, N.; Kahou, S.E.; Chassang, A.; Gatta, C.; Bengio, Y. Fitnets: Hints for thin deep nets. arXiv, 2014; arXiv:1412.6550. [Google Scholar]
- Pan, S.J.; Yang, Q. A survey on transfer learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
- Yosinski, J.; Clune, J.; Bengio, Y.; Lipson, H. How transferable are features in deep neural networks. In Proceedings of the Conference on Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 3320–3328. [Google Scholar]
- Marmanis, D.; Datcu, M.; Esch, T.; Stilla, U. Deep learning earth observation classification using ImageNet pretrained networks. IEEE Geosci. Remote Sens. Lett. 2016, 13, 105–109. [Google Scholar] [CrossRef]
- Li, M.; Zhang, T.; Chen, Y.; Smola, A.J. Efficient Mini-Batch Training for Stochastic Optimization; ACM Press: New York, NY, USA, 2014; pp. 661–670. [Google Scholar] [CrossRef]
- Vapnik, V.; Izmailov, R. Learning using privileged information: similarity control and knowledge transfer. J. Machine Learn. Res. 2015, 16, 55. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 1998; Volume 1. [Google Scholar]
- Cheng, G.; Han, J.; Lu, X. Remote Sensing Image Scene Classification: Benchmark and State of the Art. Proc. IEEE 2017, 105, 1865–1883. [Google Scholar] [CrossRef]
- Chollet, F. Keras; GitHub: San Francisco, CA, USA, 2015. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M. TensorFlow: A system for large-scale machine learning. arXiv, 2016; arXiv:1605.08695. [Google Scholar]
- Thompson, W.D.; Walter, S.D. A reappraisal of the kappa coefficient. J. Clin. Epidemiol. 1988, 41, 949–958. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.E.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Zeiler, M.D. ADADELTA: An adaptive learning rate method. arXiv, 2012; arXiv:1212.5701. [Google Scholar]
- Lin, M.; Chen, Q.; Yan, S. Network in network. arXiv, 2013; arXiv:1312.4400. [Google Scholar]
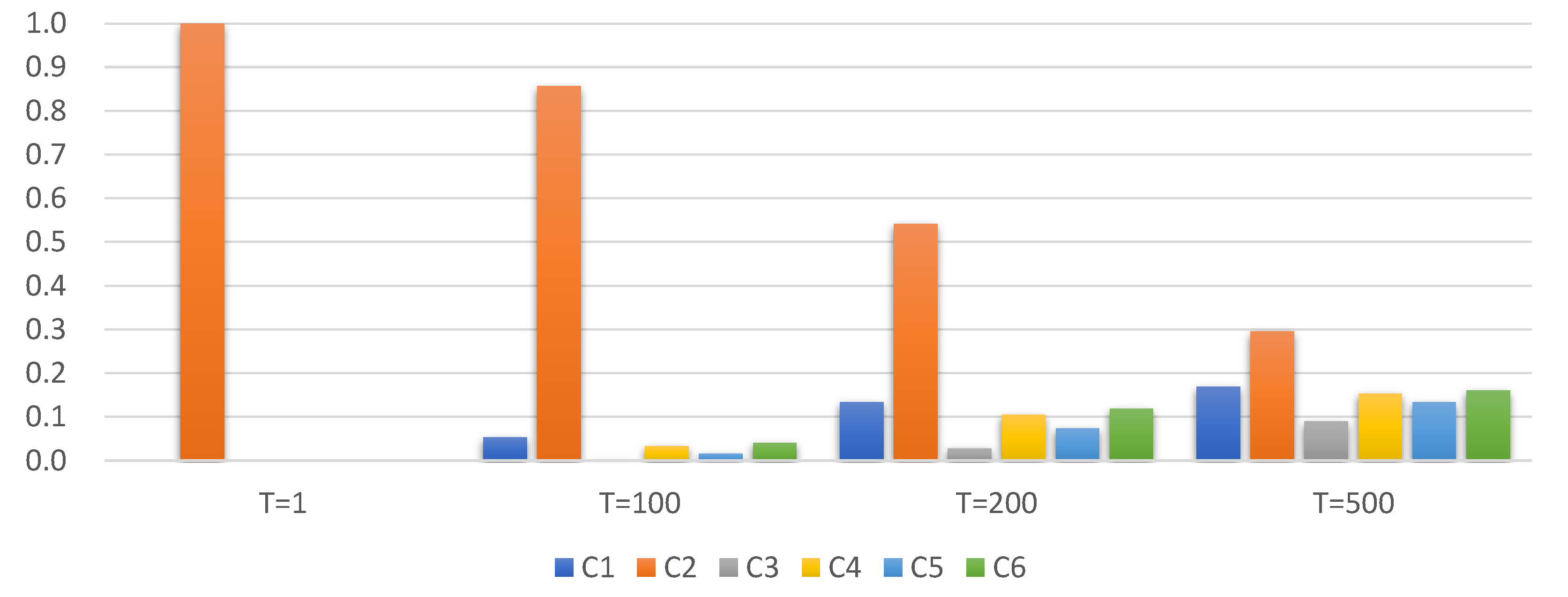

| Temperature | C1 | C2 | C3 | C4 | C5 | C6 | Entropy 1 |
|---|---|---|---|---|---|---|---|
| 1 | 0.0000 | 1.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 100 | 0.0523 | 0.8566 | 0.0022 | 0.0320 | 0.0160 | 0.0409 | 0.8764 |
| 200 | 0.1338 | 0.5416 | 0.0275 | 0.1046 | 0.0741 | 0.1183 | 1.9934 |
| 500 | 0.1687 | 0.2951 | 0.0896 | 0.1529 | 0.1331 | 0.1606 | 2.4898 |
| logits |
| Dataset | Resolution | Size | Category Count | Training Samples | Validation Samples | Test Samples |
|---|---|---|---|---|---|---|
| AID | 0.5–8 m | 600 × 600 | 30 | 5000 | 2507 | 2493 |
| UCMerced | 0.3 m | 256 × 256 | 21 | 1050 | 525 | 525 |
| NWPU-RESISC | 0.2–3 m | 256 × 256 | 45 | 15,750 | 7875 | 7875 |
| EuroSAT | 10–60 m | 64 × 64 | 10 | 16,200 | 5400 | 5400 |
| VOA | OA | K | F1 | FPS | Parameters | ||||
|---|---|---|---|---|---|---|---|---|---|
| student model | direct training | 0.8466 | 0.8295 | 0.8234 | 0.8299 | 113.96 | 1,012,830 | ||
| ML training | |||||||||
| 1 | 0.7140 | 0.7084 | 0.6980 | 0.7098 | |||||
| 100 | 0.8161 | 0.8087 | 0.8018 | 0.8070 | |||||
| KD training | T | ||||||||
| 1 | 1 | 0.8373 | 0.8448 | 0.8392 | 0.8438 | ||||
| 1 | 0.1 | 0.8289 | 0.8287 | 0.8226 | 0.8282 | ||||
| 5 | 1 | 0.8516 | 0.8480 | 0.8426 | 0.8484 | ||||
| 5 | 0.1 | 0.8524 | 0.8363 | 0.8305 | 0.8348 | ||||
| 10 | 1 | 0.8500 | 0.8367 | 0.8309 | 0.8352 | ||||
| 10 | 0.1 | 0.8560 | 0.8580 | 0.8530 | 0.8593 | ||||
| 20 | 1 | 0.8416 | 0.8355 | 0.8297 | 0.8347 | ||||
| 20 | 0.1 | 0.8484 | 0.8383 | 0.8326 | 0.8353 | ||||
| 50 | 1 | 0.8404 | 0.8335 | 0.8276 | 0.8336 | ||||
| 50 | 0.1 | 0.8400 | 0.8307 | 0.8247 | 0.8308 | ||||
| 100 | 1 | 0.8536 | 0.8484 | 0.8430 | 0.8478 | ||||
| 100 | 0.1 | 0.8444 | 0.8311 | 0.8251 | 0.8304 | ||||
| teacher model (ResNet-101) | 0.8888 | 0.8524 | 0.8471 | 0.8542 | 71.31 | 42,437,278 | |||
| Dataset | Training Method | VOA | OA | K | F1 | Training Time per Epoch (s) |
|---|---|---|---|---|---|---|
| 100% | direct training | 0.8466 | 0.8295 | 0.8234 | 0.8299 | 128.1 |
| 20% | direct training | 0.7219 | 0.5872 | 0.5728 | 0.5929 | 32.0 |
| KD training (T = 10, = 0.1) | 0.7298 | 0.6554 | 0.6432 | 0.6567 | ||
| KD training (T = 10, = 1.0) | 0.7416 | 0.6221 | 0.6089 | 0.6234 |
| Category Name | Direct Training | KD Training without Airport | Fine-Tuned on Unlabeled Data | ||||||
|---|---|---|---|---|---|---|---|---|---|
| P | R | F1 | P | R | F1 | P | R | F1 | |
| airport | 0.7359 | 0.8667 | 0.7959 | 0.9130 | 0.2333 | 0.3717 | 0.7234 | 0.7556 | 0.7391 |
| average | 0.8421 | 0.8295 | 0.8299 | 0.8461 | 0.8363 | 0.8306 | 0.8588 | 0.8420 | 0.8438 |
| Student Model | T | 30 Categories | 25 Categories | 20 Categories | 15 Categories | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| OA | K | F1 | OA | K | F1 | OA | K | F1 | OA | K | F1 | ||
| direct training | 0.830 | 0.823 | 0.830 | 0.840 | 0.833 | 0.840 | 0.870 | 0.863 | 0.870 | 0.878 | 0.869 | 0.876 | |
| KD training | 1 | 0.829 | 0.823 | 0.828 | 0.837 | 0.830 | 0.837 | 0.863 | 0.856 | 0.863 | 0.884 | 0.875 | 0.883 |
| 5 | 0.836 | 0.831 | 0.835 | 0.837 | 0.830 | 0.833 | 0.872 | 0.865 | 0.872 | 0.869 | 0.860 | 0.869 | |
| 10 | 0.858 | 0.853 | 0.859 | 0.846 | 0.839 | 0.846 | 0.868 | 0.861 | 0.867 | 0.879 | 0.870 | 0.879 | |
| 20 | 0.838 | 0.833 | 0.835 | 0.841 | 0.835 | 0.841 | 0.871 | 0.864 | 0.870 | 0.880 | 0.871 | 0.880 | |
| 50 | 0.831 | 0.825 | 0.831 | 0.851 | 0.845 | 0.850 | 0.870 | 0.863 | 0.871 | 0.871 | 0.861 | 0.870 | |
| 100 | 0.831 | 0.825 | 0.830 | 0.839 | 0.832 | 0.839 | 0.873 | 0.866 | 0.873 | 0.890 | 0.882 | 0.890 | |
| teacher model | 0.852 | 0.847 | 0.854 | 0.870 | 0.865 | 0.871 | 0.880 | 0.874 | 0.880 | 0.894 | 0.886 | 0.893 | |
| OA | K | F1 | FPS | Parameters | ||||
|---|---|---|---|---|---|---|---|---|
| student model | direct training | 0.6838 | 0.6680 | 0.6710 | 334.40 | 66,933 | ||
| KD training | T | |||||||
| 1 | 1 | 0.6933 | 0.6780 | 0.6918 | ||||
| 1 | 0.1 | 0.7105 | 0.6960 | 0.7079 | ||||
| 5 | 1 | 0.7200 | 0.7060 | 0.7201 | ||||
| 5 | 0.1 | 0.6933 | 0.6780 | 0.6820 | ||||
| 10 | 1 | 0.7124 | 0.6980 | 0.7092 | ||||
| 10 | 0.1 | 0.6990 | 0.6840 | 0.6871 | ||||
| 20 | 1 | 0.6838 | 0.6680 | 0.6787 | ||||
| 20 | 0.1 | 0.7067 | 0.6920 | 0.7063 | ||||
| 50 | 1 | 0.7181 | 0.7040 | 0.7098 | ||||
| 50 | 0.1 | 0.7067 | 0.6920 | 0.6993 | ||||
| 100 | 1 | 0.7352 | 0.7220 | 0.7338 | ||||
| 100 | 0.1 | 0.6724 | 0.6560 | 0.6691 | ||||
| teacher model | 0.8438 | 0.8360 | 0.8402 | 137.12 | 3,658,389 | |||
| OA | K | F1 | FPS | Parameters | ||||
|---|---|---|---|---|---|---|---|---|
| student_model | direct training | 0.7896 | 0.7848 | 0.7894 | 303.67 | 1,389,165 | ||
| KD training | T | |||||||
| 1 | 1 | 0.7911 | 0.7864 | 0.7904 | ||||
| 1 | 0.1 | 0.7705 | 0.7653 | 0.7705 | ||||
| 5 | 1 | 0.7945 | 0.7899 | 0.7923 | ||||
| 5 | 0.1 | 0.8000 | 0.7955 | 0.7983 | ||||
| 10 | 1 | 0.7945 | 0.7899 | 0.7940 | ||||
| 10 | 0.1 | 0.7926 | 0.7879 | 0.7912 | ||||
| 20 | 1 | 0.7939 | 0.7892 | 0.7933 | ||||
| 20 | 0.1 | 0.7873 | 0.7825 | 0.7862 | ||||
| 50 | 1 | 0.7907 | 0.7860 | 0.7891 | ||||
| 50 | 0.1 | 0.7893 | 0.7845 | 0.7880 | ||||
| 100 | 1 | 0.7915 | 0.7868 | 0.7907 | ||||
| 100 | 0.1 | 0.7912 | 0.7865 | 0.7892 | ||||
| teacher model (ResNet-101) | 0.8703 | 0.8674 | 0.8692 | 88.90 | 42,468,013 | |||
| OA | K | F1 | FPS | Parameters | ||||
|---|---|---|---|---|---|---|---|---|
| student model | direct training | 0.9333 | 0.9258 | 0.9336 | 440.00 | 511,050 | ||
| KD training | T | |||||||
| 1 | 1 | 0.9363 | 0.9291 | 0.9360 | ||||
| 1 | 0.1 | 0.9363 | 0.9291 | 0.9362 | ||||
| 5 | 1 | 0.9376 | 0.9305 | 0.9376 | ||||
| 5 | 0.1 | 0.9300 | 0.9221 | 0.9299 | ||||
| 10 | 1 | 0.9352 | 0.9279 | 0.9352 | ||||
| 10 | 0.1 | 0.9335 | 0.9260 | 0.9334 | ||||
| 20 | 1 | 0.9389 | 0.9320 | 0.9388 | ||||
| 20 | 0.1 | 0.9283 | 0.9203 | 0.9286 | ||||
| 50 | 1 | 0.9320 | 0.9243 | 0.9319 | ||||
| 50 | 0.1 | 0.9391 | 0.9322 | 0.9389 | ||||
| 100 | 1 | 0.9430 | 0.9365 | 0.9429 | ||||
| 100 | 0.1 | 0.9398 | 0.9330 | 0.9397 | ||||
| teacher model (ResNet-101) | 0.9474 | 0.9415 | 0.9471 | 98.93 | 42,396,298 | |||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, G.; Zhang, X.; Tan, X.; Cheng, Y.; Dai, F.; Zhu, K.; Gong, Y.; Wang, Q. Training Small Networks for Scene Classification of Remote Sensing Images via Knowledge Distillation. Remote Sens. 2018, 10, 719. https://doi.org/10.3390/rs10050719
Chen G, Zhang X, Tan X, Cheng Y, Dai F, Zhu K, Gong Y, Wang Q. Training Small Networks for Scene Classification of Remote Sensing Images via Knowledge Distillation. Remote Sensing. 2018; 10(5):719. https://doi.org/10.3390/rs10050719
Chicago/Turabian StyleChen, Guanzhou, Xiaodong Zhang, Xiaoliang Tan, Yufeng Cheng, Fan Dai, Kun Zhu, Yuanfu Gong, and Qing Wang. 2018. "Training Small Networks for Scene Classification of Remote Sensing Images via Knowledge Distillation" Remote Sensing 10, no. 5: 719. https://doi.org/10.3390/rs10050719
APA StyleChen, G., Zhang, X., Tan, X., Cheng, Y., Dai, F., Zhu, K., Gong, Y., & Wang, Q. (2018). Training Small Networks for Scene Classification of Remote Sensing Images via Knowledge Distillation. Remote Sensing, 10(5), 719. https://doi.org/10.3390/rs10050719







