1. Introduction
Recognition of tree species and acquiring geospatial information about tree species composition is essential in forest management, as well as in the management of other wooded habitats. In forest management, information about tree species dominance or species composition is needed, among other things, for estimating the woody biomass and growing stock and the estimation of the monetary value of the forest, e.g., [
1,
2,
3]. Furthermore, information about tree species is required for designing appropriate silvicultural treatments for stands or individual trees and for forecasting future yields and cutting potential, e.g., [
4]. For assessing non-timber forest resources, such as forest biodiversity or mapping wildlife habitats, knowledge of the tree species is equally essential, e.g., [
5]. In addition, controlling for biohazards caused by invasive and/or exotic pest insects brought about by timber trade or the use of wooden packing materials, trees of certain species or genus may need to be urgently located and/or removed from the infested area, such as in the case of the widely-spread Dutch elm disease [
6], or the recent Asian long-horned beetle (
Anoplophora glabripennis) infestation in Southern Finland [
7].
Traditionally, forest inventory methods based on the utilization of remote sensing data have used forest stands or sample plots as inventory units when estimating forest variables, such as the amount of biomass volume of growing stock, as well as averaged variables, such as the stand age or height. However, stand level forest variables are typically an average or sum from a set of trees, of which the stand or sample plot are composed, and a certain amount of information is lost even when aiming at ecologically homogeneous inventory units. In the calculation, forest inventory variables, such as the volume and biomass of the growing stock, and tree level models are typically used nowadays, e.g., [
1,
2,
3]. Very high resolution remote sensing data allows moving from the stand level to the level of individual trees, e.g., [
8], which has certain benefits in forest management planning. In temperate and boreal forests stands often have several tree species which may differ from each other in relation to their growing characteristics. Furthermore, the size and growth of individual stems varies due to genetic properties and due to their position in relation to the dominance and competition within the stand. Especially for harvest management purposes, information on single trees is desirable, as harvesting decisions based on average stand characteristics may not provide optimal results [
9]. Increasing the level of detail can also improve detailed modelling of forests and this can be used to predict forest growth and to improve satellite-based remote sensing by modelling the radiative transfer more accurately within the forest canopy.
Forest and tree species classification using multi- or hyperspectral (HS) imaging or laser scanning has been widely studied [
10,
11,
12,
13,
14,
15]. However, the data has mainly been captured from manned aircraft or satellites, and the studies have focused more on the forest or plot level. The challenge for passive imaging has been the dependence on sunlight (i.e., the object reflectance anisotropy) and the high impact of changing and different illumination conditions on the radiometry of the data, e.g., [
16,
17,
18]. Shadowing and brightening of individual tree crowns causes the pixels of a single tree crown to range from very dark pixels to very bright pixels. Few methods have been developed and suggested to reduce the effect of the changing illumination of the forest canopy, e.g., [
19,
20,
21,
22,
23].
Individual trees have been detected using passive data mainly using image segmentation, e.g., [
24,
25], but the development of dense image matching methods and improved computing power have enabled the production of high resolution photogrammetric point clouds. Their ability to provide structural information of forest has been examined by e.g., Baltsavias et al. [
26], Haala et al. [
27] and St-Onge et al. [
28]. Photogrammetric point clouds provide accurate top-of-the-canopy information that enables the computation of canopy height models (CHM), e.g., [
26], and thus provides a means for the detection of individual trees. However, the notable limitation of photogrammetric point clouds compared to laser scanning is that passive imaging does not have good penetration ability, especially with aerial data from manned aircraft. Thus, laser scanning, which can deeper penetrate forest canopies, has been the main operational method to provide information about the forest structure. Photogrammetric point clouds derived from data captured using manned aircraft have been used, but the spatial resolution is not usually accurate enough to produce good detection results.
The use of UAVs in aerial imaging has enabled aerial measurements with very high spatial resolution and has improved the resolution of photogrammetric point clouds of forests to a level of 5 cm point interval, or even denser. The development of light-weight HS cameras has enabled the measurement of high spectral resolution data from UAVs [
29]. In several studies push-broom HS imaging sensors have been implemented in UAVs [
30,
31,
32,
33]. One of the recent innovations are HS cameras operating in a 2D frame format [
34,
35,
36,
37]. These sensors provide the ability to capture very high spatial resolution HS images with GSDs of 10 cm and even less and to carry out 3D data analysis, thus giving very detailed spectral information about tree canopies. Since UAVs are usually small in size, their sensor load and the flying range are somewhat limited, which makes their use less feasible in typical operational forest inventory areas.
Some studies have used data from UAV-borne sensors for individual tree detection with excellent results, e.g., [
38]. Tree species classification from UAV data has not been widely studied, especially concerning simultaneous individual tree detection. Näsi et al. [
39] used UAV-based HS data on an individual tree scale to study damage caused by bark beetles. Previously, Nevalainen et al. [
22] have studied individual tree detection and species classification in boreal forests using UAV-borne photogrammetric point clouds and HS image mosaics.
Novel HS camera technology based on a tunable Fabry-Pérot interferometer (FPI) was used in this study. The first prototypes of the FPI-based hyperspectral cameras were operating in the visible to near-infrared spectral range (500–900 nm; VNIR) [
35,
36,
37]. The FPI camera can be easily mounted on a small UAV together with an RGB camera which enables simultaneous HS imaging with high spatial resolution photogrammetric point cloud creation. The objective of this study was to investigate the use of high resolution photogrammetric point clouds in combination with HS imagery based on two novel cameras in VNIR (400–1000 nm) and short-wavelength infrared, an SWIR (1100–1600 nm) spectral ranges in tree species recognition in an arboretum with large numbers of tree species. The effect of the applied classifier and the importance of different spectral and 3D structural features, as well as reflectance calibration for tree species classification in complex environments, were also investigated. The preliminary analysis results have been described earlier by Näsi et al. [
40]. This article is an extended version of a conference paper by Tuominen et al. [
23].
4. Discussion
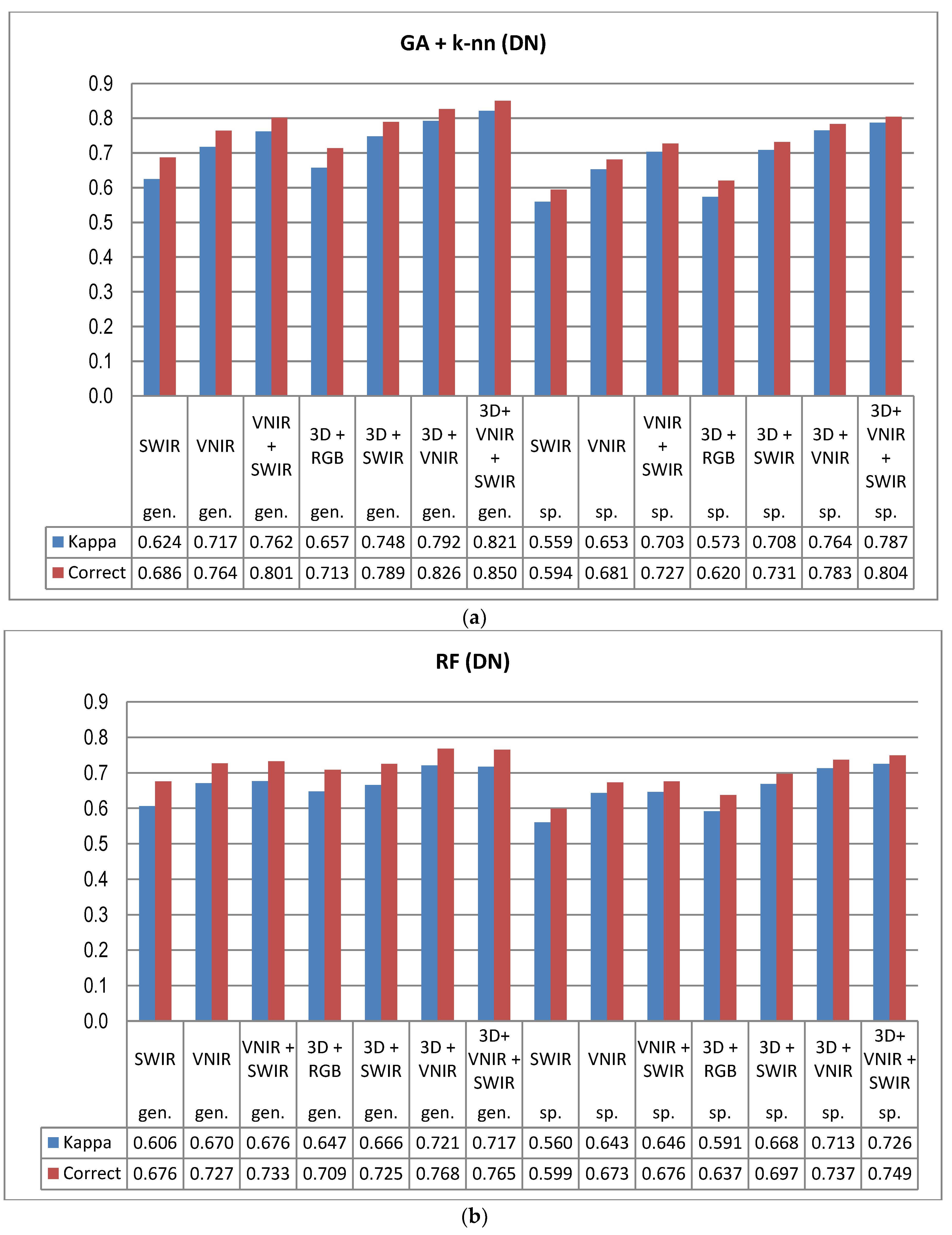
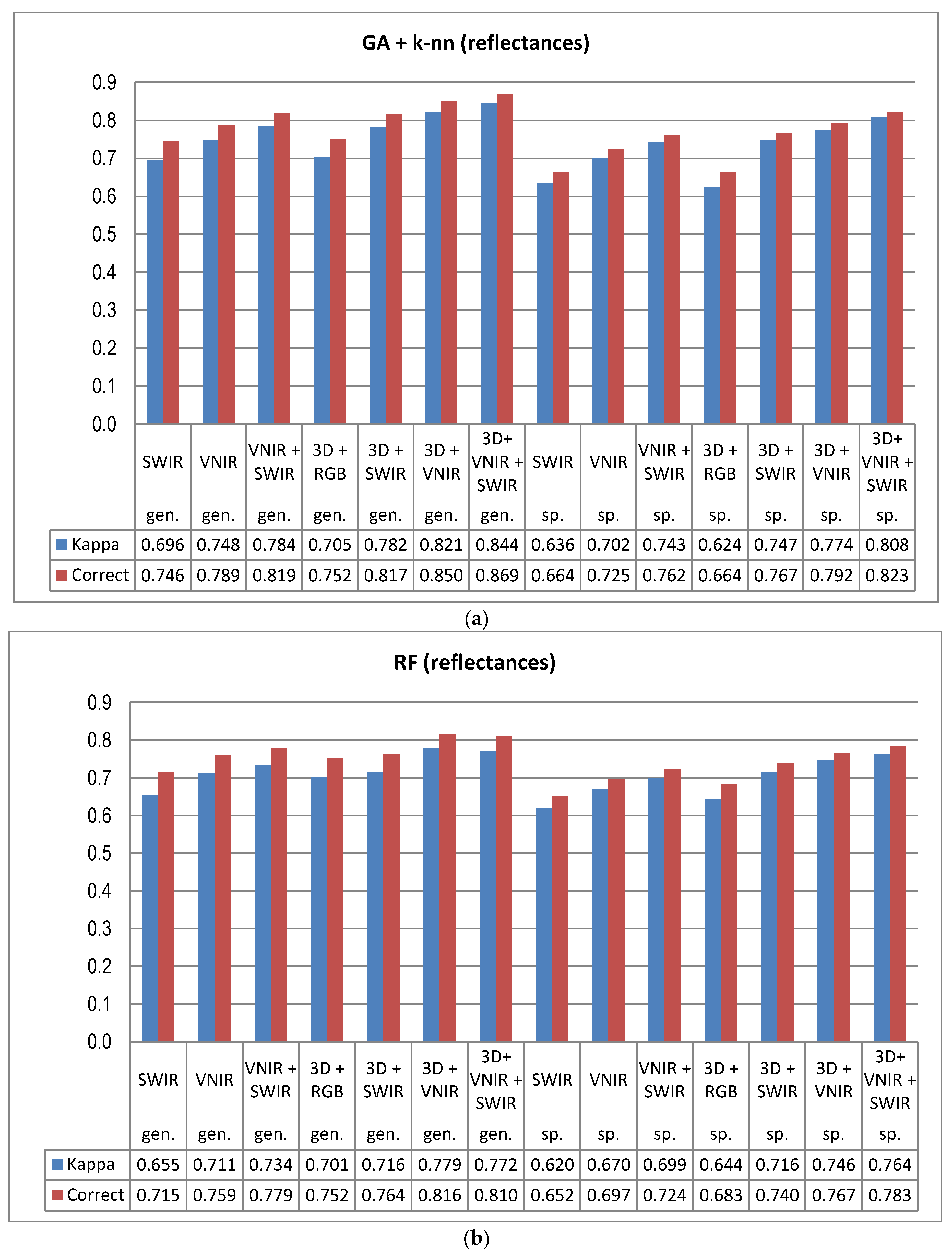
The combination of HS bands over a wide spectral range and 3D features from point cloud data allows the extraction of a very high number of remote sensing features for the classification task. As a consequence, the classification task is carried out in a high-dimensional feature space. As the dimensionality grows, all data typically become sparse in relation to the dimensions [
50], which causes problems for classifiers based on the distance or proximity in the feature space, such as k-nn, e.g., [
49]. In hyper-dimensional feature space, the distances from any point to its nearest and farthest neighbors tend to become similar [
49], which makes it questionable whether the nearest neighbors found are the true nearest neighbors. Therefore, the number of remote sensing features must be reduced for producing an appropriate subset of features for the classification task considering their usefulness in recognizing the classes, as well as their mutual correlation. In recent forest estimation and classification studies various algorithms have been applied for this purpose [
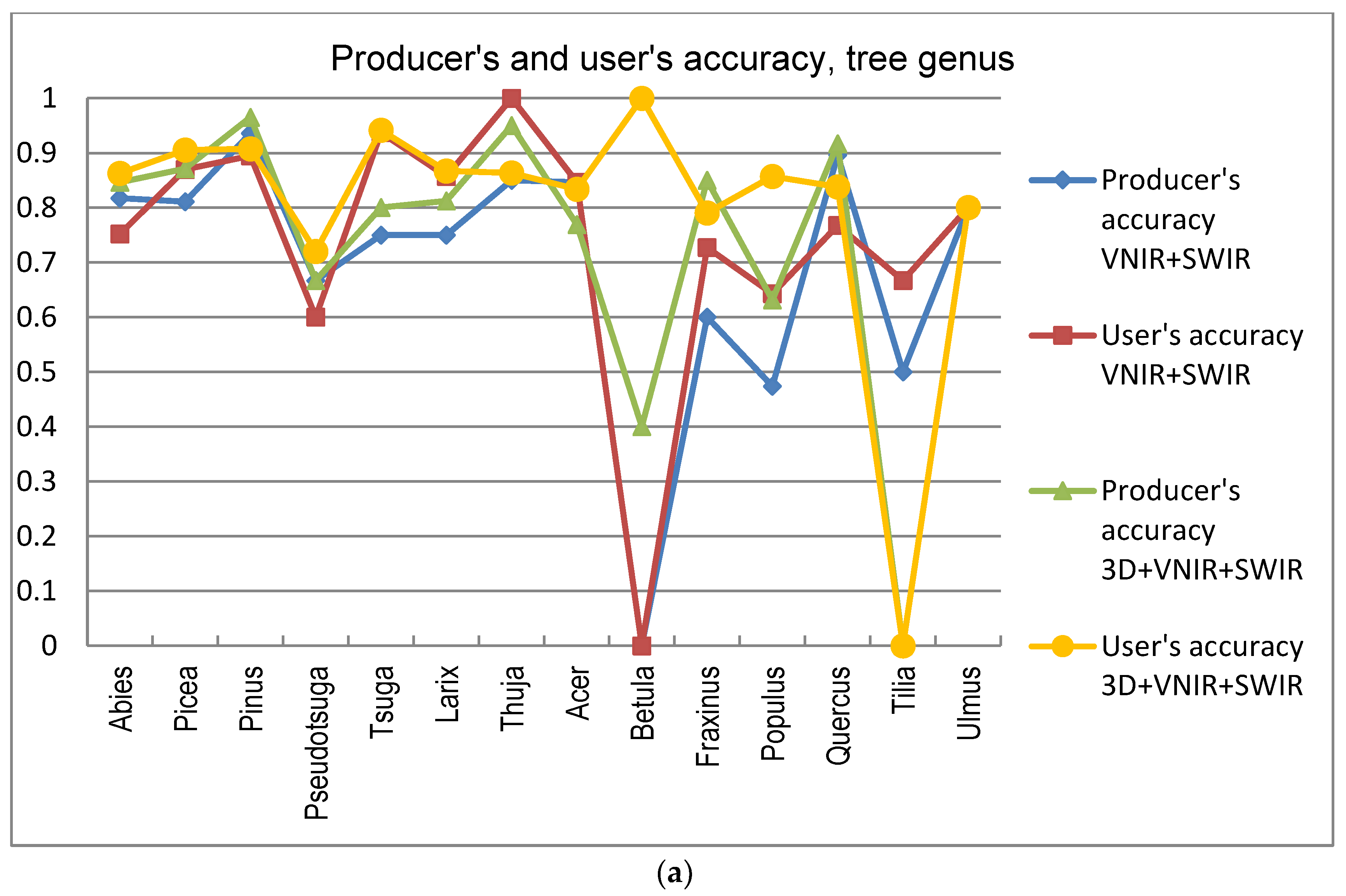
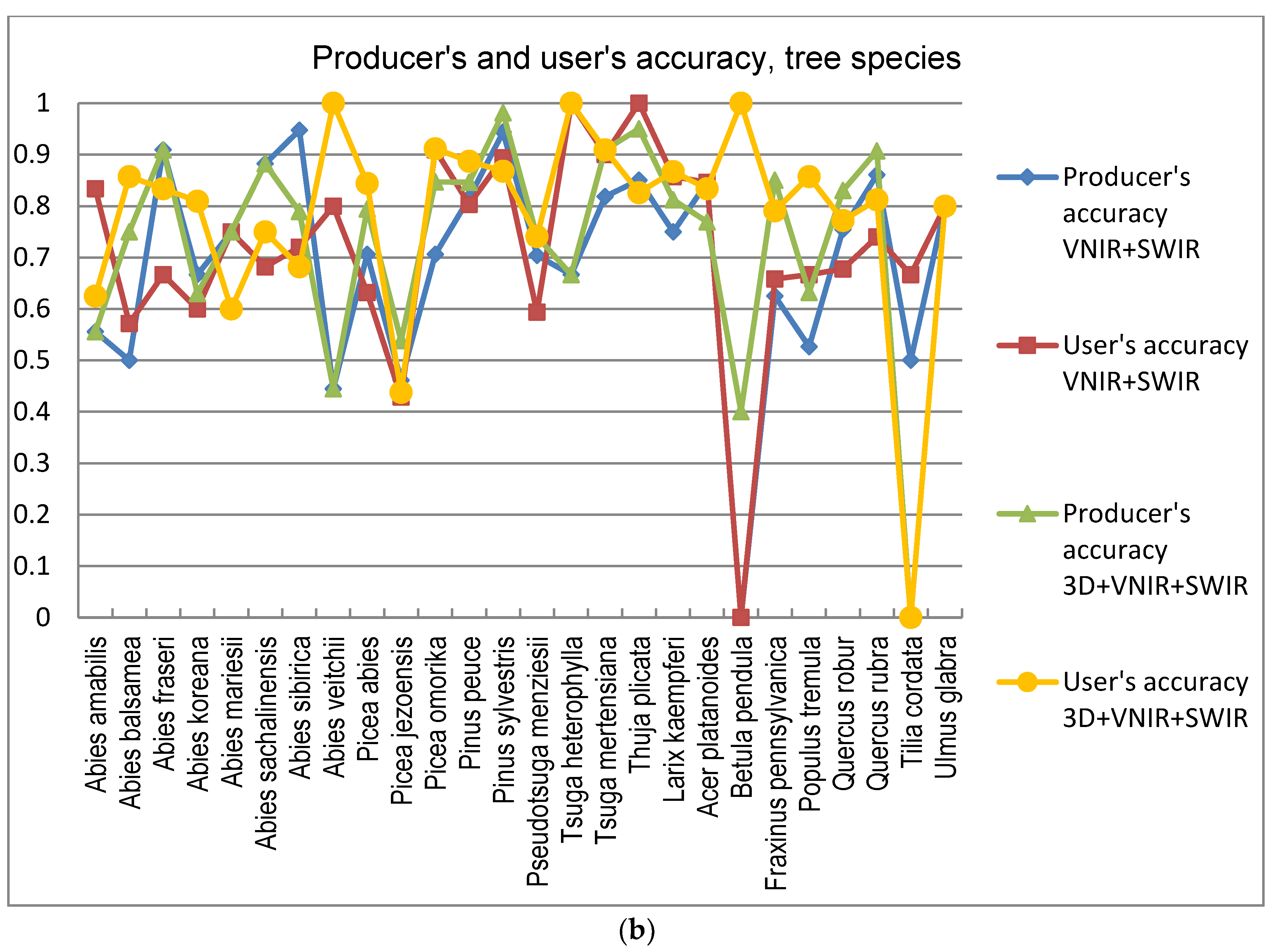
5]. In this study the GA procedure used in combination with a k-nn classifier provided otherwise consistently better results in tree species and genus recognition than RF, with the exception of 3D+RGB (the dataset having the lowest number of features) where RF performed slightly better. Thus, the GA algorithm applied here was found to be a viable tool for finding an appropriate set of features for this task, especially in a very high-dimensional feature space, such as that tested in this study. Both classification methods applied in this study have feature selection components which are stochastic by nature, which means that there is a random effect in their results. This effect was apparent especially in those tree species which had few test trees, and the user’s and producer’s accuracy of these species varied highly between 0–1 with different feature combinations (see
Figure 9a,b).
Another main finding of this study was the significance of the calibration of the HS imagery for tree species recognition. Compared to pixel DN values that were disturbed according to the variations in the illumination levels and sensor characteristics, the calibrated reflectance consistently provided better results in tree species and genus recognition, and this trend was similar across all the spectral band combinations tested here. Although the HS image acquisition was carried out in clear sunny weather conditions, it was necessary to compensate for the illumination changes caused by varying solar elevation over the 5–6 h of data capture each day. We used the empirical line method to carry out the calibration. In UAV campaigns, there are always variations in pixel values that are caused by other factors than the properties of the target of observation (i.e., tree canopies), such as changing illumination by solar elevation and azimuth angles, as well as object reflectance anisotropy effects or illumination changes due to clouds, which necessitate, in most cases, the use of advanced methods for image calibration in order to be able to utilize the full potential of HS imagery. The radiometric block adjustment is an example of such a method [
22,
35,
39].
Despite the high spectral and radiometric resolution of the HS imagery applied, the inclusion of 3D features extracted from point cloud data of the stereo-photogrammetric canopy surface model always improved the accuracy of tree species recognition. The dataset having the least spectral information (i.e., 3D+RGB) generally resulted in similar accuracy as the poorest performing HS data (SWIR) without 3D. To a certain extent, the effect of reflectance calibration and 3D features was also complementary; when original pixel values were applied, the effect of 3D features was more prominent than with calibrated reflectances and the use of calibrated reflectances had smaller effects on the accuracy when the classification was based on data combinations that included 3D features. It is possible that the calibration could have resulted in even greater improvements to the results, if the weather had been more variable [
23]. In operational forest inventories the significance of 3D data is typically considerably higher, since there are many other variables of importance, such as the volume of growing stock and the amount of biomass, as well as variables related to the size of the trees, e.g., stand mean diameter and height, where 3D data is a key factor in their accurate prediction. Based on our results, the SWIR-range data did not provide advantages for the classification, thus VNIR-hyperspectral data was sufficient. The approach integrating spectral and 3D features has significant potential to develop a high-performing automatic classifier.
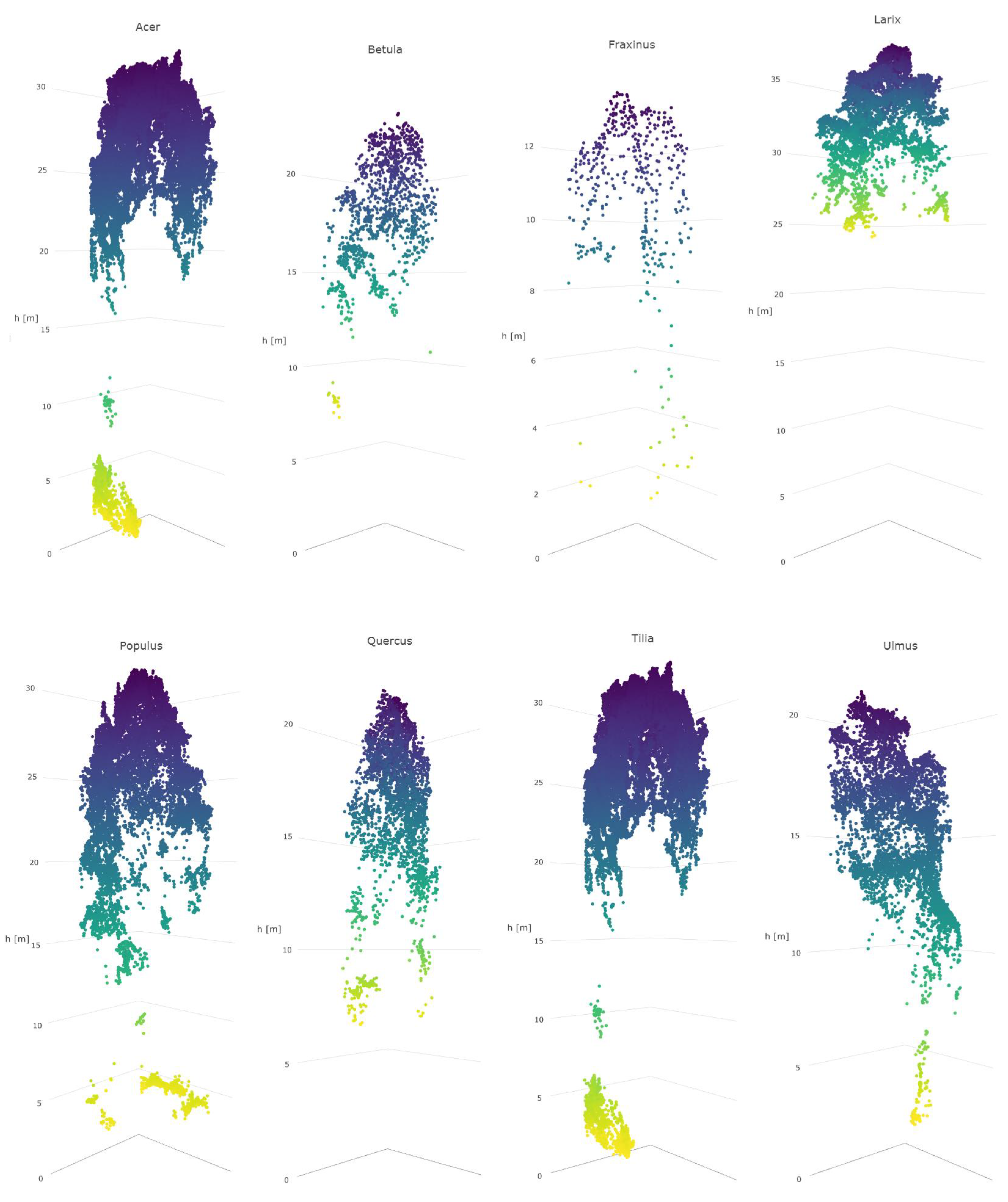
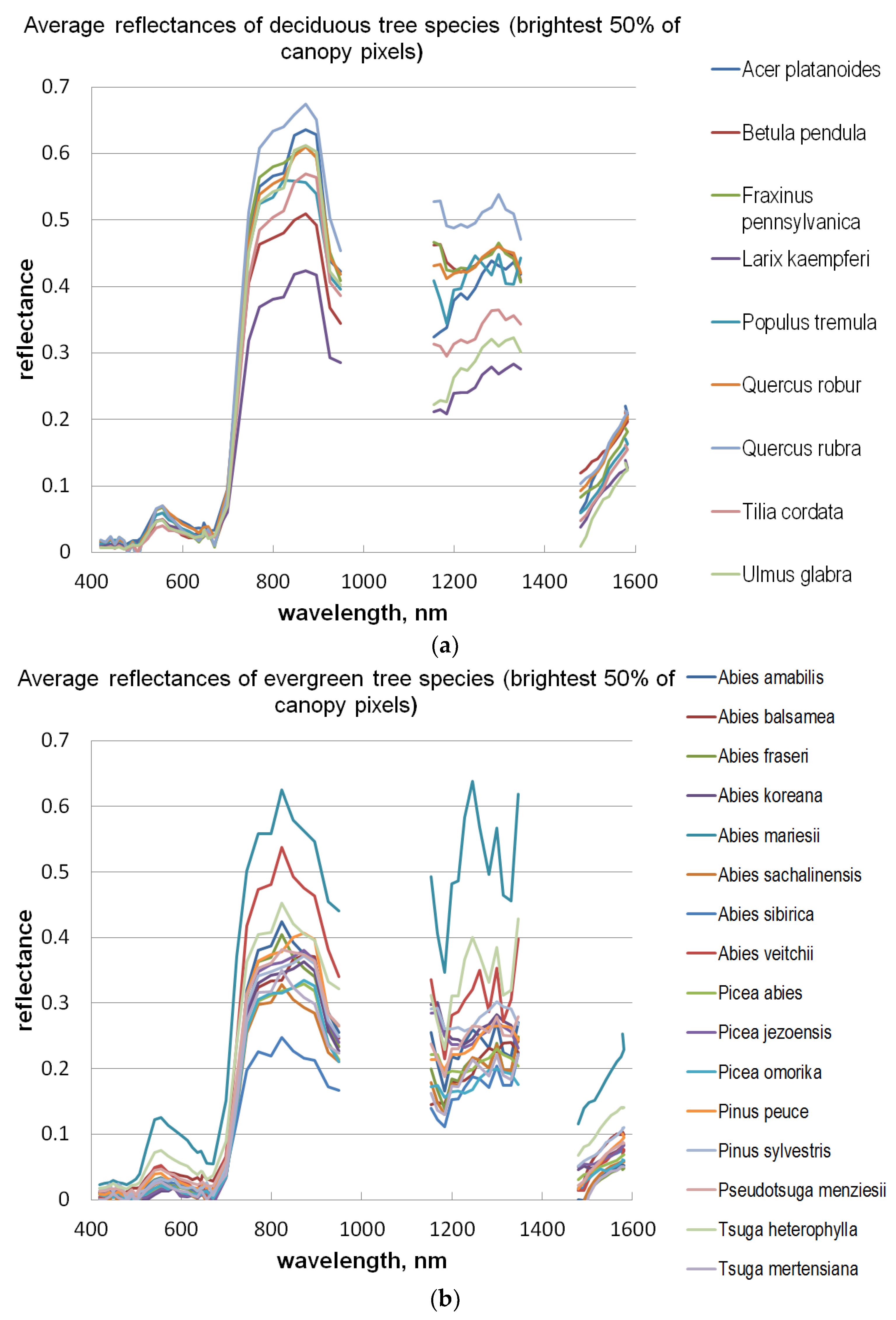
A number of broadleaved tree species that occur naturally primarily in the temperate vegetation zone and in the study area are on the northern edge of the distribution map, such as
Tilia cordata,
Ulmus glabra,
Acer platanoides, and
Quercus sp., are difficult to distinguish from each other, even with a combination of HS and 3D data. Apparently, their spectral properties, as well as the geometric shape of the canopy, seem to resemble each other (see
Figure 8). Additionally, the classification of
Betula had a very low level of accuracy, and it was often confused with other broadleaved trees. This is somewhat contrary to expectations, since the leaves of
Betula sp. somewhat differ from other broadleaved trees in the test material. The poor accuracy of these species may be partly because some of these species had a low number of trees in the test data.
Trees belonging to
Larix sp. which, botanically, are classified as conifers, have spectral characteristics mainly resembling broadleaved trees, due to the properties of their needles, e.g., [
63]. Here, also,
Larix sp. trees were partly confused with broadleaved trees, which was otherwise rare for other coniferous trees. Trees belonging to
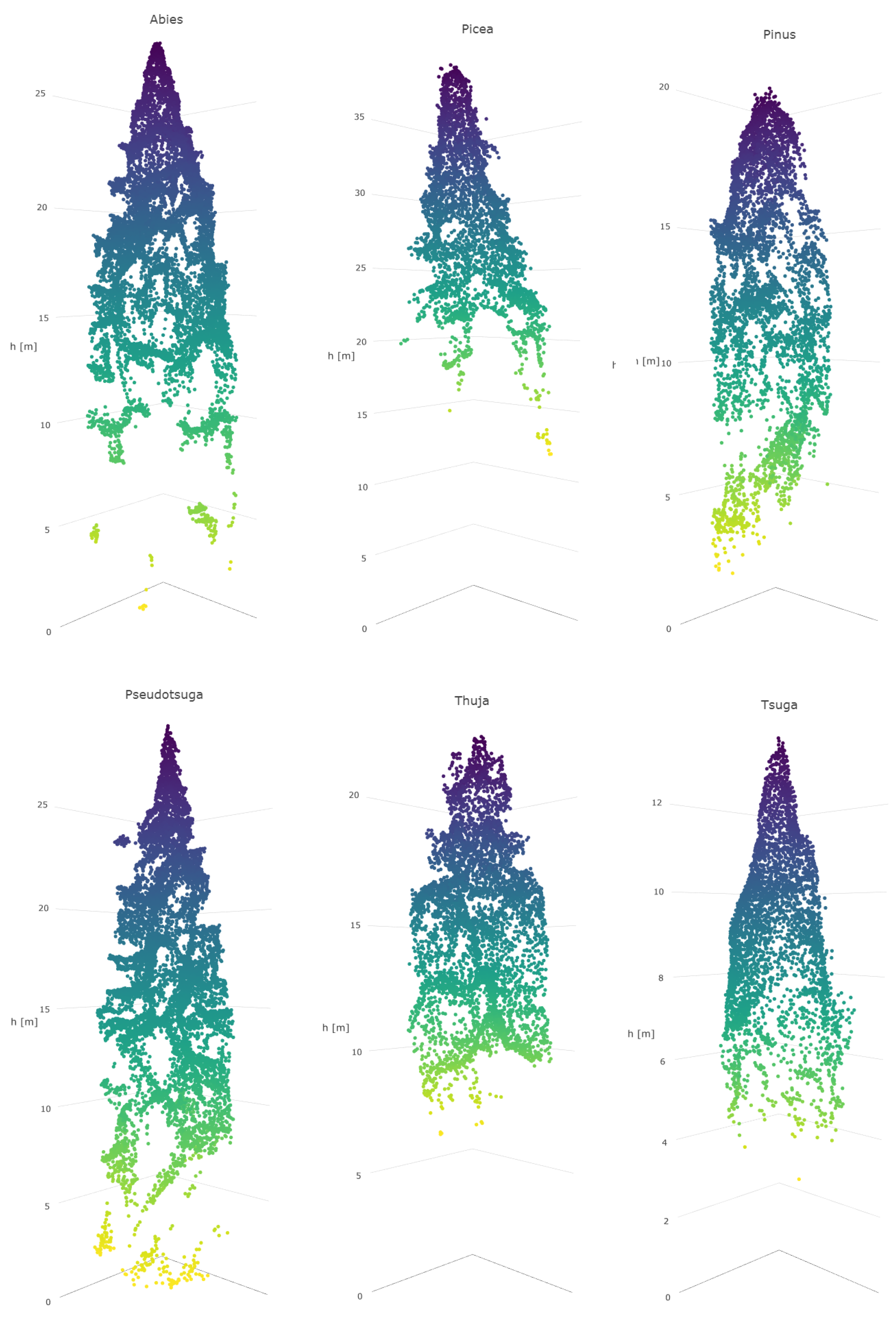
Abies sp.,
Picea sp.,
Pseudotsuga sp., and
Tsuga sp. were sometimes difficult to distinguish from each other due to the similar physical appearance of their canopies in the 3D data. Furthermore, in the classification on the individual tree species level, members of
Abies sp. were often confused with each other, due to their similarity even when observed in the field. Of all the tree genera,
Thuja sp. (only one species included in the study material,
Thuja plicata) had the highest producer’s level of accuracy, which was intuitively foreseen since
Thuja sp. has a peculiar needle form, which apparently can be clearly distinguished by HS bands. This was obvious since the classification accuracy of
Thuja sp. is high even when HS bands are used without 3D data. In addition, also the canopy form of
Thuja sp. was somewhat unique among the test trees.
In this study we used test material, where trees formed stands or tree groups that showed homogeneous species composition. In natural forests, however, canopies of different species are often intermingled with each other, causing further complication for individual tree-level recognition, whose effect was not studied here. Due to the selection of the test material, a similar level of accuracy may not be achieved in operational forest inventories where the target forests are often mixed.
Most previous studies concerning tree species classification using the UAV-based (as well as other airborne) datasets have been carried out in forests with less-diverse species structure. Generally, in studies concerning Nordic conditions there are few tree species present [
14]. Nevalainen et al. [
19] used an FPI camera operating in the wavelength range of 500–900 nm in the classification of five species in a boreal forest. The best results were obtained with RF and multilayer perceptron (MLP), which both gave 95% overall accuracies and kappa values of 0.90–0.91. Our analysis in the study area of higher species diversity did not reach as high an accuracy, but also the task was more complex. In Norwegian boreal forest conditions Dalponte et al. [
13] have used ALS and hyperspectral data for separating pine, spruce, and broadleaved species using support vector machines, achieving overall accuracies as high as of 93.5% and kappa values of 0.89 for those three species. Dalponte et al. [
13] have noted that using automatic tree delineation instead of manual delineation lowered the accuracy markedly. We delineated tree crowns manually for this study in order to focus on the performance of the input data and classifiers. In operational applications automatic delineation of tree crowns should be applied, which brings an additional source of potential errors in species recognition. Thus, for an operational application, the results of this study may give too optimistic an impression.
In studies applying more diverse species material the level of accuracy similar to this study have been reported by, e.g., Zhang and Hu [
15], who achieved an overall accuracy of 86.1% and kappa coefficient of 0.826 using a combination of spectral, textural, and longitudinal crown profile features extracted from high-resolution multispectral imagery. However, their test material covered only six tree species from an urban environment. Zhang and Hu [
15] argue that the shape of trees is likely to be more species-specific in urban areas (due to lower competition) than in forests. Waser et al. [
12] have used LiDAR in combination with RGB and CIR imagery in an alpine forest, achieving overall accuracies between 0.76 and 0.83, and kappa values between 0.70 and 0.73 with multinomial regression models. The test data of Waser et al. [
12]. consisted of nine tree species. Ballanti et al. [
64]. have tested combination of LiDAR and hyperspectral imagery in the Western USA using support vector machines and RF as classifiers, achieving accuracies between 91 and 95%, their test data consisted of eight tree species with a relatively wide range of physiological characteristics.
Accurate tree species recognition was achieved by Kim et al. [
65] with test material of even higher species diversity (15 species) using LiDAR data, but their best recognition (over 90%) was achieved by combining LiDAR data from both leaf-on and leaf-off seasons. However, with single-season data, the species recognition accuracy was approx. 80%, and the leaf-off data performed markedly better than data from the leaf-on season [
65]. Kim et al. [
65] have especially noted the capability of LiDAR intensity values from different seasons to distinguish various tree species. Zhang and Qiu [
66] have used a combination of LiDAR data and hyperspectral imagery for species recognition in test material of even higher species diversity (40 species), achieving an accuracy of 68.8% and a kappa value of 0.66. Aforementioned studies have used conventional aircraft as sensor platforms and, thus, applied somewhat lower spatial resolution data than this study.
It is highly likely that further improvement in species recognition accuracy can be achieved by utilizing multitemporal data in the classification process. For example, Somers and Asner [
67] found the phenology to be key to spectral separability analysis when using low spatial-resolution Hyperion data. Similar findings were made by Kim et al. [
65] using LiDAR data and Mickelson et al. [
68] using optical satellite imagery.