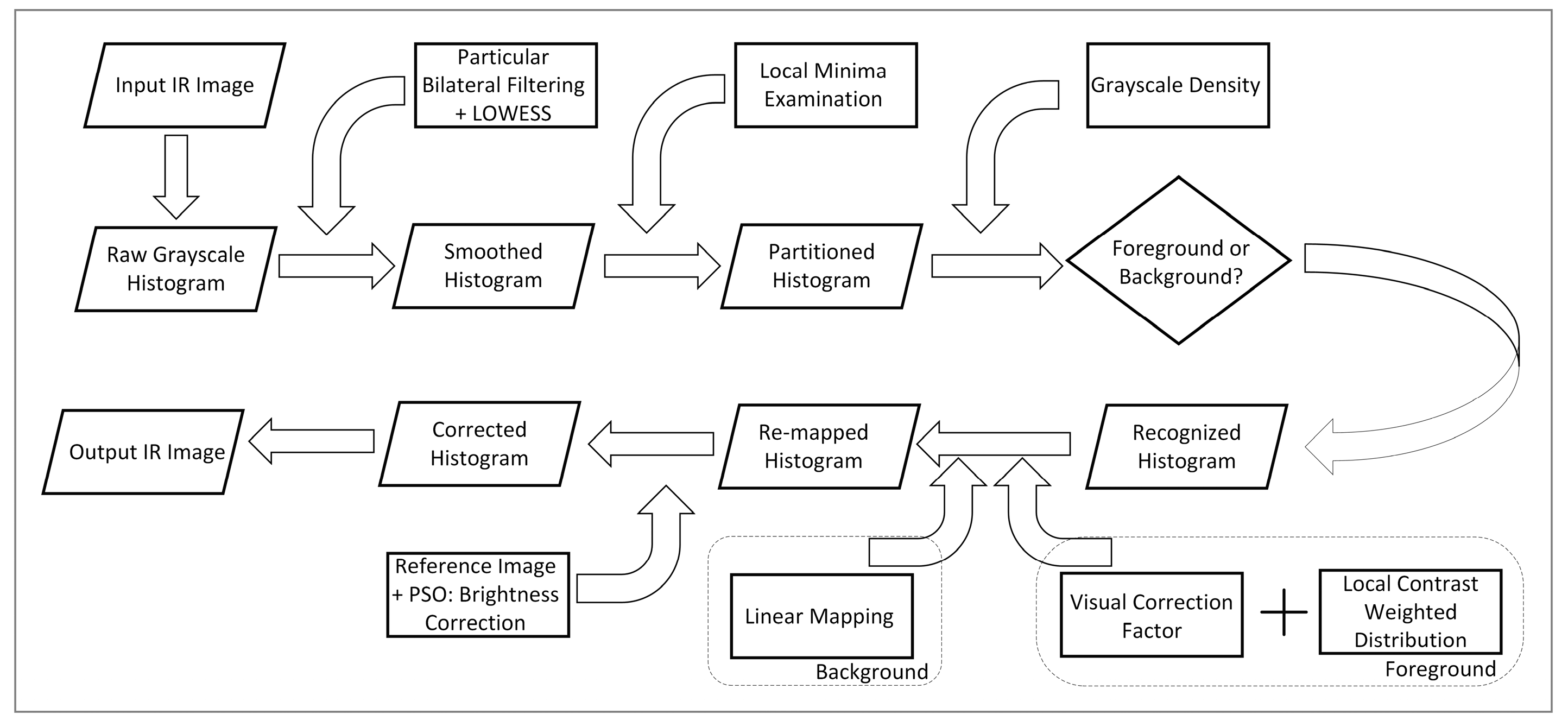
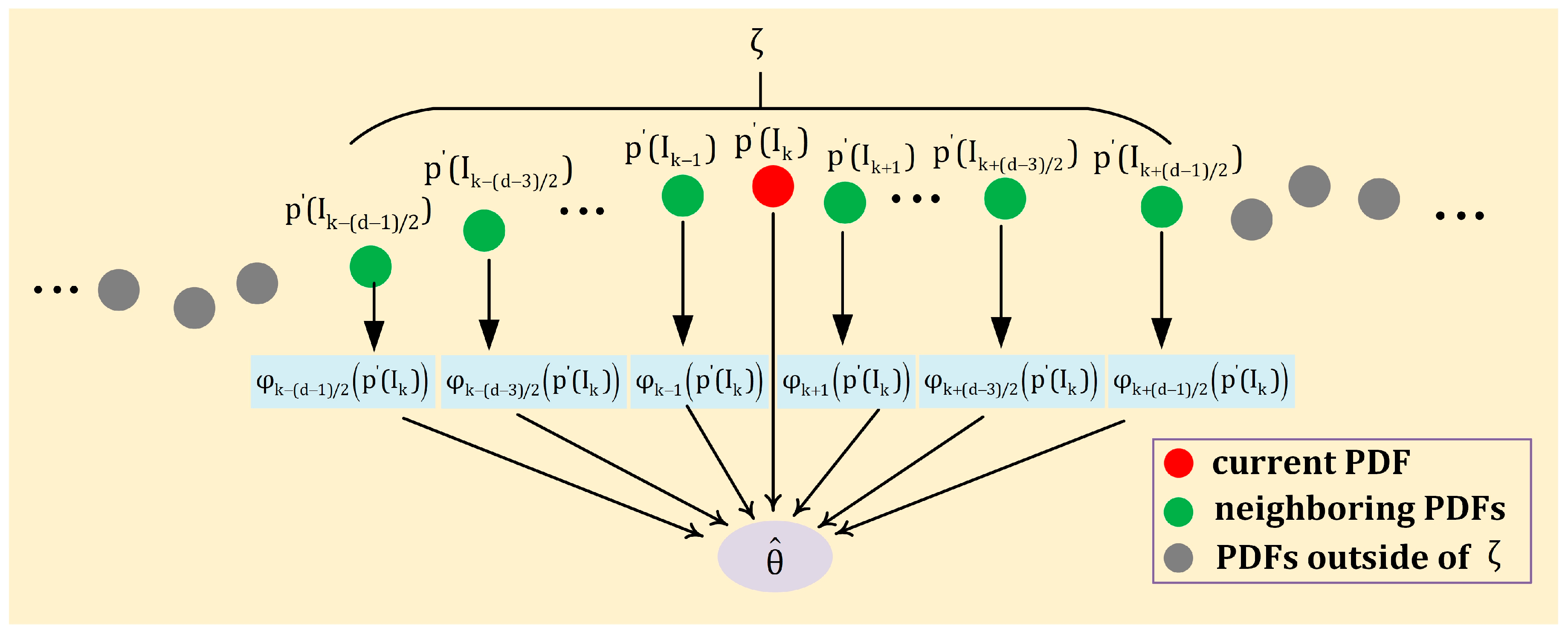
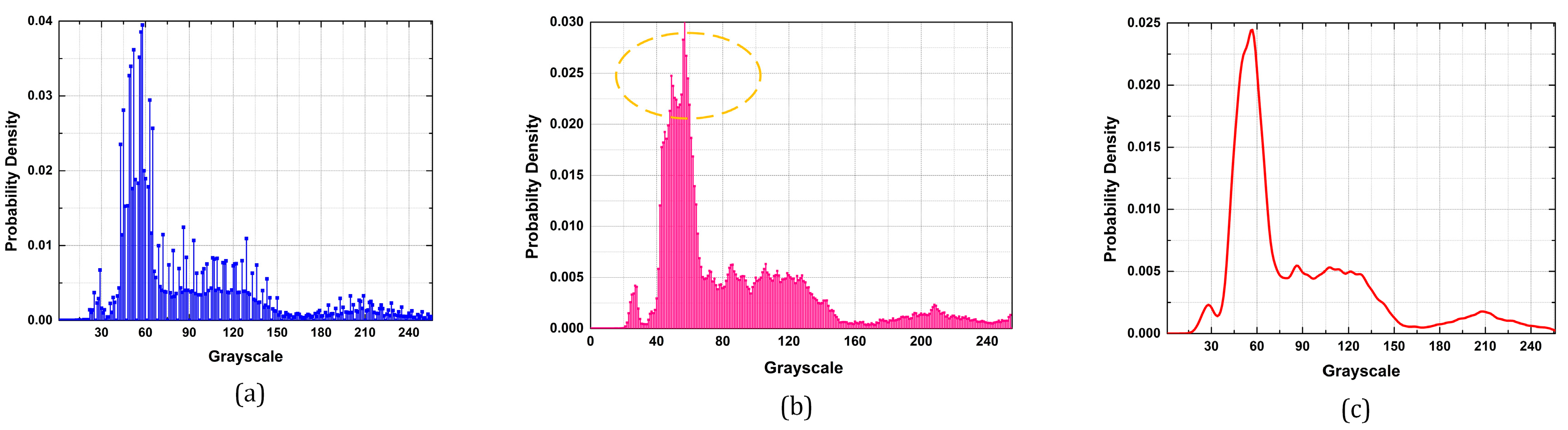
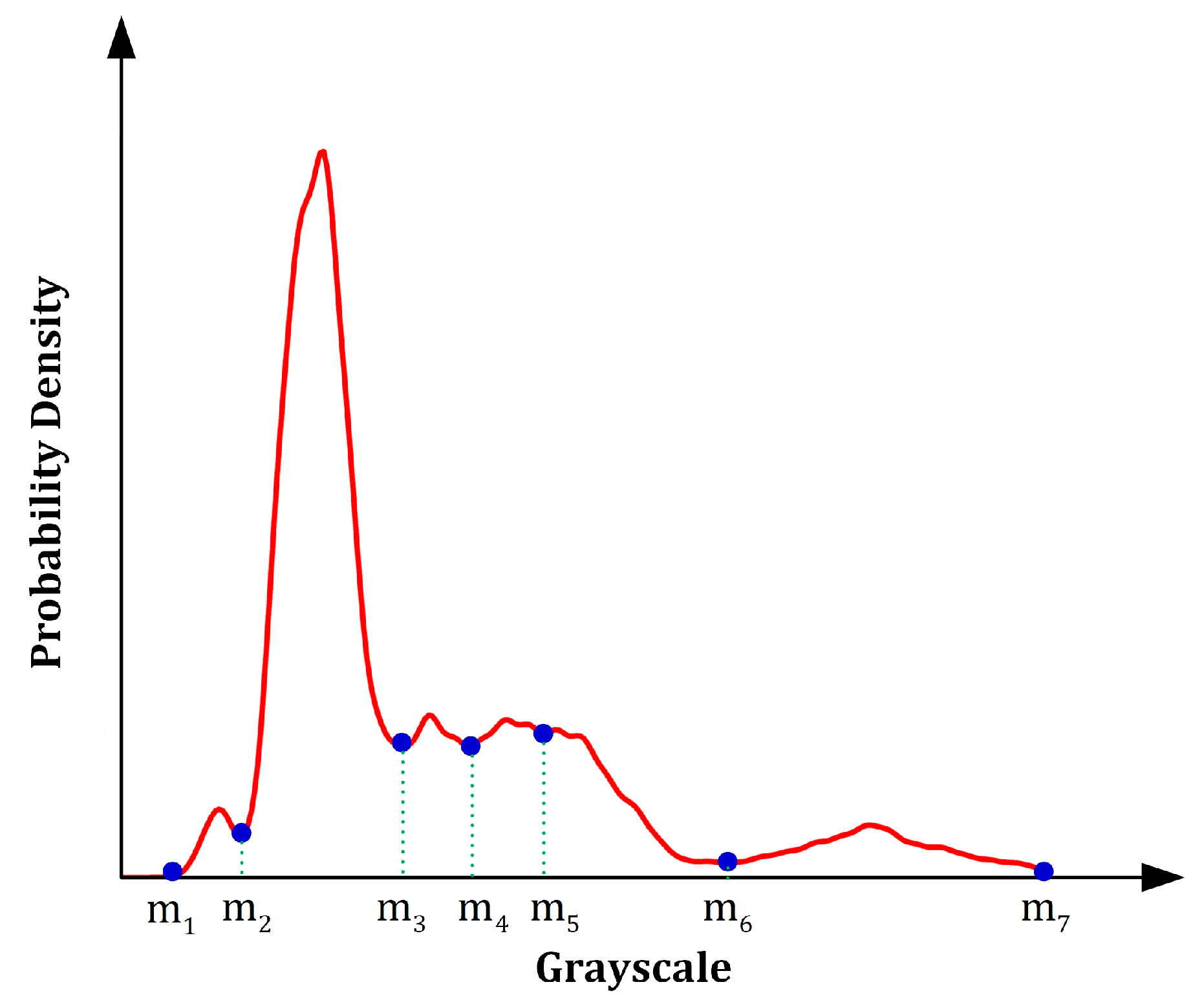
4.3.1. Comparison of Processed Result
To further verify the superiority of the presented algorithm, several extensively used metrics are applied to make quantified comparisons in this section.
First of all, the definitions of all the metrics utilized in this paper are introduced:
(1) Linear index of fuzziness
[
35] is widely applied to analyze the performance of image enhancement, which is defined as:
where, O represents the enhanced image and its width and height are M and N, respectively. and,
where, max(O) represents the maximal grayscale of O. A smaller value of
indicates a better performance of the enhanced image with fewer clutters [
36].
(2) Peak signal-to-noise ratio (PSNR) [
37,
38,
39] is commonly used for evaluating image quality and measures how much the enhanced image has degraded when referred to the input image in the area of image enhancement [
38]. Here, the formula of PSNR is given in Equation (37).
where,
denotes the maximal gray level and
for 8-bit digital images; MSE(O,I) is the mean square error between the output O and input I, which is defined as:
Besides, a larger PSNR refers to a higher image quality of the output.
(3) Image definition
[
40] is a comprehensive index integrating
and PSNR and is always used to reflect the overall definition of an enhanced image. Below, its specific definition is given as:
Ideally, a qualified result should not only improve the global contrast, but also has less degradation. Thus, for a high-quality enhanced image, a small is expected.
(4) Roughness
[
41] is used as a metric for evaluating the performance of an algorithm for noise reduction in many IR imaging applications. Here, we employ it in the following experiments for measuring the effect of noise suppression of the enhanced image. Further, the calculation of
is introduced below:
where,
and
stand for the horizonal and vertical difference filters, respectively;
is a convolution operator; and
stands for the
norm. Obviously, a smaller
is related to a smoother result with less residual noise.
(5) Discrete entropy (DE) [
42] characterizing the information amount contained in an enhanced image is employed to measure the degree of over-enhancement in our experiment. Additionally, DE is a globally statistical index which is defined as:
A larger DE means fewer gray levels are merged, leading to a clearer visual performance. Note that the essence of DE is different from the one of local entropy H defined in Equation (20), although their formulas are seemingly the same. DE is a globally counted index, but H is calculated in a local window.
(6) Logarithmic Michelson Contrast Measure (AME) [
43] denotes a measure of local contrast, and Equation (42) gives its definition as:
where, the output O is segmented into
blocks;
and
denote the maximal and minimal grayness of the block, respectively; and
is a constant for preventing the invalid values. AME aims to use the relationship between the spread and the sum of the two intensity values in each block, and a smaller AME means a better performance [
33].
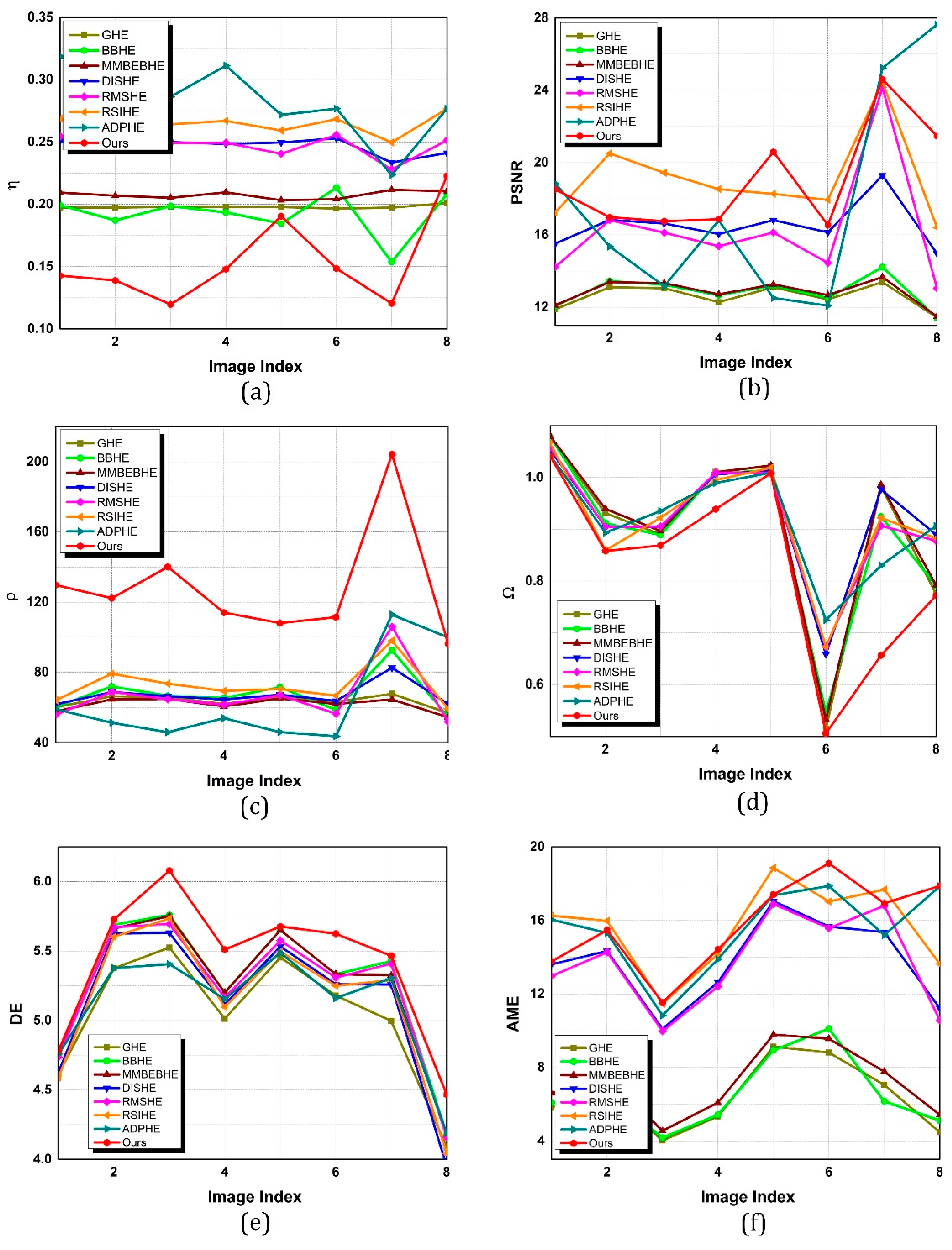
Table 3,
Table 4,
Table 5,
Table 6,
Table 7 and
Table 8 list the statistical results of the six indexes and the average values are also given in the last row of each table. To present a clearer comparison, the corresponding line graphs are also presented in
Figure 20.
On the one hand,
denotes the target/background contrast, and it also measures the quantity of clutters to a certain degree. As is shown in
Table 3 and
Figure 20a, our method achieves the best average
, implying that the foregrounds become brighter while the background clutters become darker after our enhancement. More specifically, we argue that it is the strategy of sub-histogram segmentation that enlarges the intensity difference between the fore- and background. We notice that BBHE, GHE, and MMBEBHE also result in low
values (<2) in most scenes, which matches the experimental fact that the intensity differences between target and background regions are always remarkable in their enhanced images. Besides, the average
of RSIHE is the worst, which is about 10% larger than ours and it proves that the serious over-enhancement is somewhat related to the degradation of global contrast.
Unlike its poor performance related to
, RSIHE has the most satisfactory PSNR on the whole, while our method still takes second place in this metric. Since PSNR reflects the degree of image degradation, we consider that if the PSNR value is excessively large, a large amount of detail information is lost at the same time. That is the reason why the enhanced images processed by RSIHE are fogged and their PSNRs are always very high. By contrast, our method maintains a balance between PSNR (slightly larger than ADPHE and RMSHE) and exhibits the preservation of details, meaning that not only the visual performance presented in
Section 4.2, but also the quantitative evaluation of image degradation, is qualified.
As is mentioned above, is a comprehensive index measuring the overall performance of image enhancement. Since our method results in comparatively remarkable performances in both and PSNR, its values of all the test images thus keep the advantage. Relying on its outstanding achievements in , the average value of our method is almost two times that of RSIHE, which possesses the second largest value. One point that should be noticed is that those algorithms overly emphasizing input brightness preservation, e.g., BBHE, MMBEBHE, DISHE, RMSHE and RSIHE, sacrifice the fore- and background contrast instead, which leads to their poor performances in and .
is commonly utilized to reflect the smoothness of image. As is shown in
Figure 20d, BBHE and our method obtain the top two
values, whereas DISHE presents the worst one. Since the background occupies the majority of an image and the background histograms are not equalized in our method, the noise is not amplified and the smoothness is thus satisfactory. However, some grayscale histogram equalization-based algorithms, like GHE and MMBEBHE, quite easily generate over-enhancement in high grayscales and image noise precisely tends to center on high grayscales, so the effects of the noise suppression of these algorithms greatly decrease. According to
Table 6, we also see that ADPHE’s capability of removing noise through the adaptive upper threshold is limited in IR images considering its comparatively high
values.
DE is a significant index that directly measures the degree of over-enhancement. Through observing its definition, we can easily find that if more grayscales are merged by equalization, the entropy of the image will decrease more. Clearly, our method has a distinct advantage in DE which is approximately 3% greater than the second largest one (BBHE). On the contrary, GHE and DISHE decrease the DE value of the original image seriously, and this is mainly because these methods tend to merge different gray levels together through enhancement. Interestingly, RSIHE achieves a satisfactory performance in PSNR, but its DE performance is poor. Furthermore, BBHE undergoes an opposing situation. We infer that a high DE value can indicate relatively low image degradation to a certain degree.
To evaluate the local contrast of the enhanced image,
Table 8 reports the comparison result in terms of AME. Among all the comparative algorithms, the average AME of our method is the best, while the one of GHE is the worst. Even though the
values of GHE and MMBEBHE, which represent the global contrast, are large, plenty of local regions turn to be homogenous due to the fact that it is highly likely that pixels in the same region will merge in these algorithms, contributing to the low AMEs.
4.3.2. Evaluation of Running Time
A comparison of running time is made in
Table 9. All the algorithms are implemented for five times and the average running time is recorded.
As we can see, BBHE achieves the fastest running speed, which is about 88 fps. Besides, DISHE and ADPHE also perform well, and their running speeds can reach more than 60 fps and 40 fps, respectively. In regard to our method, the PSO-based optimization consists of multiple iterations of the procedures introduced in
Section 3.2. That is to say, these parts of codes need to be executed for
times in total, which leads to the long computation time. As a matter of fact, computation burden is a common problem existing in all the iterative algorithms which needs to be urgently settled. Motivated by the extensive applications of multi-core digital signal processors, e.g., GPU, in practical engineering, we propose to increase our running efficiency using the strategy of parallel processing. Considering that each particle in PSO is individual, the executable codes of all the particles in the same iteration can be regarded as a group of parallel tasks and can be implemented in different cores at the same time. Under the circumstances, even real-time running can be expected.
In order to demonstrate the advantage of PSO optimization among concurrent methods, three other concurrent optimization algorithms: the genetic algorithm (GA) [
44], ant colony optimization (ACO) [
45], and the bat algorithm (BA) [
46] are applied to make a comparison. For a fair comparison, all these algorithms are implemented with the same number of particles and iterations (
), and
Table 10 clearly reports the running time of the four algorithms. Note that the execution time listed is the average of five times of running.
As is indicated from
Table 10, the average running time of GA and ACO is obviously longer than that of BA and PSO. This is because GA contains several genetic operations, e.g., crossover and mutation, and ACO contains a series of combinatorial optimizations. BA and PSO achieve almost the same average execution time due to the fact that their update mechanisms of position and velocity are similar.