Spatial Downscaling of Gross Primary Productivity Using Topographic and Vegetation Heterogeneity Information: A Case Study in the Gongga Mountain Region of China
Abstract
:1. Introduction
2. Materials and Methods
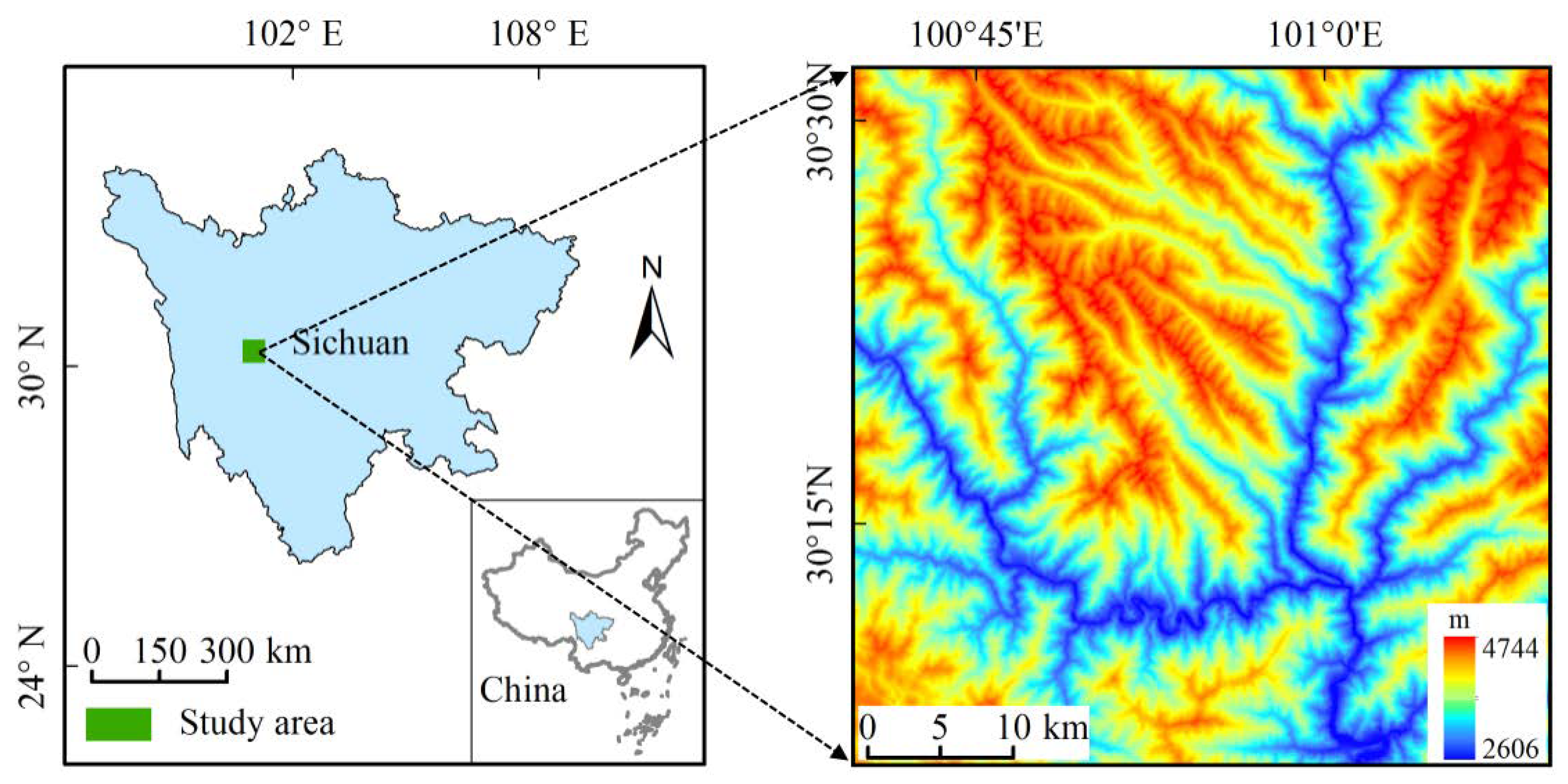
2.1. Study Area
2.2. Data and Processing
2.2.1. GPP Images at 500 m and 1 km
2.2.2. LAI Data
2.2.3. DEM Data
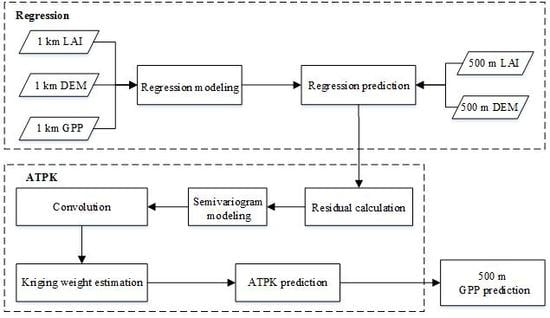
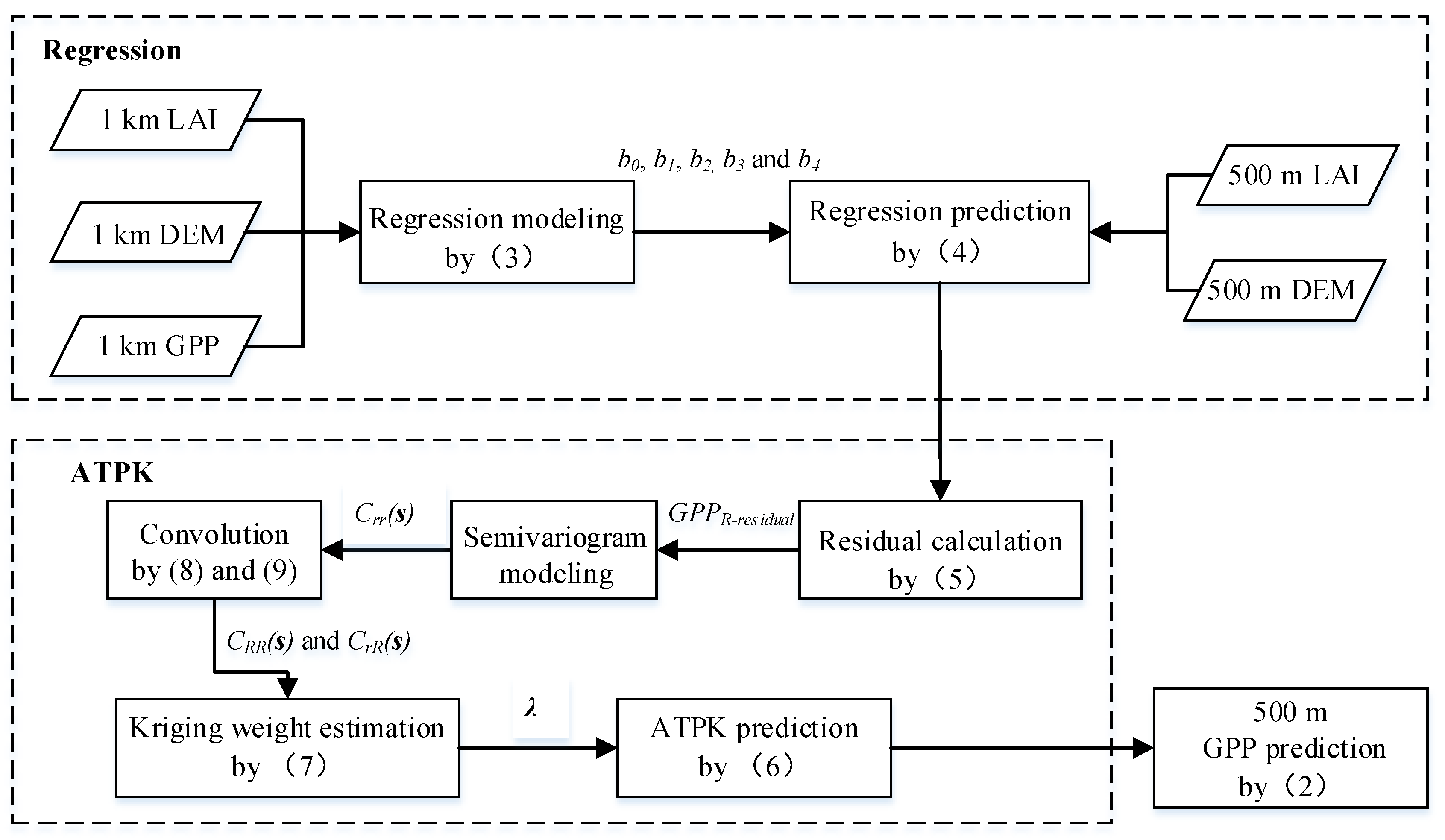
2.3. Algorithm for Downscaling
2.3.1. Problem Formulation
2.3.2. Regression between GPP and Topographic Factors
2.3.3. ATPK for Downscaling Residuals
2.4. Result Validation and Method Evaluation
3. Results and Analyses
3.1. Topographic and Vegetation Heterogeneities at Two Scales
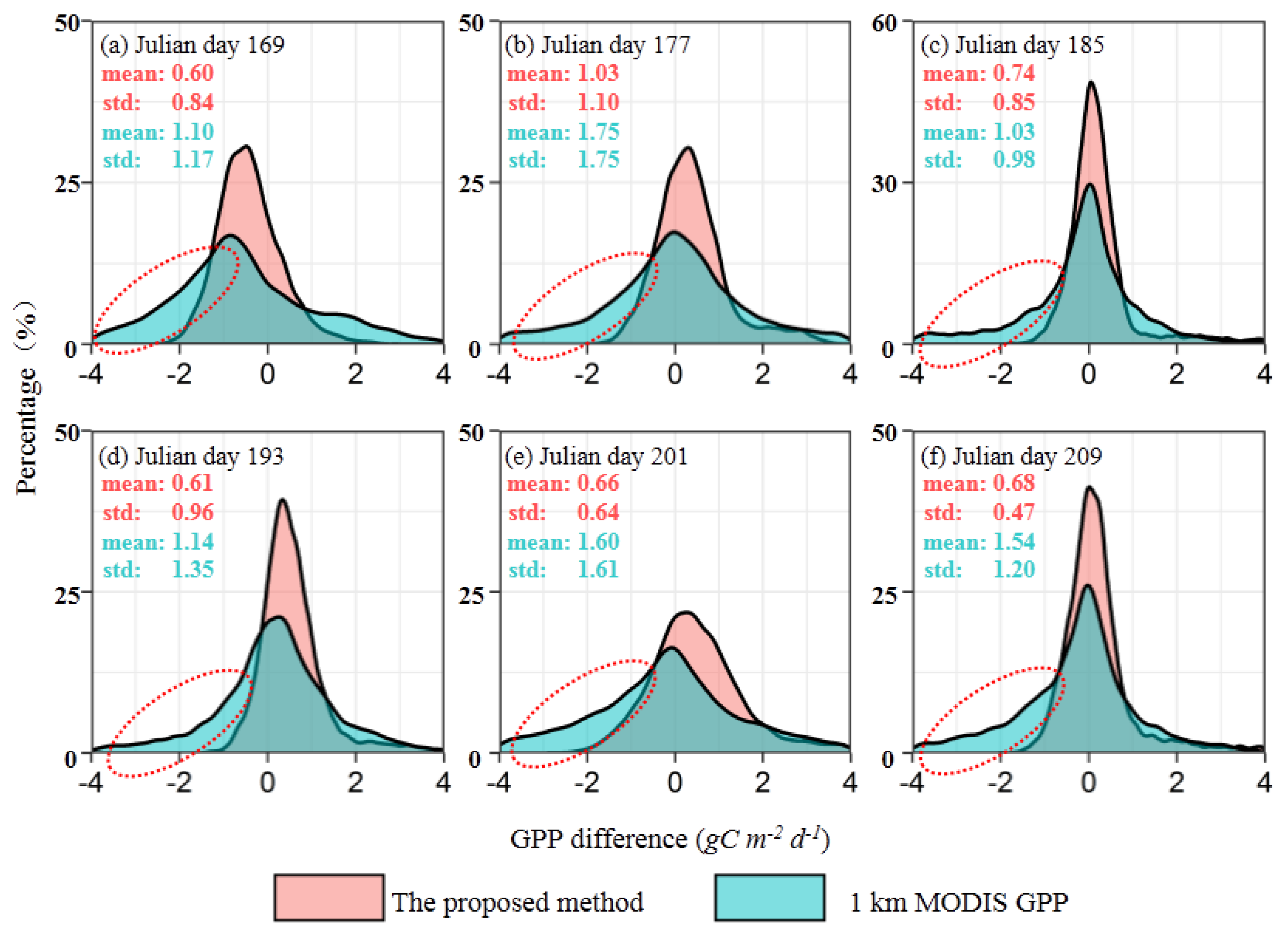
3.2. GPP Difference of the Two MODIS Products
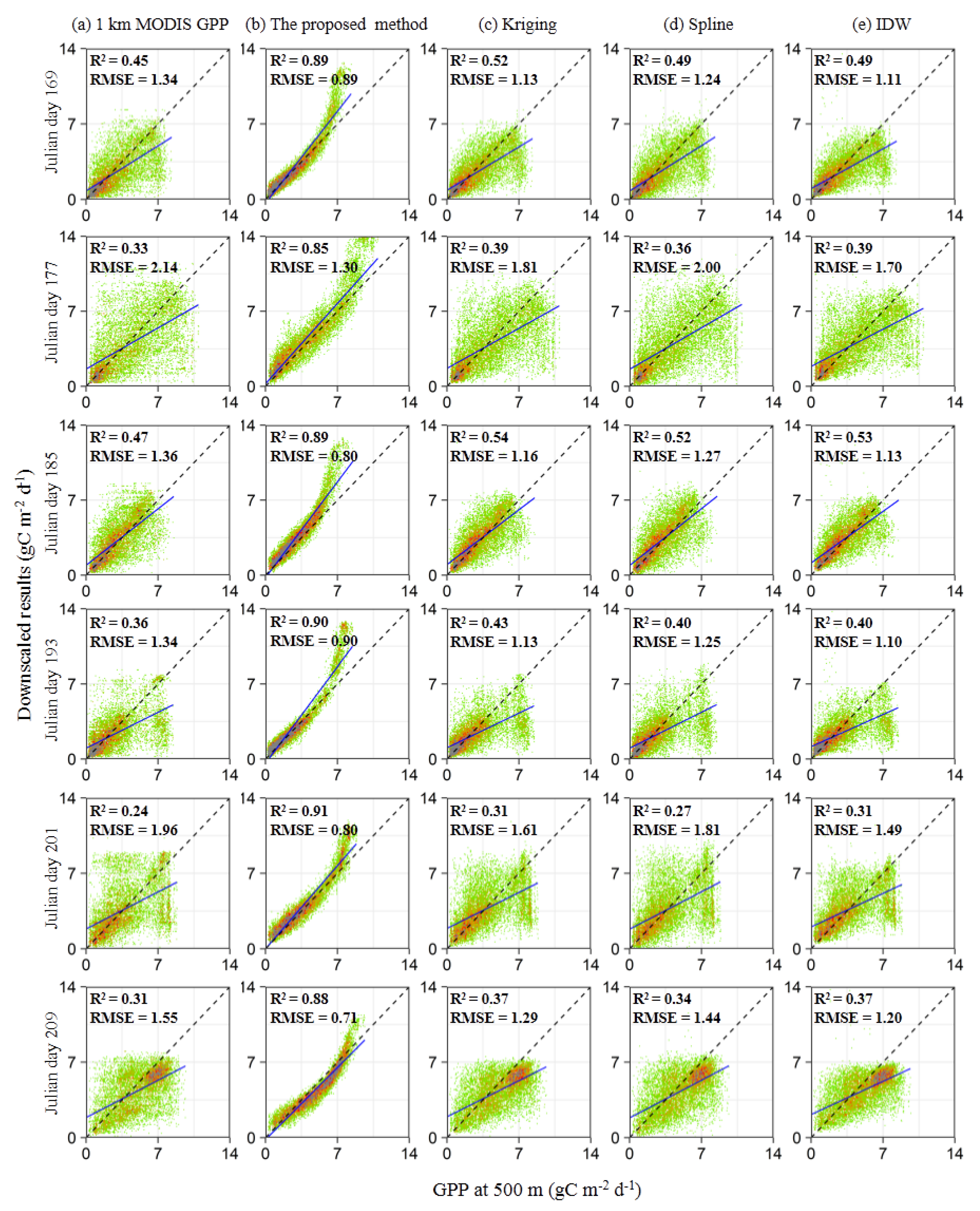
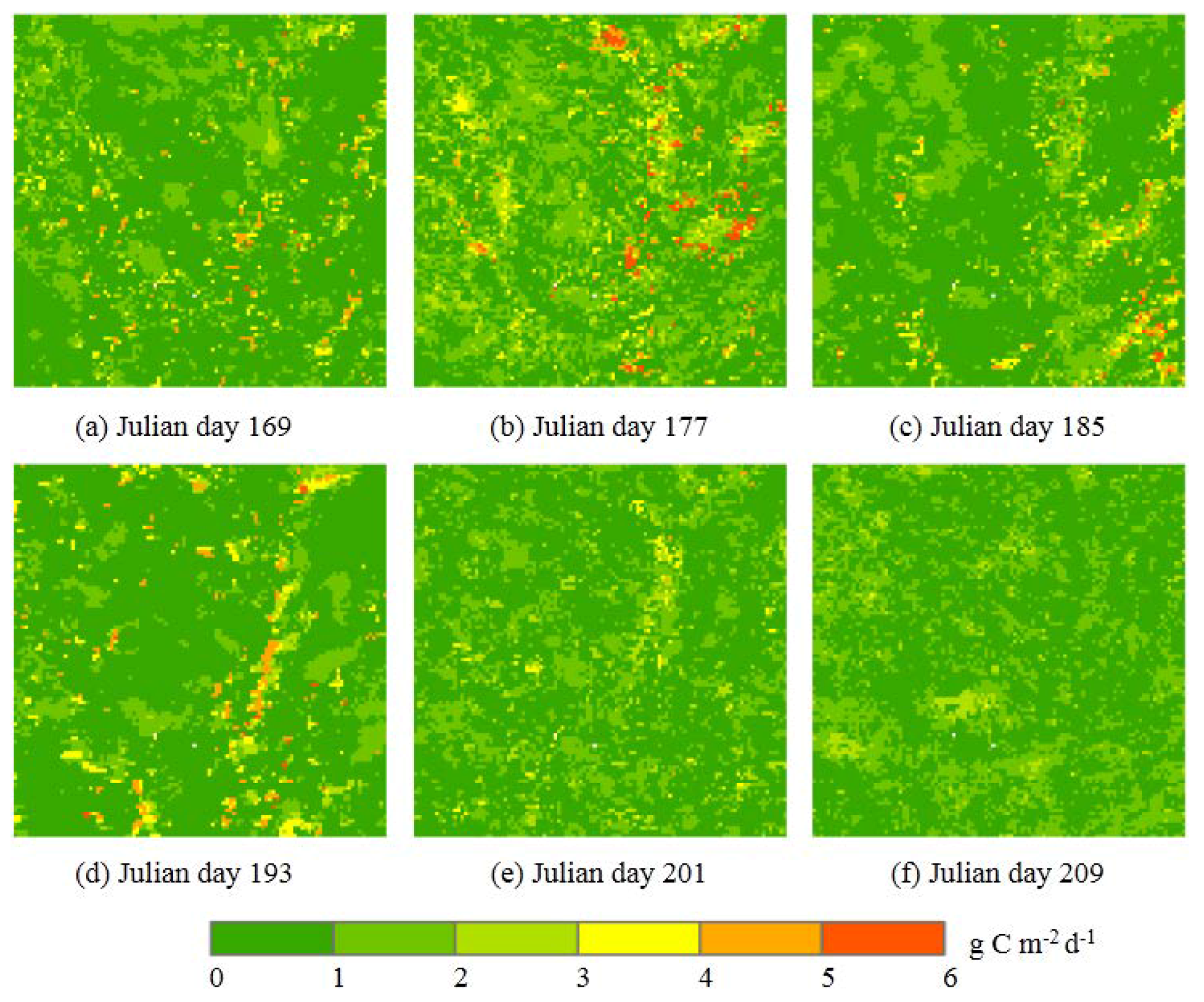
3.3. Downscaled Results
4. Discussions
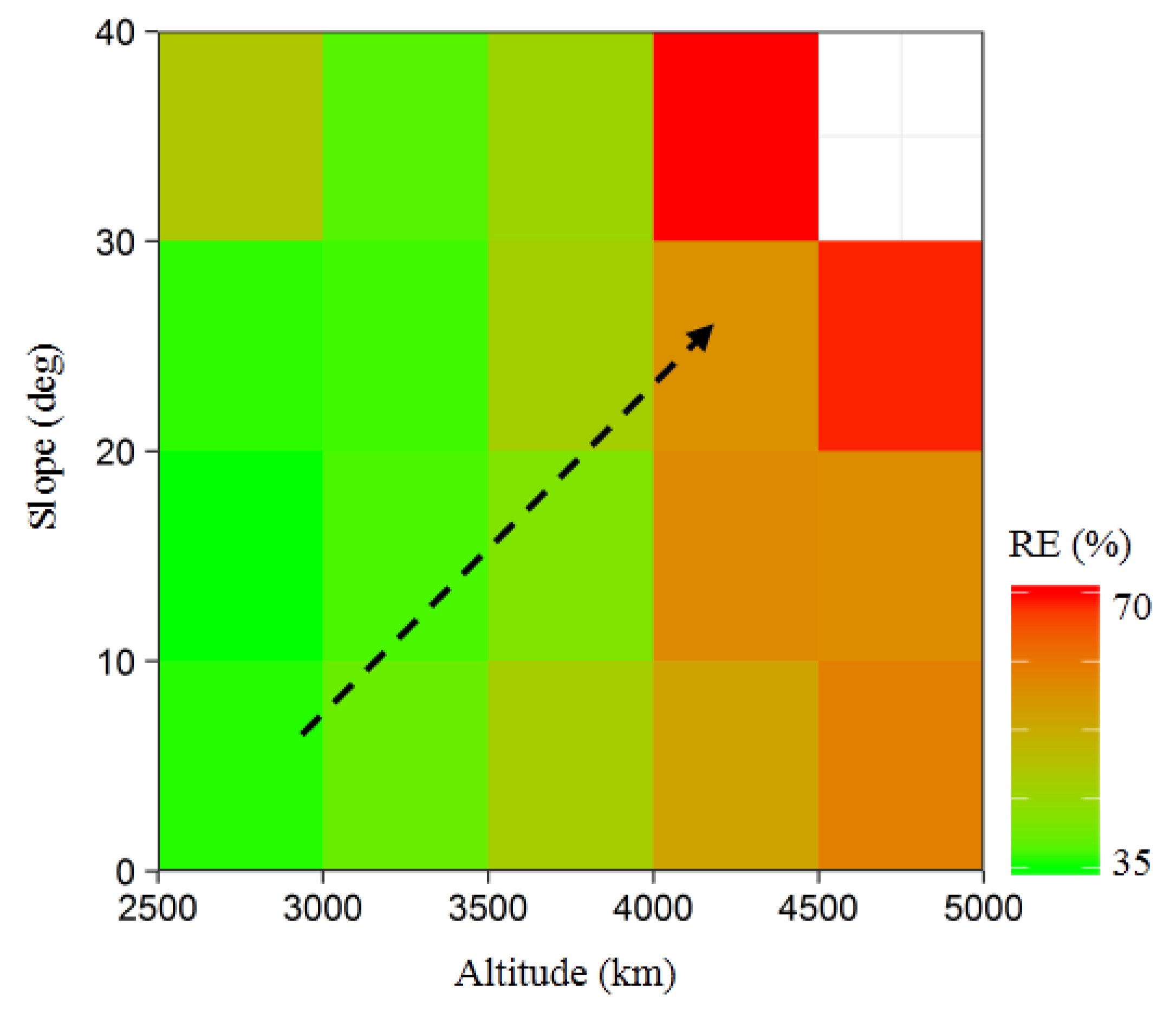
4.1. The Topographic Effects on GPP Inconsistency at Two Resolutions
4.2. Evaluations of the Proposed Downscaling Method
4.3. Limitations of the Current Work and Prospects for Future Studies
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Li, A.; Bian, J.; Lei, G.; Huang, C. Estimating the maximal light use efficiency for different vegetation through the casa model combined with time-series remote sensing data and ground measurements. Remote Sens. 2012, 4, 3857–3876. [Google Scholar] [CrossRef]
- Zhou, Y.; Hilker, T.; Ju, W.; Coops, N.C.; Black, T.A.; Chen, J.M.; Wu, X. Modeling gross primary production for sunlit and shaded canopies across an evergreen and a deciduous site in canada. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1859–1873. [Google Scholar] [CrossRef]
- Liu, L.; Guan, L.; Liu, X. Directly estimating diurnal changes in gpp for c3 and c4 crops using far-red sun-induced chlorophyll fluorescence. Agric. For. Meteorol. 2017, 232, 1–9. [Google Scholar] [CrossRef]
- Ju, W.; Chen, J.M.; Black, T.A.; Barr, A.G.; Liu, J.; Chen, B. Modelling multi-year coupled carbon and water fluxes in a boreal aspen forest. Agric. For. Meteorol. 2006, 140, 136–151. [Google Scholar] [CrossRef]
- Alemu, G.; Chen, J.M.; Price, D.T.; Kurz, W.A.; Liu, J.; Céline, B.; Hember, R.A.; Wu, C.; Chang, K.H. Improved assessment of gross and net primary productivity of canada’s landmass. J. Geophys. Res. Atmos. 2013, 99, 1089–1104. [Google Scholar]
- Xie, X.; Li, A.; Jin, H. The simulation models of the forest carbon cycle on a large scale : A review. Acta Ecol. Sin. 2018, 38, 1–14. [Google Scholar]
- Chen, J.M.; Chen, X.; Ju, W. Effects of vegetation heterogeneity and surface topography on spatial scaling of net primary productivity. Biogeosciences 2013, 10, 4879–4896. [Google Scholar] [CrossRef]
- El Maayar, M.; Chen, J.M. Spatial scaling of evapotranspiration as affected by heterogeneities in vegetation, topography, and soil texture. Remote Sens. Environ. 2006, 102, 33–51. [Google Scholar] [CrossRef]
- Mitchell, S.W.; Csillag, F.; Tague, C. Impacts of spatial partitioning in hydroecological models: Predicting grassland productivity with rhessys. Trans. GIS 2005, 9, 421–442. [Google Scholar] [CrossRef]
- MacKay, D.S.; Ahl, D.E.; Ewers, B.E.; Gower, S.T.; Burrows, S.N.; Samanta, S.; Davis, K.J. Effects of aggregated classifications of forest composition on estimates of evapotranspiration in a northern wisconsin forest. Glob. Chang. Biol. 2002, 8, 1253–1265. [Google Scholar] [CrossRef]
- Jin, H.; Li, A.; Bian, J.; Nan, X.; Zhao, W.; Zhang, Z.; Yin, G. Intercomparison and validation of modis and glass leaf area index (lai) products over mountain areas: A case study in southwestern china. Int. J. Appl. Earth Observ. Geoinf. 2017, 55, 52–67. [Google Scholar] [CrossRef]
- Zhao, W.; Li, A.N. A review on land surface processes modelling over complex terrain. Adv. Meteorol. 2015, 2015, 607181. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; Petersen, L.; Ragettli, S.; Pellicciotti, F. The importance of observed gradients of air temperature and precipitation for modeling runoff from a glacierized watershed in the nepalese himalayas. Water Resour. Res. 2014, 50, 2212–2226. [Google Scholar] [CrossRef]
- Mizukami, N.; Clark, M.P.; Slater, A.G.; Brekke, L.D.; Elsner, M.M.; Arnold, J.R.; Gangopadhyay, S. Hydrologic implications of different large-scale meteorological model forcing datasets in mountainous regions. J. Hydrometeorol. 2014, 15, 474–488. [Google Scholar] [CrossRef]
- Helbig, N.; Loewe, H. Shortwave radiation parameterization scheme for subgrid topography. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Li, A.; Bian, J.; Jin, H.; Zhao, W.; Zhang, Z.; Nan, X.; Yin, G.; Lei, G. Mountain Remote Sensing; Science Press: Beijing, China, 2016. [Google Scholar]
- Chen, J.M. Spatial scaling of a remotely sensed surface parameter by contexture. Remote Sens. Environ. 1999, 69, 30–42. [Google Scholar] [CrossRef]
- Liang, S.; Li, X.; Wang, J. Advanced Remote Sensing; Academic Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Hong, S.-H.; Hendrickx, J.M.H.; Borchers, B. Up-scaling of sebal derived evapotranspiration maps from landsat (30 m) to modis (250 m) scale. J. Hydrol. 2009, 370, 122–138. [Google Scholar] [CrossRef]
- Thomas, A. Overview of the geoecology of the gongga shan range, sichuan province, china. Mt. Res. Dev. 1999, 19, 17–30. [Google Scholar] [CrossRef]
- Zhu, W.; Fu, X.; Feng, X.; Lu, J.Y. Annual time-series analyses of total gaseous mercury measurement and its impact factors on the gongga mountains in the southeastern fringe of the qinghai-tibetan plateau. J. Mt. Sci. Engl. 2008, 5, 17–31. [Google Scholar] [CrossRef]
- Running, S.W.; Nemani, R.R.; Heinsch, F.A.; Zhao, M.S.; Reeves, M.; Hashimoto, H. A continuous satellite-derived measure of global terrestrial primary production. Bioscience 2004, 54, 547–560. [Google Scholar] [CrossRef]
- Heinsch, F.A.; Zhao, M.; Running, S.W.; Kimball, J.S.; Nemani, R.R.; Davis, K.J.; Bolstad, P.V.; Cook, B.D.; Desai, A.R.; Ricciuto, D.M.; et al. Evaluation of remote sensing based terrestrial productivity from modis using regional tower eddy flux network observations. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1908–1925. [Google Scholar] [CrossRef]
- Jung, M.; Reichstein, M.; Margolis, H.A.; Cescatti, A.; Richardson, A.D.; Arain, M.A.; Arneth, A.; Bernhofer, C.; Bonal, D.; Chen, J.; et al. Global patterns of land-atmosphere fluxes of carbon dioxide, latent heat, and sensible heat derived from eddy covariance, satellite, and meteorological observations. J. Geophys. Res. Biogeo 2011, 116. [Google Scholar] [CrossRef]
- Turner, D.P.; Ritts, W.D.; Cohen, W.B.; Gower, S.T.; Running, S.W.; Zhao, M.S.; Costa, M.H.; Kirschbaum, A.A.; Ham, J.M.; Saleska, S.R.; et al. Evaluation of modis npp and gpp products across multiple biomes. Remote Sens. Environ. 2006, 102, 282–292. [Google Scholar] [CrossRef]
- Myneni, R.B.; Hoffman, S.; Knyazikhin, Y.; Privette, J.L.; Glassy, J.; Tian, Y.; Wang, Y.; Song, X.; Zhang, Y.; Smith, G.R.; et al. Global products of vegetation leaf area and fraction absorbed par from year one of modis data. Remote Sens. Environ. 2002, 83, 214–231. [Google Scholar] [CrossRef]
- Knyazikhin, Y.; Martonchik, J.V.; Myneni, R.B.; Diner, D.J.; Running, S.W. Synergistic algorithm for estimating vegetation canopy leaf area index and fraction of absorbed photosynthetically active radiation from modis and misr data. J. Geophys. Res. Atmos. 1998, 103, 32257–32275. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, Q.; Liu, G.; Ding, S.; Li, H.; Dong, J. Elevation quality evaluation of aster gdem data in china’s eastern region. J. Geomat. Sci. Technol. 2014, 31, 67–72. [Google Scholar]
- Zhang, C.; Liu, Q.; Liu, G.; Ding, S.; Wang, P.; Dong, J. Data processing and application progress of srtm3 and aster gdem. Geogr. Geo-inf. Sci. 2012, 28, 29–34. [Google Scholar]
- Frey, H.; Paul, F. On the suitability of the srtm dem and aster gdem for the compilation of topographic parameters in glacier inventories. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 480–490. [Google Scholar] [CrossRef]
- Dozier, J.; Frew, J. Rapid calculation of terrain parameters for radiation modeling from digital elevation data. IEEE Trans. Geosci. Remote Sens. 1990, 28, 963–969. [Google Scholar] [CrossRef]
- Wang, Q.; Shi, W.; Atkinson, P.M.; Zhao, Y. Downscaling modis images with area-to-point regression kriging. Remote Sens. Environ. 2015, 166, 191–204. [Google Scholar] [CrossRef]
- Gao, F.; Kustas, W.P.; Anderson, M.C. A data mining approach for sharpening thermal satellite imagery over land. Remote Sens. 2012, 4, 3287–3319. [Google Scholar] [CrossRef]
- Wang, Q.; Shi, W.; Atkinson, P.M. Area-to-point regression kriging for pan-sharpening. ISPRS J. Photogramm. Remote Sens. 2016, 114, 151–165. [Google Scholar] [CrossRef]
- Knotters, M.; Brus, D.J.; Voshaar, J.H.O. A comparison of kriging, co-kriging and kriging combined with regression for spatial interpolation of horizon depth with censored observations. Geoderma 1995, 67, 227–246. [Google Scholar] [CrossRef]
- Tait, A.; Henderson, R.; Turner, R.; Zheng, X. Thin plate smoothing spline interpolation of daily rainfall for new zealand using a climatological rainfall surface. Int. J. Climatol. 2006, 26, 2097–2115. [Google Scholar] [CrossRef]
- Watson, D.F.; Philip, G.M. A refinement of inverse distance weighted interpolation. Geo-Processing 1985, 2, 315–327. [Google Scholar]
- Simic, A.; Chen, J.M.; Liu, J.; Csillag, F. Spatial scaling of net primary productivity using subpixel information. Remote Sens. Environ. 2004, 93, 246–258. [Google Scholar] [CrossRef]
- Jin, H.; Li, A.; Bian, J.; Zhang, Z.; Huang, C.; Li, M. Validation of global land surface satellite (glass) downward shortwave radiation product in the rugged surface. J. Mt. Sci. Engl. 2013, 10, 812–823. [Google Scholar] [CrossRef]
- Jin, H.A.; Li, A.N.; Bian, J.H. Comparative analysis of hj-1, spot, and tm data for leaf area index estimation in a mountainous area. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium, Melbourne, Australia, 21–26 July 2013; pp. 2782–2785. [Google Scholar]
- Bonan, G.B. The land surface climatology of the ncar land surface model coupled to the ncar community climate model. J. Clim. 1998, 11, 1307–1326. [Google Scholar] [CrossRef]
- Qiu, Y.; Fu, B.J.; Wang, J.; Chen, L.D. Soil moisture variation in relation to topography and land use in a hillslope catchment of the loess plateau, china. J. Hydrol. 2001, 240, 243–263. [Google Scholar] [CrossRef]
- Govind, A.; Chen, J.M.; Margolis, H.; Ju, W.; Sonnentag, O.; Giasson, M.-A. A spatially explicit hydro-ecological modeling framework (beps-terrainlab v2.0): Model description and test in a boreal ecosystem in eastern north america. J. Hydrol. 2009, 367, 200–216. [Google Scholar] [CrossRef]
- Sabetraftar, K.; Mackey, B.; Croke, B. Sensitivity of modelled gross primary productivity to topographic effects on surface radiation: A case study in the cotter river catchment, australia. Ecol. Model. 2011, 222, 795–803. [Google Scholar] [CrossRef]
- Konzelmann, T.; Calanca, P.; Muller, G.; Menzel, L.; Lang, H. Energy balance and evapotranspiration in a high mountain area during summer. J. Appl. Meteorol. 1997, 36, 966–973. [Google Scholar] [CrossRef]
- Huang, W.; Zhang, L.; Furumi, S.; Muramatsu, K.; Daigo, M.; Li, P. Topographic effects on estimating net primary productivity of green coniferous forest in complex terrain using landsat data: A case study of yoshino mountain, japan. Int. J. Remote Sens. 2010, 31, 2941–2957. [Google Scholar] [CrossRef]
- Gelybo, G.; Barcza, Z.; Kern, A.; Kljun, N. Effect of spatial heterogeneity on the validation of remote sensing based gpp estimations. Agric. For. Meteorol. 2013, 174, 43–53. [Google Scholar] [CrossRef]
- Chen, J.M.; Mo, G.; Pisek, J.; Liu, J.; Deng, F.; Ishizawa, M.; Chan, D. Effects of foliage clumping on the estimation of global terrestrial gross primary productivity. Glob. Biogeochem. Cycle 2012, 26. [Google Scholar] [CrossRef]
- Lin, S.; Jing, C.; Coles, N.A.; Chaplot, V.; Moore, N.J.; Wu, J. Evaluating dem source and resolution uncertainties in the soil and water assessment tool. Stoch. Environ. Res. Risk Assess. 2013, 27, 209–221. [Google Scholar] [CrossRef]
- Xu, F.; Dong, G.; Wang, Q.; Liu, L.; Yu, W.; Men, C.; Liu, R. Impacts of dem uncertainties on critical source areas identification for non-point source pollution control based on swat model. J. Hydrol. 2016, 540, 355–367. [Google Scholar] [CrossRef]
- Grohmann, C.H. Effects of spatial resolution on slope and aspect derivation for regional-scale analysis. Comput. Geosci. 2015, 77, 111–117. [Google Scholar] [CrossRef]
- Wechsler, S.P.; Kroll, C.N. Quantifying dem uncertainty and its effect on topographic parameters. Photogramm. Eng. Remote Sens. 2006, 72, 1081–1090. [Google Scholar] [CrossRef]
- Oksanen, J.; Sarjakoski, T. Error propagation of dem-based surface derivatives. Comput. Geosci. 2005, 31, 1015–1027. [Google Scholar] [CrossRef]
- Zhou, Q.M.; Liu, X.J. Analysis of errors of derived slope and aspect related to dem data properties. Comput. Geosci. 2004, 30, 369–378. [Google Scholar] [CrossRef]
- Liu, H.H.; Kiesel, J.; Hormann, G.; Fohrer, N. Effects of dem horizontal resolution and methods on calculating the slope length factor in gently rolling landscapes. Catena 2011, 87, 368–375. [Google Scholar] [CrossRef]
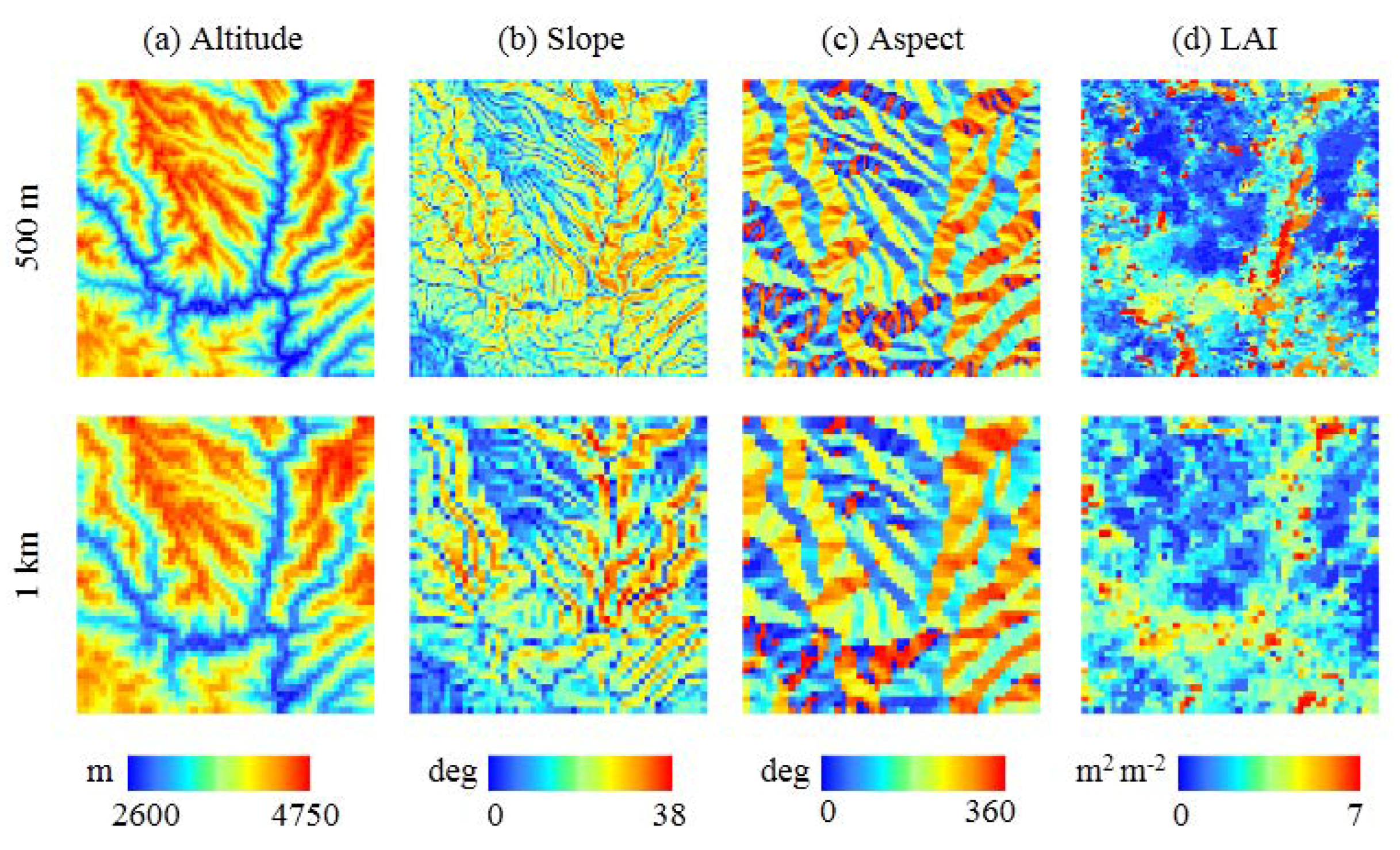
| Pixel Resolution (m) | Min | Max | Mean | STD | ||||
|---|---|---|---|---|---|---|---|---|
| 500 | 1000 | 500 | 1000 | 500 | 1000 | 500 | 1000 | |
| Altitude (m) | 2606 | 2647 | 4744 | 4671 | 3784 | 3787 | 501 | 489 |
| Slope (deg) | 0 | 0 | 38 | 28 | 18 | 12 | 8 | 6 |
| Aspect (deg) | 0 | 0 | 360 | 360 | 178 | 177 | 101 | 100 |
| LAI (m2 m−2) | 0 | 0 | 7.0 | 5.7 | 1.88 | 1.58 | 1.93 | 1.61 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, X.; Li, A.; Jin, H.; Yin, G.; Bian, J. Spatial Downscaling of Gross Primary Productivity Using Topographic and Vegetation Heterogeneity Information: A Case Study in the Gongga Mountain Region of China. Remote Sens. 2018, 10, 647. https://doi.org/10.3390/rs10040647
Xie X, Li A, Jin H, Yin G, Bian J. Spatial Downscaling of Gross Primary Productivity Using Topographic and Vegetation Heterogeneity Information: A Case Study in the Gongga Mountain Region of China. Remote Sensing. 2018; 10(4):647. https://doi.org/10.3390/rs10040647
Chicago/Turabian StyleXie, Xinyao, Ainong Li, Huaan Jin, Gaofei Yin, and Jinhu Bian. 2018. "Spatial Downscaling of Gross Primary Productivity Using Topographic and Vegetation Heterogeneity Information: A Case Study in the Gongga Mountain Region of China" Remote Sensing 10, no. 4: 647. https://doi.org/10.3390/rs10040647
APA StyleXie, X., Li, A., Jin, H., Yin, G., & Bian, J. (2018). Spatial Downscaling of Gross Primary Productivity Using Topographic and Vegetation Heterogeneity Information: A Case Study in the Gongga Mountain Region of China. Remote Sensing, 10(4), 647. https://doi.org/10.3390/rs10040647