Geographically Weighted Area-to-Point Regression Kriging for Spatial Downscaling in Remote Sensing
Abstract
1. Introduction
2. Methodology
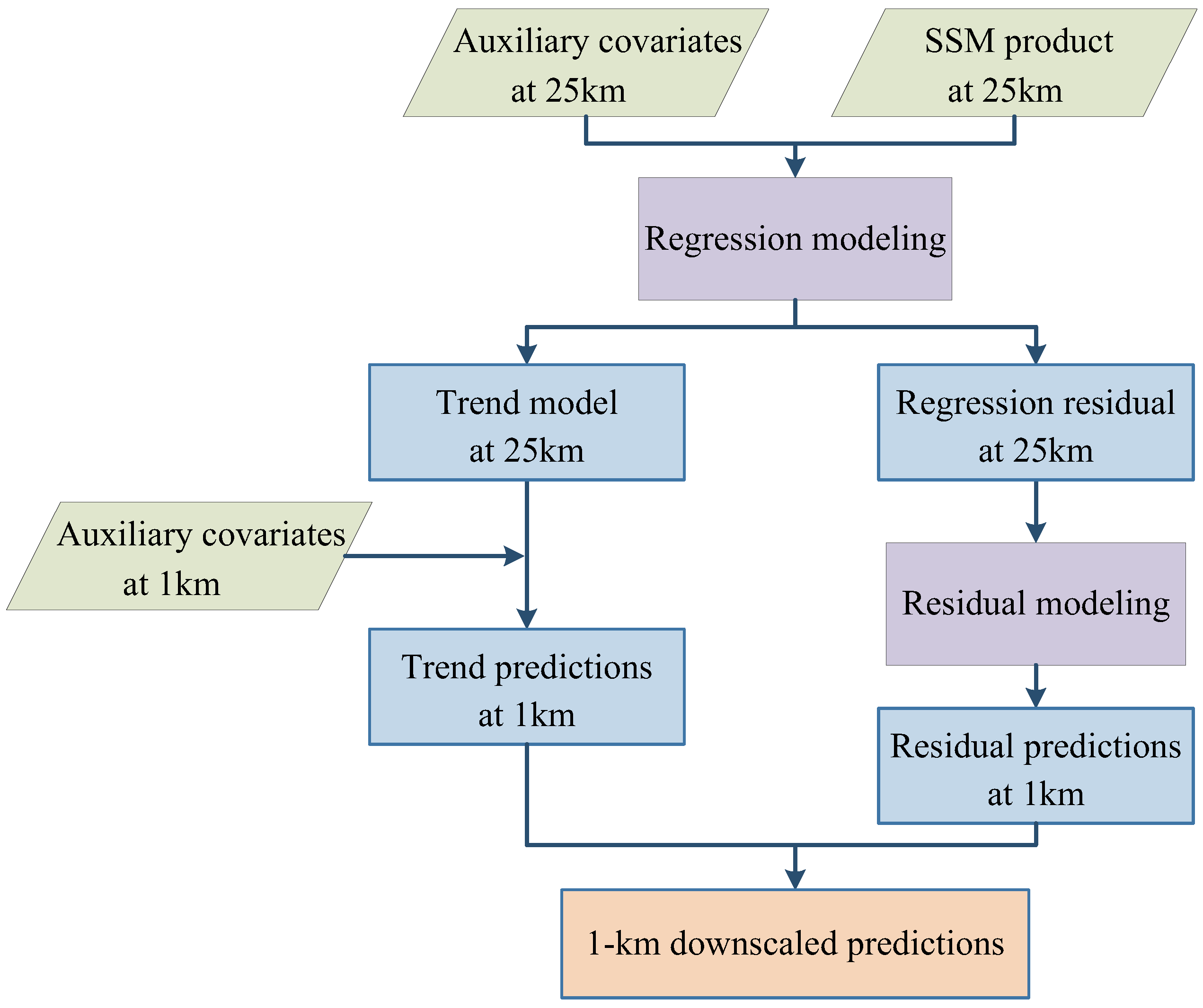
2.1. Generic Formulation
2.2. ATPRK
2.3. GWATPRK
3. Experimental Design
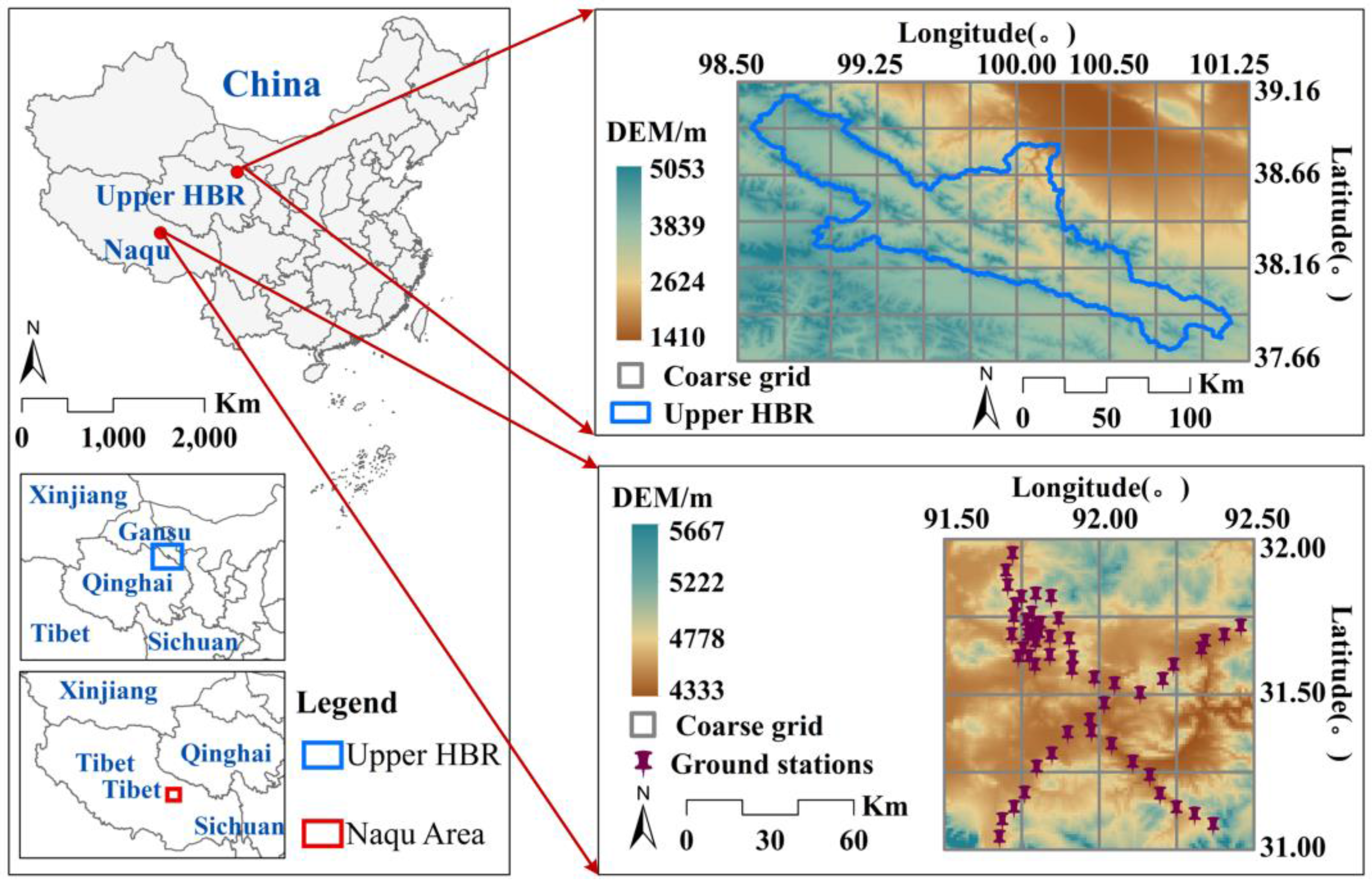
3.1. Study Area
3.2. Data Description
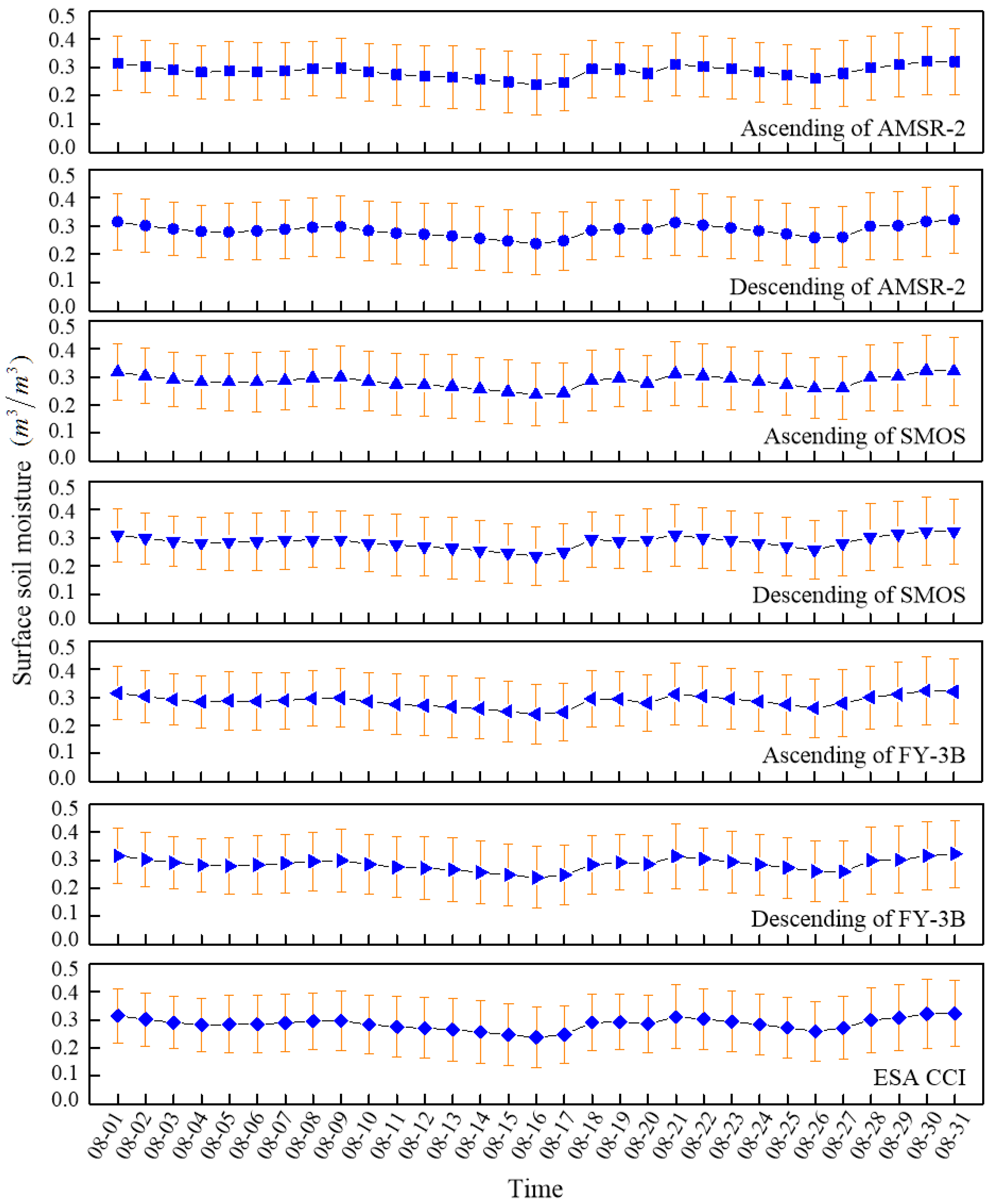
3.2.1. Ground Measurements of SSM
3.2.2. Brightness Temperature
3.2.3. Coarse SSM Products
3.2.4. MODIS Products
3.3. Process of Experiment Implementation
4. Results and Discussion
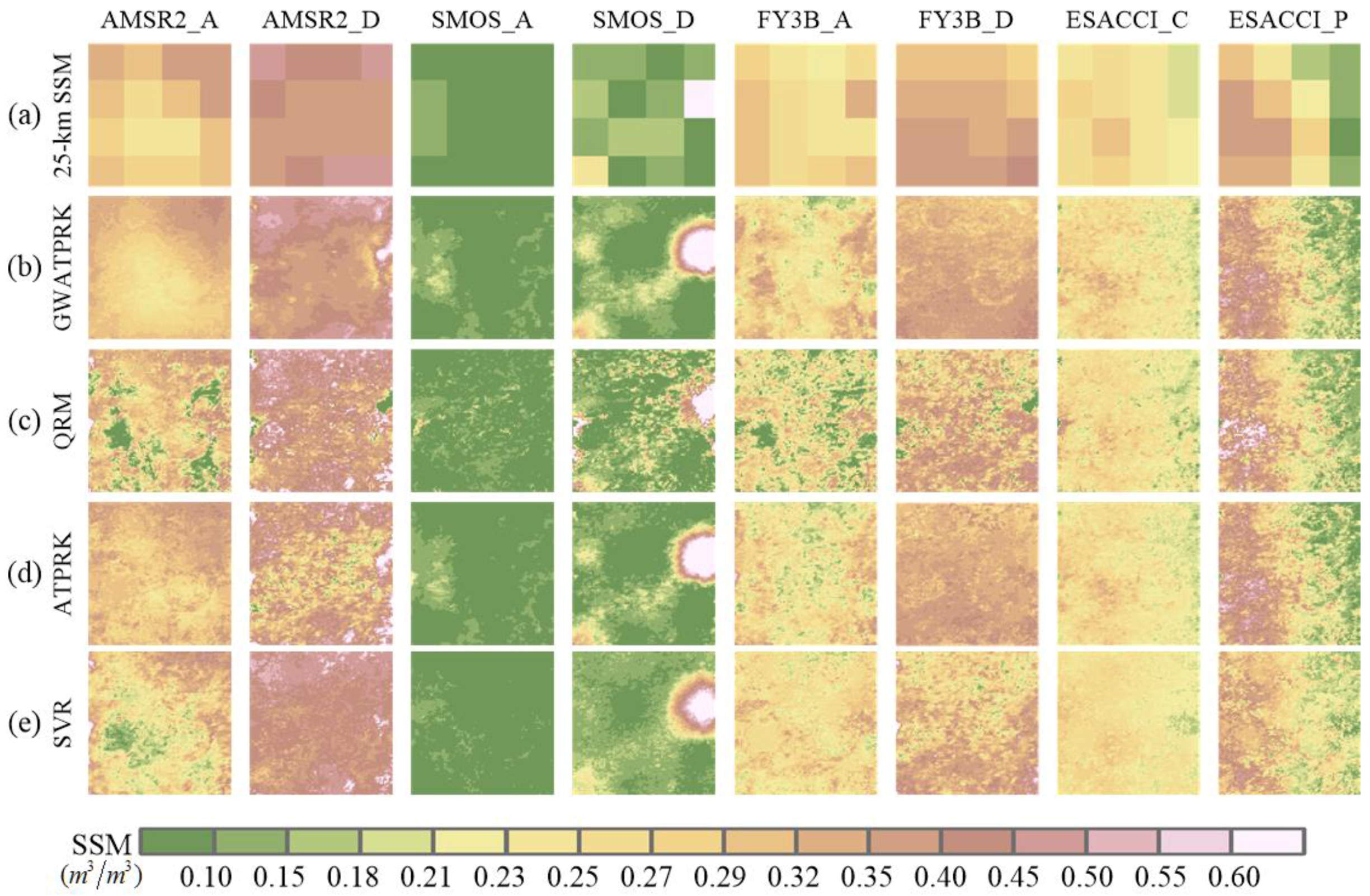
4.1. Downscaled Results
4.2. Direct Validation
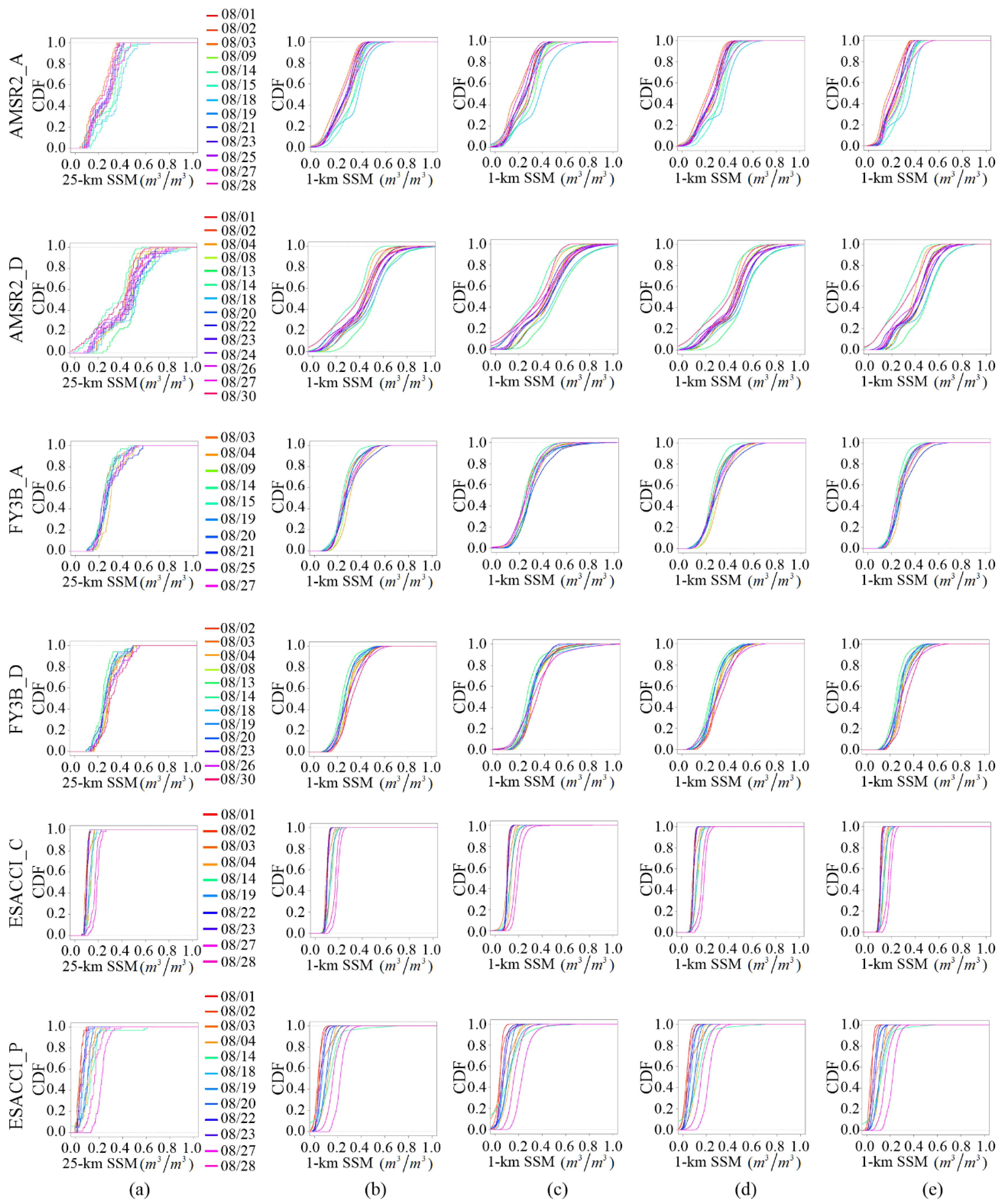
4.3. Indirect Validation
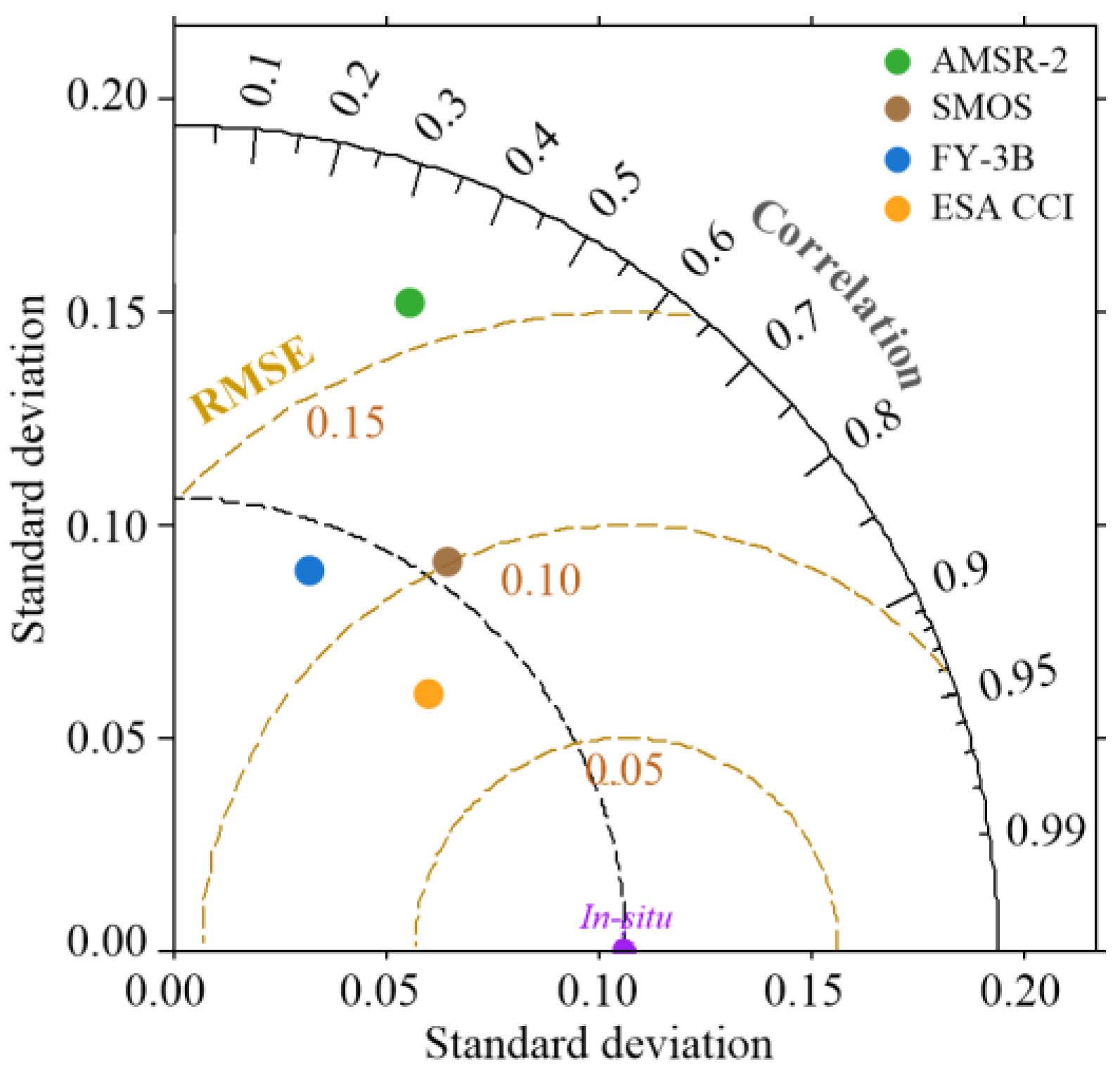
4.4. Cross Validation
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hall, F.G.; Townshend, J.R.; Engman, E.T. Status of remote sensing algorithms for estimation of land surface state parameters. Remote Sens. Environ. 1995, 51, 138–156. [Google Scholar] [CrossRef]
- Zavorotny, V.U.; Voronovich, A.G. Scattering of GPS signals from the ocean with wind remote sensing application. IEEE Trans. Geosci. Remote Sens. 2002, 38, 951–964. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Tanré, D.; Remer, L.A.; Vermote, E.F.; Chu, A.; Holben, B.N. Operational remote sensing of tropospheric aerosol over land from EOS moderate resolution imaging spectroradiometer. J. Geophys. Res. 1997, 102, 17051–17067. [Google Scholar] [CrossRef]
- Atkinson, P.M.; Tate, N.J. Spatial scale problems and geostatistical solutions: A review. Prof. Geogr. 2000, 52, 607–623. [Google Scholar] [CrossRef]
- Peng, J.; Loew, A.; Merlin, O.; Verhoest, N.E.C. A review of spatial downscaling of satellite remotely-sensed soil moisture. Rev. Geophys. 2017, 55, 341–366. [Google Scholar] [CrossRef]
- Atkinson, P.M. Downscaling in remote sensing. Int. J. Appl. Earth Obs. Geoinf. 2012, 22, 106–114. [Google Scholar] [CrossRef]
- Chen, Y.H.; Ge, Y.; Jia, Y.X. Integrating object boundary in super-resolution land-cover mapping. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 219–230. [Google Scholar] [CrossRef]
- Bergant, K.; Kajfež-Bogataj, L.; Črepinšek, Z. Statistical downscaling of general-circulation-model- simulated average monthly air temperature to the beginning of flowering of the dandelion (Taraxacum officinale) in Slovenia. Int. J. Biometeorol. 2002, 46, 22–32. [Google Scholar] [CrossRef] [PubMed]
- Pardo-Igúzquiza, E.; Chica-Olmo, M.; Atkinson, P.M. Downscaling cokriging for image sharpening. Remote Sens. Environ. 2006, 102, 86–98. [Google Scholar] [CrossRef]
- Hutengs, C.; Vohland, M. Downscaling land surface temperatures at regional scales with random forest regression. Remote Sens. Environ. 2016, 178, 127–141. [Google Scholar] [CrossRef]
- Wood, A.W.; Leung, L.R.; Sridhar, V.; Lettenmaier, D.P. Hydrologic implications of dynamical and statistical approaches to downscaling climate model outputs. Clim. Chang. 2004, 62, 189–216. [Google Scholar] [CrossRef]
- Rahman, S.; Bagtzoglou, A.C.; Hossain, F.; Tang, L.; Yarbrough, L.; Easson, G. Investigating spatial downscaling of satellite rainfall data for streamflow simulation in a medium-sized basin. J. Hydrometeorol. 2008, 10, 1063–1079. [Google Scholar] [CrossRef]
- Tao, K.; Barros, A.P. Using fractal downscaling of satellite precipitation products for hydrometeorological applications. J. Atmos. Ocean. Technol. 2010, 27, 409–427. [Google Scholar] [CrossRef]
- Kaheil, Y.H.; Rosero, E.; Gill, M.K.; Mckee, M.; Bastidas, L.A. Downscaling and forecasting of evapotranspiration using a synthetic model of wavelets and support vector machines. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2692–2707. [Google Scholar] [CrossRef]
- Cressie, N.A. Change of support and the modifiable unit problem. Geogr. Syst. 1996, 3, 159–180. [Google Scholar]
- Gotway, C.A.; Young, L.J. Combining incompatible spatial data. J. Am. Stat. Assoc. 2002, 97, 632–648. [Google Scholar] [CrossRef]
- Kyriakidis, P.C. A geostatistical framework for area-to-point spatial interpolation. Geogr. Anal. 2004, 36, 259–289. [Google Scholar] [CrossRef]
- Yoo, E.H.; Kyriakidis, P.C. Area-to-point kriging with inequality-type data. J. Geogr. Syst. 2006, 8, 357–390. [Google Scholar] [CrossRef]
- Goovaerts, P. Geostatistical analysis of disease data: Accounting for spatial support and population density in the isopleth mapping of cancer mortality risk using area-to-point poisson kriging. Int. J. Health Geogr. 2006, 5, 52. [Google Scholar] [CrossRef] [PubMed]
- Yoo, E.H.; Kyriakidis, P.C.; Tobler, W. Reconstructing population density surfaces from areal data: A comparison of Tobler’s pycnophylactic interpolation method and area-to-point kriging. Geogr. Anal. 2010, 42, 78–98. [Google Scholar] [CrossRef]
- Yoo, E.H.; Kyriakidis, P.C. Area-to-point kriging in spatial hedonic pricing models. J. Geogr. Syst. 2009, 11, 381–406. [Google Scholar] [CrossRef]
- Kerry, R.; Goovaerts, P.; Haining, R.P.; Ceccato, V. Applying geostatistical analysis to crime data: Car-related thefts in the Baltic States. Geogr. Anal. 2010, 42, 53–77. [Google Scholar] [CrossRef] [PubMed]
- Atkinson, P.M.; Pardo-Iguzquiza, E.; Chica-Olmo, M. Downscaling cokriging for super-resolution mapping of continua in remotely sensed images. IEEE Trans. Geosci. Remote Sens. 2008, 46, 573–580. [Google Scholar] [CrossRef]
- Wang, Q.M.; Shi, W.Z.; Atkinson, P.M. Area-to-point regression kriging for pan-sharpening. ISPRS J. Photogramm. Remote Sens. 2016, 114, 151–165. [Google Scholar] [CrossRef]
- Kerry, R.; Goovaerts, P.; Rawlins, B.G.; Marchant, B.P. Disaggregation of legacy soil data using area to point kriging for mapping soil organic carbon at the regional scale. Geoderma 2012, 170, 347–358. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.M.; Shi, W.Z.; Atkinson, P.M.; Zhao, Y. Downscaling MODIS images with area-to-point regression kriging. Remote Sens. Environ. 2015, 166, 191–204. [Google Scholar] [CrossRef]
- Hengl, T.; Heuvelink, G.B.M.; Rossiter, D.G. About regression-kriging: From equations to case studies. Comput. Geosci. 2007, 33, 1301–1315. [Google Scholar] [CrossRef]
- Liu, X.H.; Kyriakidis, P.C.; Goodchild, M.F. Population-density estimation using regression and area-to-point residual kriging. Int. J. Geogr. Inf. Sci. 2008, 22, 431–447. [Google Scholar] [CrossRef]
- Poggio, L.; Gimona, A. Modelling high resolution RS data with the aid of coarse resolution data and ancillary data. Int. J. Appl. Earth Obs. Geoinf. 2013, 23, 360–371. [Google Scholar] [CrossRef]
- Zhang, Y.H.; Atkinson, P.M.; Ling, F.; Wang, Q.M.; Li, X.D.; Shi, L.F.; Du, Y. Spectral–spatial adaptive area-to-point regression kriging for MODIS image downscaling. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 1883–1896. [Google Scholar] [CrossRef]
- Wang, Q.M.; Shi, W.Z.; Atkinson, P.M.; Wei, Q. Approximate area-to-point regression kriging for fast hyperspectral image sharpening. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 286–295. [Google Scholar] [CrossRef]
- Goodchild, M.F. The Validity and Usefulness of Laws in Geographic Information Science and Geography. Ann. Assoc. Am. Geogr. 2004, 94, 300–303. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Charlton, M.E.; Brunsdon, C. Geographically weighted regression: A natural evolution of the expansion method for spatial data analysis. Environ. Plan. A Econ. Space 1998, 30, 1905–1927. [Google Scholar] [CrossRef]
- Harris, P.; Fotheringham, A.S.; Crespo, R.; Charlton, M. The use of geographically weighted regression for spatial prediction: An evaluation of models using simulated data sets. Math. Geosci. 2010, 42, 657–680. [Google Scholar] [CrossRef]
- Zhao, N.; Chen, C.F.; Zhou, X.; Yue, T.X. A comparison of two downscaling methods for precipitation in china. Environ. Earth Sci. 2015, 74, 6563–6569. [Google Scholar] [CrossRef]
- Kumari, M.; Singh, C.K.; Bakimchandra, O.; Basistha, A. Geographically weighted regression based quantification of rainfall–topography relationship and rainfall gradient in central himalayas. Int. J. Climatol. 2017, 37, 1299–1309. [Google Scholar] [CrossRef]
- Jin, Y.; Ge, Y.; Wang, J.H.; Chen, Y.H.; Heuvelink, G.B.M.; Atkinson, P.M. Downscaling amsr-2 soil moisture data with geographically weighted area-to-area regression kriging. IEEE Trans. Geosci. Remote Sens. 2017, 56, 1–15. [Google Scholar] [CrossRef]
- Jin, Y.; Ge, Y.; Wang, J.H.; Heuvelink, G.B.M. Deriving temporally continuous soil moisture estimations at fine resolution by downscaling remotely sensed product. Int. J. Appl. Earth Obs. Geoinf. 2018, 68, 8–19. [Google Scholar] [CrossRef]
- Piles, M.; Camps, A.; Vall-Llossera, M.; Corbella, I.; Panciera, R.; Rudiger, C.; Kerr, Y.; Walker, J. Downscaling SMOS-derived soil moisture using MODIS visible/infrared data. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3156–3166. [Google Scholar] [CrossRef]
- Tripathi, S.; Srinivas, V.V.; Nanjundiah, R.S. Downscaling of precipitation for climate change scenarios: A support vector machine approach. J. Hydrol. 2006, 330, 621–640. [Google Scholar] [CrossRef]
- Hengl, T.; Heuvelink, G.B.M.; Stein, A. A generic framework for spatial prediction of soil variables based on regression-kriging. Geoderma 2004, 120, 75–93. [Google Scholar] [CrossRef]
- Goovaerts, P. Kriging and semivariogram deconvolution in the presence of irregular geographical units. Math. Geosci. 2008, 40, 101–128. [Google Scholar] [CrossRef]
- Zawadzki, J.; Cieszewski, C.J.; Zasada, M.; Lowe, R.C. Applying geostatistics for investigations of forest ecosystems using remote sensing imagery. Silva Fenn. 2005, 39, 599–617. [Google Scholar] [CrossRef]
- Li, X.; Cheng, G.D.; Liu, S.M.; Xiao, Q.; Ma, M.G.; Jin, R.; Che, T.; Liu, Q.H.; Wang, W.Z.; Qi, Y.; et al. Heihe Watershed Allied Telemetry Experimental Research (HiWATER): Scientific objectives and experimental design. Bull. Am. Meteorol. Soc. 2013, 94, 1145–1160. [Google Scholar] [CrossRef]
- Yang, K.; Qin, J.; Zhao, L.; Chen, Y.Y.; Tang, W.J.; Han, M.L.; La, Z.; Chen, Z.Q.; Lv, N.; Ding, B.H.; et al. A multi-scale soil moisture and freeze-thaw monitoring network on the third pole. Bull. Am. Meteorol. Soc. 2013, 94, 1907–1916. [Google Scholar] [CrossRef]
- Zeng, J.Y.; Li, Z.; Chen, Q.; Bi, H.Y.; Qiu, J.X.; Zou, P.F. Evaluation of remotely sensed and reanalysis soil moisture products over the tibetan plateau using in-situ observations. Remote Sens. Environ. 2015, 163, 91–110. [Google Scholar] [CrossRef]
- Kim, S.; Balakrishnan, K.; Liu, Y.; Johnson, F.; Sharma, A. Spatial disaggregation of coarse soil moisture data by using high-resolution remotely sensed vegetation products. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1604–1608. [Google Scholar] [CrossRef]
- Cui, C.; Xu, J.; Zeng, J.; Chen, K.S.; Bai, X.; Lu, H.; Chen, Q.; Zhao, T.J. Soil moisture mapping from satellites: An intercomparison of SMAP, SMOS, FY3B, AMSR2, and ESA CCI over two dense network regions at different spatial scales. Remote Sens. 2018, 10, 33. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.P.; Martinuzzi, J.M.; Font, J.; Berger, M. Soil moisture retrieval from space: The soil moisture ocean salinity (SMOS) mission. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1729–1735. [Google Scholar] [CrossRef]
- Parinussa, R.M.; Wang, G.; Holmes, T.R.H.; Liu, Y.Y.; Dolman, A.J.; Jeu, R.A.M.D.; Jiang, T.; Zhang, P.; Shi, J. Global surface soil moisture from the microwave radiation imager onboard the Fengyun-3B satellite. Int. J. Remote Sens. 2014, 35, 7007–7029. [Google Scholar] [CrossRef]
- Dorigo, W.; Wagner, W.; Albergel, C.; Albrecht, F.; Balsamo, G.; Brocca, L. ESA CCI soil moisture for improved earth system understanding: State-of-the art and future directions. Remote Sens. Environ. 2017, 203, 185–215. [Google Scholar] [CrossRef]
- Sachindra, D.A.; Huang, F.; Barton, A.; Perera, B.J.C. Least square support vector and multi-linear regression for statistically downscaling general circulation model outputs to catchment streamflows. Int. J. Climatol. 2013, 33, 1087–1106. [Google Scholar] [CrossRef]
- Zhang, H.; Huang, B. Support vector regression-based downscaling for intercalibration of multiresolution satellite images. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1114–1123. [Google Scholar] [CrossRef]
- Alaya, M.A.B.; Chebana, F.; Ouarda, T.B.M.J. Multisite and multivariable statistical downscaling using a gaussian copula quantile regression model. Clim. Dyn. 2016, 1–15. [Google Scholar] [CrossRef]
- Merlin, O.; Rudiger, C.; Bitar, A.A.; Richaume, P.; Walker, J.P.; Kerr, Y.H. Disaggregation of SMOS soil moisture in southeastern Australia. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1556–1571. [Google Scholar] [CrossRef]
- Djamai, N.; Magagi, R.; Goïta, K.; Merlin, O.; Kerr, Y.; Roy, A. A combination of dispatch downscaling algorithm with class land surface scheme for soil moisture estimation at fine scale during cloudy days. Remote Sens. Environ. 2016, 184, 1–14. [Google Scholar] [CrossRef]
- Miralles, D.G.; Crow, W.T.; Cosh, M.H. Estimating spatial sampling errors in coarse-scale soil moisture estimates derived from point-scale observations. J. Hydrometeorol. 2010, 11, 1423–1429. [Google Scholar] [CrossRef]
- Kang, J.; Jin, R.; Li, X.; Zhang, Y.; Zhu, Z. Spatial Upscaling of Sparse Soil Moisture Observations Based on Ridge Regression. Remote Sens. 2018, 10, 192. [Google Scholar] [CrossRef]
- Yilmaz, M.T.; Crow, W.T. Evaluation of assumptions in soil moisture triple collocation analysis. J. Hydrometeorol. 2013, 15, 1293–1302. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2014; Available online: http://www.r-project.org/ (accessed on 27 March 2018).
- Cha, S.H.; Srihari, S.N. On measuring the distance between histograms. Pattern Recognit. 2002, 35, 1355–1370. [Google Scholar] [CrossRef]
- Bisquert, M.; Sánchez, J.M.; Caselles, V. Evaluation of disaggregation methods for downscaling modis land surface temperature to Landsat spatial resolution in Barrax test site. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 1430–1438. [Google Scholar] [CrossRef]
- Eweys, O.A.; Escorihuela, M.J.; Villar, J.M.; Er-Raki, S.; Amazirh, A.; Olivera, L.; Jarlan, L.; Khabba, S.; Merlin, O. Disaggregation of SMOS soil moisture to 100 m resolution using MODIS optical/thermal and sentinel-1 radar data: Evaluation over a bare soil site in morocco. Remote Sens. 2017, 9, 1155. [Google Scholar] [CrossRef]
- Zreda, M.; Desilets, D.; Ferré, T.P.A.; Scott, R.L. Measuring soil moisture content non-invasively at intermediate spatial scale using cosmic-ay neutrons. Geophys. Res. Lett. 2008, 35, L21402. [Google Scholar] [CrossRef]
- Kędzior, M.A.; Zawadzki, J. SMOS data as a source of the agricultural drought information: Case study of the Vistula catchment, Poland. Geoderma 2017, 306, 167–182. [Google Scholar] [CrossRef]




| Data Source | Short Name | Spatial Resolution | Temporal Resolution | Coverage | |
|---|---|---|---|---|---|
| AMSR-2 | Ascending product | AMSR2_A | 25 km | Daily | Global 2012– |
| Descending product | AMSR2_D | ||||
| SMOS | Ascending product | SMOS_A | 25 km | Daily | Global 2010– |
| Descending product | SMOS_D | ||||
| FY-3B | Ascending product | FY3B_A | 25 km | Daily | Global 2011– |
| Descending product | FY3B_D | ||||
| ESA CCI | Combined product | ESACCI_C | 25 km | Daily | Global 1978–2016 |
| Passive product | ESACCI_P | ||||
| Study Area | Coarse SSM | Other Variables | Downscaling Method | Validation | ||
|---|---|---|---|---|---|---|
| Name | Trend | Residual | ||||
| Upper HRB area | AMSR-2 (25 km) ESA CCI (25 km) FY-3B (25 km) | LST (1 km/25 km) NDVI (1 km/25 km) BSA (1 km/25 km) Tb (1 km) | GWATPRK | GWR | ATPK | Cross validation using the TC method Indirect validation using Tb data |
| QRM | Quadratic regression | Bilinear interpolation | ||||
| ATPRK | Ordinary linear regression | ATPK | ||||
| SVR | Support vector regression | Bilinear interpolation | ||||
| Naqu area | AMSR-2 (25 km) ESA CCI (25 km) FY-3B (25 km) SMOS (25 km) | LST (1 km/25 km) NDVI (1 km/25 km) BSA (1 km/25 km) In situ (1 km) | GWATPRK | GWR | ATPK | Direct validation using ground observations Cross validation using the TC method |
| QRM | Quadratic regression | Bilinear interpolation | ||||
| ATPRK | Ordinary linear regression | ATPK | ||||
| SVR | Support vector regression | Bilinear interpolation | ||||
| AMSR2_A | AMSR2_D | SMOS_A | SMOS_D | FY3B_A | FY3B_D | ESACCI_C | ESACCI_P | ||
|---|---|---|---|---|---|---|---|---|---|
| RMSE | GWATPRK | 0.114 * | 0.175 * | 0.114 * | 0.083 * | 0.079 * | 0.195 * | 0.056 * | 0.075 * |
| QRM | 0.158 | 0.198 | 0.166 | 0.107 | 0.089 | 0.260 | 0.096 | 0.126 | |
| ATPRK | 0.140 | 0.188 | 0.148 | 0.087 | 0.087 | 0.233 | 0.073 | 0.078 | |
| SVR | 0.154 | 0.176 | 0.147 | 0.093 | 0.088 | 0.245 | 0.061 | 0.079 | |
| ME | GWATPRK | 0.050 * | 0.093 * | −0.092 * | −0.023 * | 0.016 * | −0.189* | 0.002 * | 0.003 * |
| QRM | 0.081 | 0.171 | −0.134 | −0.028 | 0.030 | −0.205 | −0.040 | 0.034 | |
| ATPRK | 0.054 | 0.134 | −0.134 | −0.025 | 0.024 | −0.203 | −0.003 | −0.007 | |
| SVR | 0.060 | 0.151 | −0.116 | −0.026 | 0.027 | −0.190 | 0.016 | 0.022 | |
| R | GWATPRK | 0.469 * | 0.382 * | 0.449 * | 0.688* | 0.676* | 0.341 * | 0.772 * | 0.699 * |
| QRM | 0.346 | 0.311 | 0.342 | 0.612 | 0.439 | 0.315 | 0.668 | 0.399 | |
| ATPRK | 0.463 | 0.373 | 0.408 | 0.663 | 0.566 | 0.332 | 0.766 | 0.675 | |
| SVR | 0.369 | 0.338 | 0.383 | 0.660 | 0.611 | 0.317 | 0.723 | 0.576 | |
| SLOP | GWATPRK | 0.694 * | 0.586 * | 0.675 * | 0.630 * | 0.809 * | 0.534 * | 1.036 * | 0.811 * |
| QRM | 0.621 | 0.536 | 0.527 | 0.556 | 0.597 | 0.508 | 0.816 | 0.663 | |
| ATPRK | 0.679 | 0.576 | 0.675* | 0.602 | 0.744 | 0.519 | 1.045 | 0.766 | |
| SVR | 0.680 | 0.542 | 0.568 | 0.535 | 0.624 | 0.509 | 1.076 | 0.701 | |
| AMSR2_A | AMSR2_D | ESACCI_C | ESACCI_P | ||
|---|---|---|---|---|---|
| R | GWATPRK | 0.514 | 0.478 | 0.703 | 0.647 |
| QRM | 0.398 | 0.386 | 0.501 | 0.412 | |
| ATPRK | 0.477 | 0.434 | 0.571 | 0.519 | |
| SVR | 0.459 | 0.457 | 0.601 | 0.500 | |
| ID | GWATPRK | 0.419 | 0.382 | 0.589 | 0.547 |
| QRM | 0.328 | 0.313 | 0.422 | 0.361 | |
| ATPRK | 0.347 | 0.332 | 0.469 | 0.416 | |
| SVR | 0.431 | 0.351 | 0.511 | 0.482 | |
| K-L | GWATPRK | 0.617 | 0.622 | 0.542 | 0.551 |
| QRM | 0.686 | 0.700 | 0.631 | 0.647 | |
| ATPRK | 0.665 | 0.681 | 0.586 | 0.602 | |
| SVR | 0.583 | 0.652 | 0.570 | 0.573 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, Y.; Ge, Y.; Wang, J.; Heuvelink, G.B.M.; Wang, L. Geographically Weighted Area-to-Point Regression Kriging for Spatial Downscaling in Remote Sensing. Remote Sens. 2018, 10, 579. https://doi.org/10.3390/rs10040579
Jin Y, Ge Y, Wang J, Heuvelink GBM, Wang L. Geographically Weighted Area-to-Point Regression Kriging for Spatial Downscaling in Remote Sensing. Remote Sensing. 2018; 10(4):579. https://doi.org/10.3390/rs10040579
Chicago/Turabian StyleJin, Yan, Yong Ge, Jianghao Wang, Gerard B. M. Heuvelink, and Le Wang. 2018. "Geographically Weighted Area-to-Point Regression Kriging for Spatial Downscaling in Remote Sensing" Remote Sensing 10, no. 4: 579. https://doi.org/10.3390/rs10040579
APA StyleJin, Y., Ge, Y., Wang, J., Heuvelink, G. B. M., & Wang, L. (2018). Geographically Weighted Area-to-Point Regression Kriging for Spatial Downscaling in Remote Sensing. Remote Sensing, 10(4), 579. https://doi.org/10.3390/rs10040579







