Modeling Surface Energy Fluxes over a Dehesa (Oak Savanna) Ecosystem Using a Thermal Based Two-Source Energy Balance Model (TSEB) I
Abstract
:1. Introduction
2. Materials and Methods
2.1. Two-Source Energy Balance Model (TSEB)—Basic Formulations
Aerodynamic Resistance Scheme and Wind-Speed Profile
2.2. Modifications to TSEB Formulations and Parameters
2.2.1. Roughness Length and Zero Plane Displacement Height (z0M − d0)
2.2.2. Within-Canopy Wind-Speed Profile Scheme
2.2.3. Within-Canopy Wind-Speed Profile Scheme Modified to Account for Different Vegetation Layers
2.2.4. Priestley–Taylor Coefficient Evaluation
2.3. Ground Measurements (TSEB Inputs and Validation)
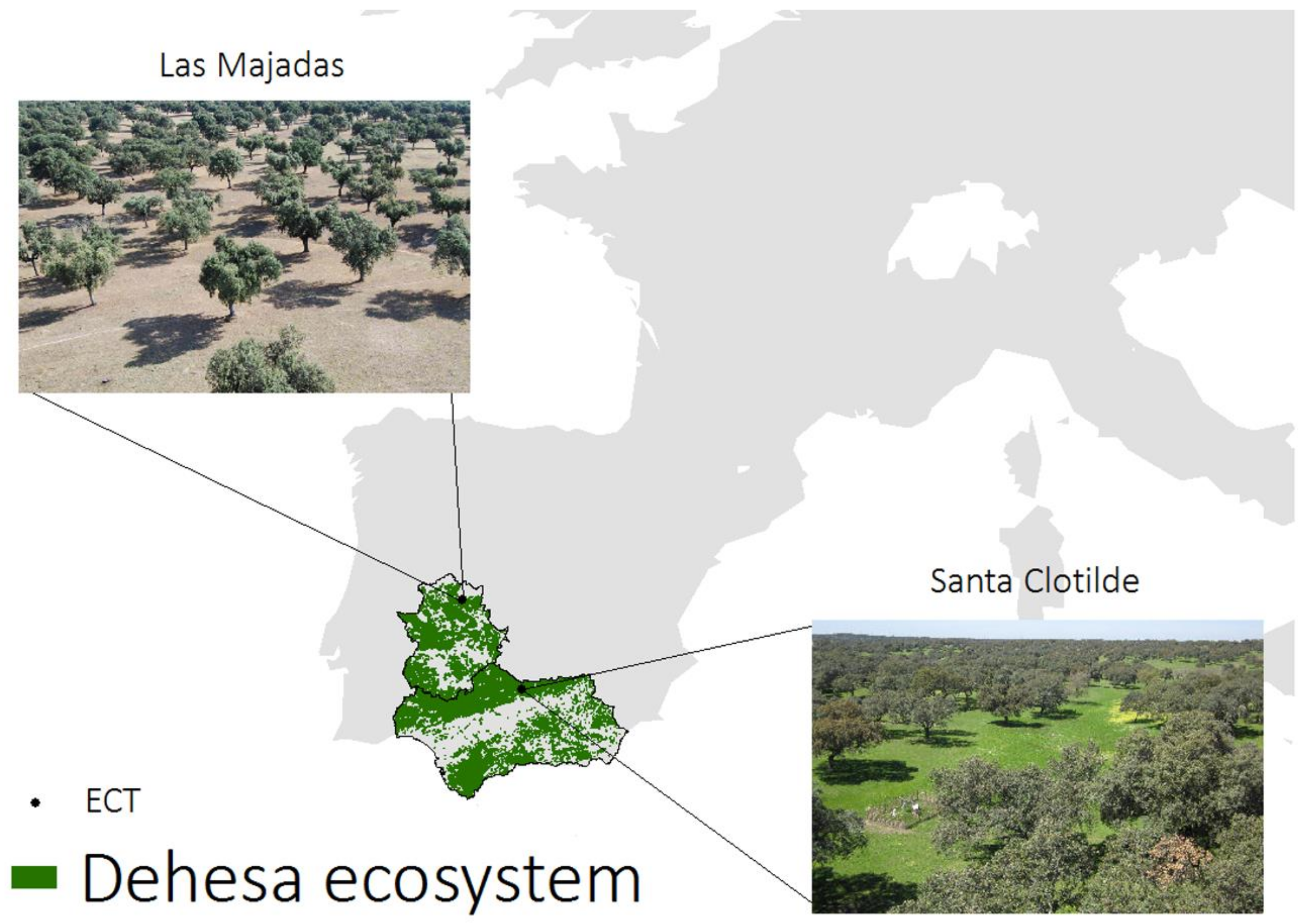
2.3.1. Santa Clotilde
2.3.2. Las Majadas del Tiétar
2.3.3. Energy Balance Closure Error and Footprint
2.3.4. Remotely Sensed Inputs for TSEB
2.4. Evaluation of TSEB Performance in the Dehesa
3. Results
3.1. Evaluation of the Ground Measurements and TSEB Inputs
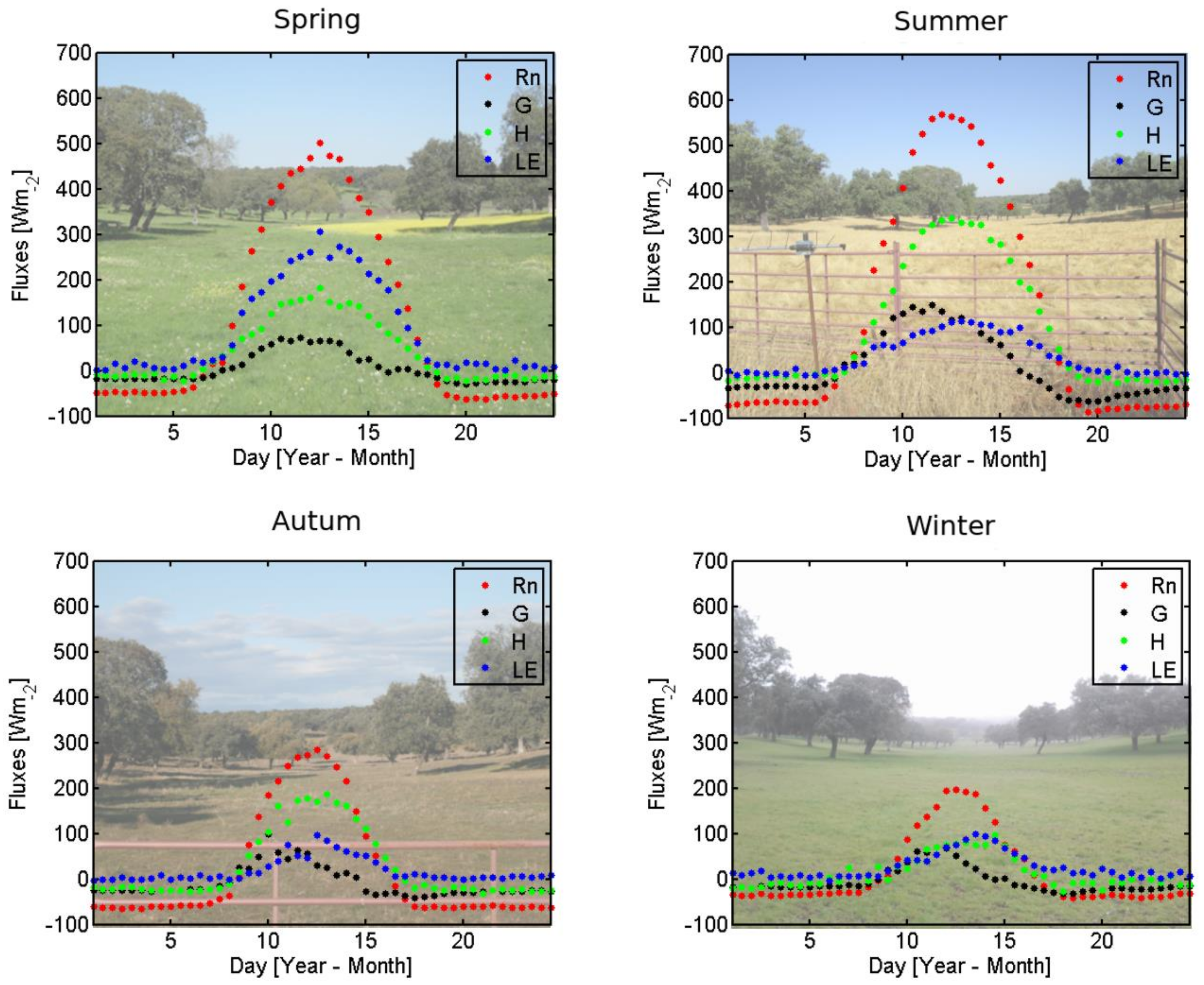
3.1.1. Evaluation of the Surface Energy Fluxes Measured at the EC Sites
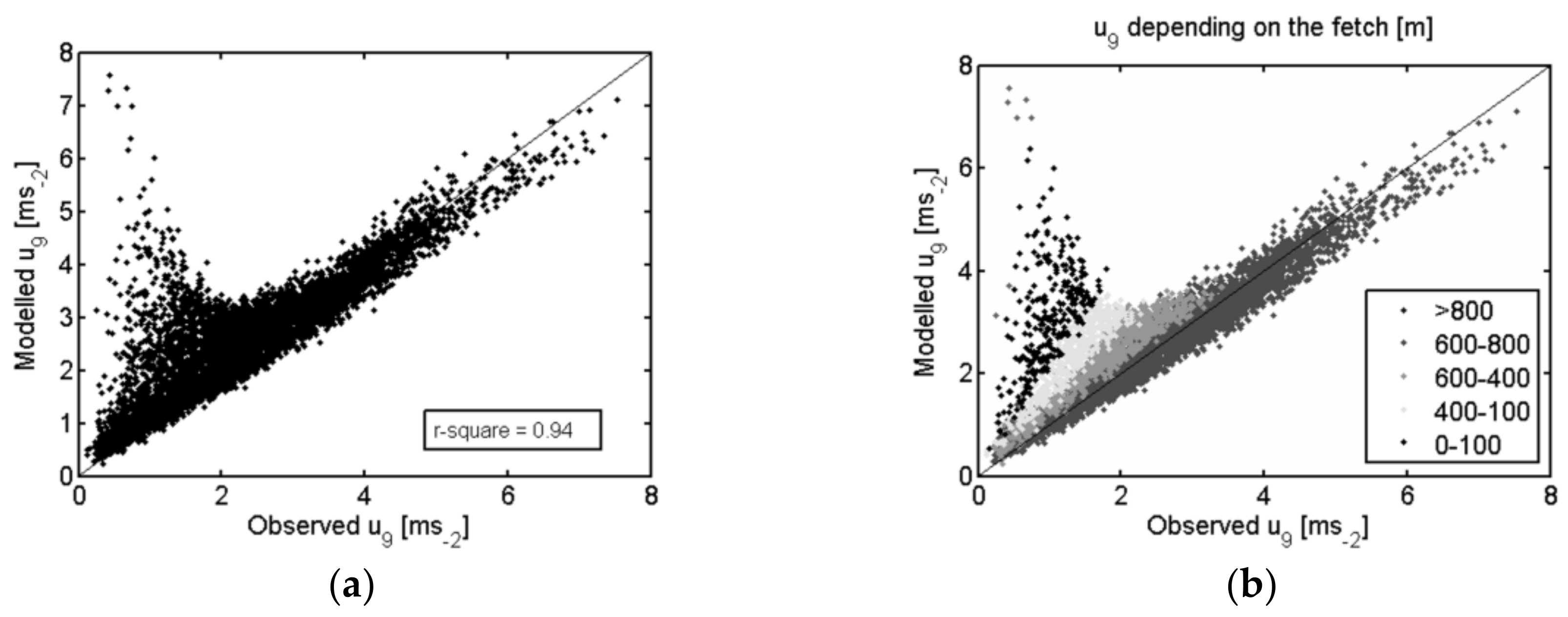
3.1.2. Evaluation of the Remote Sensing Data Used to Derive TSEB Inputs
3.2. Evaluation of TSEB Formulation
3.2.1. Roughness Length and Zero-Plane Displacement Height
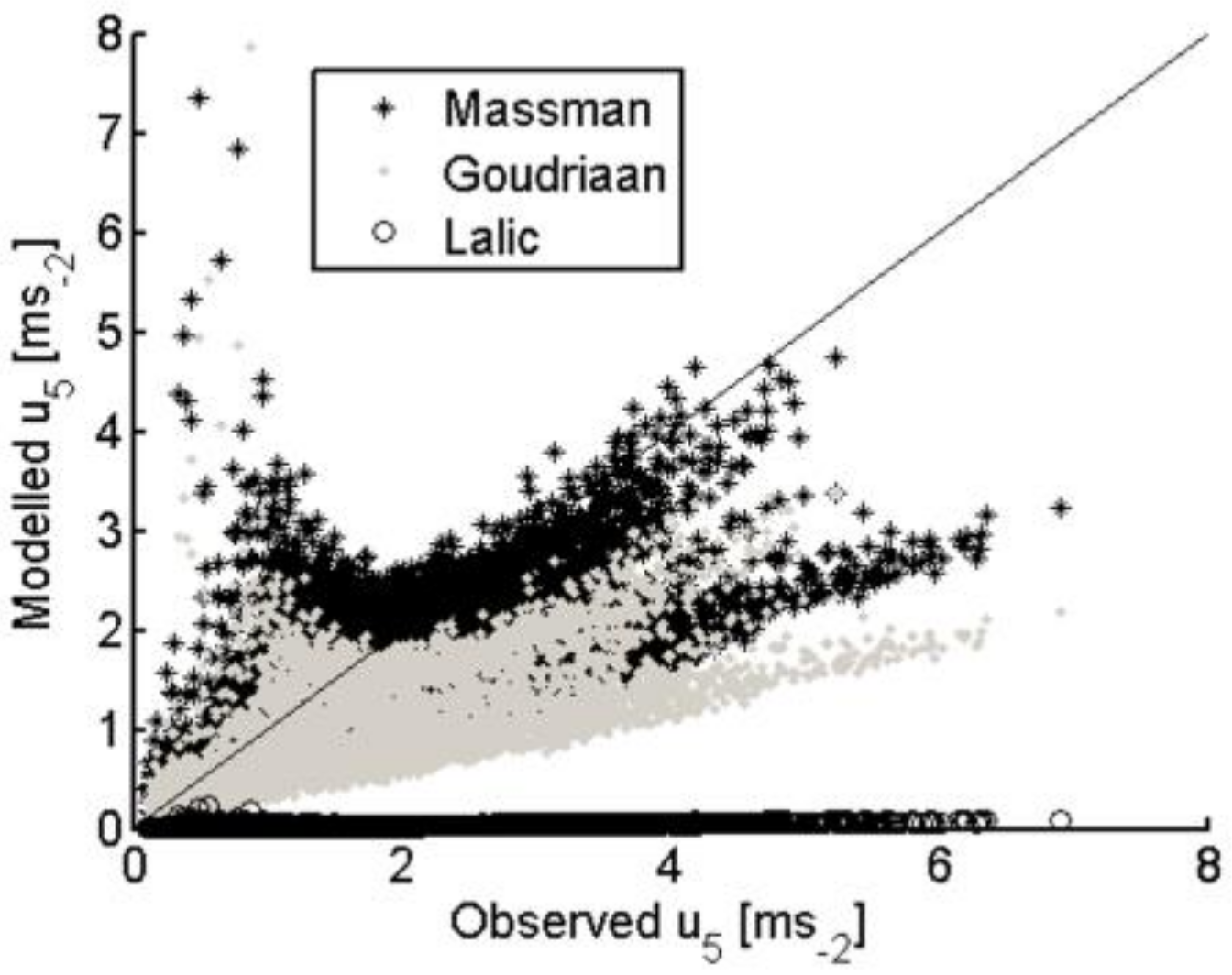
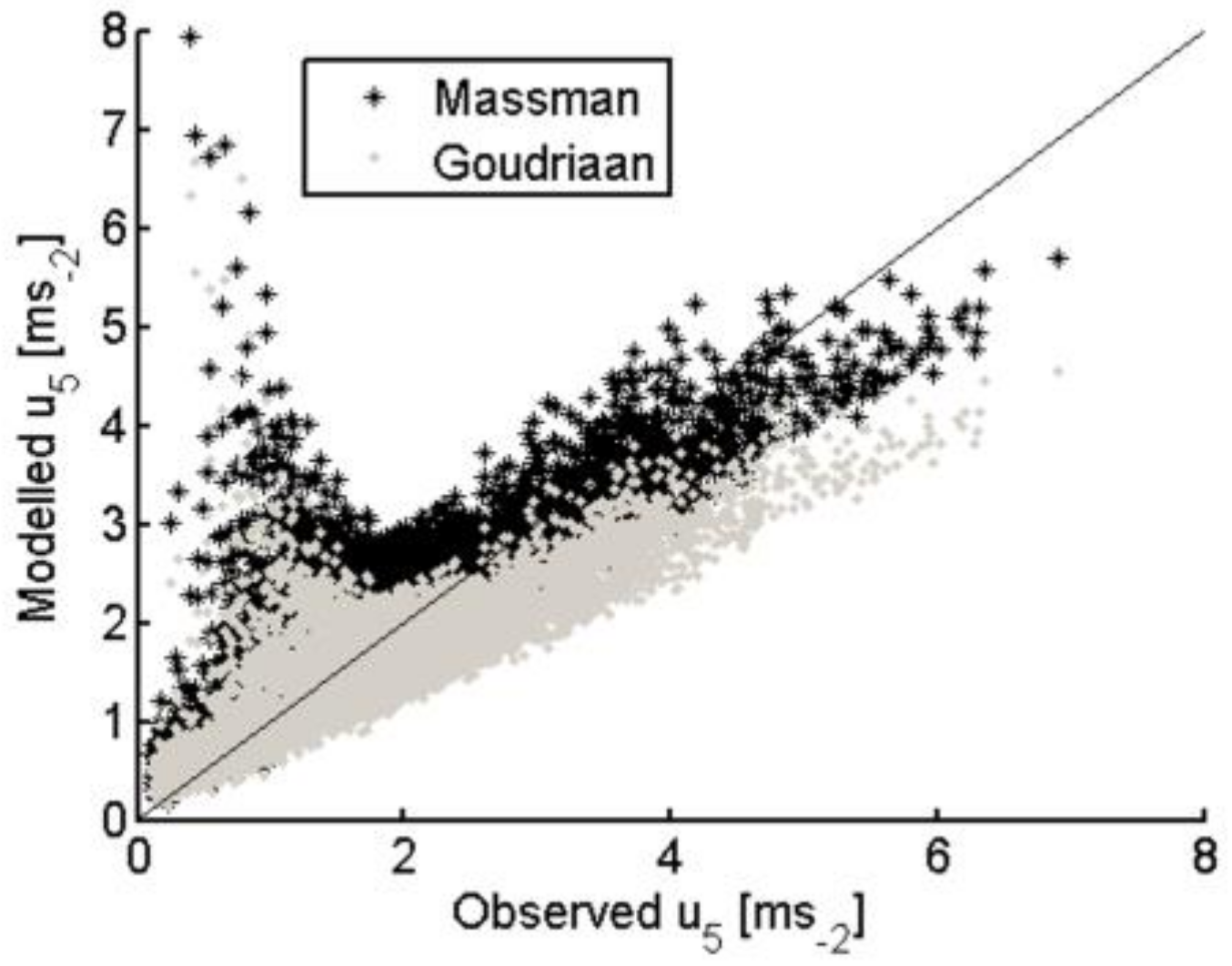
3.2.2. Within-Canopy Wind-Speed Profile Scheme
3.2.3. Within-Canopy Wind-Speed Profile Scheme with the Modification to Account for Different Vegetation (Grass and Tree) Layers
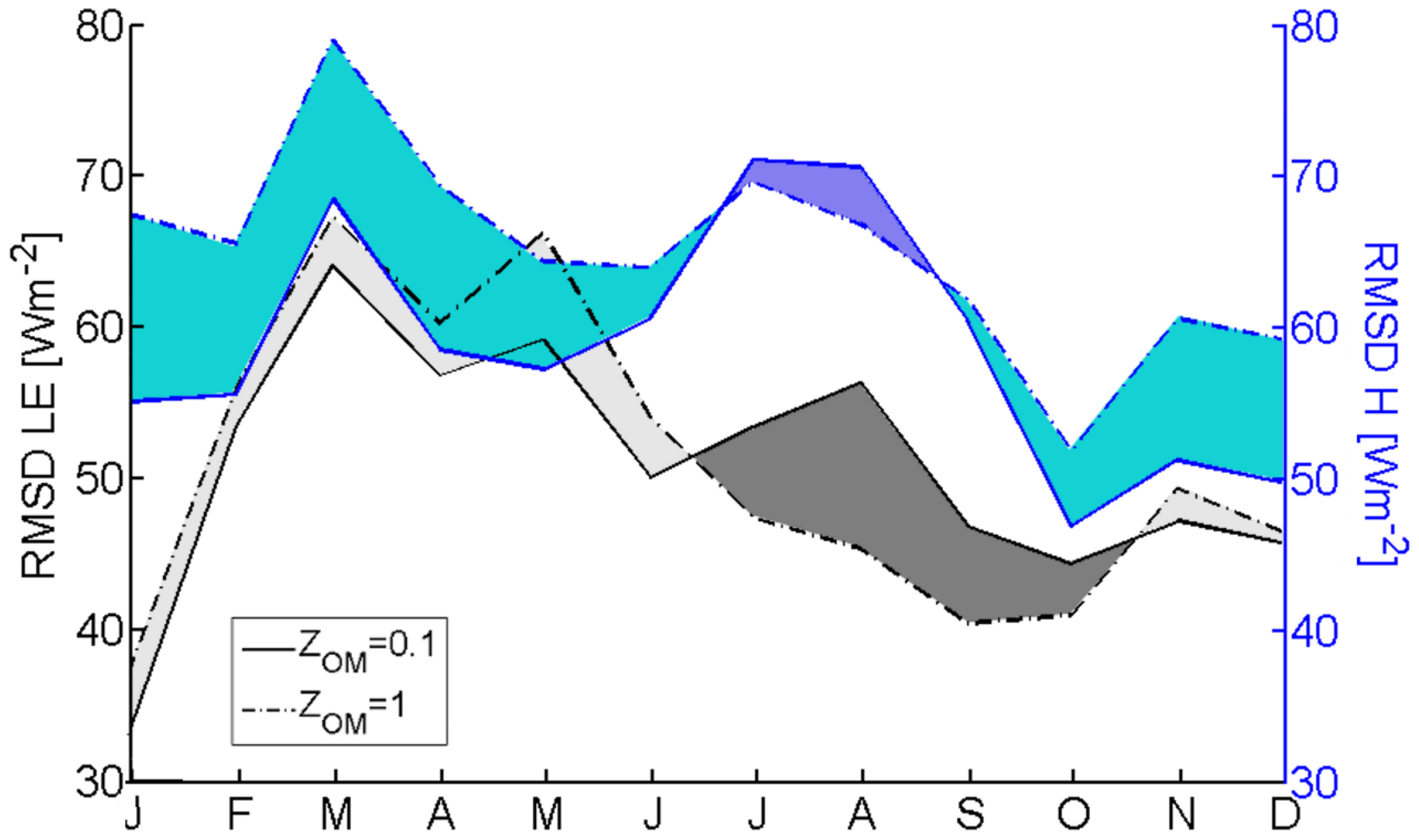
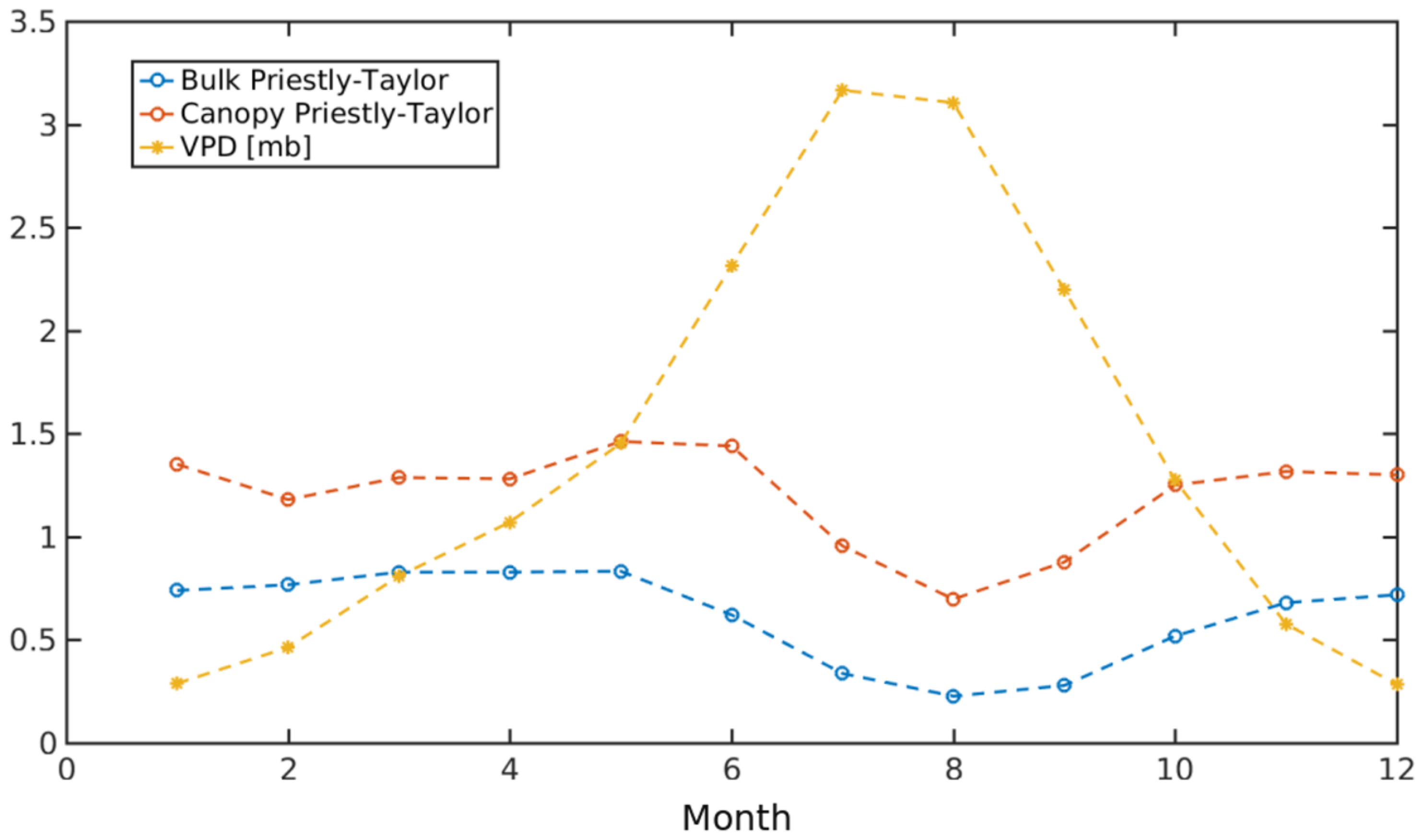
3.2.4. Priestley–Taylor Coefficient Evaluation
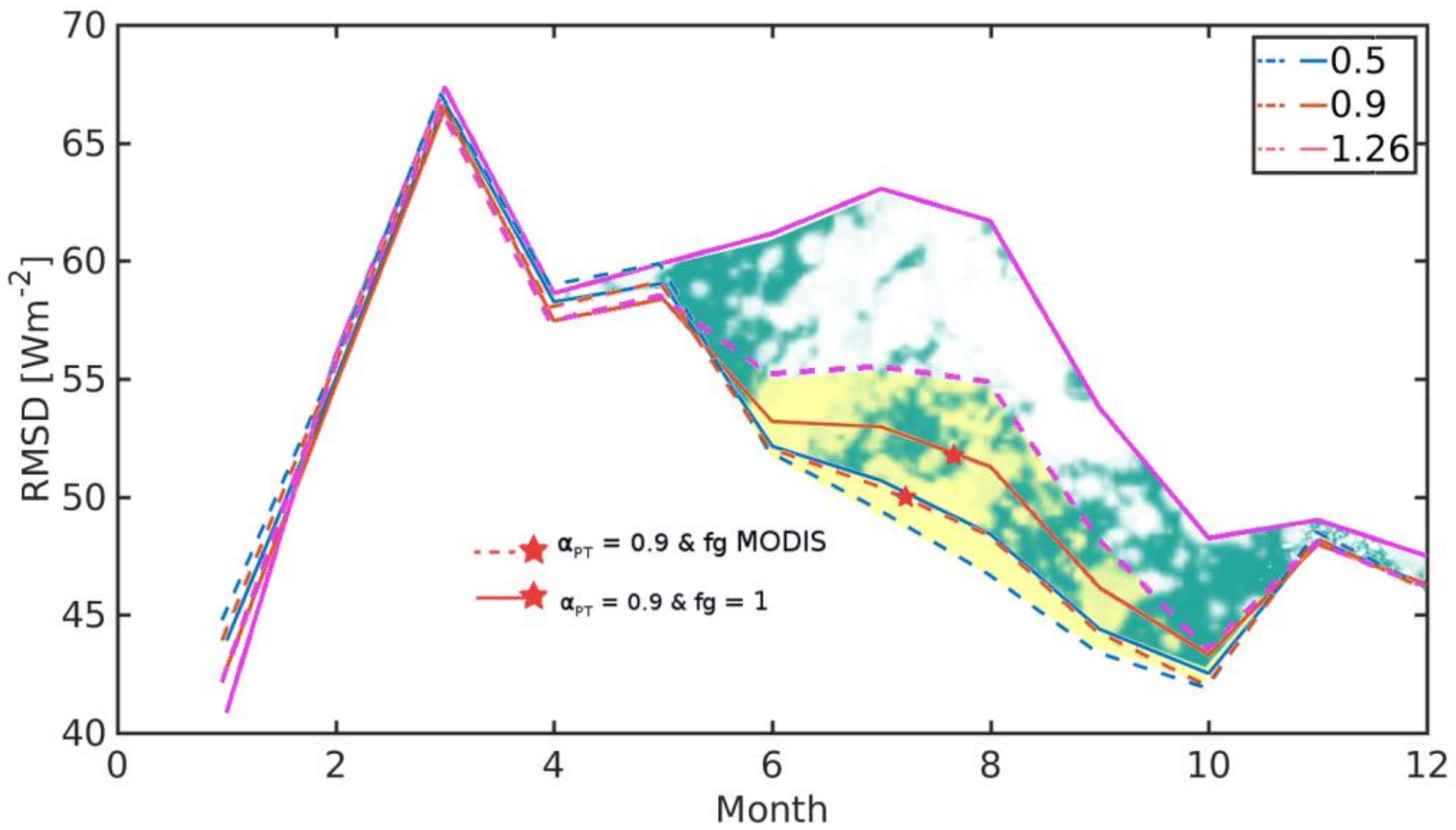
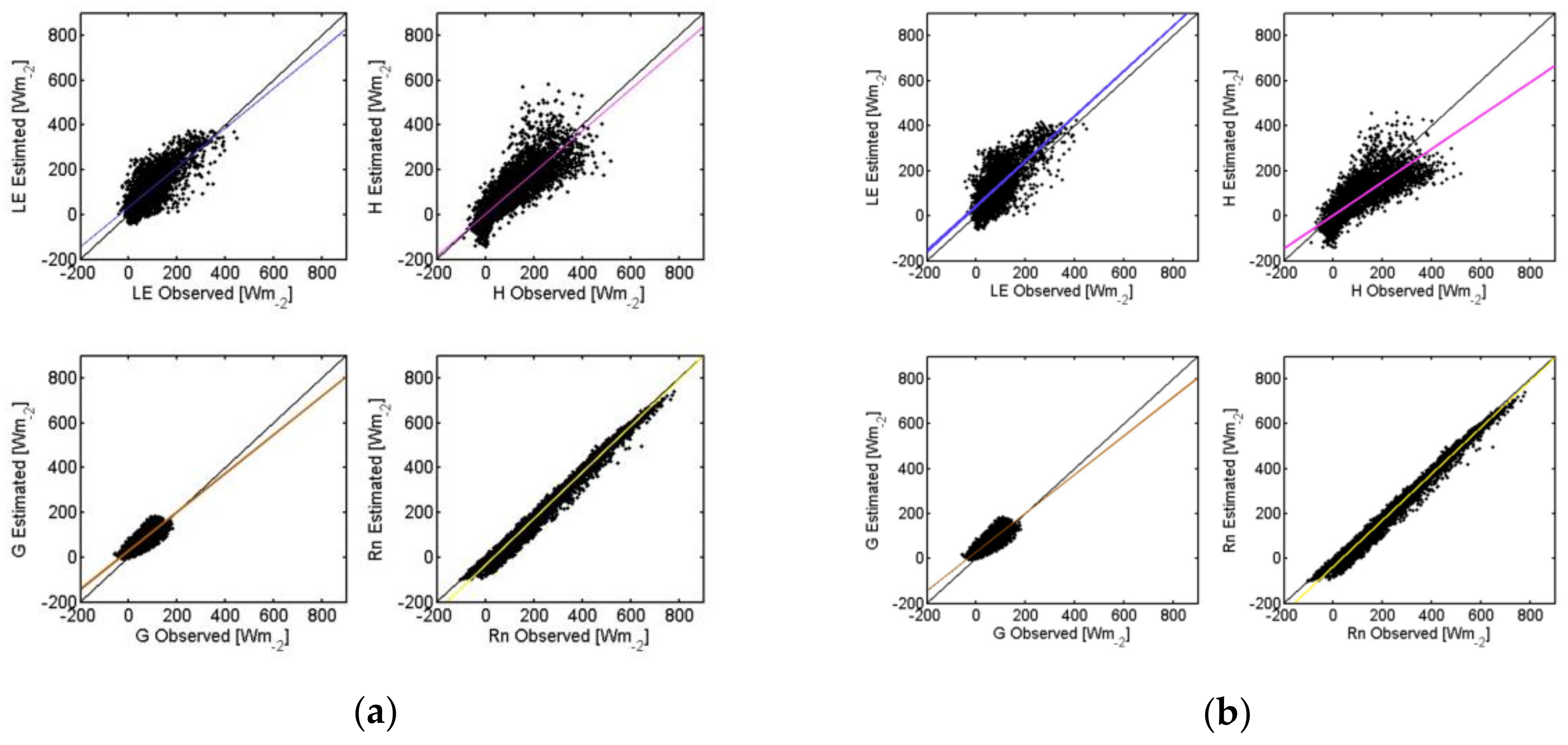
3.3. Evaluation of TSEB Performance in Savanna Ecosystem
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sankaran, M.; Ratnam, J. African and Asian Savannas A2—Levin, Simon A. In Encyclopedia of Biodiversity, 2nd ed.; Academic Press: Waltham, MA, USA, 2013; pp. 58–74. ISBN 978-0-12-384720-1. [Google Scholar]
- Papanastasis, V.P. Vegetation degradation and land use changes in agrosilvopastoral systems. In Sustainability of Agrosilvopastoral Systems: Dehesas, Montados; Advances in Geoecology; Catena Verlag: Reiskirchen, Germany, 2004; Volume 37, pp. 1–12. ISBN 3-923381-50-6. [Google Scholar]
- Schnabel, S.; Dahlgren, R.A.; Moreno, G. Soil and water dynamics. In Mediterranean Oak Woodland Working Landscapes: Dehesas of Spain and Ranchlands of California; Springer: New York, NY, USA, 2013; pp. 91–121. [Google Scholar]
- Pachauri, R.K.; Meyer, L.A. (Eds.) IPCC Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2014. [Google Scholar]
- Baldocchi, D.D.; Xu, L. What limits evaporation from Mediterranean oak woodlands—The supply of moisture in the soil, physiological control by plants or the demand by the atmosphere? Recent Dev. Hydrol. Anal. 2007, 30, 2113–2122. [Google Scholar] [CrossRef]
- Jeltsch, F.; Weber, G.E.; Grimm, V. Ecological buffering mechanisms in savannas: A unifying theory of long-term tree-grass coexistence. Plant Ecol. 2000, 150, 161–171. [Google Scholar] [CrossRef]
- Bond, W.J.; Keeley, J.E. Fire as a global “herbivore”: The ecology and evolution of flammable ecosystems. Trends Ecol. Evol. 2005, 20, 387–394. [Google Scholar] [CrossRef] [PubMed]
- Andreu, A. Water Monitoring in Vegetation Covers through Multi-Scale Energy Balance Modelling Using Time Series of Remotely Sensed Data; University of Cordoba: Cordoba, Spain, 2014. [Google Scholar]
- Campos, P. Mediterranean Oak Woodland Working Landscapes: Dehesas of Spain and Ranchlands of California; Springer: New York, NY, USA, 2013. [Google Scholar]
- McCabe, M.F.; Wood, E.F. Scale influences on the remote estimation of evapotranspiration using multiple satellite sensors. Remote Sens. Environ. 2006, 105, 271–285. [Google Scholar] [CrossRef]
- Gamon, J.A. Reviews and Syntheses: Optical sampling of the flux tower footprint. Biogeosciences 2015, 12, 4509–4523. [Google Scholar] [CrossRef]
- Kustas, W.P.; Norman, J.M. A two-source energy balance approach using directional radiometric temperature observations for sparse canopy covered surfaces. Agron. J. 2000, 92, 847–854. [Google Scholar] [CrossRef]
- González-Dugo, M.P.; Neale, C.M.U.; Mateos, L.; Kustas, W.P.; Prueger, J.H.; Anderson, M.C.; Li, F. A comparison of operational remote sensing-based models for estimating crop evapotranspiration. Agric. For. Meteorol. 2009, 149, 1843–1853. [Google Scholar] [CrossRef]
- Shuttleworth, W.J.; Wallace, J.S. Evaporation from sparse crops-an energy combination theory. Q. J. R. Meteorol. Soc. 1985, 111, 839–855. [Google Scholar] [CrossRef]
- Shuttleworth, W.J.; Gurney, R.J. The theoretical relationship between foliage temperature and canopy resistance in sparse crops. Q. J. R. Meteorol. Soc. 1990, 116, 497–519. [Google Scholar] [CrossRef]
- Norman, J.M.; Kustas, W.P.; Humes, K.S. Source approach for estimating soil and vegetation energy fluxes in observations of directional radiometric surface temperature. Therm. Remote Sens. Energy Water Balance Veg. 1995, 77, 263–293. [Google Scholar] [CrossRef]
- Kustas, W.P.; Norman, J.M. Evaluation of soil and vegetation heat flux predictions using a simple two-source model with radiometric temperatures for partial canopy cover. Agric. For. Meteorol. 1999, 94, 13–29. [Google Scholar] [CrossRef]
- Timmermans, W.J.; Kustas, W.P.; Anderson, M.C.; French, A.N. An intercomparison of the Surface Energy Balance Algorithm for Land (SEBAL) and the Two-Source Energy Balance (TSEB) modeling schemes. Remote Sens. Environ. 2007, 108, 369–384. [Google Scholar] [CrossRef]
- Kustas, W.P.; Norman, J.M. A two-source approach for estimating turbulent fluxes using multiple angle thermal infrared observations. WRCR Water Resour. Res. 1997, 33, 1495–1508. [Google Scholar] [CrossRef]
- French, A.N.; Jacob, F.; Anderson, M.C.; Kustas, W.P.; Timmermans, W.; Gieske, A.; Su, Z.; Su, H.; McCabe, M.F.; Li, F. Surface energy fluxes with the Advanced Spaceborne Thermal Emission and Reflection radiometer (ASTER) at the Iowa 2002 SMACEX site (USA). Remote Sens. Environ. 2005, 99, 55–65. [Google Scholar] [CrossRef]
- Cammalleri, C.; Anderson, M.C.; Ciraolo, G.; D’Urso, G.; Kustas, W.P.; La Loggia, G.; Minacapilli, M. The impact of in-canopy wind profile formulations on heat flux estimation in an open orchard using the remote sensing-based two-source model. Hydrol. Earth Syst. Sci. 2010, 14, 2643–2659. [Google Scholar] [CrossRef] [Green Version]
- Guzinski, R.; Anderson, M.C.; Kustas, W.P.; Nieto, H.; Sandholt, I. Using a thermal-based two source energy balance model with time-differencing to estimate surface energy fluxes with day–night MODIS observations. Hydrol. Earth Syst. Sci. 2013, 17, 2809–2825. [Google Scholar] [CrossRef]
- Morillas, L.; Garcia, M.; Nieto, H.; Villagarcia, L.; Sandholt, I.; Gonzalez-Dugo, M.P.; Zarco-Tejada, P.J.; Domingo, F. Using radiometric surface temperature for surface energy flux estimation in Mediterranean drylands from a two-source perspective. Remote Sens. Environ. 2013, 136, 234–246. [Google Scholar] [CrossRef]
- Kustas, W.P.; Anderson, M.C.; Alfieri, J.G.; Nieto, H.; Morillas, L.; Hipps, L.E.; Villagarcia, L.; Domingo, F.; Garcia, M. Revisiting the paper Using radiometric surface temperature for surface energy flux estimation in Mediterranean drylands from a two-source perspective. Remote Sens. Environ. 2016, 184, 645–653. [Google Scholar] [CrossRef]
- Campos, I.; Villodre, J.; Carrara, A.; Calera, A. Remote sensing-based soil water balance to estimate Mediterranean holm oak savanna (dehesa) evapotranspiration under water stress conditions. J. Hydrol. 2013, 494, 1–9. [Google Scholar] [CrossRef]
- Joffre, R.; Rambal, S. How tree cover influences the water balance of Mediterranean rangelands. Ecology 1993, 74, 570. [Google Scholar] [CrossRef]
- Baldocchi, D.D.; Xu, L.; Kiang, N. How plant functional-type, weather, seasonal drought, and soil physical properties alter water and energy fluxes of an oak–grass savanna and an annual grassland. Agric. For. Meteorol. 2004, 123, 13–39. [Google Scholar] [CrossRef]
- Li, F.; Kustas, W.P.; Prueger, J.H.; Neale, C.M.U.; Jackson, T.J. Utility of Remote Sensing Based Two-Source Energy Balance Model under Low- and High-Vegetation Cover Conditions. J. Hydrometeorol. 2005, 6, 878–891. [Google Scholar] [CrossRef]
- Choudhury, B.J. Relationships between vegetation indices, radiation absorption, and net photosynthesis evaluated by a sensitivity analysis. Remote Sens. Environ. 1987, 22, 209–233. [Google Scholar] [CrossRef]
- Campbell, G.S.; Norman, J.M. An Introduction to Environmental Biophysics; Springer: Delhi, India, 2009; ISBN 978-0-387-94937-6. [Google Scholar]
- Ross, J. Radiative transfer in plant communities. In Vegetation and the Atmosphere; Monteith, J.L., Ed.; 1975; Volume 1, pp. 13–55. [Google Scholar]
- Lhomme, J.-P.; Chehbouni, A. Comments on dual-source vegetation-atmosphere transfer models. Agric. For. Meteorol. 1999, 94, 269–273. [Google Scholar] [CrossRef]
- Kustas, W.P.; Daughtry, C.S. Estimation of the soil heat flux/net radiation ratio from spectral data. Agric. For. Meteorol. 1990, 49, 205–223. [Google Scholar] [CrossRef]
- Friedl, M.A. Relationships among remotely sensed data, surface energy balance, and area-averaged fluxes over partially vegetated land surfaces. J. Appl. Meteorol. 1996, 35, 2091–2103. [Google Scholar] [CrossRef]
- Cellier, P.; Richard, G.; Robin, P. Partition of sensible heat fluxes into bare soil and the atmosphere. Agric. For. Meteorol. 1996, 82, 245–265. [Google Scholar] [CrossRef]
- Brutsaert, W. Evaporation into the Atmosphere: Theory, History and Applications; Kluwer: Dordrecht, The Netherlands, 2010. [Google Scholar]
- Priestley, C.H.B.; Taylor, R.J. On the Assessment of Surface Heat Flux and Evaporation Using Large-Scale Parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Dyer, A.J. A review of flux-profile relationships. Bound.-Layer Meteorol. 1974, 7, 363–372. [Google Scholar] [CrossRef]
- Kondo, J.; Ishida, S. Sensible Heat Flux from the Earth’s Surface under Natural Convective Conditions. J. Atmos. Sci. 1997, 54, 498–509. [Google Scholar] [CrossRef]
- Goudriaan, J. Crop Micrometeorology: A Simulation Study; PUDOC: Wageningen, The Netherlands, 1977; ISBN 90-220-0614-X. [Google Scholar]
- Massman, W.J. An analytical one-dimensional model of momentum transfer by vegetation of arbitrary structure. Bound.-Layer Meteorol. 1997, 83, 407–421. [Google Scholar] [CrossRef]
- Massman, W.J.; Weil, J.C. An Analytical one-dimensional second-order closure model of turbulence statistics and the lagrangian time scale within and above plant canopies of arbitrary structure. Bound.-Layer Meteorol. 1999, 91, 81. [Google Scholar] [CrossRef]
- Choudhury, B.J.; Monteith, J.L. A four-layer model for the heat budget of homogeneous land surfaces. Q. J. R. Meteorol. Soc. 1988, 114, 373–398. [Google Scholar] [CrossRef]
- Raupach, M.R. Simplified expressions for vegetation roughness length and zero-plane displacement as functions of canopy height and area index. Bound.-Layer Meteorol. 1994, 71, 211–216. [Google Scholar] [CrossRef]
- Shaw, R.H.; Pereira, A. Aerodynamic roughness of a plant canopy: A numerical experiment. Agric. Meteorol. 1982, 26, 51–65. [Google Scholar] [CrossRef]
- Schaudt, K.; Dickinson, R. An approach to deriving roughness length and zero-plane displacement height from satellite data, prototyped with BOREAS data. Agric. For. Meteorol. 2000, 104, 143–155. [Google Scholar] [CrossRef]
- Rooney, G.G. Comparison of upwind land use and roughness length measured in the urban boundary layer. Bound.-Layer Meteorol. 2001, 100, 469–486. [Google Scholar] [CrossRef]
- Nakai, T.; Sumida, A.; Daikoku, K.; Matsumoto, K.; van der Molen, M.K.; Kodama, Y.; Kononov, A.V.; Maximov, T.C.; Dolman, A.J.; Yabuki, H.; et al. Parameterisation of aerodynamic roughness over boreal, cool- and warm-temperate forests. Agric. For. Meteorol. 2008, 148, 1916–1925. [Google Scholar] [CrossRef]
- De Bruin, H.A.R.; Moore, C.J. Zero-plane displacement and roughness length for tall vegetation, derived from a simple mass conservation hypothesis. Bound.-Layer Meteorol. 1985, 31, 39–49. [Google Scholar] [CrossRef]
- Massman, W. A comparative study of some mathematical models of the mean wind structure and aerodynamic drag of plant canopies. Bound.-Layer Meteorol. 1987, 40, 179–197. [Google Scholar] [CrossRef]
- Lalic, B.; Mihailovic, D.T.; Rajkovic, B.; Arsenic, I.D.; Radlovic, D. Wind profile within the forest canopy and in the transition layer above it. Environ. Model. Softw. 2003, 18, 943–950. [Google Scholar] [CrossRef]
- Shaw, R.H. Secondary wind-speed Maxima inside Plant Canopies. J. Appl. Meteorol. 1977, 16, 514–521. [Google Scholar] [CrossRef]
- Raupach, M.R.; Thom, A.S. Turbulence in and above Plant Canopies. Annu. Rev. Fluid Mech. 1981, 13, 97–129. [Google Scholar] [CrossRef]
- Agam, N.; Kustas, W.P.; Anderson, M.C.; Norman, J.M.; Colaizzi, P.D.; Howell, T.A.; Prueger, J.H.; Meyers, T.P.; Wilson, T.B. Application of the Priestley-Taylor approach in a two-source surface energy balance model. J. Hydrometeorol. 2010, 11, 185–198. [Google Scholar] [CrossRef]
- Monteith, J.L.; Unsworth, M.H. Principles of Environmental Physics; Arnold, E., Ed.; Routledge: New York, NY, USA; Chapman and Hall: London, UK, 1990; ISBN 0-7131-2981-6. [Google Scholar]
- Raupach, M.R. Combination theory and equilibrium evaporation. Q. J. R. Meteorol. Soc. 2001, 127, 1149–1181. [Google Scholar] [CrossRef]
- De Bruin, H.A.R.; Keijman, J.Q. The Priestley-Taylor evaporation model applied to a large, shallow lake in the Netherlands. J. Appl. Meteorol. 1979, 18, 898–903. [Google Scholar] [CrossRef]
- Komatsu, H. Forest categorization according to dry-canopy evaporation rates in the growing season: Comparison of the Priestley-Taylor coefficient values from various observation sites. Hydrol. Process. 2005, 19, 3873–3896. [Google Scholar] [CrossRef]
- Alameda, D.; Villar, R.; Iriondo, J.M. Spatial pattern of soil compaction: Trees footprint on soil physical properties. For. Ecol. Manag. 2012, 283, 128–137. [Google Scholar] [CrossRef]
- Quero, J.L.; Villar, R.; Marañon, T.; Zamora, R.; Poorter, L. Seed-mass effects in four Mediterranean Quercus species (Fagaceae) growing in contrasting light environments. Am. J. Bot. 2007, 94, 1795–1803. [Google Scholar] [CrossRef] [PubMed]
- Mauder, M.; Foken, T. Documentation and Instruction Manual of the Eddy-Covariance Software Package TK3; Universities Bayreuth: Bayreuth, Germany, 2013. [Google Scholar]
- Fuchs, M.; Tanner, C.B. Evaporation from a Drying Soil. J. Appl. Meteorol. 1967, 6, 852–857. [Google Scholar] [CrossRef]
- Fernandez-Rebollo, P.; Carbonero-Muñoz, M.D.; García-Moreno, A. Control y Seguimiento de Los Programas Agroambientales en la Comunidad Autónoma Andaluza. El Estado de Los Recursos en la Dehesa y el Papel de Las Medidas Agroambientales; Consejería de Agricultura y Pesca, Junta de Andalucía: Andalucía, Spain, 2009. [Google Scholar]
- Aubinet, M.; Grelle, A.; Ibrom, A.; Rannik, Ü.; Moncrieff, J.; Foken, T.; Kowalski, A.S.; Martin, P.H.; Berbigier, P.; Bernhofer, C.; et al. Estimates of the Annual Net Carbon and Water Exchange of Forests: The EUROFLUX Methodology. In Advances in Ecological Research; Fitter, A.H., Raffaelli, D.G., Eds.; Academic Press: London, UK, 1999; Volume 30, pp. 113–175. [Google Scholar]
- Twine, T.E.; Kustas, W.P.; Norman, J.M.; Cook, D.R.; Houser, P.R.; Meyers, T.P.; Prueger, J.H.; Starks, P.J.; Wesely, M.L. Correcting eddy-covariance flux underestimates over a grassland. Agric. For. Meteorol. 2000, 103, 279–300. [Google Scholar] [CrossRef]
- Foken, T. The energy balance closure problem: An overview. Ecol. Appl. 2008, 18, 1351–1367. [Google Scholar] [CrossRef] [PubMed]
- Schuepp, P.H.; Leclerc, M.Y.; MacPherson, J.I.; Desjardins, R.L. Footprint prediction of scalar fluxes from analytical solutions of the diffusion equation. Bound.-Layer Meteorol. 1990, 50, 355–373. [Google Scholar] [CrossRef]
- Stewart, J.B.; Thom, A.S. Energy budgets in pine forest. Q. J. R. Meteorol. Soc. 1973, 99, 154–170. [Google Scholar] [CrossRef]
- Stewart, J.B. Measurement and Prediction of Evaporation from Forested and Agricultural Catchments. In Developments in Agricultural and Managed Forest Ecology; Sharma, M.L., Ed.; Elsevier: Amsterdam, The Netherlands, 1984; Volume 13, pp. 1–28. ISBN 0166-2287. [Google Scholar]
- Wilson, K.B.; Hanson, P.J.; Mulholland, P.J.; Baldocchi, D.D.; Wullschleger, S.D. A comparison of methods for determining forest evapotranspiration and its components: Sap-flow, soil water budget, eddy covariance and catchment water balance. Agric. For. Meteorol. 2001, 106, 153–168. [Google Scholar] [CrossRef]
- Choudhury, B.J.; Ahmed, N.U.; Idso, S.B.; Reginato, R.J.; Daughtry, C.S.T. Relations between evaporation coefficients and vegetation indices studied by model simulations. Remote Sens. Environ. 1994, 50, 1–17. [Google Scholar] [CrossRef]
- Fisher, J.B.; Tu, K.P.; Baldocchi, D.D. Global estimates of the land–atmosphere water flux based on monthly AVHRR and ISLSCP-II data, validated at 16 FLUXNET sites. Remote Sens. Environ. 2008, 112, 901–919. [Google Scholar] [CrossRef]
- Trigo, I.F.; Peres, L.F.; DaCamara, C.C.; Freitas, S.C. Thermal Land Surface Emissivity Retrieved from SEVIRI/Meteosat. IEEE Trans. Geosci. Remote Sens. 2008, 46, 307–315. [Google Scholar] [CrossRef]
- Franssen, H.J.H.; Stöckli, R.; Lehner, I.; Rotenberg, E.; Seneviratne, S.I. Energy balance closure of eddy-covariance data: A multisite analysis for European FLUXNET stations. Agric. For. Meteorol. 2010, 150, 1553–1567. [Google Scholar] [CrossRef]
- Perez-Priego, O.; El-Madany, T.S.; Migliavacca, M.; Kowalski, A.S.; Jung, M.; Carrara, A.; Kolle, O.; Martín, M.P.; Pacheco-Labrador, J.; Moreno, G.; et al. Evaluation of eddy covariance latent heat fluxes with independent lysimeter and sapflow estimates in a Mediterranean savannah ecosystem. Agric. For. Meteorol. 2017, 236, 87–99. [Google Scholar] [CrossRef]
- Entekhabi, D.; Rodriguez-Iturbe, I. Analytical framework for the characterization of the space-time variability of soil moisture. Adv. Water Resour. 1994, 17, 35–45. [Google Scholar] [CrossRef]
- Kobayashi, H.; Baldocchi, D.D.; Ryu, Y.; Chen, Q.; Ma, S.; Osuna, J.L.; Ustin, S.L. Modeling energy and carbon fluxes in a heterogeneous oak woodland: A three-dimensional approach. Agric. For. Meteorol. 2012, 152, 83–100. [Google Scholar] [CrossRef] [Green Version]
- Businger, J.A. A note on the Businger-Dyer profiles. Bound.-Layer Meteorol. 1988, 42, 145–151. [Google Scholar] [CrossRef]
- Droppo, J.G. Experimental Variability in the Determination of the Energy Balance in a Deciduous Forest; American Meteorological Society: New York, NY, USA, 1973. [Google Scholar]
- Kelliher, F.M.; Köstner, B.M.M.; Hollinger, D.Y.; Byers, J.N.; Hunt, J.E.; McSeveny, T.M.; Meserth, R.; Weir, P.L.; Schulze, E.-D. Evaporation, xylem sap flow, and tree transpiration in a New Zealand broad-leaved forest. Agric. For. Meteorol. 1992, 62, 53–73. [Google Scholar] [CrossRef]
- Kanda, M.; Moriwaki, R.; Takayanagi, Y.; Yokoyama, H.; Hamada, T. Environmental effect of Meiji Shrine Forest as a sink for atmospheric energy and pollutants. (I) Field observation in summer 1996. Tenki 1997, 44, 713–722. [Google Scholar]
- Tanaka, K.; Kosugi, Y.; Ohte, N.; Kobashi, S.; Nakamura, A. Model of CO2 flux between a plant community and the atmosphere, and simulation of CO2 flux over a planted forest. Jpn. J. Ecol. 1998, 48, 265–268. [Google Scholar]
- Meiresonne, L.; Nadezhdin, N.; Cermak, J.; Van Slycken, J.; Ceulemans, R. Measured sap flow and simulated transpiration from a poplar stand in Flanders (Belgium). Agric. For. Meteorol. 1999, 96, 165–179. [Google Scholar] [CrossRef]
- Black, T.A. Evapotranspiration from Douglas fir stands exposed to soil water deficits. Water Resour. Res. 1979, 15, 164–170. [Google Scholar] [CrossRef]
- Shuttleworth, W.J.; Calder, I.R. Has the Priestley-Taylor equation any relevance to forest evaporation? J. Appl. Meteorol. 1979, 18, 639–646. [Google Scholar] [CrossRef]
- Giles, D.G.; Black, T.A.; Spittlehouse, D.L. Determination of growing season soil water deficits on a forested slope using water balance analysis. Can. J. For. Res. 1985, 15, 107–114. [Google Scholar] [CrossRef]

| TSEB-GM | TSEB-GR | TSEB-MR | TSEB-GGT | TSEB-MGT | TSEB-GM-PT | |
|---|---|---|---|---|---|---|
| d0 − z0M | ||||||
| Massman [41] | x | x (grass) | x (grass) | x | ||
| Raupach [44] | x | x | x (oak) | x (oak) | ||
| Wind-speed profile | ||||||
| Goudriaan [40] | ||||||
| a | x | x | x | |||
| a(oak)—a (grass) | x | |||||
| Massman [50] | ||||||
| β | x | |||||
| β(oak)—β (grass) | x | |||||
| αPTC | ||||||
| 1.26 | x | |||||
| 0.9 | x | x | x | x | x | |
| Date | fg from Spectral Information | fg from MODIS | ||
|---|---|---|---|---|
| Oak | Grass | Oak + grass | Oak + grass | |
| 23 July 2013 | 0.73 | 0.75 | 0.75 | 0.81 |
| 23 July 2013 | 0.76 | 0.75 | 0.81 | |
| 20 October 2013 | 0.78 | 0.66 | ||
| 20 December 2013 | 1 | |||
| 7 April 2014 | 0.94 | |||
| 5 May 2014 | 0.98 | 0.98 | 0.74 | |
| 13 May 2014 | 0.87 | 0.9 | 0.74 | |
| 19 May 2014 | 1 | |||
| 30 June 2014 | 0.78 | 0.82 | 0.81 | 0.71 |
| “Observed Values” | (2/3 hC) and (1/8 hC) | Raupach (1994) | Choudhury and Montheith (1988) | Massman (1997) | |
|---|---|---|---|---|---|
| d0 | Mean: 3.35 Std: 1.94 | 5.33 | 5 | Mean: 4.66 Std: 0.23 | Mean: 4.05 Std: 0.43 |
| z0M | Mean: 0.52 Std: 0.3 | 1 | 0.687 | Mean: 1.13 Std: 0.2967 | Mean: 1.24 Std: 0.06 |
| RMSD (W m−2) | TSEB-GM | TSEB-GR | TSEB-MR | TSEB-GGT | TSEB-MGT | TSEB-GM-PT |
|---|---|---|---|---|---|---|
| Rn | 27 | 27 | 27.5 | 30 | 30 | 27 |
| G | 28 | 28 | 28 | 28 | 27 | 28 |
| H | 47 | 48 | 46 | 55 | 53 | 50 |
| LE | 50 | 46 | 46 | 48 | 44 | 60 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andreu, A.; Kustas, W.P.; Polo, M.J.; Carrara, A.; González-Dugo, M.P. Modeling Surface Energy Fluxes over a Dehesa (Oak Savanna) Ecosystem Using a Thermal Based Two-Source Energy Balance Model (TSEB) I. Remote Sens. 2018, 10, 567. https://doi.org/10.3390/rs10040567
Andreu A, Kustas WP, Polo MJ, Carrara A, González-Dugo MP. Modeling Surface Energy Fluxes over a Dehesa (Oak Savanna) Ecosystem Using a Thermal Based Two-Source Energy Balance Model (TSEB) I. Remote Sensing. 2018; 10(4):567. https://doi.org/10.3390/rs10040567
Chicago/Turabian StyleAndreu, Ana, William P. Kustas, Maria Jose Polo, Arnaud Carrara, and Maria P. González-Dugo. 2018. "Modeling Surface Energy Fluxes over a Dehesa (Oak Savanna) Ecosystem Using a Thermal Based Two-Source Energy Balance Model (TSEB) I" Remote Sensing 10, no. 4: 567. https://doi.org/10.3390/rs10040567
APA StyleAndreu, A., Kustas, W. P., Polo, M. J., Carrara, A., & González-Dugo, M. P. (2018). Modeling Surface Energy Fluxes over a Dehesa (Oak Savanna) Ecosystem Using a Thermal Based Two-Source Energy Balance Model (TSEB) I. Remote Sensing, 10(4), 567. https://doi.org/10.3390/rs10040567







