Comparison of the Retrieval of Sea Surface Salinity Using Different Instrument Configurations of MICAP
Abstract
1. Introduction
2. Datasets and Model
2.1. Datasets
2.2. Forward Models of L/C/K Band Radiometers
2.3. Backscatter Coefficient Model of L-Band Scatterometer
3. Description of MICAP
3.1. Instrument Characteristics
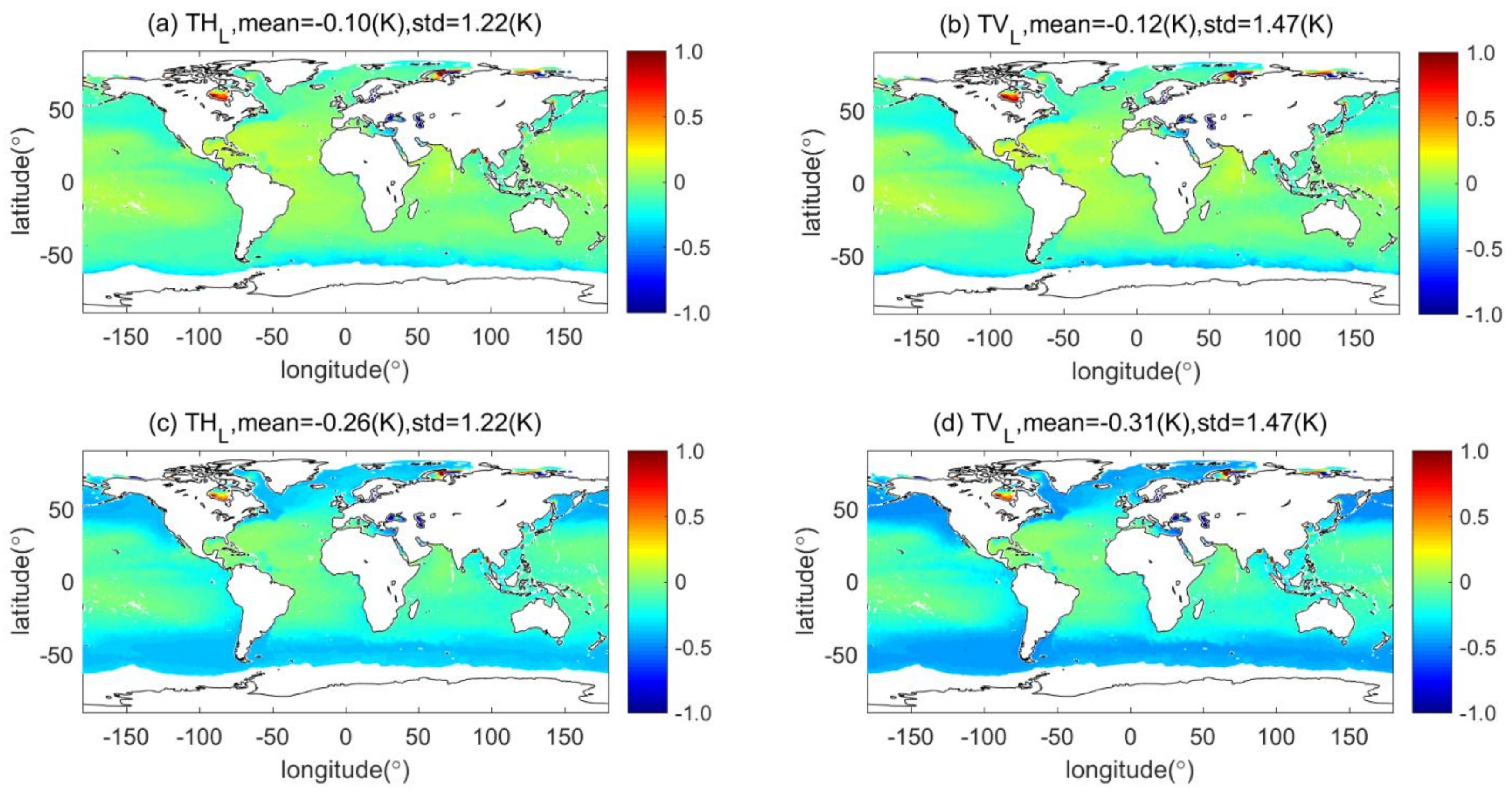
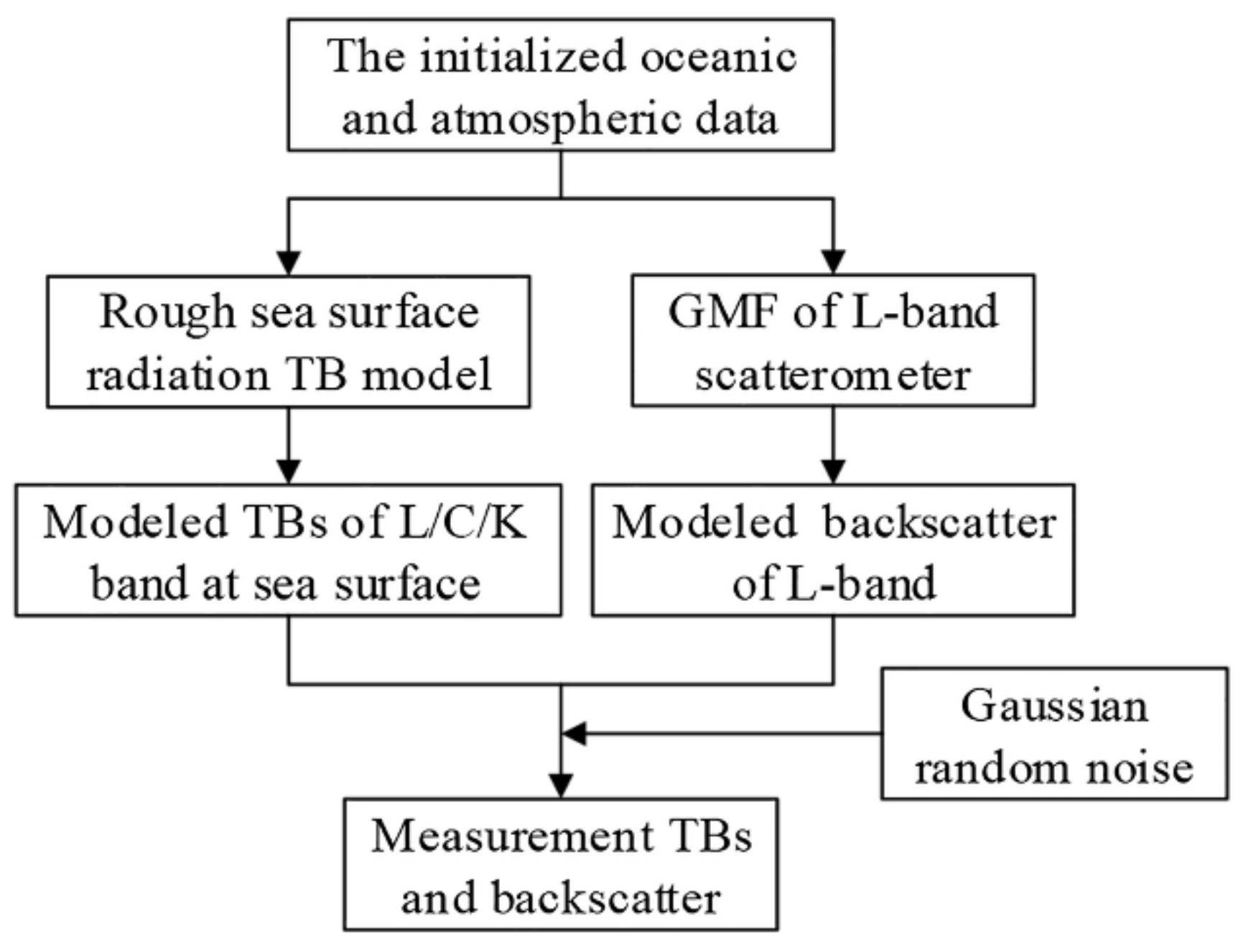
3.2. Simulate TBs and Backscatter of MICAP
4. Algorithm and Configurations
4.1. Combined Active/Passive SSS Retrieval Algorithm
4.2. Different Instrument Configurations of MICAP
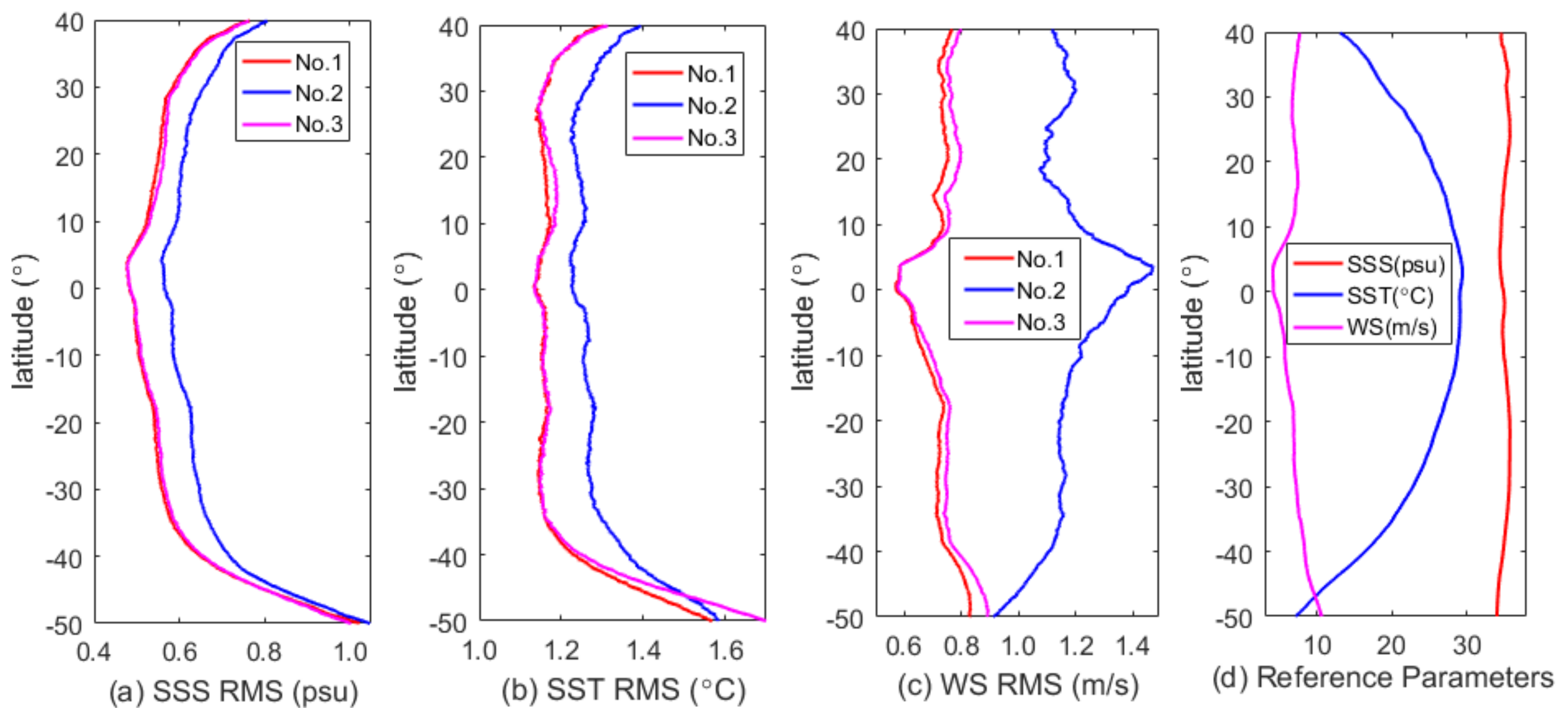
5. Results
5.1. The Retrieval Results at Single Pixel
5.2. Comparison of Retrieval Results with Different Configurations Over the Globe
5.2.1. Default Configuration and without 23.8 GHz
5.2.2. Default Configuration and Without Scatterometer
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Batteen, M.L.; Collins, C.A.; Gunderson, C.R.; Nelson, C.S. The effect of salinity on density in the California Current System. J. Geophys. Res. Oceans 1995, 100, 8733–8749. [Google Scholar] [CrossRef]
- Emery, W.J.; Meincke, J. Global water masses-summary and review. Oceanol. Acta 1986, 9, 383–391. [Google Scholar]
- Lagerloef, G.S.; Swift, C.T.; Le Vine, D.M. Sea surface salinity: The next remote sensing challenge. Oceanography 1995, 8, 44–50. [Google Scholar] [CrossRef]
- Schmitt, R.W. The ocean freshwater cycle. In JSC Ocean Observing System Development Panel; Texas A & M University: College Station, TX, USA, 1994. [Google Scholar]
- Reul, N.; Fournier, S.; Boutin, J.; Hernandez, O.; Maes, C.; Chapron, B.; Alory, G.; Quilfen, Y.; Tenerelli, J.; Morisset, S.; et al. Sea surface salinity observations from space with the SMOS satellite: A new means to monitor the marine branch of the water cycle. Surv. Geophys. 2014, 35, 681–722. [Google Scholar] [CrossRef]
- Schmitt, R.W. Salinity and the global water cycle. Oceanography 2008, 21, 12–19. [Google Scholar] [CrossRef]
- Font, J.; Boutin, J.; Reul, N.; Spurgeon, P.; Ballabrera-Poy, J.; Chuprin, A.; Gabarró, C.; Gourrion, J.; Guimbard, S.; Hénocq, C.; et al. SMOS first data analysis for sea surface salinity determination. Int. J. Remote Sens. 2013, 34, 3654–3670. [Google Scholar] [CrossRef]
- Lagerloef, G.; Boutin, J.; Chao, Y.; Delcroix, T.; Font, J.; Niiler, P.; Reul, N.; Riser, S.J.; Schmitt, R.; Stammer, D.; et al. Resolving the global surface salinity field and variations by blending satellite and in situ observations. In OceanObs 09; European Space Agency: Paris, France, 2010; pp. 587–597. [Google Scholar]
- Le Vine, D.M.; Lagerloef, G.S.; Colomb, F.R.; Yueh, S.H.; Pellerano, F.A. Aquarius: An instrument to monitor sea surface salinity from space. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2040–2050. [Google Scholar] [CrossRef]
- Boutin, J.; Martin, N.; Yin, X.B.; Font, J.; Reul, N.; Spurgeon, P. First assessment of SMOS data over Open Ocean: Part II—Sea surface salinity. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1662–1675. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.P.; Martinuzzi, J.A.M.J.; Font, J.; Berger, M. Soil moisture retrieval from space: The Soil Moisture and Ocean Salinity (SMOS) mission. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1729–1735. [Google Scholar] [CrossRef]
- Sabia, R. Sea Surface Salinity Retrieval Error Budget within the Esa Soil Moisture and Ocean Salinity Mission; Universitat Politècnica de Catalunya: Barcelona, Spain, 2008. [Google Scholar]
- Font, J.; Lagerloef, G.S.; Le Vine, D.M.; Camps, A.; Zanife, O.Z. The determination of surface salinity with the European SMOS space mission. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2196–2205. [Google Scholar] [CrossRef]
- Lagerloef, G.; Colomb, F.R.; Le Vine, D.; Wentz, F.; Yueh, S.; Ruf, C.; Lilly, J.; Gunn, J.; Chao, Y.; Decharon, A.; et al. The Aquarius/SAC-D mission: Designed to meet the salinity remote-sensing challenge. Oceanography 2008, 21, 68–81. [Google Scholar] [CrossRef]
- Entekhabi, D.; Njoku, E.G.; O’Neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Kimball, J. The soil moisture active passive (SMAP) mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Le Vine, D.M.; Lagerloef, G.S.; Torrusio, S.E. Aquarius and remote sensing of sea surface salinity from space. Proc. IEEE 2010, 98, 688–703. [Google Scholar] [CrossRef]
- Fore, A.G.; Yueh, S.H.; Tang, W.; Stiles, B.W.; Hayashi, A.K. Combined Active/Passive Retrievals of Ocean Vector Wind and Sea Surface Salinity with SMAP. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7396–7404. [Google Scholar] [CrossRef]
- Akhil, V.P.; Lengaigne, M.; Durand, F.; Vialard, J.; Chaitanya, A.V.S.; Keerthi, M.G.; Gopalakrishna, V.V.; Boutin, J.; de Boyer Montégut, C. Assessment of seasonal and year-to-year surface salinity signals retrieved from SMOS and Aquarius missions in the Bay of Bengal. Int. J. Remote Sens. 2016, 37, 1089–1114. [Google Scholar] [CrossRef]
- Philipps, S.; Boone, C.; Obligis, E. The role of averaging for improving sea surface salinity retrieval from the Soil Moisture and Ocean Salinity (SMOS) satellite and impact of auxiliary data. J. Atmos. Ocean. Technol. 2007, 24, 255–269. [Google Scholar] [CrossRef]
- Yueh, S.H.; West, R.; Wilson, W.J.; Li, F.K.; Njoku, E.G.; Rahmat-Samii, Y. Error sources and feasibility for microwave remote sensing of ocean surface salinity. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1049–1060. [Google Scholar] [CrossRef]
- Zhang, L.J.; Yin, X.; Wang, Z.Z.; Liu, H.; Lin, M.S. Preliminary Analysis of the Potential and Limitations of MICAP for the Retrieval of Sea Surface Salinity. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2018. submitted. [Google Scholar]
- Gaillard, F. ISAS-13 temperature and salinity gridded fields. SEANOE 2015. [Google Scholar] [CrossRef]
- Wentz, F.J.; Ricciardulli, L.; Gentemann, C.; Meissner, T.; Hilburn, K.A.; Scott, J. Remote Sensing Systems GCOM-W1 AMSR2 Monthly Environmental Suite on 0.25 Deg Grid, Version 7.0; Remote Sensing Systems: Santa Rosa, CA, USA, 2014; Available online: www.remss.com/missions/amsr (accessed on 1 March 2017).
- Wentz, F.J.; Ricciardulli, L.; Gentemann, C.; Meissner, T.; Hilburn, K.A.; Scott, J. Remote Sensing Systems Coriolis WindSat Monthly Environmental Suite on 0.25 Deg Grid, Version 7.0.1; Remote Sensing Systems: Santa Rosa, CA, USA, 2013; Available online: www.remss.com/missions/windsat (accessed on 2 March 2017).
- Font, J.; Camps, A.; Borges, A.; Martín-Neira, M.; Boutin, J.; Reul, N.; Mecklenburg, S. SMOS: The challenging sea surface salinity measurement from space. Proc. IEEE 2010, 98, 649–665. [Google Scholar] [CrossRef]
- Yin, X.B.; Boutin, J.; Martin, N.; Spurgeon, P.; Vergely, J.L.; Gaillard, F. Errors in SMOS Sea Surface Salinity and their dependency on a priori wind speed. Remote Sens. Environ. 2014, 146, 159–171. [Google Scholar] [CrossRef][Green Version]
- Revision 13 SMOS L2 OS Algorithm Theoretical Baseline Document, SO-TN-ARG-GS-0007. Available online: http://www.argans.co.uk/smos/docs/deliverables/delivered/ATBD/SO-TN-ARG-GS-007_L2OS-ATBD_v3.7_110622.pdf. (accessed on 13 March 2017).
- Meissner, T.; Wentz, F.J.; Ricciardulli, L. The emission and scattering of L-band microwave radiation from rough ocean surfaces and wind speed measurements from the Aquarius sensor. J. Geophys. Res. Oceans 2014, 119, 6499–6522. [Google Scholar] [CrossRef]
- Dinnat, E.P.; Boutin, J.; Yin, X.; Le Vine, D.M.; Waldteufel, P.; Vergely, J.L. Comparison of SMOS and Aquarius Sea Surface Salinity and analysis of possible causes for the differences. In Proceedings of the XXXIth URSI IEEE General Assembly and Scientific Symposium (URSI GASS), Beijing, China, 16–23 August 2014. [Google Scholar]
- Klein, L.; Swift, C. An improved model for the dielectric constant of sea water at microwave frequencies. IEEE J. Ocean. Eng. 1977, 2, 104–111. [Google Scholar] [CrossRef]
- Meissner, T.; Wentz, F.J. The emissivity of the ocean surface between 6 and 90 GHz over a large range of wind speeds and earth incidence angles. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3004–3026. [Google Scholar] [CrossRef]
- Zhou, Y.; Lang, R.H.; Dinnat, E.P.; Le Vine, D.M. L-Band Model Function of the Dielectric Constant of Seawater. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6964–6974. [Google Scholar] [CrossRef]
- Zine, S.; Boutin, J.; Font, J.; Reul, N.; Waldteufel, P.; Gabarró, C.; Delwart, S. Overview of the SMOS sea surface salinity prototype processor. IEEE Trans. Geosci. Remote Sens. 2008, 46, 621–645. [Google Scholar] [CrossRef]
- Yin, X.B.; Boutin, J.; Martin, N.; Spurgeon, P. Optimization of L-band sea surface emissivity models deduced from SMOS data. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1414–1426. [Google Scholar] [CrossRef]
- Liebe, H.J.; Hufford, G.A.; Cotton, M.G. Propagation modeling of moist air and suspended water/ice particles at frequencies below 1000 GHz. In Proceedings of the AGARD 52nd Specialists’ Meeting Electromagnetic Wave Propagation Panel, Palma de Mallorca, Spain, May 1993. [Google Scholar]
- Wentz, F.J.; Meissner, T. Algorithm Theoretical Basis Document (atbd), Version 2; RSS Tech. Proposal 121599A-1; Remote Sensing Systems: Santa Rosa, CA, USA, 2000. [Google Scholar]
- Isoguchi, O.; Shimada, M. An L-band ocean geophysical model function derived from PALSAR. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1925–1936. [Google Scholar] [CrossRef]
- Liu, H.; Zhu, D.; Niu, L.; Wu, L.; Wang, C.; Chen, X.; Wu, J. MICAP (Microwave imager combined active and passive): A new instrument for Chinese ocean salinity satellite. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 184–187. [Google Scholar]

| Instruments | L-Band Radiometer | C-Band Radiometer | K-Band Radiometer | L-Band Scatterometer |
|---|---|---|---|---|
| frequency | 1.4 GHz | 6.9 GHz | 18.7 GHz, 23.8 1 GHz | 1.26 GHz |
| sensitivity | 0.1 K | 0.3 K | 0.3 K | 0.1 dB |
| polarization | H, V, T3 | H, V, | H, V, | HH, HV, VV, VH |
| incident angle | 30–55° | |||
| spatial resolution | along-track: 65/15/15 km; cross-track: 50–100 km | |||
| antenna size | Reflector: 3.0 m × 5.5 m (after deployment), Feed array: 4 m × 0.5 m | |||
| FOV | >1000 km | |||
| revisit | 3 days | |||
| SSS accuracy | <1 psu, over one satellite pass; < 0.1 psu, over 200 km and 30 days | |||
| Number | Configurations |
|---|---|
| No. 1 | 1.26 GHz, 1.4 GHz, 6.9 GHz, 18.7 GHz and 23.8 GHz (default) |
| No. 2 | without 1.26 GHz scatterometer |
| No. 3 | without 23.8 GHz |
| Scene | SSS (psu) | SST (°C) | WS (m/s) |
|---|---|---|---|
| Reference | 35 | 15 | 7 |
| High SST | 35 | 25 | 7 |
| High SST and SSS | 38 | 25 | 7 |
| High SST, Low WS | 35 | 25 | 3 |
| Low SST | 35 | 5 | 7 |
| Low SST and SSS | 33 | 5 | 7 |
| Low SST and WS | 35 | 5 | 3 |
| Scene | SSS (psu) | SST (°C) | WS (m/s) |
|---|---|---|---|
| Reference | 0.64 | 1.19 | 0.68 |
| High SST | 0.52 | 1.12 | 0.68 |
| High SST and SSS | 0.57 | 1.13 | 0.76 |
| High SST, Low WS | 0.49 | 1.00 | 0.46 |
| Low SST | 1.17 | 1.54 | 0.78 |
| Low SST and SSS | 1.22 | 1.50 | 0.79 |
| Low SST and WS | 1.10 | 1.44 | 0.50 |
| Scene | SSS (psu) | SST (°C) | WS (m/s) |
|---|---|---|---|
| Reference | 0.64 | 1.19 | 0.68 |
| σsss = 0.5 | 0.82 | 1.19 | 0.68 |
| σsst = 1 | 0.64 | 1.50 | 0.68 |
| σsst = 2 | 0.64 | 2.24 | 0.68 |
| σws = 1 | 0.64 | 1.19 | 1.10 |
| σws = 2 | 0.64 | 1.19 | 2.03 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Wang, Z.; Yin, X. Comparison of the Retrieval of Sea Surface Salinity Using Different Instrument Configurations of MICAP. Remote Sens. 2018, 10, 550. https://doi.org/10.3390/rs10040550
Zhang L, Wang Z, Yin X. Comparison of the Retrieval of Sea Surface Salinity Using Different Instrument Configurations of MICAP. Remote Sensing. 2018; 10(4):550. https://doi.org/10.3390/rs10040550
Chicago/Turabian StyleZhang, Lanjie, Zhenzhan Wang, and Xiaobin Yin. 2018. "Comparison of the Retrieval of Sea Surface Salinity Using Different Instrument Configurations of MICAP" Remote Sensing 10, no. 4: 550. https://doi.org/10.3390/rs10040550
APA StyleZhang, L., Wang, Z., & Yin, X. (2018). Comparison of the Retrieval of Sea Surface Salinity Using Different Instrument Configurations of MICAP. Remote Sensing, 10(4), 550. https://doi.org/10.3390/rs10040550






