Spatiotemporal Dynamics in Vegetation GPP over the Great Khingan Mountains Using GLASS Products from 1982 to 2015
Abstract
1. Introduction
2. Materials and Methods
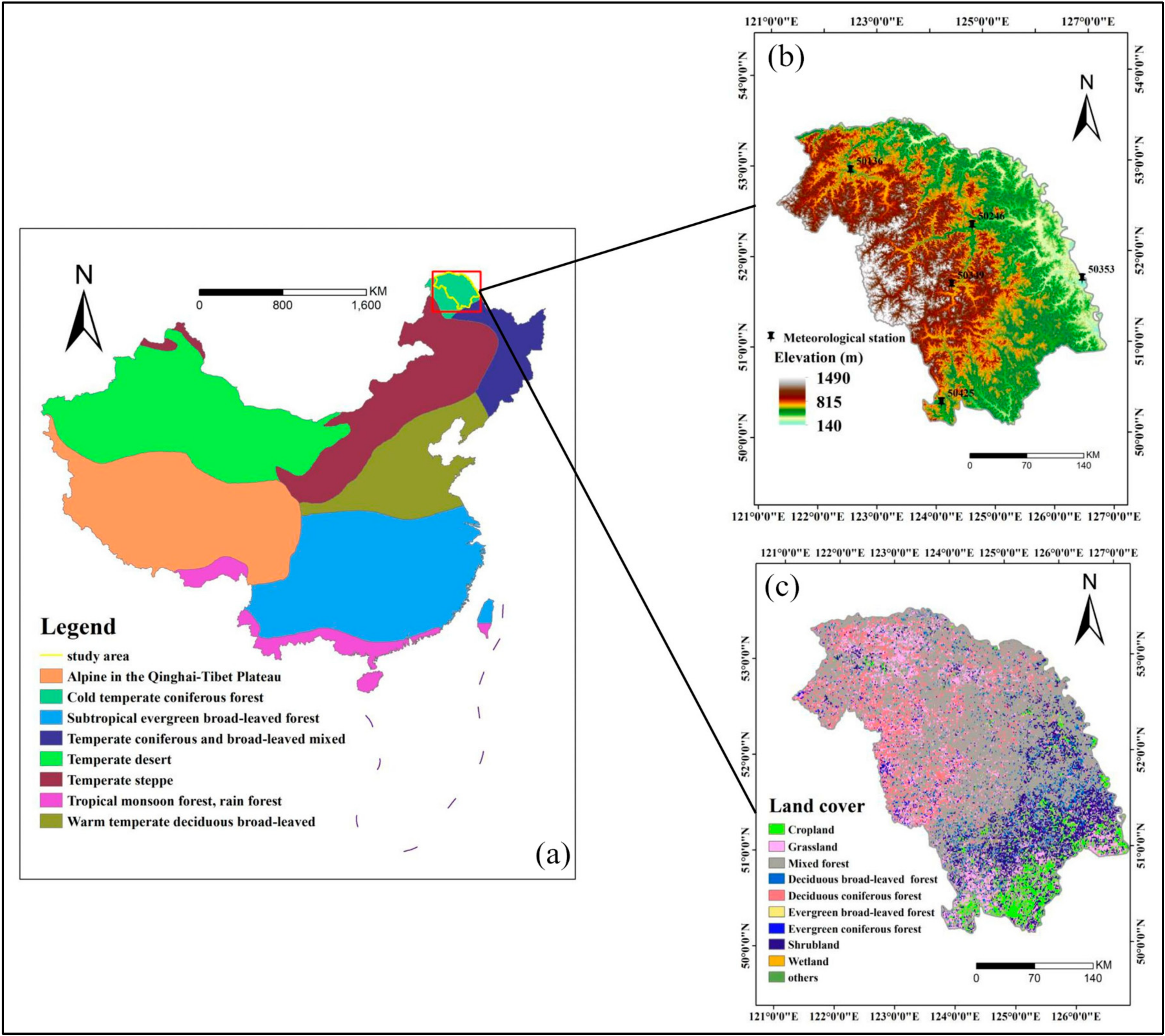
2.1. Study Area
2.2. Data
2.2.1. GLASS GPP Dataset
2.2.2. Datasets for Auxiliary Analysis
2.3. Methods
2.3.1. Unary Linear Regression
2.3.2. Pearson Correlation
2.3.3. Standardized Multivariate Linear Regression (SMLR) Model
3. Results
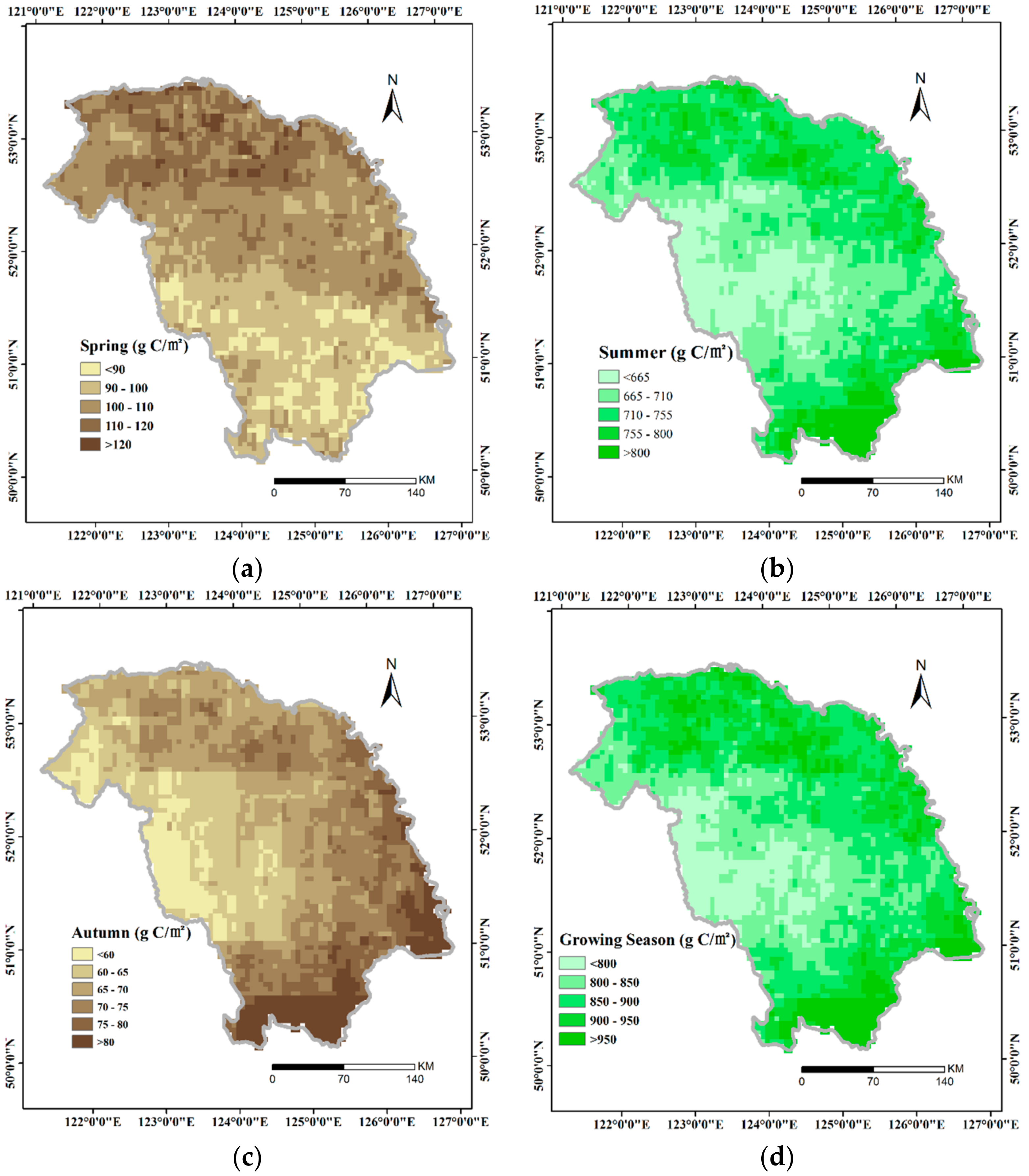
3.1. Spatial Distribution of GPP
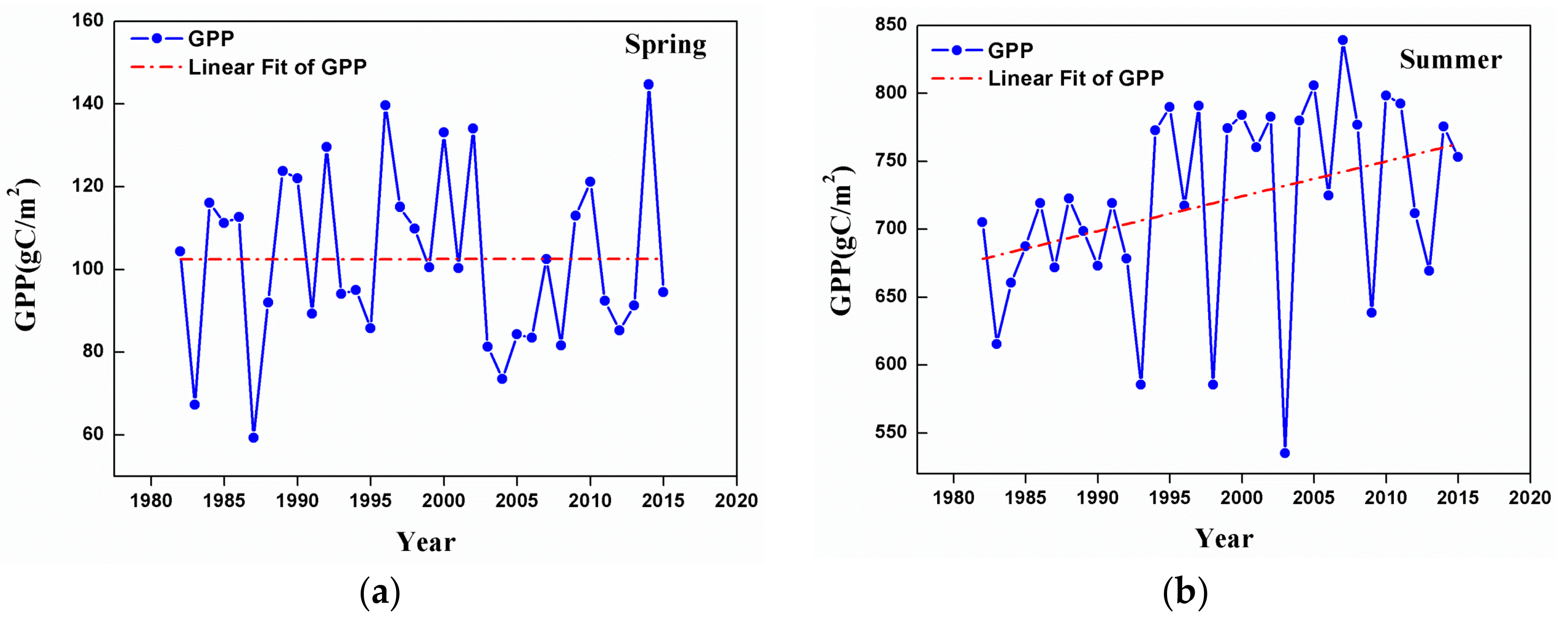
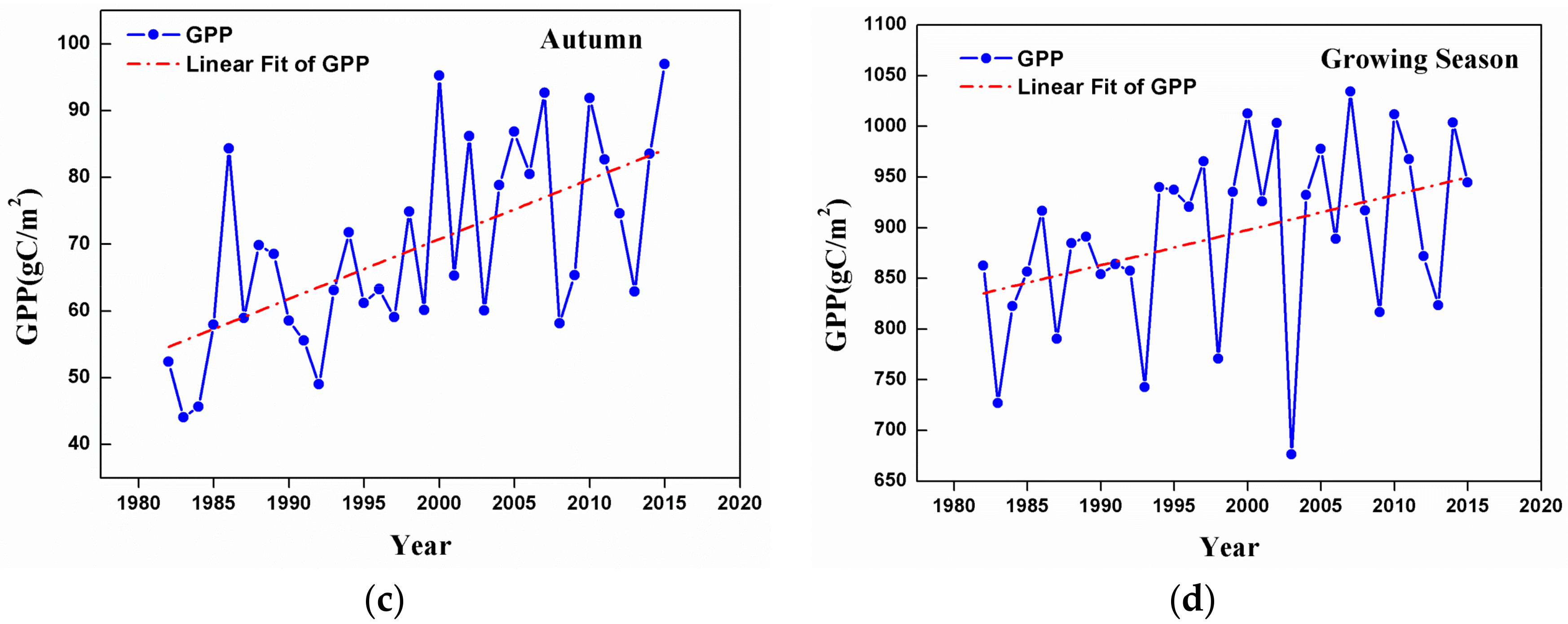
3.2. Changes in GPP at a Regional Scale
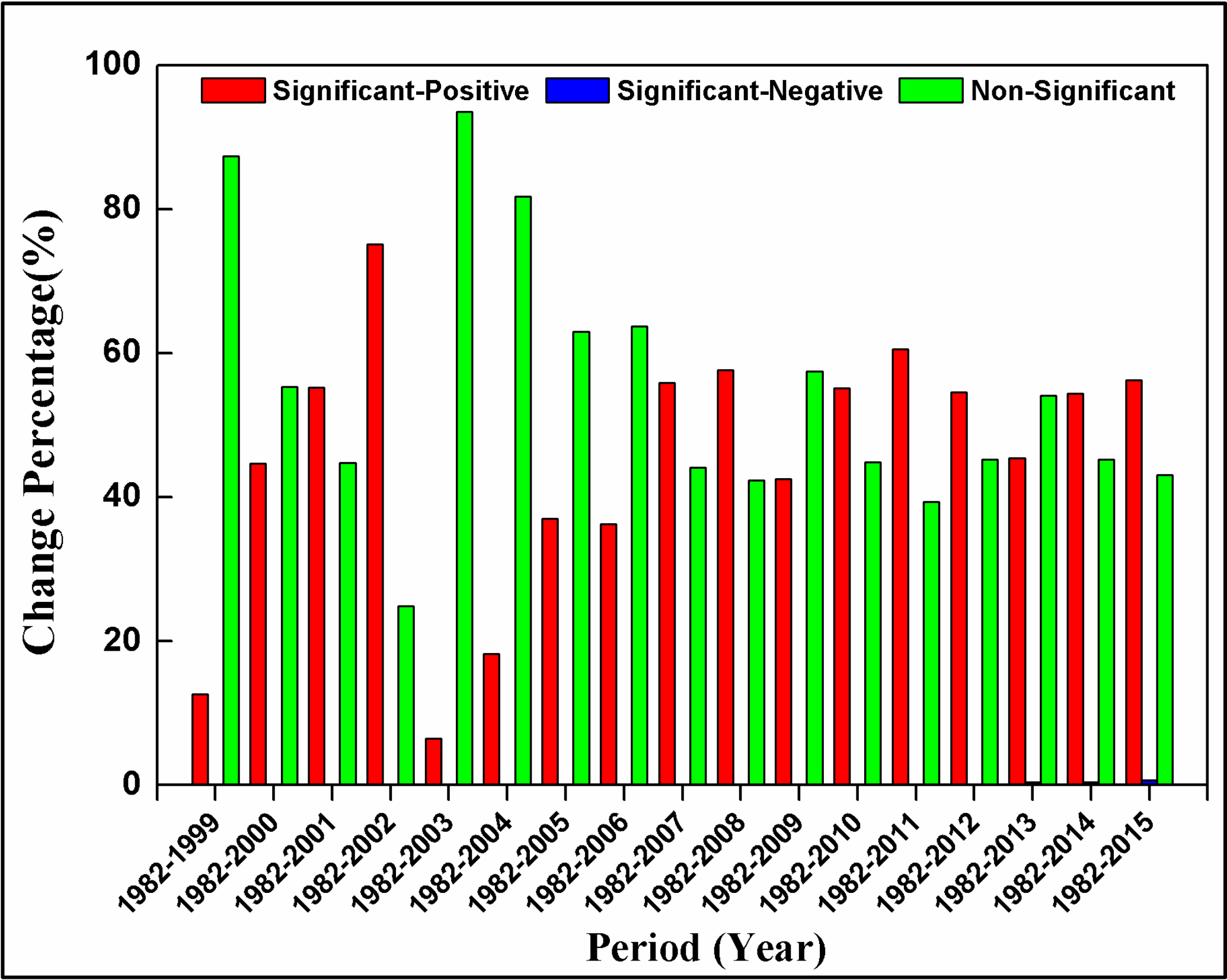
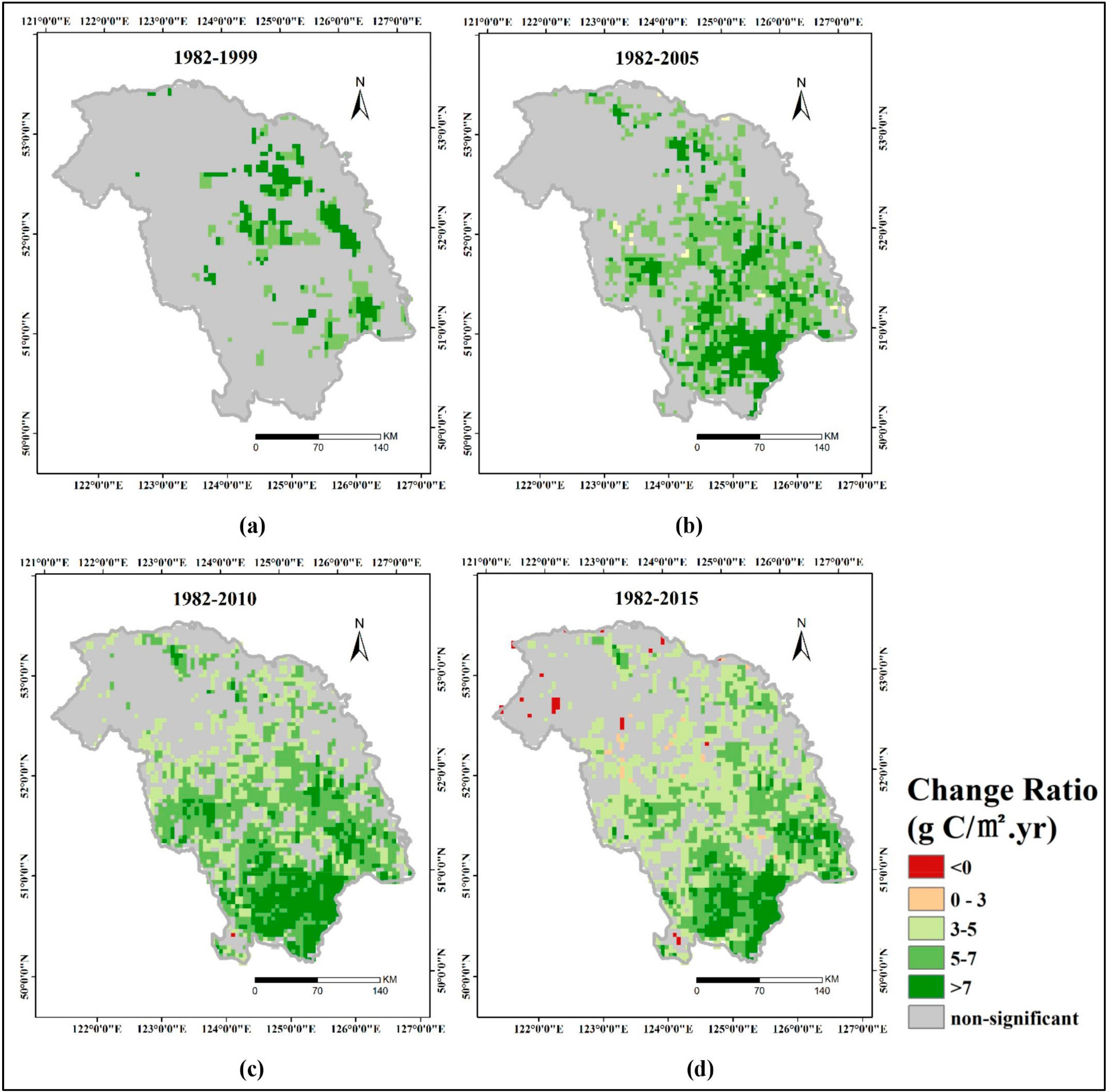
3.3. Spatial Patterns of GPP Trend
3.4. Correlations between GPP and Driving Factors
3.4.1. Effects of Local Meteorological Factors on GPP
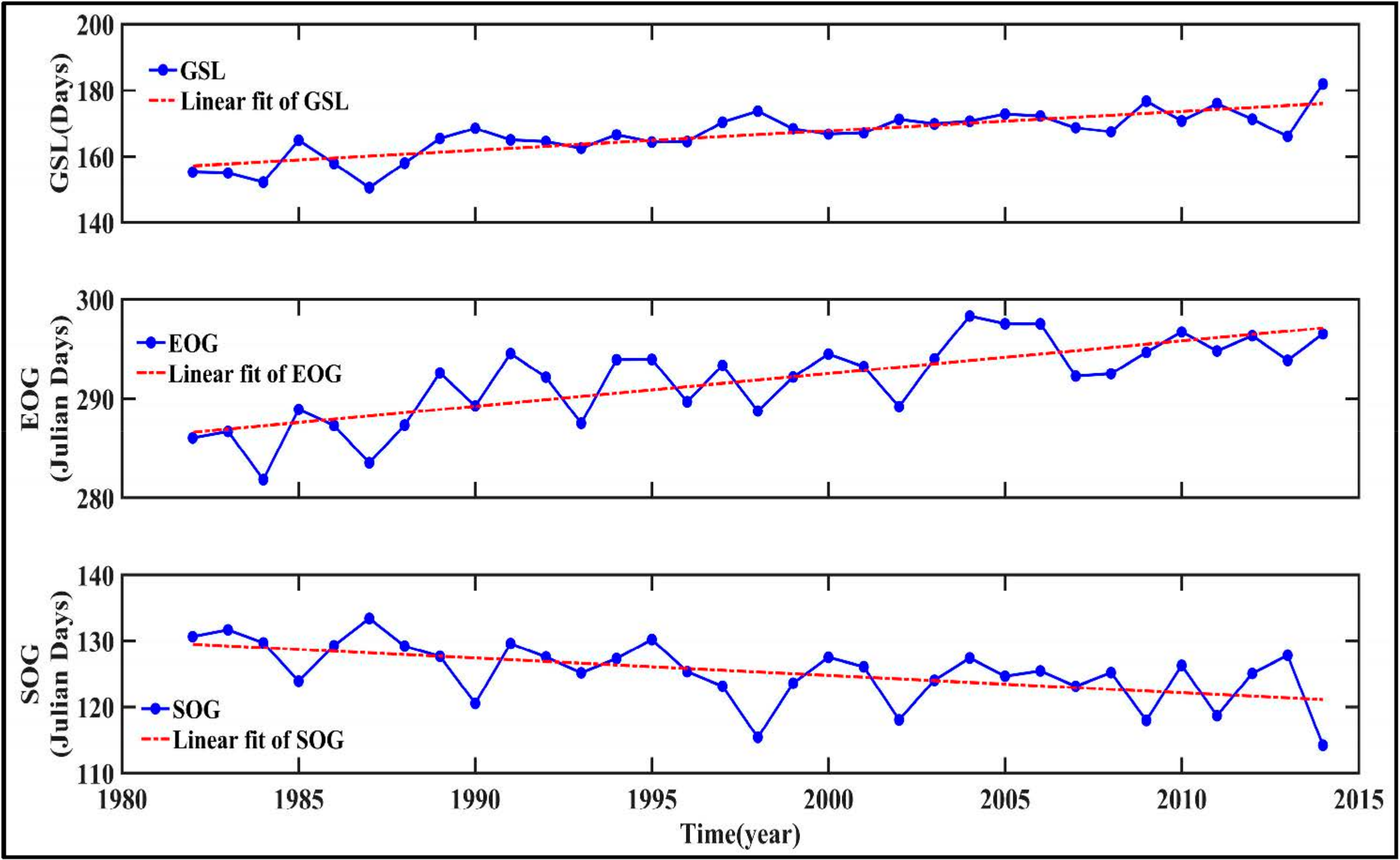
3.4.2. Effects of Phenological Parameters and FPAR on GPP
3.4.3. Dominant Factor for GPP Variation
4. Discussions
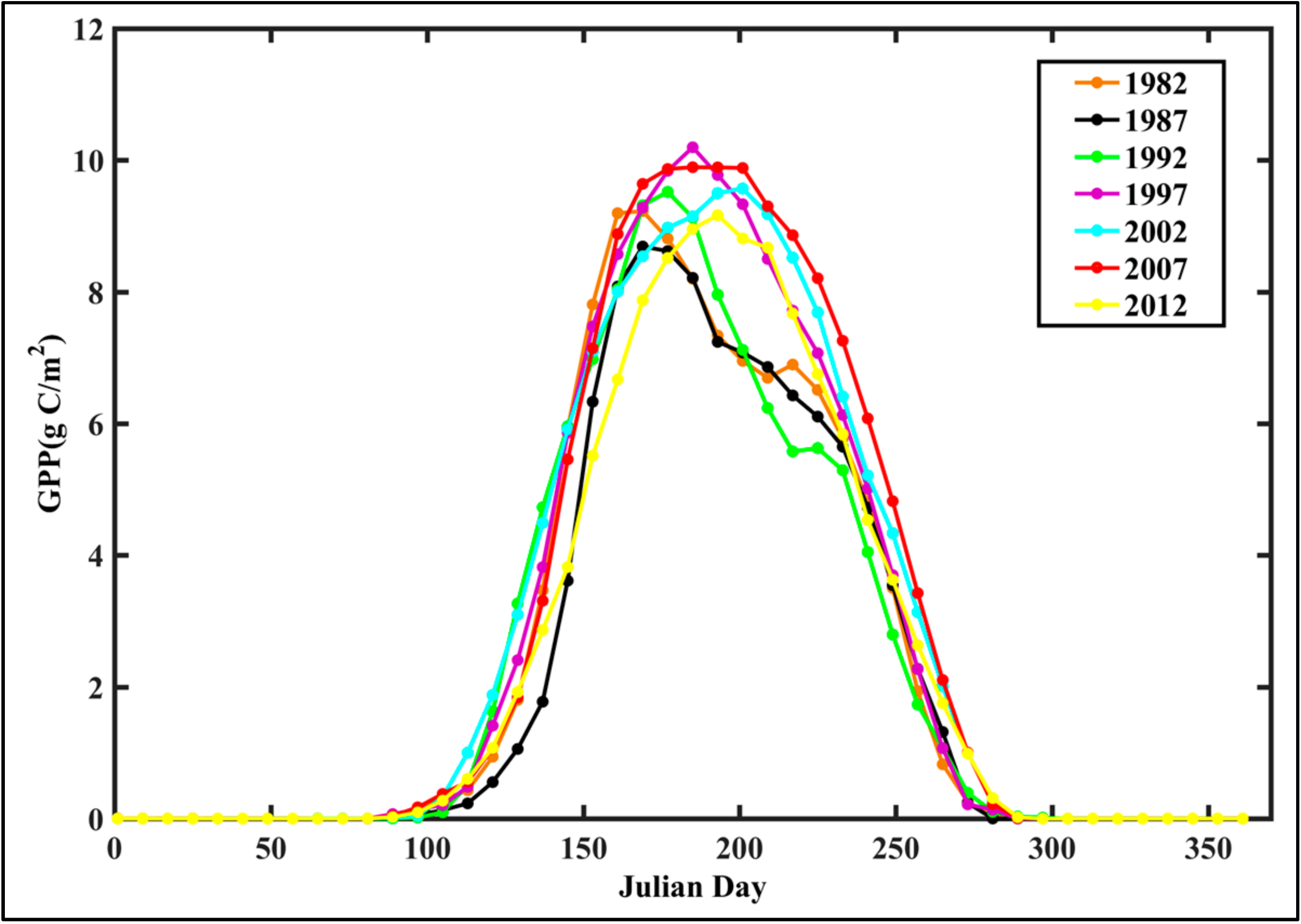
4.1. Analysis of GPP Spatiotemporal Dynamics
4.2. The Response of GPP to Driving Factors
4.3. Study Limitations
5. Conclusions
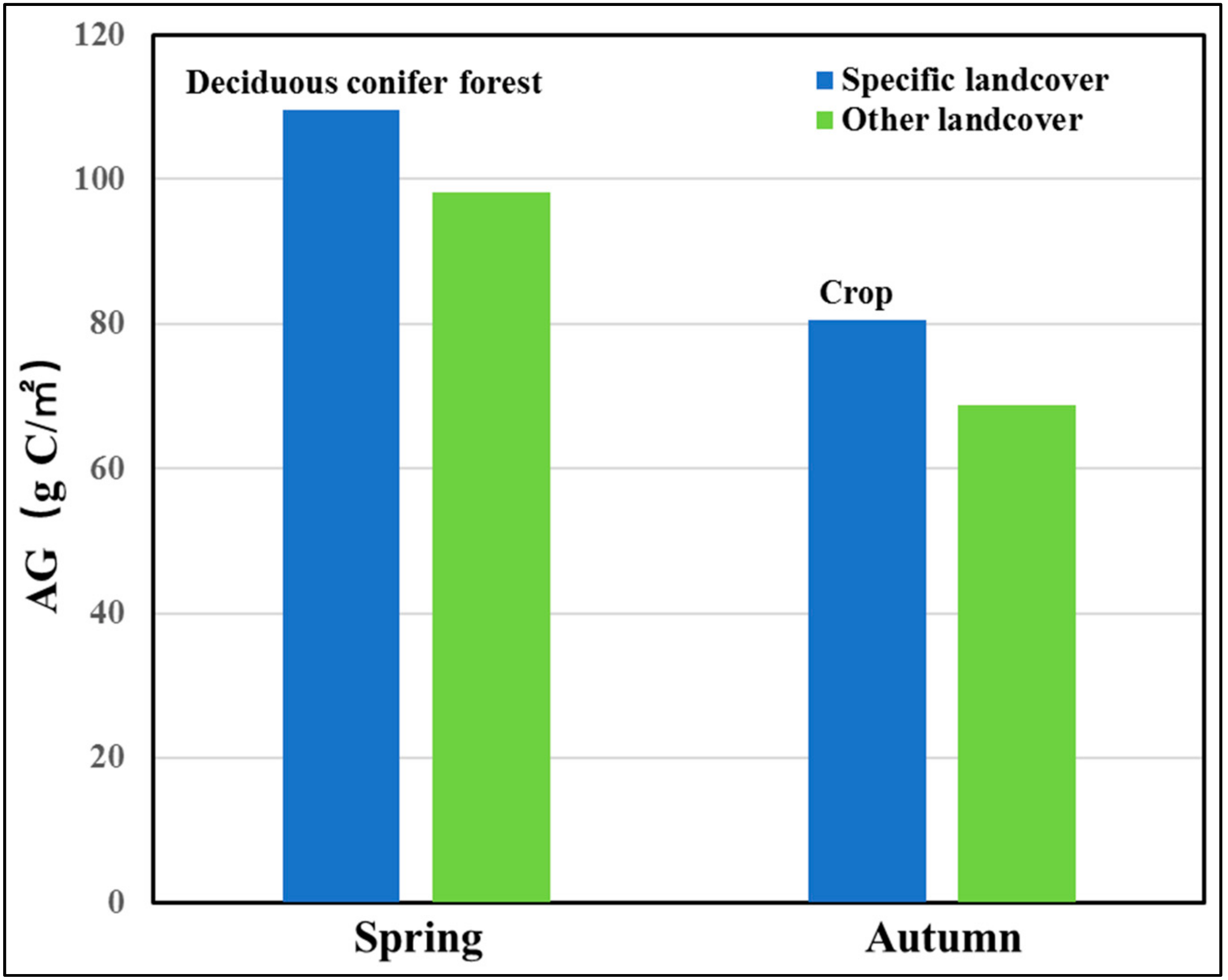
- In the GKM, different seasons displayed different patterns of spatial distribution because of the difference in understory vegetation, altitude and land cover. Areas with bright conifer forest always have a larger GPP because the understory vegetation contributes a great deal to vegetation total productivities. Altitude impacts GPP by changing temperature. Land cover with intense human intervention showed different seasonal changes in AGG.
- Temporal trends of AG at the regional scale showed a dramatic increase from 1982 to 2015 in summer, autumn, and the growing season. This observation could be considered to be a result of the warming and drying trend that is seen in the GKM over the past 34 years.
- Interannual GPP trends at the pixel scale showed that the areas with significant AGG variation (mostly significant increasing trends) were strikingly expanded after 2000 because of the natural forest protection project launched in 1998, but the AGG variation displayed a flattened trend over the last five years due to the formation of a relatively stable vegetation community.
- Upon aggregating all of the above factors, daily sunshine duration in summer, instead of GSL, acted as the dominant factor in most of the areas, whereas daily mean temperature in summer was the dominant factor in a fraction of the GKM. FPAR also acted as the dominant factor in part of the northern GKM and was closely related to vegetation change that was caused by the fire in 1987.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Tans, P.P.; Fung, I.Y.; Takahashi, T. Observational constraints on the global atmospheric CO2 budget. Science 1990, 247, 1431–1438. [Google Scholar] [CrossRef] [PubMed]
- Schimel, D.S.; Braswell, B.H.; McKeown, R.; Ojima, D.S.; Parton, W.J.; Pulliam, W. Climate and nitrogen controls on the geography and timescales of terrestrial biogeochemical cycling. Glob. Biogeochem. Cycles 1996, 10, 677–692. [Google Scholar] [CrossRef]
- Zhou, L.M.; Tucker, C.J.; Kaufmann, R.K.; Slayback, D.; Shabanov, N.V.; Myneni, R.B. Variations in northern vegetation activity inferred from satellite data of vegetation index during 1981 to 1999. J. Geophys. Res. 2001, 106, 20069–20083. [Google Scholar] [CrossRef]
- Melillo, J.M.; Mcguire, A.D.; Kicklighter, D.W.; Moore, B.; Vorosmarty, C.J.; Schloss, A.L. Global climate-change and terrestrial net primary production. Nature 1993, 363, 234–240. [Google Scholar] [CrossRef]
- Fang, J.Y.; Chen, A.P.; Peng, C.H.; Zhao, S.Q.; Ci, L.J. Changes in forest biomass carbon storage in China between 1949 and 1998. Science 2001, 292, 2320–2322. [Google Scholar] [CrossRef] [PubMed]
- Xiao, X.M.; Hollinger, D.; Aber, J.; Goltz, M.; Davidson, E.A.; Zhang, Q.Y.; Moore, B. Satellite-based modeling of gross primary production in an evergreen needleleaf forest. Remote Sens. Environ. 2004, 89, 519–534. [Google Scholar] [CrossRef]
- Nemani, R.; Keeling, C.; Hashimoto, H.; Jolly, W.; Piper, S.; Tucker, C.; Myneni, R.; Running, S. Climate-driving increases in global terrestrial net primary production from 1982 to 1999. Science 2003, 300, 1560–1563. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Z.C.; Piao, S.L.; Myneni, R.B.; Huang, M.T.; Zeng, Z.Z.; Canadell, J.G.; Ciais, P.; Sitch, S.; Friedlingstein, P.; Arneth, A.; et al. Greening of the Earth and its drivers. Nat. Clim. Chang. 2016, 6, 791–795. [Google Scholar] [CrossRef]
- Chapin, M.C.; Matson, P.A.; Mooney, H.A. Principles of Terrestrial Ecosystem Ecology, 2nd ed.; Spring: New York, NY, USA, 2002; p. 102. [Google Scholar]
- Beer, C.; Reichstein, M.; Tomelleri, E.; Ciais, P.; Jung, M.; Carvalhais, N.; Rodenbeck, C.; Arain, M.A.; Baldocchi, D.; Bonan, G.B.; et al. Terrestrial gross carbon dioxide uptake: Global distribution and covariation with climate. Science 2010, 329, 834–838. [Google Scholar] [CrossRef] [PubMed]
- Anav, A.; Friedlingstein, P.; Beer, C.; Ciais, P.; Harper, A.; Jones, C.; Murray-Tortarolo, G.; Papale, D.; Parazoo, N.C.; Peylin, P.; et al. Spatiotemporal patterns of terrestrial gross primary production: A review. Rev. Geophys. 2015, 53, 785–818. [Google Scholar] [CrossRef]
- Jensen, M.N. Consensus on ecological impacts remains elusive. Science 2003, 299, 38. [Google Scholar] [CrossRef] [PubMed]
- Cox, P.; Jones, C. Illuminating the modern dance of climate and CO2. Science 2008, 321, 1642–1644. [Google Scholar] [CrossRef] [PubMed]
- Battin, T.J.; Kaplan, L.A.; Findlay, S.; Hopkinson, C.S.; Marti, E.; Packman, A.I.; Newbold, J.D.; Sabater, F. The boundless carbon cycle. Nat. Geosci. 2009, 2, 598–600. [Google Scholar] [CrossRef]
- NASA. Earth System Science: A Closer View; NASA: Washington, DC, USA, 1988; p. 208. [Google Scholar]
- Myneni, R.; Hoffman, R.; Knyazikhin, Y.; Privette, J.; Glassy, J.; Tian, H. Global products of vegetation leaf area and fraction absorbed PAR from one year of MODIS data. Remote Sens. Environ. 2002, 83, 214–231. [Google Scholar] [CrossRef]
- Gutman, G.; Ignatov, A. Global land monitoring from AVHRR: Potential and limitations. Int. J. Remote Sens. 1995, 16, 2301–2309. [Google Scholar] [CrossRef]
- Privette, J.L.; Fowler, C.; Wick, G.A.; Baldwin, D.; Emery, W.J. Effect of orbital drift on advanced very high resolution radiometer products Normalized difference vegetation index and sea surface temperature. Remote Sens. Environ. 1995, 53, 164–17l. [Google Scholar] [CrossRef]
- Rao, C.R.N.; Chen, J. Inter-satellite calibration linkages for the visible and near-infrared channels of the Advanced Very High Resolution Radiometer on the NOAA-7,-9, and-11 spacecraft. Int. J. Remote Sens. 1995, 16, 1931–1942. [Google Scholar]
- Rao, C.R.N.; Chen, J. Post-launch calibration of the visible and near-infrared channels of the Advanced Very High Resolution Radiometer (AVHRR) on the NOAA-14 spacecraft. Int. J. Remote Sens. 1996, 17, 2743–2747. [Google Scholar] [CrossRef]
- Myneni, R.B.; Tucker, C.J.; Asrar, G.; Keeling, C.D. Interannual variations in satellite-sensed vegetation index data from 1981 to 1991. J. Geophys. Res. 1998, 103, 6145–6160. [Google Scholar] [CrossRef]
- Gutman, G.G. On the use of long-term global data of land reflectances and vegetation indices derived from the advanced very high resolution radiometer. J. Geophys. Res. 1999, 104, 6241–6255. [Google Scholar] [CrossRef]
- Monteith, J.L. Solar radiation and productivity in tropical ecosystems. J. Appl. Ecol. 1972, 9, 747–766. [Google Scholar] [CrossRef]
- Monteith, J.L. Climate and the efficiency of crop production in Britain. Phil. Trans. R. Soc. B. 1977, 281, 277–294. [Google Scholar] [CrossRef]
- Goetz, S.J.; Prince, S.D. Modelling terrestrial carbon exchange and storage: Evidence and implications of functional convergence in light-use efficien Cycles. Adv. Ecol. Res. 1999, 28, 57–92. [Google Scholar]
- Tucker, C.J.; Pinzon, J.E.; Brown, M.E.; Slayback, D.A.; Pak, E.W.; Mahoney, R.; Vermote, E.F.; Saleous, N.E. An extended AVHRR 8-km NDVI dataset compatible with MODIS and SPOT vegetation NDVI data. Int. J. Remote Sens. 2005, 26, 4485–4498. [Google Scholar] [CrossRef]
- Hilker, T.; Coops, N.C.; Hall, F.G.; Black, T.A.; Wulder, M.A.; Nesic, Z.; Krishnan, P. Separating physiologically and directionally induced changes in PRI using BRDF models. Rem. Sens. Environ. 2008, 112, 2777–2788. [Google Scholar] [CrossRef]
- Prince, S.D.; Goward, S.N. Global net primary production: A remote sensing approach. J. Biogeogr. 1995, 22, 815–835. [Google Scholar] [CrossRef]
- Wei, S.H.; Yi, C.X.; Fang, W.; Hendrey, G. A global study of GPP focusing on light-use efficiency in a random forest regression model. Ecosphere 2017, 8, e01724. [Google Scholar] [CrossRef]
- Potter, C.S.; Randers, J.T.; Field, C.B.; Matson, P.A.; Vitousek, P.M.; Mooney, H.A.; Klooster, S.A. Terrestrial ecosystem production: A process model based on global satellite and surface data. Glob. Biogeochem. Cycles 1993, 7, 811–841. [Google Scholar] [CrossRef]
- Field, C.B.; Randerson, J.T.; Malmström, C.M. Global net primary production: Combining ecology and remote sensing. Remote Sens. Environ. 1995, 51, 74–88. [Google Scholar] [CrossRef]
- Yuan, W.P.; Liu, S.G.; Zhou, G.S.; Zhou, G.Y.; Tieszen, L.L.; Baldocchi, D.; Bernhofer, C.; Gholz, H.; Goldstein, A.H.; Goulden, M.L.; et al. Deriving a light use efficiency model from eddy covariance flux data for predicting daily gross primary production across biomes. Agric. For. Meteorol. 2007, 143, 189–207. [Google Scholar] [CrossRef]
- Yuan, W.P.; Liu, S.G.; Yu, G.R.; Bonnefond, J.M.; Chen, J.Q.; Davis, K.; Desai, A.R.; Goldstein, A.H.; Gianelle, D.; Rossi, F.; et al. Global estimates of evapotranspiration and gross primary production based on MODIS and global meteorology data. Remote Sens. Environ. 2010, 114, 1416–1431. [Google Scholar] [CrossRef]
- Veroustraete, F.; Sabbe, H.; Eerens, H. Estimation of carbon mass fluxes over Europe using the C-Fix model and Euroflux data. Remote Sens. Environ. 2002, 83, 376–399. [Google Scholar] [CrossRef]
- Running, S.W.; Nemani, R.R.; Heinsch, F.A.; Zhao, M.S.; Reeves, M.; Hashimoto, H. A continuous satellite-derived measure of global terrestrial primary production. Bioscience 2004, 54, 547–560. [Google Scholar] [CrossRef]
- Xiao, X.M.; Zhang, Q.Y.; Braswell, B.; Urbanski, S.; Boles, S.; Wofsy, S.; Moore, B., III; Ojima, D. Modeling gross primary production of temperate deciduous broadleaf forest using satellite images and climate data. Remote Sens. Environ. 2004, 91, 256–270. [Google Scholar] [CrossRef]
- Turner, D.P.; Ritts, W.D.; Styles, J.M.; Yang, Z.; Cohen, W.B.; Law, B.E.; Thornton, P.E. A diagnostic carbon flux model to monitor the effects of disturbance and interannual variation in climate on regional NEP. Tellus B 2006, 58, 476–490. [Google Scholar] [CrossRef]
- King, D.A.; Turner, D.P.; Ritts, W.D. Parameterization of a diagnostic carbon cycle model for continental scale application. Remote Sens. Environ. 2011, 115, 1653–1664. [Google Scholar] [CrossRef]
- Yao, Y.T.; Wang, X.H.; Li, Y.; Wang, T.; Shen, M.G.; Du, M.Y.; He, H.L.; Li, Y.; Luo, W.; Ma, M.; et al. Spatiotemporal pattern of gross primary productivity and its covariation with climate in China over the last thirty years. Glob. Change Biol. 2017, 24, 184–196. [Google Scholar] [CrossRef] [PubMed]
- Zscheischler, J.; Mahecha, M.D.; Buttlar, J.; Harmeling, S.; Jung, M.; Rammig, A.; Randerson, J.T.; Schölkopf, B.; Seneviratne, S.; Tomelleri, E.; et al. A few extreme events dominate global interannual variability in gross primary production. Environ. Res. Lett. 2014, 9, 035001. [Google Scholar] [CrossRef]
- Churkina, G.; Running, S.W. Contrasting climatic controls on the estimated productivity of global terrestrial biomes. Ecosystems 1998, 1, 206–215. [Google Scholar] [CrossRef]
- Piao, S.L.; Ciais, P.; Friedlingstein, P.; Noblet-Ducoudré, N.; Cadule, P.; Viovy, N.; Wang, T. Spatiotemporal patterns of terrestrial carbon cycle during the 20th century. Glob. Biogeochem. Cycles 2009, 23, GB4026. [Google Scholar] [CrossRef]
- Goulden, M.L.; Munger, J.W.; Fan, S.M.; Daube, B.C.; Wofsy, S.C. Exchange of carbon dioxide by a deciduous forest: Response to interannual climate variability. Science 1996, 271, 1576–1578. [Google Scholar] [CrossRef]
- Fang, J.Y.; Chen, A.P. Dynamic forest biomass carbon pools in China and their significance. Acta Bot. Sin. 2001, 43, 967–973. [Google Scholar]
- Zhao, H.Y.; Gong, L.J.; Qu, H.H.; Zhu, H.X.; Li, X.F.; Zhao, F. The climate change variations in the northern Greater Khingan Mountains during the past centuries. J. Geogr. Sci. 2016, 26, 585–602. [Google Scholar] [CrossRef]
- Cai, H.Y.; Zhang, S.W.; Yang, X.H. Forest Dynamics and Their Phenological Response to Climate Warming in the Khingan Mountains, Northeastern China. Int. J. Environ. Res. Pub. Health 2012, 9, 3943–3953. [Google Scholar] [CrossRef] [PubMed]
- Editorial Board of Vegetation Map of China. Chinese Academy of Science. In Vegetation Atlas of China (1:1,000,000); Geological Publishing House: Beijing, China, 2007. [Google Scholar]
- Global Land Surface Satellite (GLASS) Products Download and Service. Available online: http://glass-product.bnu.edu.cn/ (accessed on 1 December 2016).
- Savitzky, A.; Golay, M. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1638. [Google Scholar] [CrossRef]
- Eklundh, L.; Jonsson, P. TIMESAT 3.0 Software Manual; Malmö University: Malmö, Sweden, 2010. [Google Scholar]
- Chinese Meteorological Data Service Center (CMDC). Available online: http://data.cma.cn/ (accessed on 1 October 2016).
- NASA Ames Ecological Forecasting Lab. Available online: https://ecocast.arc.nasa.gov/data/pub/gimms/3g.v1/ (accessed on 20 December 2016).
- You, X.Z.; Meng, J.H.; Zhang, M.; Dong, T.F. Remote Sensing Based Detection of Crop Phenology for Agricultural Zones in China Using a New Threshold Method. Remote Sens. 2013, 5, 3190–3211. [Google Scholar] [CrossRef]
- Zhao, J.J.; Wang, Y.Y.; Zhang, Z.X.; Zhang, H.Y.; Hong, Y.; Guo, X.Y.; Yu, S.; Du, W.L.; Huang, F. The Variations of Land Surface Phenology in Northeast China and Its Responses to Climate Change from 1982 to 2013. Remote Sens. 2016, 8, 400. [Google Scholar] [CrossRef]
- Xiao, Z.Q.; Liang, S.L.; Sun, R.; Wang, J.D.; Jiang, B. Estimating the fraction of absorbed photosynthetically active radiation from the MODIS data based GLASS leaf area index product. Remote Sens. Environ. 2015, 171, 105–117. [Google Scholar] [CrossRef]
- Huang, K.; Zhang, Y.J.; Zhu, J.T.; Liu, Y.J.; Zu, J.X.; Zhang, J. The Influences of Climate Change and Human Activities on Vegetation Dynamics in the Qinghai-Tibet Plateau. Remote Sens. 2016, 8, 876. [Google Scholar] [CrossRef]
- Weber, U.; Jung, M.; Reichstein, M.; Beer, C.; Braakhekke, M.C.; Lehsten, V.; Ghent, D.; Kaduk, J.; Viovy, N.; Ciais, P.; et al. The interannual variability of Africa's ecosystem productivity: A multi-model analysis. Biogeosciences 2009, 6, 285–295. [Google Scholar] [CrossRef]
- Peng, S.S.; Piao, S.L.; Ciais, P.; Myneni, R.B.; Chen, A.; Chevallier, F.; Dolman, A.J.; Janssens, I.A.; Peñuelas, J.; Zhang, G.X.; et al. Asymmetric effects of daytime and night-time warming on Northern Hemisphere vegetation. Nature 2013, 501, 88–92. [Google Scholar] [CrossRef] [PubMed]
- Zhao, M.; Running, S.W. Drought-induced reduction in global terrestrial net primary production from 2000 through 2009. Science 2010, 329, 940–943. [Google Scholar] [CrossRef] [PubMed]
- Davis, C.L.; Hoffman, M.T.; Roberts, W. Long-term trends in vegetation phenology and productivity over Namaqualand using the GIMMS AVHRR NDVI3g data from 1982 to 2011. S. Afr. J. Bot. 2017, 111, 76–85. [Google Scholar] [CrossRef]
- Tang, H.; Li, Z.W.; Zhu, Z.L.; Chen, B.; Zhang, B.H.; Xin, X.P. Variability and Climate Change Trend in Vegetation Phenology of Recent Decades in the Greater Khingan Mountain Area, Northeastern China. Remote Sens. 2015, 7, 11914–11932. [Google Scholar] [CrossRef]
- Piao, S.L.; Friedlingstein, P.; Ciais, P.; Viovy, N.; Demarty, J. Growing season extension and its impact on terrestrial carbon cycle in the Northern Hemisphere over the past 2 decades. Global Biogeochem. Cycles 2007, 21, GB3018. [Google Scholar] [CrossRef]
- Murray-Tortarolo, G.; Anav, A.; Friedlingstein, P.; Sitch, S.; Piao, S.L.; Zhu, Z.; Poulter, B.; Zaehle, S.; Ahlström, A.; Lomas, M.; et al. Evaluation of land surface models in reproducing satellite-derived LAI over the high-latitude Northern Hemisphere. Part I: Uncoupled DGVMs. Remote Sens. 2013, 5, 4819–4838. [Google Scholar] [CrossRef]
- Nilsson, M.C.; Wardle, D.A. Understory vegetation as a forest ecosystem driver: Evidence from the northern Swedish boreal forest. Front Ecol. Environ. 2005, 3, 421–428. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, R.G.; Pisek, J.; Chen, J.M. Separating overstory and understory leaf area indices for global needleleaf and deciduous broadleaf forests by fusion of MODIS and MISR data. Biogeosciences 2017, 14, 1093–1110. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, J. Quantifying ecological drivers of ecosystem productivity of the early successional boreal Larix gmelinii forest. Ecosphere 2014, 5, 1–16. [Google Scholar] [CrossRef]
- Myneni, R.B.; Keeling, C.; Tucker, C.; Asrar, G.; Nemani, R. Increased plant growth in the northern high latitudes from 1981 to 1991. Nature 1997, 386, 698–702. [Google Scholar] [CrossRef]
- Zhang, Y.P.; Hu, H.Q. Climatic Change and Its Impact on Forest Fire in Daxing’ anling Mountains. J. North-East For. Univ. 2008, 36, 29–31. [Google Scholar]
- Gao, Y.G.; Zhao, H.Y.; Gao, F.; Zhu, H.X.; Qu, H.H.; Zhao, F. Climate change trend in future and its influence on wetlands in the Greater Khingan Mountains. J. Glaciol. Geocryol. 2016, 38, 47–56. [Google Scholar]
- Han, X.C.; Zhao, Y.S.; Xin, Y. Succession process of Larix gmelinii forest with artificial restoration after fire in Daxing’ anling. Sci. Soil Water Conserv. 2015, 13, 70–76. [Google Scholar]
- Rull, V. A palynological record of a secondary succession after fire in the Gran Sabana, Venezuela. J. Quat. Sci. 1999, 14, 137–152. [Google Scholar] [CrossRef]
- Wang, C.K.; Gower, S.T.; Wang, Y.H.; Zhao, H.X.; Yan, P.; Bond-Lamberty, B.P. The influence of fire on carbon distribution and net primary production of boreal Larix gmelinii forests in north-eastern China. Glob. Chang. Biol. 2001, 7, 719–730. [Google Scholar] [CrossRef]
- Wang, X.G.; Li, X.Z.; He, H.S.; Leng, W.F.; Wen, Q.C. Postfire succession of larch forest on the northern slope of Daxinganling. Chin. J. Ecol. 2004, 23, 35–41. [Google Scholar]
- Artz, R.; Ball, G.; Behrens, K.; Bonnin, G.M.; Bower, C.A.; Canterford, R.; Childs, B.; Claude, H.; Crum, T.; Dombrowsky, R.; et al. Measurement of Sunshine Duration. In Guide to Meteorological Instruments and Methods of Observation, 7th ed.; 7 bis, avenue de la Paix P.O. Box No. 2300 CH-1211 Geneva 2; WMO: Geneva, Switzerland, 2008; Volume 8, p. 199. ISBN 978-92-63-10008-5. [Google Scholar]
- Wikipedia. Available online: https://en.wikipedia.org/wiki/Sunshine_duration (accessed on 1 May 2017).
- Piao, S.L.; Nan, H.J.; Huntingford, C.; Ciais, P.; Friedlingstein, P.; Sitch, S.; Peng, S.S.; Ahlström, A.; Canadell, J.G.; Cong, N.; et al. Evidence for a weakening relationship between inter-annual temperature variability and northern vegetation activity. Nat. Commun. 2014, 5, 5018. [Google Scholar] [CrossRef] [PubMed]
- Peng, D.L.; Zhang, B.; Liu, L.Y.; Fang, H.L.; Chen, D.M.; Hu, Y.; Liu, L.L. Characteristics and drivers of global NDVI-based FPAR from 1982 to 2006. Global Biogeochem. Cycles 2012, 26, GB3015. [Google Scholar] [CrossRef]
- Karami, M.; Hansen, B.U.; Nielsen, A.W.; Abermann, J.; Lund, M.; Schmidt, N.M.; Elberling, B. Vegetation phenology gradients along the west and east coasts of Greenland from 2001 to 2015. Ambio 2017, 46 (Suppl. 1), S94–S105. [Google Scholar] [CrossRef] [PubMed]
- Qiu, B.W.; Zeng, C.Y.; Tang, Z.H.; Chen, C.C. Characterizing spatiotemporal non-stationarity in vegetation dynamics in China using MODIS EVI dataset. Environ. Monit. Assess. 2013, 185, 9019–9035. [Google Scholar] [CrossRef] [PubMed]
- Hou, X.H.; Niu, Z.; Gao, S. Phenology of Forest Vegetation in Northeast of China in Ten Years Using Remote Sensing. Spectrosc. Spectr. Anal. 2013, 34, 515–519. [Google Scholar]
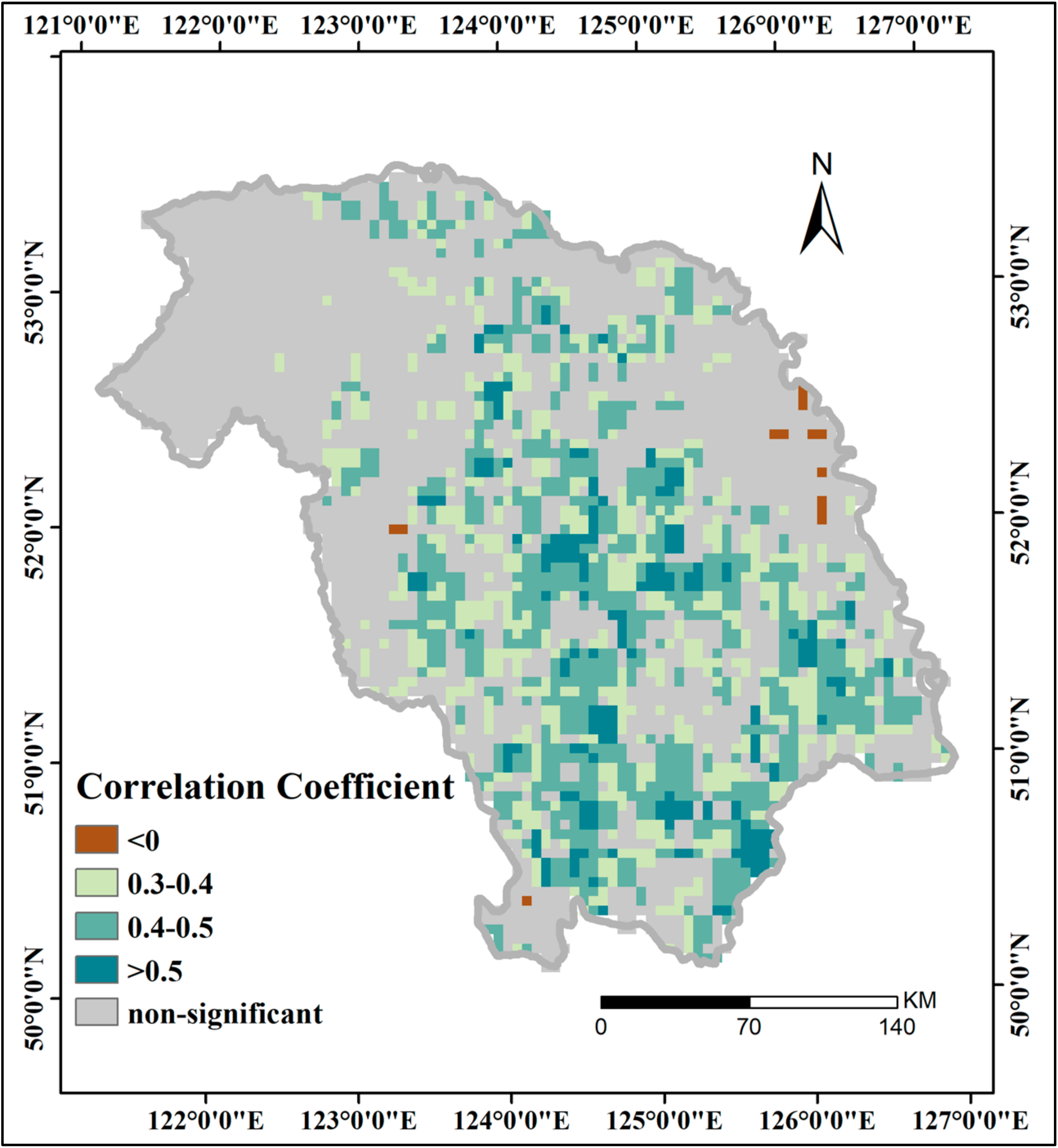
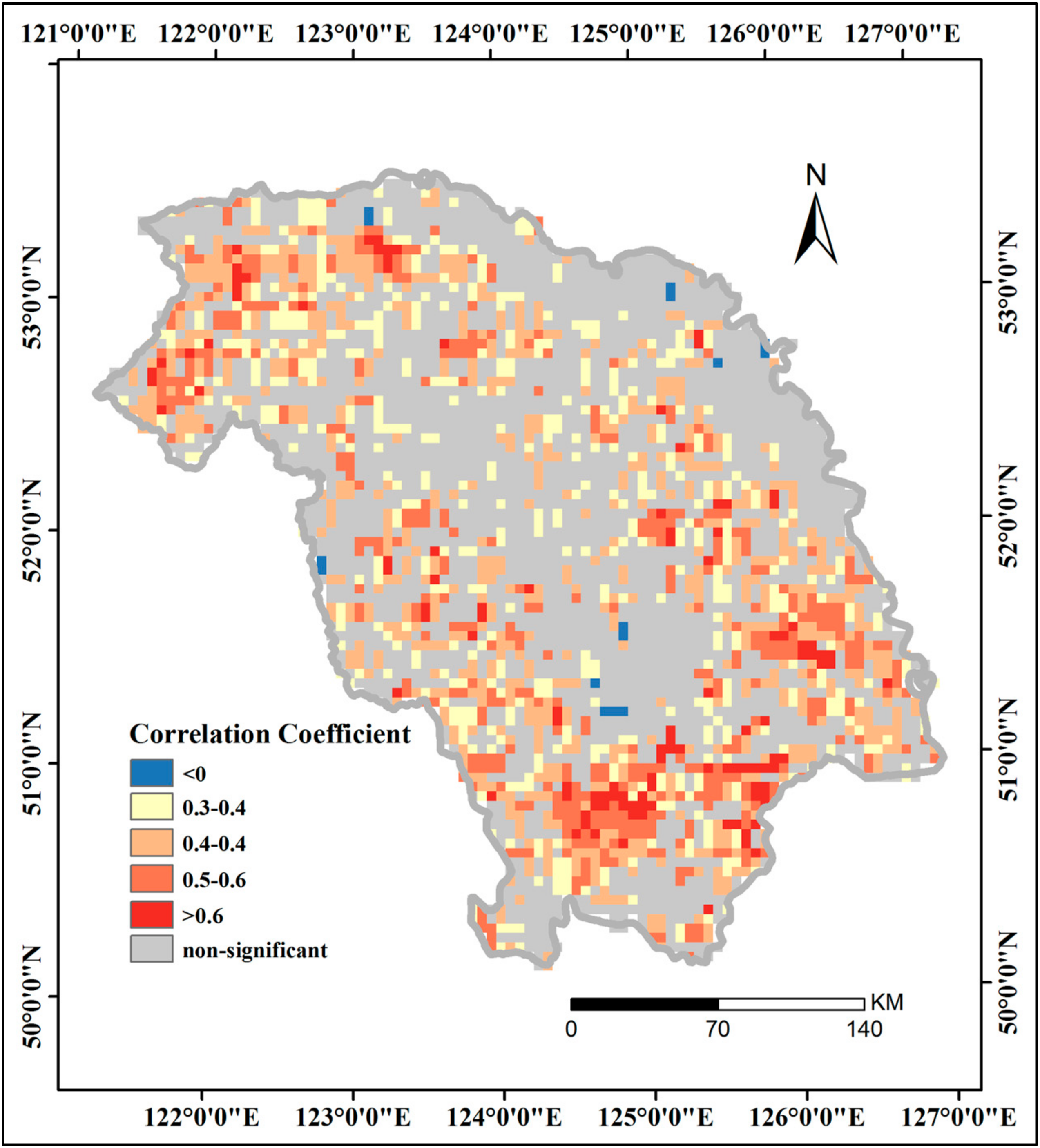
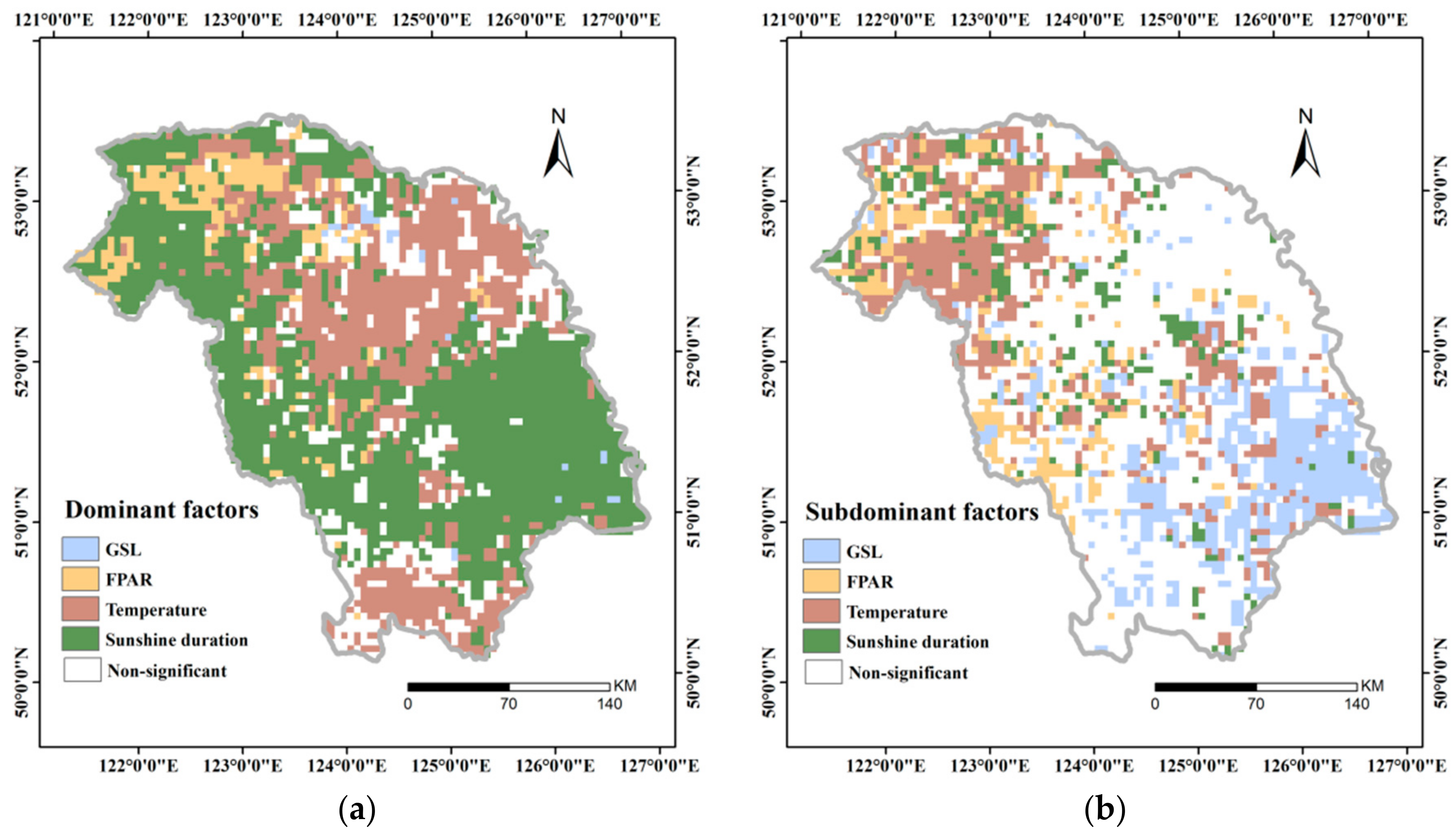
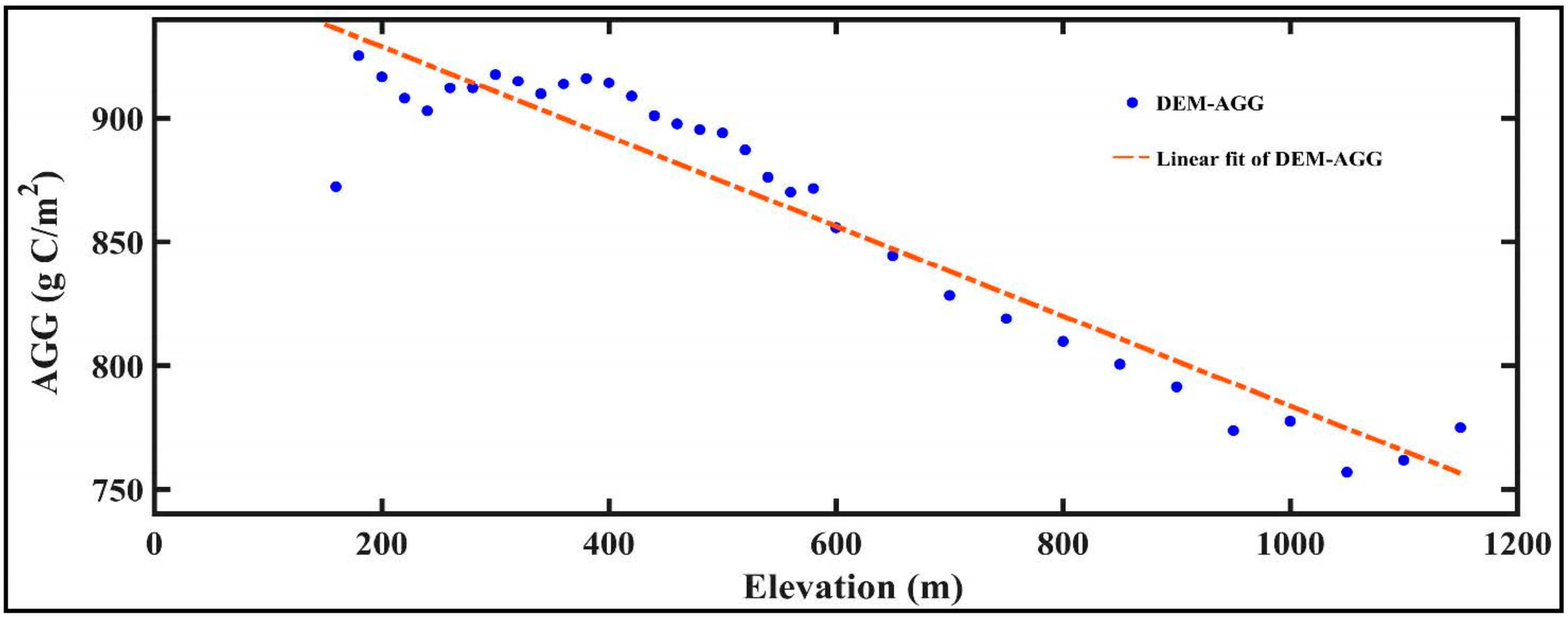
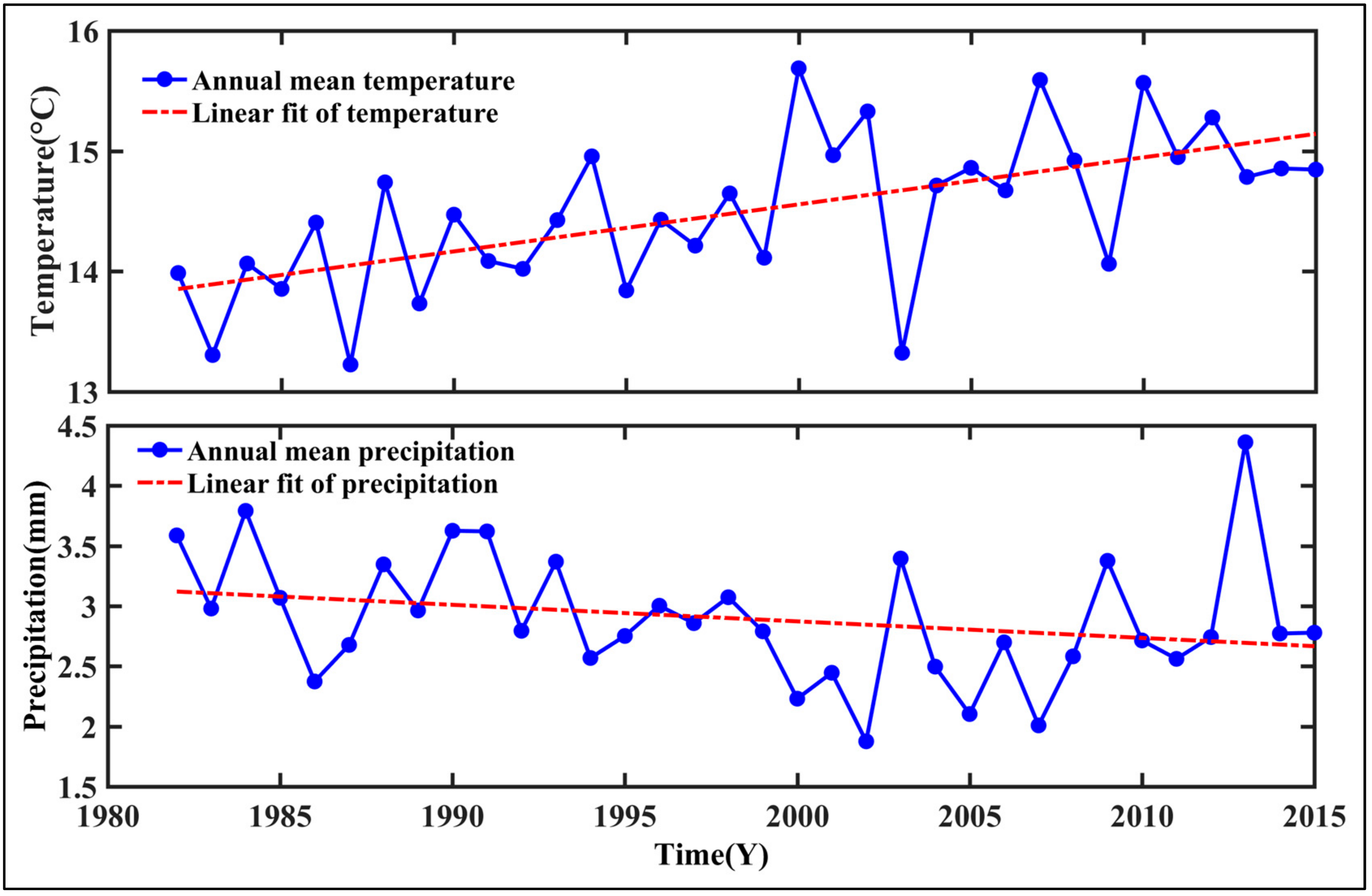
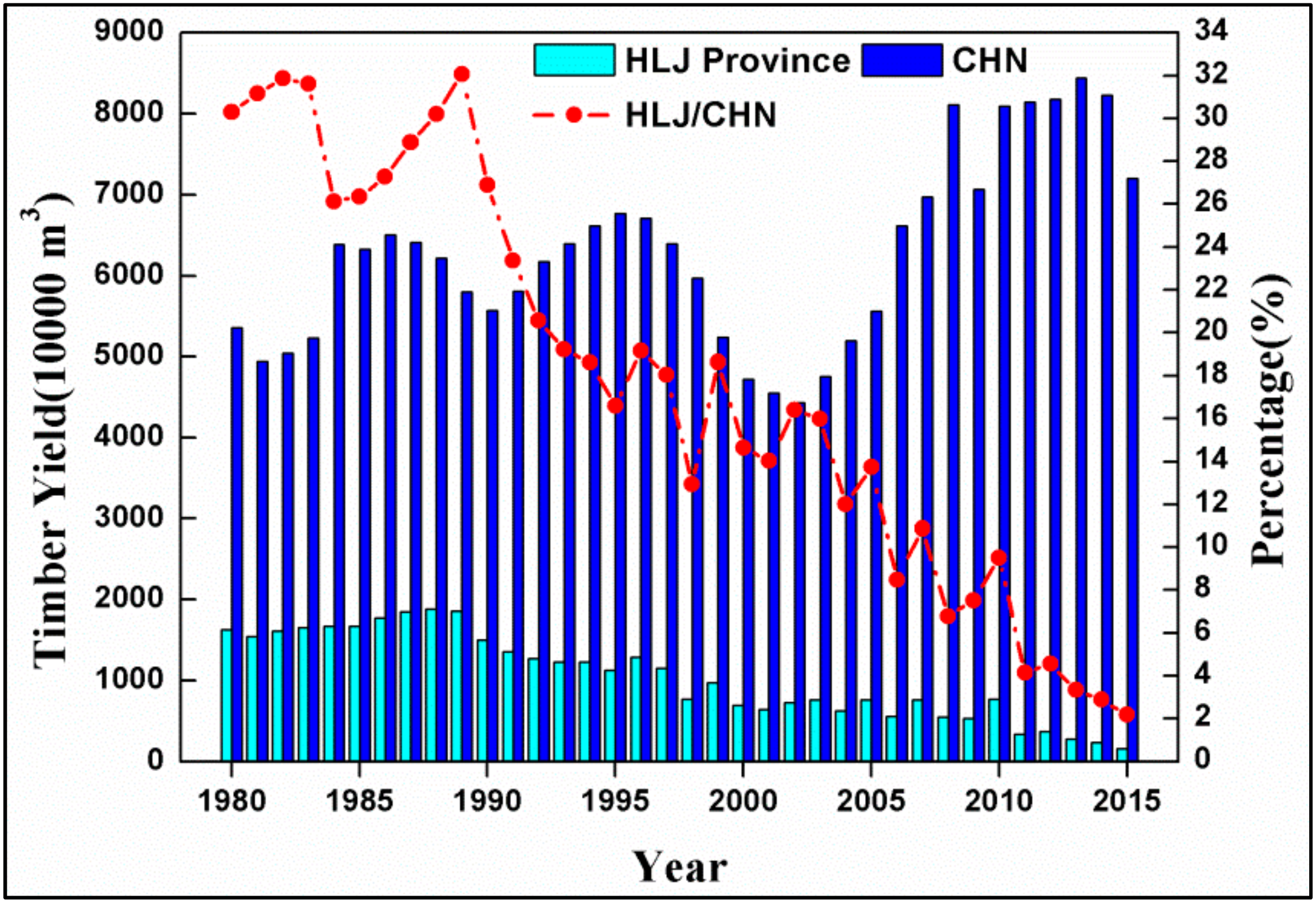
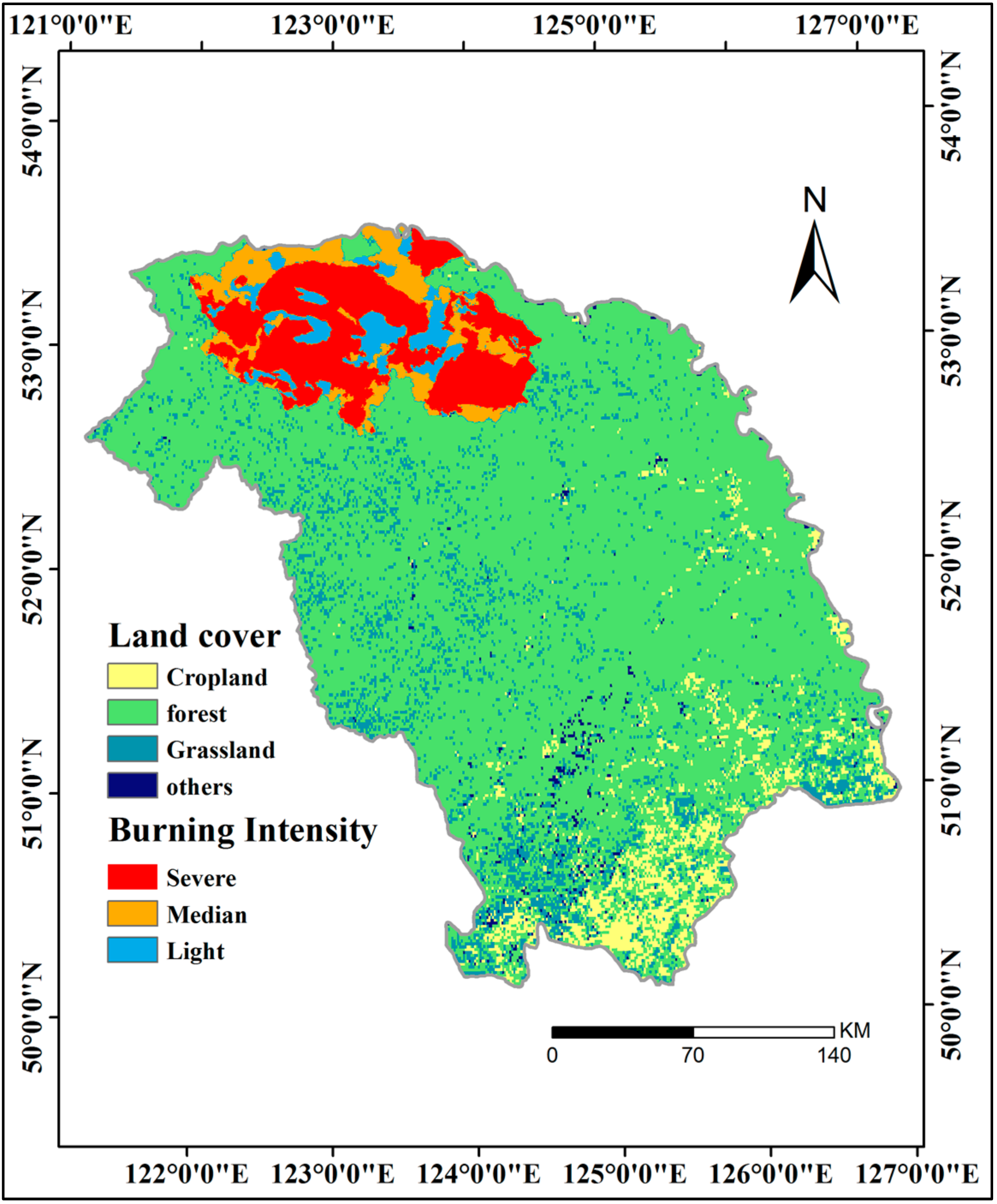
| Station | SD | DAT | DMAT | DMIT | DP | |
|---|---|---|---|---|---|---|
| Spring | 50,136 | 0.419 ** | 0.335 * | 0.398 ** | 0.257 | −0.153 |
| 50,246 | 0.279 | 0.435 ** | 0.495 ** | 0.279 | −0.179 | |
| 50,349 | 0.397 * | 0.448 ** | 0.482 ** | 0.292 * | −0.310 * | |
| 50,353 | 0.390 * | 0.381 * | 0.493 ** | 0.200 | −0.150 | |
| 50,425 | 0.295 * | 0.445 ** | 0.419 ** | 0.407 ** | −0.070 | |
| Summer | 50,136 | 0.631 ** | 0.339 * | 0.459 ** | −0.144 | −0.324 * |
| 50,246 | 0.614 ** | 0.669 ** | 0.811 ** | −0.155 | −0.580 ** | |
| 50,349 | 0.814 ** | 0.717 ** | 0.810 ** | −0.017 | −0.482 ** | |
| 50,353 | 0.835 ** | 0.665 ** | 0.753 ** | 0.247 | −0.640 ** | |
| 50,425 | 0.565 ** | 0.590 ** | 0.642 ** | 0.304 * | −0.470 ** | |
| Autumn | 50,136 | 0.474 ** | −0.041 | 0.349 * | −0.255 | −0.608 ** |
| 50,246 | 0.491 ** | −0.026 | 0.410 ** | −0.328 * | −0.484 ** | |
| 50,349 | 0.677 ** | −0.041 | 0.314 * | −0.335 * | −0.441 ** | |
| 50,353 | 0.134 | 0.176 | 0.317 * | −0.051 | −0.429 ** | |
| 50,425 | 0.466 ** | 0.304 * | 0.333 * | 0.206 | −0.447 ** | |
| Growing Season | 50,136 | 0.620 ** | 0.385 * | 0.50,2 ** | −0.055 | −0.371 * |
| 50,246 | 0.587 ** | 0.602 ** | 0.789 ** | −0.137 | −0.544 ** | |
| 50,349 | 0.753 ** | 0.626 ** | 0.773 ** | 0.005 | −0.513 ** | |
| 50,353 | 0.659 ** | 0.604 ** | 0.704 ** | 0.294 * | −0.623 ** | |
| 50,425 | 0.577 ** | 0.572 ** | 0.603 ** | 0.367 * | −0.470 ** |
| Dominant Factor | GSL | FPAR | Temperature | Sunshine Duration |
|---|---|---|---|---|
| Zonal mean coefficients | 0.399134 | 0.453251 | 0.448733 | 0.518619 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, L.; Fan, W.; Ren, H.; Liu, S.; Cui, Y.; Zhao, P. Spatiotemporal Dynamics in Vegetation GPP over the Great Khingan Mountains Using GLASS Products from 1982 to 2015. Remote Sens. 2018, 10, 488. https://doi.org/10.3390/rs10030488
Hu L, Fan W, Ren H, Liu S, Cui Y, Zhao P. Spatiotemporal Dynamics in Vegetation GPP over the Great Khingan Mountains Using GLASS Products from 1982 to 2015. Remote Sensing. 2018; 10(3):488. https://doi.org/10.3390/rs10030488
Chicago/Turabian StyleHu, Ling, Wenjie Fan, Huazhong Ren, Suhong Liu, Yaokui Cui, and Peng Zhao. 2018. "Spatiotemporal Dynamics in Vegetation GPP over the Great Khingan Mountains Using GLASS Products from 1982 to 2015" Remote Sensing 10, no. 3: 488. https://doi.org/10.3390/rs10030488
APA StyleHu, L., Fan, W., Ren, H., Liu, S., Cui, Y., & Zhao, P. (2018). Spatiotemporal Dynamics in Vegetation GPP over the Great Khingan Mountains Using GLASS Products from 1982 to 2015. Remote Sensing, 10(3), 488. https://doi.org/10.3390/rs10030488









