1. Introduction
Starting with European Remote Sensing 1 (ERS-1) in 1991 and TOPography Experiment (TOPEX)/Poseidon in 1992, satellite missions carrying radar altimeters have resulted in invaluable continuous measurements being obtained over the ocean, ice, rivers and lakes for more than 25 years. This has been made possible through the joint effort of various space agencies: the European Space Agency (ESA), the Centre National d’Études Spatiales (CNES), European Organisation for the Exploitation of Meteorological Satellites (EUMETSAT), the National Aeronautics and Space Administration (NASA), the Jet Propulsion Laboratory (JPL), the National Oceanic and Atmospheric Administration (NOAA), and the Indian Space Research Organization (ISRO). ESA supported the 35-day repeat missions ERS-1 (1991), ERS-2 (1995), and Envisat (2002), the geodetic mission CryoSat-2 (2010), and more recently, the 27-day repeat mission Sentinel-3A (2016), the latter in collaboration with EUMETSAT. Satellite with ARgos and ALtika (SARAL), a 35-day mission follow-up of Envisat, is a joint effort between the CNES and ISRO. Partly or in collaboration, NASA, NOAA, JPL, CNES, and EUMETSAT have been responsible for the so-called reference 10-day repeat missions: TOPEX/Poseidon (1991), Jason-1 (2002), Jason-2 (2008), and Jason-3 (2016) [
1]. For a detailed and update review of satellite altimetry, see e.g., [
2].
These missions have been designed to provide complementary spatial and temporal resolutions, allowing e.g., a better characterisation of the mesoscale oceanic circulation [
3,
4], the determination of accurate global and regional sea level trends [
5,
6,
7,
8,
9], and unprecedented observations over river, lakes and reservoirs [
10,
11] as well as ice surfaces [
12].
Satellite altimetry allows the determination of the height of e.g., the sea or lake surface above a reference ellipsoid by means of the following equation [
13]:
where
is the spacecraft height above a reference ellipsoid provided by precise orbit determination, referred to as an International Terrestrial Reference Frame,
is the measured altimeter range corrected for all instrument effects, and
is the corresponding range corrected for all instrument, range, and geophysical effects. The term
includes all corrections that need to be applied to the observed range due to the signal propagation delay through the atmosphere, its interaction with the sea surface and terms related with specific geophysical phenomena being given by Equation (2):
The first four terms in Equation (2) are the range corrections, accounting for the interaction of the altimeter radar signal with the atmosphere (dry, wet and ionospheric corrections) and with the sea surface (sea state bias). The last two terms refer to geophysical phenomena, dynamic atmospheric correction, and tides (ocean, load, solid earth and pole tides), which should be removed if they are not part of the signals of interest. A detailed description of the range and geophysical corrections can be found e.g., in [
13,
14].
Equation (1) evidences that the determination of an accurate surface height requires the knowledge of the spacecraft orbit, the range measurement, and of all correction terms in Equation (2) with the same accuracy. Amidst these terms is the wet tropospheric correction (WTC), due to the water vapour and liquid water content in the atmosphere. Since these variables have large space–time variability, if not properly modelled, the WTC is one of the major sources of uncertainty in many satellite altimetry applications [
13,
15,
16].
Due to its variability, the most precise way to account for the WTC in satellite altimetry is by means of collocated measurements from a microwave radiometer (MWR), obtained on the same spacecraft. Two main types of radiometers have been deployed on the altimeter satellites: three-band radiometers on board the reference missions and two-band radiometers on all ESA missions and SARAL. Over the open ocean they provide accurate WTC retrievals within 1 cm [
17].
The algorithms adopted in the WTC retrieval from the measured brightness temperatures (TBs) in the various spectral bands have been designed for the open ocean, assuming a constant ocean emissivity. In the presence of other surfaces such as land or ice, the measurements lay outside the predicted validity interval and the observations become unusable. Moreover, these instruments possess large footprints from 10 to 40 km depending on the frequency [
18,
19]. Therefore, in the coastal regions they sense land well before the altimeter, originating bands of invalid measurements around the coastline of a width of 10–40 km. In recent years, several methods have been developed to improve the MWR-derived WTC in the coastal zones, extending the validity of the correction up to the coast. An overview of these methods is given in [
16].
Building directly on the proven heritage of ERS-1, ERS-2, and Envisat, launched on 16 February 2016, Sentinel-3A (S3A) carries a suite of innovative instruments that include [
20]: (1) the Sea and Land Surface Temperature Radiometer (SLSTR) based on Envisat’s Advanced Along Track Scanning Radiometer (AATSR), to determine global sea surface temperatures to an accuracy of better than 0.3 K; the Ocean and Land Colour Instrument (OLCI), based on Envisat’s Medium Resolution Imaging Spectrometer (MERIS), with 21 bands, (compared to 15 bands on MERIS), a design optimised to minimise Sun-glint, and a resolution of 300 m over all surfaces; a dual-frequency (Ku and C-band) advanced Synthetic Aperture Radar Altimeter (SRAL) developed from Envisat RA-2, CryoSat Synthetic Aperture Interferometric Radar Altimeter (SIRAL) and Jason-2/Poseidon-3, providing accurate surface topography measurements; and a microwave radiometer for accurate measurement of the wet pat delay of the SRAL observations [
20].
SRAL and the MWR constitute the topography package, providing accurate measurements of sea surface height, significant wave height, and wind speed, essential for ocean forecasting systems and climate monitoring. Accurate SRAL measurements also extend to sea-ice, ice sheets, rivers, and lakes. Being the first altimeter mission to operate, globally, a radar altimeter in the SAR closed burst mode, with an improved along track resolution of about 300 m [
21], Sentinel-3A is a pioneer and challenging mission in many aspects, pushing the experts of the various fields to the limit to tune the retrieval algorithms to its instruments and exploit the derived geophysical parameters.
As mentioned above, amongst its suite of instruments, Sentinel-3A carries a dual channel (23.8-GHz and 36.5-GHz) microwave radiometer aiming at the retrieval of the wet path delay, which provides important support for the quality of the SRAL measurements. Due to their instrumental characteristics and retrieval algorithms, the two-band MWRs deployed on ESA altimeter missions are known for their good performance in the open ocean [
22]. However, when they approach the coast, the retrieval algorithm, which was designed for surfaces with ocean emissivity, generates very noisy values, as the footprint encounters surfaces with different levels of emissivity. The same happens at high latitudes in regions covered with ice [
23,
24].
This work aims at performing an independent assessment of S3A MWR-based WTC, in the open and coastal ocean, in support of S3A data improvement and exploitation.
The validation is performed by means of comparisons with independent data sets namely: wet path delays derived from the Global Precipitation Measurement (GPM) Microwave Imager (GMI); Global Navigation Satellite System (GNSS)-derived path delays determined at coastal stations; and wet path delays from the MWR on board Jason-2 (J2), Jason-3 (J3), and SARAL/AltiKa. In addition, the overall along-track performance is compared against independent estimates obtained from the GNSS-derived Path Delay Plus (GPD+) algorithm [
24] and from atmospheric models. From this thorough analysis, a deeper knowledge of the measurement capabilities and limitations of the dual-frequency radiometer aboard S3A and of the present WTC retrieval algorithms is expected.
This paper is organised in five sections.
Section 2 describes the data sets and the methodology used in the S3A WTC assessment.
Section 3 describes the results obtained with the various datasets. Finally,
Section 4 and
Section 5 present the discussions of the results and conclusions, respectively.
4. Discussion
This section presents a thorough discussion of the results presented in
Section 3.
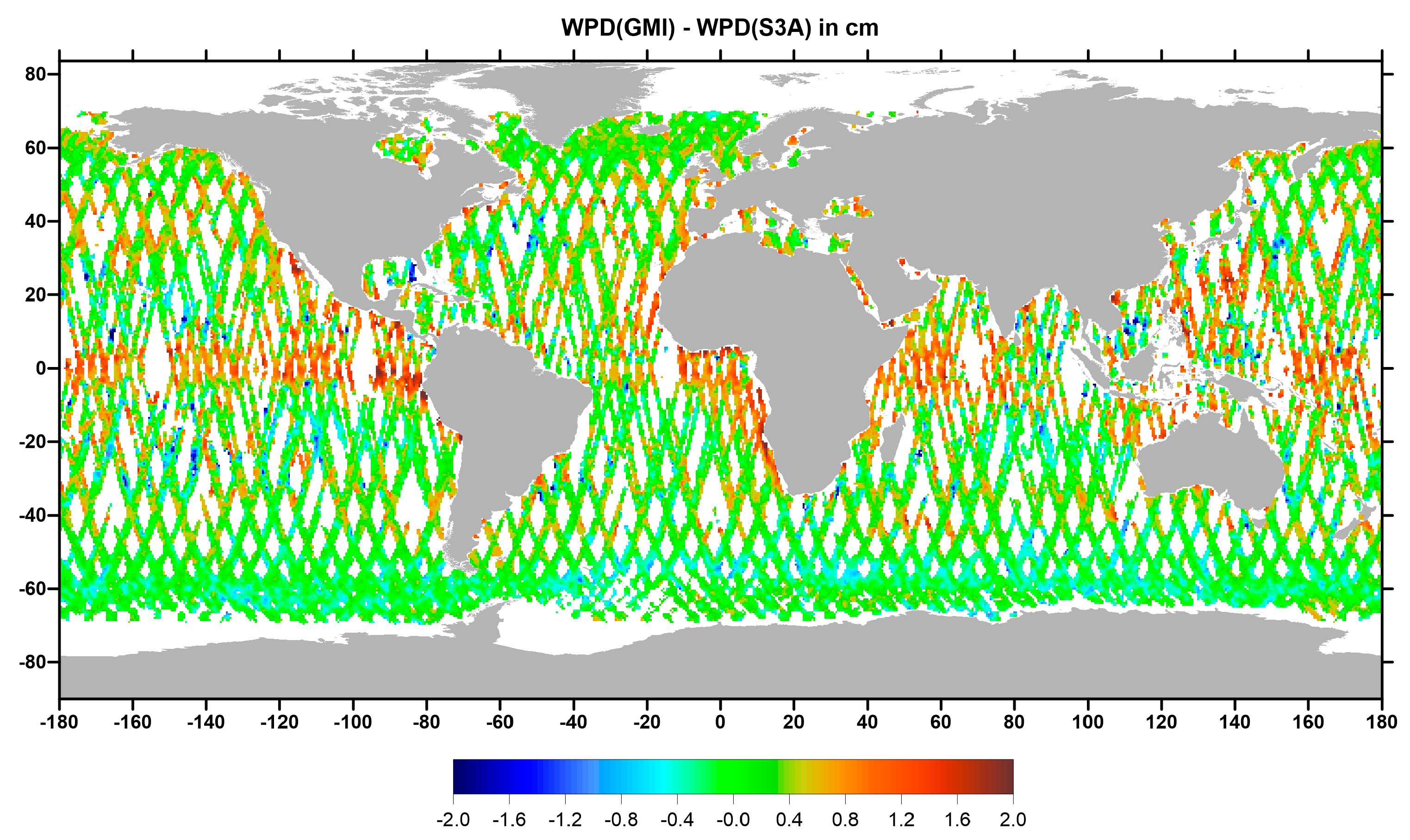
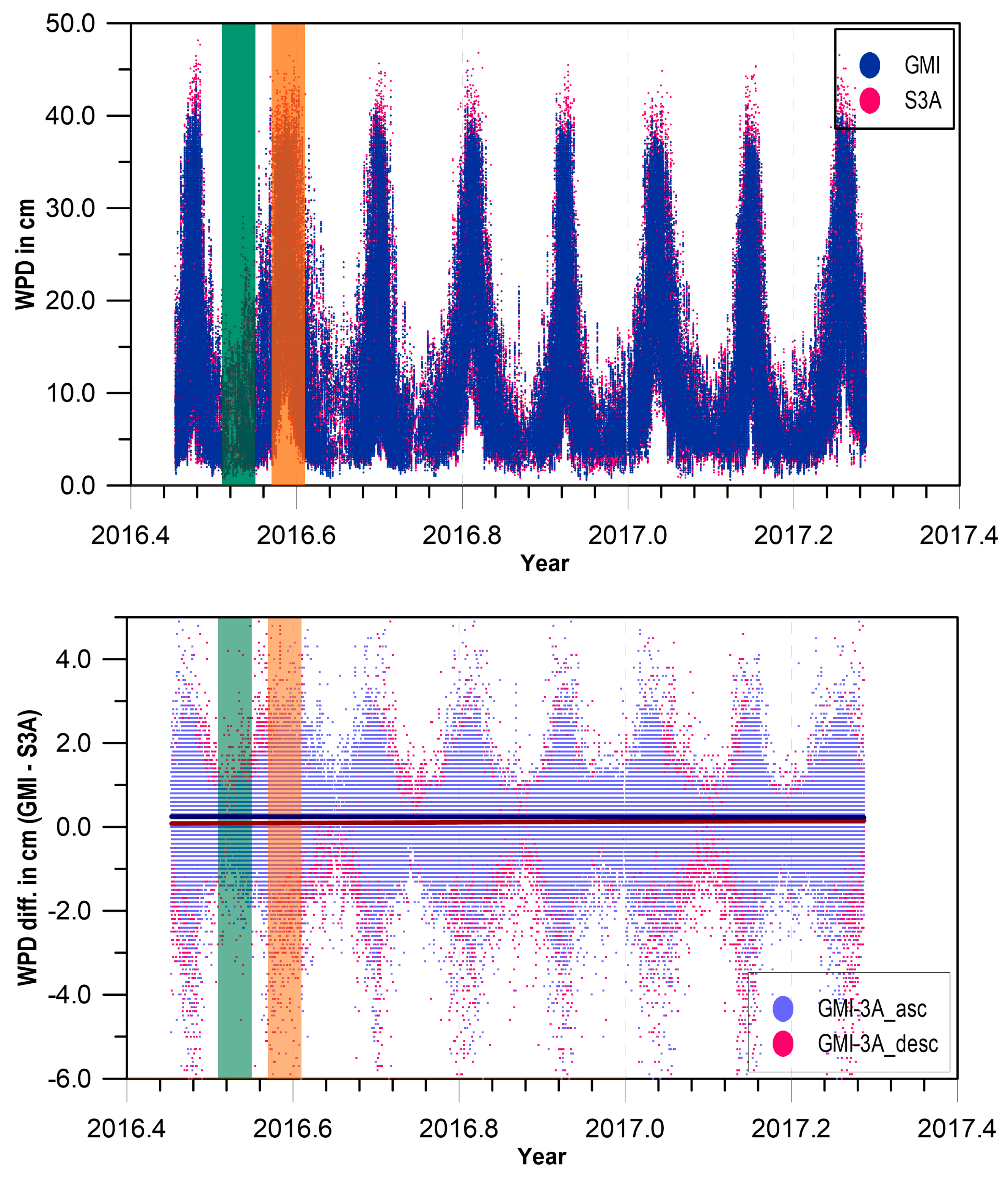
In terms of the global statistical parameters, GMI and Sentinel-3A agree very well, with mean and RMS of WPD differences (WPD(GMI)–WPD(S3A)) of 0.17 cm and 0.95 cm, respectively. The overall pattern of the WPD differences at match points shown in
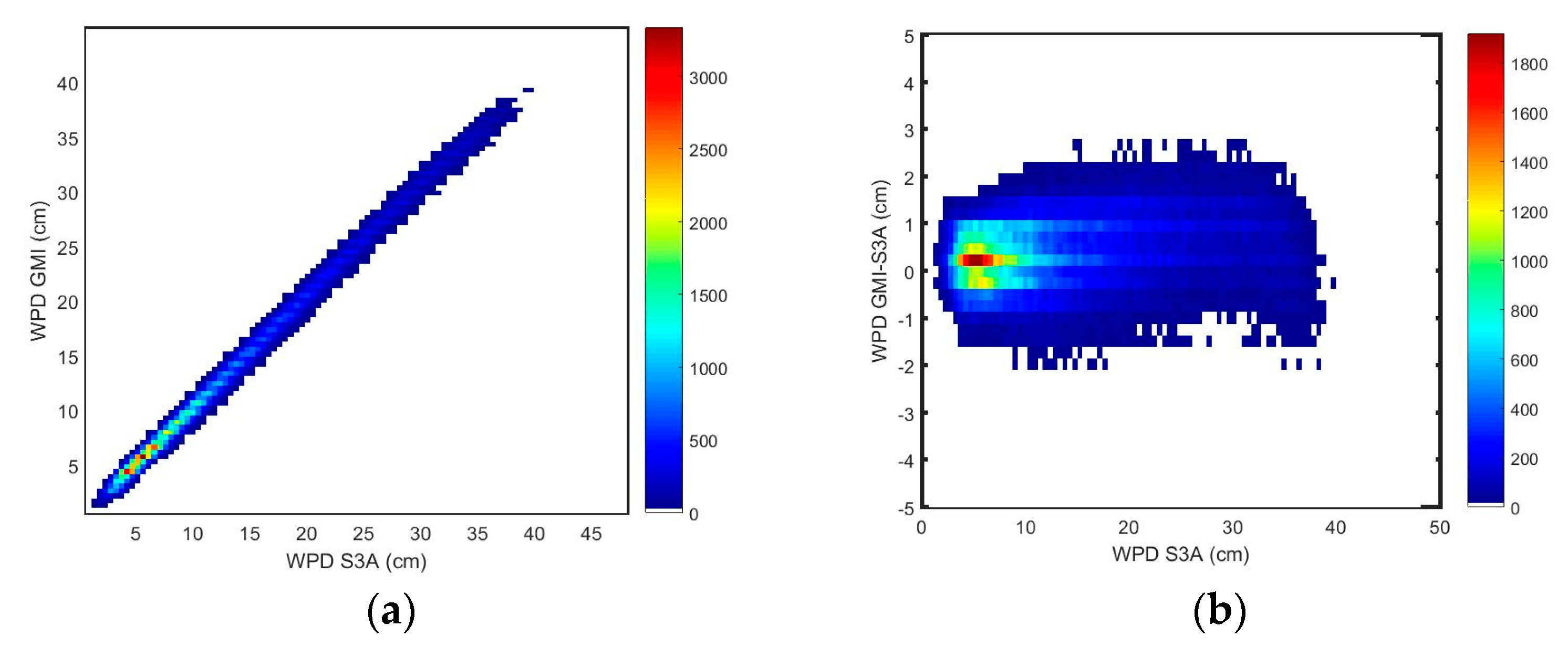
Figure 3 seems to indicate that at the low latitudes, where the WPD is larger, GMI measures wetter than S3A, while at the extreme southern latitudes, corresponding to regions of low WPD values, there is a tendency for GMI to measure drier than S3A. However, the scale factor (1.004) and small offset (0.12 cm) reveal a very good overall match between the two sensors, also demonstrated by the very small scatter of the scatter plot of the two WPDs illustrated in
Figure 4.
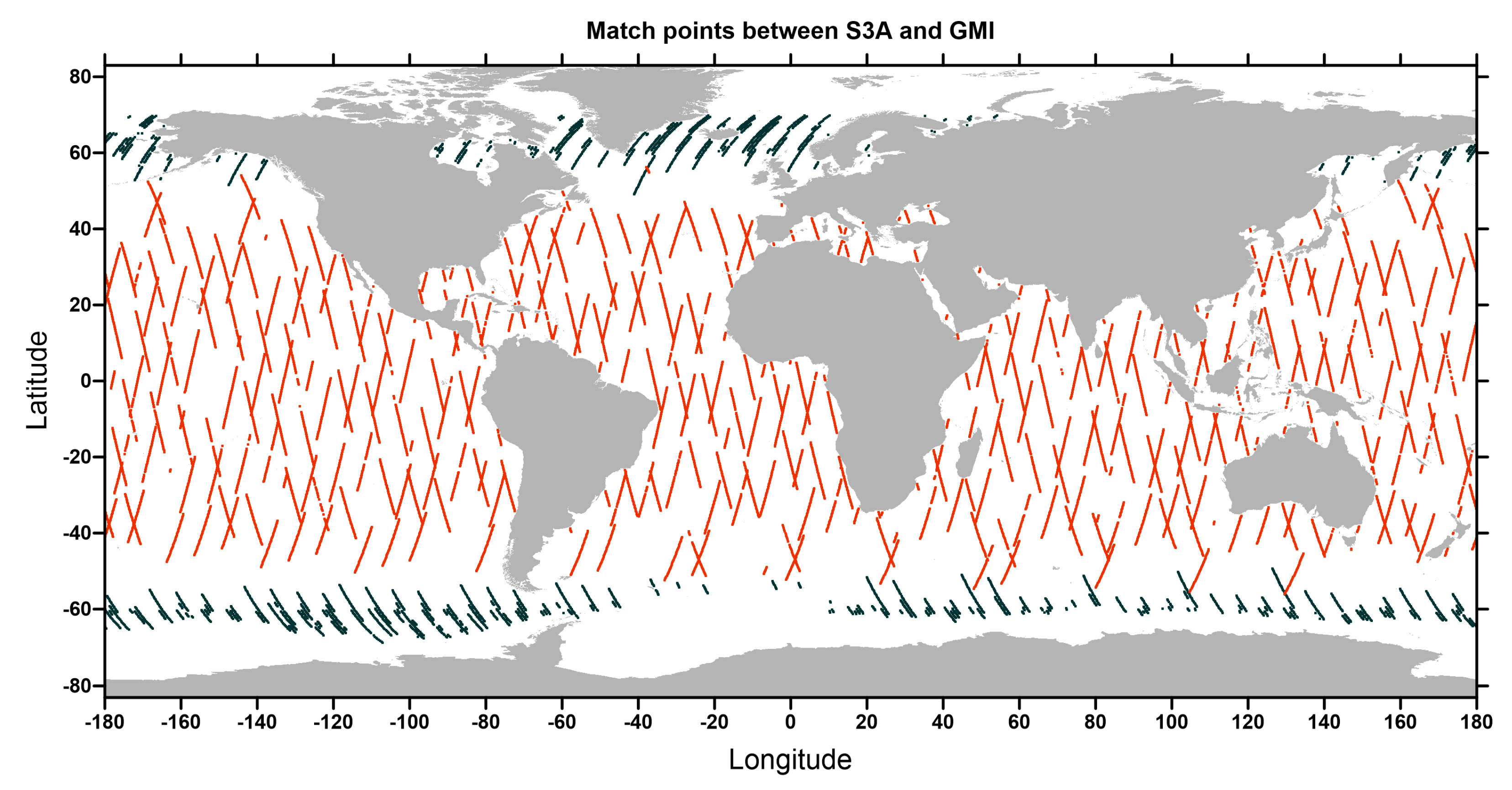
The most curious feature of the comparison between GMI and S3A is the observed strong periodic pattern of 41 days. When analysing the way the spatial pattern of the match points changes with time (
Figure 5 and
Figure 6), it can be observed that there are periods for which all match points between the two sensors are located only at high latitudes. An example of these periods is the one corresponding to the green bar in
Figure 5, to which the points with the same green colour in
Figure 7 (all above latitude 50°N or below latitude 50°S) correspond. During these periods, since the WPD at high latitudes is low (only a few cm) and with low variability, the differences between the two sensors are very small, with absolute values of less than 1 cm. On the contrary, during periods such as the one corresponding to the orange bar in
Figure 5, the match points are located at the low latitudes, between ±50° (orange points in
Figure 6). Over these periods, the WPD reaches higher values (up to 40–50 cm) and has larger variability, inducing larger differences between the two sensors. These results are a clear demonstration of the impact of data sampling in this type of study, which, if not properly accounted for, can lead to misinterpretations.
The authors of [
26] report that the S3A MWR L1 brightness temperatures exhibit a difference of up to 1 K between ascending and descending tracks for the 23.8-GHz channel, with unknown origin. With a view to investigate if this potential bias can be observed in the current L2 products, the differences WPD (GMI)—WPD(S3A) have been represented in the bottom panel of
Figure 5 separately for ascending (in blue) and descending (in red) tracks. No significant differences can be observed between the ascending and descending track differences. In terms of overall statistics, the S3A WPD differences with respect to GMI for the ascending tracks are about 1 mm larger than those for the descending tracks (compare dark blue with dark red lines in the bottom panel of
Figure 5). This difference is too small, insignificant and cannot be related with the reported 1 K difference since the latter can lead to WPD differences ranging from 0.2 cm to 1 cm.
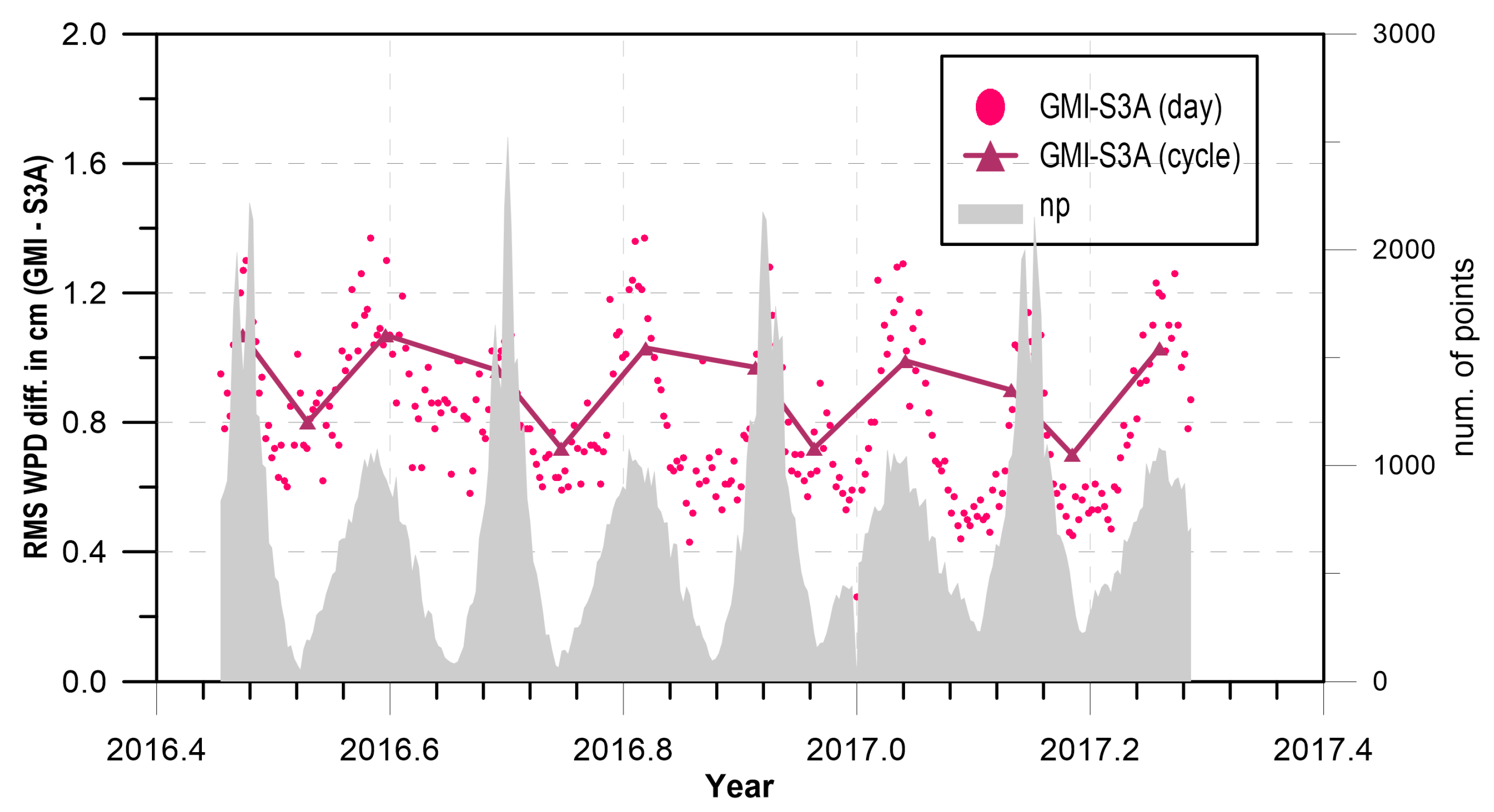
In spite of the small analysis period, the RMS differences (between GMI and S3A) computed for periods of the S3A cycles (27-day) evidence a long-term stable signal with an 82-day periodic pattern. This pattern occurs due to the fact that S3A orbit is Sun-synchronous, while GPM orbit is not. Due to its orbit characteristics, the GPM orbital plane takes 82 days to complete a full rotation with respect to the Sun and therefore with respect to the S3A orbital plane, explaining the observed periodic signal. In spite of these periodicities observed in the differences between GMI and the S3A MWR, due to the fact that GMI is on a non-Sun-synchronous orbit with a 65° inclination, the number of match points with S3A is larger than for example with any SSM/IS sensor, as these are on Sun-synchronous orbits, out of phase with respect to the S3A orbit by 3–6 h.
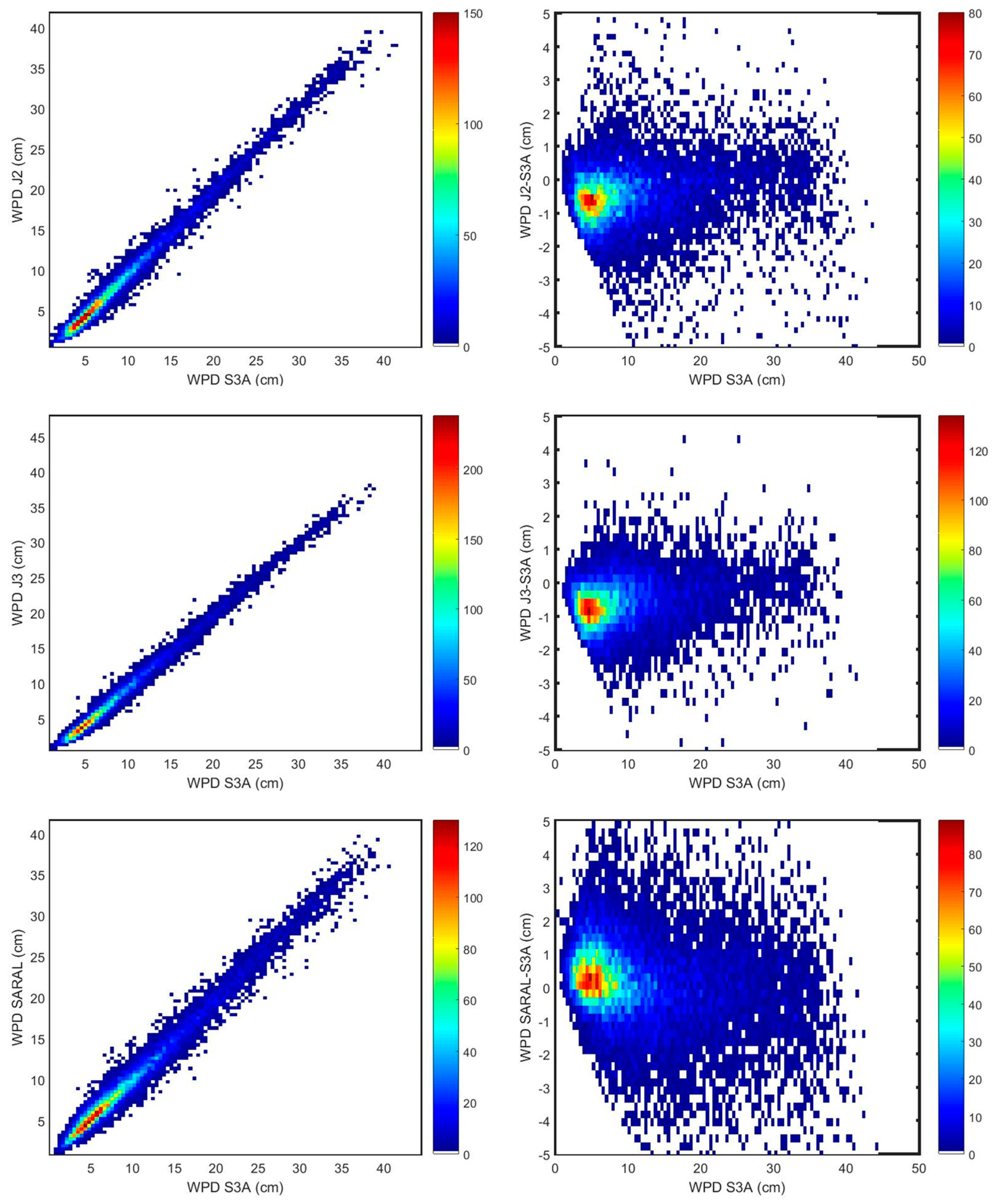
The comparison with the radiometers on board J2 and J3 indicate that on average these sensors measure drier than S3A by about 0.6–0.7 cm, while the RMS of the differences is within 1.2–1.3 cm. The scale factor (1.01), the negative offset of −0.7 and −0.8 cm and the blue predominant colour in the spatial pattern of the WPD differences shown in the top and medium panels of
Figure 8 confirm this tendency.
For SARAL, the results are a bit different. The RMS of the differences is larger (1.5 cm) which can be explained by the fact that the crossover differences span a larger time interval (240 min versus 180 min used for J2 and J3). The scale factor of 0.96, offset of 0.6 cm, and the larger scatter observed in
Figure 8 (bottom panel) and 9 (bottom panel) indicate a slightly larger difference between these two sensors, partly explained by the mentioned time difference between the corresponding crossovers.
The statistical parameters of the comparisons between S3A and the MWR aboard the other three altimeter missions are in agreement with the results presented in [
24] and further work by these authors, comparing the same sensors with the SSM/I and SSM/IS sensors, which also indicate that J2 and J3 measure drier than the latter sensors by about 0.6 cm and 1 cm, respectively.
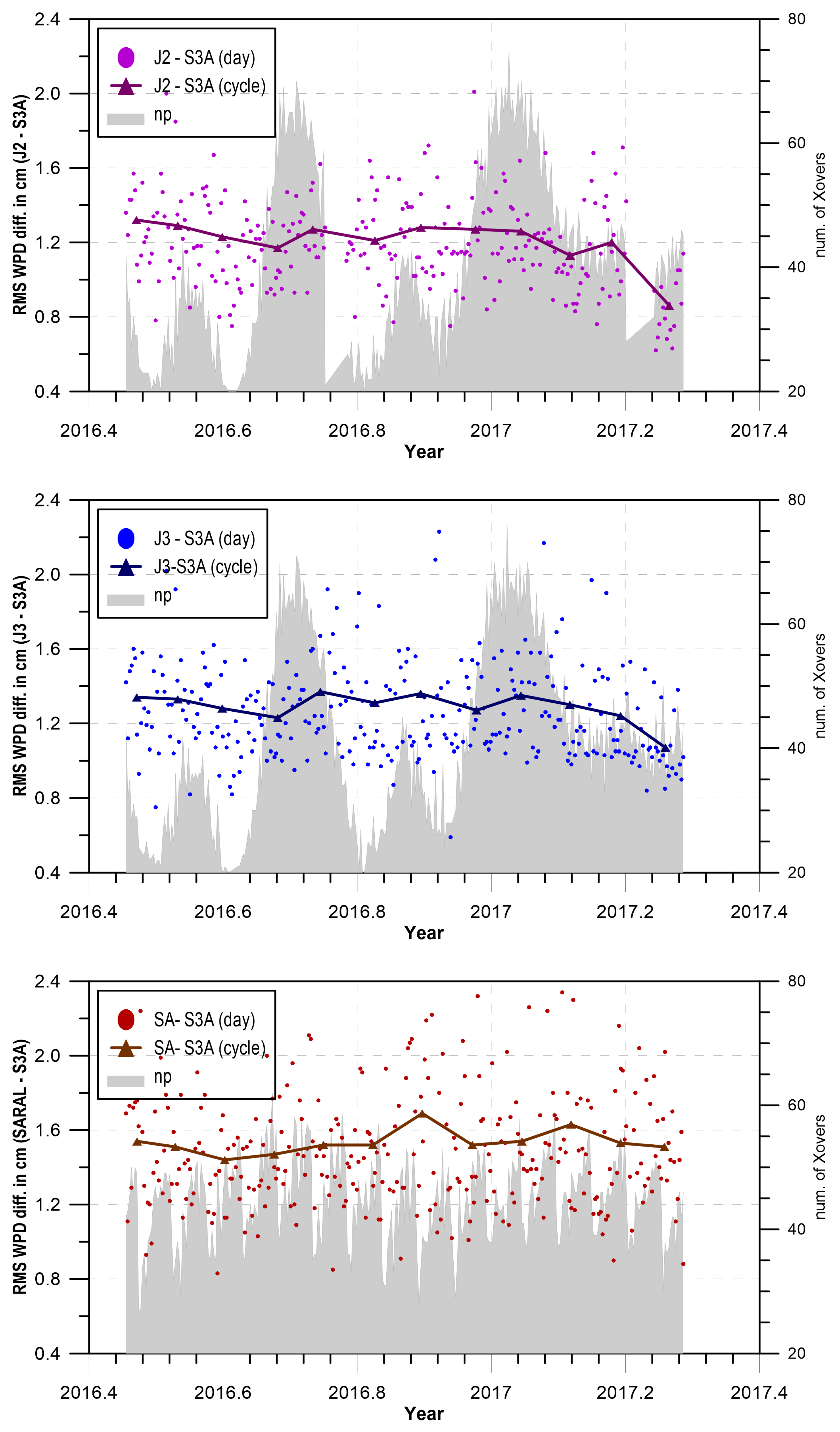
The time evolution of the daily and 27-day RMS differences between J2, J3, SARAL, and S3A illustrated in
Figure 10 indicates a stable behaviour of the Sentinel-3A radiometer with respect to these sensors.
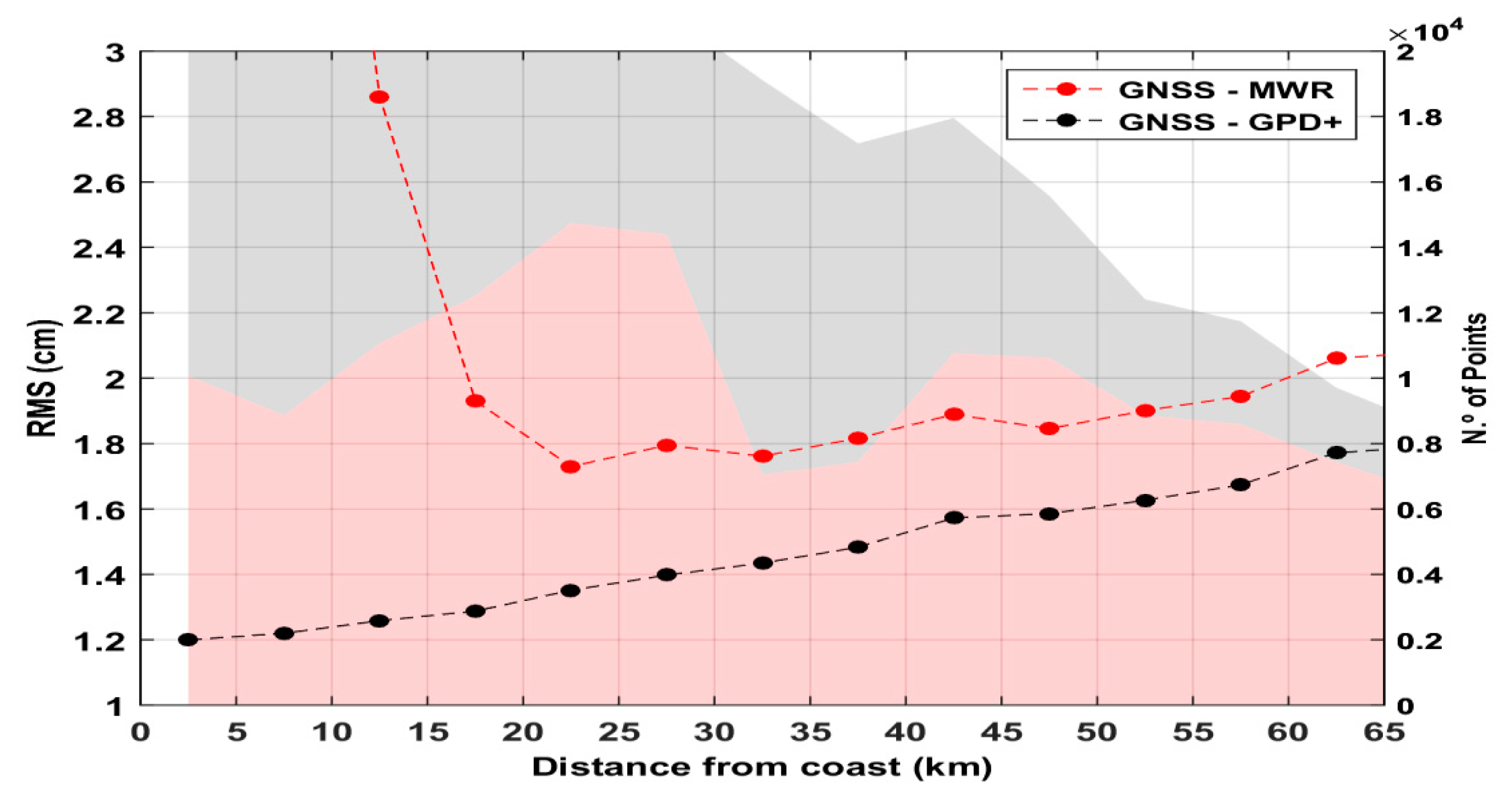
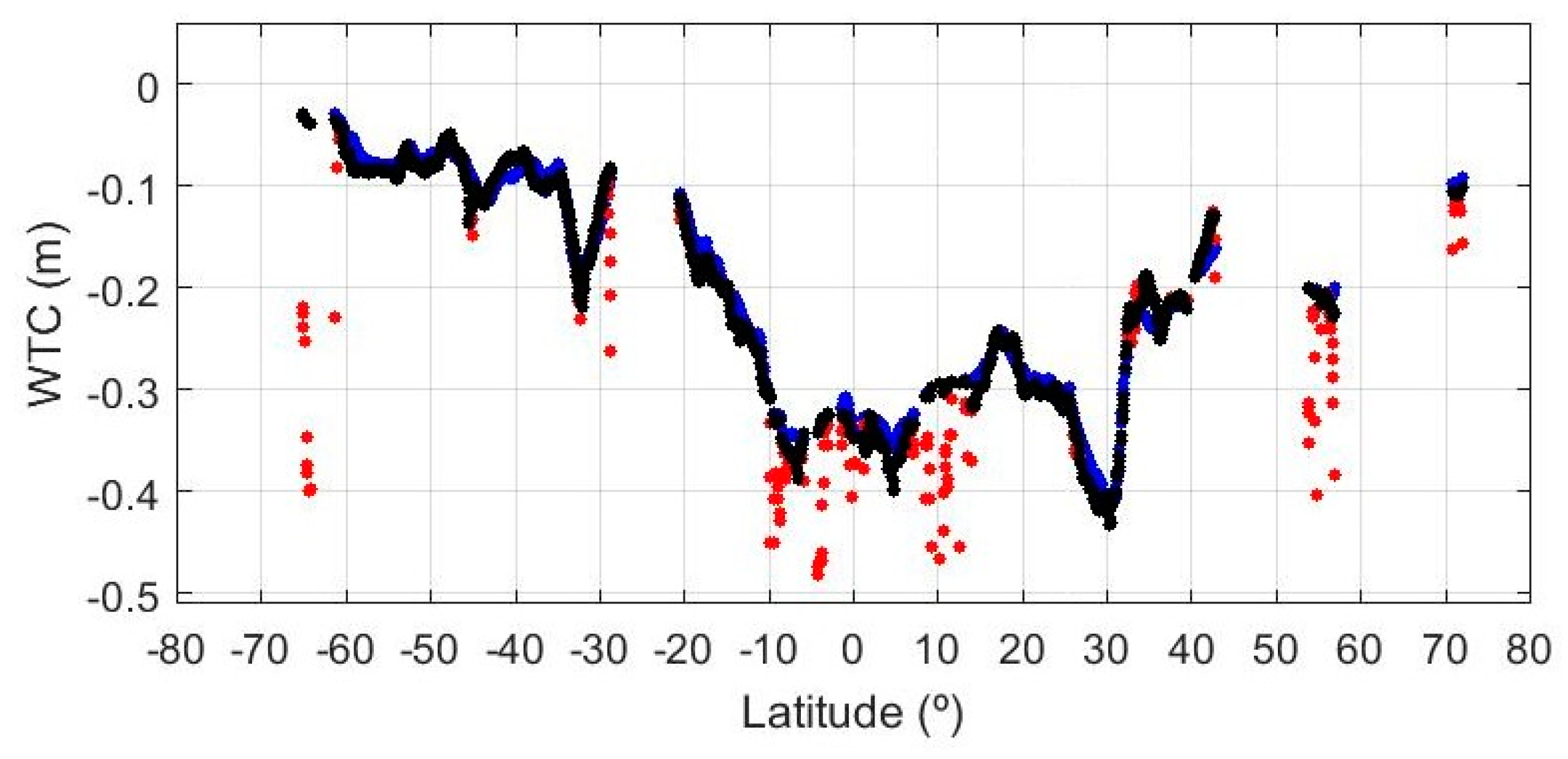
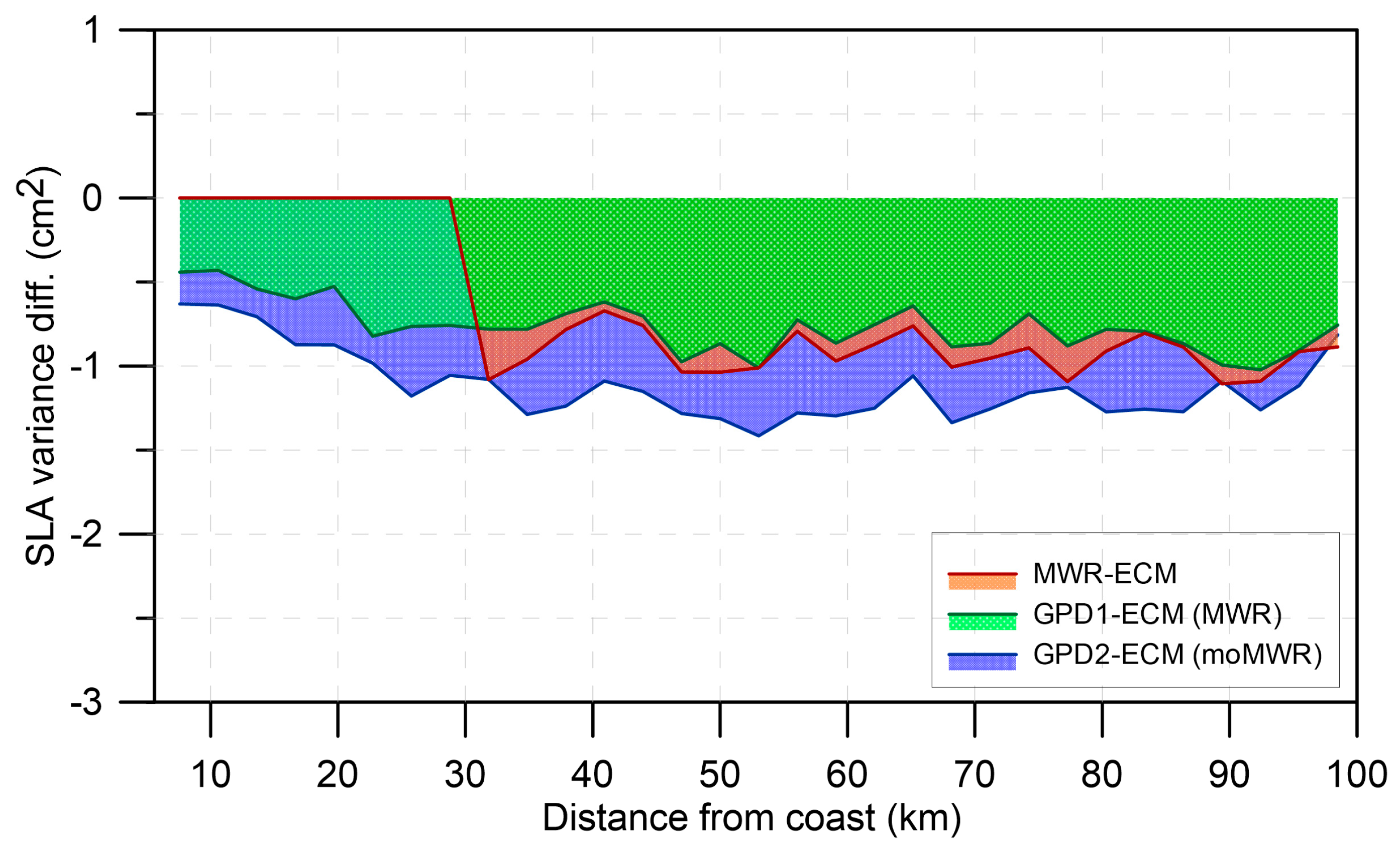
The comparisons with WTC derived at coastal GNSS stations show that land contamination can be observed in the S3A MWR observations up to 20–25 km from the coast. At this distance, the RMS of the differences between the WTC from S3A and the GNSS-derived ZWD is about 1.8 cm, increasing rapidly towards the coast, a clear indication that in the band of 0 km up to 25 km the MWR observations are not valid. On the contrary, no land contamination can be observed in the GPD1 WTC, derived solely from third party data. This stresses the need for robust criteria to remove the land-contaminated MWR observations and the important role of solutions such as GPD+ in providing valid WTC in the coastal regions.
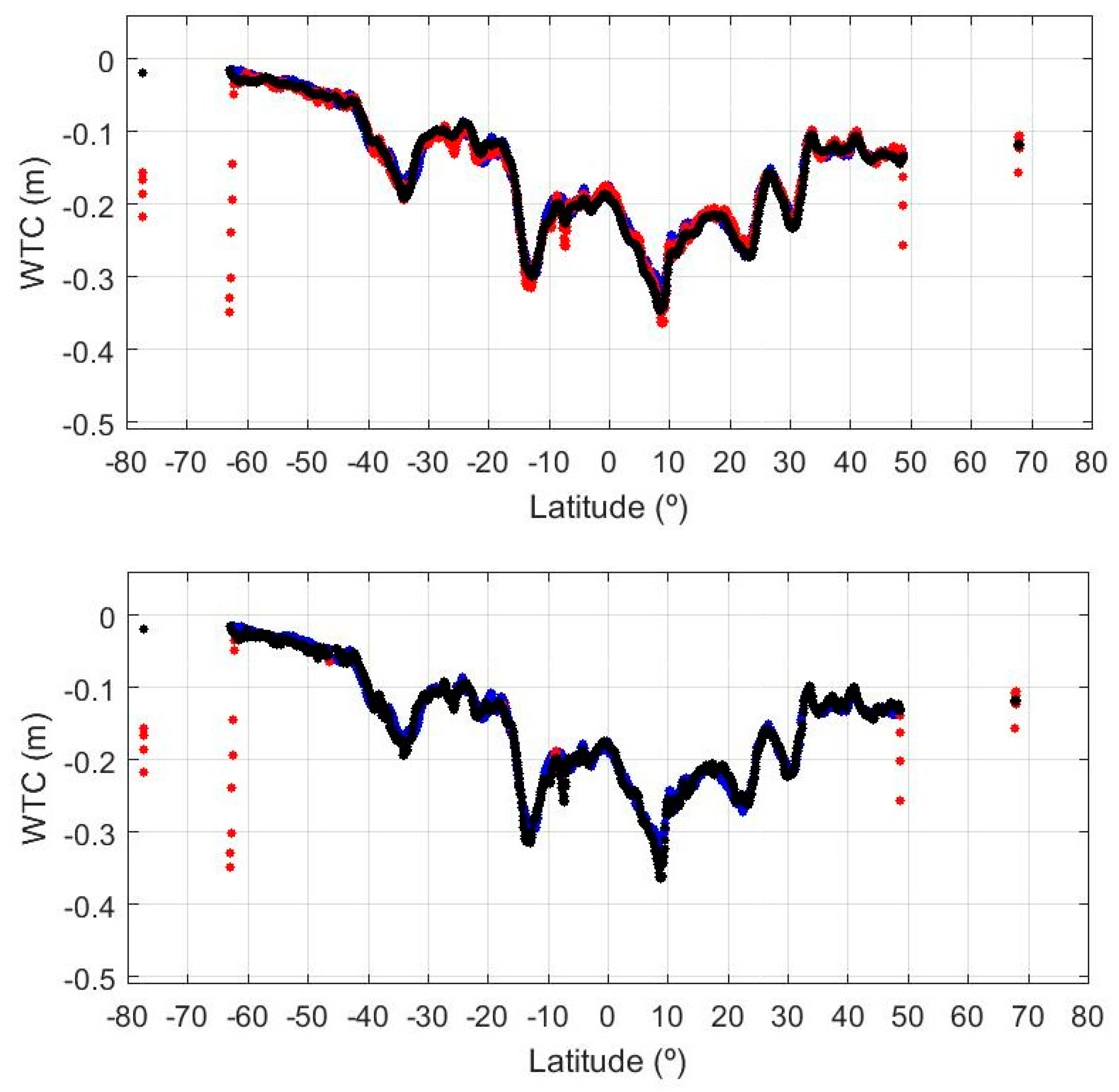
Section 3.3 presents an extensive comparison between the S3A WTC and various corrections: GPD1 (from the GPD+ algorithm using only third party data), GPD2 (from the GPD+ algorithm, preserving the valid S3A MWR observations), the ECMWF operational model, and the composite WTC. In
Figure 12 and
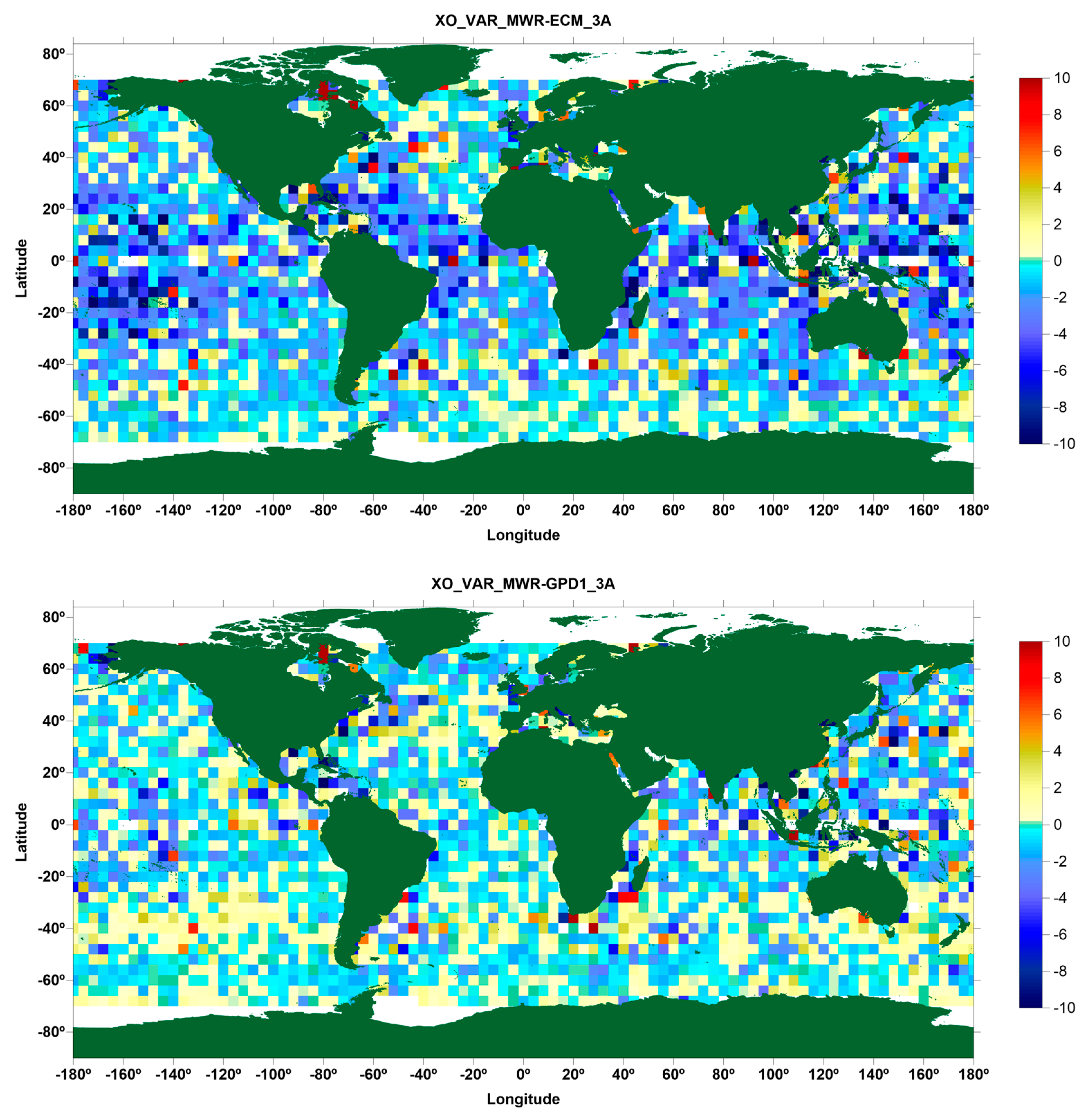
Figure 13, it can be observed that GPD1 and GPD2 are very similar, in spite of the fact that GPD1 does not use any observations from the S3A on-board MWR. It can also be concluded that, in regions with a valid MWR, the ECMWF operational model values are also very close, the main difference being that some, though important, small scale features are missing. These figures are clear illustration of typical S3A MWR-derived WTCs, where invalid observations can be observed near the coast, at high latitudes and at low latitudes, associated with heavy rain events.
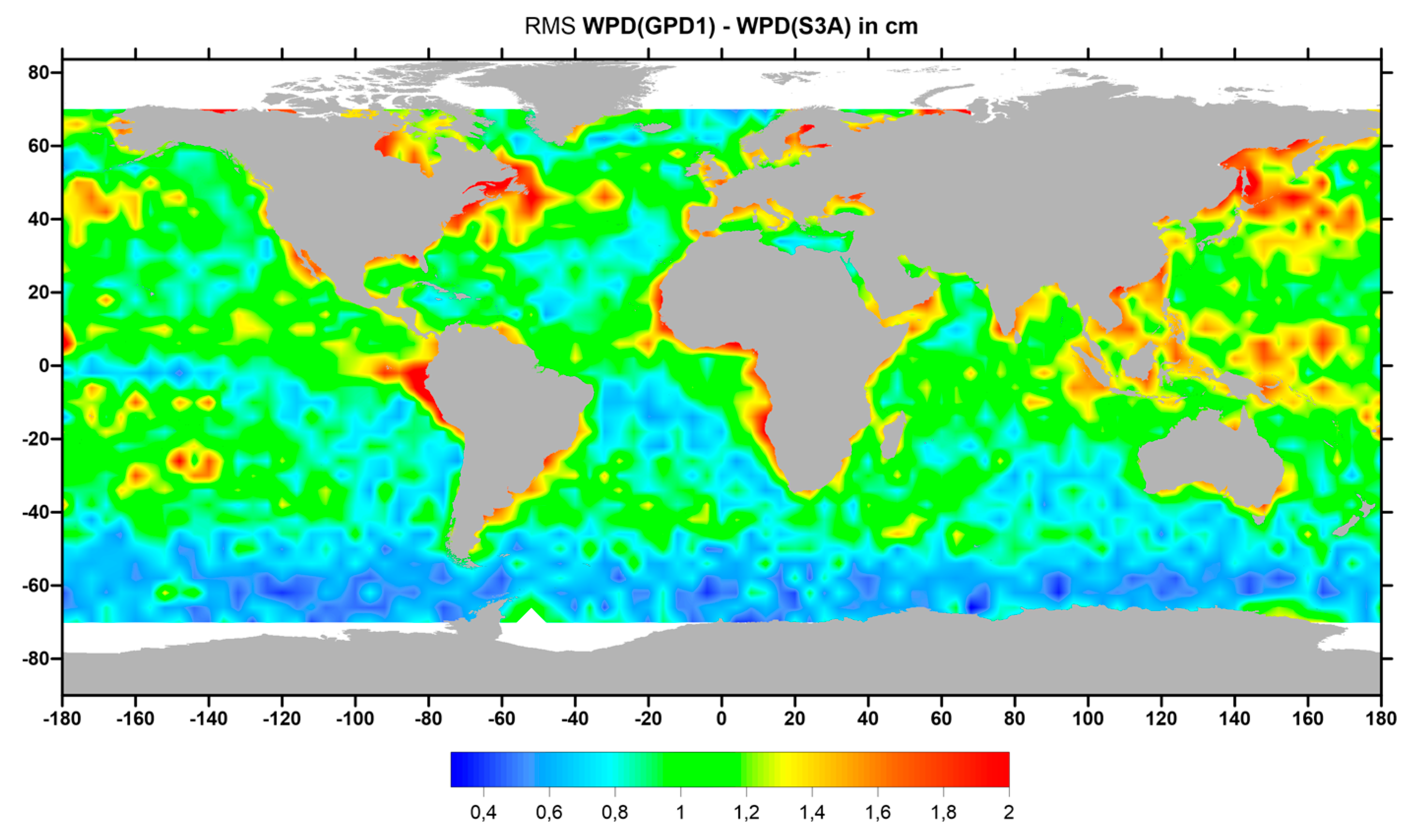
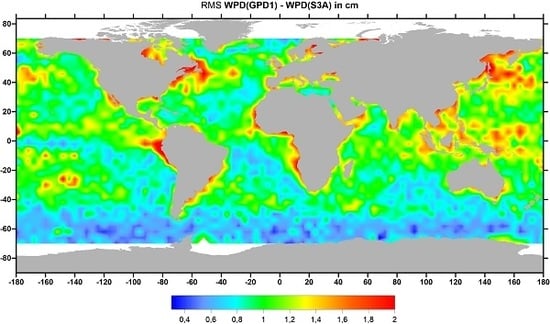
The spatial distribution of the RMS of WPD differences between GPD1 and S3A MWR for the whole period of study (cycles 05 to 16), shown in
Figure 14, indicates that the largest differences between these two WTCs are associated with regions with the largest WTC variability and ocean circulation patterns. Large differences also occur in some coastal regions, a possible indicator that some noisy MWR observations may still be present, in spite of the fact that all MWR measurements at distances from coast less than 30 km have been removed.
Both the statistical parameters in
Table 1 and
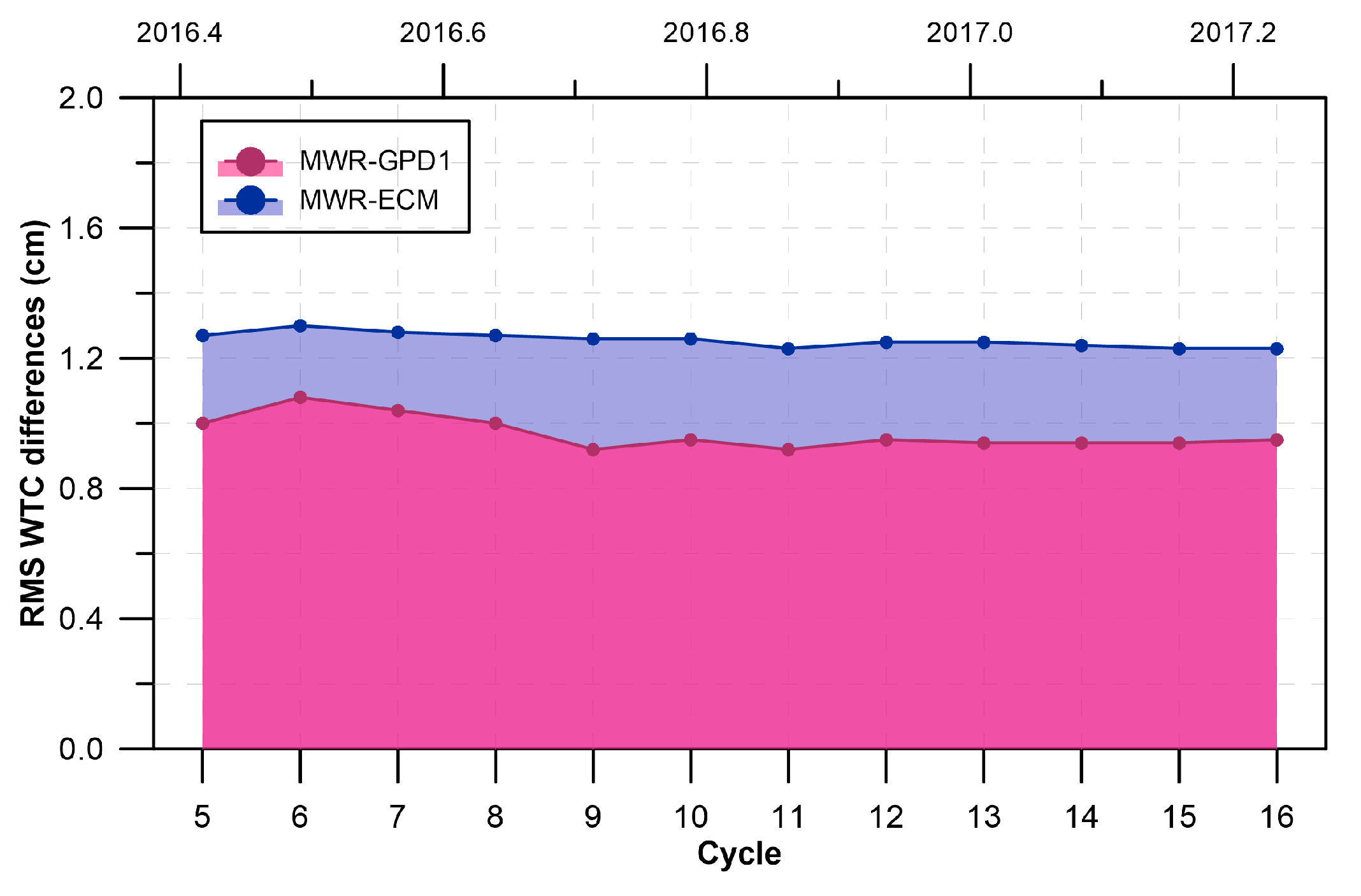
Figure 16 evidence that the S3A WPD is closer to GPD1 (RMS difference less than 1 cm) than to the ECMWF model (RMS difference 1.3 cm). The mean values of these differences are very small (0.1 cm and 0.2 cm for the comparison with GPD1 and ECMWF, respectively). The scale factors are both 1.01 and the offsets are also very small (0.2 cm, −0.1 cm). The time evolution of these differences, shown as 27-day RMS values in
Figure 15, is stable.
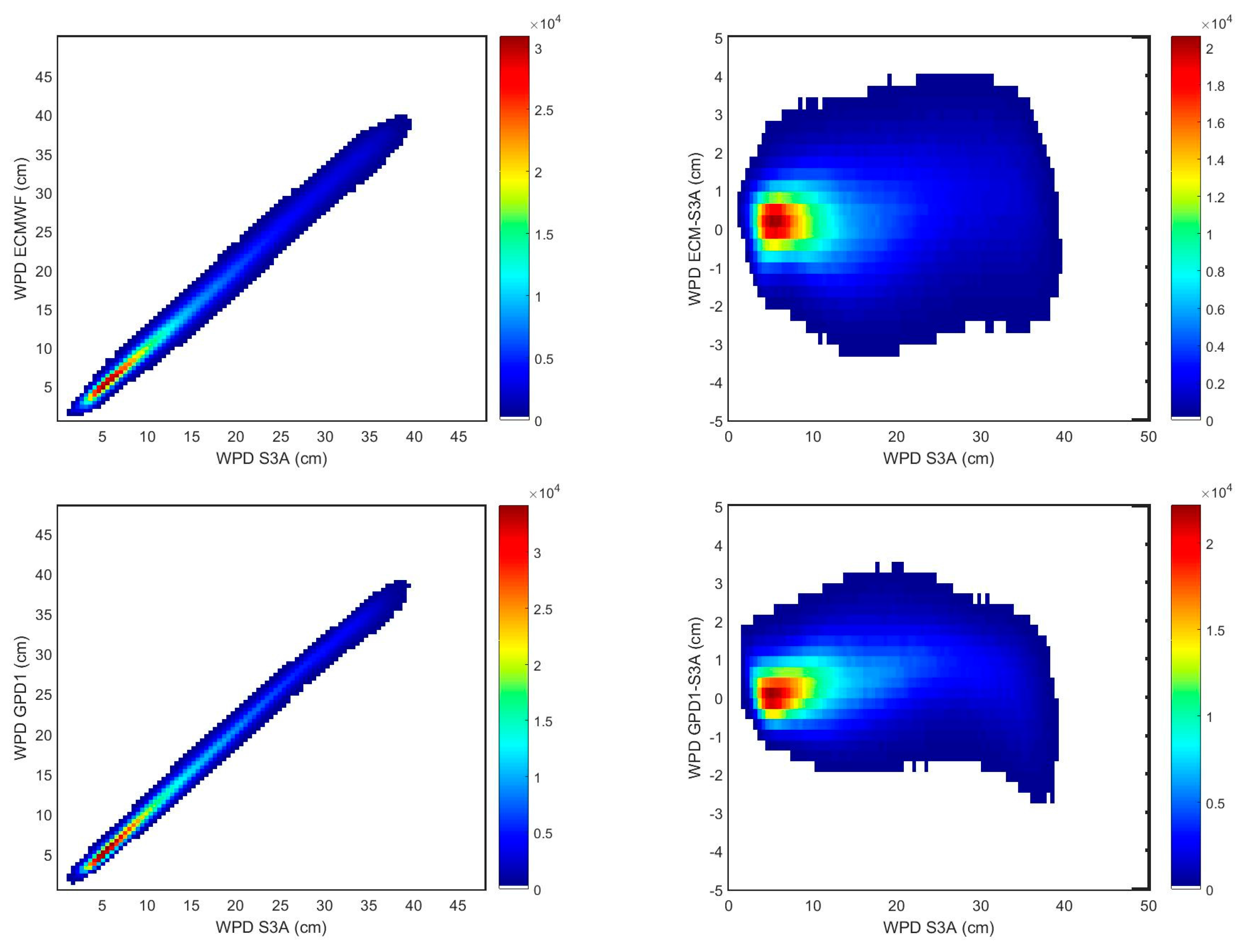
The better agreement of S3A MWR-derived WTC with GPD1 in comparison with the ECMWF model is also observed in the scatterplots of
Figure 16, where a smaller scatter can be observed for the former WTC pair. The better agreement of the S3A MWR with GPD1 than with the ECMWF model is explained by the fact that GPD1 WTC is also based on observations and the model has a poor temporal sampling of 6 h.
Figure 17,
Figure 18,
Figure 19,
Figure 20 and
Figure 21 present the assessment of the S3A MWR-based WTC by means of SLA variance analysis. In this analysis, the WTC from S3A MWR, GPD1, and GPD2 are compared against the ECMWF model. In this way, both the performance of each WTC with respect to this model and their relative performance can be analysed.
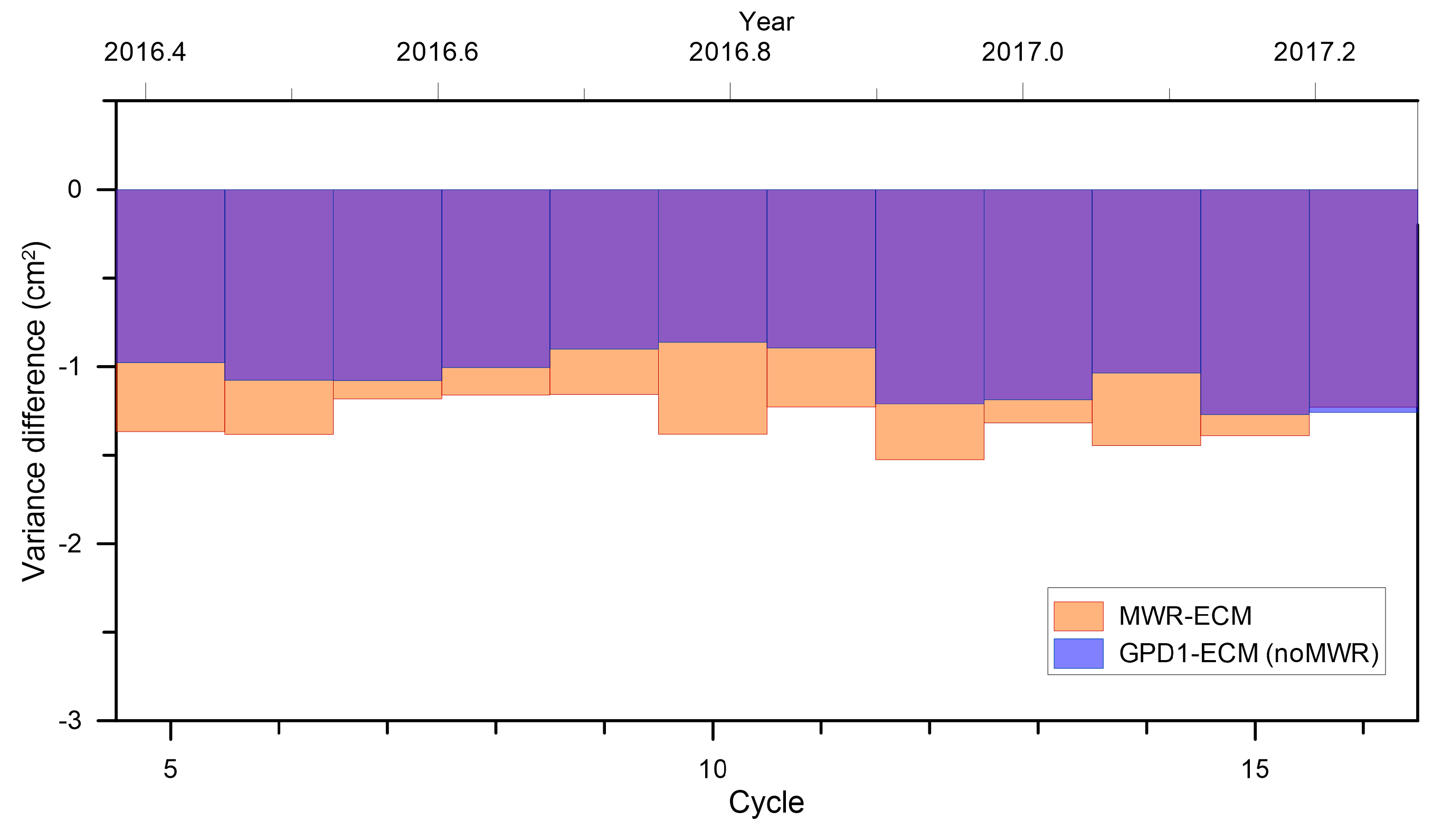
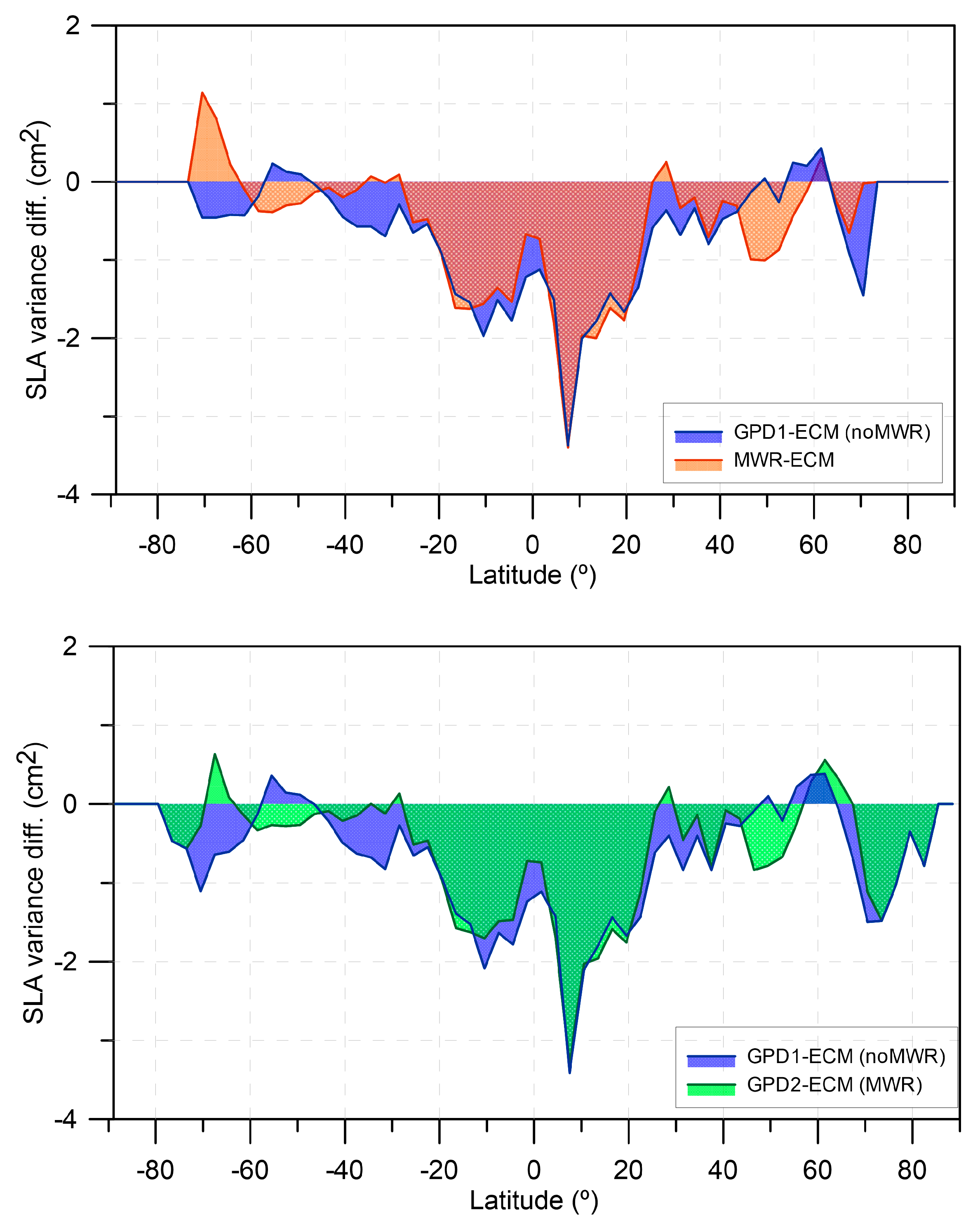
The SLA variance analysis at crossovers presented in
Figure 17 and
Figure 18 indicates that the S3A MWR reduces the variance both with respect to ECMWF and GPD1 (
Figure 18, top panel), the first reduction being significant (mean cycle values of 1.1–1.5 cm
2), while the latter (not shown, inferred from
Figure 18, top panel) is quite small (mean cycle values of 0.1–0.3 cm
2). The same is observed when comparing the performance of GPD1 and GPD2 against ECMWF (
Figure 18, bottom panel). GPD1 reduces the mean cycle variance by 0.8–1.4 cm
2 while GPD2 reduces by 1.0–1.6 cm
2. Note that the comparisons involving the MWR only use the valid MWR points, while the comparisons involving only GPD1 and GPD2 use all points with valid SLA.
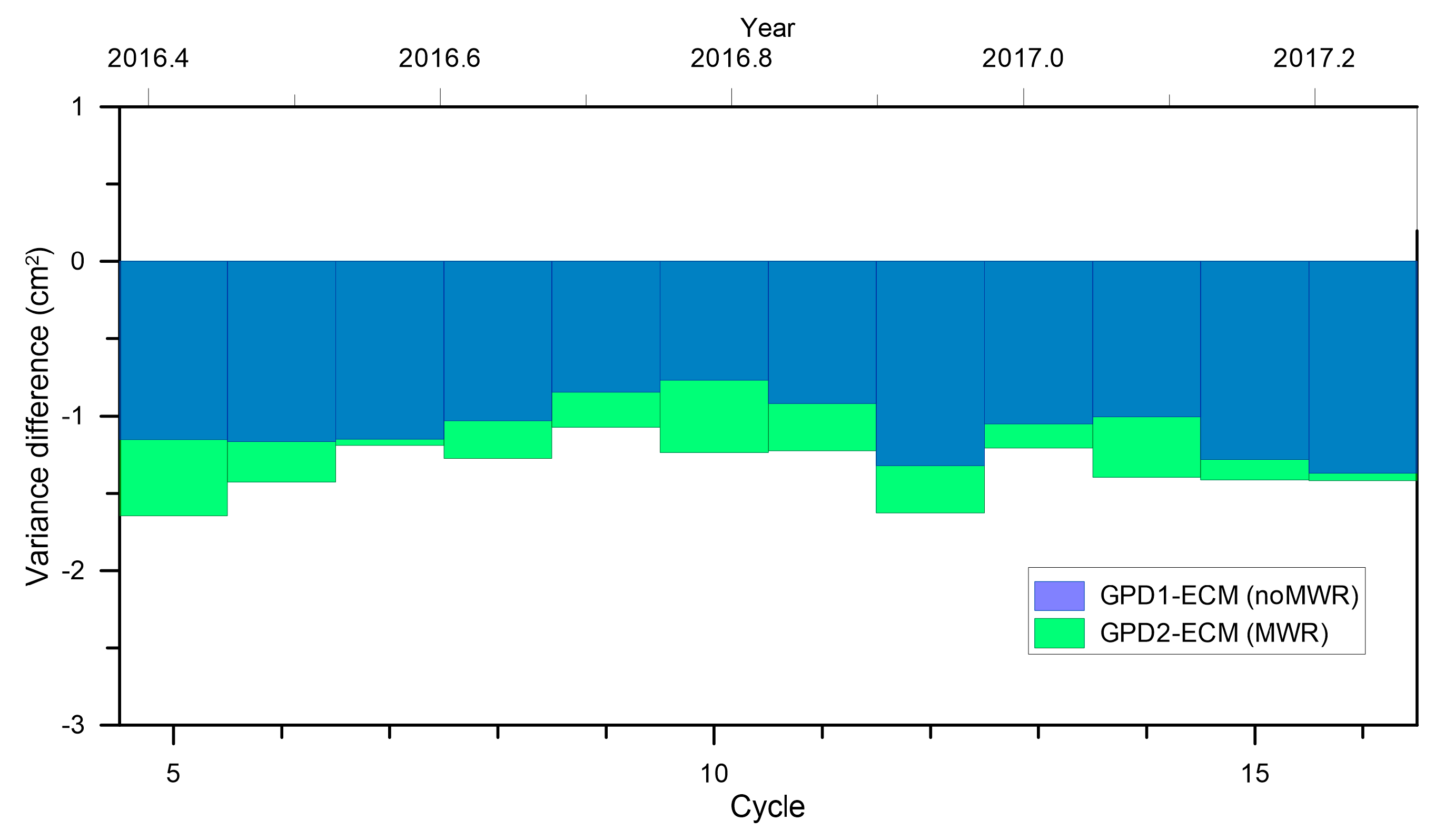
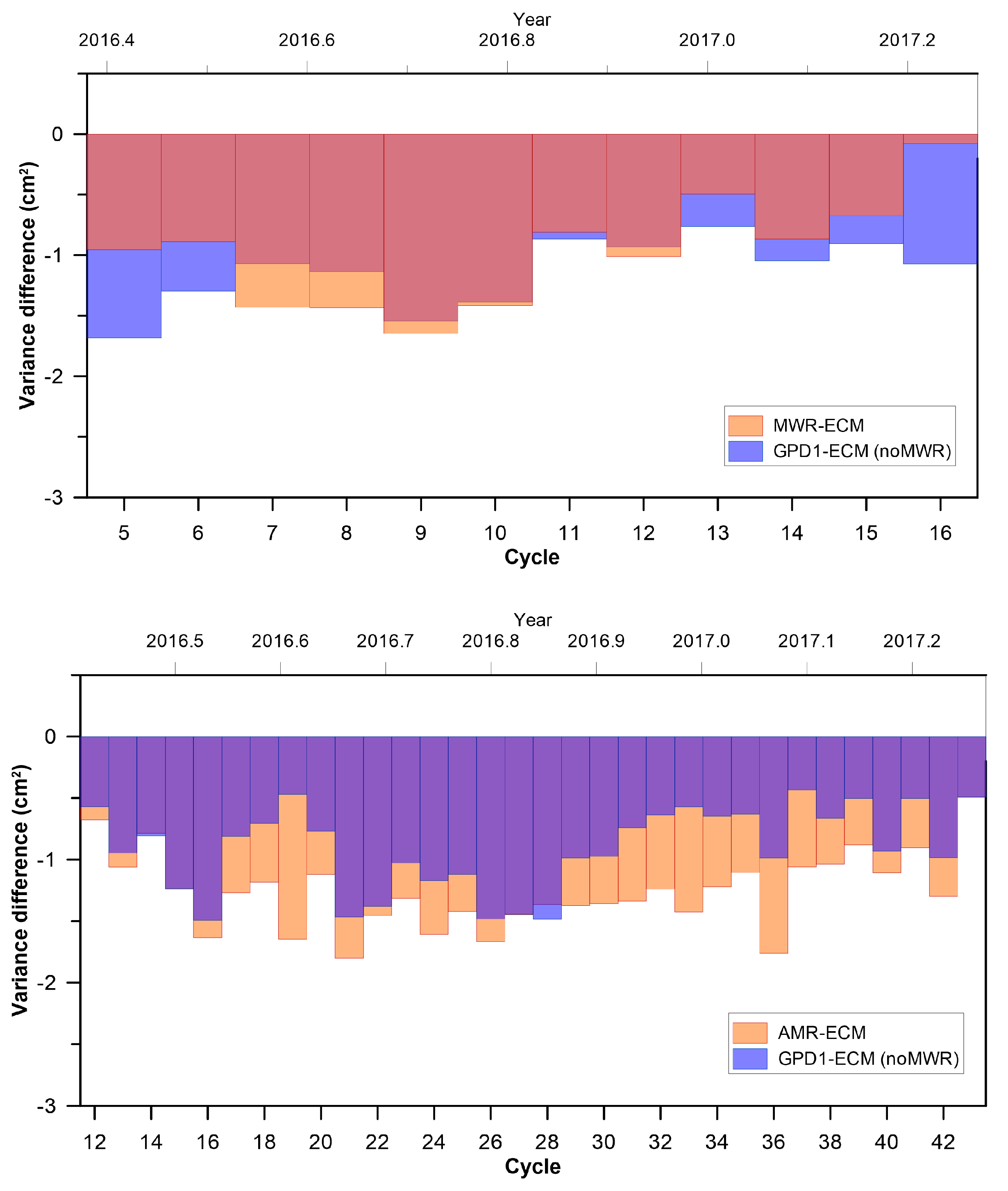
While the results from the variance analysis at crossovers indicate that the S3A MWR consistently reduces the SLA variance with respect to the WTC that only incorporates non-collocated radiometers (GPD1) and that the latter increases the variance with respect to the GPD+ WTC that makes use of the S3A MWR (GPD2), the same does not happen in along-track SLA variance analysis. In the along-track SLA variance differences, computed cycle by cycle (
Figure 19), in most cycles GPD1 leads to a slightly larger SLA variance reduction with respect to ECMWF than the GPD WTC that incorporates the S3A MWR (GPD2). This is also demonstrated in
Figure 20 and
Figure 21, which present the along-track variance differences in function of latitude and distance from coast, respectively. The top panel of
Figure 20 shows that, in comparison with the MWR, GPD1 conducts to a slightly larger variance reduction with respect to ECMWF, except for some high-latitude bands. The bottom panel of the same figure shows that, in comparison with GPD2, with the exception of some high latitude bands, GPD1 also leads to a slightly larger SLA variance reduction with respect to ECMWF. In the first comparison only valid MWR points have been used, while in the latter all points with valid SLA have been analysed. This result is more evident in the SLA variance analysis function of distance from coast (
Figure 21) where GPD1 consistently reduces the variance with respect to both MWR and GPD2.
This result is not expected since, in all previous analyses performed by the authors, the WTC derived from observations of the on-board MWR always reduced the SLA variance with respect to the WTC that only uses non-collocated observations, in all types of diagnoses and when only valid MWR points are selected. As an example, the bottom panel of
Figure 19 illustrates for J3 the same variance analysis shown in the top panel for S3A, for the same period, proving that, contrary to S3A, the J3 AMR-2 WTC is consistently better than that of GPD1. Similar results have been obtained for Envisat, confirming that the GPD+ WTC that incorporates the valid observations from the Envisat radiometer consistently reduces the SLA variance with respect to the correction that only uses third party observations. These results indicate that although the overall performance of the S3A MWR seems good, improvements are still required to retrieve a WTC with the quality of that for J3.
In the latitude plots (
Figure 20) some ice contamination can still be observed in the MWR-derived WTC and GPD2, suggesting that more robust editing is still desirable in the polar regions. We recall that a strong editing has already been performed by rejecting all MWR observations above latitude 70°N and below 70°S. Consequently, the preliminary version of the GPD+ WTC that makes use of the on-board MWR (GPD2) can still be improved, even with the present MWR dataset.
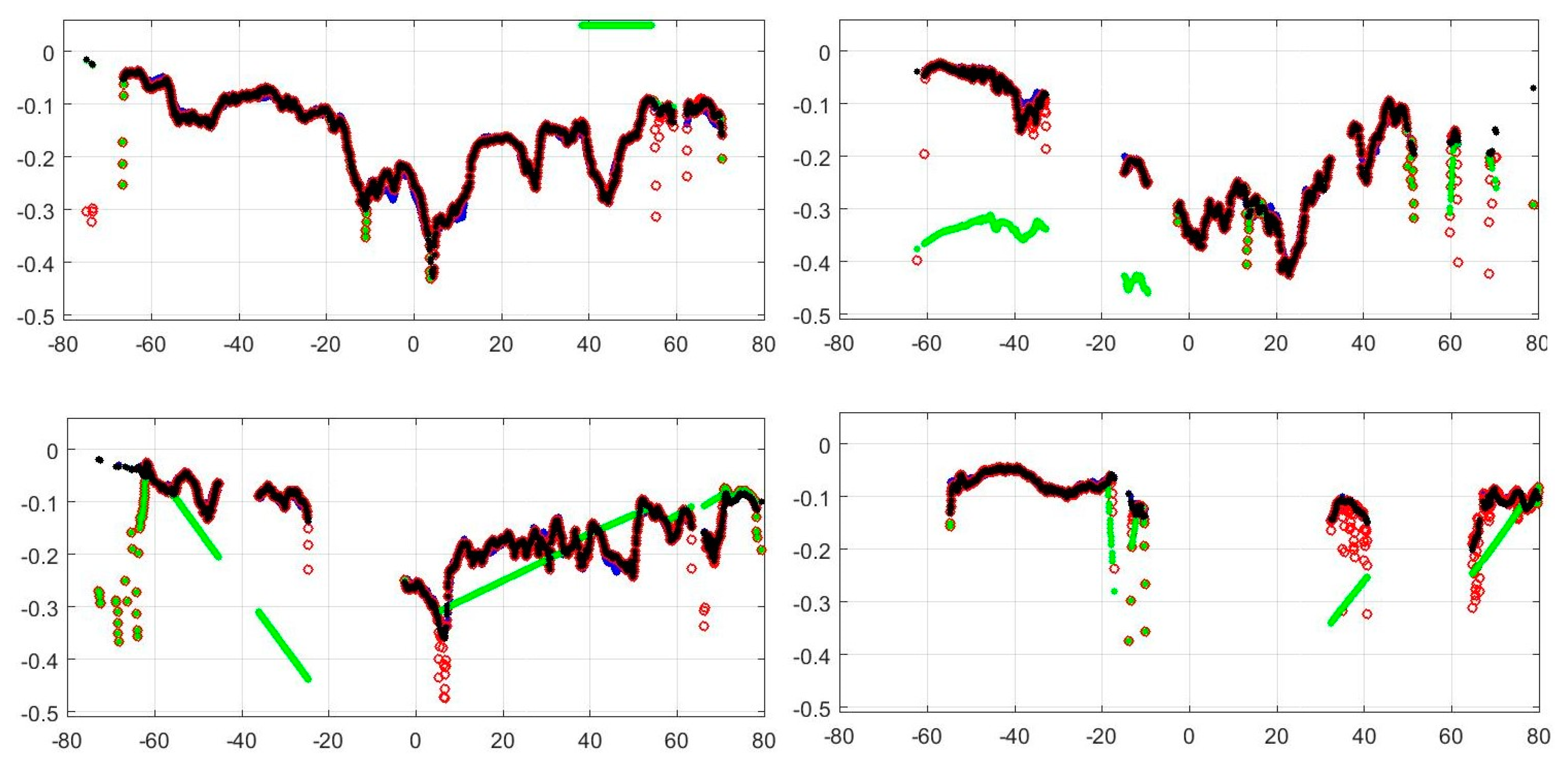
The examination of the composite correction present on the analysed S3A products shows that the implementation of this WTC still has serious problems, depicted in
Figure 22. Moreover, the correction is not present in a large percentage of points, e.g., 21% of the points with valid SLA for cycle 06. Similar to the GPD+ WTC, the composite WTC aims at generating a continuous correction, valid everywhere, including the coastal zones and high latitudes. Also, similar to the GPD2 type of correction described in this paper, it also preserves the valid MWR values. The main difference between GPD+ and the composite WTC is that, on every invalid point, the former retrieves a new estimate by data combination of all available observations, while the latter uses the model values, adjusted to the closest valid MWR points. This requires robust criteria to detect valid/invalid MWR values, otherwise the model will be adjusted to spurious MWR observations, resulting in large biases as shown e.g., in the bottom left panel of
Figure 22 or straight lines as shown in the right panels of the same figure. Similar behaviour has been observed, though in only a few occurrences, in the composite correction present in the Archiving, Validation and Interpretation of Satellite Oceanographic data (AVISO) Corrected Sea Surface Heights (CORSSH) products of TOPEX/Poseidon [
23]. Due to potential implementation problems and the fact that GPD+ use observations while the composite is solely based on model values, it has been shown that the GPD type of WTC is a significant improvement with respect to the composite WTC, particularly in the coastal zone [
9,
23].
5. Conclusions
This study presents an independent assessment of the wet tropospheric correction derived from the two-band microwave radiometer deployed on Sentinel-3A, present on the L2 NTC products from the “Spring 2017” Reprocessing Campaign”, Processing Baseline 2.15.
Studies such as this one play an important role in the improvement of altimeter-derived products, as satellite-derived data improvement is a long and continuous process. Sentinel-3 is a challenging mission in many aspects, with the research community having a long way to go to fully exploit the capabilities of its instruments, in particular SRAL. Six years after its end of mission, Envisat data are still being reprocessed and the reprocessing of TOPEX/Poseidon data has been delayed for several years.
Considering the relatively short time span of the dataset (10 months), the overall performance of the S3A MWR seems stable, with no drifts or irregular behaviour having been observed. A pronounced periodic signal has been observed in the differences with respect to GMI, due to the orbit configurations of the spacecraft housing these sensors.
When considering the linear adjustment of S3A MWR-derived WPD to those from four different sensors, scale factors very close to 1 have been obtained: GMI (1.00); J2 and J3 (1.11); and SARAL (0.96). The corresponding values for the WTC are the same since WTC is symmetric to WPD. All WPD offsets have absolute values of less than 1 cm: GMI (0.1 cm), J2 (−0.7 cm), J3 (−0.8 cm), and SARAL (0.6 cm). The corresponding offsets for the WTC are symmetric to those for WPD. The mean WPD differences have absolute values below 1 cm: GMI (0.2 cm), J2 (−0.6 cm), J3 (−0.7 cm) and SARAL (0.0 cm), the mean WTC differences being the corresponding symmetric values. RMS WPD (or WTC) differences (cm) of 0.95 (GMI), 1.3 (J2), 1.3 (J3), and 1.5 (SARAL) demonstrate a good agreement with all these sensors, in particular with GMI.
The comparison with GNSS shows land contamination in the S3A MWR observations up to 20–25 km and RMS differences between S3A MWR WTC and GNSS-derived ZWD of 1.8 cm at these distances. These results are in agreement with those found for the radiometers of other altimetric missions, for which the corresponding RMSs of differences are 1.7–1.8 cm [
43].
Extensive comparison has been performed with the ECMWF model-derived WTC and two WTC versions from the GPD+ algorithm: one using only third party data (GPD1) and another preserving the valid S3A MWR points (GPD2). Direct WTC comparisons show small statistical parameters for the differences between all these corrections. As expected, smaller RMS values have been observed for the differences with respect to the GPD+ WTC (1 cm for GPD1) than for the differences with respect to ECMWF (1.3 cm). The scale factors with respect to both GPD1 and ECMWF are 1.01 and both offsets and mean differences have absolute values smaller than or equal to 0.2 cm.
As expected, all SLA variance analyses evidence a reduction of 1–2 cm2 of the SLA computed with the S3A MWR WTC with respect to the ECMWF model, when mean cycle values are considered. The SLA variance analysis at crossover points indicates a small (mean cycle values less than 0.5 cm2) but consistent variance reduction with respect to GPD1, however, the opposite is observed in the along-track variance analysis. This seems to suggest that improvements in both the retrieval algorithm and the criteria used to detect valid/invalid MWR observations are required to achieve a WTC with accuracy similar to the AMR-2 WTC for Jason-3. These results also highlight that the along-track comparison with the GPD1 type of WTC provides complementary and very important insight into the quality of the S3A MWR-derived WTC, not evident in the assessment against the other.
Similar to other dual-frequency radiometers on board the previous ESA missions, strong ice and land contamination is observed, the former in particular making the establishment of validation criteria for the MWR observations difficult at the high latitudes. Consequently, all observations with latitude absolute values larger than 70° have been rejected.
The composite WTC present in the analysed products was revealed to have implementation problems and was unsuitable for use, improvements being required in future versions of S3A data.
As a whole, this study contributes to a better knowledge of the wet path delay affecting satellite altimeter observations. In spite of the good overall performance of the S3A MWR when compared against other state-of-the-art radiometers, current limitations are also identified. Once a tuned retrieval algorithm is achieved, meeting the state-of-the art performances of current and past similar instruments, the inability of this type of radiometer to measure over non-ocean surfaces such as e.g., land, ice, or wetlands, prevent its use in these regions. Therefore, in regions where accurate satellite altimetry measurements are of crucial importance such as coastal or inland water zones, and accurate MWR-derived WTC retrieval is not possible, alternative methods such as the GPD+ type of corrections must be used.
The GPD+ WTC solely based on third-party observations, together with microwave radiometers on board other altimeter missions and GMI, were revealed to be very useful and independent tools to validate the Sentinel-3 radiometer-based wet tropospheric correction. Future work includes the monitoring of upcoming versions of this dataset and generation of updated versions of the GPD+ WTC making use of ameliorated MWR data, which will contribute to the generation of an accurate version of this important range correction for S3A SRAL measurements over the whole ocean, including coastal zones and at high latitudes.
In regions such as coastal and continental water zones, radiometers with additional high-frequency channels, such as the one being built for Jason-CS/Sentinel-6 [
51] will provide smaller footprints, of great relevance for resolution of smaller scales of variability of the WTC.
Over inland water regions and to some extent in coastal regions, the availability of tropospheric corrections at high rate (frequency higher than 1 Hz), either from radiometers with smaller footprints or from high-resolution atmospheric models is also of great relevance, in particular in the exploitation of Sentinel-3 high-rate altimeter data. The advantage of having range corrections at a high rate applies not only to the WTC but also to the dry component of the tropospheric path delay, the dry tropospheric correction (DTC). In regions of sharp topography variations such as some steep coastal regions, lakes or rivers, one of the factors with most impact on the retrieval of accurate tropospheric corrections is their height dependence, particularly large for the DTC (1 cm per 40 m of height variation) [
13].
The future of tropospheric corrections for satellite altimetry includes: WTC from MWRs with additional high-frequency channels and improved retrieval algorithms (over the open and coastal ocean and over lakes); and WTC and DTC from high-resolution atmospheric models, both computed at surface height using accurate Digital Elevation Models (DEM) or the altimeter-measured surface height (over inland water regions). In all cases, high-rate (e.g., 20 Hz) corrections are desirable to better account for spatial variability of km order or less, in particular the variability associated with the surface height variations.