1. Introduction
As of 1997, about 37% of the global population was living within 100 km of a coastline [
1] and that number is still increasing. Coastal areas also contain a significant concentration of the world’s economic activities and urbanization. Climate change and related global warming are expected to cause sea levels to rise, forcing people to abandon certain coastal areas that may become submerged. Thus, accurate and effective monitoring of sea level change and its impact on social development is of vital importance.
Since the nineteenth century, tide gauges (TG) have been used to measure global sea level changes by providing a relative measure with respect to land [
2], but land motions around a land-based TG can result in inaccuracies in sea level measurements. Globally, there is also a decreasing number of TGs, thus limiting extensive sea level measurements. There is therefore a need for additional sea level monitoring techniques. Satellite radar altimetry is a powerful technique used for monitoring sea level changes [
3] and studying circulation [
4] in the open ocean. Radar altimetry provides high-precision sea surface topography data, but it often has poor precision in near-shore regions because of the complex and fast changing dynamics of the ocean in these areas [
5,
6]. Moreover, it is unable to provide information on mesoscale phenomena, such as swell and waves, which need better spatiotemporal sampling [
7].
Global navigation satellite system reflectometry (GNSS-R) was first proposed for use in ocean altimetry by Martin-Neira in 1993 [
8]. Over the last twenty years, this technique has been used to retrieve accurate sea surface heights from various ground-based and airborne platforms using an upward Right-Handed Circular Polarization (RHCP) antenna, a downward Left-Handed Circular Polarization (LHCP) antenna and a specialized receiver [
9,
10,
11,
12,
13,
14]. Space-borne GNSS-R altimetry has been used to retrieve sea surface height (SSH) data with an accuracy of ~7.0 m using data from the British TechDemoSat-1 (TDS-1) satellite [
15]. Both of these studies were conducted using a specialized setup, and most needed a customized GNSS-R receiver, which requires significant computing power and vast amounts of data for analysis.
Another ground-based GNSS-R altimetry setup consists of only one upward antenna and one geodetic receiver, which is the same as the GNSS positioning application. It is known as the Interference Pattern Technique (IPT) and measures the power and phase fluctuations of the interference of direct and reflected electric fields as the GNSS satellite moves [
16,
17].
Analysis of the multipath effect in GNSS observables allows the properties of the reflector surface to be inferred. Larson et al. [
18,
19] first proposed the positive use of multipath effects for retrieval of soil moisture data without modifying existing geodetic global positioning system (GPS) stations. Later, the same authors and Small et al. [
20,
21] expanded the application to estimate snow depth and vegetation by analyzing the signal-to-noise (SNR) data from the geodetic receiver. Some other studies using GPS L5, L2P, and L2C signals with a dipole antenna have also been tested [
22,
23,
24].
Ozeki and Heki [
25] first used GPS to measure snow depth by using geometry-linear combinations of carrier phases, and then Qian and Jin [
26] extended the combinations of carrier phases to GLONASS (Global Navigation Satellite System) signals for snow depth retrieval. Yu et al. [
27] proposed a new snow depth estimation approach using a linear combination of phase measurements of triple-frequency (L1, L2 and L5) GPS signals, because the inter-frequency ionospheric delay was contained in the dual-frequency phase combination.
Monitoring of sea level change is another application of this GPS multipath method. Several researchers have concentrated on the SSH retrieval technique using SNR data [
23,
24,
25,
26]. Santamar´ıa-Gomez et al. [
28] used both L1 and L2 SNR data at a tide gauge site with GNSS to estimate a leveling tie between the two instruments and hence, estimate the ellipsoidal height of the tide gauge datum. Jin et al. [
29] were the first to use BDS (Beidou Navigation Satellite System)-Reflectometry to estimate sea level change based on SNR and triple-frequency phase and code combinations. Strandberg et al. proposed a new method to retrieve sea level information from GNSS SNR data that relies upon inverse modelling of the detrended SNR, and the method was found to give an RMS error of 1.8 cm in the year of 2016 [
30]. However, SNR is not always available in the raw GPS data files because it was thought to be of little or no use to most users of GPS [
20]. Although L5 has been included in GPS, it is rarely included in the distributed data, such as in the public observation data of Plate Boundary Observation (PBO), and in the stations of the IGS (International GNSS Service) GPS network. Conversely, the combination of the two L-band carriers, L1 and L2, is always available and can be used to study multipath effects.
In this paper, the GPS observations from PBO station SC02 are used to test our algorithms. Data from this GPS station have been used by several previous researchers. Sea level changes were successfully derived for the first time from SC02 GPS data by Larson et al. [
31]. Lofgren et al. [
32] used a standard analysis method to derive the sea level variances based on one-year of GPS L1 data at this station. Larson et al. [
33] used SC02 GPS station data to assess the quality of ten years of GPS-derived water levels. Wang et al. used the GPS SNR data to derive the sea level at this station to verify their azimuth selection method. In order to verify the possibility of sea level retrieval using the L4 method, we also adopted this station as our test site [
34].The aim of this paper is to present a method for retrieving sea level change data based on geometry-free linear combinations of dual-frequency carrier phase observations. At the same time, the SNR data from dual-frequency signals are also analyzed for extensive comparisons. The reminder of this paper is organized as follows: In
Section 2, the methods of ground-based GNSS-R altimetry retrieval using the GNSS multipath effect are described in detail. In
Section 3, an overall introduction to the experimental data and data processing strategies is provided, and the results of a data comparison with a nearby TG are analyzed. Finally,
Section 4 and
Section 5 provide a discussion and conclusion of the study, respectively.
2. Methods
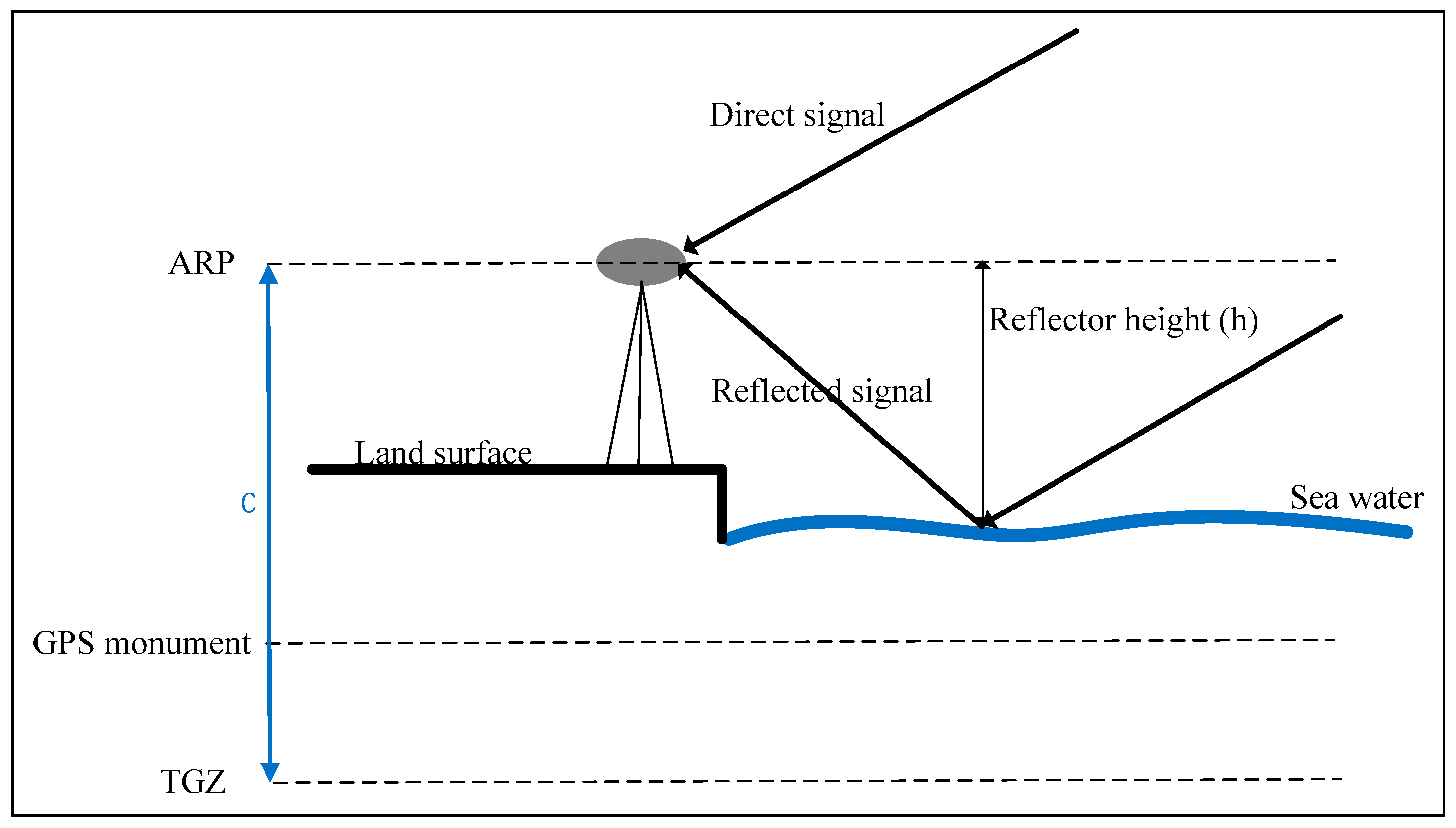
Figure 1 illustrates a scenario where direct and the reflected signals from the sea surface arrive at the zenith-facing GNSS antenna. It is shown that the antenna height above the sea surface is reduced by rising sea levels, and vice versa. The point in the GNSS antenna where the signals are detected is the antenna phase center (APC), the location of which is defined with respect to the antenna reference point (ARP). The vector between the averaged APC and the ARP is the modelled antenna phase center offset (PCO). The GNSS data used in this paper are all at low elevation, and the vertical errors caused by PCO are in the millimeter range. As a result, these effects will not be considered further in this paper. The geodetic height of the antenna can be obtained with high precision using Precise Point Positioning (PPP) or other geodetic positioning methods, and the vertical distance between the ARP and the specular point can be estimated by our approach described in the following parts of this paper. Then, after subtraction of the geodetic height of the antenna and the vertical distance is performed, the absolute sea surface height can be estimated.
The algorithm theories used for retrieval of the antenna height from the sea surface using GNSS SNR, and the phase combination can be found in the literature [
26,
27] and, for convenience, these are briefly summarized in the next section.
2.1. Fundamentals of the GNSS-R Altimetry Using the Multipath Effect
Scattered GNSS signals from the ocean surface in the vicinity of the GNSS antenna will interfere with the direct signal, thus contributing to the measured phase, power and amplitude [
35]. According to [
27,
36], when only the specular reflection path is considered, the sum of the direct and reflected signals is given by
where
where
Ad and
Am are the amplitudes of the direct and reflected signals, respectively, and
δφ(
t) is the phase caused by the excess range of the reflected signal compared with the direct one. The factors
A and
represent the amplitude and phase of the composite signals received by the antenna, and
ψ(
t) represents the phase of the direct signal. The factor
β(
t) is the composite excess phase with respect to the direct phase,
h is the vertical height between the antenna and the sea surface,
θ is the satellite elevation angle and
λ is the electromagnetic wave length of the GNSS signal.
2.2. Sea Level Based on SNR Data
The values of SNR in decibels (dB) for the GNSS signals can be found from some of their RINEX (Receiver Independent Exchange Format) observation files. SNR refers to the ratio of signal power to noise power, and although the reflected signals will be suppressed by the antenna gain of geodetic GPS receivers, it can still be received at low satellite elevation angles (<30°).
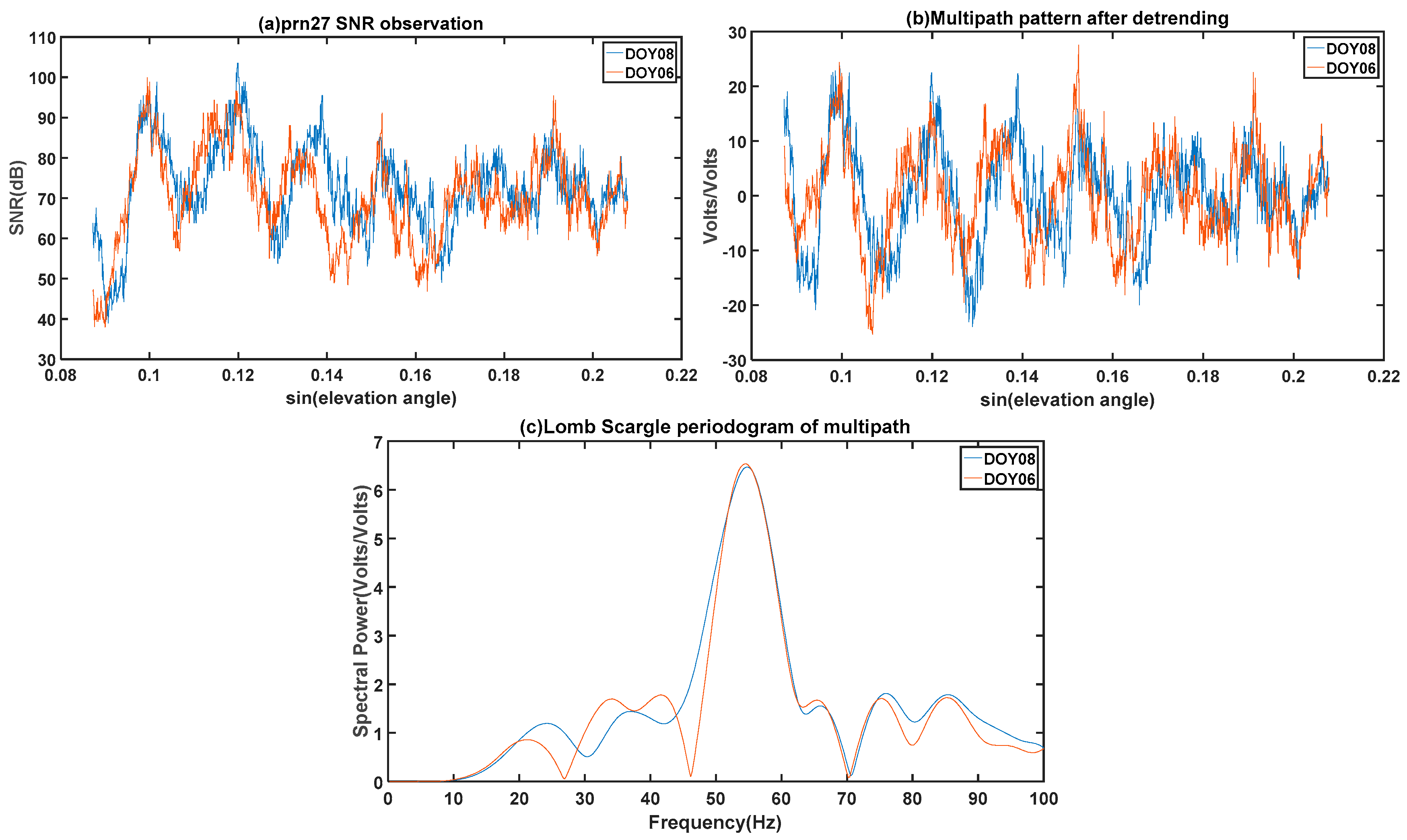
Figure 2a shows the oscillations of the SNR data from the SC02 GPS station of the PRN27 satellite on 6 and 8 January 2015 with the sinusoidal values of the satellite elevation angle. The oscillations of SNR are caused by multipath effects.
The signal power is expressed in the form of the squared amplitude of the receiving signals, and therefore the SNR is calculated as follows [
27]:
where
Pnoise is the noise power. In order to solve for reflector height (
h), it is necessary to isolate the last item from Equation (6) by removing the first two items using a fifth-order polynomial detrending. The detrending of the
SNR becomes
According to Equation (7),
dSNR is a quasi-sinusoidal function, oscillating with the sine of the elevation angle at a frequency of
f = 2
h/
λ.
Figure 2b shows the
dSNR sequence for the PRN 27 GPS satellite with the trend removed. After obtaining the dominant multipath frequency of the detrended SNR data by Lomb–Scargle Periodogram (LSP) spectral analysis (see
Figure 2c), the reflector heights can be calculated as follows:
It should be noted that the multipath pattern is expressed as a function of the sine of the elevation angle, not time (t). The SNRs are evenly sampled in time, but not as a function of the sine of elevation. Thus, spectral analysis is usually performed using the LSP or wavelet analysis, because these methods can handle an unevenly spaced sampling sequence. The reflector height is negatively correlated with sea level, and the sea surface heights can be obtained from the vertical difference between the geodetic height of the receiver antenna and the estimated reflector heights.
2.3. Sea Level Based on Carrier Phase-Combination Measurements
For carrier phase observables, it is difficult to isolate the multipath from several other effects, such as the satellite–antenna pseudorange, ionospheric and tropospheric delay. However, when considering the multipath, the carrier phase contains two quantities: the phase of the direct signal and the composite excess phase with respect to the direct phase, as shown in Equation (3). Thus, the GNSS phase observation for carriers L1 and L2 can be expressed as
In GNSS positioning, the carrier phase of the direct signal can be expressed as
where
i = 1 or 2, which stands for the two signals of different frequencies. The geometric distance between the GNSS satellite and antenna is represented by
ρ, and
Ii represents ionospheric delays.
T represents tropospheric delays, and Δ accounts for all other carrier-independent effects. To isolate the multipath, the L1–L2 combination of carrier phase measurements, shown in Equation (12), is used. For simplicity, this combination is referred to as L4 in this paper.
Some measurement errors can be eliminated in Equation (12), including clock errors and tropospheric delays. Meanwhile, the geometric distance between the GNSS satellite and antenna is eliminated because of the subtraction of carrier phase measurements with two frequencies. Thus, L4 is also known as the geometry-free linear combination of the carrier phase. However, the ionospheric delays are related to the signal frequency, so they cannot be eliminated using this combination. According to [
37], ionospheric delays are first order phenomena that are inversely proportional to the square of the frequency. Ionospheric delays in the L1 or L2 carrier phase signal can be expressed as the first two items [
38] in Equation (13),
where
TVEC is the total electronic density. From Equation (13), it is evident that the L4 data contain two kinds of effects. One is the change from ionospheric delay, and the other is from the multipath. To analyze the multipath, the ionospheric delay should be eliminated. Considering the magnitudes of the items in Equation (13), a high-pass filter can be used to remove the ionospheric error components. A 10-degree polynomial fit was adopted in this paper, such that
can be determined as follows:
In general,
x =
ε when tan
x =
ε and
ε ≈ 0. Making use of this approximation, and in the case of
AmAd, after substituting Equations (4) and (5) into Equation (14), Equation (14) can be further simplified as follows:
According to Equation (14),
dL4 is the linear combination of two quasi-sinusoidal functions, oscillating at the sine of the elevation angle with a different frequency of
fi = 2
h/
λi. Similar to the SNR method, a spectral analysis, such as LSP, is used to deal with the
dL4 data because of the irregular sampling intervals of sin
θ. As
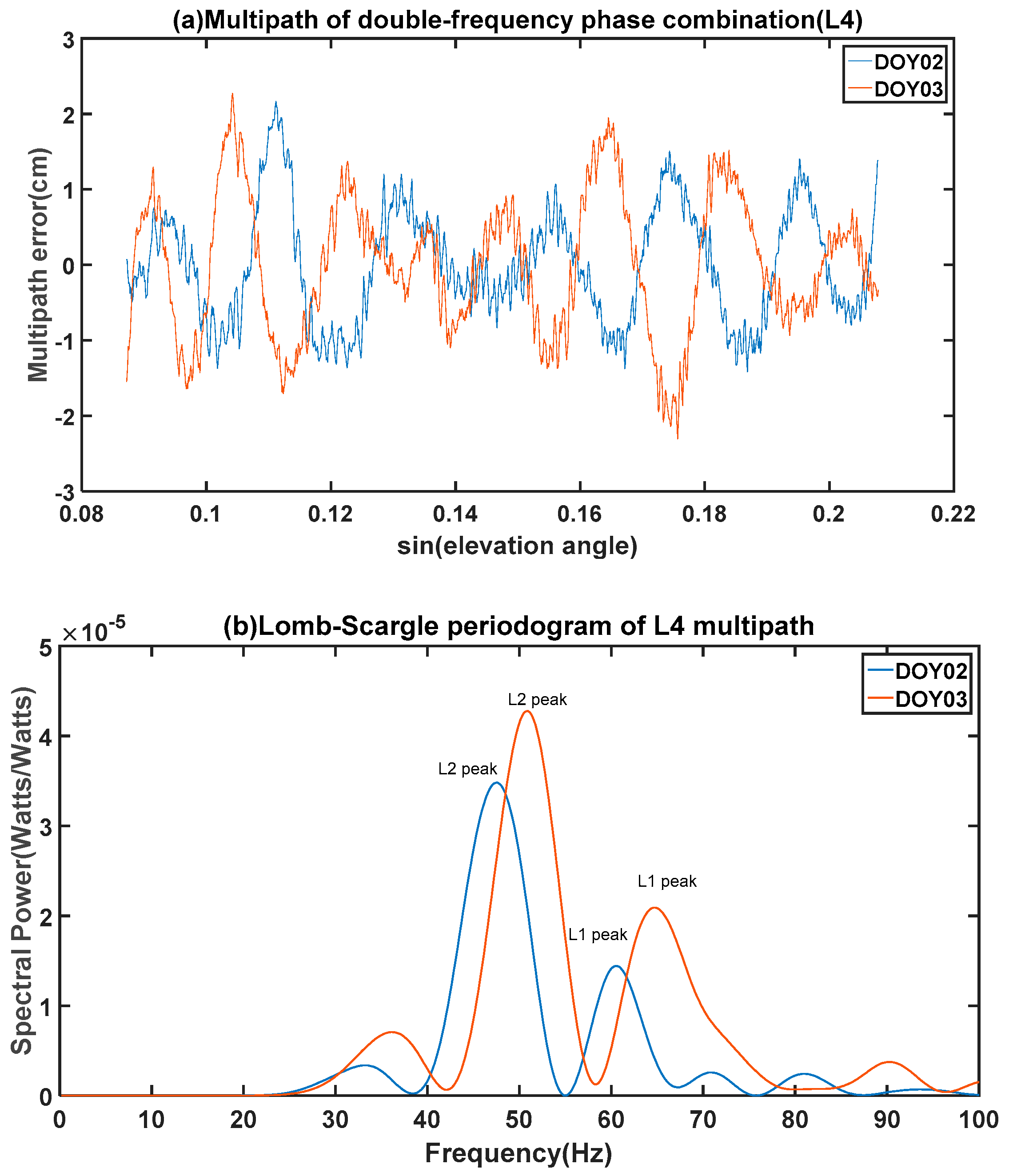
dL4 is the linear combination of L1 and L2, shown as a linear combination of two quasi-sinusoidal functions in Equation (15), there will be two peaks in its spectrogram (
Figure 3b,d). The peak at the lower frequency is caused by L2, and the peak at the higher frequency is caused by L1. Their different frequencies depend on the carrier wavelengths, and L2 peaks are usually used because they show clearer spectral peaks than L1.
2.4. Theoretical Model for Calculating Reflector Height
The values of peak frequency from the spectral analysis based on SNR and geometry-free linear combinations of the carrier phase can be determined using the methods described in
Section 2.2 and
Section 2.3. The peak frequencies for L4 are determined from the
dL4 sequence using LSP, and they consist of two components with different frequencies. There is an interaction between the two different frequencies; thus, peak frequencies will contain some errors. Therefore, the reflector height usually cannot be calculated accurately using Equation (8).
To address this problem, the relationship between the multipath signature peak frequency and the reflector height can be established using a theoretical model [
25,
27]. First, the dL4 for different reflector heights are computed using Equation (14) using simulated carrier phase multipath errors [
39]. Then, a series of spectral peak frequencies, which vary with reflector heights, can be determined using LSP. A linear relationship between them can be established as follows:
where
a and
b represent constants,
f is the peak frequency determined from the spectral analysis and
h is the reflector height.
The L1, L2 and L4 carrier phase multipath errors are simulated using forward modeling of the GPS multipath, as proposed by Nievinski and Larson [
39]. This simulator is mainly used in multipath research to simulate the multipath error in GNSS SNR, carrier phase and code pseudorange observables. Different surfaces, including soil, snow and seawater, and different antenna types and orientations, together with polarization and coherence, are considered. The surface height standard deviation also serves as a parameter when considering the loss of coherent power in the simulator, which may be of importance for multipath research into rough surfaces, such as the ocean surface.
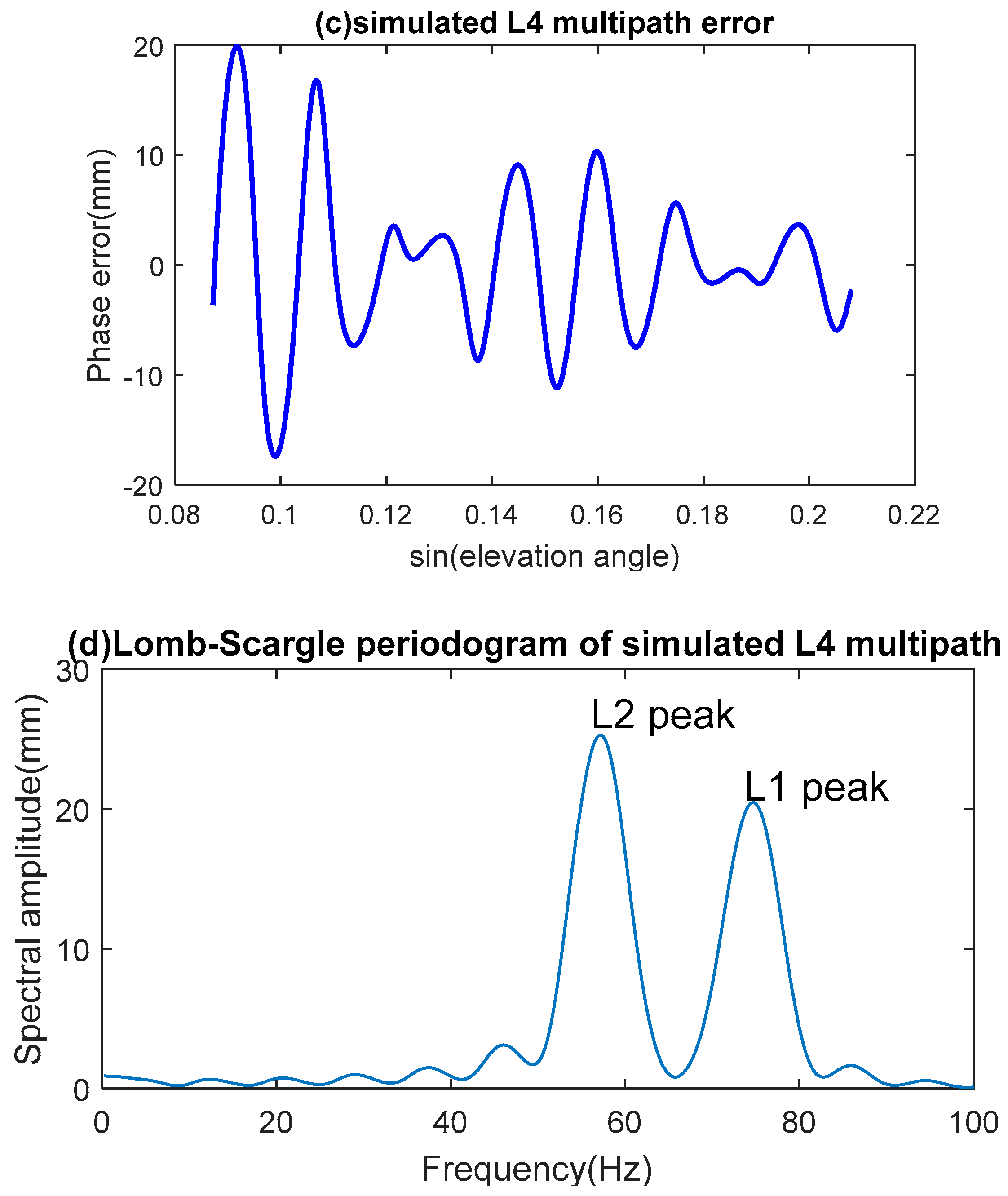
The simulated results are shown in
Figure 3c,d, in which two peaks in the LSP signature are clearly evident. These peaks were derived from the modeled L4 multipath pattern, and can also be seen from the observed data shown in
Figure 3a,b. The modeled data are almost identical to the simulated results shown in
Figure 3c,d.
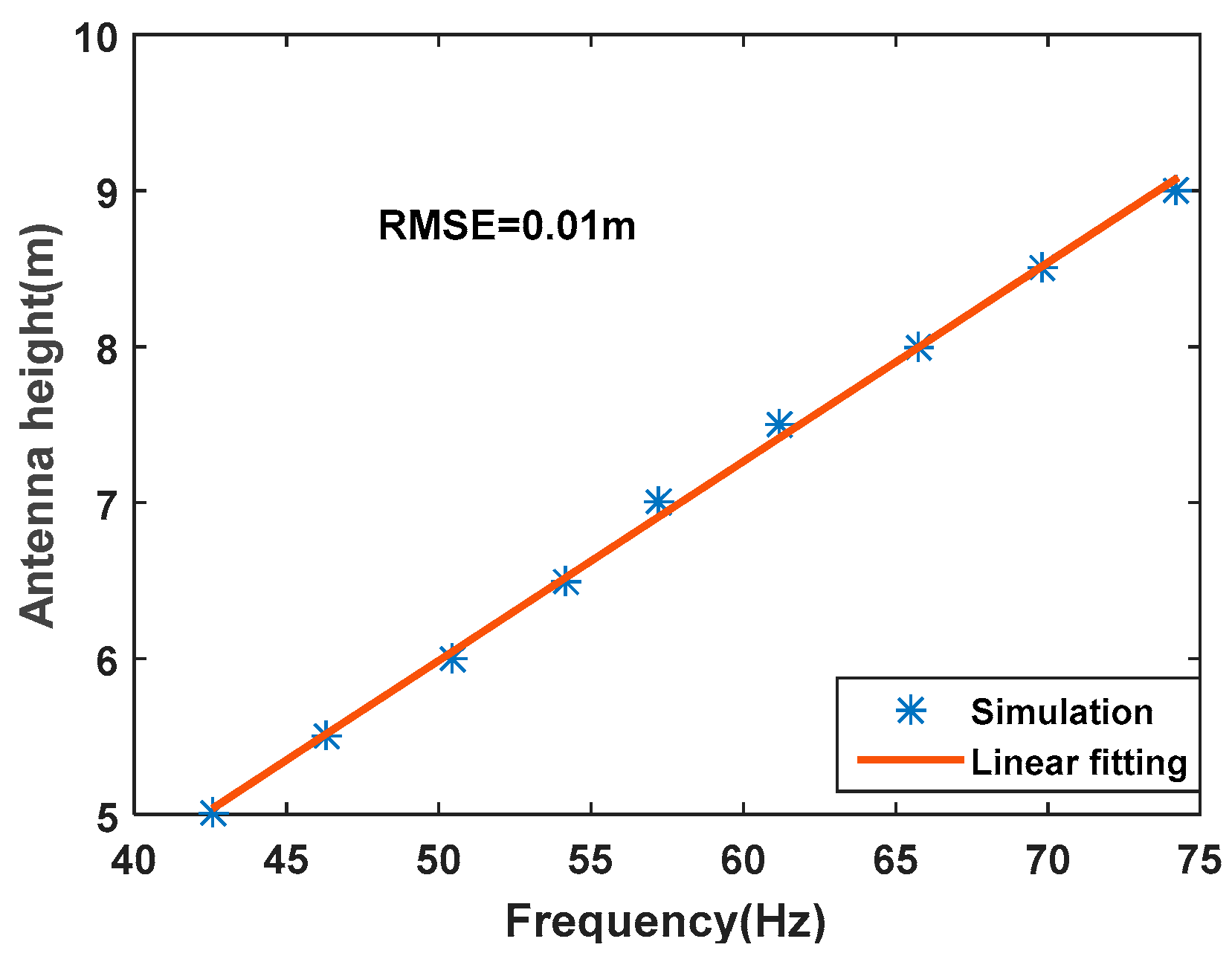
Simulation results for the relationship between antenna height and peak frequency are shown in
Figure 4. It is evident that the antenna height can be well-modeled as a linear function of the spectral peak frequency within specific elevation ranges. For (5–12°) and (5–15°), they are as follows:
Equation (17) is obtained from simulations of the particular antenna used in the following experiment and the common surface permittivity, and does not consider the actual temperature, salinity or surface roughness. The fitting error in terms of root-mean-square error (RMSE) of the linear model is 1 cm. After obtaining the spectral peak frequency of L2 from the combined raw phase measurements, the reflector height can be calculated using Equation (17).
3. Experiment and Analysis of Results
The aim of this paper is to retrieve sea level data based on the geometry-free linear combinations of GNSS carrier phase measurements. In this section, we introduce the GPS station SC02 and the data obtained from it. Then, five data processing strategies are proposed for obtaining sea level information from the GNSS multipath effect. Last, the solutions are evaluated by comparing the results with data from a nearby TG.
3.1. Brief Introduction to Station SC02
The experimental data were obtained from the GPS station SC02, which is co-located with a TG and belongs to the Plate Boundary Observation (PBO) Network of the American Earth Scope Plan. As seen in
Figure 5, station SC02 overlooks the sea and can receive reflected signals across a relatively large azimuth range. The station is located near the Friday Harbor Port in Washington State, USA (48.5°N; 123°W). It is situated at an altitude of −15.03 m with reference to ITRF08, and is equipped with a Trimble
® NETR9 receiver and TRM29659.00 choke-ring antenna (Trimble Inc., Sunnyvale, CA, USA) with a hemispherical radome. However, it only provides GPS measurements which contain a pseudo-random code with a single frequency (C/A1), a precise code (P2), a carrier phase with two frequencies (L1 and L2) and the SNR data at two frequencies (S1 and S2).
From 1 January until 31 January 2015, several available satellite signals were used, at a sampling rate of 1 s, to estimate sea level change, and data from the co-located TG station were collected. The TG station is 359 m from station SC02, and consists of an Aquatrak® air acoustic sensor (Aquatrak Corp., Sanford, FL, USA) in a protective well. Sea level data at this TG are recorded at 6-min sampling intervals and were obtained from National Oceanic and Atmospheric Administration (NOAA) for comparison.
To ensure that the signals used in the experiment were reflected by the sea surface, data with elevation angles in the 5–12° and 5–15° ranges and azimuth angles in the 90–150° range were selected. It was found that approximately 14 GPS satellites met the above azimuth and elevation angle criteria each day. However, some satellites did not provide high-quality data that could be used to retrieve reflector height. Ultimately, observations were obtained from satellites PRN 01, PRN 07, PRN15, PRN19, PRN23, PRN27 and PRN30 for use in data processing. This included L1/L2 carrier phases and their SNRs.
3.2. Data Processing Strategies
As described in
Section 2, the methods used to retrieve the reflector heights can be divided into two steps: spectral analysis and reflector height calculation. In the second step, the reflector heights can be calculated directly using Equation (8) and can also be solved using the theoretical model described in
Section 2.3.
For spectral analysis, the daily SNR and carrier phases were clustered into ascending or descending sections according to satellite elevation. SNR and L4 geometry-free linear combinations of carrier phase observations were arranged according to the values of the sine of the elevation angles. Spectral analysis based on L1 SNR, L2 SNR and L4 carrier phase combinations were performed separately using the methods mentioned in
Section 2 and the peak frequencies for each spectral analysis can be obtained. For reflector height calculation, the reflector height between the ARP of the GPS antenna and the sea surface can be retrieved using Equation (8) or Equation (17).
We proposed five strategies to retrieve the reflector height to evaluate the different methods. The reflector heights were then calculated using Equation (8) based on the peak frequency from the SNR of L1 signals and L2 signals separately, and their solutions are denoted by SNR_L1 and SNR_L2, respectively. The reflector heights were calculated using Equations (8) and (17) with the peak frequencies from L4 carrier phase combinations, and their solutions are denoted by L4_d and L4_model, respectively. As stated in
Section 2.2, L4 is the combination of L1 and L2, and L2 peaks were usually used for the analysis. The reflector heights were also calculated using Equation (17) based on SNR of L2 signals to compare the capability of L4 and SNR. The solutions are denoted by the SNR_L2_model.
The precision of the solutions is elevated by using measurements from a TG near the GPS station, such as with the co-located Friday Harbor TG near the GPS station SC02. However, the GPS-derived reflector heights are relative to the antenna phase center, whereas the TG sea level observations are relative to the TG benchmark. There is a fixed difference between the antenna phase center and the TG benchmark, as shown in
Figure 1. For convenience, the letter ‘C’ is used to represent this difference here. After removing the reflector height from C, the sea level heights can be deduced from the TG benchmark based on GNSS observations. The values of C can be estimated by using the least squares match between the estimated sea level and that determined from the TG.
When comparing the GPS-derived sea level changes with TG measurements, we noted that they have different sampling rates. The co-located TG observations are sampled every 6 min, while the GPS-derived sea surface heights are estimated for a chosen elevation interval (between 5° and 12° or between 5° and 15°), which is generally about 20 min. Thus, the TG measurements are averaged over each 20-minute period and at the same time as the GPS measurements.
3.3. Results Analysis
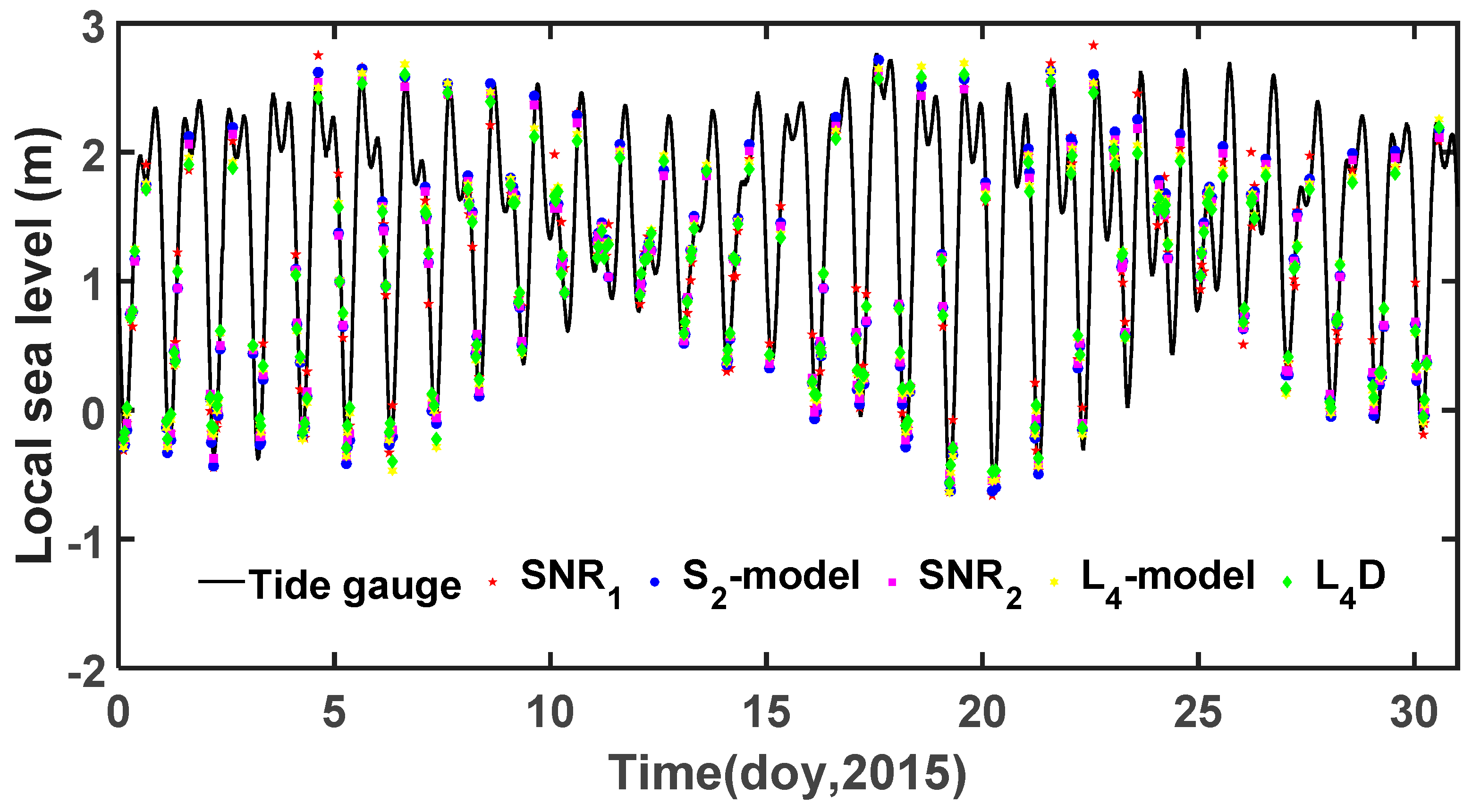
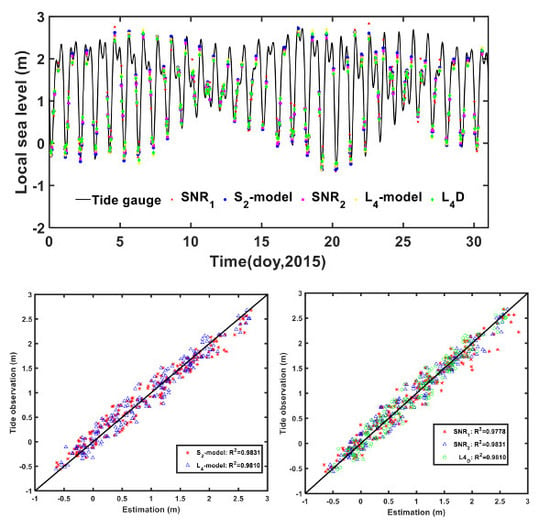
Figure 6 shows the sea level changes over the 31-day period from 1–31 January 2015, determined from the SNR_L1, SNR_L2, L4_d, L4_model and SNR_L2_model. Note that the horizontal axis is in units of “days of year” for 2015, and the vertical axis represents the local sea level in meters. It is evident from
Figure 6 that the derived results show good agreement with TG observations.
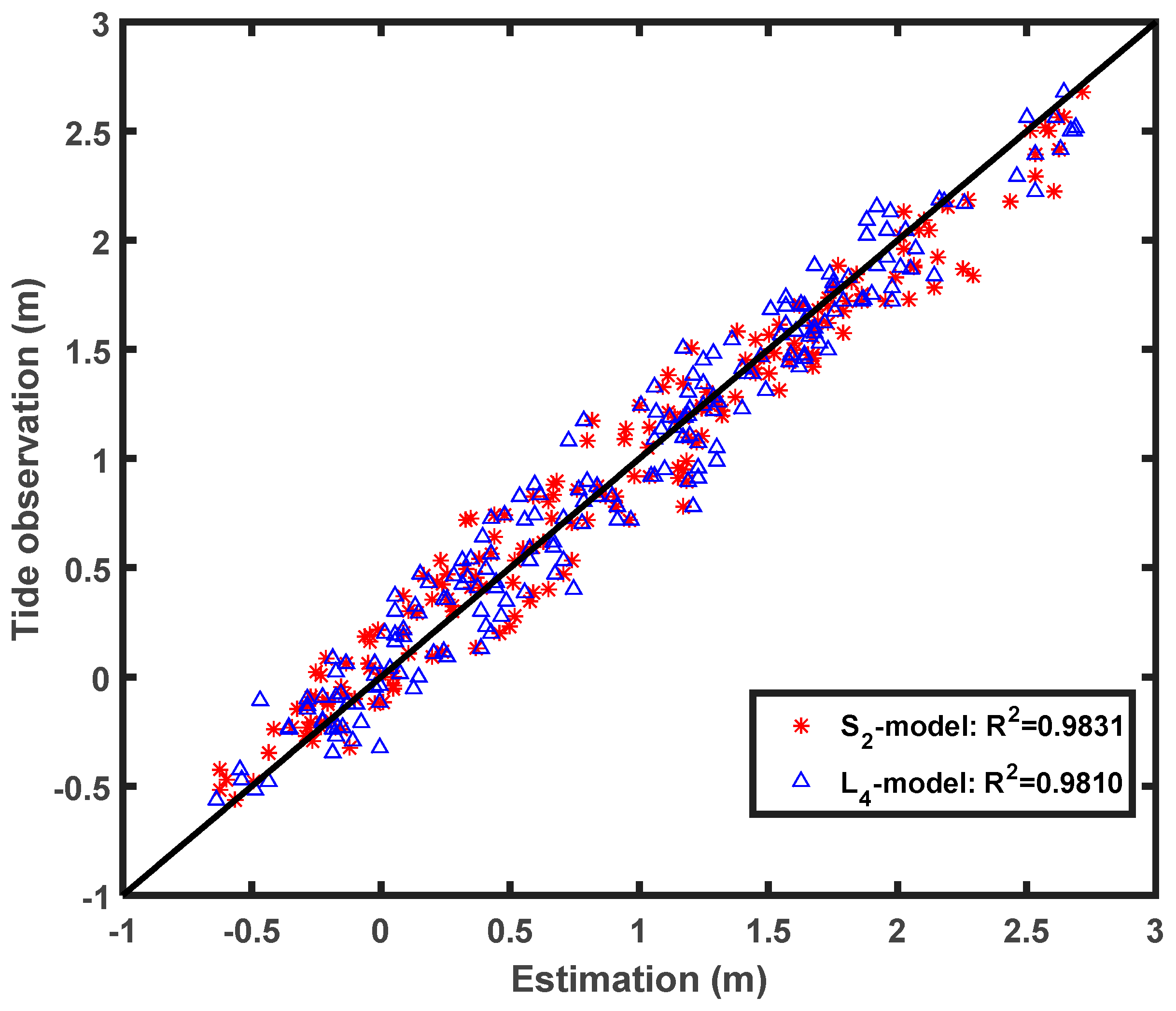
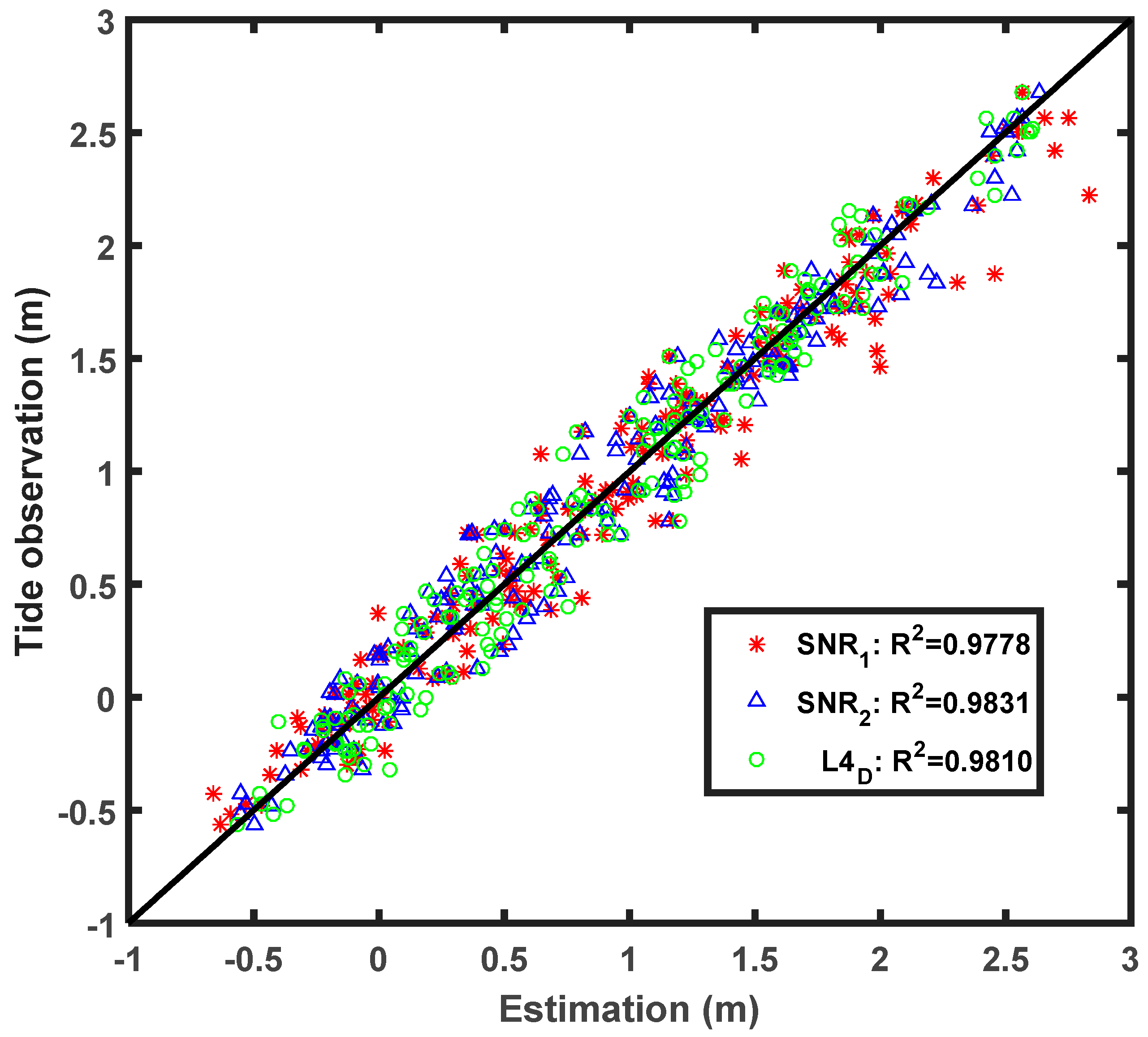
Figure 7 and
Figure 8 show the correlations of L4 and the SNR method with TG observations, and all the methods used in this paper have a correlation coefficient with TG in excess of 0.97.
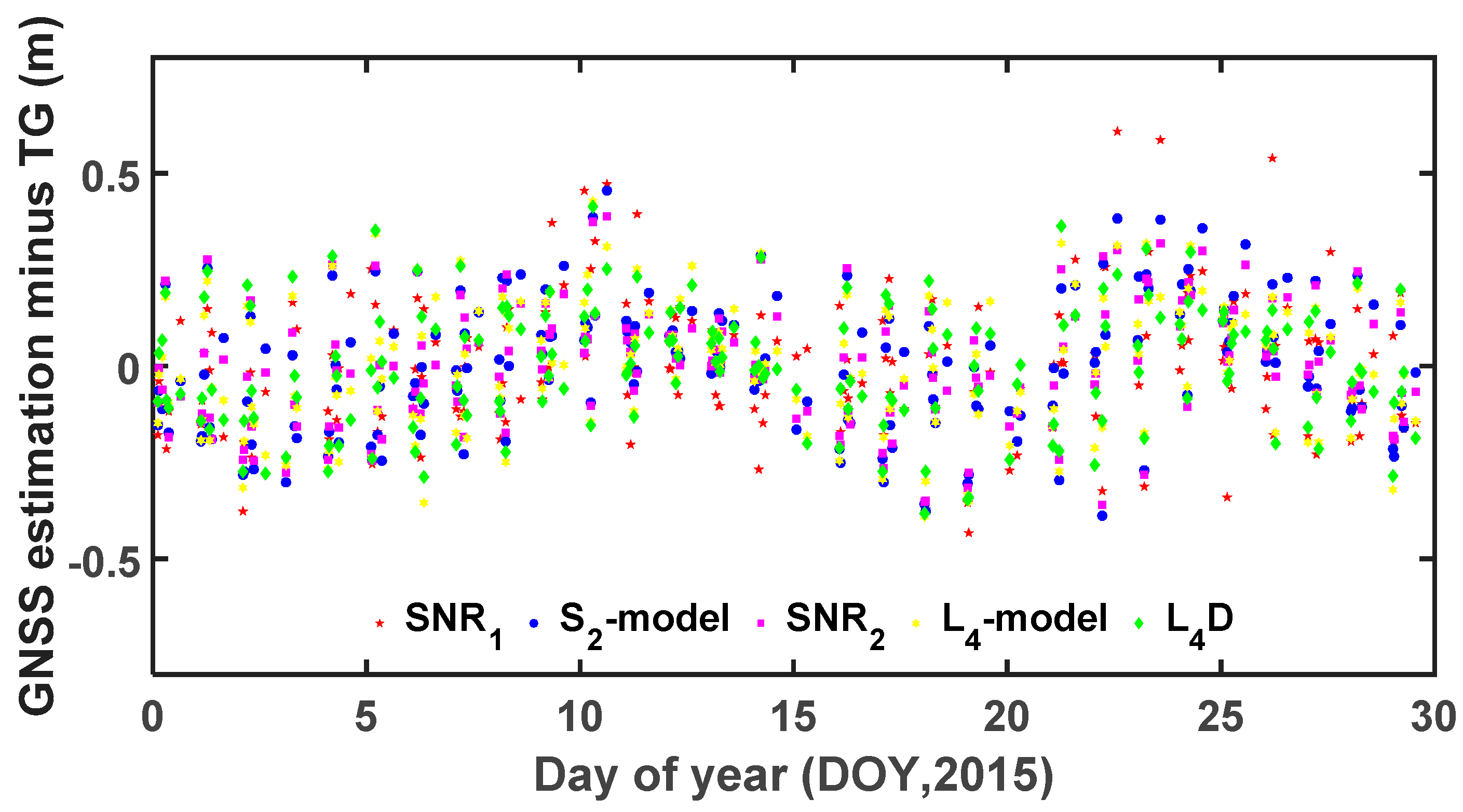
Figure 9 shows the sea surface height differences between GPS-derived solutions and TG measurements for the five strategies used from 1–31 January 2015, in which gross errors have not been removed. In the process of statistical evaluation in this paper, gross errors were removed when the residuals were larger than three times their RMSE.
Statistical results from the comparison between the GPS-derived sea level data and TG measurements for different elevation ranges are summarized in
Table 1. The values of RMSE for different methods fluctuate around 20 cm, which is acceptable when using the multipath effect in GNSS-R altimetry.
In addition,
Table 1 lists the statistical results of five data processing strategies for the elevation ranges, 5°–12° and 5°–15°. We can see that the RMSs of solutions for the elevation angle range, 5°–15°, are better than those for the elevation angle range, 5°–12°. The reason for this is that the one pass period of the available SNR data is longer for the 5°–15° range than that for the 5°–12° range. This makes the SNR oscillations clearer, and, as a result, the retrieved reflector heights have higher precision.
In the L4_d method, it was found that the remaining result was dL4 after partial removal of ionospheric delays using high-order polynomial fitting, which consists of two series with different frequencies. Then, Equation (8) was used to calculate the reflector heights from L2 peak frequencies based on the combined dual-frequency carrier phase measurements. However, because the L1 and L2 coexist in dL4, using Equation (8) to calculate the reflector height from the L2 peak frequency ignores the effect of the L1 term. As a result, the accuracy of data results using this method is still very good. Analysis of the data shows that this might be caused by the frequency difference between L1 and L2, which makes it possible to distinguish between L2 and L1 terms in dL4. It is also evident that L1 has an impact on L2 because of the slight difference in accuracy of the L4_d method.
4. Discussion
The use of GNSS reflection signals for remote sensing was proposed in 1988 [
40] and is now popular in the field of remote sensing. GNSS-R has its own advantages, such as all-weather and all-day observation, multi-signal sources, wide coverage, and high spatiotemporal resolution, which has provided it wide scope in the field of ocean altimetry. In this paper, the first known use of the L4 carrier phase dual-frequency combination from GNSS data to obtain sea surface height has been presented.
The L4_d method also obtained very similar accuracy results to the L4_ model method, indicating that the L1 quantity in dL4 has no significant impact on the L2 quantity in spectral analysis. This is probably because of the frequency difference between carrier phases L1 and L2. In future work, it is anticipated that we will focus on researching a new method with which to distinguish these two quantities in . If this can be achieved, the L4_d method will be able to achieve higher measurement accuracy, thus avoiding the low precision caused by inaccuracy of the linear model when using the L4_model.
Ionospheric error is an important quantity that affects the accuracy of the L4_model method. Although the L4 carrier phase geometry-free linear combinations of GNSS dual-frequency signals contain ionospheric delays, it has been shown here that the residual error from the ionospheric effect after high-order polynomial fitting will not strongly impact the L4 data, provided the order of the polynomial is appropriate. Although high-order polynomial fitting is used to weaken its influence, the remaining error still affects the accuracy of the solutions. In future research, the proper order of polynomials that can satisfy the accuracy of the L4_model method will be investigated. Moreover, ionospheric error will be calculated in advance using geodetic positioning methods, and this error will be subtracted in L4 observations to see if the accuracy of L4_model method can be improved.
The correctness of the linear model is also an important element when determining the measurement accuracy of the L4_model and SNR2_model methods. The linear model was obtained from a forward model of the multipath effect in this paper. The forward model takes into account many influences when considering the multipath effect reflected from the ocean surface, such as water temperature, salinity and surface roughness. However, because of the lack of on-site observation of these quantities, and the fact that all quantities adopted in this paper are commonly used values, the forward model cannot really simulate the multipath effect. This is especially true for surface roughness, which has a significant impact on the scattering of GPS signals on the ocean surface and therefore needs detailed study in the future. Additionally, although the forward model simulates multipath effects as much as possible, there are inevitably still errors. Seeking a more accurate multipath simulation model is also a way to improve accuracy.
The precision of our solutions based on SNR show a slight difference with the results in other papers. This may result from the following three points. (1) The GPS elevation of the data used in this paper ranges from 5° to 12° and 5° to 15°, and five-order polynomial fitting method was used to obtain detrended SNR. In contrast, Löfgren et al. [
32], adopted the measurements from very low elevation angles down to 0.5° and a three-order polynomial fitting method. (2) In order to improve the accuracy, Larson et al. used two methods for quality control: a normalized spectrogram peak of 1 dB-Hz and a peak-to-noise ratio >3 in LSP; “nonphysical” reflector height (RH) peaks were discarded (i.e., RH <3 or >11 m) [
41]. (3) In previous research [
33,
41], sea level retrievals were corrected with the time derivatives of RH or the height vertical velocity, H’. However, we did not correct the reflector height vertical velocity in this work, which might have caused worse RMS values in comparison with other works in the literature. In general, the constraints of elevation angles, quality of the detrended SNR, amplitudes of spectrogram peaks, and ranges of RH peaks would affect the accuracy of the solutions [
18,
19,
20,
31,
33]. Still, our purpose of this paper is to verify the possibility of sea level retrievals using the L4 method, and our initial results have strongly proved this feasibility.
5. Conclusions
Previous research has shown that ground-based GNSS-R altimetry based on SNR and triple-frequency combinations from a single GPS station can be achieved. However, the SNR data in dB and triple-frequency carrier phase measurements are not usually provided in their RINEX observation files. However, the carrier phase measurements from two signals with different frequencies are always obtainable from permanent GNSS stations.
In this paper, the reflector heights from the sea surface were retrieved using dual-frequency carrier phase linear combinations, and the precision of the solutions were similar to those derived from SNR data. The geometry-free linear combinations of GPS carrier phase observations were used to estimate the snow depth by Ozeki and Heki, in 2012, for the first time [
25]. We successfully used their method to retrieve changes in sea level.
Data processing and reflector height calculation methods have been described, including analysis of the remaining errors for methods based on L4 measurements. Peak frequencies from L4 measurements contain some errors because of the interaction between the two series of signals with different frequencies, but the methods are suitable for use with other GNSS signals from BDS, Galileo and GLONASS.
Five reflector height determination strategies were proposed to process the 10-day GPS data. SNR data and L4 measurements can all be used to solve the reflector heights separately, and a comparison with sea level changes observed from TG showed that the five strategies produce valid results. However, the solutions derived from phase combinations were not as good as those based on SNR data, and although there were some remaining ionospheric errors in the L4 measurements, their solutions can still achieve good accuracy.
The L4 and SNR analyses were performed using two different methods, respectively: a direct use of the formula method, using Equation (8), and a linear model method to obtain sea surface height after obtaining the peak frequency from spectral analysis. However, the use of L4 should be discussed under low or high solar activities with longer-period observation data, because L4 is influenced by ionospheric changes, which are due to the periodic activity of sunspots.
In summary, this paper has shown that the geometry-free linear combinations of GPS carrier phase observations can be used to estimate sea level changes, which were previously considered to have poor accuracy because of ionospheric error. However, when the appropriate polynomial fit is used to remove the ionospheric error, the measurement results achieve good accuracy. Here, double-frequency phase combination with a 10-order polynomial fit was used to remove this error to allow for estimation of sea level changes at station SC02. SNR data were also processed at the same time to provide a comparison. The results of the phase combination are not as good as that of SNR data when compared with TG observations, but they still maintain a certain degree of accuracy. All the results show good agreement with TG observations with correlation coefficients of 0.97–0.98 and RMSEs of 12–20 cm.
From this study it can be concluded that, in the absence of SNR data and triple-frequency phase data, the dual-frequency phase combination method can be used to reliably monitor sea level changes. This is, of course, not surprising, since this method has been used to estimate snow depth and soil moisture. However, sea level fluctuates considerably more than snow depth and soil moisture over time and space, particularly over a duration of approximate 20 min. There are also significant changes in spatial coverage by measurement points because of changes in the elevation angle during multipath analysis, resulting in inevitably lower retrieval accuracy of sea surface height. However, the analysis presented in this paper shows that sea level changes can be measured with considerable accuracy using the double-frequency phase combination method.
Ongoing and related work will focus on further improving the precision of the L4 method. For example, the sea surface roughness will be considered an influencing factor, thereby reducing bias, and improvements will be made to the temporal resolution of sea surface height retrieval. It is anticipated that this will be achieved by refining the estimation method by taking the temporal changes in sea surface height into consideration. In addition, continued work will focus on making use of multiple satellite constellations at the same time to improve the spatial resolution of the height measurements.