2.1. Instrumental Design
The thermal imaging PiCam developed here is based on the Raspberry Pi camera module (v1.3), with the integrated Omnivision OV5467 sensor modified as described in Wilkes et al. [
15]. As discussed in
Section 1, this procedure, which involves removal of the Bayer filter, produces a uniform sensor with heightened sensitivity at both ultraviolet and near infrared wavelengths; the latter spectral band is pertinent to this work.
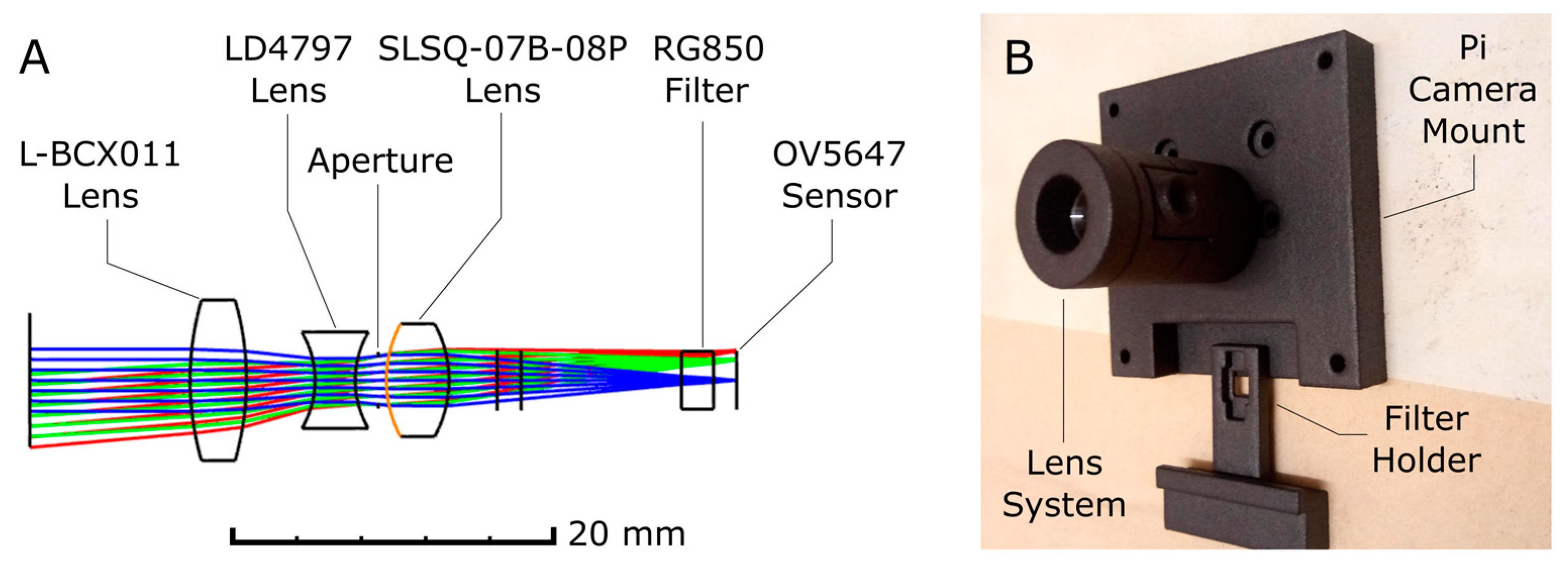
An optical system, shown in
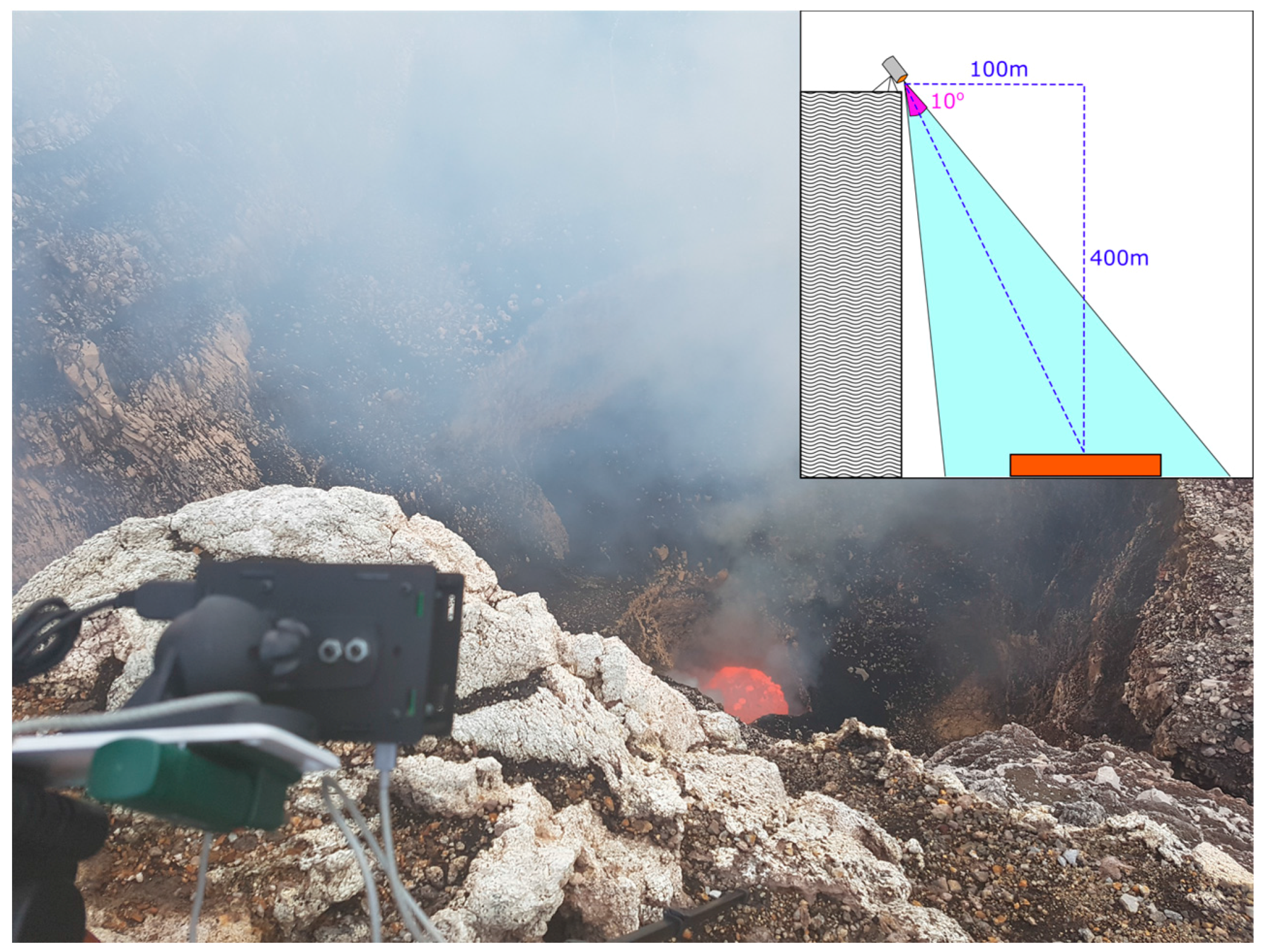
Figure 1A, was designed in OpticStudio (Zemax Ltd., Kirkland, WA, USA), to provide a 10° field of view (FOV) for the camera; this FOV had been determined to be appropriate based on estimates of the viewing geometry (
Figure 2) and Masaya’s lava lake size provided by Instituto Nicaragüense de Estudios Territoriales (INETER; Personal Communication, 2017). The lens configuration was a triplet comprising off-the-shelf lenses (Ross Optical, L-BCX011; Thorlabs, LD4797; Optosigma, SLSQ-07B-08P), with a long-pass 850 nm filter (Thorlabs, RG850) positioned behind this lens system; a metal aperture of 3 mm diameter was located between the LD4797 and SLSQ-07B-08P lenses. A lens holder was then designed in SolidWorks and 3D printed with selective laser sintering (3dprintdirect.co.uk), to house the optical system and mount it to the camera board (
Figure 1B).
The camera module was controlled by a Raspberry Pi 3 Model B computer (
www.raspberrypi.org/), which in turn was controlled by a laptop connected wirelessly by the use of the Pi 3’s built in wireless hotspot capabilities. A Python3-based graphical user interface, developed in-house, was used to communicate with the Raspberry Pi and camera module and receive images from the Pi to be displayed on the laptop in real-time. For all work discussed herein, images were converted to temperatures post-acquisition and, thus, there was no real-time display of retrieved temperatures.
The Python package
picamera allows relatively comprehensive control of the Pi Camera module. Analog gain was fixed at 1 and an optimal shutter speed, which gave a maximum pixel saturation in an image of approximately 80%, was then found experimentally; greater levels of saturation should be avoided, since sensors can begin to respond non-linearly as they approach saturation. These steps ensure a high signal-to-noise ratio (SNR) for each image. As discussed in
Section 2.4, we find our calibration fits well to a square root dependence on signal. This indicates that the system is shot noise limited and, thus, SNR will increase proportionally to
t1/2, where
t is the integration time (i.e., shutter speed). Pixels were also software-binned from the full resolution 2592 × 1944 to 648 × 486, to further increase SNR, and saved in this smaller format. It could be argued here, however, that maintaining the high pixel resolution would be advantageous for retrieving accurate temperatures, especially when imaging small features which are sub-pixel scale in the 648 × 486 images. In such a scenario, the high resolution of this sensor (5 mega-pixels), relative to commercial MWIR/LWIR thermal cameras, could prove highly beneficial for accurate determination of small feature temperatures (e.g., [
14]).
2.2. Calibration Procedure
The camera was calibrated using a blackbody furnace (Landcal P1200B), with a thermocouple providing UKAS [
www.ukas.com] certified temperature measurements of the source. The effective emissivity of the furnace is quoted as 0.998 if its cavity is isothermal. Images were then taken of the source at temperatures between 500 and 1000 °C, in 50 °C increments, and at a number of shutter speeds. For each temperature/shutter speed 30 images were taken and pixel Digital Numbers (DNs) were averaged in both the spatial and temporal domain, to provide a single DN representative of that temperature/shutter speed. To improve the calibration, the upper end of the temperature range could be increased, to extend the calibration beyond the maximum temperature expected from the lava lake. Issues with the furnace prevented capturing the whole range of lake temperatures (maximum of ≈1100 °C) in our calibration here; however, the calibration fit is extremely strong, with a standard error of 1.08 °C (see
Table 1 and
Table A1) and, thus, we are confident of the retrieved temperatures even when extrapolating beyond the 1000 °C. Although here we perform a single calibration to be applied to all pixels across an image, it is possible to perform the calibration for each pixel individually, which can account for non-uniform pixel sensitivity (e.g., [
22]).
The recorded signals,
(discussed as the DN herein), at the given temperatures in Kelvin,
, were fitted to the Planckian form of the Sakuma-Hattori equation (e.g., [
23]) with 3 fitting coefficients,
A0,
A1,
A2:
where
is the surface emissivity,
is the path transmission coefficient and
is the second radiation constant (1.43877736 × 10
−2). Results of this fit are displayed in
Appendix B. Inversely, with known fitting parameters and for a given signal, temperature can be retrieved with:
Finally, we can differentiate Equation (1), producing a derivative which is utilised in the uncertainty analysis in
Section 2.4.
In view of later discussion, we note here that since is monotonic, = .
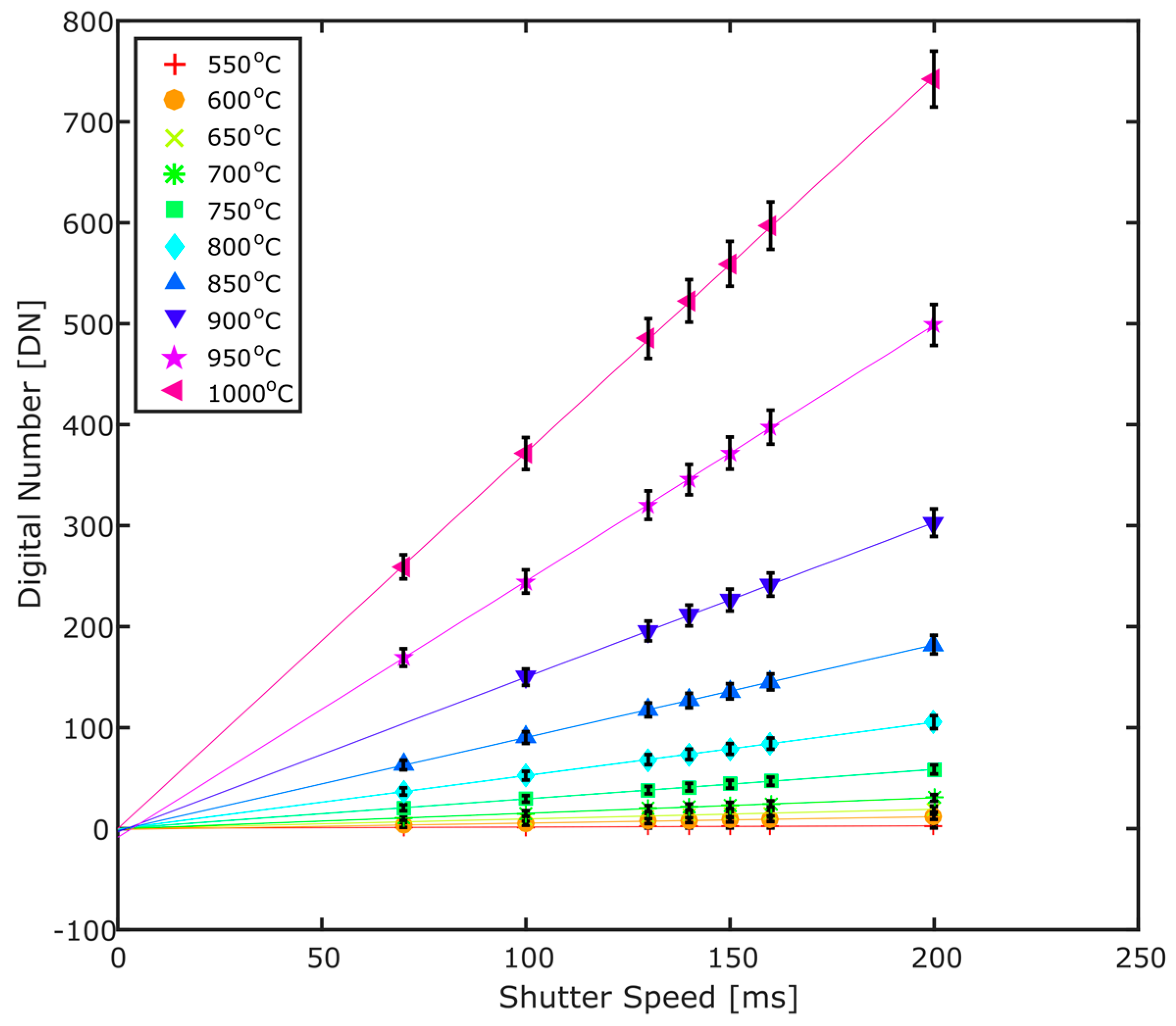
Two methods of calibration were attempted. In the first, Sakuma-Hattori fit coefficients were determined individually for each shutter speed, i.e., calibration with the furnace was performed for a small set of known shutter speeds; thus, we generate fit coefficients
A0,
A1,
A2 specific to a single shutter speed. Although the sensor response is linear with changing shutter speed, as demonstrated by Wilkes et al. [
15] and confirmed here with the blackbody furnace (
Appendix C), we performed a separate calibration for each specific shutter speed used throughout the campaign, to ensure integrity of results. This method can be time consuming, especially if a large number of different shutter speeds are used in field deployment. In the second method, the sensor response was assumed to be perfectly linear in DN vs. radiance and passing through the origin; thus, a single set of fit parameters were determined for a shutter speed of 1 μs and all signals were scaled to a 1 μs signal by dividing by the shutter speed of that acquisition. This technique depends on perfectly linear response of the sensor and an accurate dark current/offset correction; however, as can be seen from the calibration data (
Appendix C), dark current subtractions do not always perfectly account for the offset in an image, for reasons which are unclear. Hence, although we see an extremely linear response of the sensor to incident radiation with increasing shutter speed, a perfect calibration, which covers all shutter speeds is difficult to establish. Furthermore, Lane and Whitenton [
22] recommend cross-checking calibration points which have been scaled for varying integration times, acknowledging the difficulty of providing one calibration to fit all sensor integration times. The results presented here are therefore only based on the first method of calibration.
2.3. Extinction and Emissivity
From Equation (1), it can be seen that in order to retrieve accurate temperature measurements from our NIR thermal images, two final parameters need to be considered: the extinction of radiation between the object and the observer and the emissivity of the object. Both can have significant effects on the apparent temperatures observed by the instrument.
Atmospheric extinction comes in two forms, absorption and scattering of radiation by particles between the emitting object and the measuring instrument. Neglecting re-emission of radiation, extinction and transmission must sum to unity and, thus, understanding extinction can allow us to calculate
in Equation (2). Arguably, scattering due to aerosols is a significantly more complex radiative transfer problem than absorption. If imaging through an optically thick plume can be avoided this is preferential, otherwise, retrieving accurate temperatures would be extremely difficult and beyond the scope of this paper. If the aerosol loading is relatively stable with time, temperature measurements may still be able to provide useful insights into changing lake dynamics, without providing accurate absolute temperatures. Conditions where no plume condensation occurs are always preferable; nevertheless, in cases where aerosol is an issue, MWIR/LWIR cameras may perform better than a NIR alternative (e.g., [
2]). Conversely, with regards to extinction through absorption, the NIR system is possibly less affected than a MWIR/LWIR system (e.g., [
11,
12]). Sawyer and Burton [
24] addressed this issue well for MWIR/LWIR imaging, whilst Radebaugh et al. [
12] give a good discussion for the NIR application. However, the latter only discuss this issue and do not correct their temperatures for absorption. Here, we estimate the amount of absorption across the viewing path and subsequently correct our temperatures for this effect.
Within the spectral sensitivity band of our instrument (≈850–1100 nm), only H
2O exhibits significant absorption, therefore simplifying the absorption correction to this single gas species. Furthermore, attenuation due to absorption is relatively straightforward to quantify, since high resolution absorption/transmission spectra for most, if not all, common gaseous species are openly available via the High Resolution Transmission database (HITRAN; [
25]). Using the bytran software [
26], which utilises the HITRAN Application Programming Interface (HAPI; [
27]) to extract and manipulate molecular line intensities, we generated data for transmission vs. wavelength. Relative humidity (RH) and temperature data, logged during the Masaya field campaign, and an estimated atmospheric pressure were then used to scale the transmission spectrum according to the column density of water in the instrument’s line-of-site. The two extremes of measured conditions, 26.5 °C and 82% RH and 31.9 °C and 60% RH, were used in these calculations, assuming that conditions do not change across the viewing path; in reality, this assumption will not be perfect, since conditions close to the lava lake surface are likely to be significantly different from our measurements made on the crater rim. Using these spectra, along with the spectral response of the PiCam with the long-pass filter in place (determined using a monochromator), we determined the effect on observed temperature by integrating Planck’s equation with these two filter spectra applied. The ratio of this calculated signal to the signal without the H
2O spectrum filter provides a path transmission coefficient,
, which can be directly used in Equation (2) during temperature retrievals. If all atmospheric parameters remained constant, the path transmission coefficient would still be a non-constant scalar, since it is dependent on the temperature of the emitting body. This is because the shape of the blackbody curve varies with temperature and, therefore, the proportion of absorption from each H
2O absorption line changes with this changing distribution of spectral radiance. Since the majority of, if not all, lava lake temperatures range between 800–1200 °C (see
Section 3), we calculate the transmission coefficients between these temperatures, in 100 °C increments and take an average. We therefore have a single
, averaged across both temparature and atmospheric conditions, which can be used in temperature retrievals; for this work,
. In
Section 2.4 we quantify the uncertainty associated with using this single transmission coefficient for the Masaya lava lake dataset.
The water absorption effect could be almost entirely removed by using a second optical filter to attenuate radiation around the absorption peak at ≈940 nm. Rudimentary tests of this were attempted in the field using band-pass filters, centred at 850 and 1080 nm (10 nm full-width-at-half-maximum; Knight Optical), mounted to the fore of the lens system. Due to this optical setup, however, images appear to display some vignetting/aberrations. Furthermore, longer shutter speeds (100–200 ms) were required in order to obtain greater signal, due to the decrease in radiation incident upon the sensor caused by the filters. Since Masaya’s lava lake was moving extremely rapidly, this caused some blurring of the image scene. In cases of extremely humid conditions or long path lengths, or where the scene is relatively stationary, an additional filter could be advantageous. Here, however, we discuss only data acquired using the single long-pass 850 nm filter.
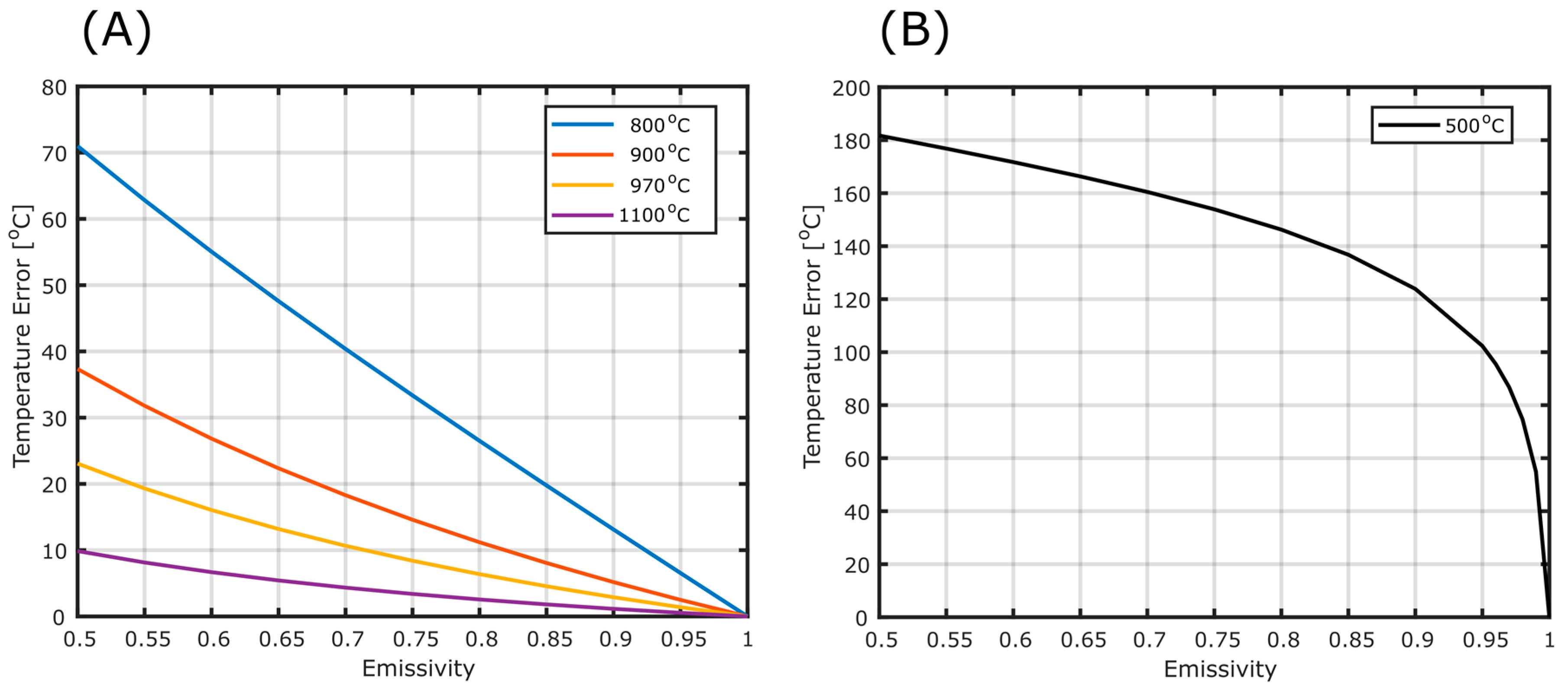
In the literature, hitherto, a range of emissivities (≈0.5–1.0) have been used for basalts within the wavelength range of 0.8–1.1 μm ([
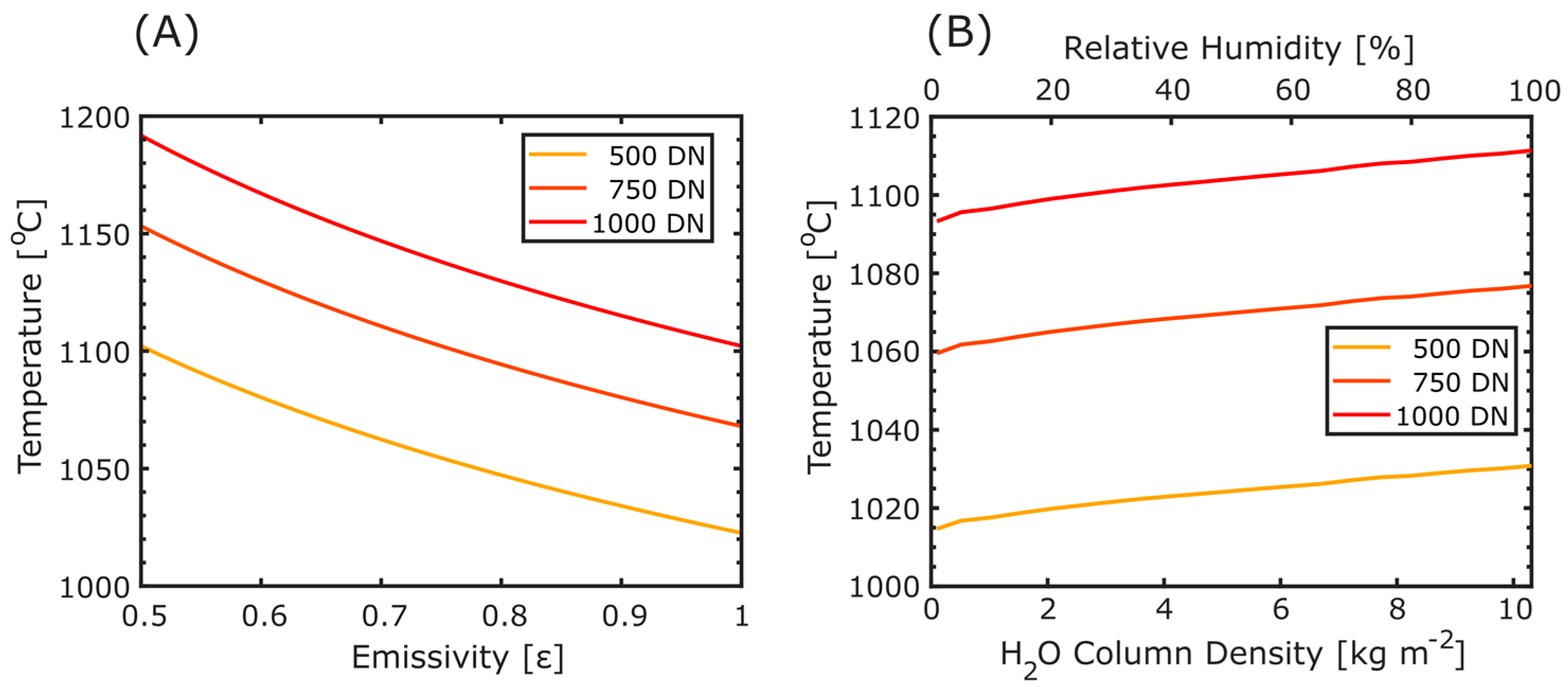
28] and references therein). Nevertheless, at a signal DN of 750, assuming an emissivity of 1 only underestimates the temperature by ≈12 °C if the actual emissivity were 0.9 (
Figure 3A); this emissivity is also very much at the lower end of most estimates, if excluding the broad range (0.5–0.9) presented by Rothery et al. [
29] where emissivity was not directly measured, rather, it was inferred from Kirchoff’s law and reflectance determined through satellite imagery. Ideally, for each application, a rock sample would be taken from the field and its emissivity measured; however, if this experiment is not conducted in a rigorous manner, to obtain a freely radiating surface, significant errors can be incorporated into this calculation. We therefore, somewhat arbitrarily, assume an emissivity of 0.95 and acknowledge that this will affect the absolute temperatures presented herein. Due to the paucity of emissivity data in the NIR, we then assume a bounding range of 0.9–1.0, with a uniform distribution, to calculate
(Equation (10)) for the uncertainty analysis in
Section 2.4.
The emissivity of an object is a function of a number of parameters, including: chemical composition, surface roughness, viewing angle and porosity. When the lava lake is in a relatively non-turbulent state, it may be reasonable to assume that the change in emissivity is relatively small. Under such conditions erroneous estimation of this parameter will only cause over- or under-estimation of the absolute temperature by a constant value during an acquisition sequence; however, between states of turbulence and relative stability, emissivity may vary, making such an assumption less valid. Similarly, atmospheric conditions, volcanic gas emissions and the mixing ratio of the two, can vary quite considerably over relatively short time periods and, thus, could result in a variable path transmission coefficient. Were this variation significant, it would not only affect the absolute calibration of the instrument but could also mask/influence any trends or periodicities in a temperature time series; this latter effect may be more problematic, since it is likely that volcanologists are more concerned with thermal signatures which can relate to changes in volcanic activity (e.g., [
1,
2,
30]), rather than a perfect radiometric calibration of temperature. As part of the following section we show that, for conditions experienced on Masaya, the uncertainty caused by a variable path transmission coefficient is negligible for this PiCam instrument.
2.4. Uncertainty Analysis
A number of uncertainties can be quantified with respect to the final quoted temperatures. Quite often these are neglected or poorly constrained within the field of volcano remote sensing, however, it is important to understand these constraints when evaluating datasets. We therefore give a detailed discussion of our uncertainty analysis herein. We will discuss each uncertainty separately, as they are considered independent and can, therefore, be added in quadrature to provide a total uncertainty estimate of a retrieved temperature. Lane et al. [
31] provide a comprehensive overview of much of the work presented in this section.
The calibration uncertainty consists of four sources (
Table 1). These uncertainties are, again, assumed uncorrelated and, thus, added in quadrature to provide a total calibration uncertainty (
). In this case, we multiply the total by a factor of 2 to provide a 95% confidence interval:
It can be seen that this uncertainty is temperature dependent due to the temperature dependence of the blackbody furnace’s emissivity uncertainty. Therefore, this standard uncertainty can be plotted against temperature and a linear regression is performed to estimate
given any temperature,
:
The measurement noise is specific to the camera sensor. In an optical system which is performing optimally this will be dominated by shot noise, which has a square root dependence on signal:
where, in this case, the fit coefficients
and
were empirically determined to be 0.109768 and 0.15447, respectively. This can be converted to a temperature uncertainty, again at 95% confidence level, using:
In this study, we do not employ any flat-field (i.e., uniform pixel illumination) correction, which can account for variation in pixel-to-pixel sensitivity, vignetting and other optical effects, and dust or scratches on the sensor. By imaging a homogenous surface, or clear sky at dusk or dawn, variations across the field of the camera can be accounted for; thus, it should be possible to totally remove, or at least make negligible, this uncertainty. Instead, here we quantify this uncertainty as another contributor to the overall uncertainty estimate. An image was taken of a flat reflecting object and the standard deviation of signal across the sensor was determined. The fraction of this standard deviation relative to the mean signal across the sensor can then be used to quantify the flat-field related temperature uncertainty,
, as follows:
where
is the temperature uncertainty at 95% confidence level and
= 0.03 is the empirically derived fractional standard deviation across the sensor. It should be noted that this flat-field image will also contain other associated sensor noise components, such as shot noise. To remove this uncertainty from the image we average a sequence of 30 images, on a pixel-by-pixel basis, making the contribution from this noise source negligible. The uncertainty associated with random sensor noise is equal to
where
N is the sample size and
is the standard deviation. Therefore, it is important to use enough images to make this uncertainty negligible; we found that 30 images were adequate here. The standard deviation of the resulting image is therefore almost entirely due to deviation from a perfect flat-field setup.
The total temperature uncertainty is now calculated by adding all considered uncertainties in quadrature:
where
represents the sum of the squares of any further uncertainties which may not be directly associated with the PiCam instrument or calibration. In our case, we further estimate transmission coefficient and emissivity uncertainties, following from the discussion in
Section 2.3.
There are two uncertainties associated with the transmission coefficient
. The first uncertainty pertains to atmospheric variability. For simplicity, we assume that the extreme values of atmospheric conditions stated in
Section 2.3 provide the bounds for a uniform distribution function of the path transmission coefficient. The standard deviation,
, can then be calculated by the general equation:
where
and
are the lower and upper limits of a variable,
, respectively; in this case this is the path transmission coefficient
.
There is also a transmission coefficient uncertainty associated with object temperature (see
Section 2.3). Using the extremes of temperatures to calculate two transmission coefficients, again we use Equation (10) to find the standard deviation of
with respect to temperature changes. The final transmission coefficient, therefore, incorporates uncertainties related to both atmospheric conditions and the temperature of the emitting object. These are independent of each other and are, therefore, added in quadrature to be incorporated into the final uncertainty. We do not include extinction through scattering in our quantification of uncertainties, since it is difficult to constrain; however, we acknowledge and later show (see
Section 3), that it can have a significant impact on measurements.
The uncertainty of
can now be calculated using the general equation:
where
for the uncertainty at 95% confidence level of variable
, which is in this case
;
is then the product of any further scaling factors from Equation (1), which in this case is simply the emissivity,
.
As stated in the previous section, emissivity was also assumed to have a uniform distribution, between 0.9 and 1.0, due to the paucity of data on this parameter; furthermore, its high dependence on composition suggests that drawing values from articles at different volcanoes may be somewhat fallible. Again, the standard deviation, , is defined by Equation (10) and the standard uncertainty, , is calculated from Equation (11), where is now the path transmission coefficient .
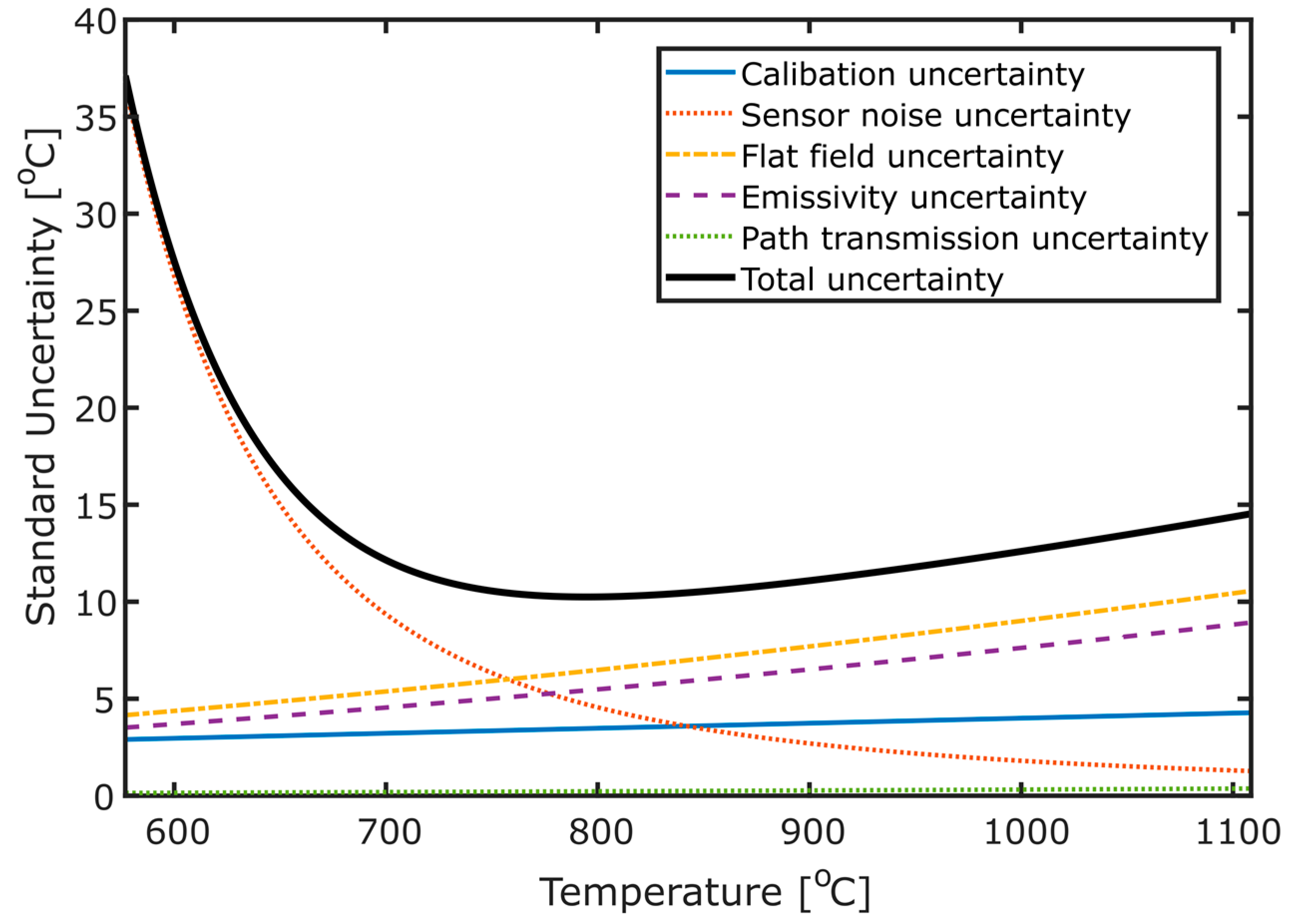
All uncertainties have a signal or temperature dependence, displayed in
Figure 4 for a calibration at 1 ms shutter speed. Signal noise shows a very strong temperature dependence at lower temperatures, since this is approaching a signal of 0 and, thus, the SNR is extremely low. Neglecting these large low-temperature uncertainties, we find that the flat-field uncertainty contribution is the largest uncertainty in a measurement. This indicates that a flat-field correction would be highly advantageous and could markedly reduce the overall error. However, poor knowledge of the emissivity of the image object also limits the precision of the instrument; as discussed, accurately constraining this parameter can be difficult. Furthermore, it is likely that the total uncertainty quantified here somewhat underestimates the overall uncertainty of this instrument, due to other contributions which are more difficult to accurately quantify. For instance, we do not consider the point spread function herein (e.g., [
31,
32]), which introduces another uncertainty into temperature measurements. Due to pixel cross-talk and imperfections in the optical system, the signal of a pixel is a function of an area surrounding that pixel, not just the area imaged by the pixel itself. For example, this can lead to small hot objects appearing cooler than they are. Although it is important to be aware of this phenomenon, reconciling this error is a topic of current research in radiometry; therefore, it is beyond the scope of this article.
Notably, within the bounds of conditions measured at Masaya on this field campaign, the H
2O uncertainty is negligible. Use of a single path transmission coefficient, rather than varying it with changing atmospheric conditions and source temperatures, is therefore adequate. However,
Figure 3B shows that the lack of any water vapour correction may lead to a relatively significant underestimation of the object’s temperature. Overall, our results somewhat corroborate those of Furukawa [
11] and Radebaugh et al. [
12], who both identified that NIR silicon sensors show relatively low dependence on water vapour column in the observation path and suggest that thermal imaging at these wavelengths is less susceptible to instabilities in atmospheric conditions relative to at MWIR/LWIIR wavelengths. Nevertheless, we advise that some form of correction should still be applied if accurate temperature retrievals are required.
The lower limit of temperature that can be imaged by this instrument is not directly addressed in this study. Furukawa [
11] suggest their system is imaging fumaroles of temperatures a little above 300 °C. Since our system is also based on a silicon focal plane array, a similar temperature sensitivity should be attainable; however, with the large sensor noise temperature uncertainty present in the 1 ms measurement at 600 °C (
Figure 4), we more conservatively estimate that the system can work well for temperatures of ≥500 °C. This would require an increase in the exposure time, to increase the SNR and, therefore, reduce the associated temperature uncertainty. Furthermore, this would require more consideration of the effects of reflected solar radiation, which can become more of an issue when attempting to image lower temperature targets (see
Appendix A).
2.5. Field Deployment
The camera system was deployed at Masaya Volcano, Nicaragua, where a lava lake has been visible in the Santiago crater since 2015. Masaya is a basaltic volcano which stands at an altitude of 635 m in the west of Nicaragua, approximately 20 km south-east of the capital Managua. The volcano is currently displaying a vigorously overturning lava lake, one of fewer than 10 known current lava lakes on Earth. Nevertheless, to the best of our knowledge there are currently no articles in the scientific literature which report ground-based data on the thermal characteristics of this most recent phase of Masaya’s activity.
Between 12 and 17 June 2017, a range of tests were performed with the thermal imaging PiCam. Here, we discuss a dataset from 12 June, acquired after sundown; therefore, any uncertainty due to reflected solar radiation was avoided. Images were acquired at a framerate 0.5 Hz. Due to extracting the RAW sensor data here, which is packed into the start of the standard JPEG files, this framerate is at the upper limit of what is currently achievable with our software. One significant advantage of previous PiCam work by Radebaugh et al. [
12] is the high framerate afforded by use of the video port. Current work to directly access the RAW sensor data, bypassing image post-processing on the board itself, could open up much higher framerates for our system in the future.
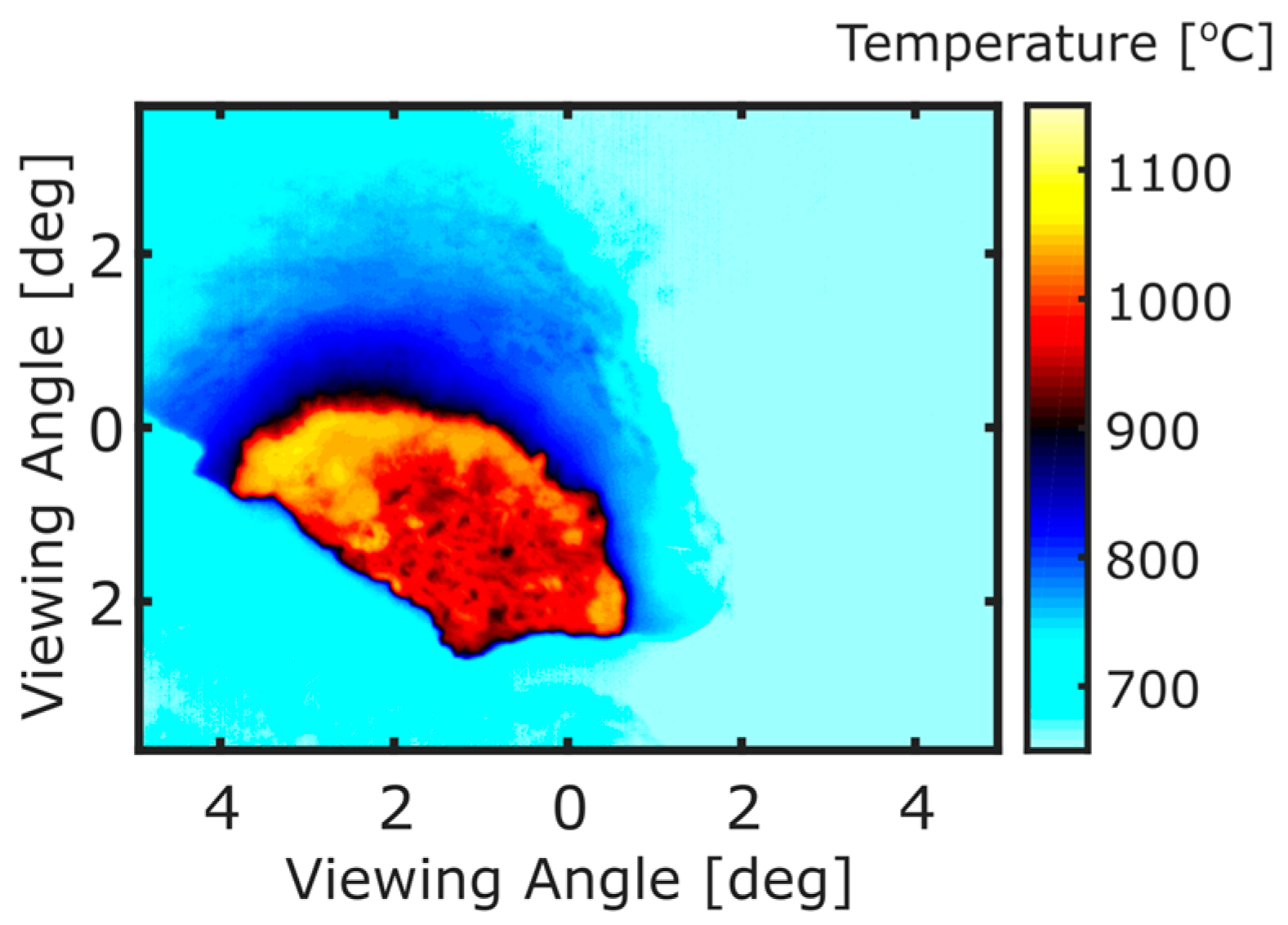
The viewing platform was located approximately 400 m above the lake; viewing geometry is displayed in
Figure 2. From this position, a region of the lava lake is obscured by a crater terrace and, thus, it should be noted that work presented here does not represent measurements of the entire exposed lava lake surface.
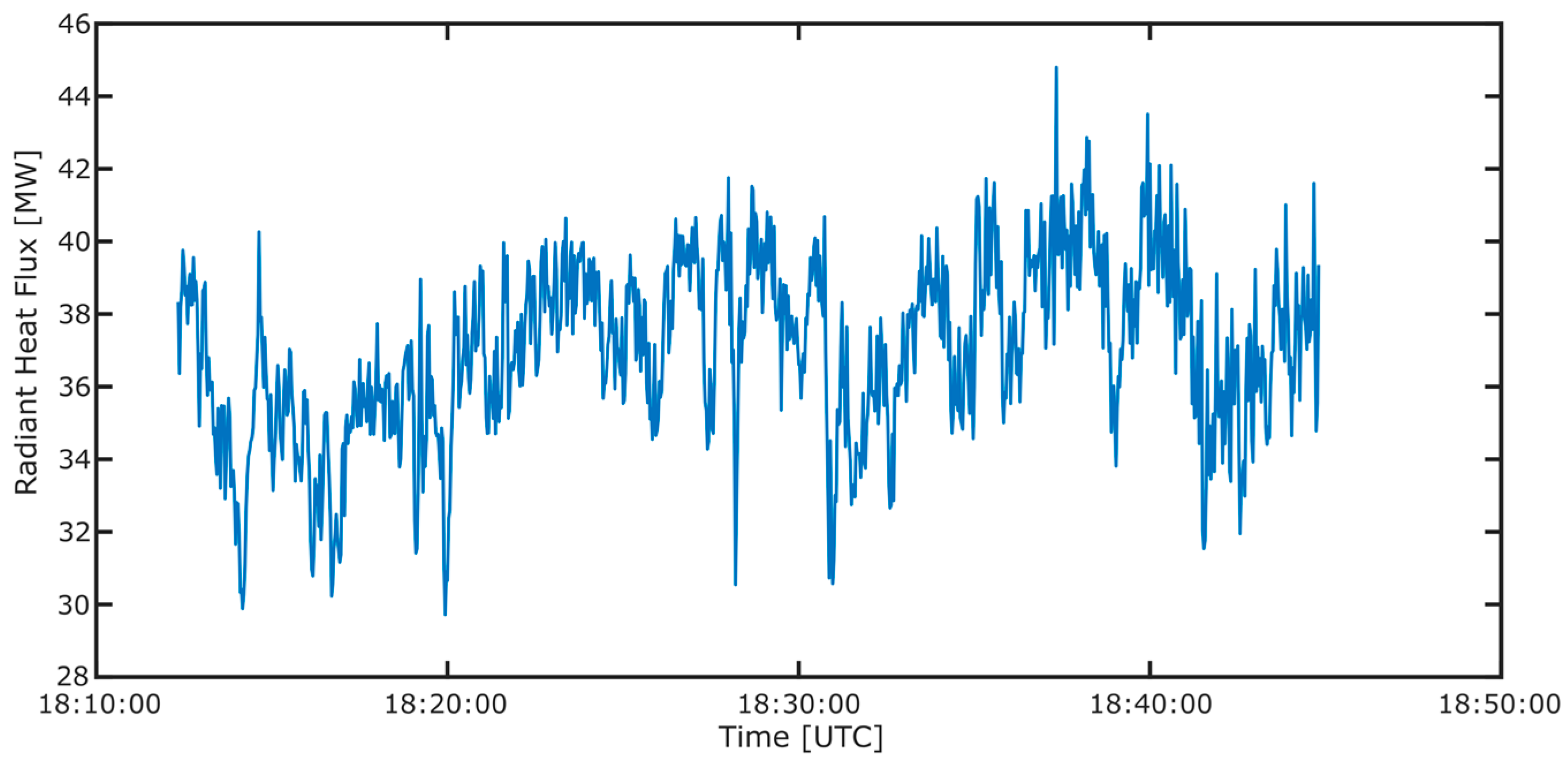
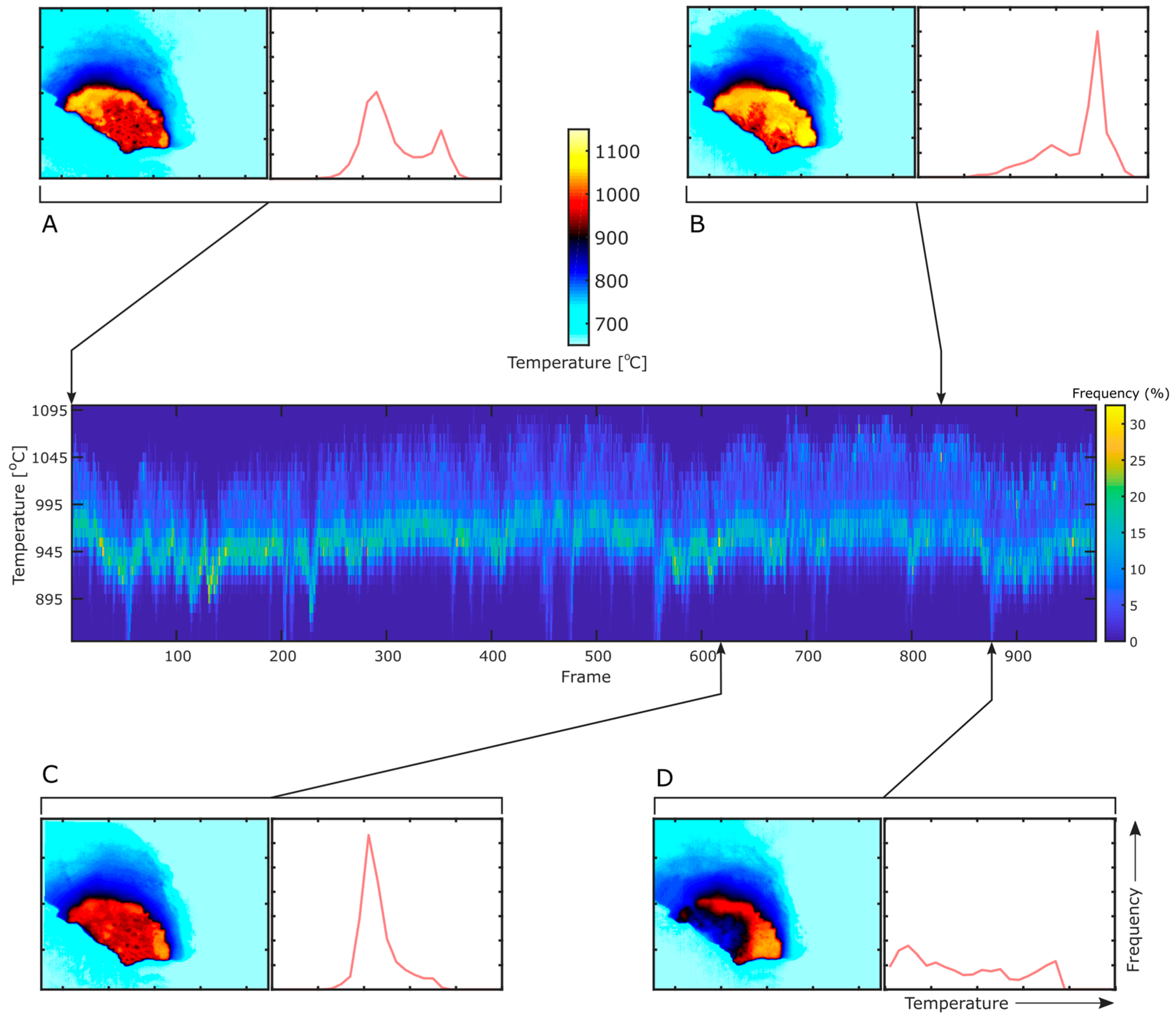
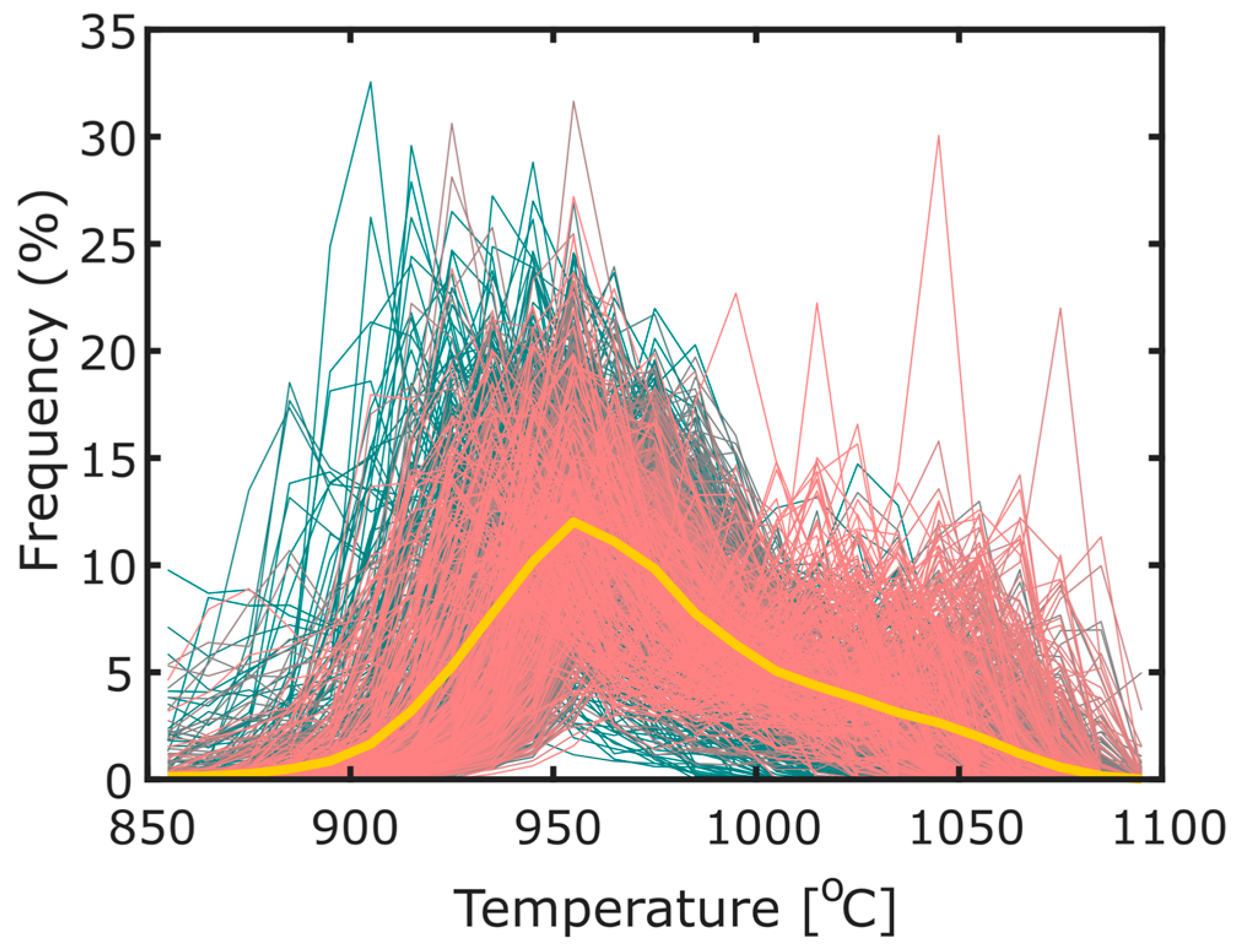
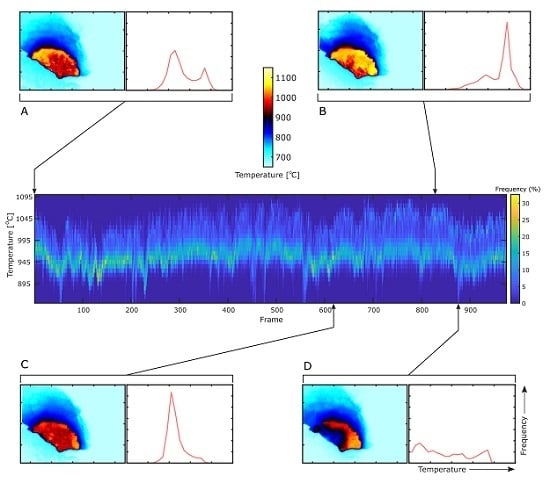
To accurately interrogate the lava lake and its thermal features it is important to isolate the lake from its surroundings; however, due to windy conditions, there is a relatively significant camera shake apparent in the image sequences (
Video S1). Two methods were therefore tested for defining the lava lake region of interest (ROI) in each frame. Firstly, the image sequences were stabilised by utilising a Lucas-Kanade image registration [
33] of each frame to the template of the first frame; this was implemented in Matlab using the Image Alignment Toolbox [
34]. From here, a ROI, i.e., the lava lake, can be extracted by defining its extent with a polygon; for each subsequent frame the same polygon is then extracted. However, the image registration in most cases here was not perfect, possibly due to the fast-flowing lava lake and intermittent presence of aerosols, as well as the difficulty in finding optimal input parameters for this algorithm. Some camera shake is, therefore, still observable in a video stabilised in this manner (
Video S2); although the larger image shifts have been removed, it appears that smaller shake has been exacerbated. We therefore attempted to define the lava lake in a separate manner, using a threshold of any temperature above 850 °C representing the lake. This temperature was determined first by a best estimate and refined by observing how the resultant threshold mask visibly compares to the lake surface. A video of this threshold mask shows that in places it can provide an accurate determination of the lava lake extent, where clearly defined edge features are tracked from frame to frame (
Video S3); however, in regions where there is spattering at the lake edges, or intense scattering from aerosols, the lava lake can become over or under-defined; the former issue is also commented on in Radebaugh et al. [
12]. For the data discussed in this article we apply the first method, image registration, since we believe this to be the most robust method in most cases; it also has the potential to be much improved relative to our example here. However, there are a number of studies in which thresholding could be extremely useful, for example, for calculating the extent of cooled plates within a lava lake, or where there is minimal aerosol and spattering such that the lava lake boundary can easily be defined by a temperature contrast with the surrounding crater wall.