kCCA Transformation-Based Radiometric Normalization of Multi-Temporal Satellite Images
Abstract
1. Introduction
2. Relative Radiometric Normalization Based on kCCA Transformation
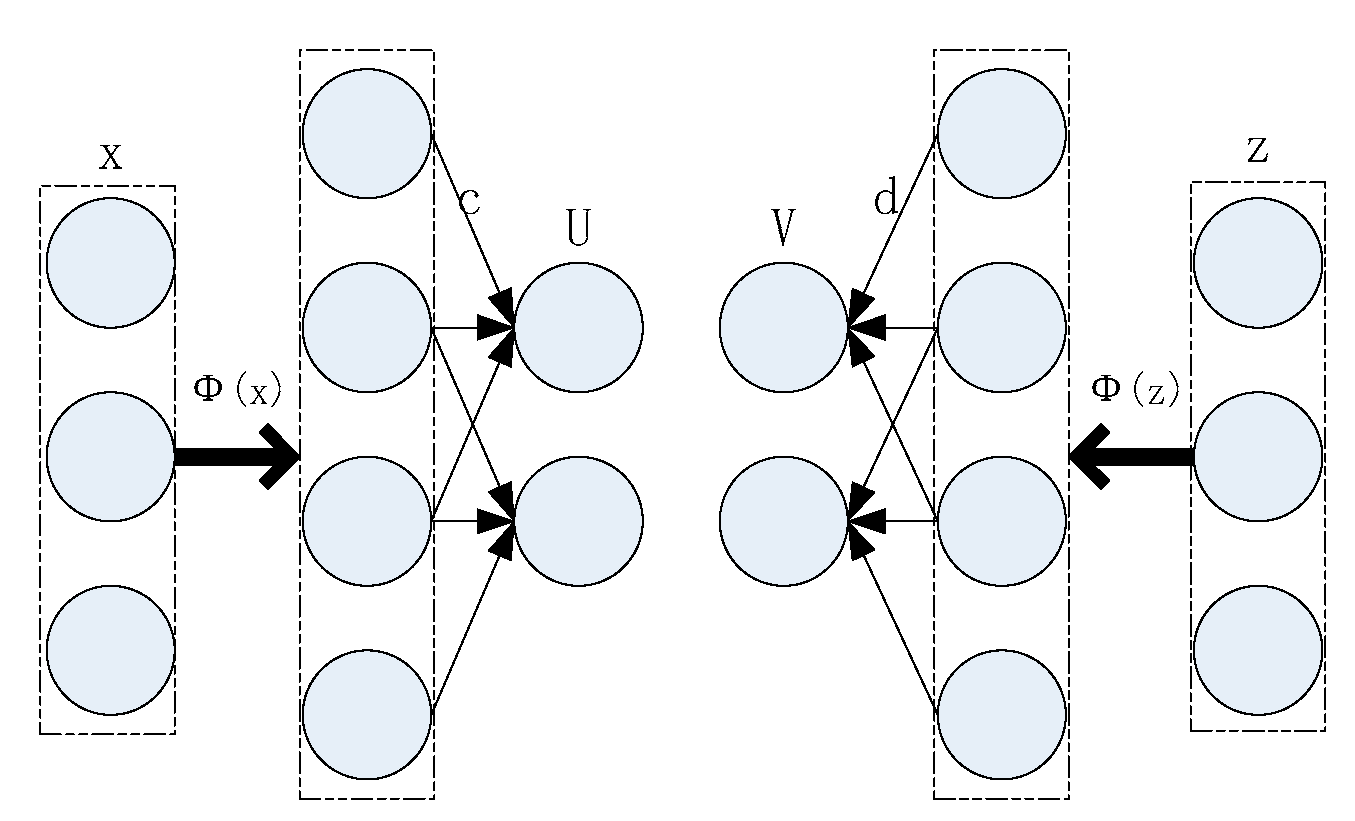
2.1. kCCA Transformation and NIFs Extraction
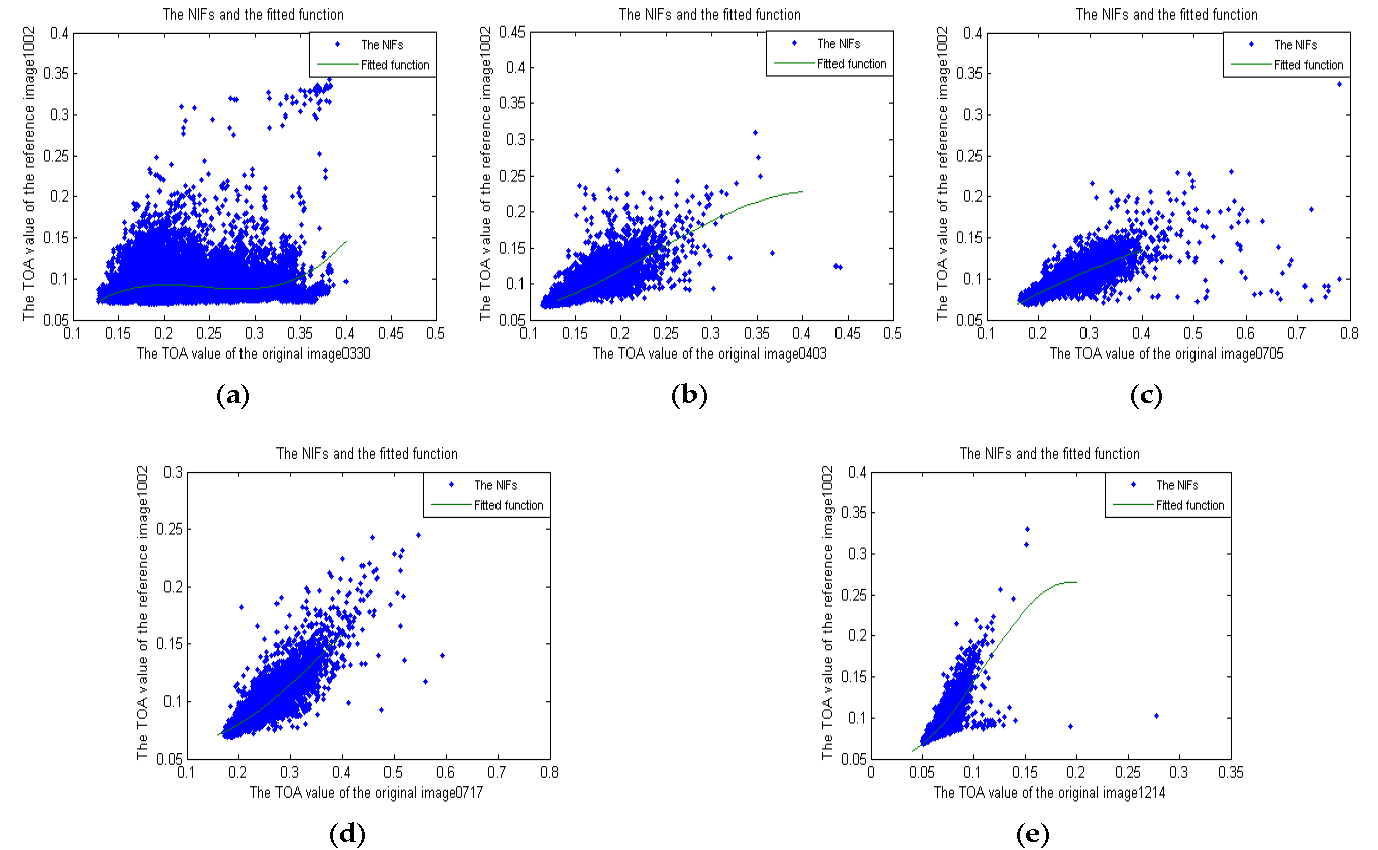
2.2. Fitting Non-Linear Transformation for Radiometric Normalization
3. Data and Results
3.1. Test Data
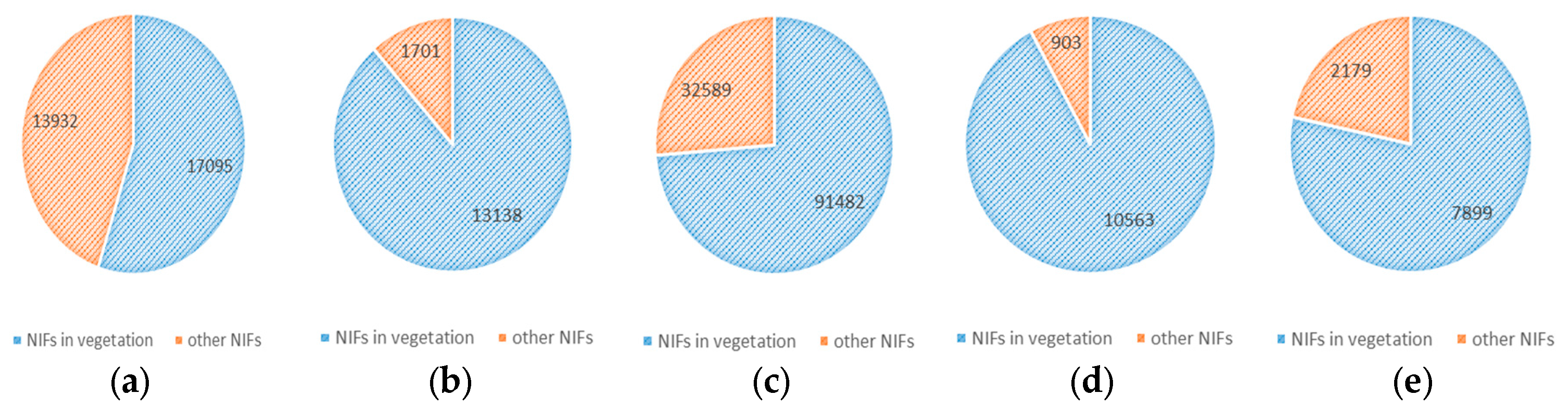
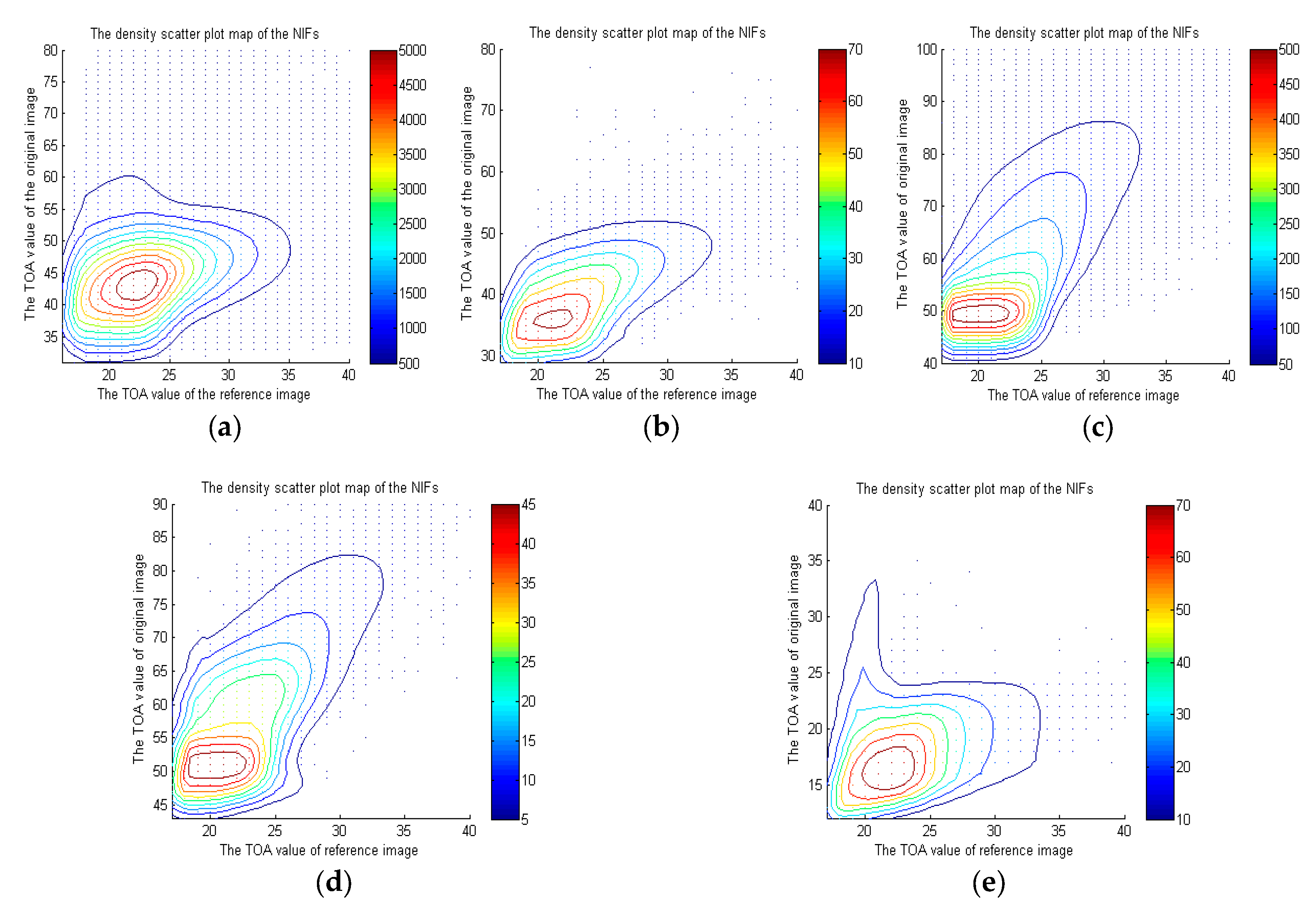
3.2. NIFs Distribution Map
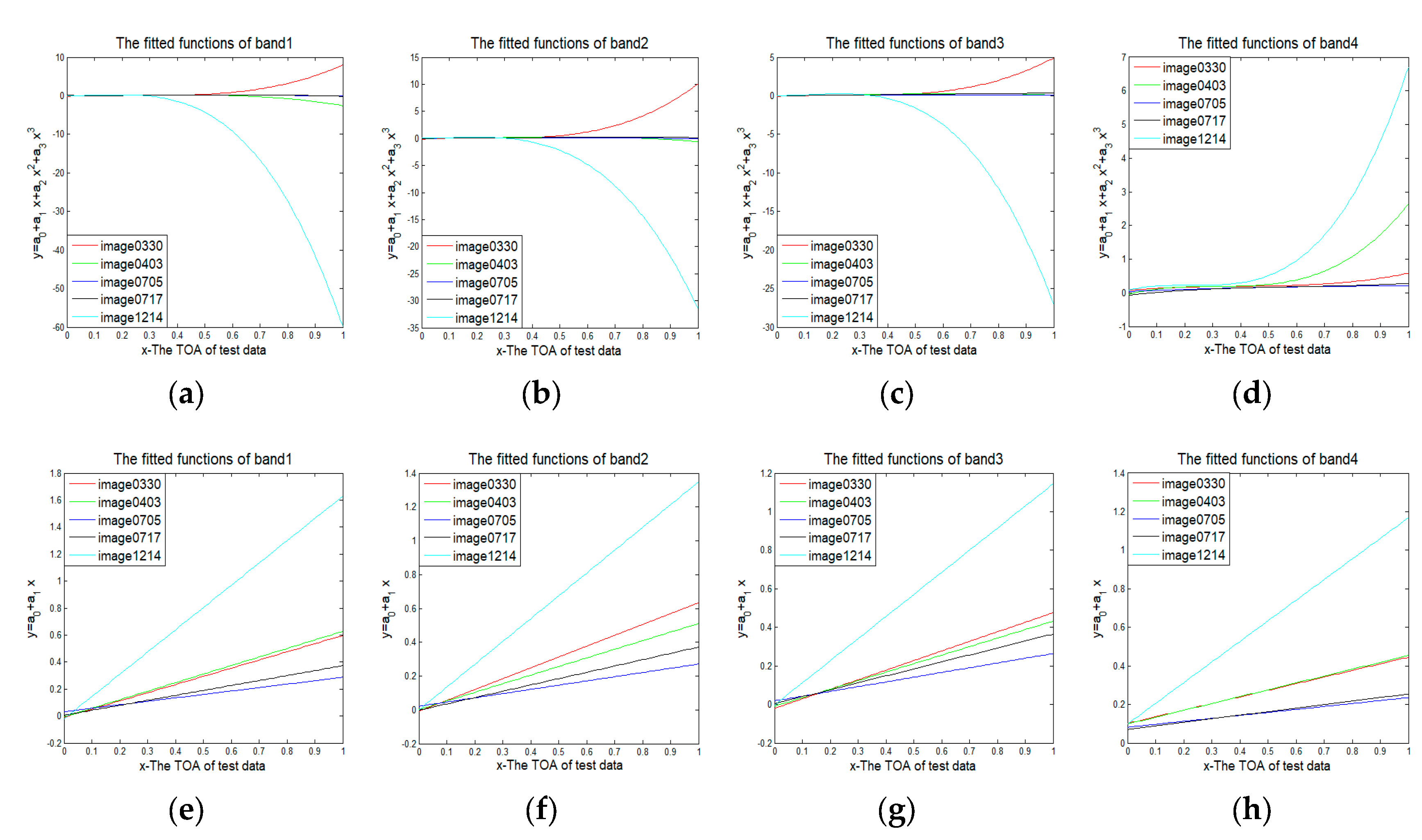
3.3. Derive Nonlinear Transformations from NIFs
3.4. Radiometric Normalization Results
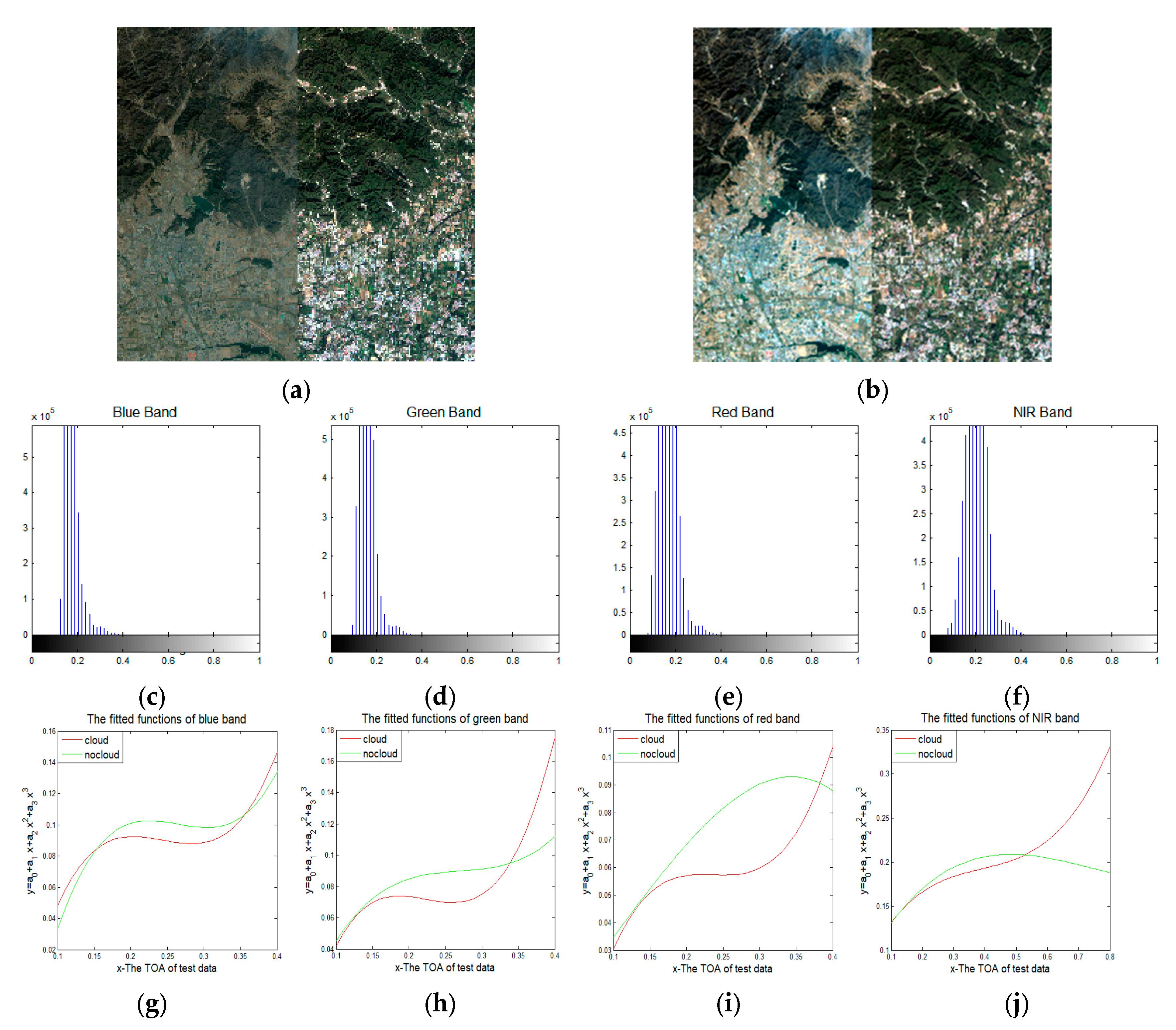
3.4.1. Clouds Pixels in the Image
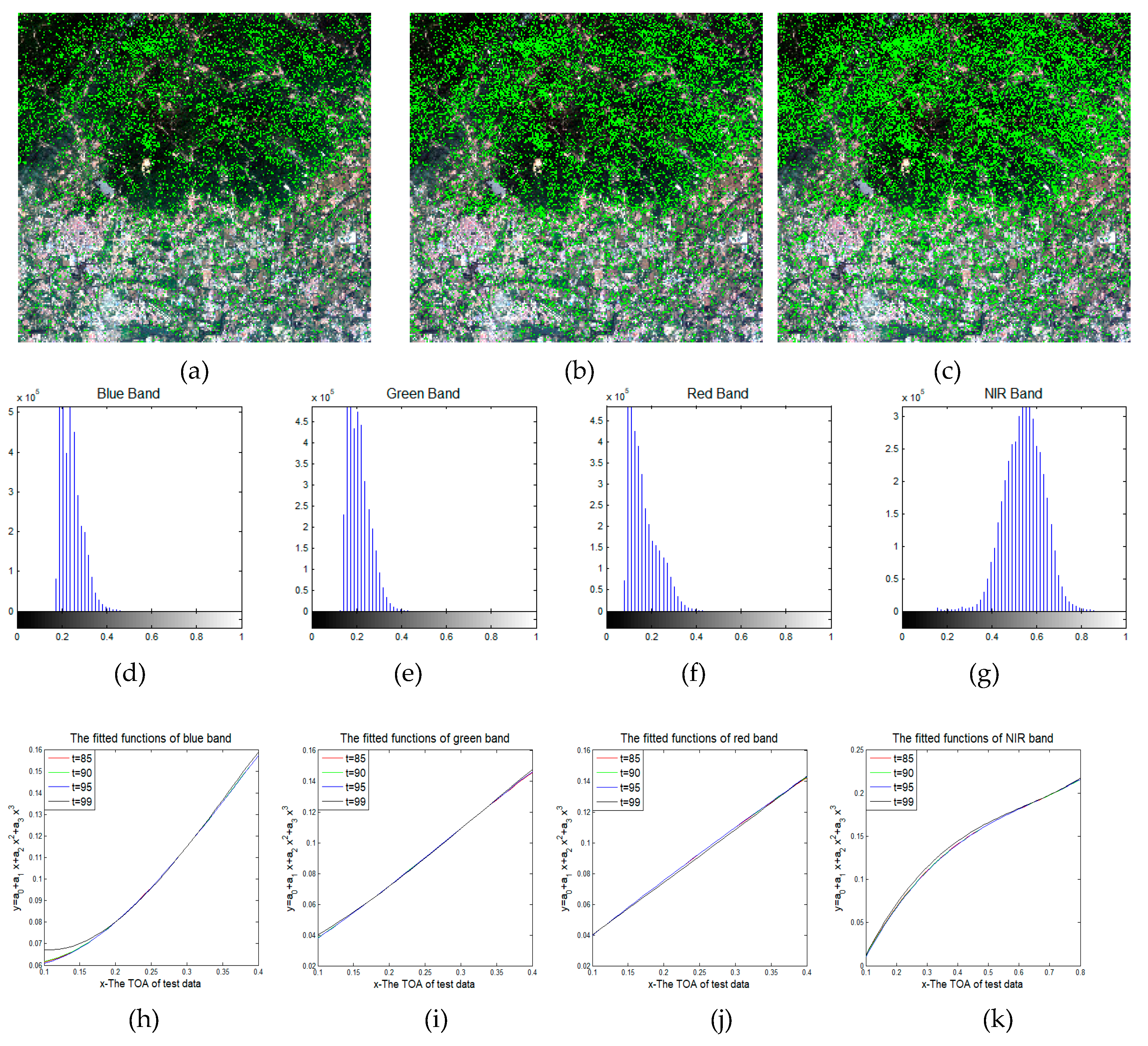
3.4.2. The Threshold Parameters τ for NIFs Extraction
3.4.3. Quantitative Comparison of the Radiometric Normalization Results
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | Directory of open access journals |
| TLA | Three letter acronym |
| LD | linear dichroism |
References
- Bai, Y.; Tang, P.; Hu, C.M. Kernel Mad Algorithm for Relative Radiometric Normalization. Int. Arch. Photogramm. 2016, 3, 49–53. [Google Scholar] [CrossRef]
- Song, C.; Woodcock, C.E.; Seto, K.C.; Lenney, M.P.; Macomber, S.A. Classification and change detection using Landsat TM data: When and how to correct atmospheric effects? Remote Sens. Environ. 2001, 75, 230–244. [Google Scholar] [CrossRef]
- Yang, Q.-H.; Qi, J.-W.; Sun, Y. The application of high-resolution satellite remotely sensed data to landuse dynamic monitoring. Remote Sens. Land Resour. 2002, 4, 20–27. [Google Scholar]
- Yang, X.J.; Lo, C.P. Relative radiometric normalization performance for change detection from multi-date satellite images. Photogramm. Eng. Remote Sens. 2000, 66, 967–980. [Google Scholar]
- Barazzetti, L.; Gianinetto, M.; Scaioni, M. Radiometric Normalization with Multi-image Pseudo-invariant Features. In Proceedings of the Fourth International Conference on Remote Sensing and Geoinformation of the Environment (Rscy2016), Paphos, Cyprus, 4–8 April 2016. [Google Scholar]
- Hu, C.M.; Tang, P. Automatic algorithm for relative radiometric normalization of data obtained from Landsat TM and HJ-1A/B charge-coupled device sensors. J. Appl. Remote Sens. 2012, 6. [Google Scholar] [CrossRef]
- Volpi, M.; Camps-Valls, G.; Tuia, D. Spectral alignment of multi-temporal cross-sensor images with automated kernel canonical correlation analysis. J. Photogramm. Remote Sens. 2015, 107, 50–63. [Google Scholar] [CrossRef]
- Berk, A.; Anderson, G.P. Impact of MODTRAN®5.1 on atmospheric compensation. In Proceedings of the 2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 6–11 July 2008; pp. 127–129. [Google Scholar]
- El Hajj, M.; Begue, A.; Lafrance, B.; Hagolle, O.; Dedieu, G.; Rumeau, M. Relative radiometric normalization and atmospheric correction of a SPOT 5 time series. Sensors 2008, 8, 2774–2791. [Google Scholar] [CrossRef] [PubMed]
- Philpot, W.; Ansty, T. Analytical Description of Pseudoinvariant Features. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2016–2021. [Google Scholar] [CrossRef]
- Canty, M.J.; Nielsen, A.A.; Schmidt, M. Automatic radiometric normalization of multitemporal satellite imagery. Remote Sens. Environ. 2004, 91, 441–451. [Google Scholar] [CrossRef]
- De Carvalh, O.A.; Guimaraes, R.F.; Silva, N.C.; Gillespie, A.R.; Gomes, R.A.T.; Silva, C.R.; de Carvalho, A.P.F. Radiometric Normalization of Temporal Images Combining Automatic Detection of Pseudo-Invariant Features from the Distance and Similarity Spectral Measures, Density Scatterplot Analysis, and Robust Regression. Remote Sens. 2013, 5, 2763–2794. [Google Scholar] [CrossRef]
- Schott, J.R.; Salvaggio, C.; Volchok, W.J. Radiometric Scene Normalization Using Pseudo-invariant Features. Remote Sens. Environ. 1988, 6, 1–16. [Google Scholar] [CrossRef]
- Andrefouet, S.; Muller-Karger, F.E.; Hochberg, E.J.; Hu, C.M.; Carder, K.L. Change detection in shallow coral reef environments using Landsat 7 ETM+ data. Remote Sens. Environ. 2001, 78, 150–162. [Google Scholar] [CrossRef]
- Chen, X.X.; Vierling, L.; Deering, D. A simple and effective radiometric correction method to improve landscape change detection across sensors and across time. Remote Sens. Environ. 2005, 98, 63–79. [Google Scholar] [CrossRef]
- Kennedy, R.E.; Cohen, W.B. Automated designation of tie-points for image-to-image coregistration. Int. J. Remote Sens. 2003, 24, 3467–3490. [Google Scholar] [CrossRef]
- Hall, F.G.; Strebel, D.E.; Nickeson, J.E.; Goetz, S.J. Radiometric Rectification—Toward a Common Radiometric Response among Multidate, Multisensor Images. Remote Sens. Environ. 1991, 35, 11–27. [Google Scholar] [CrossRef]
- Elvidge, C.D.; Yuan, D.; Weerackoon, R.D.; Lunetta, R.S. Relative Radiometric Normalization of Landsat Multispectral Scanner (Mss) Data Using an Automatic Scattergram-Controlled Regression. Photogramm. Eng. Remote Sens. 1995, 61, 1255–1260. [Google Scholar]
- Yu, X.; Chen, Y. Relative radiometric normalization of remotely sensed images based on improved automatic scattergram-controlled regression. Opt. Tech. 2007, 22, 185–188. [Google Scholar]
- Canty, M.J.; Nielsen, A.A. Unsupervised classification of changes in multispectral satellite imagery. Proc. SPIE 2004, 5573, 356–363. [Google Scholar] [CrossRef]
- Canty, M.J.; Nielsen, A.A. Automatic radiometric normalization of multitemporal satellite imagery with the iteratively re-weighted MAD transformation. Remote Sens. Environ. 2008, 112, 1025–1036. [Google Scholar] [CrossRef]
- Nielsen, A.A. Multiset canonical correlations analysis and multispectral, truly multitemporal remote sensing data. IEEE Trans. Image Process. 2002, 11, 293–305. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, A.A.; Conradsen, K.; Simpson, J.J. Multivariate alteration detection (MAD) and MAF postprocessing in multispectral, bitemporal image data: New approaches to change detection studies. Remote Sens. Environ. 1998, 64, 1–19. [Google Scholar] [CrossRef]
- Sadeghi, V.; Ebadi, H.; Ahmadi, F.F. A new model for automatic normalization of multitemporal satellite images using Artificial Neural Network and mathematical methods. Appl. Math. Model. 2013, 37, 6437–6445. [Google Scholar] [CrossRef]
- Helmer, E.H.; Ruefenacht, B. A comparison of radiometric normalization methods when filling cloud gaps in Landsat imagery. Can. J. Remote Sens. 2007, 33, 457–458. [Google Scholar] [CrossRef]
- Canty, M.J.; Nielsen, A.A. Linear and kernel methods for multivariate change detection. Comput. Geosci. 2012, 38, 107–114. [Google Scholar] [CrossRef]
- Huang, S.Y.; Lee, M.H.; Hsiao, C.K. Nonlinear measures of association with kernel canonical correlation analysis and applications. J. Stat. Plan. Inference 2009, 139, 2162–2174. [Google Scholar] [CrossRef]
- Nielsen, A.A. Kernel Methods in Orthogonalization of Multi- and Hypervariate Data. In Proceedings of the 2009 16th IEEE International Conference on Image Processing (ICIP), Cairo, Egypt, 7–10 November 2009; pp. 3729–3732. [Google Scholar]
- Nielsen, A.A.; Vestergaard, J.S. A Kernel Version of Multivariate Alteration Detection. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Melbourne, VIC, Australia, 21–26 July 2013; pp. 3451–3454. [Google Scholar]
- Yoshida, K.; Yoshimoto, J.; Doya, K. Sparse kernel canonical correlation analysis for discovery of nonlinear interactions in high-dimensional data. BMC Bioinform. 2017, 18. [Google Scholar] [CrossRef] [PubMed]
- Shao, J.; Wang, L.Q.; Zhao, Z.C.; Su, F.; Cai, A.N. Deep canonical correlation analysis with progressive and hypergraph learning for cross-modal retrieval. Neurocomputing 2016, 214, 618–628. [Google Scholar] [CrossRef]
- Hotelling, H. Relations between two sets of variates. Biometrika 1936, 28, 321–377. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Bruzzone, L. Kernel Methods for Remote Sensing Data Analysis; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Shawe-Taylor, J.; Cristianini, N. Kernel Methods for Pattern Analysis; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Nielsen, A.A.; Conradsen, K.; Andersen, O. A change oriented extension of EOF analysis applied to the 1996–1997 AVHRR sea surface temperature data. Phys. Chem. Earth 2002, 27, 1379–1386. [Google Scholar] [CrossRef]
- Hu, C.M.; Bai, Y.; Tang, P. Automatic cloud detection for GF-4 series images. J. Remote Sens. 2018, 22, 132–142. [Google Scholar]





| Satellite Performance | Technical Capability | |
|---|---|---|
| Satellite Orbit | type | Solar synchronous circular orbit |
| Average orbit height | 644.5 km | |
| descending/ascending nod sun-synchronous | 10:30 a.m. | |
| regressive period | 41 days | |
| Revisit/Coverage characteristic | Revisit: 4 days for 2/8 m camera under side sway | |
| Coverage: 4 days for 16 m camera; 41 days for 2/8 m camera; | ||
| High resolution imaging | Spectrum/μm | Panchromatic: 0.45–0.90μm |
| B1: 0.45–0.52 μm; B2: 0.52–0.59 μm; B3: 0.63–0.69 μm; B4: 0.77–0.89 μm; | ||
| resolution | Panchromatic: better than 2 m Multispectral: better than 8 m | |
| Swath width (km) | >60 | |
| Wide imaging | Spectrum/μm | B1: 0.45–0.52 μm; B2: 0.52–0.59 μm; B3: 0.63–0.69 μm; B4: 0.77–0.89 μm; |
| resolution | Better than 16 m | |
| Swath width (km) | >800 | |
| Image Name | Image Date |
|---|---|
| Image0705 | 5 July 2013 |
| Image0717 | 17 July 2013 |
| Image1002reference | 2 October 2013 |
| Image1214 | 14 December 2013 |
| Image0330 | 30 March 2014 |
| Image0403 | 3 April 2014 |
| a3 | a2 | a1 | a0 | Mr | Sr | ||
|---|---|---|---|---|---|---|---|
| Image 0330 | Band1 | 18.3284 | −13.3953 | 3.1748 | −0.1532 | 0.019194 | 0.000002 |
| Band2 | 21.5494 | −14.4433 | 3.1393 | −0.1489 | 0.019906 | 0.000003 | |
| Band 3 | 10.9105 | −7.7441 | 1.8255 | −0.0855 | 0.02473 | 0.000004 | |
| Band4 | 1.4785 | −1.7238 | 0.7561 | 0.072 | 0.035371 | 0.000007 | |
| Image 0403 | Band1 | −7.367 | 5.2422 | −0.5349 | 0.0748 | 0.011784 | 0.000012 |
| Band2 | −3.0287 | 2.4336 | −0.0403 | 0.0372 | 0.01312 | 0.000013 | |
| Band 3 | −1.8955 | 2.0456 | −0.099 | 0.0288 | 0.018398 | 0.000015 | |
| Band4 | 7.3705 | −6.866 | 2.1832 | −0.046 | 0.030512 | 0.000037 | |
| Image 0705 | Band1 | −0.7959 | 0.4918 | 0.194 | 0.0297 | 0.010231 | 0.000024 |
| Band2 | −0.4582 | 0.0524 | 0.3273 | 0.0071 | 0.011725 | 0.00002 | |
| Band 3 | 0.173 | −0.4517 | 0.4073 | 0.0041 | 0.015785 | 0.000023 | |
| Band4 | 0.0878 | −0.2848 | 0.3699 | 0.0379 | 0.0341 | 0.000083 | |
| Image 0717 | Band1 | −2.2136 | 2.4316 | −0.445 | 0.0895 | 0.008238 | 0.000082 |
| Band2 | −0.7765 | 0.7466 | 0.1471 | 0.0187 | 0.009817 | 0.00005 | |
| Band 3 | −0.0018 | 0.0113 | 0.3381 | 0.0061 | 0.013293 | 0.000033 | |
| Band4 | 0.6642 | −1.2344 | 0.9188 | −0.0681 | 0.031373 | 0.000042 | |
| Image 1214 | Band1 | −87.0617 | 28.3288 | −1.1949 | 0.0675 | 0.010096 | 0.000023 |
| Band2 | −44.4402 | 12.7071 | 0.2623 | 0.02687 | 0.011614 | 0.000023 | |
| Band 3 | −41.5801 | 14.5948 | −0.1363 | 0.0267 | 0.017183 | 0.000032 | |
| Band4 | 13.8154 | −9.1873 | 2.0127 | 0.07651 | 0.026603 | 0.000044 |
| Total number of NIFs | 11466 | 27596 | 41421 | 53453 |
| NIFs in vegetation area | 10563 | 25319 | 38021 | 49097 |
| Ratio of NIFs in vegetation area (%) | 92.12 | 91.75 | 91.79 | 91.85 |
| RMSE | |||
|---|---|---|---|
| image pair (imag0330, image1002) | |||
| Band 1 | 0.09 | 0.32 | 0.04 |
| Band 2 | 0.09 | 0.40 | 0.03 |
| Band 3 | 0.12 | 0.45 | -0.05 |
| Band 4 | 0.06 | 0.36 | 0.74 |
| image pair (imag0403, image1002) | |||
| Band 1 | 0.07 | 0.80 | 0.02 |
| Band 2 | 0.07 | 0.77 | 0.05 |
| Band 3 | 0.10 | 0.71 | -0.02 |
| Band 4 | 0.06 | 0.51 | 0.69 |
| image pair (imag0705, image1002) | |||
| Band 1 | 0.15 | 0.80 | 0.07 |
| Band 2 | 0.15 | 0.77 | 0.09 |
| Band 3 | 0.13 | 0.78 | 0.09 |
| Band 4 | 0.42 | 0.40 | 0.24 |
| image pair (imag0717, image1002) | |||
| Band 1 | 0.15 | 0.89 | 0.07 |
| Band 2 | 0.14 | 0.87 | 0.08 |
| Band 3 | 0.11 | 0.86 | 0.07 |
| Band 4 | 0.38 | 0.46 | 0.23 |
| image pair (imag1214, image1002) | |||
| Band 1 | 0.03 | 0.81 | 0.43 |
| Band 2 | 0.02 | 0.81 | 0.78 |
| Band 3 | 0.02 | 0.73 | 0.75 |
| Band 4 | 0.11 | 0.67 | -0.04 |
| RMSECCA | RMSEkCCA | RMSEH | CCA | kCCA | H | ||||
|---|---|---|---|---|---|---|---|---|---|
| image pair (imag0330, image1002) | |||||||||
| Band 1 | 0.02 | 0.02 | 0.02 | 0.32 | 0.42 | 0.32 | 0.58 | 0.69 | 0.98 |
| Band 2 | 0.02 | 0.02 | 0.02 | 0.40 | 0.47 | 0.39 | 0.77 | 0.78 | 0.97 |
| Band 3 | 0.03 | 0.02 | 0.03 | 0.45 | 0.47 | 0.41 | 0.73 | 0.75 | 0.98 |
| Band 4 | 0.04 | 0.03 | 0.04 | 0.36 | 0.37 | 0.37 | 0.81 | 0.82 | 0.94 |
| image pair (imag0403 image1002) | |||||||||
| Band 1 | 0.01 | 0.01 | 0.01 | 0.81 | 0.81 | 0.80 | 0.95 | 0.95 | 0.98 |
| Band 2 | 0.01 | 0.01 | 0.01 | 0.78 | 0.78 | 0.77 | 0.93 | 0.93 | 0.99 |
| Band 3 | 0.02 | 0.02 | 0.02 | 0.71 | 0.72 | 0.71 | 0.86 | 0.93 | 0.99 |
| Band 4 | 0.06 | 0.03 | 0.04 | 0.51 | 0.55 | 0.55 | 0.74 | 0.89 | 0.95 |
| image pair (imag0705, image1002): | |||||||||
| Band 1 | 0.02 | 0.01 | 0.01 | 0.80 | 0.83 | 0.81 | 0.92 | 0.93 | 1.00 |
| Band 2 | 0.02 | 0.01 | 0.01 | 0.77 | 0.80 | 0.78 | 0.98 | 0.94 | 0.91 |
| Band 3 | 0.03 | 0.01 | 0.02 | 0.78 | 0.79 | 0.77 | 0.97 | 0.91 | 0.88 |
| Band 4 | 0.06 | 0.03 | 0.04 | 0.41 | 0.42 | 0.38 | 0.82 | 0.81 | 0.99 |
| image pair (imag0717, image1002): | |||||||||
| Band 1 | 0.01 | 0.01 | 0.01 | 0.89 | 0.89 | 0.89 | 0.94 | 0.94 | 0.99 |
| Band 2 | 0.01 | 0.01 | 0.01 | 0.87 | 0.87 | 0.87 | 0.94 | 0.94 | 0.98 |
| Band 3 | 0.02 | 0.01 | 0.01 | 0.86 | 0.86 | 0.86 | 0.93 | 0.93 | 0.98 |
| Band 4 | 0.06 | 0.03 | 0.04 | 0.47 | 0.47 | 0.46 | 0.88 | 0.88 | 0.99 |
| image pair (imag1214, image1002): | |||||||||
| Band 1 | 0.01 | 0.01 | 0.01 | 0.83 | 0.85 | 0.85 | 0.81 | 0.85 | 0.85 |
| Band 2 | 0.01 | 0.01 | 0.01 | 0.81 | 0.82 | 0.82 | 0.86 | 0.88 | 0.88 |
| Band 3 | 0.02 | 0.02 | 0.02 | 0.74 | 0.76 | 0.74 | 0.74 | 0.79 | 0.86 |
| Band 4 | 0.03 | 0.03 | 0.03 | 0.67 | 0.68 | 0.67 | 0.77 | 0.90 | 0.92 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, Y.; Tang, P.; Hu, C. kCCA Transformation-Based Radiometric Normalization of Multi-Temporal Satellite Images. Remote Sens. 2018, 10, 432. https://doi.org/10.3390/rs10030432
Bai Y, Tang P, Hu C. kCCA Transformation-Based Radiometric Normalization of Multi-Temporal Satellite Images. Remote Sensing. 2018; 10(3):432. https://doi.org/10.3390/rs10030432
Chicago/Turabian StyleBai, Yang, Ping Tang, and Changmiao Hu. 2018. "kCCA Transformation-Based Radiometric Normalization of Multi-Temporal Satellite Images" Remote Sensing 10, no. 3: 432. https://doi.org/10.3390/rs10030432
APA StyleBai, Y., Tang, P., & Hu, C. (2018). kCCA Transformation-Based Radiometric Normalization of Multi-Temporal Satellite Images. Remote Sensing, 10(3), 432. https://doi.org/10.3390/rs10030432





