Precise Orbit Determination of FY-3C with Calibration of Orbit Biases in BeiDou GEO Satellites
Abstract
:1. Introduction
2. BeiDou Orbit Error Analysis and Mitigation
2.1. Assessment of BeiDou Precise Orbit Products
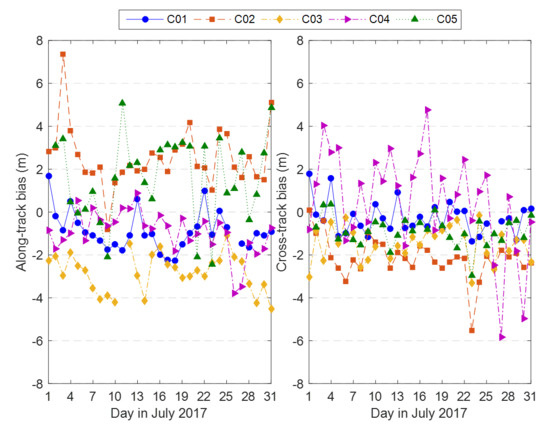
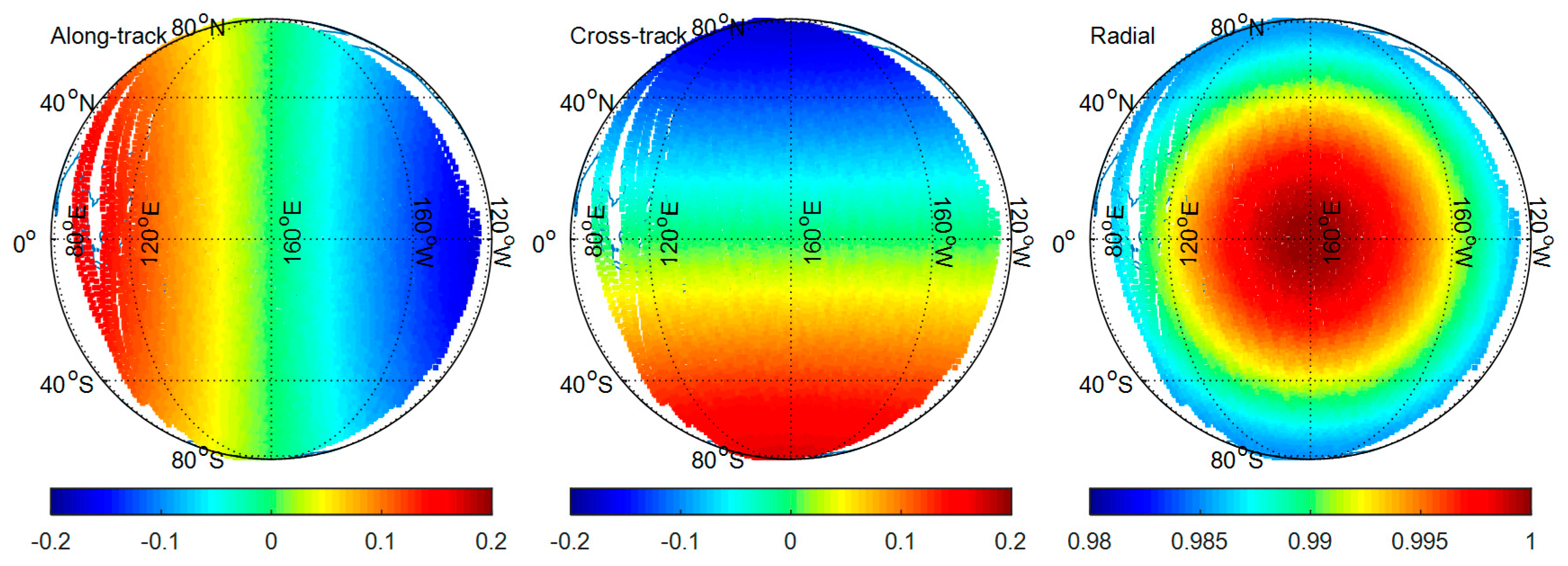
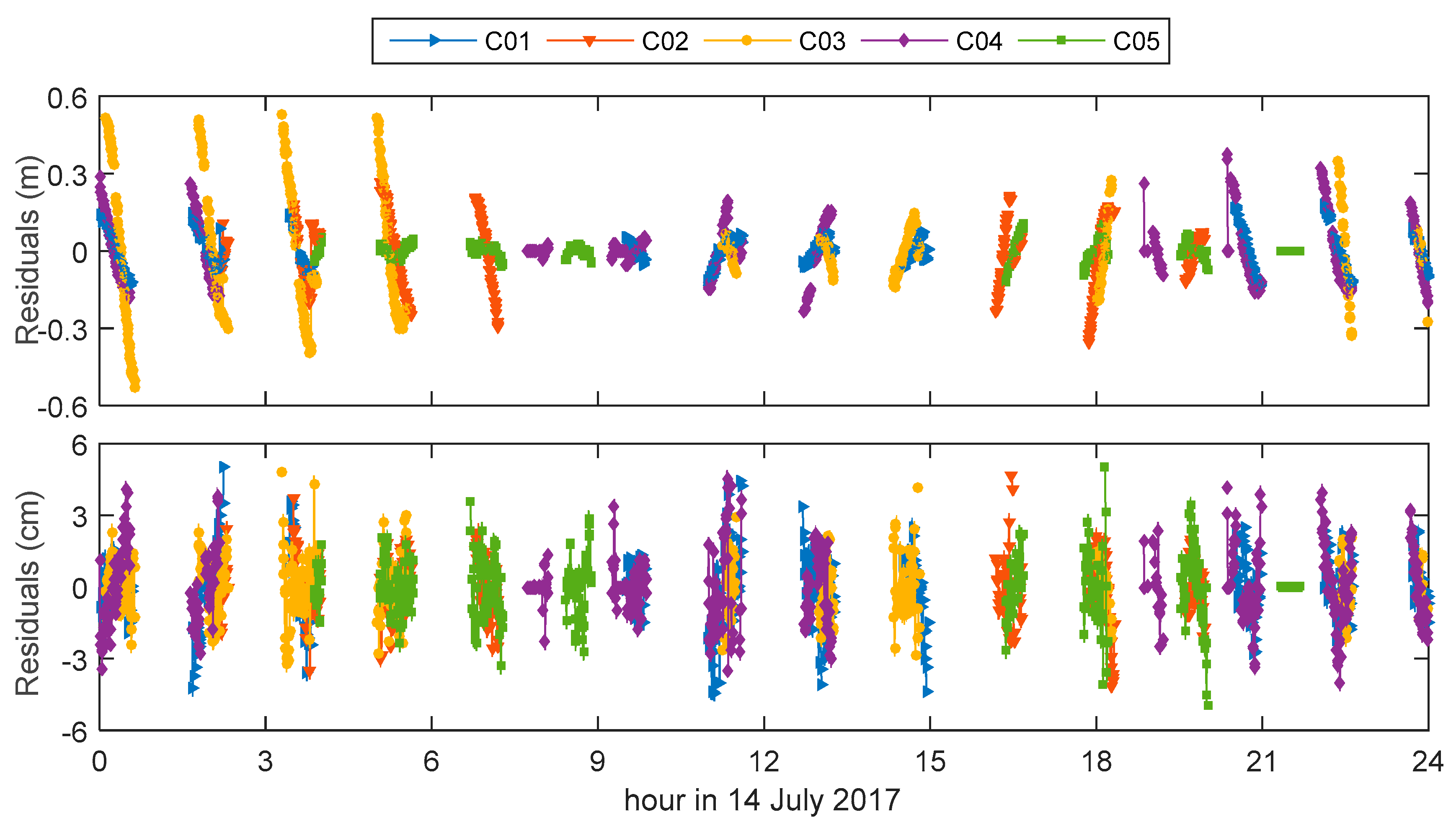
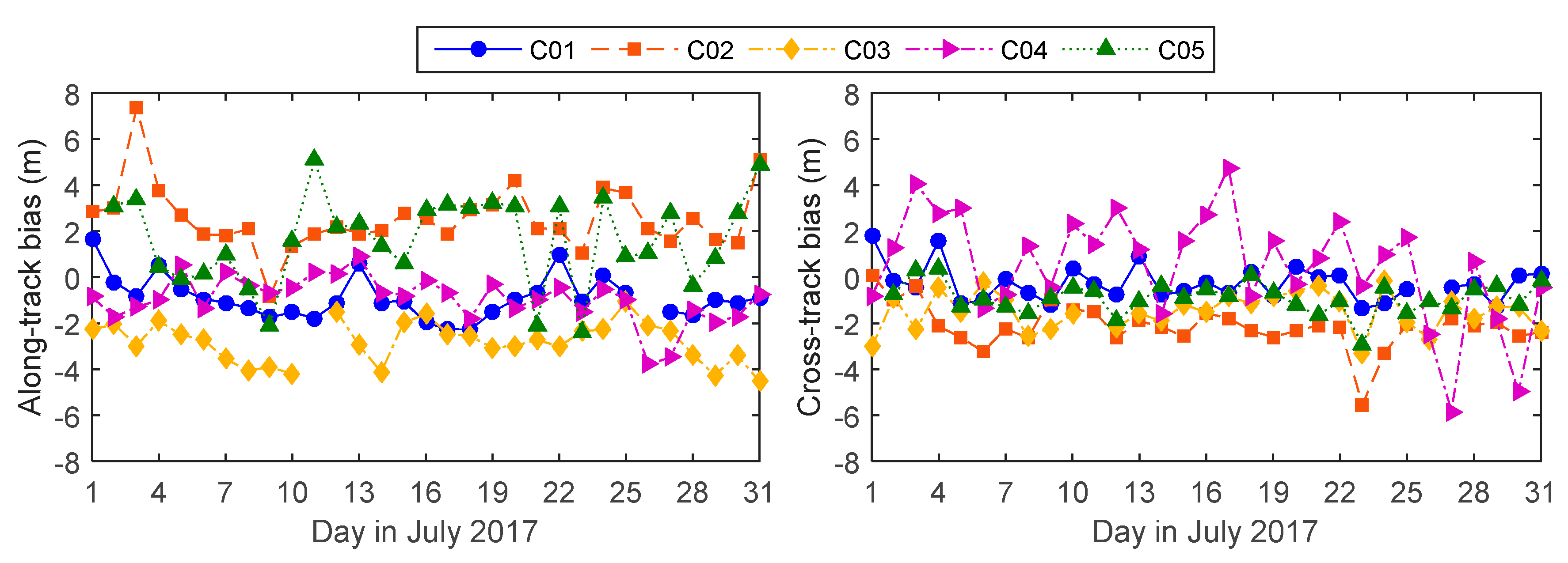
2.2. Characteristics of BeiDou GEO Orbit Errors
2.3. Mitigation of BeiDou GEO Orbit Errors
3. FY-3C POD Results and Analysis
3.1. Strategies of FY-3C POD
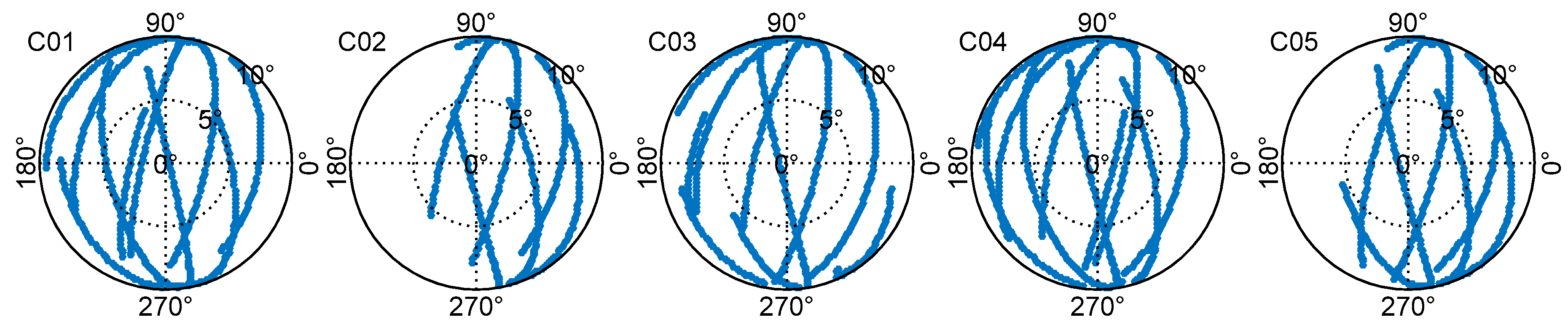
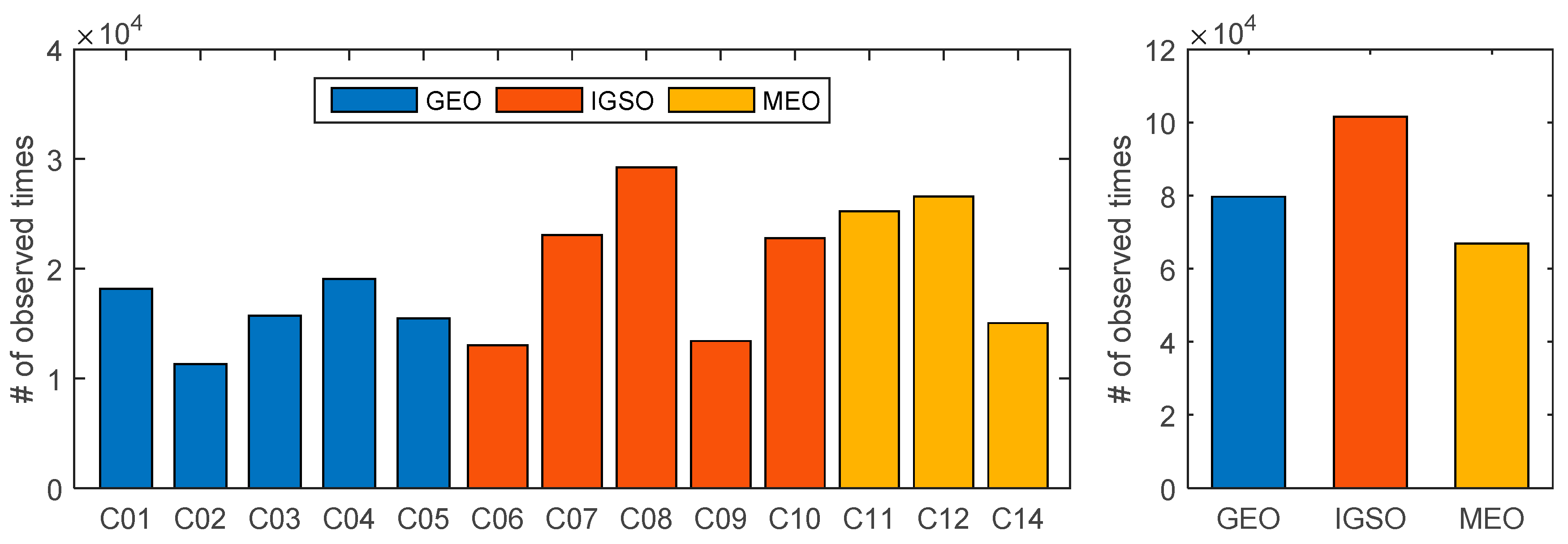
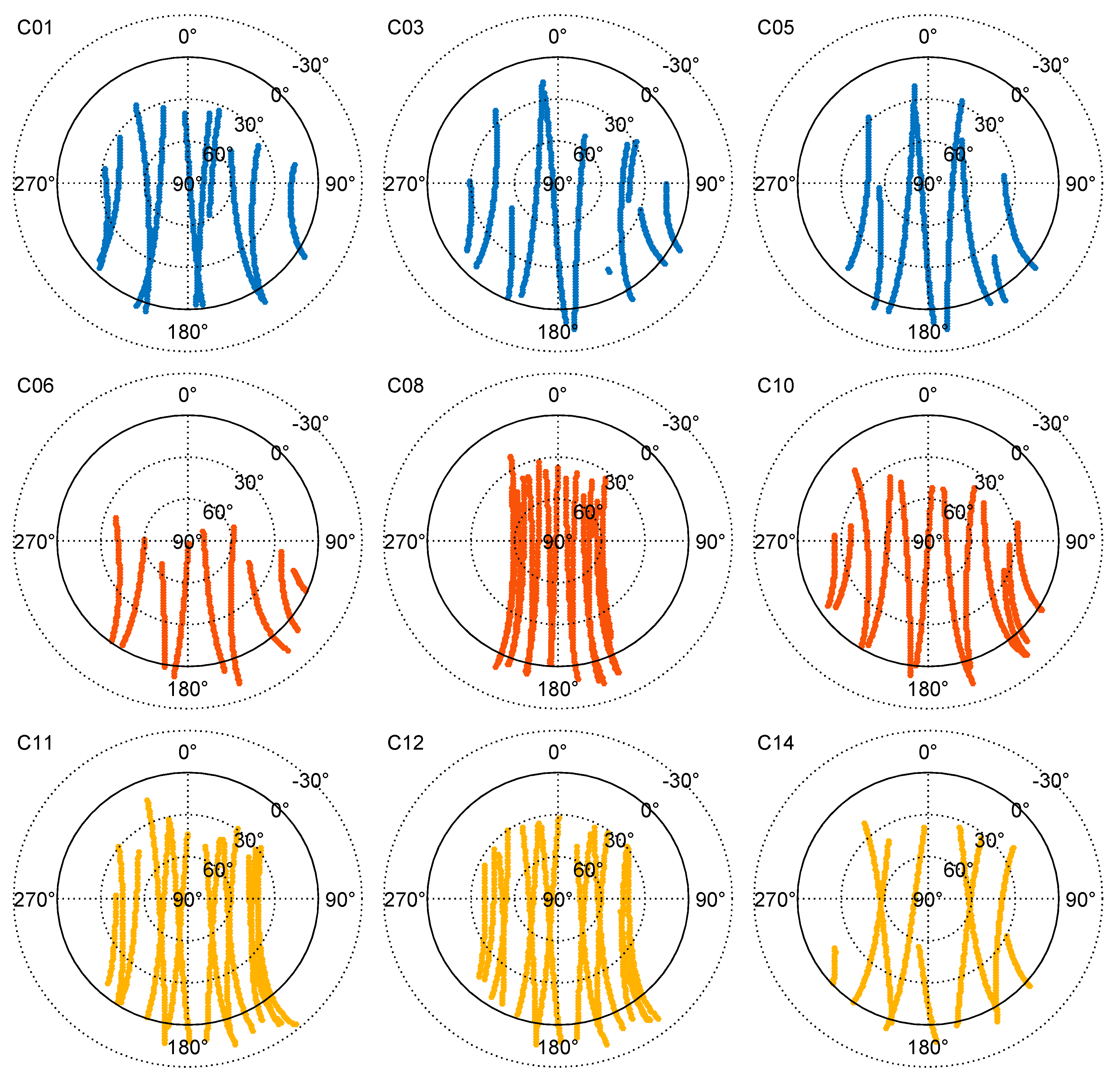
3.2. Distribution of FY-3C BeiDou Observations
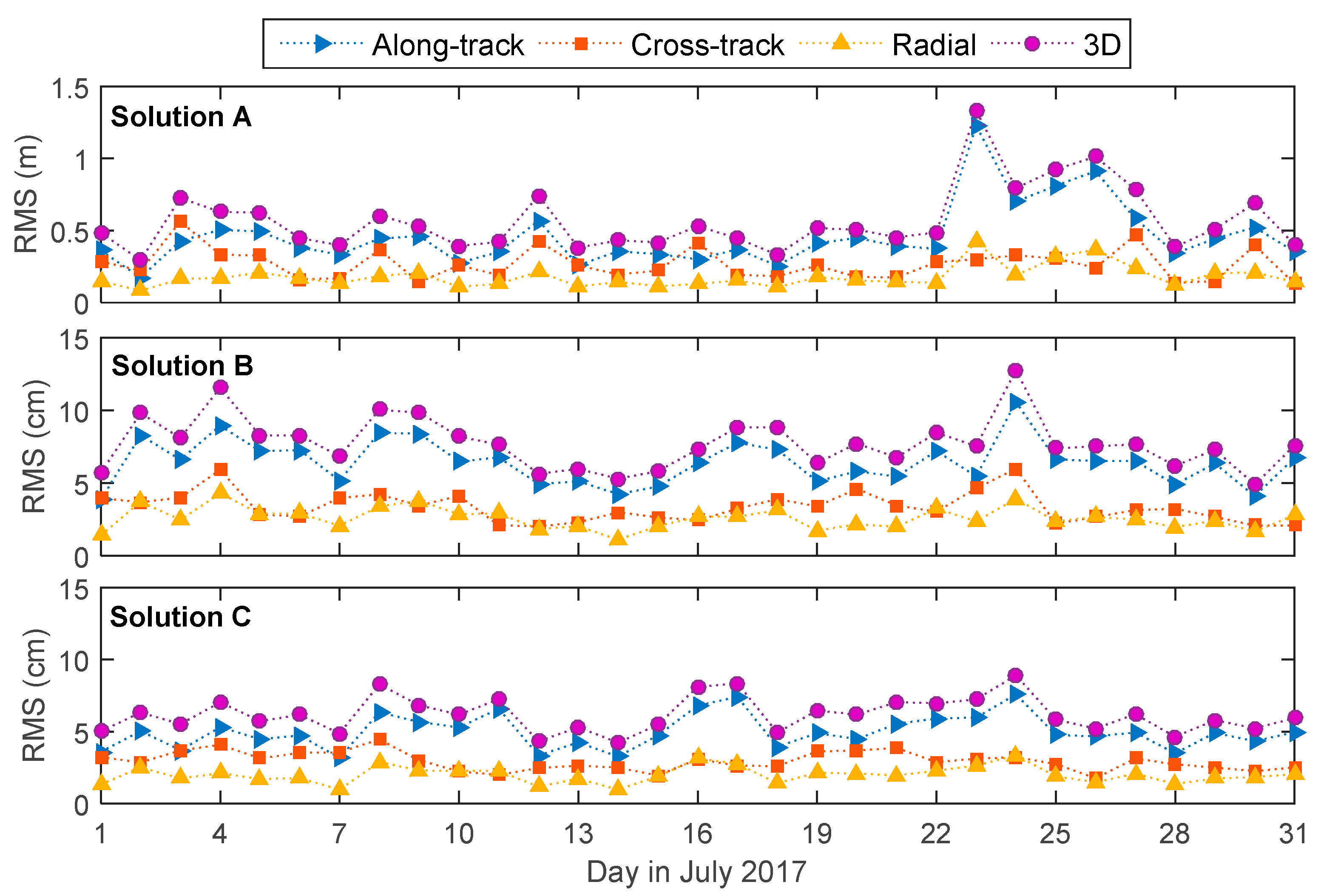
3.3. Validation of FY-3C Orbit Precision
3.4. Statistics of Observation Residuals
3.5. Assessment of Calibrated BeiDou GEO Orbits
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kang, Z.G.; Tapley, B.; Bettadpur, S.; Ries, J.; Nagel, P.; Pastor, R. Precise orbit determination for the GRACE mission using only GPS data. J. Geodesy 2006, 80, 322–331. [Google Scholar] [CrossRef]
- Bruce, H.; Yoaz, B.; Willy, B.; Shailen, D.; Pascal, W. One-Centimeter Orbit Determination for Jason-1: New GPS-Based Strategies. Mar. Geodesy 2004, 27, 299–318. [Google Scholar]
- Bock, H.; Jäggi, A.; Meyer, U.; Visser, P.; van den Ijssel, J.; van Helleputte, T.; Heinze, M.; Hugentobler, U. GPS-derived orbits for the GOCE satellite. J. Geodesy 2011, 85, 807–818. [Google Scholar] [CrossRef]
- Bock, H.; Jäggi, A.; Švehla, D.; Beutler, G.; Hugentobler, U.; Visser, P. Precise orbit determination for the GOCE satellite using GPS. Adv. Space Res. 2007, 39, 1638–1647. [Google Scholar] [CrossRef]
- Van den IJssel, J.; Encarnacao, J.; Doornbos, E.; Visser, P. Precise science orbits for the Swarm satellite constellation. Adv. Space Res. 2015, 56, 1042–1055. [Google Scholar] [CrossRef]
- Guo, J.; Zhao, X.; Liu, X.; Liu, J.; Zhou, Q. Quality assessment of onboard GPS receiver and its combination with DORIS and SLR for Haiyang 2A precise orbit determination. Sci. China Earth Sci. 2015, 138–150. [Google Scholar] [CrossRef]
- Min, L.; Qu, L.; Zhao, Q.; Jing, G.; Xing, S.; Li, X. Precise Point Positioning with the BeiDou Navigation Satellite System. Sensors 2014, 14, 927–943. [Google Scholar]
- Chen, X.; Zhao, S.; Wang, M.; Lu, M. Space-borne BDS receiver for LING QIAO satellite: Design, implementation and preliminary in-orbit experiment results. GPS Solut. 2015, 20, 837–847. [Google Scholar] [CrossRef]
- Zhao, S.; Chen, X.; Yuan, S.; Kuang, L.; Lu, M. Space-borne BDS and GPS Receiver of LING QIAO: Results over Two Years In-Orbit Operation. In Proceedings of the China Satellite Navigation Conference, Shanghai, China, 23–25 May 2017; pp. 753–762. [Google Scholar]
- Liu, J.H.; Gu, D.F.; Ju, B.; Yao, J.; Duan, X.J.; Yi, D.Y. Basic performance of BeiDou-2 navigation satellite system used in LEO satellites precise orbit determination. Chin. J. Aeronaut. 2014, 27, 1251–1258. [Google Scholar] [CrossRef]
- Xiong, C.; Lu, C.F.; Zhu, J.; Ding, H.P. Orbit determination using real tracking data from FY3C-GNOS. Adv. Space Res. 2017, 60, 543–556. [Google Scholar] [CrossRef]
- Bi, Y.M.; Yang, Z.D.; Zhang, P.; Sun, Y.Q.; Bai, W.H.; Du, Q.F.; Yang, G.L.; Chen, J.; Liao, M. An introduction to China FY3 radio occultation mission and its measurement simulation. Adv. Space Res. 2012, 49, 1191–1197. [Google Scholar] [CrossRef]
- Bai, W.H.; Sun, Y.Q.; Du, Q.F.; Yang, G.L.; Yang, Z.D.; Zhang, P.; Bi, Y.M.; Wang, X.Y.; Cheng, C.; Han, Y. An introduction to the FY3 GNOS instrument and mountain-top tests. Atmos. Meas. Tech. 2014, 7, 1817–1823. [Google Scholar] [CrossRef]
- Cai, Y.; Bai, W.; Wang, X.; Sun, Y.; Du, Q.; Zhao, D.; Meng, X.; Liu, C.; Xia, J.; Wang, D.; et al. In-orbit performance of GNOS on-board FY3-C and the enhancements for FY3-D satellite. Adv. Space Res. 2017, 60, 2812–2821. [Google Scholar] [CrossRef]
- Li, M.; Li, W.W.; Shi, C.; Jiang, K.C.; Guo, X.; Dai, X.L.; Meng, X.G.; Yang, Z.D.; Yang, G.L.; Liao, M. Precise orbit determination of the Fengyun-3C satellite using onboard GPS and BDS observations. J. Geodesy 2017, 91, 1313–1327. [Google Scholar] [CrossRef]
- Zhao, Q.L.; Wang, C.; Guo, J.; Yang, G.L.; Liao, M.; Ma, H.Y.; Liu, J.N. Enhanced orbit determination for BeiDou satellites with FengYun-3C onboard GNSS data. GPS Solut. 2017, 21, 1179–1190. [Google Scholar] [CrossRef]
- Palmerini, G. Capabilities of the GNSS Precise Point Positioning Technique for Landslide Monitoring. Disaster Adv. 2012, 5, 509–513. [Google Scholar]
- Kouba, J.; Héroux, P. Precise Point Positioning Using IGS Orbit and Clock Products. GPS Solut. 2001, 5, 12–28. [Google Scholar] [CrossRef]
- Zhao, Q.; Wang, C.; Guo, J.; Liu, X. Assessment of the Contribution of BeiDou GEO, IGSO, and MEO Satellites to PPP in Asia-Pacific Region. Sensors 2015, 15, 29970–29983. [Google Scholar] [CrossRef] [PubMed]
- Montenbruck, O.; Steigenberger, P.; Prange, L.; Deng, Z.G.; Zhao, Q.L.; Perosanz, F.; Romero, I.; Noll, C.; Sturze, A.; Weber, G.; et al. The Multi-GNSS Experiment (MGEX) of the International GNSS Service (IGS)—Achievements, prospects and challenges. Adv. Space Res. 2017, 59, 1671–1697. [Google Scholar] [CrossRef]
- Dow, J.M.; Neilan, R.E.; Rizos, C. The International GNSS Service in a changing landscape of Global Navigation Satellite Systems. J. Geodesy 2009, 83, 191–198. [Google Scholar] [CrossRef]
- Uhlemann, M.; Gendt, G.; Ramatschi, M.; Deng, Z. GFZ Global Multi-GNSS Network and Data Processing Results. In IAG 150 Years, Proceedings of the IAG Scientific Assembly, Postdam, Germany, 1–6 September 2016; Rizos, C., Willis, P., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 673–679. [Google Scholar]
- Guo, F.; Li, X.; Zhang, X.; Wang, J. Assessment of precise orbit and clock products for Galileo, BeiDou, and QZSS from IGS Multi-GNSS Experiment (MGEX). GPS Solut. 2017, 21, 279–290. [Google Scholar] [CrossRef]
- Guo, J.; Xu, X.; Zhao, Q.; Liu, J. Precise orbit determination for quad-constellation satellites at Wuhan University: Strategy, result validation, and comparison. J. Geodesy 2016, 90, 143–159. [Google Scholar] [CrossRef]
- Lou, Y.; Zhang, W.; Wang, C.; Yao, X.; Shi, C.; Liu, J. The impact of orbital errors on the estimation of satellite clock errors and PPP. Adv. Space Res. 2014, 54, 1571–1580. [Google Scholar] [CrossRef]
- Douša, J. The impact of errors in predicted GPS orbits on zenith troposphere delay estimation. GPS Solut. 2010, 14, 229–239. [Google Scholar] [CrossRef]
- Liu, J.N.; Mao-Rong, G.E. Panda Software and Its Preliminary Result of Positioning and Orbit Determination. Wuhan Univ. J. Nat. Sci. 2003, 8, 603–609. [Google Scholar]
- Rebischung, P.; Schmid, R. IGS14/igs14.atx: A New Framework for the IGS Products. In Proceedings of the AGU Fall Meeting, San Francisco, CA, USA, 12–16 December 2016. [Google Scholar]
- Wu, J.T.; Wu, S.C.; Hajj, G.A.; Bertiger, W.I.; Lichten, S.M. Effects of Antenna Orientation on GPS Carrier Phase. In Proceedings of the AAS/AIAA Astrodynamics Conference; Durango, CO, USA, 19–22 August 1991; pp. 1647–1660. [Google Scholar]
- Shako, R.; Förste, C.; Abrikosov, O.; Bruinsma, S.; Marty, J.-C.; Lemoine, J.-M.; Flechtner, F.; Neumayer, H.; Dahle, C. EIGEN-6C: A High-Resolution Global Gravity Combination Model Including GOCE Data. In Observation of the System Earth from Space—Champ, Grace, Goce and Future Missions: Geotechnologien Science Report No. 20; Flechtner, F., Sneeuw, N., Schuh, W.-D., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 155–161. [Google Scholar]
- Petit, G.; Luzum, B.; Al, E. IERS Conventions. IERS Tech. Note 2010, 36, 1–95. [Google Scholar]
- Carrere, L.; Lyard, F.; Cancet, M. FES 2012: A New Global Tidal Model Taking Advantage of Nearly 20 Years of Altimetry. In Proceedings of the 20 Years of Progress in Radar Altimatry, Venice, Italy, 24–29 September 2013; Volume 710, pp. 11–12. [Google Scholar]
- Berger, C.; Biancale, R.; IllF, M. Barlier Improvement of the empirical thermospheric model DTM: DTM94—A comparative review of various temporal variations and prospects in space geodesy applications. J. Geodesy 1998, 72, 161–179. [Google Scholar] [CrossRef]
- Folkner, W.M.; Williams, J.G.; Boggs, D.H. The Planetary and Lunar Ephemeris DE 421. Interplanet. Netw. Prog. Rep. 2009, 178, 1–34. [Google Scholar]
- Jiang, K.; Li, M.; Zhao, Q.; Li, W.; Guo, X. BeiDou Geostationary Satellite Code Bias Modeling Using Fengyun-3C Onboard Measurements. Sensors 2017, 17, 2460. [Google Scholar] [CrossRef] [PubMed]
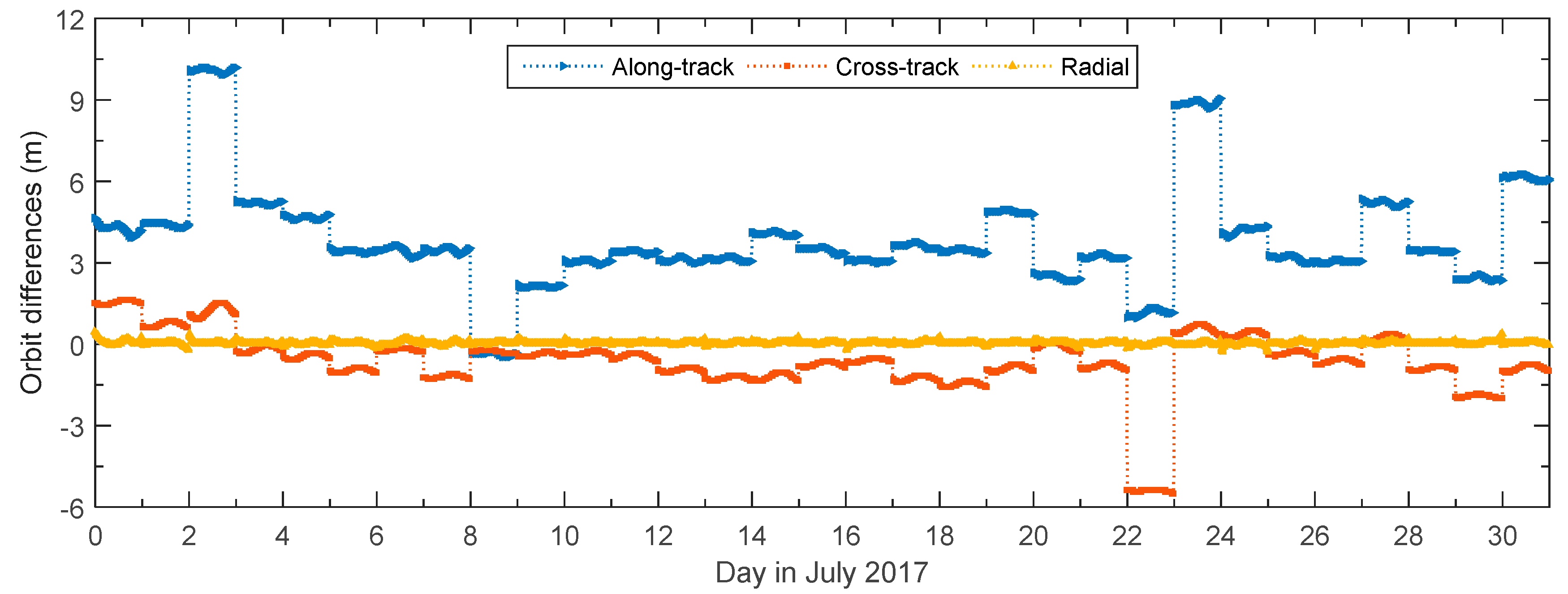
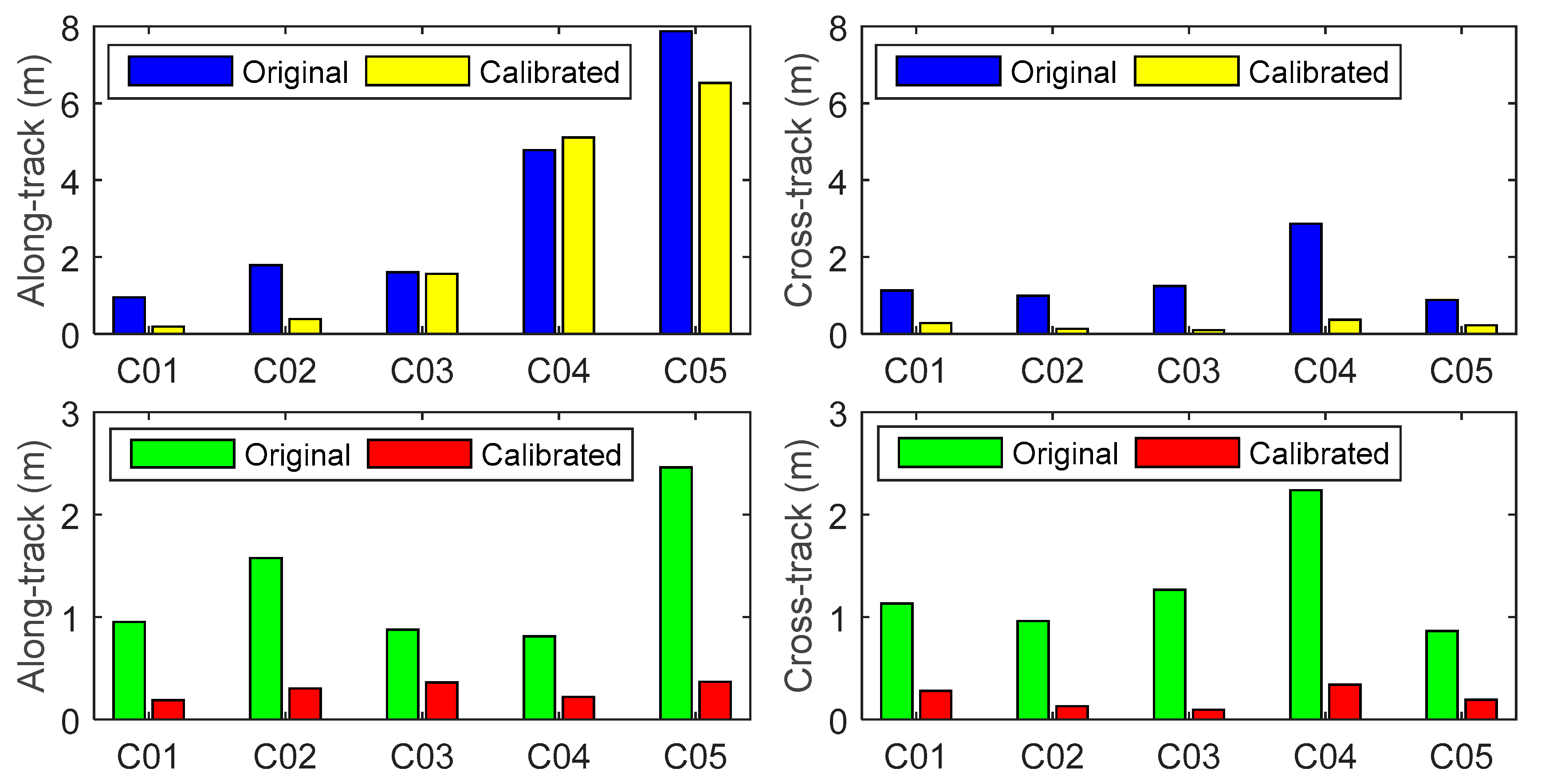
| Sat. ID | RMS of Orbit Day Boundary Discontinuities (m) | ||||
|---|---|---|---|---|---|
| Along-Track | Cross-Track | Radial | 3D | ||
| GEO | C01 | 1.10 | 1.24 | 0.09 | 1.66 |
| C02 | 1.76 | 1.02 | 0.83 | 2.20 | |
| C03 | 1.59 | 1.23 | 1.16 | 2.32 | |
| C04 | 4.71 | 2.83 | 1.96 | 5.83 | |
| C05 | 7.87 | 0.88 | 2.67 | 8.36 | |
| IGSO | C06 | 0.14 | 0.07 | 0.10 | 0.19 |
| C07 | 0.12 | 0.26 | 0.12 | 0.31 | |
| C08 | 0.09 | 0.06 | 0.11 | 0.16 | |
| C09 | 0.14 | 0.07 | 0.21 | 0.26 | |
| C10 | 0.08 | 0.11 | 0.20 | 0.25 | |
| C13 | 0.06 | 0.10 | 0.13 | 0.17 | |
| MEO | C11 | 0.12 | 0.07 | 0.12 | 0.18 |
| C12 | 0.14 | 0.07 | 0.05 | 0.17 | |
| C14 | 0.17 | 0.06 | 0.04 | 0.18 | |
| Item | Description |
|---|---|
| POD arc length | 24 h |
| Observation selection | Ionosphere-free linear combinations of space-borne dual-frequency phase and code observations of FY-3C during July 2017 |
| BeiDou orbit and clock products | GBM products generated by GFZ |
| BeiDou transmitter antenna phase center | Adopt antenna phase center patterns in IGS14_1967.atx [28] |
| Phase wind-up | Correct using the model published in [29] |
| Observation process interval | 30 s, use observations recorded at 0 s and 30 s of each minute in GPS time system |
| Cut-off elevation | Accept all available observations including those with negative elevation angles |
| Observation weighting strategy | Equal weight for phase and code respectively, and the weight ratio of phase to that of code is 40,000:1 |
| Earth gravity | EIGEN-6C model with degree 100 and order 100 [30] |
| Solid Earth tides | IERS 2010 [31] |
| Ocean tides | FES2012 model with degree 30 and order 30 [32] |
| Relativistic effects | IERS 2010 |
| Atmospheric drag | Box-wing model, atmospheric density adopts DTM94 model [33] |
| Solar radiation pressure | Box-wing model |
| Third body gravity | Consider the gravitational attraction of celestial bodies, use celestial ephemeris named DE421 published by Jet Propulsion Laboratory (JPL) [34] |
| FY-3C satellite attitude | Nominal attitude mode |
| Estimated parameters | Receiver antenna phase center coordinates in Z direction estimated as a constant Receiver clock offset estimated as white noise Phase ambiguity estimated as a float constant during each satellite tracking arc segment Satellite initial position and velocity in the inertial reference frame estimated as constants Atmospheric drag coefficient estimated as piece wise constant every 6 h Amplitudes of periodic empirical accelerations acting on the along-track and cross-track of FY-3C orbit estimated as piece wise constants every 6 h |
| Category | Along-Track | Cross-Track | Radial | 3D |
|---|---|---|---|---|
| Solution A | 45.7 | 26.6 | 17.7 | 56.9 |
| Solution B | 6.4 | 3.3 | 2.6 | 7.8 |
| Solution C | 5.0 | 3.0 | 2.0 | 6.2 |
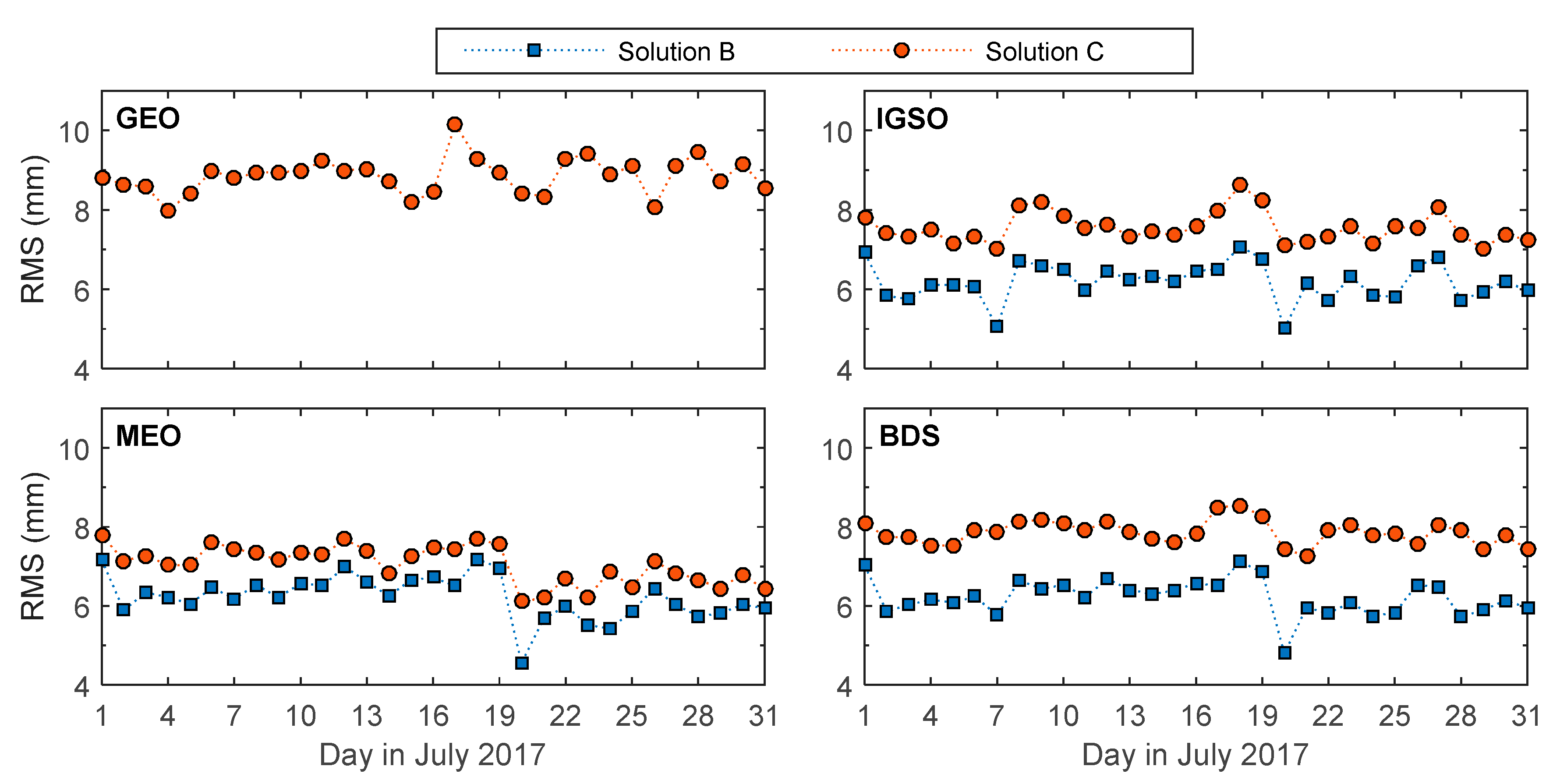
| Category | GEO Max/Min/Mean | IGSO Max/Min/Mean | MEO Max/Min/Mean | BeiDou Max/Min/Mean |
|---|---|---|---|---|
| Solution A | 126.0/35.4/63.5 | 71.0/21.9/36.5 | 47.4/18.9/29.8 | 73.1/28.4/45.8 |
| Solution B | - | 7.1/5.0/6.2 | 7.2/4.5/6.2 | 7.1/4.8/6.2 |
| Solution C | 10.1/8.0/8.9 | 8.6/7.0/7.5 | 7.8/6.1/7.1 | 8.5/7.3/7.9 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Guo, X.; Qu, L.; Zhao, Q. Precise Orbit Determination of FY-3C with Calibration of Orbit Biases in BeiDou GEO Satellites. Remote Sens. 2018, 10, 382. https://doi.org/10.3390/rs10030382
Zhang Q, Guo X, Qu L, Zhao Q. Precise Orbit Determination of FY-3C with Calibration of Orbit Biases in BeiDou GEO Satellites. Remote Sensing. 2018; 10(3):382. https://doi.org/10.3390/rs10030382
Chicago/Turabian StyleZhang, Qiang, Xiang Guo, Lizhong Qu, and Qile Zhao. 2018. "Precise Orbit Determination of FY-3C with Calibration of Orbit Biases in BeiDou GEO Satellites" Remote Sensing 10, no. 3: 382. https://doi.org/10.3390/rs10030382
APA StyleZhang, Q., Guo, X., Qu, L., & Zhao, Q. (2018). Precise Orbit Determination of FY-3C with Calibration of Orbit Biases in BeiDou GEO Satellites. Remote Sensing, 10(3), 382. https://doi.org/10.3390/rs10030382