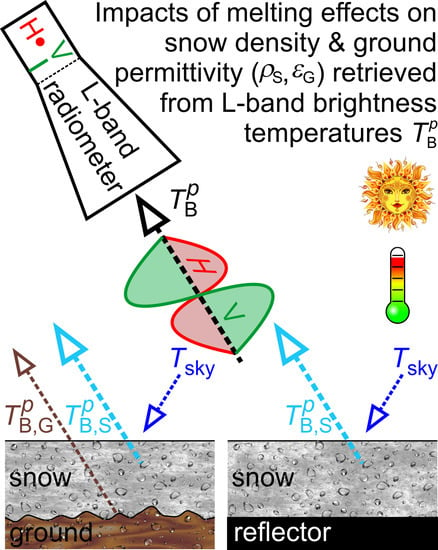
Snow Density and Ground Permittivity Retrieved from L-Band Radiometry: Melting Effects
Abstract
1. Introduction
2. Data Sets
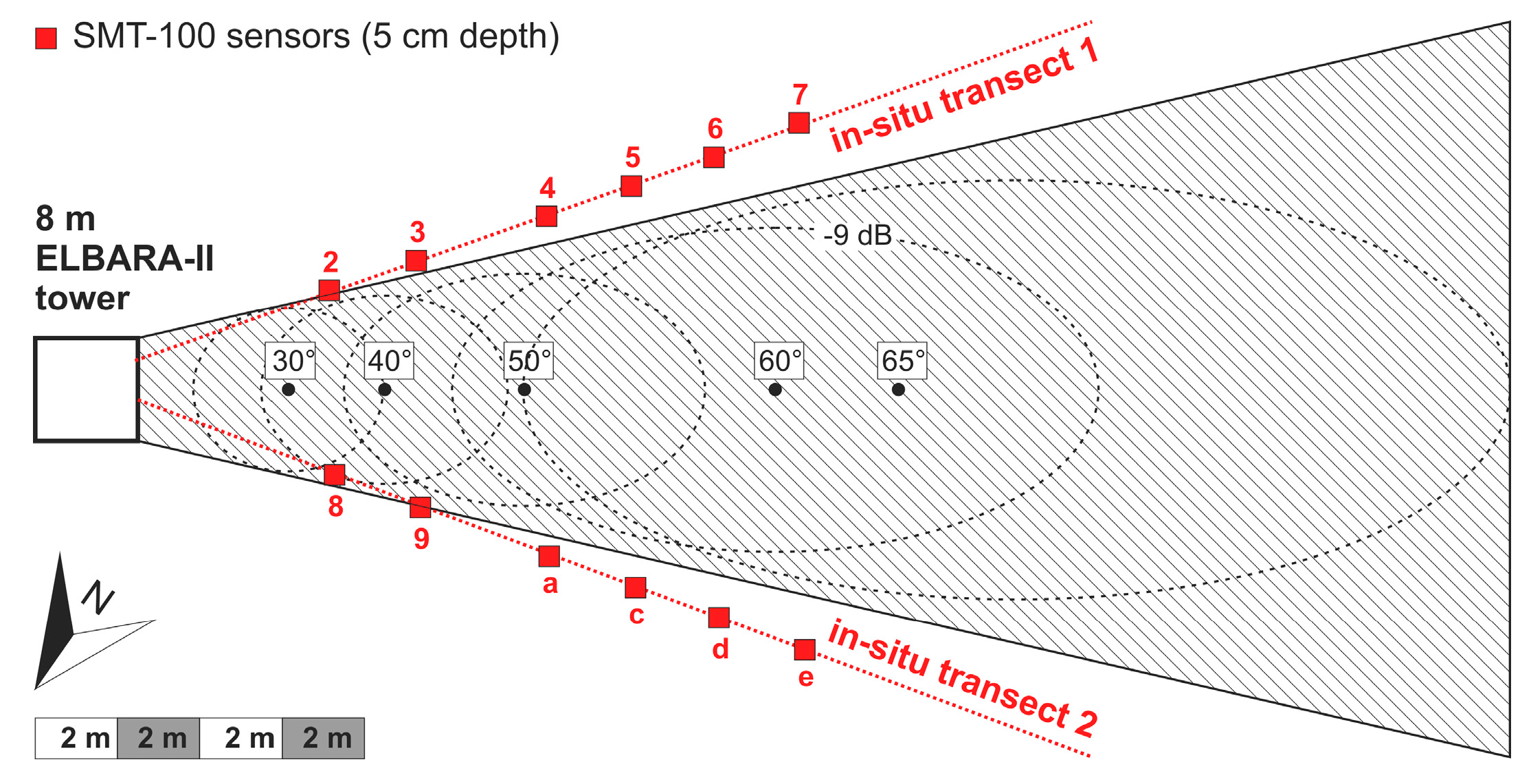
2.1. Test Site
2.2. In-Situ Measurements
2.3. Radiometry Data
3. Methodology
3.1. Multi-Angle Retrieval Approach
3.2. Single-Angle Retrieval Approach
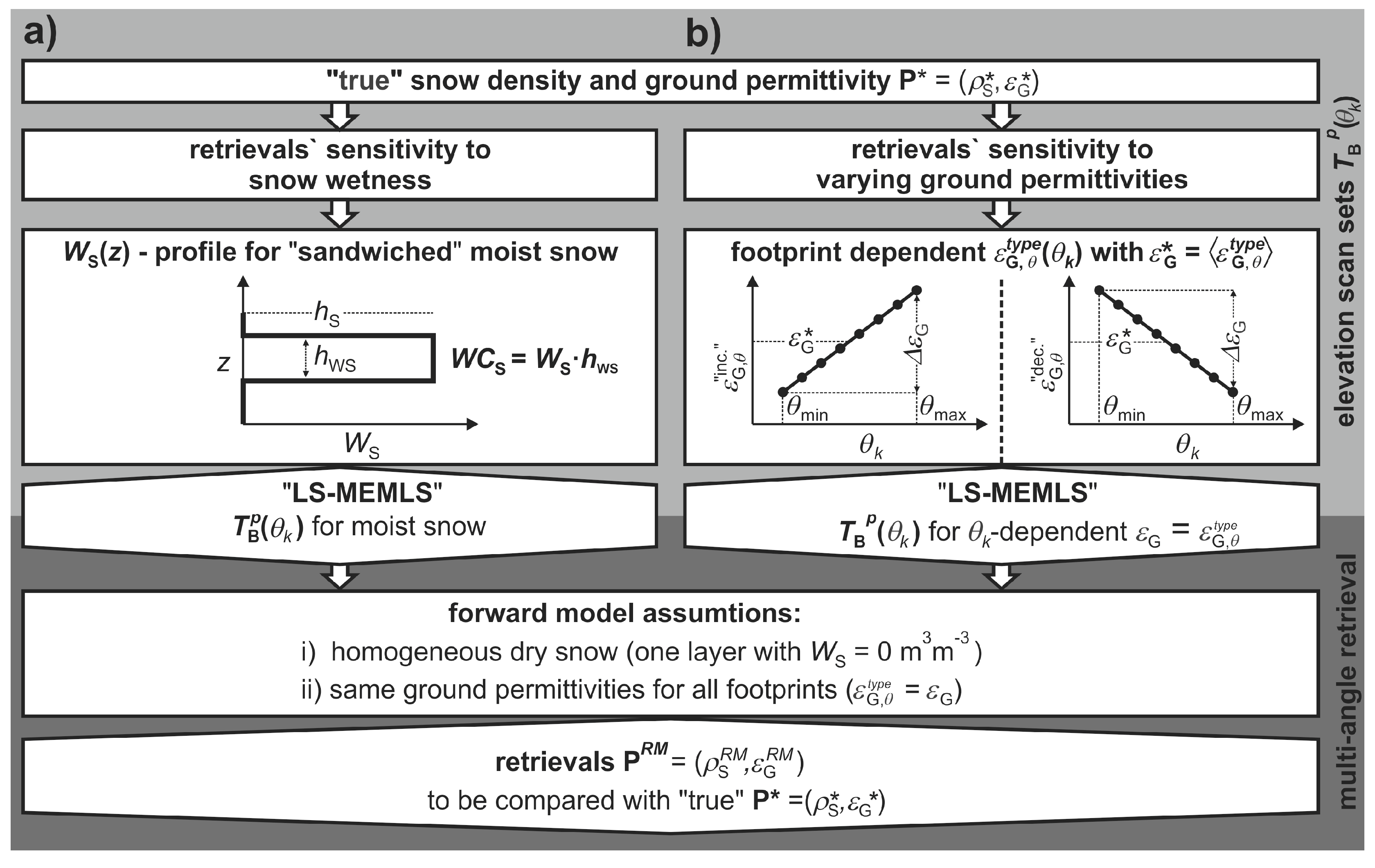
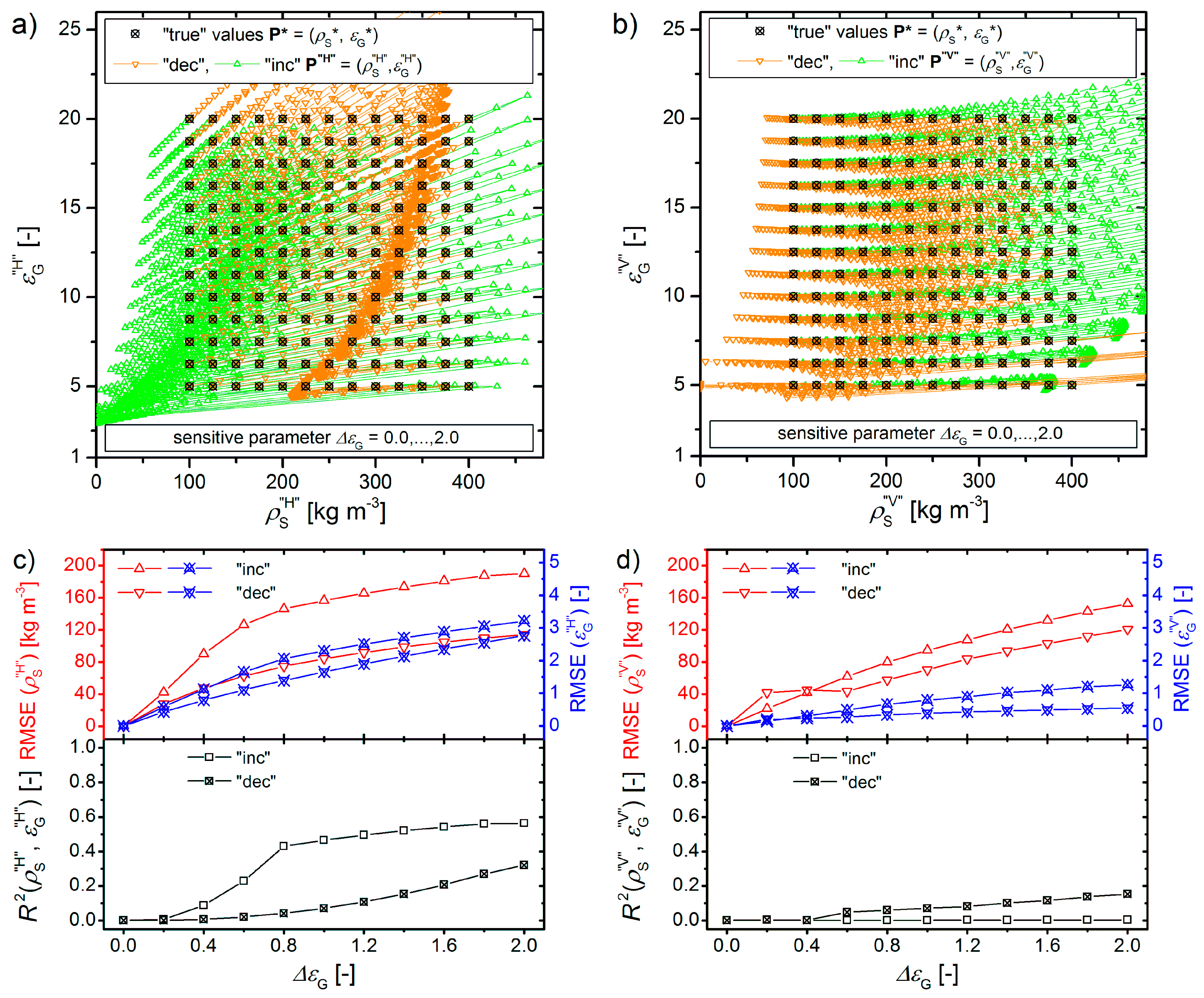
3.3. Sensitivity of Multi-Angle Retrievals to Snow Wetness and Ground Permittivity Varying among Footprints
- The initial snow density and ground permittivity values , henceforth called “true” parameter values, together with a range of (i) snow liquid water column or (ii) footprint-specific ground permittivity values, are fed in “LS—MEMLS” to simulate scan sets (p = H, V; ) of brightness temperatures. These synthetic elevation scan sets , mimic L-band measurements of a (i) moist snowpack or (ii) dry snowpack over a ground with varying permittivities among footprints.
- Using the elevation scan sets in the multi-angle retrieval scheme (Section 3.1) to derive retrievals to be compared with the “true” parameter values .
3.3.1. Elevation Scan Sets Representative of Moist Snow
3.3.2. Elevation Scan Sets Representative of Ground Permittivities Varying among Footprints
4. Synthetic Retrieval Sensitivity Analysis
4.1. Sensitivity of Multi-Angle Retrievals to Snow Wetness
4.2. Sensitivity of Multi-Angle Retrievals to Ground Permittivities Varying among Footprints
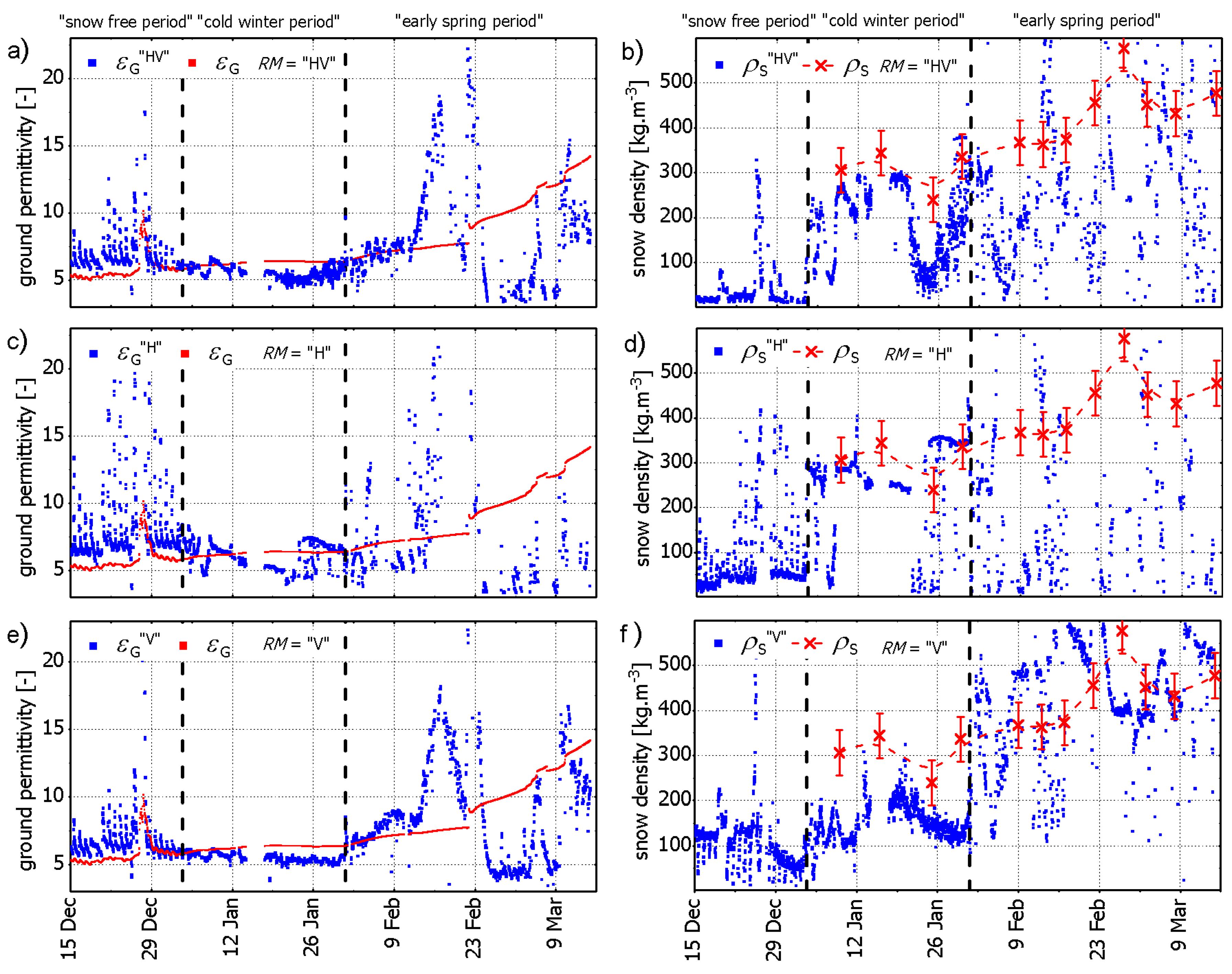
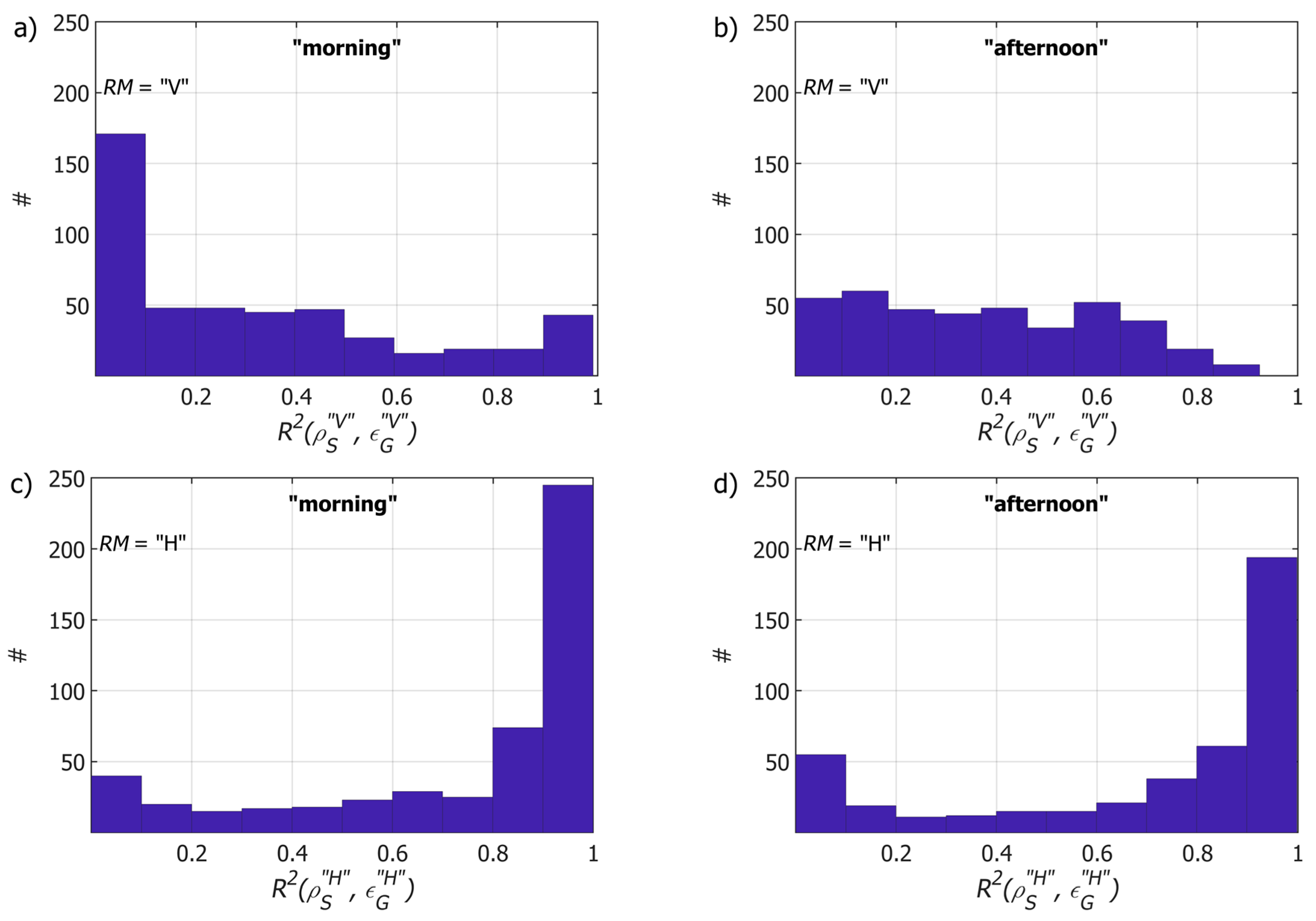
5. Experimental Retrievals
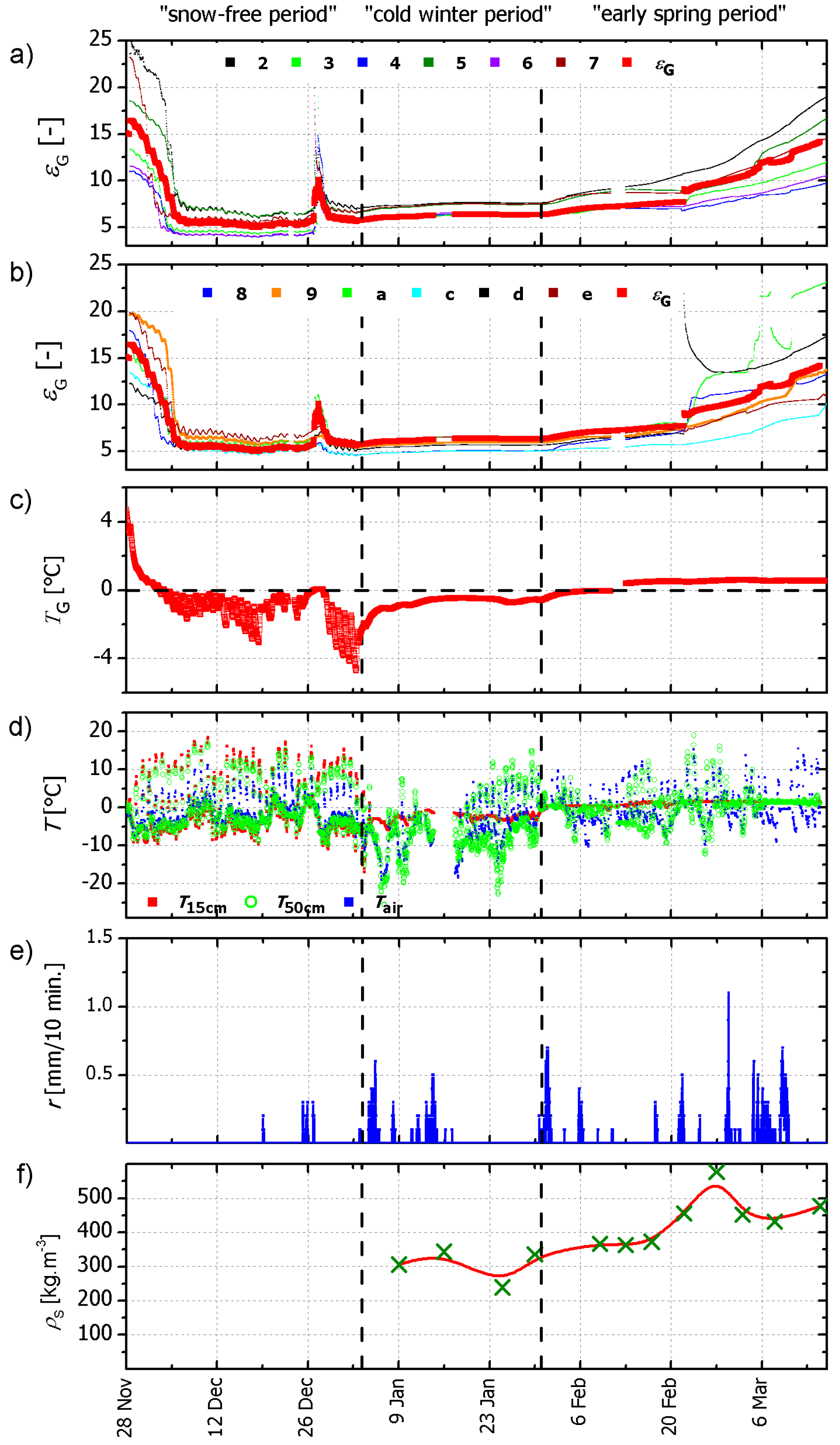
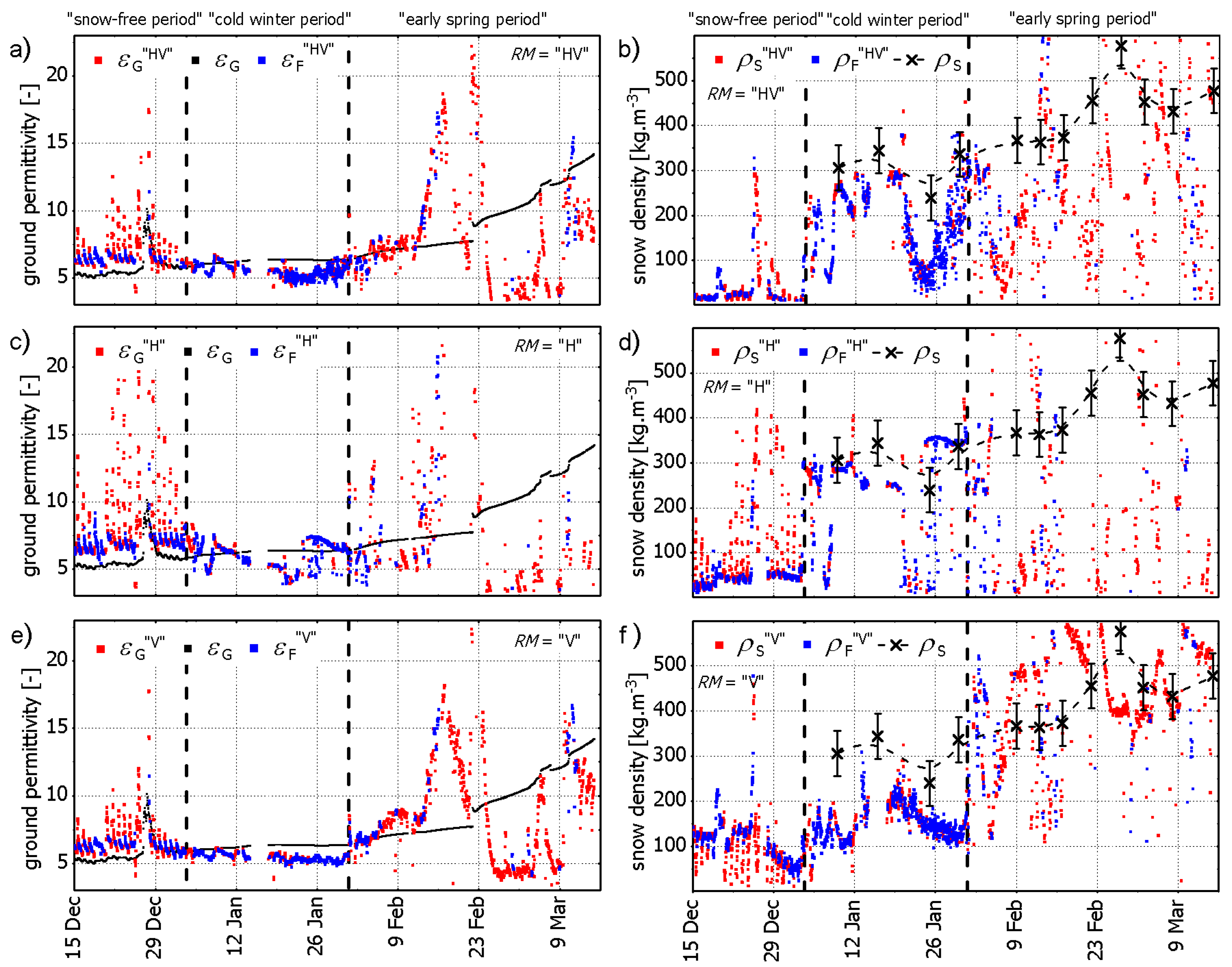
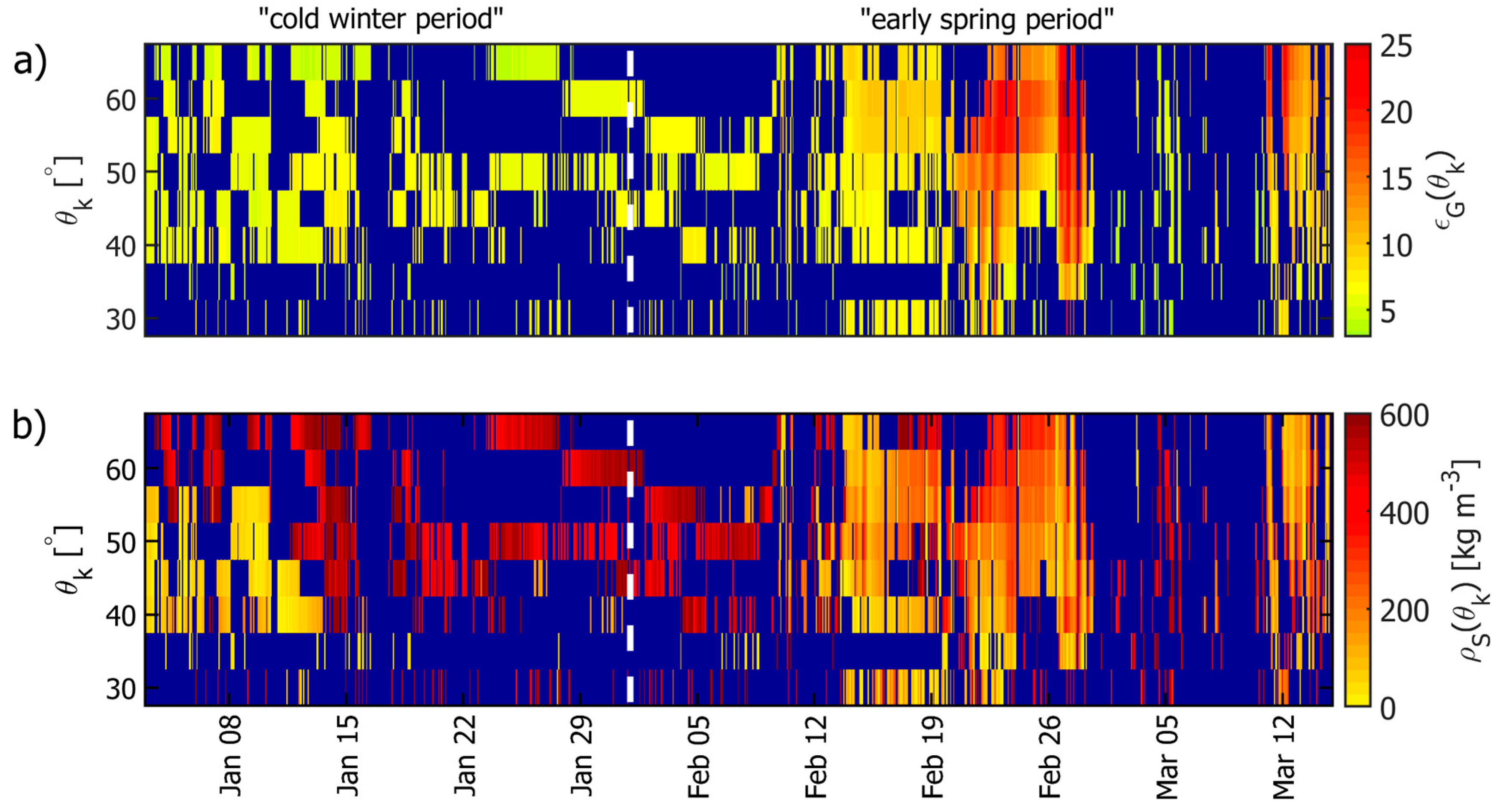
5.1. Multi-Angle Retrievals
- RM = “V”: Performs best for retrievals compared to corresponding in-situ references ; provides a suitable retrieval “quality flag” based on the threshold of retrieval coefficients of determination. The criterion can detect the onset of the “early spring period” characterized by increased snow liquid water as demonstrated in [40].
- RM = “H”: Retrievals are most suited to detect the onset of dry snow cover over frozen ground. Retrievals are generally more distorted by “geophysical noise” associated with “melting effects”, and thus are much less “successful” during the “early spring period” compared to V-mode retrievals.
- RM = “HV”: Retrievals comprise features of both retrieval modes RM = “H” and “V”. It is suggested that RM = “HV” be used for snow density retrievals as it: (a) detects and distinguishes the onset of dry snow, (b) represents in-situ references , and (c) is less prone to instrumental uncertainties because it is based on twice as many measurements .
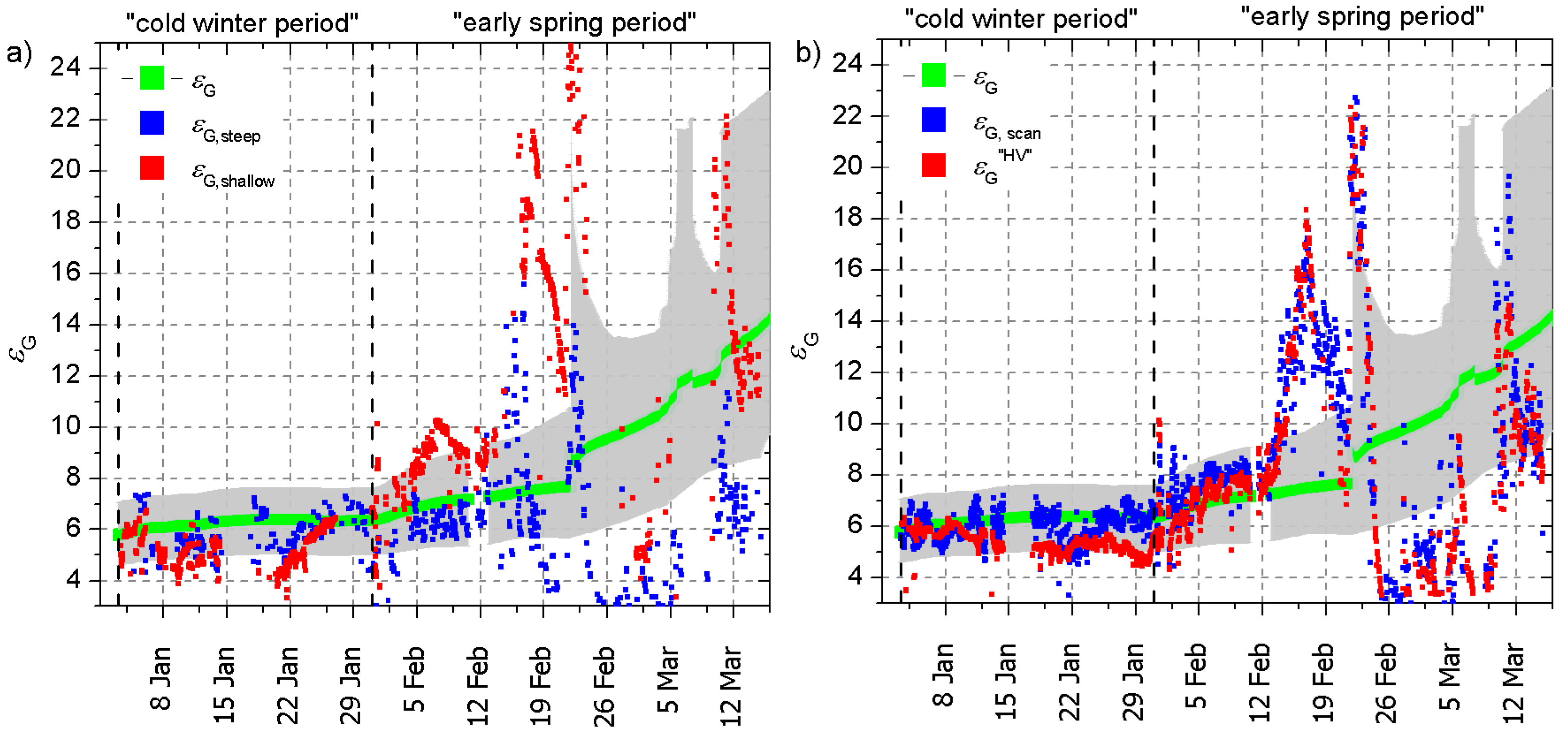
5.2. Single-Angle Retrieval
6. Summary and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Malenovský, Z.; Rott, H.; Cihlar, J.; Schaepman, M.E.; García-Santos, G.; Fernandes, R.; Berger, M. Sentinels for science: Potential of Sentinel-1, -2, and -3 missions for scientific observations of ocean, cryosphere, and land. Remote Sens. Environ. 2012, 120, 91–101. [Google Scholar] [CrossRef]
- Hollmann, R.; Merchant, C.J.; Saunders, R.; Downy, C.; Buchwitz, M.; Cazenave, A.; Chuvieco, E.; Defourny, P.; de Leeuw, G.; Forsberg, R.; et al. The ESA Climate Change Initiative: Satellite Data Records for Essential Climate Variables. Bull. Am. Meteorol. Soc. 2013, 94, 1541–1552. [Google Scholar] [CrossRef]
- Mätzler, C. Applications of SMOS over terrestrial ice and snow. In Proceedings of the 3rd SMOS Workshop, DLR, Oberpfaffenhofen, Germany, 10–12 December 2001. [Google Scholar]
- Pulliainen, J.; Hallikainen, M. Retrieval of Regional Snow Water Equivalent from Space-Borne Passive Microwave Observations. Remote Sens. Environ. 2001, 75, 76–85. [Google Scholar] [CrossRef]
- Leduc-Leballeur, M.; Picard, G.; Mialon, A.; Arnaud, L.; Lefebvre, E.; Possenti, P.; Kerr, Y. Modeling L-Band Brightness Temperature at Dome C in Antarctica and Comparison With SMOS Observations. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4022–4032. [Google Scholar] [CrossRef]
- Owe, M.; Jeu, R.d.; Walker, J. A methodology for surface soil moisture and vegetation optical depth retrieval using the microwave polarization difference index. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1643–1654. [Google Scholar] [CrossRef]
- Meesters, A.G.C.A.; Jeu, R.A.M.D.; Owe, M. Analytical derivation of the vegetation optical depth from the microwave polarization difference index. IEEE Geosci. Remote Sens. Lett. 2005, 2, 121–123. [Google Scholar] [CrossRef]
- Kim, Y.; Kimball, J.S.; McDonald, K.C.; Glassy, J. Developing a Global Data Record of Daily Landscape Freeze/Thaw Status Using Satellite Passive Microwave Remote Sensing. IEEE Trans. Geosci. Remote Sens. 2011, 49, 949–960. [Google Scholar] [CrossRef]
- Rautiainen, K.; Parkkinen, T.; Lemmetyinen, J.; Schwank, M.; Wiesmann, A.; Ikonen, J.; Derksen, C.; Davydov, S.; Davydova, A.; Boike, J.; et al. SMOS prototype algorithm for detecting autumn soil freezing. Remote Sens. Environ. 2016, 180, 346–360. [Google Scholar] [CrossRef]
- Roy, A.; Toose, P.; Williamson, M.; Rowlandson, T.; Derksen, C.; Royer, A.; Berg, A.A.; Lemmetyinen, J.; Arnold, L. Response of L-Band brightness temperatures to freeze/thaw and snow dynamics in a prairie environment from ground-based radiometer measurements. Remote Sens. Environ. 2017, 191, 67–80. [Google Scholar] [CrossRef]
- Njoku, E.G.; Entekhabi, D. Passive microwave remote sensing of soil moisture. J. Hydrol. 1996, 184, 101–129. [Google Scholar] [CrossRef]
- Kerr, Y.; Waldteufel, P.; Wigneron, J.-P.; Martinuzzi, J.-M.; Font, J.; Berger, M. Soil moisture retrieval from space: The soil moisture and ocean salinity (SMOS) mission. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1729–1735. [Google Scholar] [CrossRef]
- Njoku, E.G.; Jackson, T.J.; Lakshmi, V.; Chan, T.K.; Nghiem, S.V. Soil moisture retrieval from AMSR-E. IEEE Trans. Geosci. Remote Sens. 2003, 41, 215–229. [Google Scholar] [CrossRef]
- Melaas, E.K.; Richardson, A.D.; Friedl, M.A.; Dragoni, D.; Gough, C.M.; Herbst, M.; Montagnani, L.; Moors, E. Using FLUXNET data to improve models of springtime vegetation activity onset in forest ecosystems. Agric. For. Meteorol. 2013, 171–172, 46–56. [Google Scholar] [CrossRef]
- Xu, L.; Myneni, R.B.; Chapin, F.S., III; Callaghan, T.V.; Pinzon, J.E.; Tucker, C.J.; Zhu, Z.; Bi, J.; Ciais, P.; Tømmervik, H.; et al. Temperature and vegetation seasonality diminishment over northern lands. Nat. Clim. Chang. Lett. 2013, 3, 581–586. [Google Scholar] [CrossRef]
- Kim, Y.; Kimball, J.S.; Zhang, K.; McDonald, K.C. Satellite detection of increasing Northern Hemisphere non-frozen seasons from 1979 to 2008: Implications for regional vegetation growth. Remote Sens. Environ. 2012, 121, 472–487. [Google Scholar] [CrossRef]
- Fletcher, C.G.; Zhao, H.; Kushner, P.J.; Fernandes, R. Using models and satellite observations to evaluate the strength of snow albedo feedback. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Gouttevin, I.; Menegoz, M.; Dominé, F.; Krinner, G.; Koven, C.; Ciais, P.; Tarnocai, C.; Boike, J. How the insulating properties of snow affect soil carbon distribution in the continental pan-Arctic area. J. Geophys. Res. Biogeosci. 2012, 117. [Google Scholar] [CrossRef]
- Yang, D.; Robinson, D.; Zhao, Y.; Estilow, T.; Ye, B. Streamflow response to seasonal snow cover extent changes in large Siberian watersheds. J. Geophys. Res. Atmos. 2003, 108, 1–14. [Google Scholar] [CrossRef]
- Barnett, T.P.; Adam, J.C.; Lettenmaier, D.P. Potential impacts of a warming climate on water availability in snow-dominated regions. Nature 2005, 438, 303–309. [Google Scholar] [CrossRef] [PubMed]
- Papa, F.; Prigent, C.; Rossow, W.B. Ob’ River flood inundations from satellite observations: A relationship with winter snow parameters and river runoff. J. Geophys. Res. Atmos. 2007, 112. [Google Scholar] [CrossRef]
- Stewart, I.T. Changes in snowpack and snowmelt runoff for key mountain regions. Hydrol. Process. 2009, 23, 78–94. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.-P.; Delwart, S.; Cabot, F.; Boutin, J.; Escorihuela, M.-J.; Font, J.; Reul, N.; Gruhier, C.; et al. The SMOS mission: New tool for monitoring key elements of the global water cycle. Proc. IEEE 2010, 98, 666–687. [Google Scholar] [CrossRef]
- Mecklenburg, S.; Drusch, M.; Kerr, Y.H.; Font, J.; Martin-Neira, M.; Delwart, S.; Buenadicha, G.; Reul, N.; Daganzo-Eusebio, E.; Oliva, R.; et al. ESA’s Soil Moisture and Ocean Salinity Mission: Mission Performance and Operations. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1354–1366. [Google Scholar] [CrossRef]
- Entekhabi, D.; Njoku, E.G.; O’Neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J.; et al. The Soil Moisture Active Passive (SMAP) Mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Armstrong, R.L.; Brodzik, M.J. Recent northern hemisphere snow extent: A comparison of data derived from visible and microwave satellite sensors. Geophys. Res. Lett. 2001, 28, 3673–3676. [Google Scholar] [CrossRef]
- Dozier, J. Spectral signature of alpine snow cover from the landsat thematic mapper. Remote Sens. Environ. 1989, 28, 9–22. [Google Scholar] [CrossRef]
- Winther, J.G.; Gerland, S.; Ørbæk, J.; Ivanov, B.; Blanco, A.; Boike, J. Spectral reflectance of melting snow in a high Arctic watershed on Svalbard: Some implications for optical satellite remote sensing studies. Hydrol. Process. 1999, 13, 2033–2049. [Google Scholar] [CrossRef]
- Schwank, M.; Rautiainen, K.; Mätzler, C.; Stähli, M.; Lemmetyinen, J.; Pulliainen, J.; Vehviläinen, J.; Kontu, A.; Ikonen, J.; Ménard, C.B.; et al. Model for microwave emission of a snow-covered ground with focus on L band. Remote Sens. Environ. 2014, 154, 180–191. [Google Scholar] [CrossRef]
- Schwank, M.; Matzler, C.; Wiesmann, A.; Wegmuller, U.; Pulliainen, J.; Lemmetyinen, J.; Rautiainen, K.; Derksen, C.; Toose, P.; Drusch, M. Snow Density and Ground Permittivity Retrieved from L-Band Radiometry: A Synthetic Analysis. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3833–3845. [Google Scholar] [CrossRef]
- Lemmetyinen, J.; Schwank, M.; Rautiainen, K.; Kontu, A.; Parkkinen, T.; Mätzler, C.; Wiesmann, A.; Wegmüller, U.; Derksen, C.; Toose, P.; et al. Snow density and ground permittivity retrieved from L-band radiometry: Application to experimental data. Remote Sens. Environ. 2016, 180, 377–391. [Google Scholar] [CrossRef]
- Shi, J.; Dozier, J. Estimation of Snow Water Equivalence Using SIR-C/X-SAR, Part I: Inferring Snow Density and Subsurface Properties. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2465–2473. [Google Scholar]
- Snehmani; Venkataraman, G.; Nigam, A.K.; Singh, G. Development of an inversion algorithm for dry snow density estimation and its application with ENVISAT-ASAR dual co-polarization data. Geocarto Int. 2010, 25, 597–616. [Google Scholar] [CrossRef]
- Thakur, P.K.; Aggarwal, S.P.; Garg, P.K.; Garg, R.D.; Mani, S.; Pandit, A.; Kumar, S. Snow physical parameters estimation using space-based Synthetic Aperture Radar. Geocarto Int. 2012, 27, 263–288. [Google Scholar] [CrossRef]
- Oh, Y.; Sarabandi, K.; Ulaby, F.T. An empirical model and an inversion technique for radar scattering from bare soil surfaces. IEEE Trans. Geosci. Remote Sens. 1992, 30, 370–381. [Google Scholar] [CrossRef]
- Shi, J.; Wang, J.; Hsu, A.Y.; O’Neill, P.E.; Engman, E.T. Estimation of Bare Surface Soil Moisture and Surface Roughness Parameter Using L-band SAR Image Data. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1254–1266. [Google Scholar]
- Wiesmann, A.; Mätzler, C. Microwave emission model of layered snowpacks. Remote Sens. Environ. 1999, 70, 307–316. [Google Scholar] [CrossRef]
- Wigneron, J.-P.; Kerr, Y.; Waldteufel, P.; Saleh, K.; Escorihuela, M.-J.; Richaume, P.; Ferrazzoli, P.; de Rosnay, P.; Gurney, R.; Calvet, J.-C.; et al. L-band microwave emission of the biosphere (L-MEB) model: Description and calibration against experimental data sets over crop fields. Remote Sens. Environ. 2007, 107, 639–655. [Google Scholar] [CrossRef]
- Naderpour, R.; Schwank, M.; Mätzler, C.; Lemmetyinen, J.; Steffen, K. Snow Density and Ground Permittivity Retrieved From L-Band Radiometry: A Retrieval Sensitivity Analysis. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3148–3161. [Google Scholar] [CrossRef]
- Naderpour, R.; Schwank, M. Snow Wetness Retrieved from L-Band Radiometry. Remote Sens. 2018, 10, 359. [Google Scholar]
- Naderpour, R.; Schwank, M.; Mätzler, C. Davos-Laret Remote Sensing Field Laboratory: 2016/2017 Winter Season L-Band Measurements Data-Processing and Analysis. Remote Sens. 2017, 9, 1185. [Google Scholar] [CrossRef]
- Chang, A.; Rango, A.; Shiue, J. Remote sensing of snow properties by passive microwave. Microwave Remote Sens. Snowpack Prop. 1980, 169. Available online: https://ntrs.nasa.gov/search.jsp?R=19810010994. (accessed on 24 February 2018).
- Moeser, D.; Morsdorf, F.; Jonas, T. Novel forest structure metrics from airborne LiDAR data for improved snow interception estimation. Agric. For. Meteorol. 2015, 208, 40–49. [Google Scholar] [CrossRef]
- Bogena, H.R.; Huisman, J.A.; Schilling, B.; Weuthen, A.; Vereecken, H. Effective calibration of low-cost soil water content sensors. Sensors 2017, 17, 208. [Google Scholar] [CrossRef] [PubMed]
- Schwank, M.; Wiesmann, A.; Werner, C.; Mätzler, C.; Weber, D.; Murk, A.; Völksch, I.; Wegmüller, U. ELBARA II, An L-Band Radiometer System for Soil Moisture Research. Sensors 2010, 10, 584–612. [Google Scholar] [CrossRef] [PubMed]
- Schwank, M.; Wigneron, J.P.; Lopez-Baeza, E.; Völksch, I.; Mätzler, C.; Kerr, Y. L-Band Radiative Properties of Vine Vegetation at the SMOS Cal/Val Site MELBEX III. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1587–1601. [Google Scholar] [CrossRef]
- Or, D.; Wraith, J.M. Temperature effects on soil bulk dielectric permittivity measured by time domain reflectometry: A physical model. Water Resour. Res. 1999, 35, 371–383. [Google Scholar] [CrossRef]
- Mironov, V.; Lukin, Y.I. A Physical Model of Dielectric Spectra of Thawed and Frozen Bentonitic Clay within the Frequency Range from 1 to 15 GHz. Russ. Phys. J. 2011, 53, 956–963. [Google Scholar] [CrossRef]
- Bernier, M.; Fortin, J.P.; Gauthier, Y.; Gauthier, R.; Roy, R.; Vincent, P. Determination of snow water equivalent using RADARSAT SAR data in eastern Canada. Hydrol. Process. 1999, 13, 3041–3051. [Google Scholar] [CrossRef]
- Ishikawa, M. Thermal regimes at the snow–ground interface and their implications for permafrost investigation. Geomorphology 2003, 52, 105–120. [Google Scholar] [CrossRef]
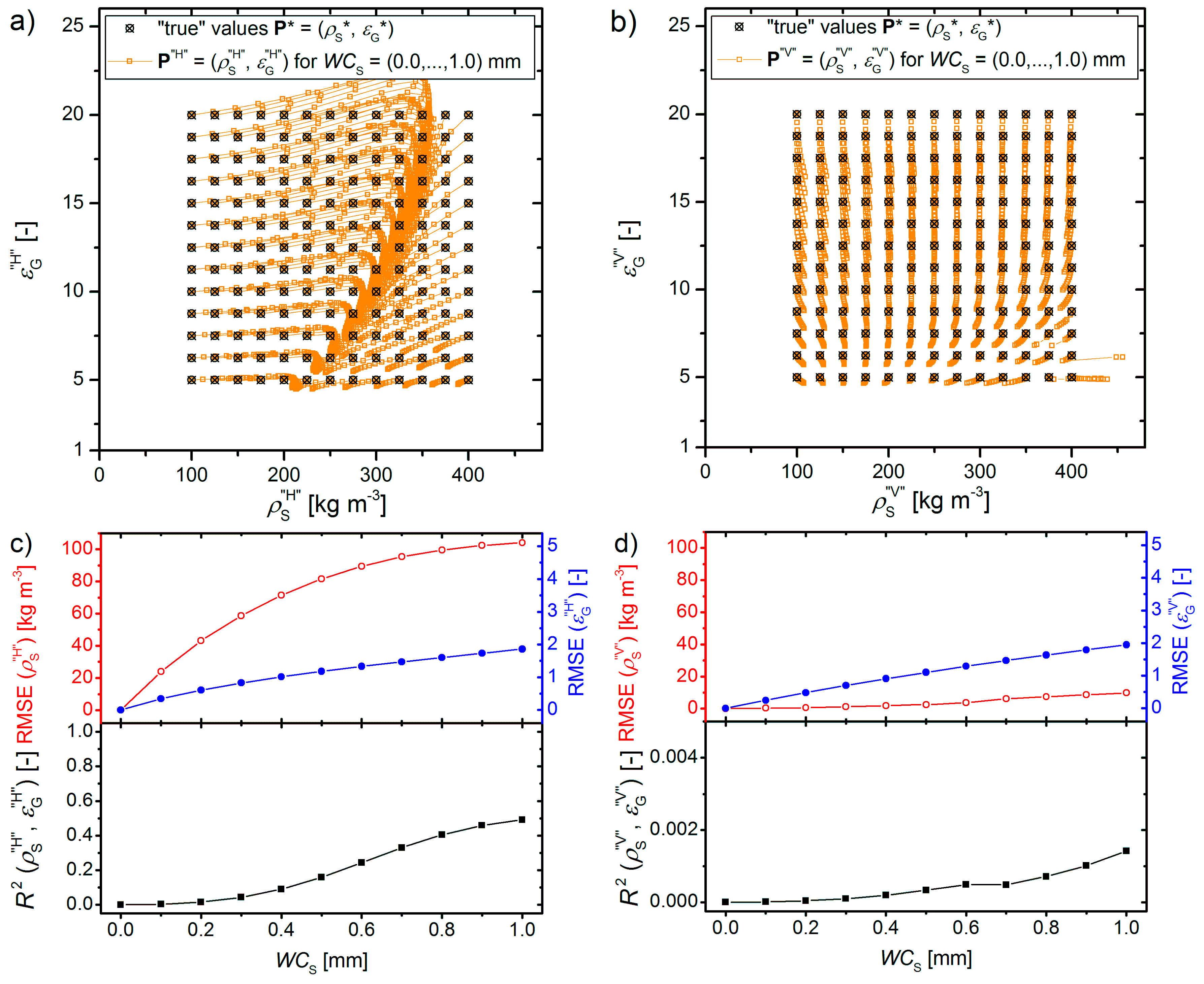
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schwank, M.; Naderpour, R. Snow Density and Ground Permittivity Retrieved from L-Band Radiometry: Melting Effects. Remote Sens. 2018, 10, 354. https://doi.org/10.3390/rs10020354
Schwank M, Naderpour R. Snow Density and Ground Permittivity Retrieved from L-Band Radiometry: Melting Effects. Remote Sensing. 2018; 10(2):354. https://doi.org/10.3390/rs10020354
Chicago/Turabian StyleSchwank, Mike, and Reza Naderpour. 2018. "Snow Density and Ground Permittivity Retrieved from L-Band Radiometry: Melting Effects" Remote Sensing 10, no. 2: 354. https://doi.org/10.3390/rs10020354
APA StyleSchwank, M., & Naderpour, R. (2018). Snow Density and Ground Permittivity Retrieved from L-Band Radiometry: Melting Effects. Remote Sensing, 10(2), 354. https://doi.org/10.3390/rs10020354