Development of a System of Compatible Individual Tree Diameter and Aboveground Biomass Prediction Models Using Error-In-Variable Regression and Airborne LiDAR Data
Abstract
:1. Introduction
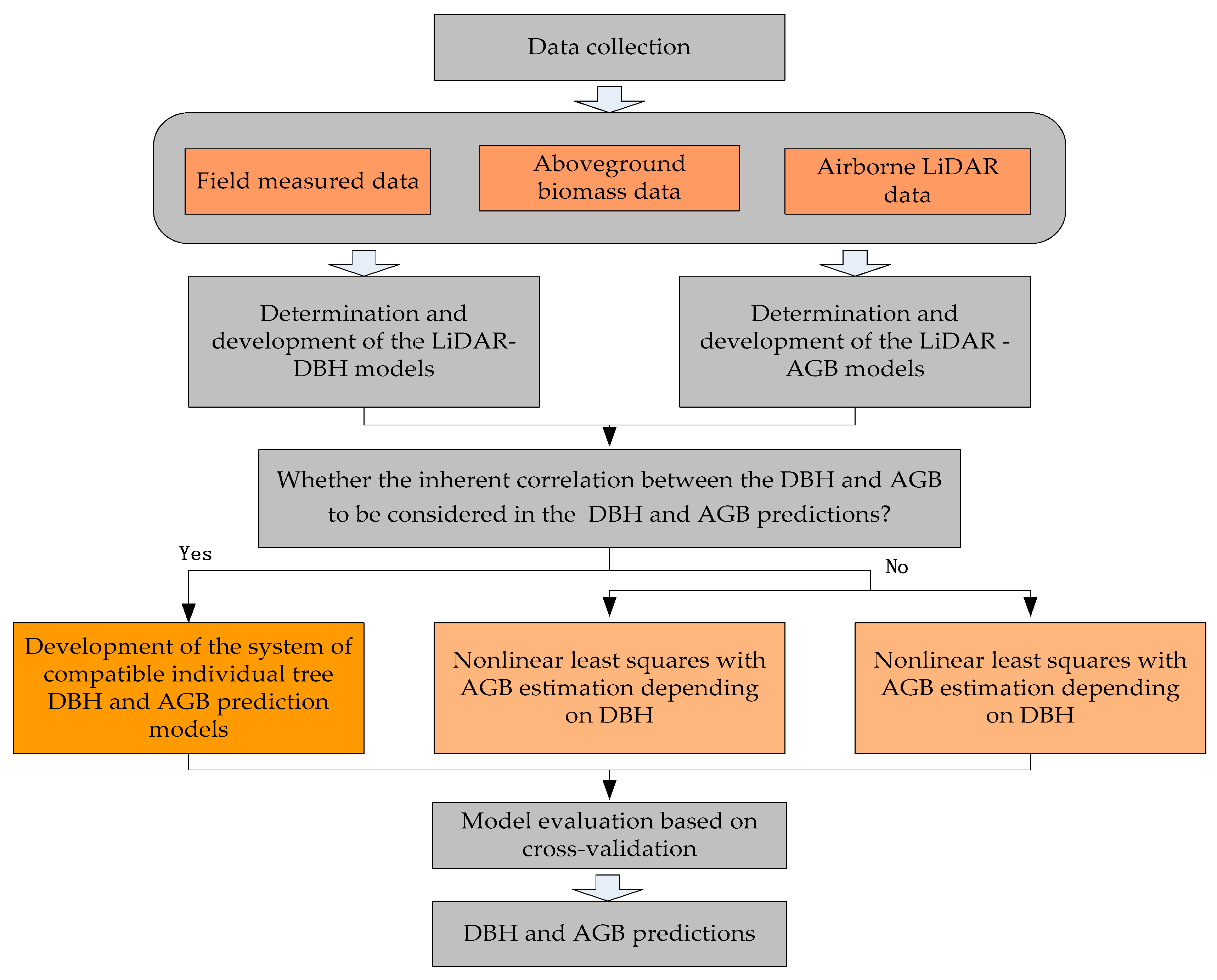
2. Materials and Methods
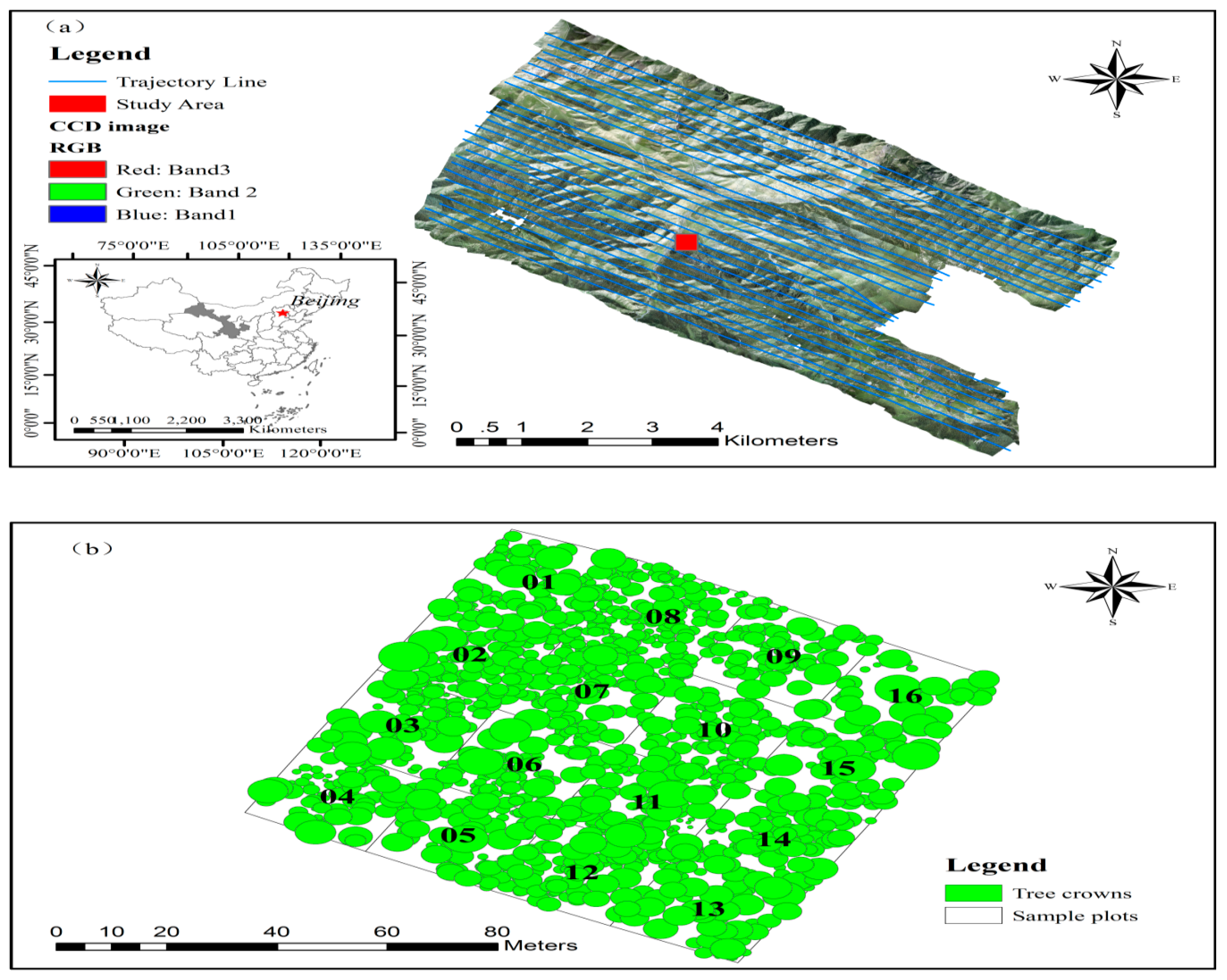
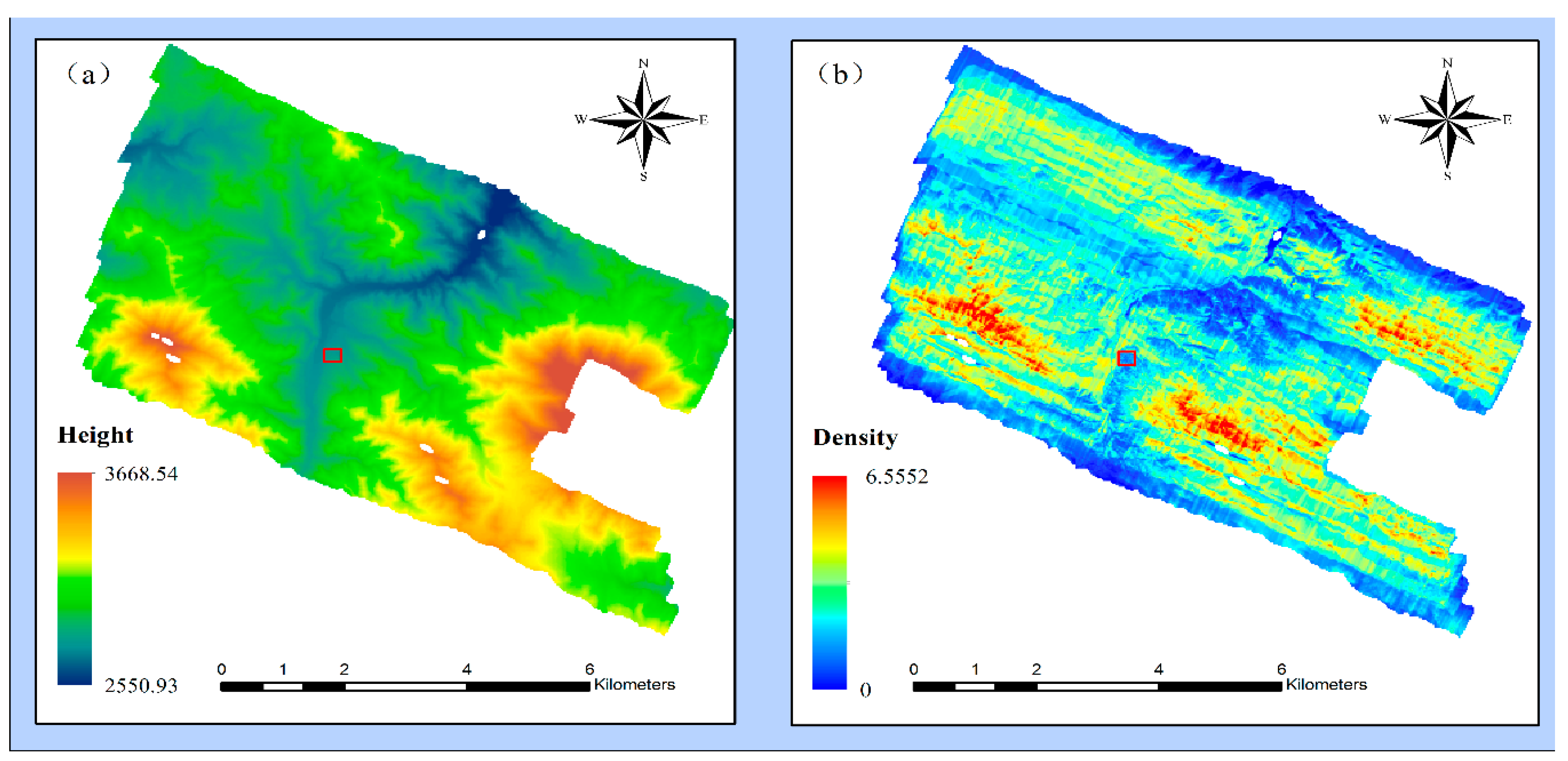
2.1. Study Area and Data
2.2. LiDAR-Derived Individual Tree Characteristics
2.3. Determination of the Base Model
2.3.1. LiDAR–DBH Model
2.3.2. LiDAR–AGB Model
2.4. A System of Compatible Individual Tree DBH and AGB Error-In-Variable Models
2.4.1. Structure for the Variance–Covariance Matrix
2.4.2. Parameter Estimation Methods
2.5. Other Model Structures for Comparison
2.5.1. Nonlinear Least Squares with AGB Estimation Depending on DBH
2.5.2. Nonlinear Least Squares with AGB Estimation Not Depending on DBH
2.6. Evaluation and Comparison of Model Predictions Based on a Leave-One-Out Cross-Validation Approach
3. Results
3.1. Estimation of the Parameters
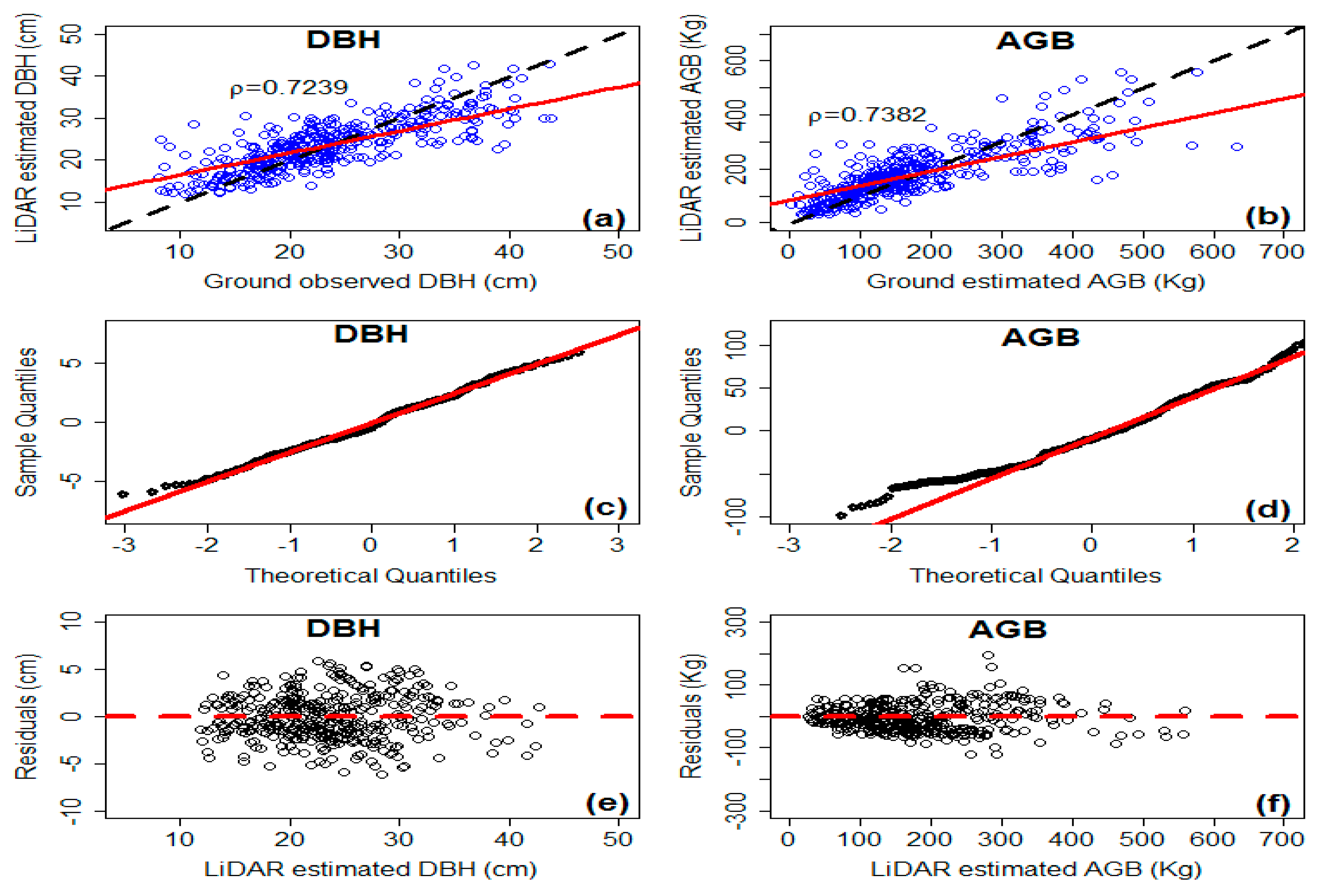
3.2. Model Evaluation
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zhang, W.; Ke, Y.; Quackenbush, L.J.; Zhang, L. Using error-in-variable regression to predict tree diameter and crown width from remotely sensed imagery. Can. J. For. Res. 2010, 40, 1095–1108. [Google Scholar] [CrossRef]
- Fu, L.; Zeng, W.; Tang, S. Individual tree biomass models to estimate forest biomass for large spatial regions developed using four pine species in China. For. Sci. 2017, 63, 42–50. [Google Scholar]
- Fu, L.; Lei, Y.; Wang, G.; Bi, H.; Tang, S.; Song, X. Comparison of seemingly unrelated regressions with multivariate errors-in-variables models for developing a system of nonlinear additive biomass equations. Trees 2016, 30, 839–857. [Google Scholar] [CrossRef]
- Zianis, D.; Mencuccini, M. On simplifying allometric analyses of forest biomass. For. Ecol. Manag. 2004, 187, 311–332. [Google Scholar] [CrossRef]
- Zianis, D.; Muukkonen, P.; Mäkipää, R.; Mencuccini, M. Biomass and stem volume equations for tree species in Europe. Silva Fenn. 2005, 4, 5–63. [Google Scholar]
- Dong, L.; Zhang, L.; Li, F. Developing additive systems of biomass equations for nine hardwood species in Northeast China. Trees 2015, 29, 1149–1163. [Google Scholar] [CrossRef]
- Fu, L.; Zeng, W.; Tang, S.; Sharma, R.P.; Li, H. Using linear mixed model and dummy variable model approaches to construct compatible single-tree biomass equations at different scales—A case study for Masson pine in southern China. J. For. Sci. 2012, 58, 101–115. [Google Scholar] [CrossRef]
- Fu, L.; Sun, W.; Wang, G. A climate-sensitive aboveground biomass model for three larch species in northeastern and northern China. Trees 2017, 31, 124–131. [Google Scholar] [CrossRef]
- Salas, C.; Ene, L.; Gregoire, T.G.; Naesset, E.; Gobakken, T. Modelling tree diameter from airborne laser scanning derived variables: A comparison of spatial statistical models. Remote Sens. Environ. 2010, 114, 1277–1285. [Google Scholar] [CrossRef]
- Popescu, S.C.; Zhao, K.; Neuenschwander, A.; Lin, C. Satellite Lidar vs. small footprint airborne lidar: Comparing the accuracy of aboveground biomass estimates and forest structure metrics at footprint level. Remote Sens. Environ. 2011, 115, 2786–2797. [Google Scholar] [CrossRef]
- Bi, H.; Fox, J.C.; Li, Y.; Lei, Y.; Pang, Y. Evaluation of nonlinear equations for predicting diameter from tree height. Can. J. Remote Sens. 2012, 42, 789–806. [Google Scholar] [CrossRef]
- Ene, L.T.; Naesset, E.; Gobakken, T.; Gregoire, T.G.; Stahl, G.; Holm, S. A simulation approach for accuracy assessment of two-phase post-stratified estimation in large-area LiDAR biomass surveys. Remote Sens. Environ. 2013, 133, 210–224. [Google Scholar] [CrossRef]
- Ahmed, R.; Siqueira, P.; Hensley, S. A study of forest biomass estimates from Lidar in the northern temperate forests of New England. Remote Sens. Environ. 2013, 130, 121–135. [Google Scholar] [CrossRef]
- Cao, L.; Coops, N.C.; Innes, J.L.; Sheppard, S.R.J.; Fu, L.; Ruan, H.; She, G. Estimation of forest biomass dynamics in subtropical forests using multi-temporal airborne LiDA R data. Remote Sens. Environ. 2016, 178, 158–171. [Google Scholar] [CrossRef]
- Popescu, S.C. Estimating biomass of individual pine trees using airborne lidar. Biomass Bioenergy 2007, 31, 646–655. [Google Scholar] [CrossRef]
- Broadbent, E.N.; Asner, G.P.; Peña-Claros, M.; Palace, M.; Soriano, M. Spatial partitioning of biomass and diversity in a lowland Bolivian forest: linking field and remote sensing measurements. For. Ecol. Manag. 2008, 255, 2602–2616. [Google Scholar] [CrossRef]
- Heurich, M. Automatic recognition and measurement of single trees based on data from airborne laser scanning over the richly structured natural forests of the Bavarian Forest National Park. For. Ecol. Manag. 2008, 255, 2416–2433. [Google Scholar] [CrossRef]
- Boudreau, J.; Nelson, R.F.; Margolis, H.A.; Beaudoin, A. Regional aboveground forest biomass using airborne and spaceborne LiDAR in Québec. Remote Sens. Environ. 2008, 112, 3876–3890. [Google Scholar] [CrossRef]
- Verma, N.K.; Lamb, D.W.; Reid, N.; Wilson, B. An allometric model for estimating DBH of isolated and clustered Eucalyptus trees from measurements of crown projection area. For. Ecol. Manag. 2014, 326, 125–132. [Google Scholar] [CrossRef]
- Detto, M.; Asner, G.; Muller-landau, H.; Sonnentag, O. Spatial variability in tropical forest leaf area density from multireturn lidar and modeling. J. Geophys. Res. 2015, 120, 294–309. [Google Scholar] [CrossRef]
- Zhao, F.; Guo, Q.; Kelly, M. Allometric equation choice impacts Lidar-based forest biomass estimates: A case study from the Sierra National Forest, CA. Agric. For. Meteorol. 2012, 165, 64–72. [Google Scholar] [CrossRef]
- He, Q.; Chen, E.; An, R.; Li, Y. Above-ground biomass and biomass components estimation using LiDAR data in a coniferous forest. Forests 2013, 4, 984–1002. [Google Scholar] [CrossRef]
- Rencher, A.C.; Schaalje, G.B. Linear Models in Statistics, 2nd ed.; Wiley: New York, NY, USA, 2008. [Google Scholar]
- Fuller, W.A. Measurement Error Models; John Wiley and Sons: New York, NY, USA, 1987. [Google Scholar]
- Moore, J.R. Allometric equations to predict the total aboveground biomass of radiata pine trees. Ann. For. Sci. 2010, 67, 806. [Google Scholar] [CrossRef]
- Kangas, A.S. Effect of error-in-variables on coefficients of a growth model and on prediction of growth. For. Ecol. Manag. 1998, 102, 203–212. [Google Scholar] [CrossRef]
- Li, Y.; Tang, S. A study on impact of measurement error on whole stand model. Sci. Silv. Sin. 2005, 41, 166–169. [Google Scholar]
- Tang, S.; Zhang, S. Measurement error models and their applications. J. Biomath. 1998, 13, 161–166. [Google Scholar]
- Tang, S.; Li, Y.; Wang, Y. Simultaneous equations, errors-invariable models, and model integration in systems ecology. Ecol. Model. 2001, 142, 285–294. [Google Scholar] [CrossRef]
- Tang, S.Z.; Li, Y.; Fu, L.Y. Statistical Foundation for Biomathematical Models, 2nd ed.; Higher Education Press: Beijing, China, 2015; p. 435. ISBN 978-7-04-042303-7. [Google Scholar]
- Tang, S.; Wang, Y. A parameter estimation program for the errors-in-variable model. Ecol. Model. 2002, 156, 225–236. [Google Scholar] [CrossRef]
- Li, Y.; Tang, S. Study on impact of measurement error on model and compare of parameter estimate methods. J. Biomath. 2006, 21, 285–290. [Google Scholar]
- Fernandes, R.; Leblanc, S.G. Parametric (modified least squares) and non-parametric (Thei-Sen) linear regression for predicting biophysical parameter in the presence of measurement errors. Remote Sens. Environ. 2005, 95, 303–316. [Google Scholar] [CrossRef]
- Dang, H.Z.; Zhao, Y.S.; Chen, X.W. Law of the water transfer process of water—Conversation forest in Qilian Mountains. Chin. J. Eco-Agric. 2004, 12, 43–46. (In Chinese) [Google Scholar]
- Ma, Y.J.; Wang, J.Y.; Liu, X.M.; Pei, W.; Jin, M. Status of Forestry Ecosystem and Protection Countermeasure in the Protection Areas in Qilian Mountains. J. Northwest For. Univ. 2005, 20, 5–8. [Google Scholar]
- Koch, B.; Heyder, U.; Weinacker, H. Detection of Individual Tree Crowns in Airborne Lidar Data. Photogramm. Eng. Remote Sens. 2006, 72, 357–363. [Google Scholar] [CrossRef]
- Parent, J.R.; Volin, J.C. Assessing the potential for leaf–off LiDAR data to model canopy closure in temperate deciduous forests. Photogramm. Eng. Remote Sens. 2014, 95, 134–145. [Google Scholar] [CrossRef]
- Liu, Q.; Li, Z.; Chen, E.; Pang, Y.; Wu, H. Extracting individual tree heights and crowns using airborne LIDAR data. J. Beijing For. Univ. 2008, 30, 83–89. [Google Scholar]
- Zhang, K.; Chen, S.C.; Whitman, D.; Shyu, M.L.; Yan, J.; Zhang, C. A progressive morphological filter for removing nonground measurements from airborne LIDAR data. IEEE Trans. Geosci. Remote 2003, 41, 872–882. [Google Scholar] [CrossRef]
- Chen, Q.; Baldocchi, D.; Gong, P.; Kelly, M. Isolating individual trees in asavanna Woodland using small footprint lidar data. Photogramm. Eng. Remote Sens. 2006, 72, 923–932. [Google Scholar] [CrossRef]
- Wu, B.; Yu, B.; Huang, C.; Wu, Q.; Wu, J. Automated extraction of groundsurface along urban roads from mobile laser scanning point clouds. Remote Sens. Lett. 2016, 7, 170–179. [Google Scholar] [CrossRef]
- Korhonen, L.; Korpela, I.; Heiskanen, J.; Maltamo, M. Airborne discrete–return LiDAR data in the estimation of vertical canopy cover, angular canopy closure and leaf area index. Remote Sens. Environ. 2011, 115, 1065–1080. [Google Scholar] [CrossRef]
- Yu, X.; Hyyppä, J.; Vastaranta, M.; Holopainen, M.; Viitala, R. Predicting individual tree attributes from airborne laser point clouds based on the random forests technique. Photogramm. Eng. Remote Sens. 2011, 66, 28–37. [Google Scholar] [CrossRef]
- Brandtberg, T.; Warner, T.A.; Landenberger, R.E.; McGraw, J.B. Detection and analysis of individual leaf-off tree crowns in small footprint, high sampling density lidar data from the eastern deciduous forest in North America. Remote Sens. Environ. 2003, 85, 290–303. [Google Scholar] [CrossRef]
- Liu, Q. Study on the Estimation Method of Forest Parameters using Airborne LiDAR. Ph.D. Thesis, Chinese Academy of Forestry, Beijing, China, 2009; p. 174. (In Chinese). [Google Scholar]
- Silva, C.A.; Hudak, A.T.; Vierling, L.A.; Loudermilk, E.L.; O’Brien, J.J.; Hiers, J.K.; Jack, B.S.; Gonzalez-Benecke, C.; Lee, H.; Falkowski, M.J.; et al. Imputation of Individual Longleaf Pine (Pinus palustris Mill.) Tree Attributes from Field and LiDAR Data. Can. J. Remote Sens. 2016, 42, 554–573. [Google Scholar] [CrossRef]
- Wang, J.Y.; Ju, K.J.; Fu, H.E.; Chang, X.X.; He, H.Y. Study on biomass of water conservation forest on North Slope of Qilian Mountains. J. Fujian Coll. For. 1998, 18, 319–325. (In Chinese) [Google Scholar]
- Dubayah, R.; Drake, J. Lidar remote sensing for forestry. J. For. 2000, 98, 44–46. [Google Scholar]
- Andersen, H.E.; Reutebuch, S.E.; McGaughey, R.J. A rigorous assessment of tree height measurements obtained using airborne lidar and conventional field methods. Can. J. Remote Sens. 2006, 32, 355–366. [Google Scholar] [CrossRef]
- Xiao, W.; Xu, S.; Elberink, S.O.; Vosselman, G. Individual Tree Crown Modeling and Change Detection from Airborne Lidar Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 3467–3477. [Google Scholar] [CrossRef]
- Venables, W.N.; Ripley, B.D. Modern Applied Statistics with S-PLUS, 3rd ed.; Springer Verlag: New York, NY, USA, 1999. [Google Scholar]
- Yang, Y.; Huang, S. Comparison of different methods for fitting nonlinear mixed forest models and for making predictions. Can. J. For. Res. 2011, 41, 1671–1686. [Google Scholar] [CrossRef]
- Fang, Z.; Bailey, R.L. Nonlinear mixed-effect modeling for Slash pine dominant height growth following intensive silvicultural treatments. For. Sci. 2001, 47, 287–300. [Google Scholar]
- Tang, S.Z.; Lang, K.J.; Li, H.K. Statistics and Computation of Biomathematical Models (ForStat Course); Science Press: Beijing, China, 2008. (In Chinese) [Google Scholar]
- Parresol, B.R. Assessing tree and stand biomass: A review with examples and critical comparisons. For. Sci. 1999, 45, 573–593. [Google Scholar]
- Parresol, B.R. Additivity of nonlinear biomass equations. Can. J. For. Res. 2001, 31, 865–878. [Google Scholar] [CrossRef]
- Bi, H.; Turner, J.; Lambert, M.J. Additive biomass equations for native eucalypt forest trees of temperate Australia. Trees 2004, 18, 467–479. [Google Scholar] [CrossRef]
- Bi, H.; Long, Y.; Turner, J.; Lei, Y.; Snowdon, P.; Li, Y.; Harper, R.; Zerihun, A.; Ximenes, F. Additive prediction of aboveground biomass for Pinus radiata (D. Don) plantations. For. Ecol. Manag. 2010, 259, 2301–2314. [Google Scholar] [CrossRef]
- Judge, G.G.; Hill, R.C.; Griffiths, W.E.; Lutkepohl, H.; Lee, T.C. Introduction to the Theory and Practice of Econometrics, 2nd ed.; Wiley: New York, NY, USA, 1988. [Google Scholar]
- Borders, B.E.; Bailey, R.L.; Ware, K.D. Slash pine site-index from a polymorphic model by joining (splining) nonpolynomial segments with an algebraic difference method. For. Sci. 1984, 30, 411–423. [Google Scholar]
- Nord-Larsen, T.; Meilby, H.; Skovsgaard, J.P. Site-specific height growth models for six common tree species in Denmark. Scand. J. For. Res. 2009, 24, 194–204. [Google Scholar] [CrossRef]
- Timilsina, N.; Staudhammer, C.L. Individual tree-based diameter growth model of slash pine in Florida using nonlinear mixed modeling. For. Sci. 2013, 59, 27–31. [Google Scholar] [CrossRef]
- Field, C.B.; Raupach, M.R.; Victoria, R. The global carbon cycle: Integrating humans, climate and the natural world. In The Global Carbon Cycle: Integrating Humans, Climate and the Natural World, 2nd ed.; Field, C.B., Raupach, M.R., Hill MacKenzie, S., Eds.; Island Press: Washington, DC, USA, 2003. [Google Scholar]
- Hall, R.J.; Morton, R.T.; Nesby, R.N. A Comparison of existing models for DBH estimation for large-scale photos. For. Chron. 1989, 65, 114–120. [Google Scholar] [CrossRef]
- Gering, L.R.; May, D.M. The relationship of diameter at breast height and crown diameter for four species groups in Hardin County, Tennessee. South. J. Appl. For. 1995, 19, 177–181. [Google Scholar]
- Fleck, S.; Mölder, I.; Jacob, M.; Gebauer, T.; Jungkunst, H.F.; Leuschner, C. Comparison of conventional eight-point crown projections with LIDAR-based virtual crown projections in a temperate old-growth forest. Ann. For. Sci. 2011, 68, 1173–1185. [Google Scholar] [CrossRef]
- Nelson, R. Modelling forest canopy heights. The effects of canopy shape. Remote Sens. Environ. 1997, 60, 327–334. [Google Scholar] [CrossRef]
- Grote, R. Estimation of crown radii and crown projection area from stem size and tree position. Ann. For. Sci. 2003, 60, 393–402. [Google Scholar] [CrossRef]
- Lindley, D.V. Regression lines and the linear functional relationship. J. R. Stat. Soc. B 1947, 9, 218–244. [Google Scholar] [CrossRef]
- Henningsen, A.; Jeff, H. Systemfit: A package for estimating systems of simultaneous equations in R. J. Stat. Softw. 2007, 23, 1–40. [Google Scholar] [CrossRef]
- SAS Institute, Inc. SAS/ETS 9.3. User’s Guide; SAS Institute, Inc.: Cary, NC, USA, 2011. [Google Scholar]
- Wang, G.; Oyana, T.; Zhang, M.; Adu-Prah, S.; Zeng, S.; Lin, H.; Se, J. Mapping and spatial uncertainty analysis of forest vegetation carbon by combining national forest inventory data and satellite images. For. Ecol. Manag. 2009, 258, 1275–1283. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, M.; Gertner, G.Z.; Oyana, T.; McRoberts, R.E.; Ge, H. Uncertainties of Mapping Forest Carbon Due to Plot Locations Using National Forest Inventory Plot and Remotely Sensed Data. Scand. J. For. Res. 2011, 26, 360–373. [Google Scholar] [CrossRef]
- Zhang, M.; Lin, H.; Zeng, S.; Li, J.; Shi, J.; Wang, G. Impacts of plot location errors on accuracy of mapping and up-scaling aboveground forest carbon using sample plot and Landsat TM data. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1483–1487. [Google Scholar] [CrossRef]

| Component | Models |
|---|---|
| Stem | |
| Branch | |
| Foliage | |
| Fruit |
| Variable | Mean | SD | Min | Max |
|---|---|---|---|---|
| DBH (cm) | 23.51 | 7.63 | 5.00 | 43.8 |
| AGB (kg) | 181.36 | 134.17 | 1.45 | 632.84 |
| LH (m) | 6.95 | 1.90 | 1.96 | 11.30 |
| CPA (m2) | 7.43 | 2.06 | 2.94 | 13.50 |
| Model No. | Model | Model Form | RMSE | |||
|---|---|---|---|---|---|---|
| I.1 | Linear | 0.0000 | 5.8187 | 5.8187 | 0.5140 | |
| I.2 | Richards | 0.0777 | 5.8294 | 5.8300 | 0.5122 | |
| I.3 | Logistic | 0.0028 | 5.7569 | 5.7569 | 0.5243 | |
| I.4 | Exponential | −0.0025 | 5.7584 | 5.7584 | 0.5241 |
| Model No. | Model | RMSE | −2LL | LRT | p Value | |||
|---|---|---|---|---|---|---|---|---|
| II.1 | −4.8730 | 31.7568 | 32.1285 | 0.9427 | −1965 | - | - | |
| II.2 | 0.4477 | 18.2123 | 18.2178 | 0.9816 | −1737 | 228 | <0.0001 | |
| II.3 | −0.5761 | 20.6800 | 20.6880 | 0.9762 | −1788 | 177 | <0.0001 | |
| II.4 | 1.9894 | 91.6294 | 91.6501 | 0.5334 | −2386 | 421 | <0.0001 | |
| II.5 | 0.4645 | 18.2086 | 18.2145 | 0.9816 | −1737 | 228 | <0.0001 |
| Parameters | Model I.4 | Model II.2 | Model (20) | Model System (7) | |
|---|---|---|---|---|---|
| NSUR | TSEM | ||||
| DBH-related parameters | |||||
| () | 8.6595 | _ | 10.9351 | 8.5799 | 8.2213 |
| () | −0.0851 | _ | -0.1117 | −0.0863 | −0.0894 |
| () | −0.05 | _ | −0.0879 | −0.0501 | −0.0522 |
| AGB-related parameters | |||||
| () | _ | 0.2267 | 0.6457 | 0.2307 | 0.2386 |
| _ | 1.7701 | _ | 1.7594 | 1.7435 | |
| _ | 0.5008 | _ | 0.5095 | 0.5188 | |
| Variance components | |||||
| _ | _ | _ | 33.3283 | 33.4050 | |
| _ | _ | _ | 13.1971 | 20.2866 | |
| _ | _ | _ | 334.7768 | 340.1165 | |
| 5.773 | 18.26 | 91.64 | _ | _ | |
| Model | ||||
|---|---|---|---|---|
| NLS&DD | ||||
| −0.0028 | 5.8341 | 5.8341 | 0.5193 | |
| 6.5972 | 91.3987 | 91.6365 | 0.5335 | |
| NLS&NDD | ||||
| −0.0028 | 5.8341 | 5.8341 | 0.5193 | |
| 0.0581 | 91.2973 | 91.2973 | 0.5370 | |
| MS-NSUR | ||||
| 0.0097 | 5.7587 | 5.7587 | 0.5251 | |
| 6.5559 | 91.0211 | 91.2569 | 0.5449 | |
| MS-TSEM | ||||
| 0.0648 | 5.7649 | 5.7653 | 0.5239 | |
| 6.1813 | 91.0873 | 91.2968 | 0.5430 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, L.; Liu, Q.; Sun, H.; Wang, Q.; Li, Z.; Chen, E.; Pang, Y.; Song, X.; Wang, G. Development of a System of Compatible Individual Tree Diameter and Aboveground Biomass Prediction Models Using Error-In-Variable Regression and Airborne LiDAR Data. Remote Sens. 2018, 10, 325. https://doi.org/10.3390/rs10020325
Fu L, Liu Q, Sun H, Wang Q, Li Z, Chen E, Pang Y, Song X, Wang G. Development of a System of Compatible Individual Tree Diameter and Aboveground Biomass Prediction Models Using Error-In-Variable Regression and Airborne LiDAR Data. Remote Sensing. 2018; 10(2):325. https://doi.org/10.3390/rs10020325
Chicago/Turabian StyleFu, Liyong, Qingwang Liu, Hua Sun, Qiuyan Wang, Zengyuan Li, Erxue Chen, Yong Pang, Xinyu Song, and Guangxing Wang. 2018. "Development of a System of Compatible Individual Tree Diameter and Aboveground Biomass Prediction Models Using Error-In-Variable Regression and Airborne LiDAR Data" Remote Sensing 10, no. 2: 325. https://doi.org/10.3390/rs10020325
APA StyleFu, L., Liu, Q., Sun, H., Wang, Q., Li, Z., Chen, E., Pang, Y., Song, X., & Wang, G. (2018). Development of a System of Compatible Individual Tree Diameter and Aboveground Biomass Prediction Models Using Error-In-Variable Regression and Airborne LiDAR Data. Remote Sensing, 10(2), 325. https://doi.org/10.3390/rs10020325









