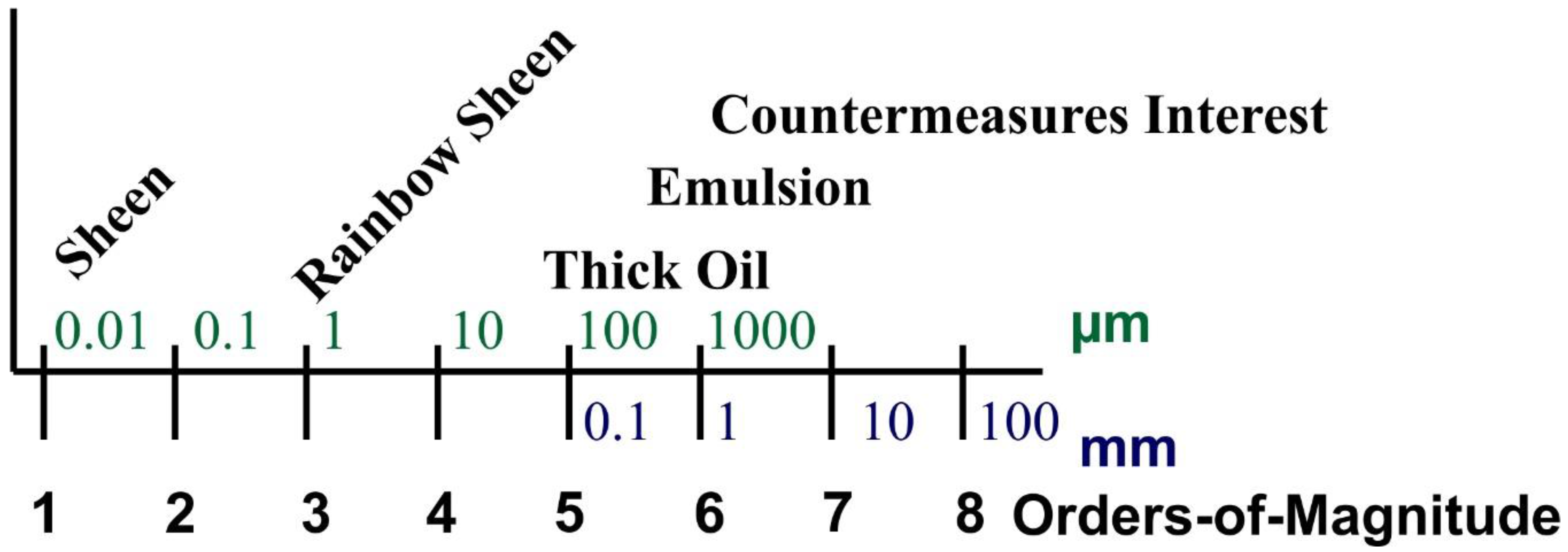
4.1. Near-Infrared Reflectance
Several workers have proposed to use reflection or specular reflection from slicks in the near-infrared (IR) region to estimate slick thickness. Cox and Munk proposed that a slick might reflect sunlight differently than a water surface. After some theoretical developments, they proposed that slick thickness might be a factor in the reflection [
34]. De Carolis et al. proposed to use this model to estimate the thickness of an actual slick, the Lebanon heavy oil spill [
35,
36]. The theory of Cox and Munk was extended to estimate that slick thickness changes the reflection coefficient. De Carolis et al. used near-IR measurements obtained from MODIS and MERIS to obtain input data.
Table 4 shows the result of their calculations (data from de Carolis et al. [
36]).
Table 4 shows that the thickness may be close to what one might estimate (1 to 5 µm), but the deviations are high and very high for case number 2. The theory behind the specular reflection is not well established, and the application was never tested against field data by this group.
Clark et al. proposed that color composite images assembled from both visible and near-IR wavelengths could be used to make images of thick oil, but such images also show strong reflections from clouds and the glint from the ocean surface [
37]. Clark et al. proposed that spectroscopic analysis of the reflectance spectra within remote sensing imagery could resolve the absorptions due to the organic compounds in oil and could better discriminate the spectral shape of the oil. A method to analyse absorptions due to specific materials is called absorption-band depth mapping. Clark et al. showed that simple three-point-band depth mapping will show the location of absorption features but cannot identify specific compositions of the compounds causing these features when multiple compounds have absorptions near the same wavelength. In the case of open ocean images, comprised of pixels containing water, oil/water mixtures, and clouds, the organic compounds in the oil and oil/water mixtures have absorption features that are distinct from those of the water and clouds. These spectral differences should allow one to map the qualitative variations in oil abundance. This scheme was ‘calibrated’ using reconstructed water-in-oil emulsions in a laboratory setting. Other than for one set of images from the Gulf of Mexico oil spill, this concept has not been proven.
Clark et al. used the NASA Airborne Visible/Infrared Imaging Spectrometer (AVIRIS) [
37,
38]. AVIRIS provides data on the spectrum of a surface at each pixel from 0.35 to 2.5 microns (the visible spectrum is: blue: 0.4 microns, green 0.53 microns, deep red 0.7 microns) in 224 channels. AVIRIS data from oil overflights are used to produce a three-point band depth map, indicating the potential locations of thick oil by the following methods: 1 the radiance data are converted to surface reflectance using a two-step process; 2 three-point-band depth images are computed using continuum-removed reflectance spectra using the equation,
where Rb is the reflectance around the absorption maximum (minimum reflectance), Rl is the reflectance of the left continuum end point, and Rr is the reflectance of the right continuum end point. The proposed adsorption scheme is shown in
Figure 8 (from Leifer et al., 2012 [
38]).
The band-depth images produced from calculations are combined into a color composite image as follows: the 2.3 micron feature in the red channel, the 1.73 micron feature in the green channel, and the 1.2 micron feature in the blue channel. The thicker oil then shows up in the green-blue regions of the image.
The Gulf of Mexico oil spill was mapped using the AVIRIS sensor in the ER aircraft, and thickness maps were plotted [
37]. This method appeared to work for the Gulf oil spill, however confirmation on other spills awaits. Clark et al. reported that AVIRIS covered about 30 percent of the core spill area, which consisted of emulsion plumes and oil sheens. The derived lower limits for oil volumes within the top few mm of the ocean surface directly probed with the near-infrared light detected in the AVIRIS scenes were from 19,000 (conservative assumptions) to 34,000 (aggressive assumptions) barrels of oil. The areas of oil sheen lacking oil emulsion plumes outside of the core spill were not evaluated in the oil volume in this study. If the core spill areas not covered by flight lines contained similar amounts of oil and oil–water emulsions, then the extrapolation to the entire core spill area defined by a MODIS (Terra) image collected on the same day indicates that a minimum of 66,000 to 120,000 barrels of oil was floating on the surface at the time of the flight on May 17, 2010 [
37].
An immediate concern one might raise about this technique is that the absorptions were measured in the laboratory, and the emulsions were ‘reconstituted’. Since emulsion formation is very complex, doubts are raised about the reliability of these laboratory emulsions.
Sun et al. used the data generated by Clarke et al. to categorize the slicks in the area measured by AVIRIS and used by Clarke et al. [
39]. In their thickness estimates, this constituted about 30% of the oil coverage by the Deepwater Horizon spill. The thickness classes were divided into four, as shown in
Table 5 below, and the slicks fitting into each of the categories were counted. Further, the dimensions of the slicks were estimated.
Table 5 shows the basic results from Sun et al. with the approximate volumes calculated [
39]. This calculation (performed by the present author) is interesting in that it shows that only about 20% of the volume estimated was in thin slicks. Most of the oil was in the thicker slicks, according to the estimations by Sun et al. and their calculations.
Macdonald et al. and Holmes et al. used the Clarke estimates for the thicker slicks to calculate the amount of oil on the sea day by day during the Deepwater Horizon spill [
40,
41]. These researchers used synthetic aperture radar data over the Deepwater Horizon spill and neural network analysis of satellite SAR images to quantify the magnitude and distribution of surface oil in the Gulf of Mexico from persistent, natural seeps and from the Deepwater Horizon (DWH) discharge. The slicks were divided into thin and thick (emulsion) slicks. The thickness was estimated to be 1 µm for the thin slicks and following the Clarke et al. data, and 70 µm for the thick slicks of oil. This analysis was able to separate the seeps from the oil from the Deepwater Horizon blowout. This analysis showed that the 87-day DWH discharge produced a surface-oil footprint fundamentally different from background seepage, with an average ocean area of 11,200 km
2 and a volume of 22,600 m
3 [
40].
Sicot et al. attempted to use the Clark et al. method to measure both the emulsification rate of a spill and its thickness [
42]. The subset of a SWIR wavelength of 1500 to 1750 nm was chosen. The spectra of various oils in states of emulsification were measured. A model was then created. After fitting the model to the experimental data, the model was applied to historical spills (Deepwater Horizon and a Norwegian experimental spill) with claimed good results. The models contain a number of constants which require manipulation, for example, for various values of one constant, a thickness of 5 mm or 200–250 µm was achieved.
Niu et al. followed the methods of Clarke et al. using AVIRIS data, however, they developed a new scheme of spectral indices which were then subjected to a support vector machine [
43]. Six spectral indices were developed, three of which were good predictors of slick thickness, which was gauged, by using visual appearances, as being medium, thick, or thin. The best index was the one dubbed ‘SR’ index, which used indicators from the spectral band of 400 to 900 nm, as well as 724 to 821 nm, and 404 to 504 nm. The details of the correlations were not given.
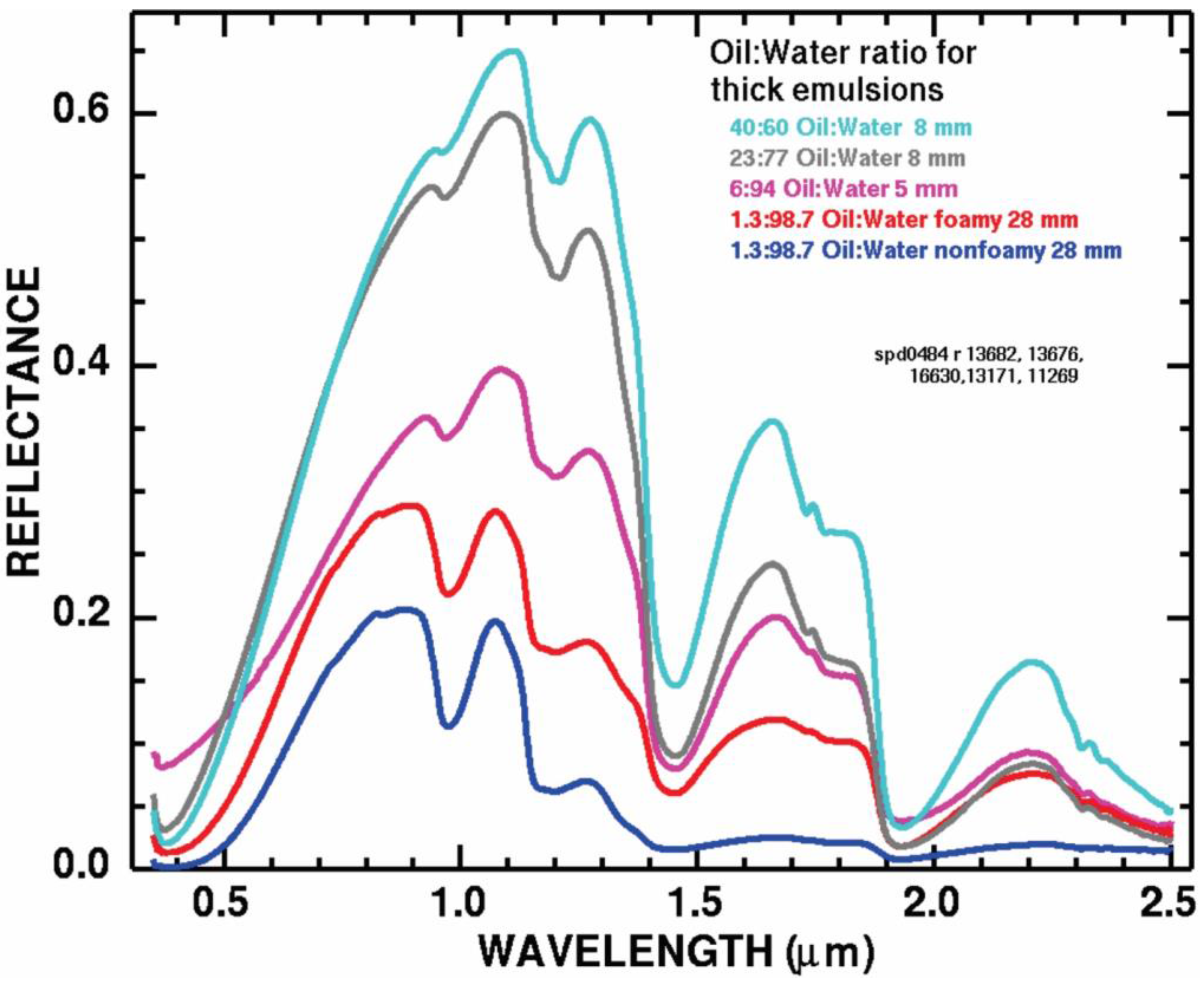
The reflectivity measurements presumed that reflectivity was greatest for the thickest oils, however other studies show this is not the case. Allik et al. measured the reflectivities of two oils and one emulsion, and the results showed that reflectivities varied [
44]. The Alaska North Slope (ANS) crude showed lesser reflectivity than its emulsions. The order of reflectivity for the ANS emulsion (highest to lowest) was 2, 5, 1, 20, 10 mm. For the non-emulsified oil, the order was 3, 2, 5, 1, and 0.5 mm. For Santa Barbara seep oil, the order was 3, 2, 5, 1, 0.5 mm. Lu et al. similarly found that the reflectance of a Bohai crude oil slick was the lowest for the thickest oil slick tested and the highest for the thinnest slick [
45]. However, intermediate thicknesses did not necessarily have reflectivities in the order of their thicknesses. It is clear that the reflectivity does not simply increase or decrease with oil thickness. Other phenomena must be occurring to explain the observations that some thicknesses have greater reflectivities than others. Reflectivity in the near-infrared cannot, at this time, be used to gauge slick thickness.
4.2. Spectral Differences
Several workers report on studies relating thickness to specific wavelengths ranging over the visible spectrum and sometimes out into the near-infrared. Most typically, wavelengths in the visible range appeared to correlate with slick thickness. The wavelengths used are summarized in
Table 6. This table also includes the near-infrared reflectance spectra as noted above.
Allik et al. carried out a reflectivity study of oils and emulsions of various thicknesses over the range of 300 to 2300 nm [
44]. It was noted that the spectra were very similar in the visible range, but the emulsions had higher reflectivity in the spectral region of 900 to 2300 nm (SWIR). It was not noted, however, that the thicker oils and emulsions had apparent reflectivities lower than those of the thin ones, negating the use of this phenomenon for oil thickness sensing.
Andreou et al. carried out a hyperspectral signature study of several oils, largely for the purpose of investigating differences between oils [
46]. Thirteen different oils and petroleum products were studied. The spectra of each oil were gathered and then correlated with age and thickness. It was found that these did correlate, however the wavelength at which the correlation occurred was different. The thickness correlated with four different wavelengths: for heavy fuel oil the wavelength was 893–918 nm, for heating fuel it was 474–500 nm, for kerosene it was 839–864 nm, and for crude oil it was 715–740 nm. Thickness equation correlations of 0.88 to 0.84 were claimed. This correlation is, however, not evident in the spectra, as for the three thicknesses used (10, 50, 100 µm), the intensity of the spectrum is significantly lower at the intermediate thicknesses. There is no theory explaining why this might work, nor was this same correlation observed by others.
Byfield tested oils in the laboratory and claimed that the relative thickness for light crude oils could be determined from the ratio of red to near-infrared radiances [
47,
48]. This ratio increased for light oils but not heavy ones. This was also tested on the Sea Empress spill with claimed success, but no results were given.
De Beaucoudrey et al. calculated the reflectivity of oil films on the surface as a function of oil thickness [
49]. They found that the reflectivity did vary with thickness and suggested this might be used to measure thickness.
Lennon et al. claimed that they were able to relate multi-spectral images from the CASI to slick thickness [
50]. They claimed they could calibrate this to a laser fluorosensor Raman suppression value (see Raman suppression below). As the Raman suppression claimed was about 1000 times the accepted physical maximum value, the claims in this paper are questionable.
Li et al. used spectral unmixing techniques to study the reflectivity of diesel fuel over a range of 1 to 127 µm [
51]. They noted that there is a strong reflectance peak at 388 nm when the thickness of the oil film is greater than 6 µm, but there were no distinguishing spectral features when the thickness was lower than this value. Li et al. concluded that spectral reflectance does show promise for the remote detection of oil spills.
Lu et al. found that the reflectance of oil changes only marginally in the infrared band from 1150 to 2500 nm, thus this could not be used for positive detection [
52]. They also found that the reflectance of oil decreased with thickness in the visible from 400 to 1150 nm. They were unable to translate this into a practical scheme to measure oil spill thickness.
Lu et al. attempted to calibrate the wavelengths used on the Hyperion satellite to oil slick thicknesses, using data from laboratory experiments [
45]. They carried out laboratory experiments over a spectral range of 350 to 2500 nm and used a crude oil native to the Bohai sea region. The reflectance spectra showed that the greater the thickness, the lower the reflection. All spectra were normalized to account for various interferences. Further, the laboratory test showed that the red-green wavelengths were the best, and correlations were carried out at 550 to 650 nm. The correlations with slick thickness were about 0.8 r
2.
Morinaga et al. claimed to estimate the thickness of leaked oil from the sunken tanker Nakhodka in the Sea of Japan, by using the relationships between the stick thickness and the upward radiance [
53]. This was investigated by experiments in a test tank. The obtained relationships and in situ oceanographic measurement data were used for the estimate of the actual oil slick thickness. In the range of slick thickness of 0.0005–0.0019 mm, white and shiny stripe patterns were observed, and the appearance was white. This was thought to be caused by the irregular reflection, which results from the oil droplets because of the small surface tension of the dirty city water. Above the slick thickness of 0.0027 mm, the white area decreased gradually with the increase of oil and became entirely brown at the thickness of 0.075 mm. When the thickness increased further, a tint of dark brown increased. No definite relationship was found between the slick thickness and the dominant wavelength of the chromaticity point of water. The relationships between the upward radiance and the oil slick thickness were purportedly measured. This method was never advanced further.
Sykas et al. measured the spectra of 13 oil types from 280 nm to 1093 nm. The oil types were grouped into four categories, i.e., crude oils, residual fuel oils, heavy fuel oils, and light oils [
54]. The spectral signatures were measured in a lab for six different thicknesses of 1, 5, 10, 50, 100 and 200 µm. Artificial hyperspectral images were created simulating the spreading of the oil from 1 to 200 µm. Spectral unmixing methods were applied for oil thickness estimation. A logarithmic equation derived from the unmixing method was found to be the best fit between the thickness and the abundance fraction values. The R
2 values ranged from 0.48 for residue oils and 0.66 for crude oils to 0.95 for heavy fuel oils. There do not appear to be any follow-up studies or corroborating studies.
Svejkovsky et al. proposed a thickness detection system based on reflective differences detected by aerial spectrometers [
55,
56,
57]. Their test appeared to show that two spectral ranges contained thickness information: 400 to 480 nm and 625 to 680 nm. The former range varies cyclically with thickness, so that the latter range is typically used. Tests also showed that the water background is quite different in different situations and therefore the measurements must be corrected for it. In practice, the ratio of 600/551 nm was used to account for thickness. A training set was developed using test rings full of oil at various thicknesses. This was used as a training set in a fuzzy logic system. Then, the resulting thicknesses were output. The thickness limits were claimed to be up to 0.5 mm. The tests were carried out in a test tank and at the Santa Barbara seeps. There have been no published physical descriptions on why this method should work.
Wettle et al. carried out a reflectivity and absorbance study of oil from 440 to 770 nm using a small-scale laboratory apparatus [
58]. The objective was to calculate the response of QuickBird and Hymap satellite sensors to such an oil spill. The authors claimed that reflectivity increased with oil thickness, although the opposite was generally observed in the data in the paper. They calculated that a medium crude could only be detected at 10 to 20 µm, and that a condensate could only be detected at 200 µm. These limits have not been substantiated in the field. There is also some randomness contained in the data regarding the relation of thickness to reflection.
Ye et al. studied the reflectivity of five oils, i.e., gasoline, diesel, lube oil, kerosene, and crude oil, over a spectrum from UV to NIR [
59]. It was noted that the spectrum related to the thickness as well as to the oil type. Not all oil types showed the same spectra with respect to thickness and, in fact, could be quite different. The reflectance curves peaked at around 380 nm, and that of crude oil was less than water at wavelengths greater than 340 nm. The authors suggested that this phenomenon might be best used for detection rather than for universal thickness measurement.
Zhan et al. used hyperspectral data from an oil spill to improve detection and purportedly calculate oil thickness [
60]. They first corrected the data to remove sun glitter and then normalized the image. This, they claimed, led to a relative thickness map. This has never been repeated.
In summary, several researchers noted spectral differences in thickness using oils of various types. Most of these studies were not repeated. Furthermore, the studies sometimes contradict each other. For example, some studies found greater spectral brightness or reflectance as a result of increasing thickness, other found the opposite, and still other found this to be varying. The wavelengths of interest also varied widely between the studies. This is highlighted in
Table 6 which shows that there are no repeats of a specific wavelength in 16 studies. This appears to suggest that wavelengths showing peaks with varying thickness may be uniquely the result of local conditions and the type of oil being used.
4.3. Infrared Emission
As the infrared appears to show a higher thickness gradation, several parties have suggested that infrared brightness could be used as a thickness scale. Over the years, there have been many attempts to ‘calibrate’ various systems to measure oil thickness, all to no avail. Surface temperatures may be confused with internal temperatures. Brown et al. carried out a series of laboratory and tank tests to determine if there was a correlation between infrared brightness and slick thickness [
61]. Two crude oils were used, a light and a heavy crude. The oils were progressively decanted into an outdoor tank with the infrared image constantly monitored by an overhead camera. Slicks ranging from 1 to 10 mm of each oil were progressively built up in the boomed area of the test tank. The slick thicknesses was confirmed by an underwater ultrasonic probe which had been laboratory-verified. The data from the infrared camera was then processed, and the brightness was compared to the slick thickness. There was no correlation between brightness and thickness, indicating that the brightness of the infrared image does not vary with the slick thickness. The infrared emission of the slick is constant after a certain minimum thickness is reached.
Several earlier workers noted that the infrared might be used to measure oil thickness [
62,
63,
64,
65,
66]. Most of these did not result in useable schemes, and the authors later suggested that the infrared might not be the way to proceed. Shih and Andrews studied the emission and reflectance from thin sheens such as seeps [
63,
64,
65]. They found that the emissions were highest in the far infrared and could provide detectability. Shih and Andrews studied infrared thickness and sensing and noted there was no information for thickness and also that the thickness difference was a matter of thermal heating, period of heating, and contrast to the unheated background [
65]. There was no signature that would yield thickness.
Allik et al. carried out a series of tests on a small pool using long-wave thermal imagery [
44]. Oils of various thicknesses were imaged over several hours, including into the night. The usual inversions were observed, that is, the thicker oil appeared to be hotter and vice versa at night. The authors claimed that this would indicate that IR could be used to measure oil thickness if one avoided the night cross-over. Quantitative measurements were not taken. Lu et al. conducted IR emission experiments with various oil thicknesses in a small tank [
67]. There were some differences detected in brightness temperature with oil thickness, however the differences may not be useable as a measurement because of the many varying conditions in actual field situations, such as varying thicknesses, water content, and lack of thermal equilibrium of the water and oil. It was noted that the greatest differences between thicknesses was due to the increase in temperature in the mornings. A useful point is that the greatest thermal differences were noted at noon local time. The nighttime detection is best at midnight local time.
4.4. Radar Methods-Wave Damping
As oil on the sea is detected using radar by the damping of capillary waves at wind speeds of about 3 to 8 m/s, some researchers felt that this might be progressive with spill thickness. Jones tried to correlate the area of dampened slicks with the wind speed and thickness [
68]. Success was not reported. True et al. proposed that regular SAR backscatter could be used to measure oil thickness [
69]. Backscatter contrast was claimed to be better for low-incidence angles. Thus, the existing radar satellites could be used to make this measurement. This was tested in a tank, but not in an actual spill. Hühnerfuss et al. noted that real aperture radar returns appeared to show thin and thick portions in oil spills [
70]. This was not pursued, probably because of the demise of the real aperture radar systems.
Cheng et al. studied the damping of capillary waves over the Deepwater Horizon spill using the capillary wave damping as measured by the radar altimeter satellites Jason 1 and -2 [
71]. These satellites operate in the Ku (13.5 GHz) and C (5.3 GHz) bands and are active sensors used to measure sea height and other parameters. Calm surfaces such as oil spills cause a surface brightness (backscatter bloom). Cheng et al. used the archival Deepwater Horizon surface coverage data that is categorized by coverage and classifies slicks as thick or thin. Jason 1 and 2 data were taken during the time that oil coverage was extensive in the Gulf of Mexico during 2010. The data were then compared between winds speeds and oil coverage. Although there were some differences in backscatter for oil and no oil in nadir (straight down-looking) data, there were significant differences in angular backscatter data, as shown in
Table 7. These differences, which were often as great as 100%, convinced Cheng et al. that radar altimetry has the potential to yield oil thickness measurements—at least in the range of thick versus thin, as shown here [
71].
Ermakov et al. studied the dampening of waves in a small oscillatory cell and calculated the dampening effect of an oil as a function of oil thickness [
71,
72]. At small thicknesses, they concluded that the oil they used had an elasticity of 10 mN/m at its existing viscosity. The maximum dampening coefficient would be observed at slick thicknesses of about 0.3 to 1 mm. They proposed that, in the future, they could extend this to a model of slick thickness with the wave dampening observed in radar.
Radar-detected wave dampening occurs with oil spills, and it appears it may increase with increasing thickness. This can be detected using radar backscatter. However, the wave dampening is largely affected by wind and waves. The effect of these would require compensation to yield a slick thickness measurement.
4.5. Water Raman Suppression
When a laser fluorosensor is used, the laser wavelength activates a water Raman signal. Raman scattering involves energy transfer between the incident light and the water molecules. When the incident ultraviolet light interacts with the water molecules, Raman scattering occurs. The water molecules absorb some of the energy as rotational–vibrational energy and emit light at wavelengths which are the sum or difference between the incident radiation and the vibration–rotational energy of the molecule. The Raman signal for water occurs at 344 nm when the incident wavelength is 308 nm (XeCl laser). With an excitation at 460 nm (tunable dye laser), the Raman occurs at about 540 nm [
73]. The water Raman signal is useful for maintaining wavelength calibration of the fluorosensor in operation, but has also been used in a limited way to estimate oil thickness, because the strong absorption by oil on the surface will suppress the water Raman signal in proportion to thickness [
74,
75,
76,
77]. The point at which the Raman signal is entirely suppressed depends on the type of oil, since each oil has a different absorption coefficient. The Raman signal suppression has led to estimates of sensor detection limits of about 0.05 to 0.1 μm. It should be noted that this thickness is well below that of interest for oil spill countermeasures.
Patsayeva et al. showed the Raman suppression thickness measurements were true for the nm oil thickness range (100 nm = 0.1 µm) [
78]. They also developed an algorithm to estimate thicknesses up to about 3 µm. The ratio of the Raman suppression at two wavelengths is taken both inside and outside the slick and used as input for an equation. Lennon et al. claimed to have calibrated their fluorosensor and Raman suppression readings to oil spill thicknesses in the laboratory [
50]. They claimed to have calibrated this up to µm, however this is impossible noting that the scientists above found that the limits were 1000 times lower than this. This lower limit (about nm) has also been noted by many operators of fluorosensors [
79,
80]. On a different tact with laser fluorosensors, Viser carried out laboratory tests using laser fluorescence with lasers at 337 nm (UV) and 633 nm(red), and one-third extending the thickness range to 490 nm (blue) [
81]. The level of fluorescence was correlated with the thickness for 32 oils and heavy fuels. This method was never extended further nor tested in the field.
4.6. Modeling and Calculations
Several researchers have employed oil slick spreading equations and the resulting area to calculate the average thickness of slicks [
82,
83,
84]. These are, at best, estimates since the spreading equations are not good predictors and since both thin and thick slicks are counted in the area calculations. The researchers typically propose backward thickness calculations using spreading equations and area estimates obtained from radar satellite data.
Goodman et al. set up a series of small test tanks to measure the spreading of oil in an attempt to determine if there was such a thing as an average thickness [
85]. The tanks were rapidly filled with an oil and monitored with a camera to measure the spreading rate. This test showed that for this oil type (a Mexican crude) spreading was differential and there was no average thickness. Boniewicz-Szmyt et al. carried out some laboratory experiments using optical methods to measure the spreading rates [
86]. They calculated spreading rates and equilibrium thicknesses of 0.02 to 1.25 cm. These thicknesses are obviously far too great for typical crude and fuel oils. Other attempts to calculate equilibrium thicknesses have not been successful in actual practice [
87,
88,
89]. It is suggested that the final thicknesses are a function of many factors, including oil properties, wind, sea conditions, temperature, etc.
Others have looked at the effect of waves, hoping that the containment in the bottom of waves might provide an answer [
90]. Kordyban studied oil in waves and found that waves do not part the oil, but simply thin them at the top [
91]. Thus, this parting cannot be used to measure oil amounts.
4.8. UnderWater Slick Thickness Measurements
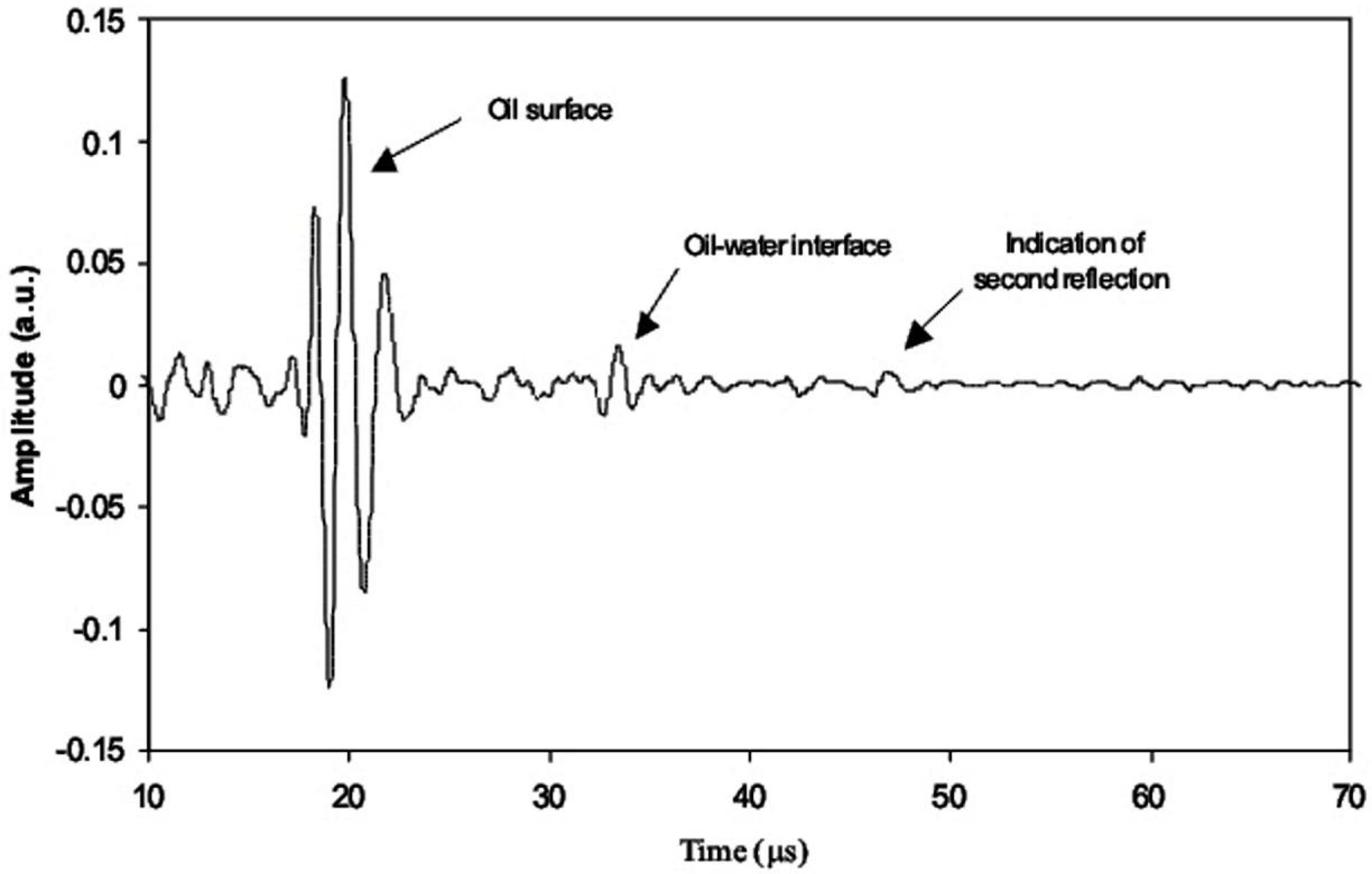
It is relatively well known that an ultrasound measuring device, such as one made for a variety of purposes, can also measure thick oil slicks on water [
94]. Workers in the oil spill field have also used this technique from below the water surface [
61]. This is possible because there are sonic reflections from the oil–water interface and from the air–oil interface. This technique can only be used in a calm situation such as in the laboratory, and the minimum measurable thicknesses are thought to be 2 mm. Fujikake first presented this technique in 1966 [
95]. An oil thickness gauging apparatus for oil of any type, density, and color was developed for direct measurements, together with a method for obtaining the oil thickness distribution from image data. The gauging apparatus, detecting the oil–water interface, consists of a composite of ultrasonic and servo-type wave gauges. The apparatus was capable of measuring a maximum thickness of 27 mm with an accuracy of 0.1 mm.
Massaro et al. studied the underwater measurement of slick thickness [
96]. They developed a model which used the Fresnel reflection of light from a slick. This was tested using two fibre optic in water under a slick. The reflection of white light was measured, and its reflection related to slick thickness using the model developed. The tests showed that the model and experiment worked in a small test cell.
Wilkinson et al. conducted experiments detecting oil under ice using cameras and ultrasound [
97]. Ultrasound was proposed to function, as the impedances of the water–oil and oil–ice layers would be such that reflections of ultrasound would result. These, in turn, could be detected and give detection and a means of measuring the oil thickness. The tests were conducted in a test tank, and oil was released under the ice and detected using a 1.1 MHz ecosounder with a 1.6° conical beam. The sounder was located 1.18 m from the ice bottom. The oil thickness detected was about a maximum of 3 cm. The researchers noted that there are possible interferences in this detection method, including the presence of air at the same location as the oil, oil penetration into the ice, and oil being encapsulated by the ice.
The measurement of oil slick thicknesses using ultrasonics works well and is limited to thicknesses of about 2 mm up to about 20 times this value. The method is, of course, a near-field method and depends on calm conditions.
4.9. Other Techniques
Several small-scale methods or methods that relate to close-in surface measurements have been proposed. Cheemalapati et al. conducted a small-scale laboratory study on thickness measurement by placing one of two types of Deepwater Horizon recovered oil between two microscope slides and measuring light transmission through the oil [
98]. Various thicknesses of oil were used between 5 to 30 µm. The transmission was measured using an optical power meter. This power was then correlated with thickness. The authors did not relate this thickness measuring method to possible at-sea methods.
Denkikian et al. and Koulakezian et al. proposed a remote transmitting sensor based on a combination of a LED spectral sensor combined with a sensor of electrical conductivity. This was not demonstrated on actual spills [
99,
100].
Kukhtarev et al. studied the use of laser optical interferometry on slick determination [
101]. This method works by the fact that different thickness layers cause different diffraction patterns. Reading these different diffraction patterns may result in a measurement of the thickness of oil. The technique was applied in the laboratory on a variety of oils including Macondo oil from the Gulf spill. This technique must certainly be limited to more transparent oils. This has not been pursued further than the paper noted.
Li et al. developed a small buoy to detect and measure oil thickness layers. The device used the absorption of radio waves to measure up to about 1 mm of oil [
102].
Lu et al. proposed a model of a beam of visible light travelling through an oil layer and being reflected off the top of the oil layer and from the top of the water surface [
103]. This would result in interference between the two beams of reflected light and would then yield interference patterns that could be detected. These could be deconvoluted to yield oil thickness. This model was proposed to be applicable to more transparent oils up to a limiting thickness. A small simulation was carried out using one type of oil. Since most oils have little to no transparency to visible light, this method may not yield results in practice.
Sun et al. studied oils in the laboratory and found that there was a polarization difference between oils and water [
104]. This peaked at a look angle of 20 to 30 degrees and at the wavelength of 785 to 880 nm. In the laboratory, they claimed to discriminate thicknesses of 20 to 220 µm. This method has never been tested in larger tanks nor at sea.
While interesting, these methods may not show potential at full scale for reasons that are fairly obvious, most are close-proximity methods only which do not show robustness under a variety of environmental variables.