Shortwave IR Adaption of the Mid-Infrared Radiance Method of Fire Radiative Power (FRP) Retrieval for Assessing Industrial Gas Flaring Output
Abstract
1. Introduction and Background
2. FRP Derivation from Earth Observing Satellite Observations
2.1. Adapting the MIR-Radiance Method of FRP Determination
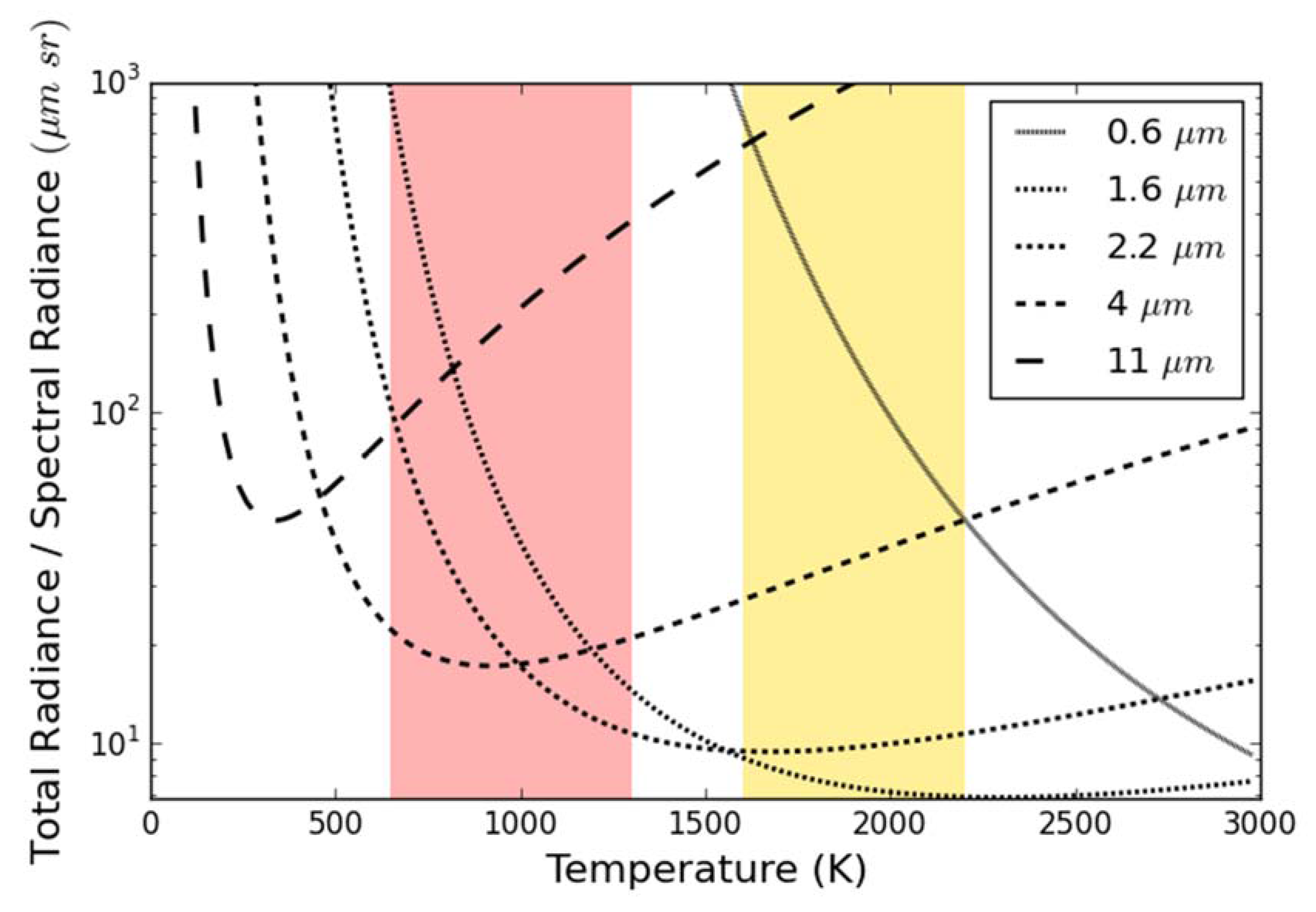
2.2. Selecting the Appropriate Spectral Measurement Band
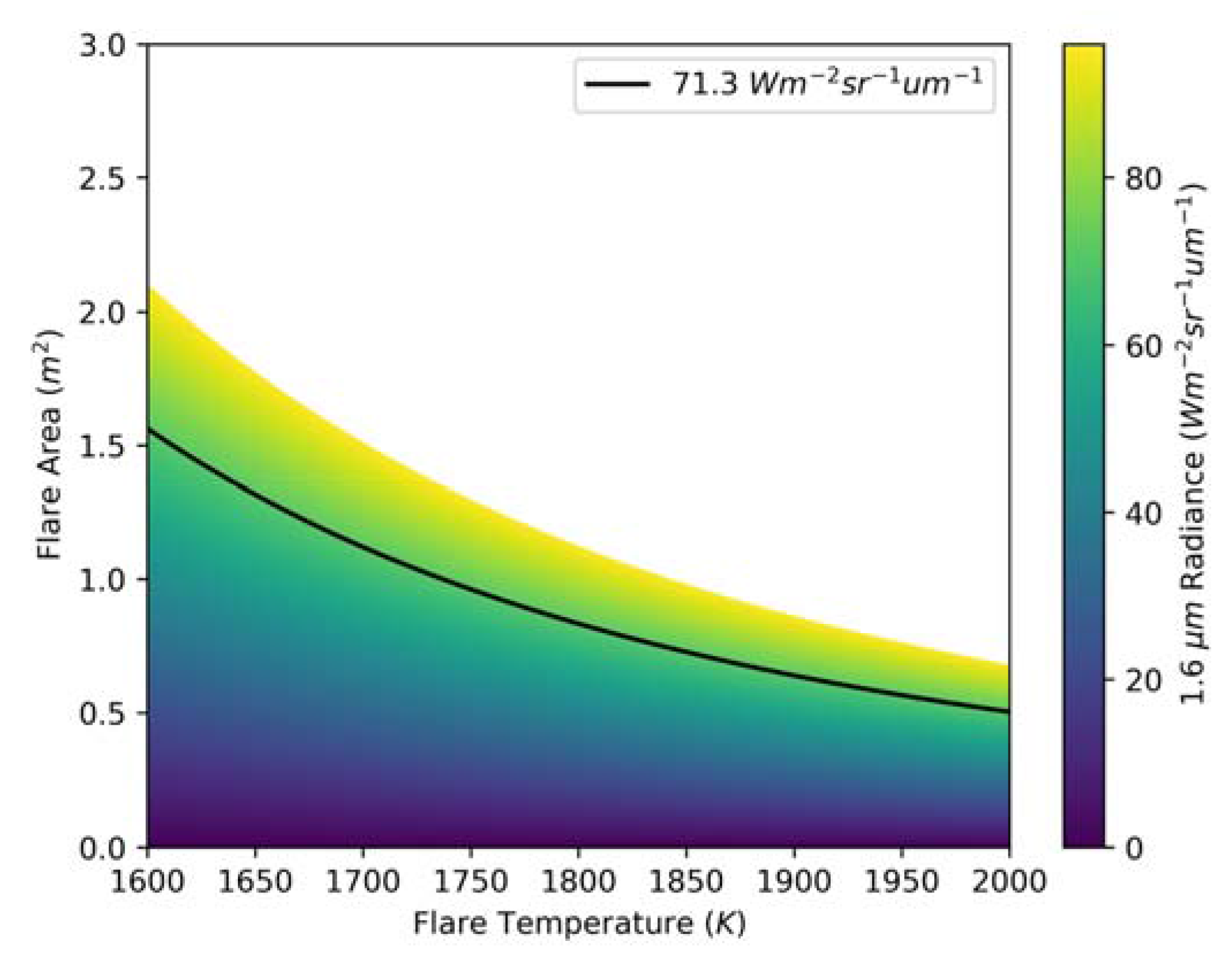
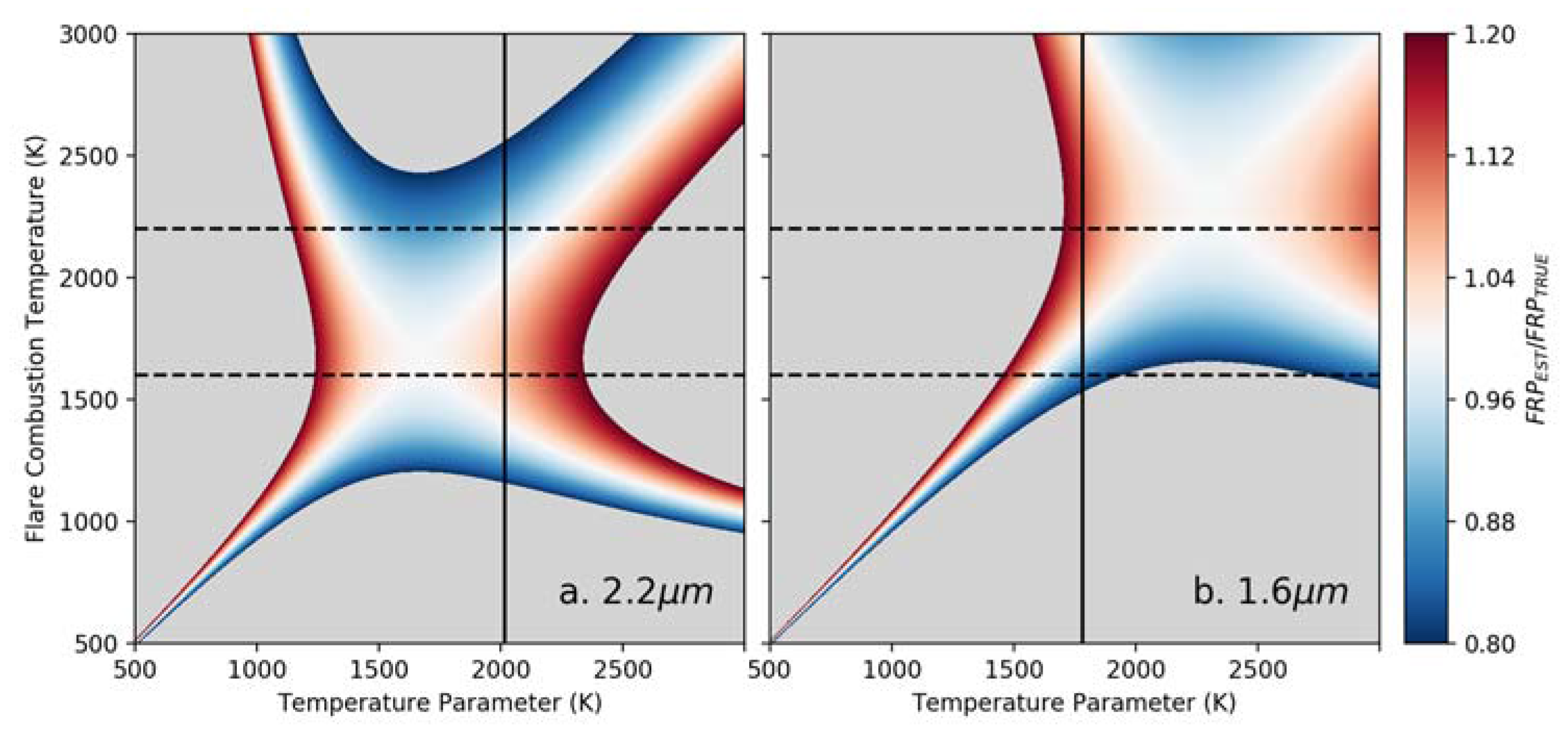
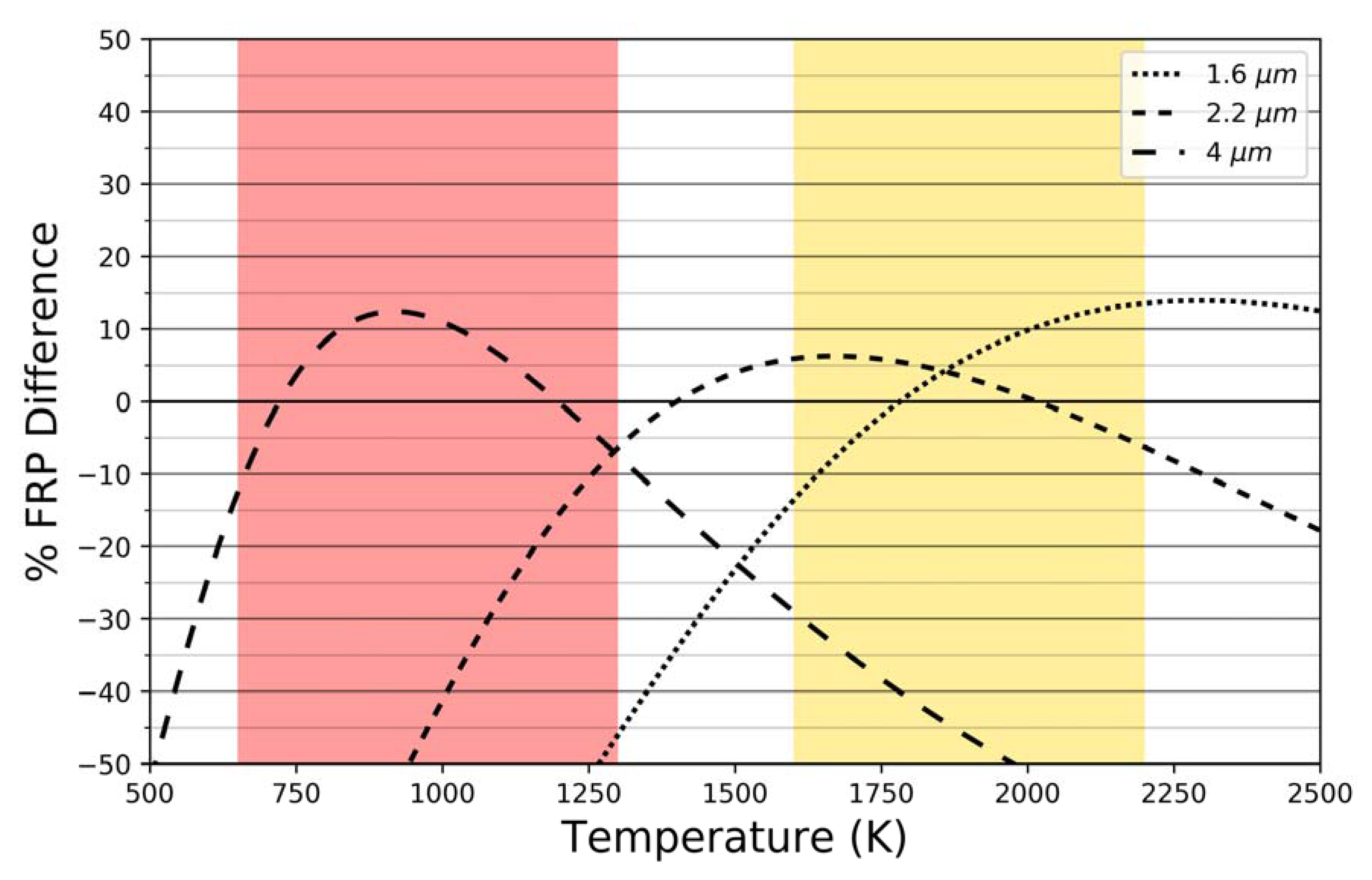
2.3. SWIR FRP Coefficients and Uncertainty Analysis
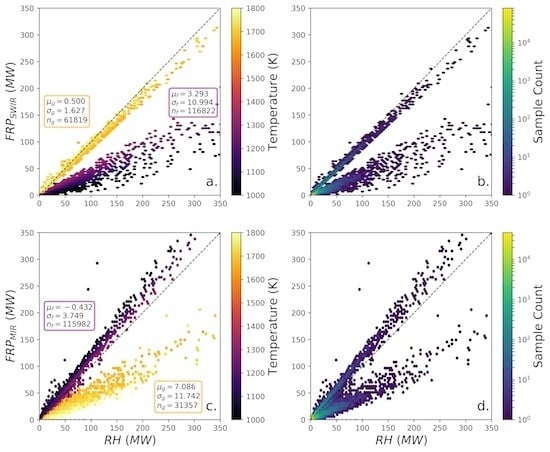
2.4. Demonstration Using Night-time VIIRS Observations
2.4.1. VIIRS Hotspot Detection
2.4.2. Comparing SWIR-Radiance FRP with NightFire RH
3. Multi-Sensor Evaluation of SWIR-Radiance Method Derived FRP
3.1. Sensors and Data
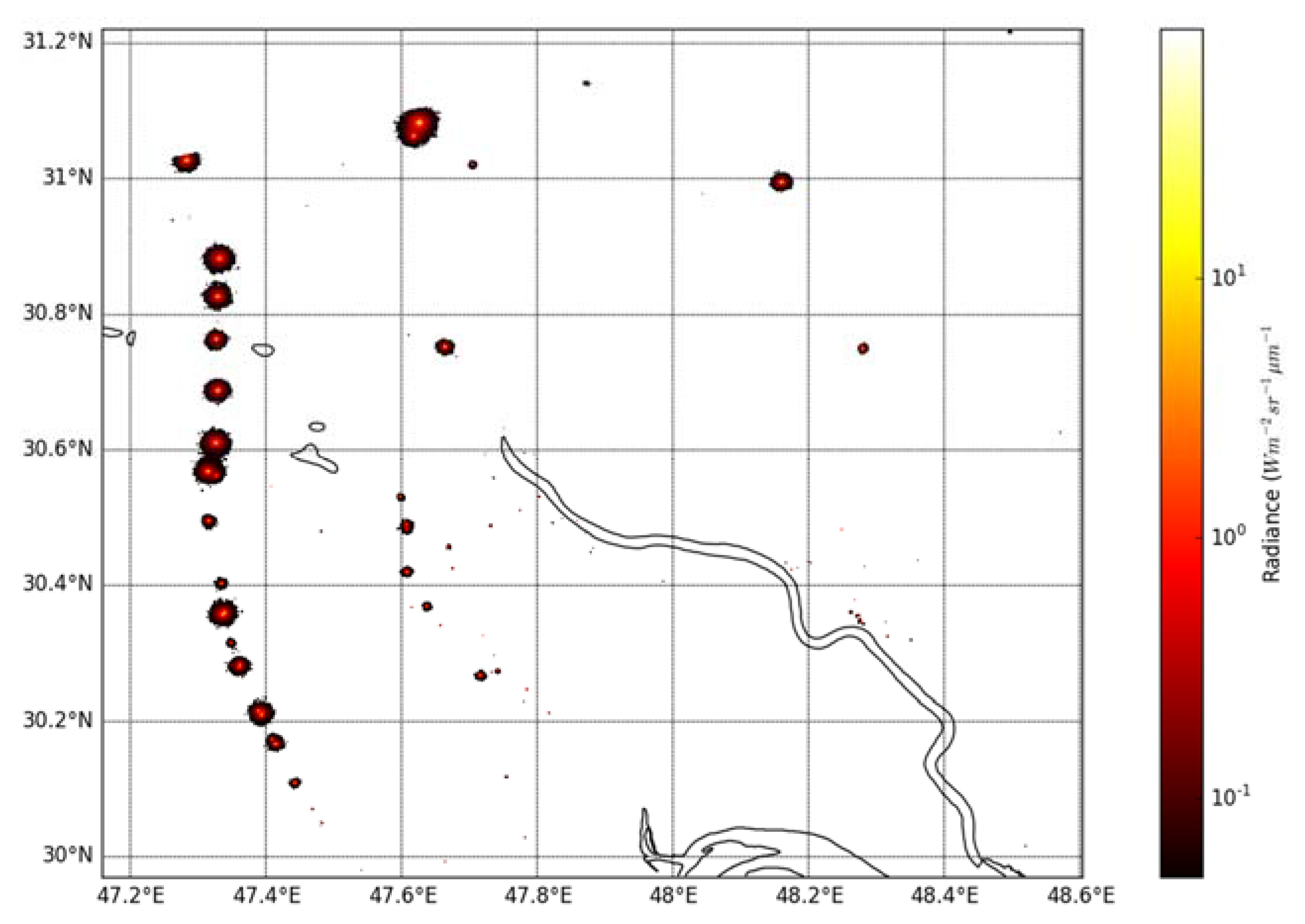
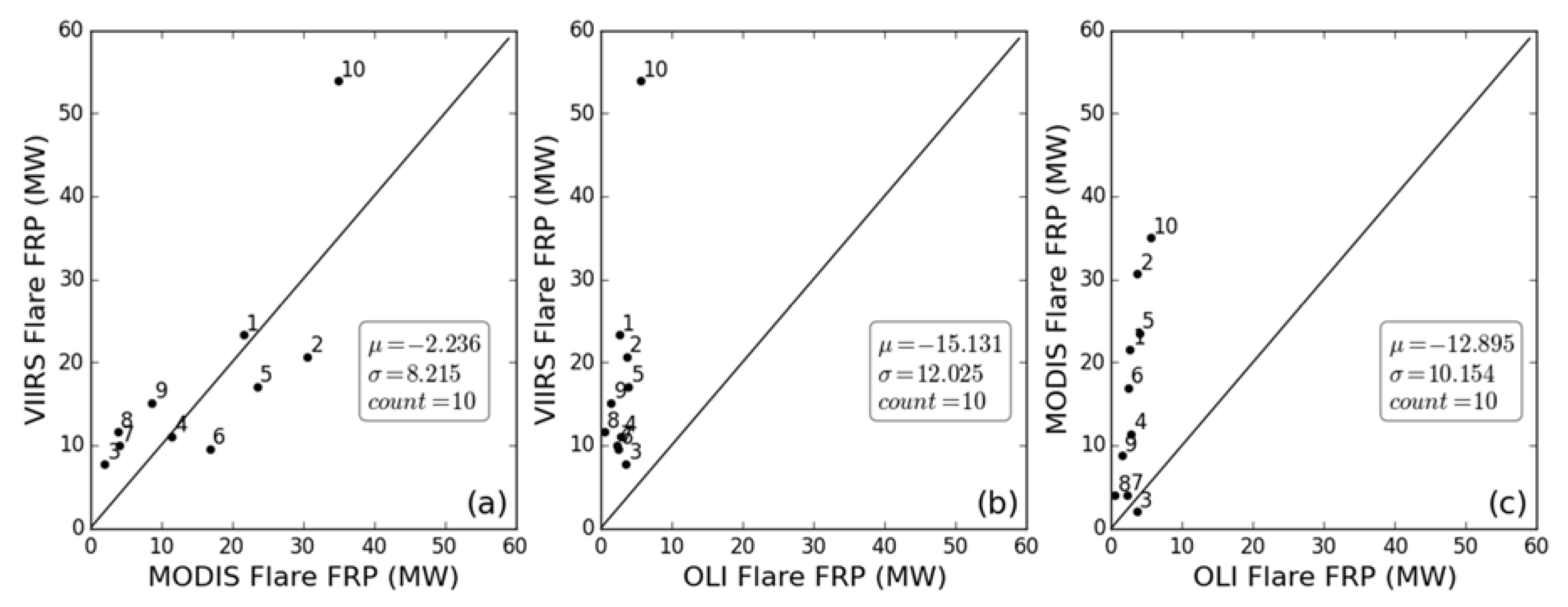
3.2. Gas Flare Detection, Characterisation and Comparison
4. Summary and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A1. Medium vs. Moderate Resolution FRP comparison
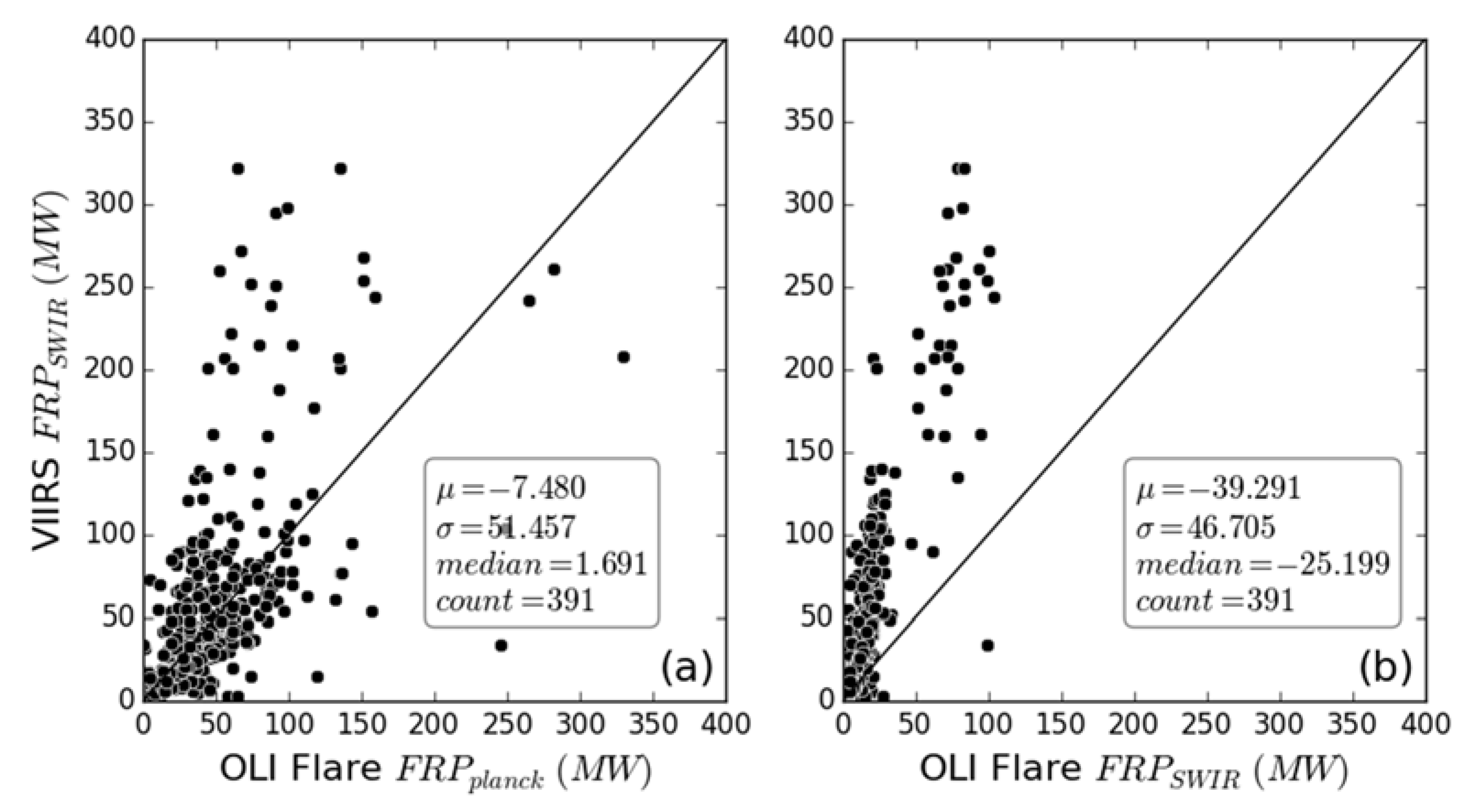
A1.1. Planck Fit Derived FRP from Landsat OLI
A1.2. Evaluation of OLI Planck Fit FRP against VIIRS M-Band SWIR-Radiance FRP
References
- Wooster, M.J.; Zhukov, B.; Oertel, D. Fire radiative energy for quantitative study of biomass burning: Derivation from the BIRD experimental satellite and comparison to MODIS fire products. Remote Sens. Environ. 2003, 86, 83–107. [Google Scholar] [CrossRef]
- Wooster, M.J.; Roberts, G.; Perry, G.L.W.; Kaufman, Y.J. Retrieval of biomass combustion rates and totals from fire radiative power observations: FRP derivation and calibration relationships between biomass consumption and fire radiative energy release. J. Geophys. Res. Atmos. 2005, 110. [Google Scholar] [CrossRef]
- Ichoku, C.; Kaufman, Y.J. A method to derive smoke emission rates from MODIS fire radiative energy measurements. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2636–2649. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Remer, L.; Ottmar, R.; Ward, D.; Li, R.R.; Kleidman, R.; Fraser, R.S.; Flynn, L.; McDougal, D.; Shelton, G. Relationship between remotely sensed fire intensity and rate of emission of smoke: SCAR-C experiment. In Global Biomass Burning; MIT Press: Cambridge, MA, USA, 1996; pp. 685–696. [Google Scholar]
- Kaufman, Y.J.; Kleidman, R.G.; King, M.D. SCAR-B fires in the tropics: Properties and remote sensing from EOS-MODIS. J. Geophys. Res. Atmos. 1998, 103, 31955–31968. [Google Scholar] [CrossRef]
- Kremens, R.L.; Dickinson, M.B.; Bova, A.S. Radiant flux density, energy density and fuel consumption in mixed-oak forest surface fires. Int. J. Wildland Fire 2012, 21, 722–730. [Google Scholar] [CrossRef]
- Roy, D.P.; Jin, Y.; Lewis, P.E.; Justice, C.O. Prototyping a global algorithm for systematic fire-affected area mapping using MODIS time series data. Remote Sens. Environ. 2005, 97, 137–162. [Google Scholar] [CrossRef]
- Roy, D.P.; Boschetti, L.; Justice, C.O.; Ju, J. The collection 5 MODIS burned area product—Global evaluation by comparison with the MODIS active fire product. Remote Sens. Environ. 2008, 112, 3690–3707. [Google Scholar] [CrossRef]
- Wooster, M.J.; Roberts, G.; Perry, G.L.; Kaufman, Y.J. Retrieval of biomass combustion rates and totals from fire radiative power observations: Application to Southern Africa using geostationary SEVIRI imagery. J. Geophys. Res. Atmos. 2005, 110. [Google Scholar] [CrossRef]
- Roberts, G.J.; Wooster, M.J. Fire detection and fire characterization over Africa using Meteosat SEVIRI. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1200–1218. [Google Scholar] [CrossRef]
- Freeborn, P.H.; Wooster, M.J.; Hao, W.M.; Ryan, C.A.; Nordgren, B.L.; Baker, S.P.; Ichoku, C. Relationships between energy release, fuel mass loss and trace gas and aerosol emissions during laboratory biomass fires. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Ellicott, E.; Vermote, E.; Giglio, L.; Roberts, G. Estimating biomass consumed from fire using MODIS FRE. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Kaiser, J.W.; Heil, A.; Andreae, M.O.; Benedetti, A.; Chubarova, N.; Jones, L.; Morcrette, J.-J.; Razinger, M.; Schultz, M.G.; Suttie, M. Biomass burning emissions estimated with a global fire assimilation system based on observed fire radiative power. Biogeosciences 2012, 9, 527–554. [Google Scholar] [CrossRef]
- Ichoku, C.; Ellison, L. Global top-down smoke-aerosol emissions estimation using satellite fire radiative power measurements. Atmos. Chem. Phys. 2014, 14, 6643–6667. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Herring, D.D.; Ranson, K.J.; Collatz, G.J. Earth Observing System AM1 mission to earth. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1045–1055. [Google Scholar] [CrossRef]
- Giglio, L.; Descloitres, J.; Justice, C.O.; Kaufman, Y.J. An enhanced contextual fire detection algorithm for MODIS. Remote Sens. Environ. 2003, 87, 273–282. [Google Scholar] [CrossRef]
- Giglio, L.; Csiszar, I.; Restás, Á.; Morisette, J.T.; Schroeder, W.; Morton, D.; Justice, C.O. Active fire detection and characterization with the advanced spaceborne thermal emission and reflection radiometer (ASTER). Remote Sens. Environ. 2008, 112, 3055–3063. [Google Scholar] [CrossRef]
- Xu, W.; Wooster, M.J.; Roberts, G.; Freeborn, P. New GOES imager algorithms for cloud and active fire detection and fire radiative power assessment across North, South and Central America. Remote Sens. Environ. 2010, 114, 1876–1895. [Google Scholar] [CrossRef]
- Wooster, M.J.; Xu, W.; Nightingale, T. Sentinel-3 SLSTR active fire detection and FRP product: Pre-launch algorithm development and performance evaluation using MODIS and ASTER datasets. Remote Sens. Environ. 2012, 120, 236–254. [Google Scholar] [CrossRef]
- Elvidge, C.D.; Zhizhin, M.; Hsu, F.-C.; Baugh, K.E. VIIRS nightfire: Satellite pyrometry at night. Remote Sens. 2013, 5, 4423–4449. [Google Scholar] [CrossRef]
- Peterson, D.; Wang, J.; Ichoku, C.; Hyer, E.; Ambrosia, V. A sub-pixel-based calculation of fire radiative power from MODIS observations: 1: Algorithm development and initial assessment. Remote Sens. Environ. 2013, 129, 262–279. [Google Scholar] [CrossRef]
- Schroeder, W.; Oliva, P.; Giglio, L.; Csiszar, I.A. The New VIIRS 375 m active fire detection data product: Algorithm description and initial assessment. Remote Sens. Environ. 2014, 143, 85–96. [Google Scholar] [CrossRef]
- Elvidge, C.D.; Zhizhin, M.; Baugh, K.; Hsu, F.-C.; Ghosh, T. Methods for global survey of natural gas flaring from visible infrared imaging radiometer suite data. Energies 2015, 9, 14. [Google Scholar] [CrossRef]
- Giglio, L.; Schroeder, W.; Justice, C.O. The collection 6 MODIS active fire detection algorithm and fire products. Remote Sens. Environ. 2016, 178, 31–41. [Google Scholar] [CrossRef]
- Wooster, M.J.; Roberts, G.; Freeborn, P.H.; Xu, W.; Govaerts, Y.; Beeby, R.; He, J.; Lattanzio, A.; Fisher, D.; Mullen, R. LSA SAF Meteosat FRP products–Part 1: Algorithms, product contents and analysis. Atmos. Chem. Phys. 2015, 15, 13217–13239. [Google Scholar] [CrossRef]
- Dennison, P.E.; Charoensiri, K.; Roberts, D.A.; Peterson, S.H.; Green, R.O. Wildfire temperature and land cover modeling using hyperspectral data. Remote Sens. Environ. 2006, 100, 212–222. [Google Scholar] [CrossRef]
- Lobert, J.M.; Warnatz, J. Emissions from the combustion process in vegetation. Fire Environ. 1993, 13, 15–37. [Google Scholar]
- Boulet, P.; Parent, G.; Acem, Z.; Kaiss, A.; Billaud, Y.; Porterie, B.; Pizzo, Y.; Picard, C. Experimental investigation of radiation emitted by optically thin to optically thick wildland flames. J. Combust. 2011, 2011. [Google Scholar] [CrossRef]
- Malvos, H.; Raj, P.K. Details of 35 m diameter LNG fire tests conducted in Montoir, France in 1987 and analysis of fire spectral and other data. In Proceedings of the AIChE Winter Conference, Orlando, FL, USA, 26 April 2006. [Google Scholar]
- Zhang, X.; Scheving, B.; Shoghli, B.; Zygarlicke, C.; Wocken, C. Quantifying gas flaring CH4 consumption using VIIRS. Remote Sens. 2015, 7, 9529–9541. [Google Scholar] [CrossRef]
- Haus, R.; Wilkinson, R.; Heland, J.; Schäfer, K. Remote sensing of gas emissions on natural gas flares. Pure Appl. Opt. 1998, 7, 853. [Google Scholar] [CrossRef]
- Ismail, O.S.; Umukoro, G.E. Global impact of gas flaring. Energy Power Eng. 2012, 4. [Google Scholar] [CrossRef]
- The World Bank Global Gas Flaring Reduction Partnership (GGFR)—Improving Energy Efficiency & Mitigating Impact on Climate Change; World Bank: Washington, DC, USA, 2011.
- Johnson, M.R.; Coderre, A.R. Compositions and greenhouse gas emission factors of flared and vented gas in the Western Canadian Sedimentary Basin. J. Air Waste Manag. Assoc. 2012, 62, 992–1002. [Google Scholar] [CrossRef] [PubMed]
- Field, R.A.; Soltis, J.; Murphy, S. Air quality concerns of unconventional oil and natural gas production. Environ. Sci. Process. Impacts 2014, 16, 954–969. [Google Scholar] [CrossRef] [PubMed]
- Smith, D.; Mutlow, C.; Delderfield, J.; Watkins, B.; Mason, G. ATSR infrared radiometric calibration and in-orbit performance. Remote Sens. Environ. 2012, 116, 4–16. [Google Scholar] [CrossRef]
- Shephard, M.W.; Kennelly, E.J. Effect of band-to-band coregistration on fire property retrievals. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2648–2661. [Google Scholar] [CrossRef]
- Giglio, L.; Kendall, J.D. Application of the Dozier retrieval to wildfire characterization: A sensitivity analysis. Remote Sens. Environ. 2001, 77, 34–49. [Google Scholar] [CrossRef]
- Giglio, L.; Schroeder, W. A global feasibility assessment of the bi-spectral fire temperature and area retrieval using MODIS data. Remote Sens. Environ. 2014, 152, 166–173. [Google Scholar] [CrossRef]
- Dozier, J. A method for satellite identification of surface temperature fields of subpixel resolution. Remote Sens. Environ. 1981, 11, 221–229. [Google Scholar] [CrossRef]
- Freeborn, P.H.; Wooster, M.J.; Roy, D.P.; Cochrane, M.A. Quantification of MODIS fire radiative power (FRP) measurement uncertainty for use in satellite-based active fire characterization and biomass burning estimation. Geophys. Res. Lett. 2014, 41, 1988–1994. [Google Scholar] [CrossRef]
- Gaydon, A.G.; Wolfhard, H.G. Flames, Their Structure, Radiation and Temperature; Halsted Press: New York, NY, USA, 1979. [Google Scholar]
- Zhukov, B.; Lorenz, E.; Oertel, D.; Wooster, M.; Roberts, G. Spaceborne detection and characterization of fires during the bi-spectral infrared detection (BIRD) experimental small satellite mission (2001–2004). Remote Sens. Environ. 2006, 100, 29–51. [Google Scholar] [CrossRef]
- Polivka, T.N.; Wang, J.; Ellison, L.T.; Hyer, E.J.; Ichoku, C.M. Improving Nocturnal Fire Detection With the VIIRS Day–Night Band. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5503–5519. [Google Scholar] [CrossRef]
- Reed, R.J. Combustion Handbook; North American Manufacturing Co.: Cleveland, OH, USA, 1986; Volume 1. [Google Scholar]
- Leifer, I.; Lehr, W.J.; Simecek-Beatty, D.; Bradley, E.; Clark, R.; Dennison, P.; Hu, Y.; Matheson, S.; Jones, C.E.; Holt, B. State of the art satellite and airborne marine oil spill remote sensing: Application to the BP Deepwater Horizon oil spill. Remote Sens. Environ. 2012, 124, 185–209. [Google Scholar] [CrossRef]
- Casadio, S.; Arino, O.; Serpe, D. Gas flaring monitoring from space using the ATSR instrument series. Remote Sens. Environ. 2012, 116, 239–249. [Google Scholar] [CrossRef]
- Griffin, M.K.; Burke, H.-h.K. Compensation of hyperspectral data for atmospheric effects. Linc. Lab. J. 2003, 14, 29–54. [Google Scholar]
- Wooster, M.J.; Rothery, D.A. Thermal monitoring of Lascar Volcano, Chile, using infrared data from the along-track scanning radiometer: A 1992–1995 time series. Bull. Volcanol. 1997, 58, 566–579. [Google Scholar] [CrossRef]
- Wooster, M.J.; Rothery, D.A.; Sear, C.B.; Carlton, R.W.T. Monitoring the development of active lava domes using data from the ERS-1 along track scanning radiometer. Adv. Space Res. 1998, 21, 501–505. [Google Scholar] [CrossRef]
- Anejionu, O.C.D.; Blackburn, G.A.; Whyatt, J.D. Satellite survey of gas flares: Development and application of a Landsat-based technique in the Niger Delta. Int. J. Remote Sens. 2014, 35, 1900–1925. [Google Scholar] [CrossRef]
- Schroeder, W.; Oliva, P.; Giglio, L.; Quayle, B.; Lorenz, E.; Morelli, F. Active fire detection using Landsat-8/OLI data. Remote Sens. Environ. 2016, 185, 210–220. [Google Scholar] [CrossRef]
- Justice, C.O.; Giglio, L.; Korontzi, S.; Owens, J.; Morisette, J.T.; Roy, D.; Descloitres, J.; Alleaume, S.; Petitcolin, F.; Kaufman, Y. The MODIS fire products. Remote Sens. Environ. 2002, 83, 244–262. [Google Scholar] [CrossRef]
- Zhang, T.; Wooster, M.J.; Xu, W. Approaches for synergistically exploiting VIIRS I-and M-Band data in regional active fire detection and FRP assessment: A demonstration with respect to agricultural residue burning in Eastern China. Remote Sens. Environ. 2017, 198, 407–424. [Google Scholar] [CrossRef]
- Freeborn, P.H.; Wooster, M.J.; Roberts, G. Addressing the spatiotemporal sampling design of MODIS to provide estimates of the fire radiative energy emitted from Africa. Remote Sens. Environ. 2011, 115, 475–489. [Google Scholar] [CrossRef]
- Gladkova, I.; Grossberg, M.; Bonev, G.; Shahriar, F. A multiband statistical restoration of the Aqua MODIS 1.6 micron band. Int. Soc. Opt. Photon. 2011, 8048, 804819. [Google Scholar]
- Johnson, M.R.; Devillers, R.W.; Thomson, K.A. A generalized Sky-LOSA method to quantify soot/black carbon emission rates in atmospheric plumes of gas flares. Aerosol Sci. Technol. 2013, 47, 1017–1029. [Google Scholar] [CrossRef]
- Morfitt, R.; Barsi, J.; Levy, R.; Markham, B.; Micijevic, E.; Ong, L.; Scaramuzza, P.; Vanderwerff, K. Landsat-8 Operational Land Imager (OLI) radiometric performance on-orbit. Remote Sens. 2015, 7, 2208–2237. [Google Scholar] [CrossRef]
- Kaldany, R. Global gas flaring reduction initiative. In Oil, Gas and Chemicals World Bank Group, Marrakesh; World Bank: Washington, DC, USA, 2001. [Google Scholar]
- Elvidge, C.D.; Zhizhin, M.; Hsu, F.-C.; Baugh, K.; Khomarudin, M.R.; Vetrita, Y.; Sofan, P.; Hilman, D. Long-wave infrared identification of smoldering peat fires in Indonesia with nighttime Landsat data. Environ. Res. Lett. 2015, 10, 065002. [Google Scholar] [CrossRef]
- Amici, S.; Wooster, M.J.; Piscini, A. Multi-resolution spectral analysis of wildfire potassium emission signatures using laboratory, airborne and spaceborne remote sensing. Remote Sens. Environ. 2011, 115, 1811–1823. [Google Scholar] [CrossRef]
- Blackett, M.; Wooster, M.J. Evaluation of SWIR-based methods for quantifying active volcano radiant emissions using NASA EOS-ASTER data. Geomat. Nat. Hazards Risk 2011, 2, 51–78. [Google Scholar] [CrossRef]




| Sensor | Band | FRP Coeff. |
|---|---|---|
| MODIS | B7 (2.13 µm) | 9.37 sr µm |
| VIIRS | M10 (1.61µm) | 7.32 sr µm |
| VIIRS | M13 (4.05 µm) | 23.14 sr µm |
| VIIRS | I3 (1.61 µm) | 7.32 sr µm |
| Landsat-OLI | B6 (1.61 µm) | 7.33 sr µm |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fisher, D.; Wooster, M.J. Shortwave IR Adaption of the Mid-Infrared Radiance Method of Fire Radiative Power (FRP) Retrieval for Assessing Industrial Gas Flaring Output. Remote Sens. 2018, 10, 305. https://doi.org/10.3390/rs10020305
Fisher D, Wooster MJ. Shortwave IR Adaption of the Mid-Infrared Radiance Method of Fire Radiative Power (FRP) Retrieval for Assessing Industrial Gas Flaring Output. Remote Sensing. 2018; 10(2):305. https://doi.org/10.3390/rs10020305
Chicago/Turabian StyleFisher, Daniel, and Martin J. Wooster. 2018. "Shortwave IR Adaption of the Mid-Infrared Radiance Method of Fire Radiative Power (FRP) Retrieval for Assessing Industrial Gas Flaring Output" Remote Sensing 10, no. 2: 305. https://doi.org/10.3390/rs10020305
APA StyleFisher, D., & Wooster, M. J. (2018). Shortwave IR Adaption of the Mid-Infrared Radiance Method of Fire Radiative Power (FRP) Retrieval for Assessing Industrial Gas Flaring Output. Remote Sensing, 10(2), 305. https://doi.org/10.3390/rs10020305