1. Introduction
The Earth Polychromatic Imaging Camera (EPIC) is a ten-channel earth monitoring spectroradiometer onboard the Deep Space Climate Observatory (DISCOVR) satellite located at Sun–Earth Lagrange-1 (L1) point (
http://epic.gsfc.nasa.gov). From this unique location it is able to observe the entire sunlit face of Earth continuously. EPIC has been in operation since June 2015, providing global spectral images of Earth every one to two hours. Together with the National Institute of Standards and Technology Advanced Radiometer (NISTAR) that measures the Earth’s total irradiance in four broadband channels, EPIC provides insights into Earth’s energy balance.
The EPIC camera captures the narrow band spectral images of Earth on a 2048 × 2048 CCD (Charge Coupled Device) array sensor by using a rotating spectral filter wheel inside the EPIC telescope. The ten-channel images include four channels (318, 325, 340 and 388 nm) in the ultra-violet (UV), four channels (443, 551, 680 and 688 nm) in the visible (VIS) and two channels (764 and 780 nm) in the near-infrared (NIR) region. The ten-channel images are used to derive ozone, SO
2, properties of aerosols, and clouds, as well as properties of vegetated surface such as leaf area index and its sunlit portion [
1,
2,
3,
4,
5,
6].
The resolution of EPIC images depends on the viewing zenith angle (VZA), and is the highest at the point where the viewing zenith angle is 0°. This point is called the sub satellite point, where a straight line from a satellite to the center of the Earth intersects the Earth’s surface. At this point, the optical resolution of EPIC images is about 10 km, and the instantaneous field of view of a pixel is about 8 km. To reduce the amount of data transmitted from DSCOVR, four pixels are averaged onboard the spacecraft for all bands except the 443 nm band [
4,
7]. This yields downloaded images of 1024 × 1024 pixels with a sub-satellite optical resolution of approximately 20 km. On the ground, these images are then resampled to match the 2048 × 2048 image size of the 443 nm band [
4]. Such images can be used to monitor the motion of clouds and weather systems, diurnal course of vegetation sunlit area, as well as events such as dust storms, biomass burnings, and volcanic eruptions.
Unlike instruments on low-orbit or geostationary satellites, EPIC measures the reflected sunlight simultaneously at all sunlit locations (including polar regions) from sunrise to sunset allowing monitoring seasonal changes in Earth reflectance. Here we take advantage of the unique capabilities of EPIC and study the daily and seasonal variations of global observations that cannot be obtained directly from other instruments.
In this paper, we report on EPIC observations of the global reflectance of the whole globe in individual channels, and on their daily and seasonal variability. We also discuss the mean and the variability of reflectances observed over ocean and land separately, and show their latitude dependence.
These observations from individual channels provide preliminary, yet helpful information to better understand variations of global reflectance and Earth radiation balance. In addition, since the EPIC measures the reflectance from Earth in the nearly backward direction (no shadows are observed), these observations can provide additional information for studying the radiative properties of vegetation surfaces [
5]. Furthermore, these observations and analysis provide useful information for studying Earth-like exoplanets [
8,
9,
10,
11,
12].
The outline of this paper is as follows: In
Section 2, we present the data used in our analysis. Then, in
Section 3, we discuss our observations of the diurnal and seasonal variations of global reflectance and show how these variations depend on factors such as land–ocean fraction over the sunlit face of Earth, atmospheric molecular scattering, latitude, and cloud distribution. Finally, in
Section 4, we summarize the main observations and the conclusions from this work.
2. Data and Methods
In this work, we use Level-1B EPIC spectral images spanning from June 2015 to August 2016. For each pixel, the EPIC products provide (1) geo-location (latitude, longitude), solar and viewing zenith and azimuthal angles, and (2) calibrated at sensor reflectance (radiance at the top of the atmosphere (TOA) multiplied by
π and normalized by the incident spectral solar irradiance). The reflectances are obtained by multiplying the original data values provided in the L1B files in engineering units of count per second by calibration factors for each wavelength (
https://eosweb.larc.nasa.gov/project/dscovr/DSCOVR_EPIC_Calibration_Factors_V02.pdf). These calibration factors were obtained by comparing EPIC observations with measurements taken by low Earth orbit satellite instruments [
4,
7], and analyzing EPIC moon observations [
7]. We use the latitude and longitude of pixels to identify the surface types according to the International Geosphere-Biosphere Programme (IGBP) surface ecosystem classifications. In addition, we use the solar zenith angle (SZA) values to select only pixels with SZA < 78°. Pixels with higher SZA values are excluded to avoid complications from the oblique illumination, large field-of-views, and slight variations in the DSCOVR satellite’s position relative to the exact L1 point (orbital data shows that the Solar-Earth-Vehicle angle varies from ~ 4° to ~12° with a mean ~8.4°). It is estimated that the excluded number of pixels is only about 4% of the total number of pixels in sunlit face of Earth, therefore excluding these pixels would not affect the global statistics. The EPIC L1B products and accompanying documentation are available from the NASA Langley Atmospheric Science Data Center (
https://eosweb.larc.nasa.gov/project/dscovr/dscovr_table).
In this study, we have considered two different global statistics of EPIC measurements.
The first one, <
R>
1, is a simple average of all observed reflectances, defined as
where
N is the total number of used Earth-viewing pixels,
Ij is the radiance observed for pixel
j,
F0 is the solar spectral irradiance for a plane perpendicular to the incoming solar rays,
Rj is the at sensor reflectance reported in the EPIC Level 1B data files for pixel
j.
We note that <
R>
1 is normalized by the solar irradiance, and so its spectral and temporal variations indicate variations in the properties of our planet, and are not affected by temporal changes in Sun–Earth distance or by spectral variations in solar irradiance. This is similar to the case of our current observations of exoplanets and to Cassini observations of Earth (
https://www.nasa.gov/mission_pages/cassini/multimedia/pia17171.html). Therefore, <
R>
1 can be considered a meaningful average from an astronomer’s perspective.
Global models of climate use surface reflectance to simulate the exchange of fluxes of energy, and mass (e.g., water and CO
2) between the surface and the planetary boundary layer and how changes in Earth surface properties impact this process. In addition to <
R>
1, we also consider statistics of TOA reflectance, <
R>
2, defined as
where
μj is the cosine of the viewing zenith angle at pixel
j.
A rigorous definition of the mean reflectance over the sunlit Earth can be found in [
13], and can be expressed as:
where Ω and Ω
0 are the view and solar direction vectors, Ω
n is outward normal to an element on Earth’s spherical surface,
μ; is the cosine of the viewing zenith angle (
μ = Ω · Ω
n), and
χ is the indicator function of sunlit points that takes the value 1 if the sensor sees a sunlit element and 0 otherwise. It characterizes mean TOA reflectance per unit of sunlit Earth area. In the backscattering direction, Equation (3) is the geometric albedo [
13].
The difference between Equations (1) and (2) is that in Equation (2), pixels are weighted by cosine of the viewing zenith angle. This weighting gives greater weight to the pixels at the center of EPIC images (around “noon” pixels) than to those near the edges (sunrise and sunset pixels).
In this paper, we will present statistics of EPIC’s L1-B reflectance data using both Equations (1) and (2) as an approximation to Equation (3). Throughout the whole paper we define the Earth “reflectance” as the ratio between radiant energy reflected by Earth into direction to the sensor and incident solar irradiance as defined by Equations (1) and (2). We note, however, that calculations using both equations gave only slightly different numerical values and displayed very similar behaviors. Therefore, for convenience, we present only the figures from Equation (2), and provide the statistical values from both methods if their differences are significant.
For each EPIC image, we calculate the global reflectance, the reflectance over land or ocean regions or the reflectance of different latitude regions. To study the daily average reflectance and its variability, we use the arithmetic mean of global reflectances of all images within a day. To reduce sampling biases and uncertainties, we process only those days that have at least five sets of full-spectrum images. The seasonal average reflectance is computed based on the arithmetic mean of daily average global reflectances within a season.
4. Conclusions
As an initial study of the radiative properties of Earth’s surface and atmosphere observed from the unique position of the DSCOVR satellite, this work studies spectral reflectance of sunlit side of earth using observations taken by the EPIC instrument.
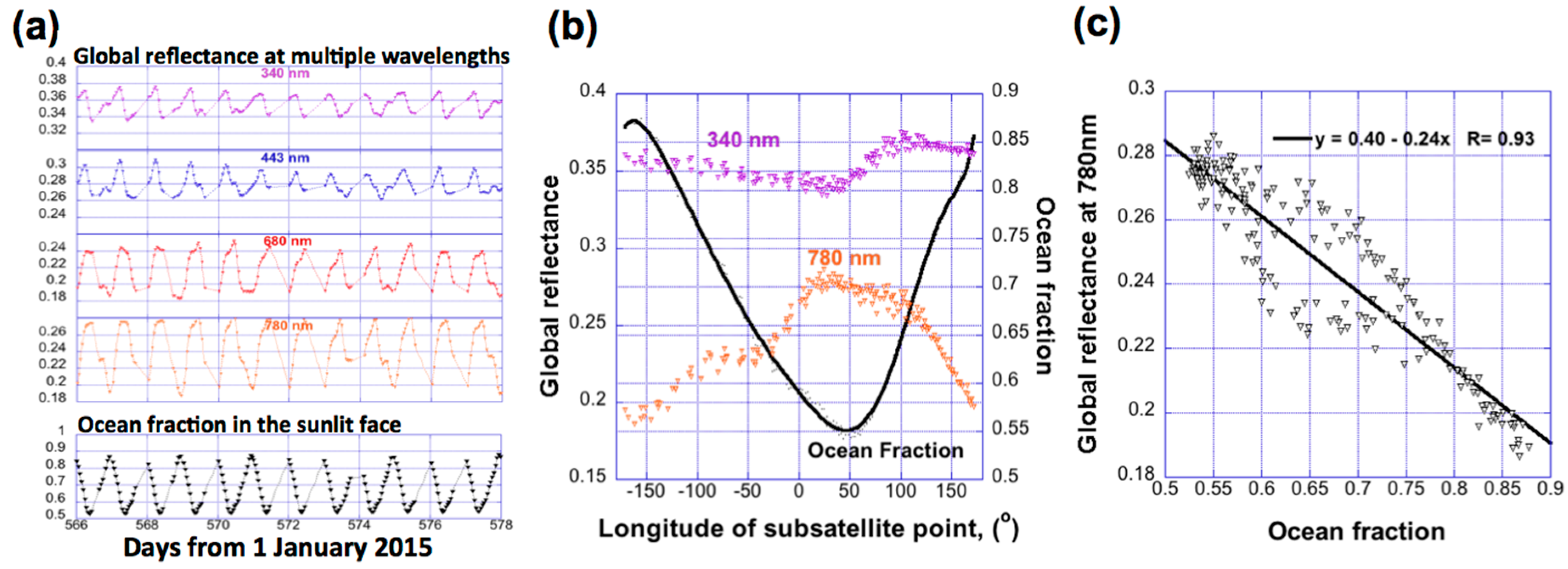
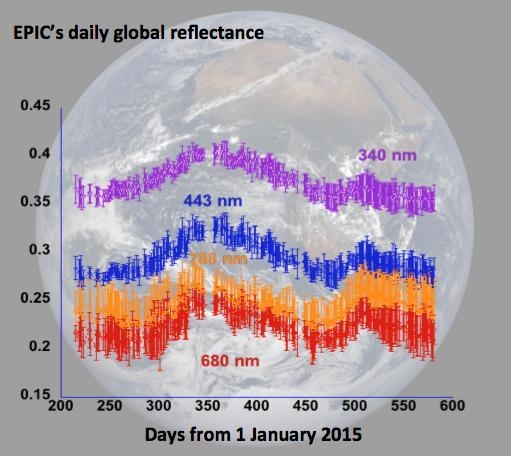
We first characterize the diurnal variability of global reflectance in a 12-day-long dataset. Compared to longer wavelengths, the shorter wavelengths show higher daily mean and lower variability mostly due to stronger molecular and aerosol scattering. At four wavelengths (340, 443, 680 and 780 nm), the daily mean are 0.35, 0.28, 0.22 and 0.25, while the daily maximum to minimum variability are 12%, 17%, 32% and 41% of the mean values, respectively. Furthermore, the global reflectances at all channels show a cycle of 24 h [
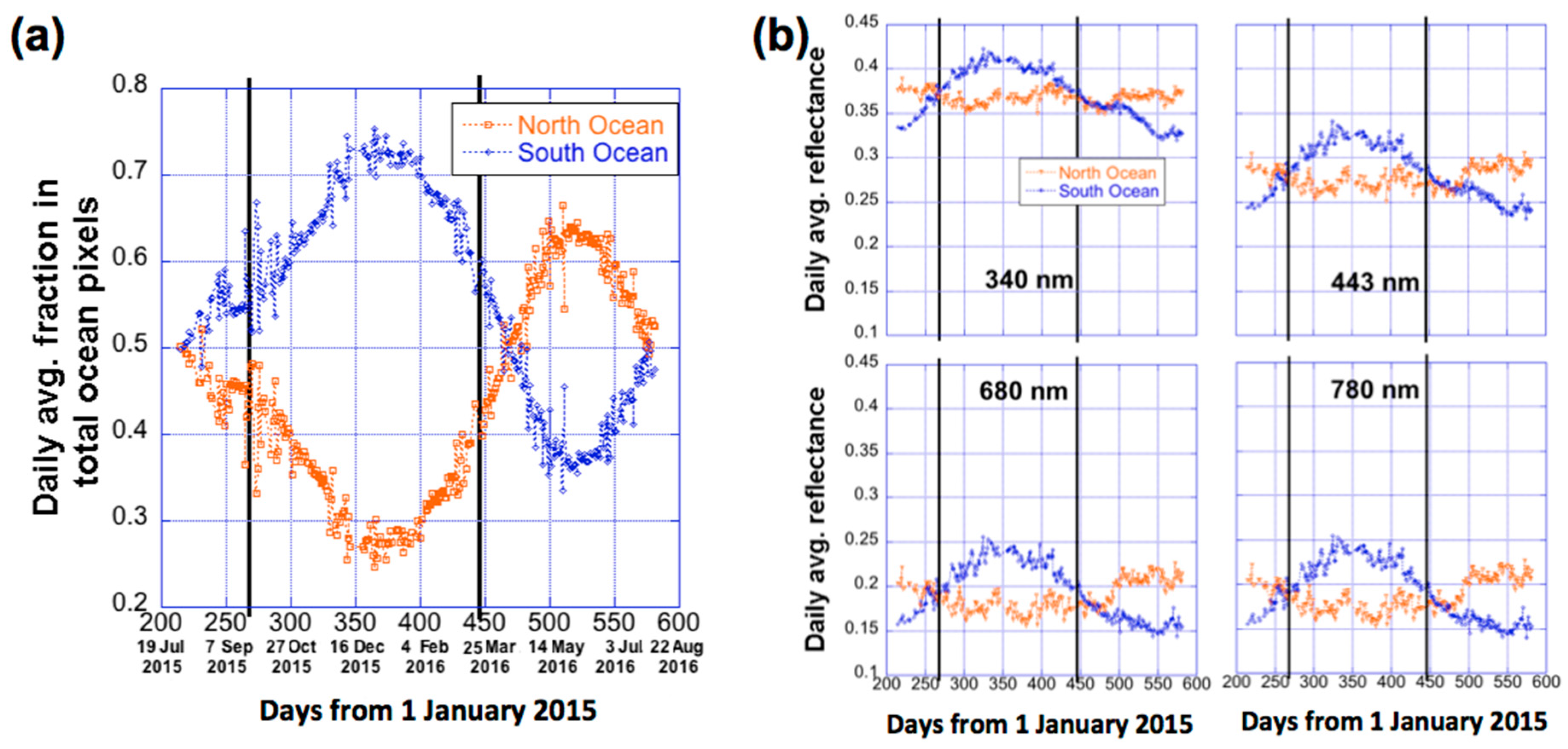
10], which, at least at the longer wavelengths, resembles a structure of ocean fraction over the sunlit face of Earth (
Figure 1a).
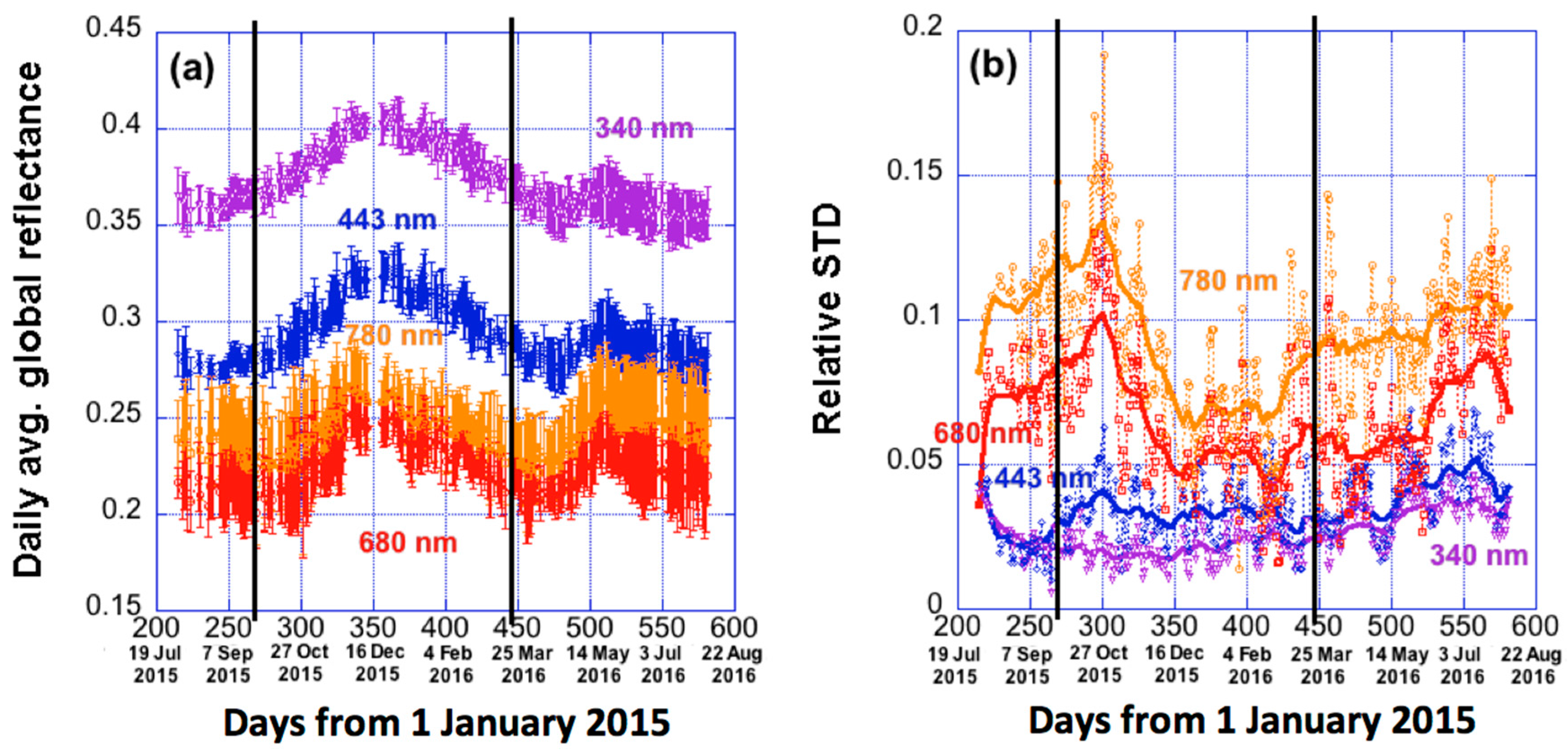
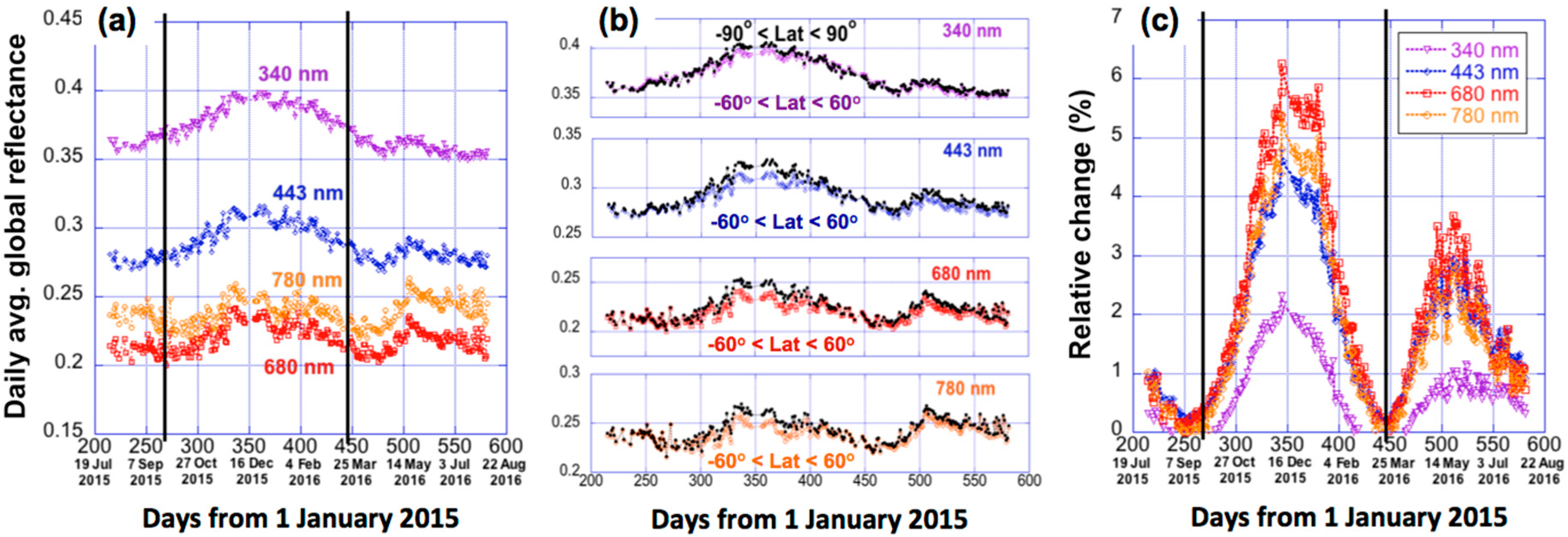
The daily averages of global reflectances display seasonal variations, with a larger peak during boreal winter, and a smaller peak during boreal summer at all wavelengths. For the whole year, the relative standard deviations of daily average reflectance values are 5%, 6%, 11%, and 18% at the four wavelengths (340, 443, 680 and 780 nm), respectfully.
We then analyzed what factors contribute the most to these seasonal variations. First, it was found that the seasonal variations do not change substantially even when the bright polar regions are not included. When the polar regions are included, the global reflectivity increases by 2–6% in winter (due to Antarctica) and 1–4% in summer (due to Arctic) relative to the values around equinoxes (the increases are weakest in UV channels).
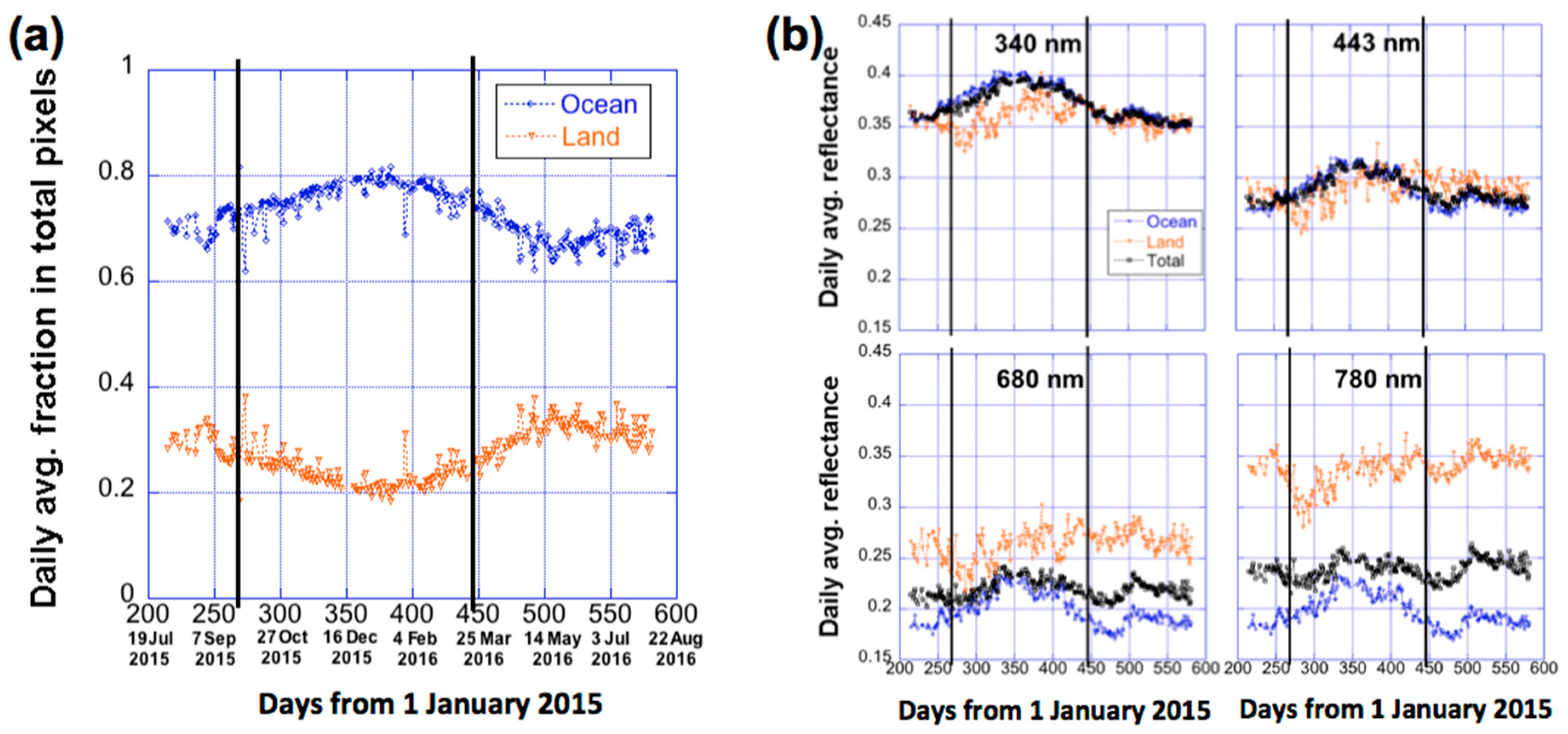
We then separated the sunlit side of Earth into land and ocean areas. It was found (
Figure 4) that the seasonal variations are mostly determined by ocean areas, simply because the daily average fraction of oceans over the sunlit side of the Earth is always much larger (65–80% depending on season; with maximum during boreal winter) than the fraction of land. It is also found that the variations over oceans are dominated in August–April by southern hemisphere and in April–August from northern hemispheres; they follow very different patterns (
Figure 5b).
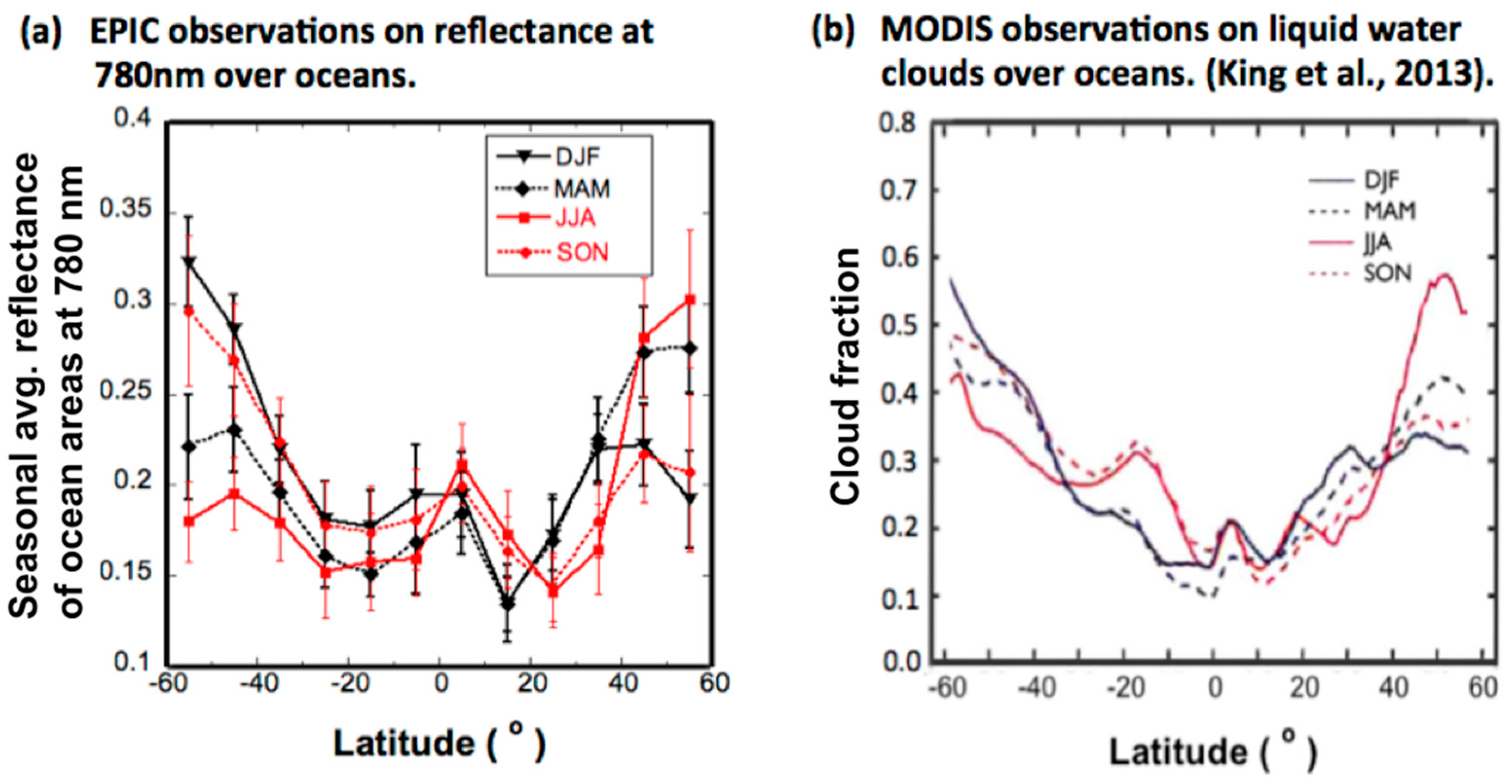
To understand the cloud effects on the northern and southern ocean reflectance, we analyzed the latitude dependence of 780 nm reflectances over oceans. Results showed that in boreal winter, reflectances of Southern oceans are larger at the high latitudes than at other latitudes, while in summer reflectances of Northern oceans are larger at the high latitudes than at other latitudes. This latitude dependence is consistent with MODIS data on cloud coverage, indicating that cloud coverage is a key factor governing the seasonal variations observed by EPIC.
Overall, EPIC observations show that while contributions from clouds are significant and important, the diurnal variations of reflectance are strongly affected by changes in the land–ocean ratio. The seasonal variations of reflectance, however, are mostly determined by the distribution of clouds. These results illustrate that studying the variations of spectral reflectances using EPIC data can provide valuable insights into the radiative properties of the Earth’s sunlit side and into their relationships to the surface and atmospheric properties.