New Adaptable All-in-One Strategy for Estimating Advanced Tropospheric Parameters and Using Real-Time Orbits and Clocks
Abstract
:1. Introduction
2. Assessment of Available RT Orbit and Clock Products and RT ZTDs
2.1. Assessment of Real-Time Orbit and Clock Corrections
2.2. Impact of IGS RTS Products on ZTD Estimates
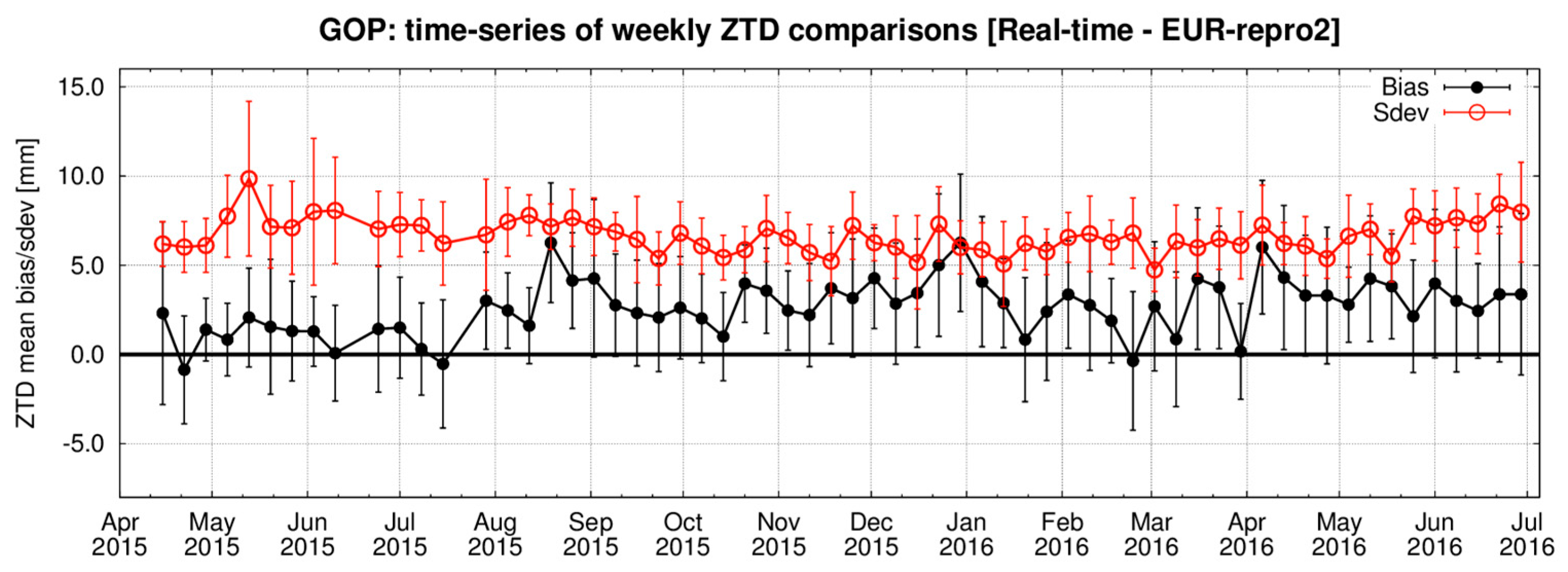
2.3. Long-Term Quality of Operational RT ZTD Production
3. New Adaptable Strategy for RT and NRT Troposphere Monitoring
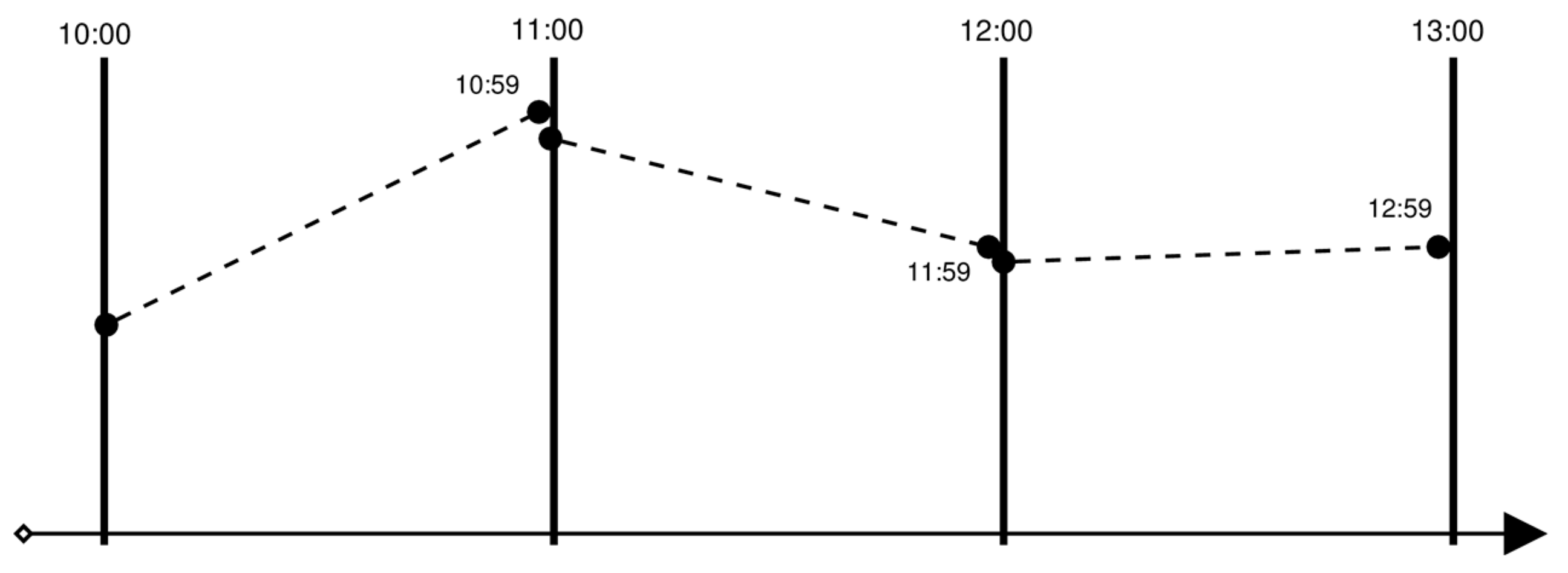
3.1. Epoch-Wise Filtering vs. Batch Processing, PPP vs. Network Approach
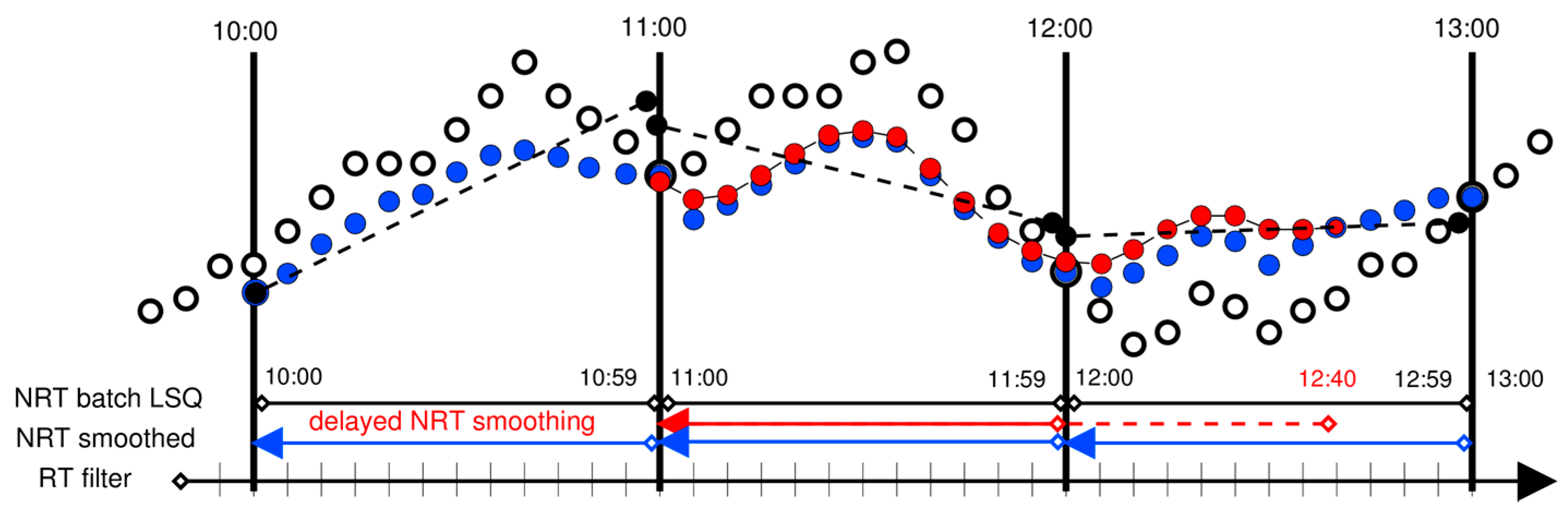
3.2. Combining RT and NRT Processing Supported by Observations from Files or Streams
3.3. Estimating High-Resolution ZTDs and Horizontal Gradients
3.4. Retrieving Slant Tropospheric Delays from Both RT and NRT Processing
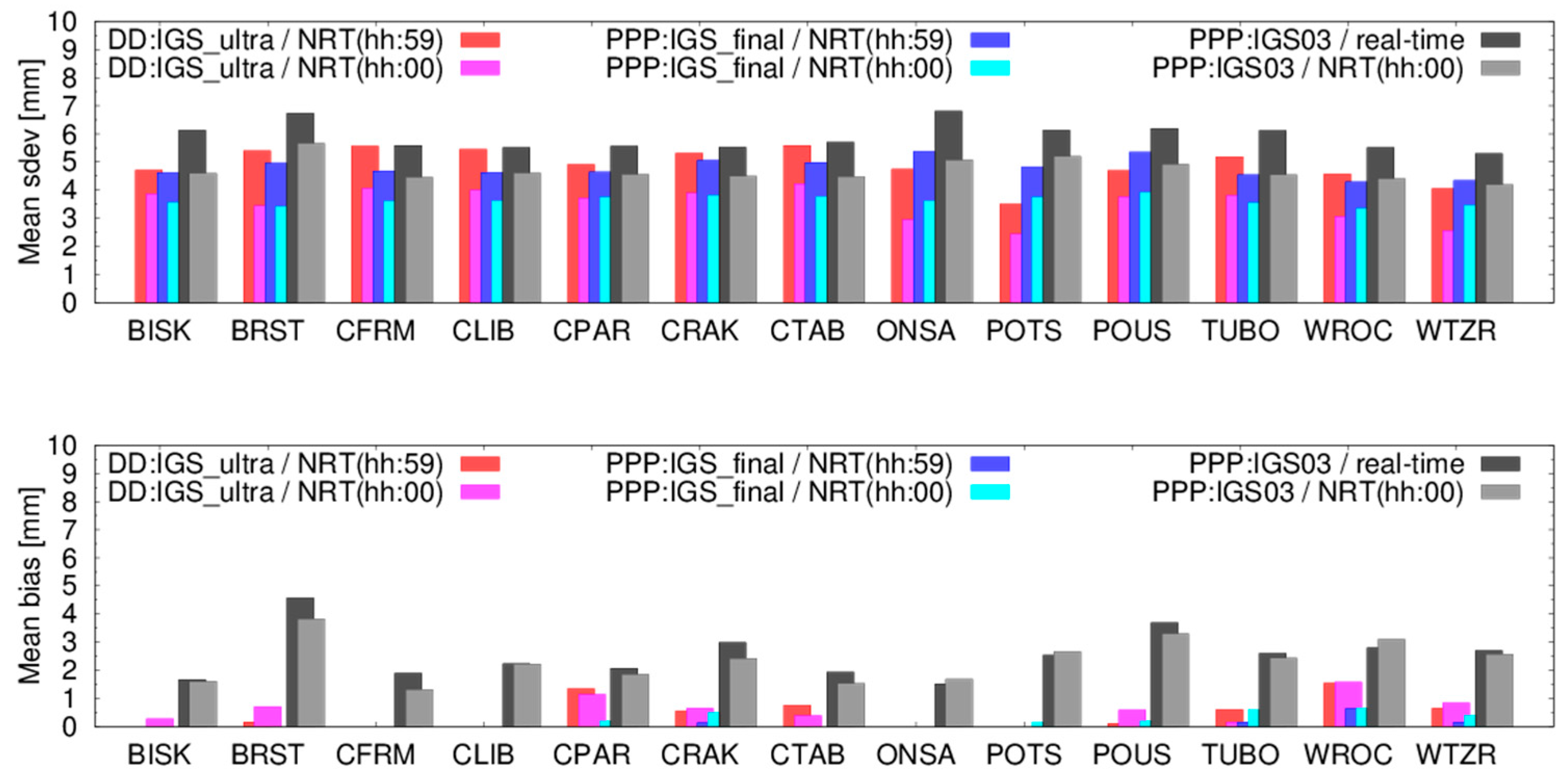
4. Assessment of New Method Compared to the Existing E-GVAP Processing
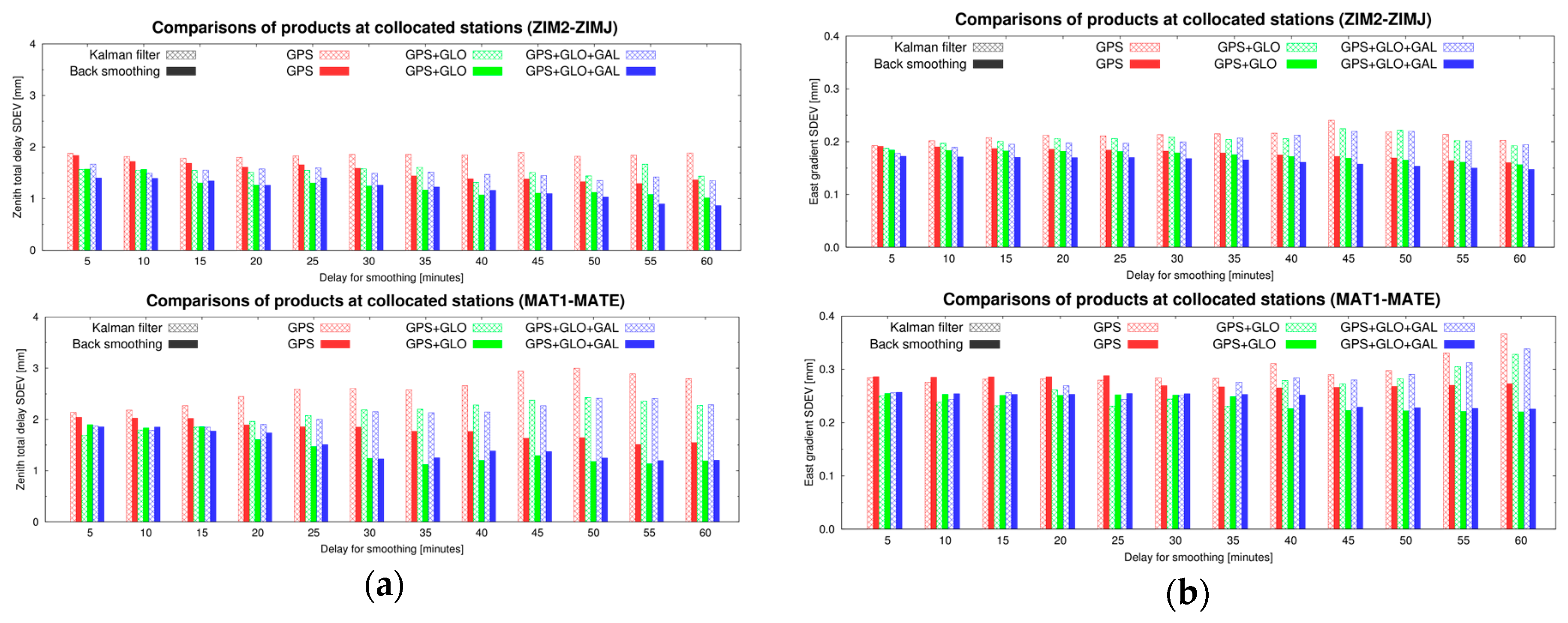
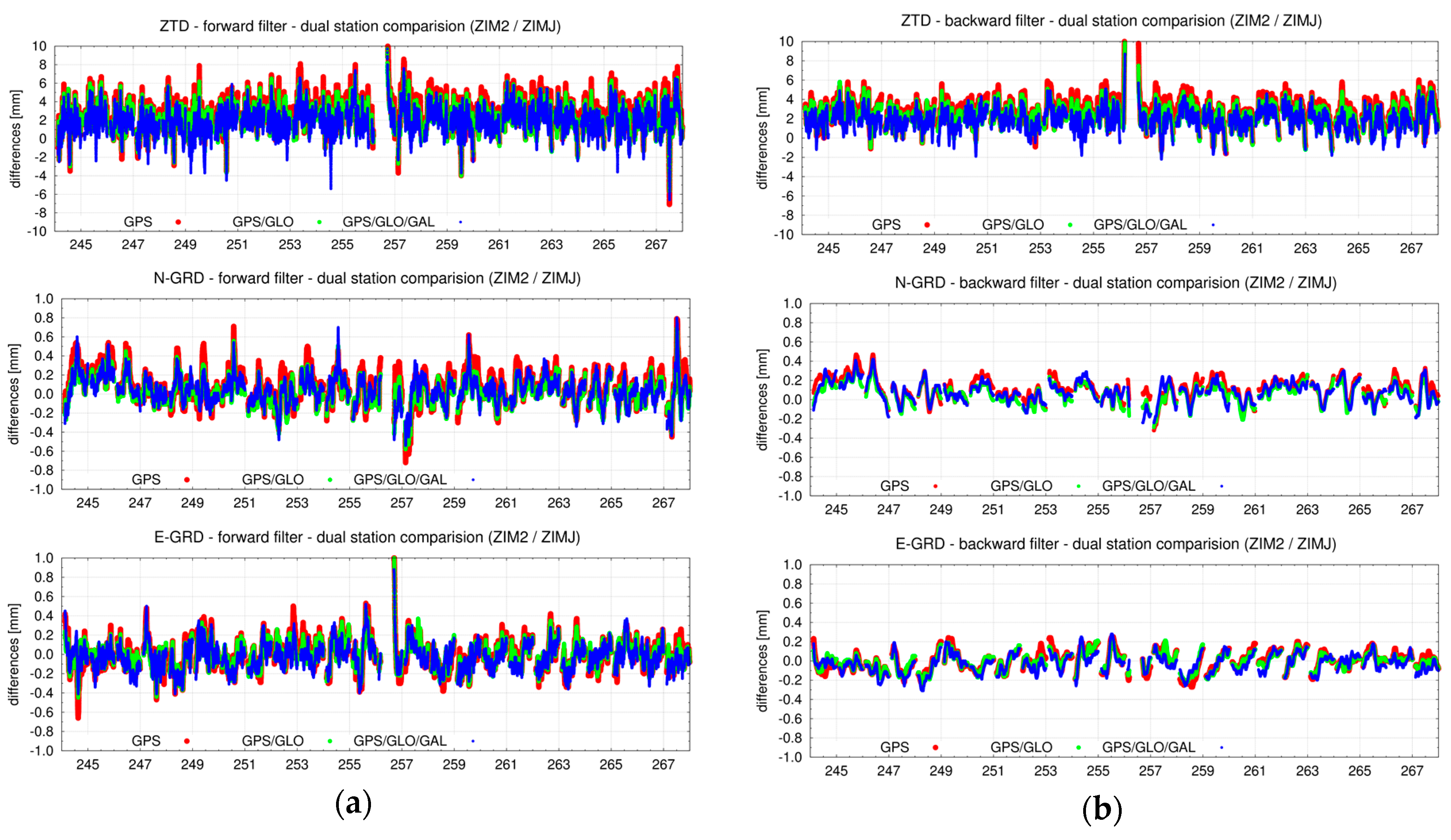
5. Impact Assessments on Estimated Parameters at Collocated Stations
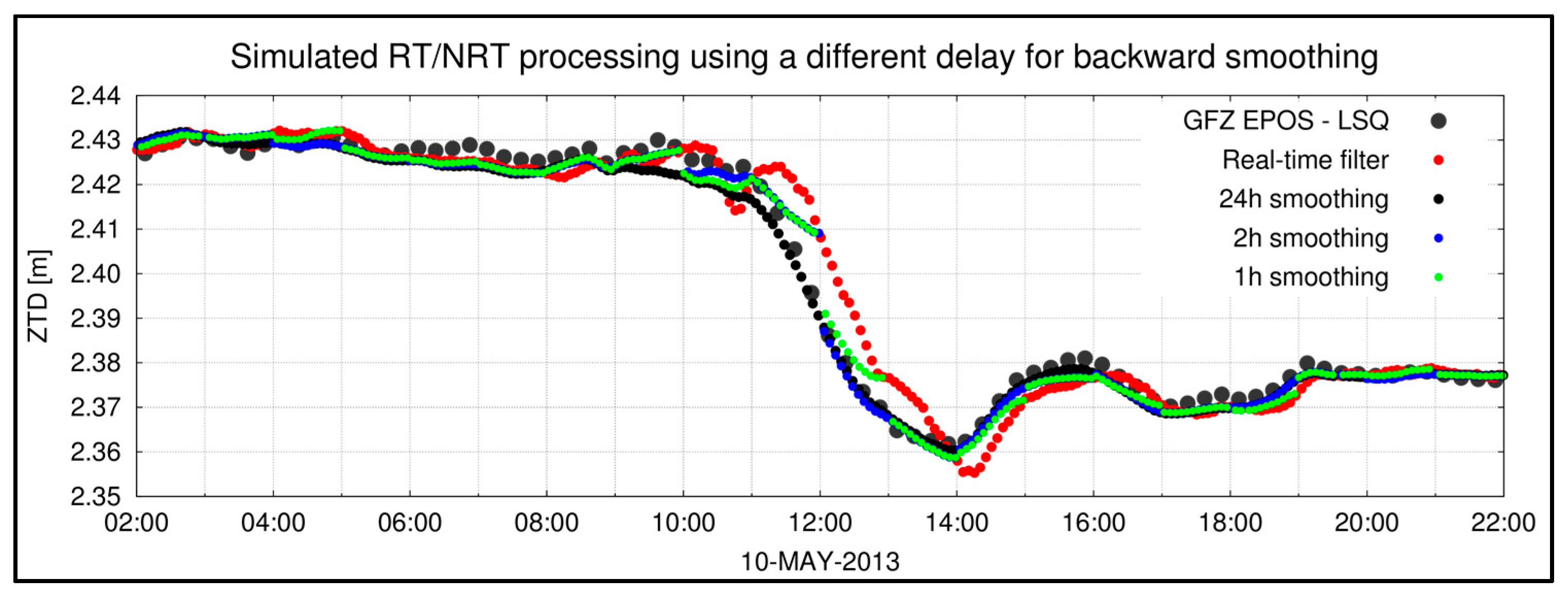
5.1. Impact of Backward Smoothing on Adaptable RT/NRT Solutions
5.2. Tropospheric Parameters from Multi-GNSS Analyses
5.3. Impact of Precise Products on ZTD and Gradient Estimates
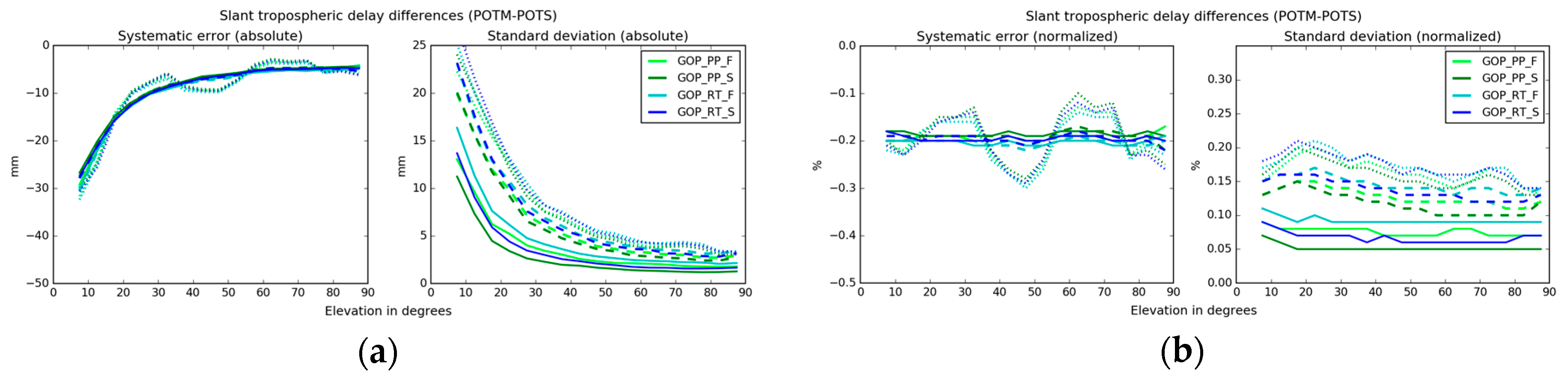
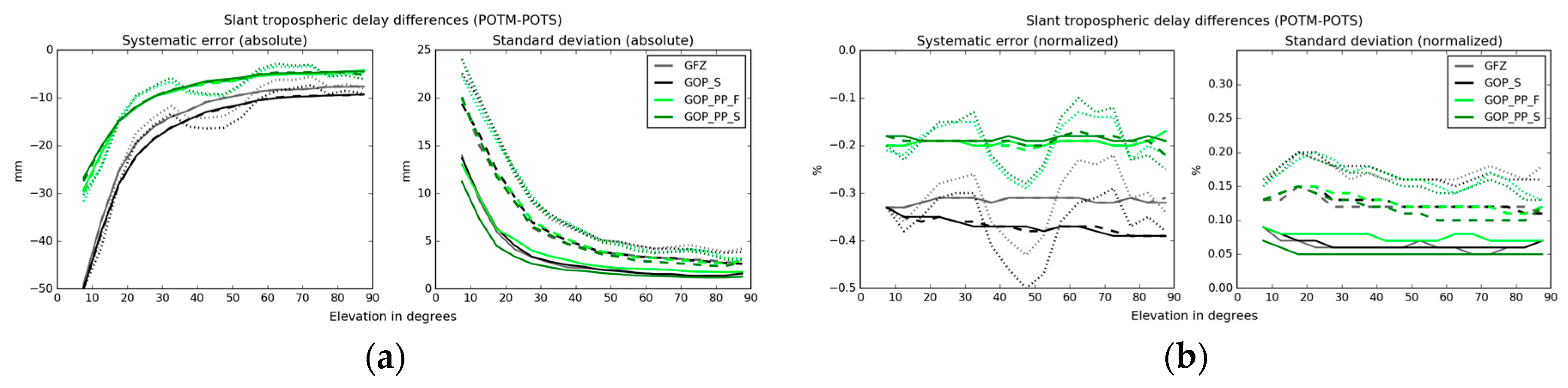
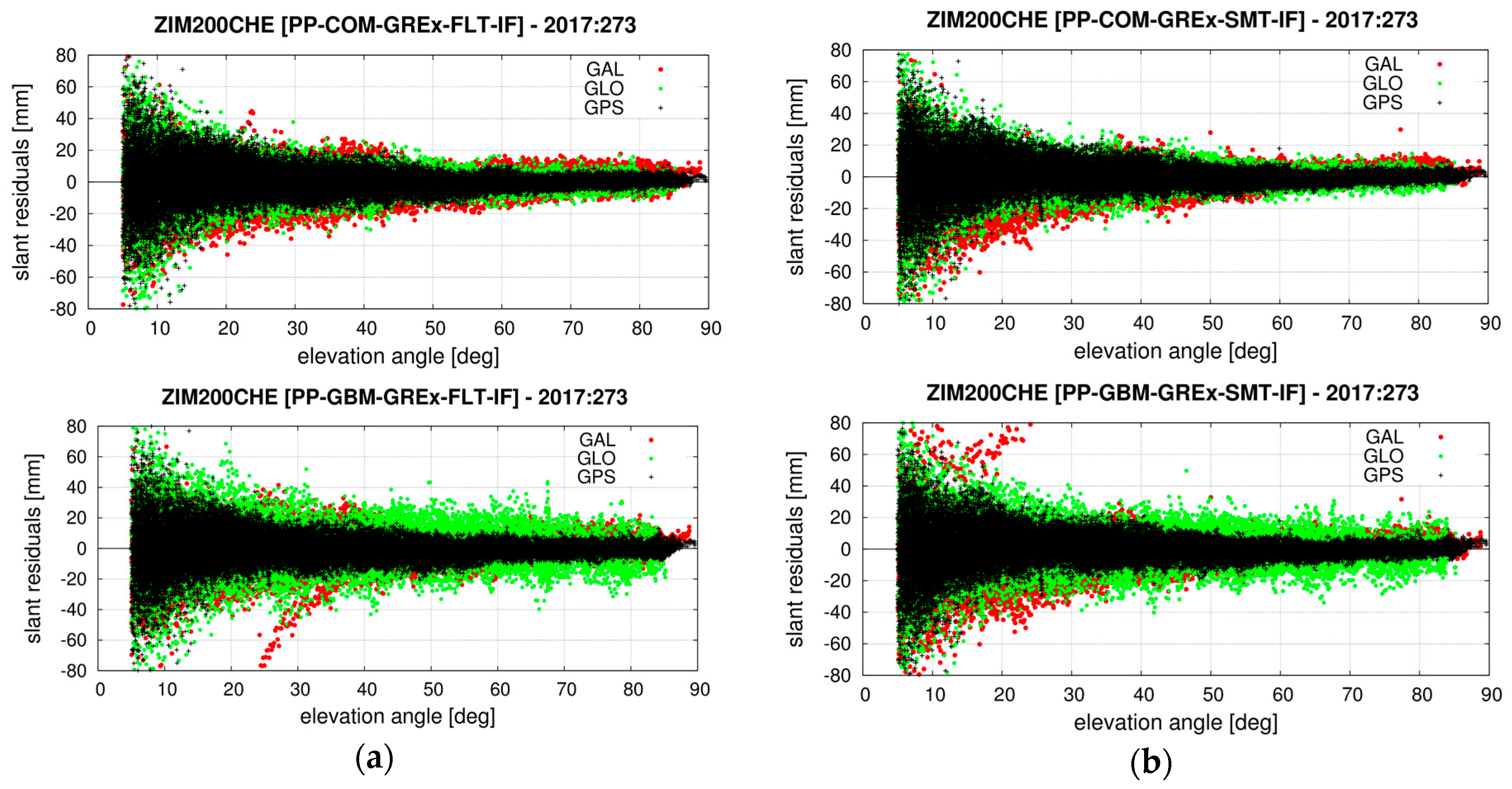
5.4. Carrier-Phase Post-Fit Residuals and Slant Delays
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bevis, M.; Businger, S.; Herring, T.A.; Rocken, C.; Anthes, R.A.; Ware, R.H. GPS Meteorology: Remote Sensing of Atmospheric Water Vapour Using the Global Positioning System. J. Geophys. Res. 1992, 97, 15787–15801. [Google Scholar] [CrossRef]
- Davis, J.; Herring, T.; Shapiro, I.; Rogers, A.; Elgered, G. Geodesy by radio interferometry: Effects of atmospheric modelling errors on estimates of baseline length. Radio Sci. 1985, 20, 1593–1607. [Google Scholar] [CrossRef]
- Gendt, G.; Reigber, C.; Dick, G. Near real-time water vapor estimation in a German GPS network: First results from the ground program of the HGF GASP Project. Phys. Chem. Earth Part A 2001, 26, 413–416. [Google Scholar] [CrossRef]
- Douša, J. Towards an Operational Near-real Time Precipitable Water Vapor Estimation. Phys. Chem. Earth Part A 2001, 26, 189–194. [Google Scholar] [CrossRef]
- Springer, T.A.; Hugentobler, U. IGS ultra rapid products for (near) real-time applications. Phys. Chem. Earth. Part A 2001, 26, 623–628. [Google Scholar] [CrossRef]
- Elgered, G.; Plag, H.P.; Marel, H.V.D.; Barlag, S.; Nash, J. Exploitation of Ground-Based GPS for Operational Numerical Weather Prediction and Climate Applications—Final Report; EU Publications Office (EUR 21639 EU): Luxembourgh, 2005; p. 258. [Google Scholar]
- Van der Marel, H.; COST-716 Team. COST-716 demonstration project for the near real-time estimation of integrated water vapour from GPS. Phys. Chem. Earth 2004, 29, 187–199. [Google Scholar] [CrossRef]
- Poli, P.; Moll, P.; Rabier, F.; Desroziers, G.; Chapnik, B.; Berre, L.; Healy, S.B.; Andersson, E.; Guelai, F.Z.E. Forecast impact studies of zenith total delay data from European near real-time GPS stations in Meteo France 4DVAR. J. Geophys. Res. 2007, 112, D06114. [Google Scholar] [CrossRef]
- Moll, P.; Poli, P.; Ducrocq, V. Use of ground based GNSS data in NWP at Météo-France. In Proceedings of the E-GVAP Workshop, Copenhagen, Denmark, 6 November 2008; Available online: http://egvap.dmi.dk/workshop/5-assimilation-meteo-france-Moll.pdf (accessed on 28 December 2017).
- Bennitt, G.V.; Jupp, A. Operational Assimilation of GPS Zenith Total Delay Observations into the Met Office Numerical Weather Prediction Models. Mon. Weather Rev. 2012, 140, 2706–2719. [Google Scholar] [CrossRef]
- Douša, J.; Bennitt, G.V. Estimation and evaluation of hourly updated global GPS Zenith Total Delays over ten months. GPS Solut. 2013, 17, 453–464. [Google Scholar] [CrossRef]
- Caissy, M.; Agrotis, L.; Weber, G.; Hernandez-Pajares, M.; Hugentobler, U. INNOVATION-Coming Soon-The International GNSS Real-Time Service. GPS World 2012, 23, 52–58. [Google Scholar]
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise Point Positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Dick, G.; Gendt, G.; Reigber, C. First experience with near real-time water vapor estimation in a German GPS network. J. Atmos. Sol. Terr. Phys. 2001, 63, 1295–1304. [Google Scholar] [CrossRef]
- Gendt, G.; Dick, G.; Reigber, C.; Tomassini, M.; Liu, Y.; Ramatschi, M. Near real time GPS water vapor monitoring for numerical weather prediction in Germany. J. Meteorol. Soc. Jpn. 2004, 82, 361–370. [Google Scholar] [CrossRef]
- Douša, J.; Vaclavovic, P. Real-time zenith tropospheric delays in support of numerical weather prediction applications. Adv. Space Res. 2014, 53, 1347–1358. [Google Scholar] [CrossRef]
- Li, X.; Dick, G.; Ge, M.; Heise, S.; Wickert, J.; Bender, M. Real-time GPS sensing of atmospheric water vapor: Precise point positioning with orbit, clock and phase delay corrections. Geophys. Res. Lett. 2014, 41, 3615–3621. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhang, K.; Rohm, W.; Choy, S.; Norman, R.; Wang, C.S. Real-time retrieval of precipitable water vapor from GPS precise point positioning. J. Geophys. Res. Atmos. 2014, 119, 10044–10057. [Google Scholar] [CrossRef]
- Douša, J.; Václavovic, P. Evaluation of ground-based GNSS tropospheric products at Geodetic Observatory Pecny. In IAG 150 Years; IAG Symposia Series; Rizos, C., Willis, P., Eds.; Springer: Cham, Switzerland, 2016; Volume 143, pp. 759–766. [Google Scholar] [CrossRef]
- Guerova, G.; Jones, J.; Douša, J.; Dick, G.; de Haan, S.; Pottiaux, E.; Bock, O.; Pacione, R.; Elgered, G.; Vedel, H.; Bender, M. Review of the state of the art and future prospects of the ground-based GNSS meteorology in Europe. Atmos. Meas. Tech. 2016, 9, 5385–5406. [Google Scholar] [CrossRef]
- Douša, J. Development of the GLONASS ultra-rapid orbit determination at Geodetic Observatory Pecný. In Geodesy for Planet Earth; IAG Symposia Series, Proceedings of the IAG Symposium, Venice, Italy, 9–12 October 2012; Kenyon, S., Pacino, M.C., Marti, U., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; Volume 136, pp. 1029–1036. [Google Scholar] [CrossRef]
- Dilssner, F.; Springer, T.; Flohrer, C.; Dow, J. Estimation of phase center corrections for GLONASS-M satellite antennas. J. Geod. 2010, 84, 467–480. [Google Scholar] [CrossRef]
- Rebischung, P.; Griffiths, J.; Ray, J.; Schmid, R.; Collilieux, X.; Garayt, B. IGS08: The IGS realization of ITRF2008. GPS Solut. 2012, 16, 483. [Google Scholar] [CrossRef]
- Iwabuchi, T.; Rocken, C.; Wada, A.; Kanzaki, M. Benefit of Multi GNSS Processing with GPS, GLONASS, and QZSS for Tropospheric Monitoring. In Proceedings of the 26th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2013), Nashville, TN, USA, 16–20 September 2013; pp. 2496–2507. [Google Scholar]
- Li, X.; Dick, G.; Lu, C.; Ge, M.; Nilsson, T.; Ning, T.; Wickert, J.; Schuh, H. Multi-GNSS meteorology: Real-time retrieving of atmospheric water vapor from BeiDou, Galileo, GLONASS and GPS observations. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6385–6393. [Google Scholar] [CrossRef]
- Li, X.; Zus, F.; Lu, C.; Dick, G.; Ning, T.; Ge, M.; Wickert, J.; Schuh, H. Retrieving of atmospheric parameters from multi-GNSS in real time: Validation with water vapor radiometer and numerical weather model. J. Geophys. Res. Atmos. 2015, 120, 7189–7204. [Google Scholar] [CrossRef]
- Ding, W.; Teferle, F.N.; Kazmierski, K.; Laurichesse, D.; Yuan, Y. An evaluation of real-time troposphere estimation based on GNSS Precise Point Positioning. J. Geophys. Res. Atmos. 2017, 122, 2779–2790. [Google Scholar] [CrossRef]
- Douša, J. The Impact of Ultra-Rapid Orbits on Precipitable Water Vapor Estimation using Ground GPS Network. Phys. Chem. Earth Part A 2001, 26, 393–398. [Google Scholar] [CrossRef]
- Douša, J.; Souček, P. The results of near real-time COST-716 GPS campaign from Geodetic observatory Pecný. In Reports on Geodesy, Proceedings of the EGU G9 Symposium, Vienna, Austria, 25–30 April 2005; Sledzinski, J., Ed.; Warsaw University of Technology, Institute of Geodesy and Geodetic Astronomy: Warsaw, Poland, 2005; pp. 139–150. [Google Scholar]
- Dach, R.; Lutz, S.; Walser, P.; Fridez, P. (Eds.) Bernese GNSS Software Version 5.2. User Manual, Astronomical Institute, University of Bern; Bern Open Publishing: Bern, Switzerland, 2015. [Google Scholar]
- Douša, J.; Dick, G.; Kacmarík, M.; Brožková, R.; Zus, F.; Brenot, H.; Stoycheva, A.; Möller, G.; Kaplon, J. Benchmark campaign and case study episode in central Europe for development and assessment of advanced GNSS tropospheric models and products. Atmos. Meas. Tech. 2016, 9, 2989–3008. [Google Scholar] [CrossRef]
- Douša, J. The impact of errors in predicted GPS orbits on zenith troposphere delay estimation. GPS Solut. 2010, 14, 229–239. [Google Scholar] [CrossRef]
- Hadas, T.; Bosy, J. IGS RTS precise orbits and clocks verification and quality degradation over time. GPS Solut. 2015, 19, 93–105. [Google Scholar] [CrossRef]
- Weber., G.; Mervart, L.; Stürze, A.; Rülke, A.; Stocker, D. BKG Ntrip Client (BNC), Version 2.12; Federal Agency for Cartography and Geodesy: Frankfurt, Germany, 2016; Volume 49, p. 140. ISBN 978-386482-083-0. [Google Scholar]
- Laurichesse, D. The CNES real-time PPP with undifferenced integer ambiguity resolution demonstrator. In Proceedings of the ION GNSS 2011, Portland, Oregon, 19–23 September 2011. [Google Scholar]
- Montenbruck, O.; Steigenberger, P.; Prange, L.; Deng, Z.; Zhao, Q.; Perosanz, F.; Romero, I.; Noll, C.; Stürze, A.; Weber, G.; et al. The Multi-GNSS Experiment (MGEX) of the International GNSS Service (IGS)—Achievements, Prospects and Challenges. Adv. Space Res. 2017, 59, 1671–1697. [Google Scholar] [CrossRef]
- Rebischung, P.; Altamimi, Z.; Ray, J.; Garayt, B. The IGS contribution to ITRF2014. J. Geod. 2016, 90, 611–630. [Google Scholar] [CrossRef]
- Ye, S.; Zhao, L.; Song, J.; Chen, D.; Jiang, W. Analysis of estimated satellite clock biases and their effects on precise point positioning. GPS Solut. 2018, 22, 16. [Google Scholar] [CrossRef]
- Pacione, R.; Araszkiewicz, A.; Brockmann, E.; Dousa, J. EPN-Repro2: A reference GNSS tropospheric data set over Europe. Atmos. Meas. Tech. 2017, 10, 1689–1705. [Google Scholar] [CrossRef]
- Václavovic, P.; Douša, J. Backward smoothing for precise GNSS applications. Adv. Space Res. 2015, 56, 627–1634. [Google Scholar] [CrossRef]
- Václavovic, P.; Douša, J.; Eliaš, M.; Kostelecký, J. Using external tropospheric corrections to improve GNSS positioning of hot-air balloon. GPS Solut. 2017, 21, 1479–1489. [Google Scholar] [CrossRef]
- Schoeneman, E.; Becker, M.; Springer, T.A. New Approach for GNSS Analysis in a Multi-GNSS and Multi-Signal Environment. J. Geod. Sci. 2011, 204–214. [Google Scholar] [CrossRef]
- Bar-Sever, Y.E.; Kroger, P.M.; Borjesson, J.A. Estimating horizontal gradients of tropospheric path delay with a single GPS receiver. J. Geophys. Res. 1998, 103, 5019–5035. [Google Scholar] [CrossRef]
- Boehm, J.; Niell, A.; Tregoning, P.; Schuh, H. Global mapping function (GMF): A new empirical mapping function based on numerical weather model data. Geophys. Res. Lett. 2006, 33, 943–951. [Google Scholar] [CrossRef]
- Boehm, J.; Heinkelmann, R.; Schuh, H. Short note: A global model of pressure and temperature for geodetic applications. J. Geod. 2007, 81, 679–683. [Google Scholar] [CrossRef]
- Pacione, P.; Douša, J. SINEX_TRO—Solution (Software/Technique) INdependent Exchange Format for TROpospheric and Meteorological Parameters, Version 2.00, 2017. Available online: http://twg.igs.org/ (accessed on 20 December 2017).
- Kačmařík, M.; Douša, J.; Dick, G.; Zus, F.; Brenot, H.; Möller, G.; Pottiaux, E.; Kapłon, J.; Hordyniec, P.; Václavovic, P.; et al. Inter-technique validation of tropospheric slant total delays. Atmos. Meas. Tech. 2017, 10, 2183–2208. [Google Scholar] [CrossRef]
- Shoji, Y.; Nakamura, H.; Iwabuchi, T.; Aonashi, K.; Seko, H.; Mishima, K.; Itagaki, A.; Ichikawa, R.; Ohtani, R. Tsukuba GPS dense net campaign observation: Improvement in GPS analysis of slant path delay by stacking one-way postfit phase residuals. J. Meteorol. Soc. Jpn. 2004, 82, 301–314. [Google Scholar] [CrossRef]
- Deng, Z.; Nischan, T.; Bradke, M. Multi-GNSS Rapid Orbit-, Clock- & EOP-Product Series. GFZ Data Services. 2017. Available online: http://gfzpublic.gfz-potsdam.de/pubman/faces/viewItemOverviewPage.jsp?itemId=escidoc:2725915 (accessed on 7 January 2018). [CrossRef]
- Prange, L.; Orliac, E.; Dach, R.; Arnold, D.; Beutler, G.; Schaer, S.; Jäggi, A. CODE’s five-system orbit and clock solution—The challenges of multi-GNSS data analysis. J. Geod. 2017, 91, 345–360. [Google Scholar] [CrossRef]
- Saastamoinen, J. Atmospheric correction for the troposphere and stratosphere in radio ranging of satellites. In The Use of Artificial Satellites for Geodesy; Henriksen, S.W., Mancini, A., Chovitz, B.H., Eds.; American Geophysical Union: Washington, DC, USA, 1972; pp. 247–251. [Google Scholar]
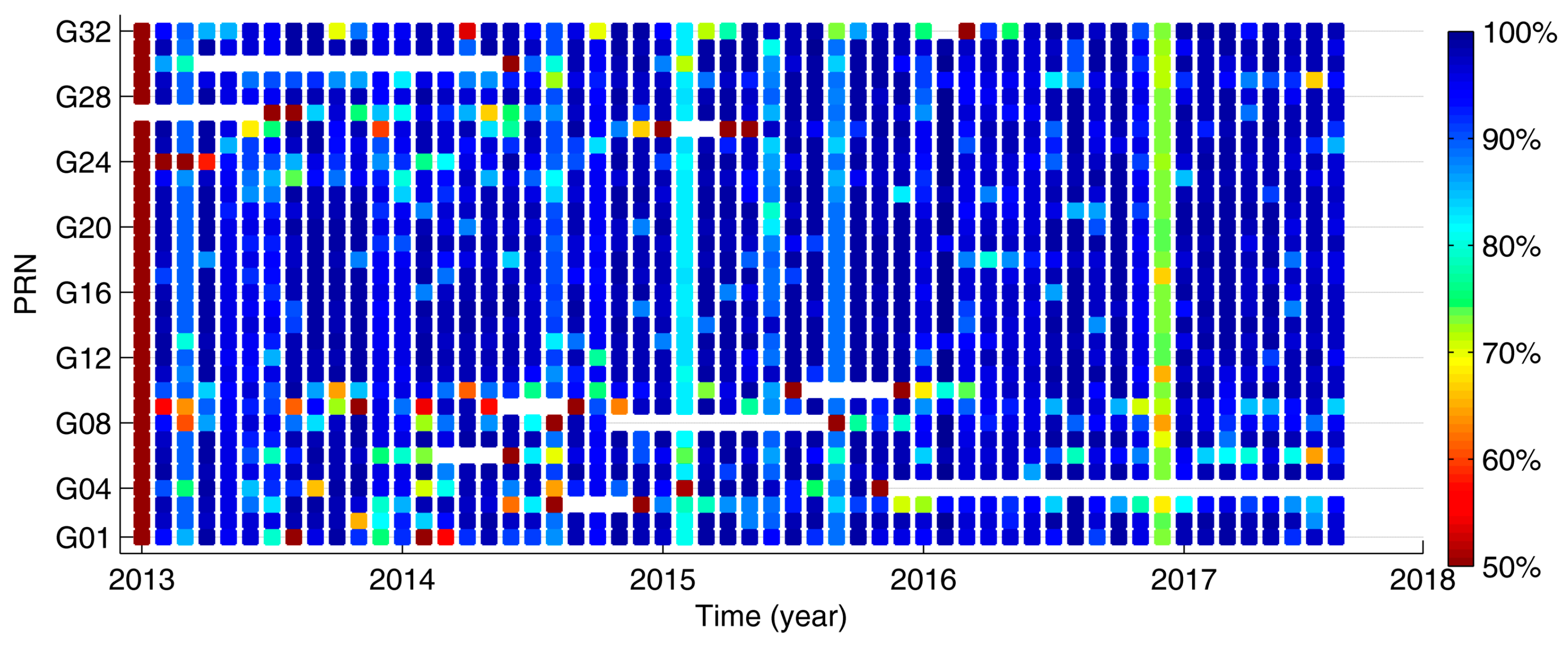
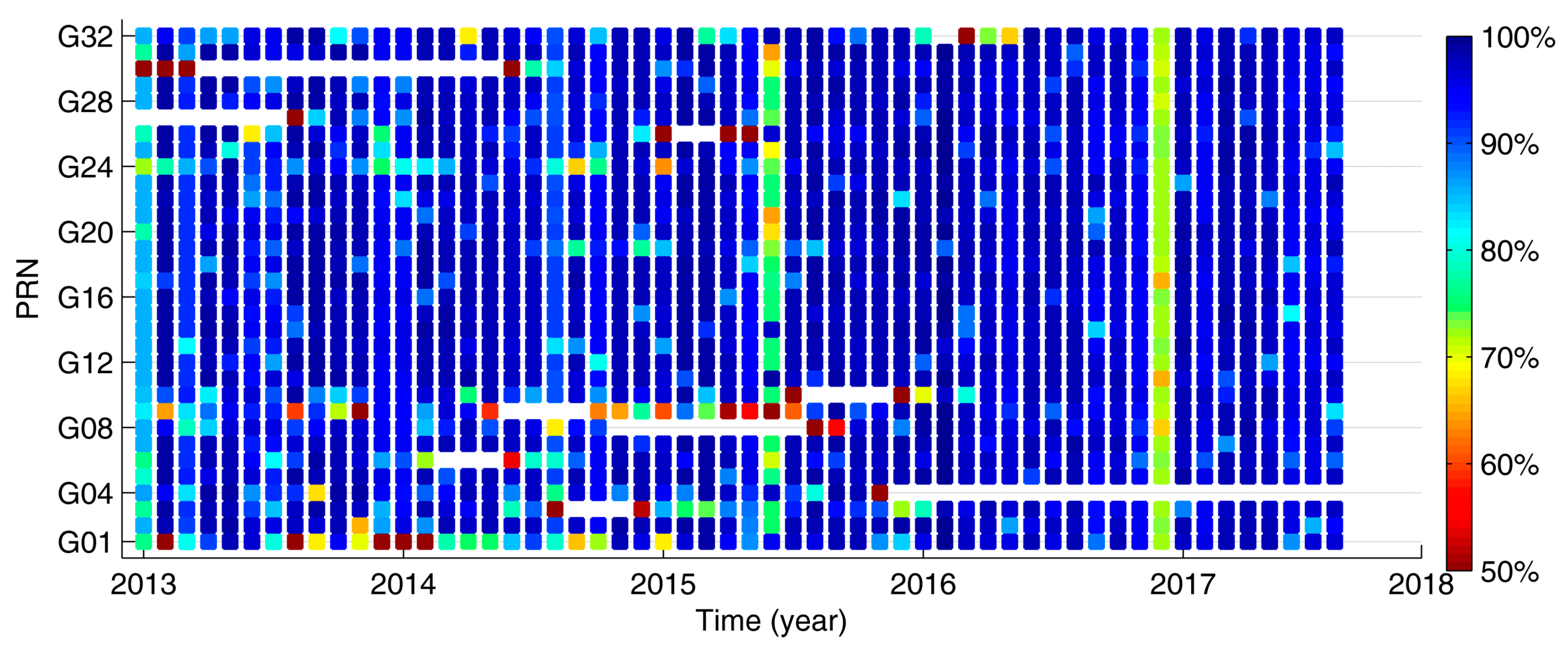
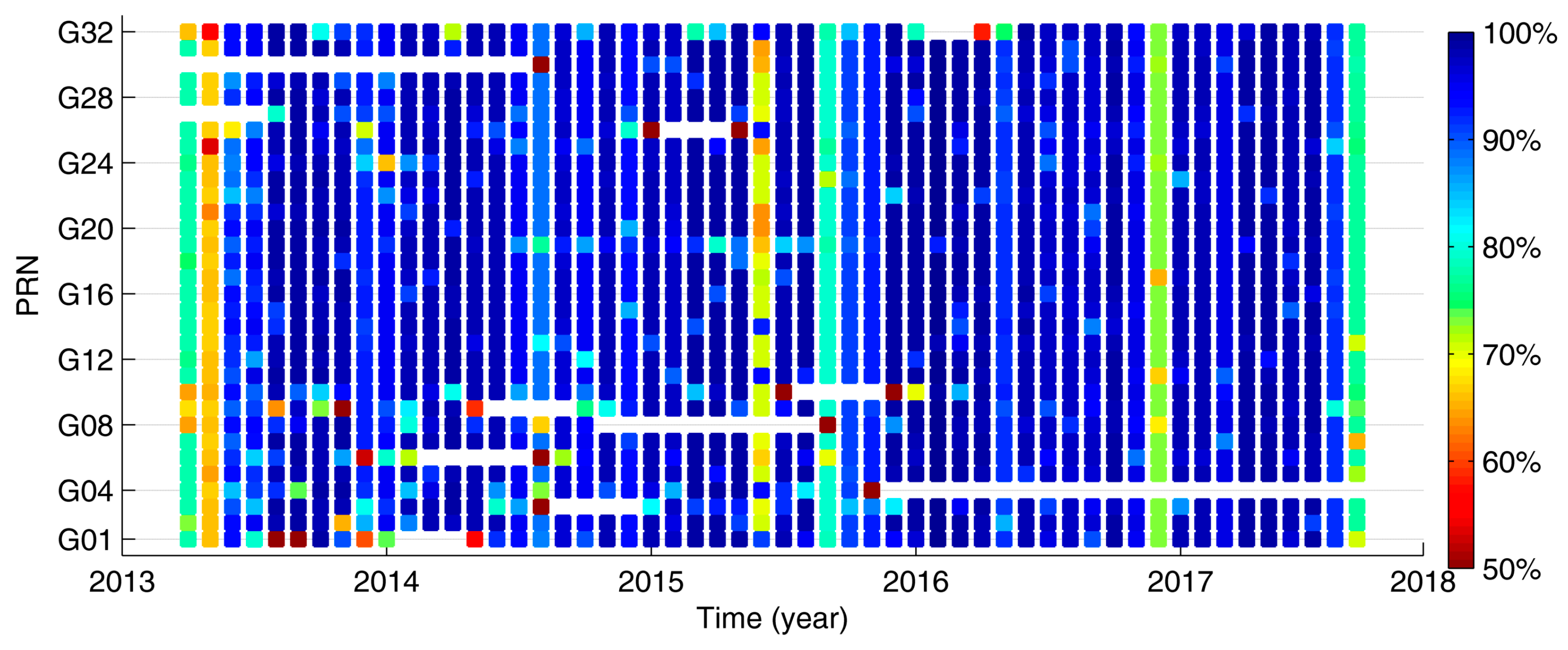
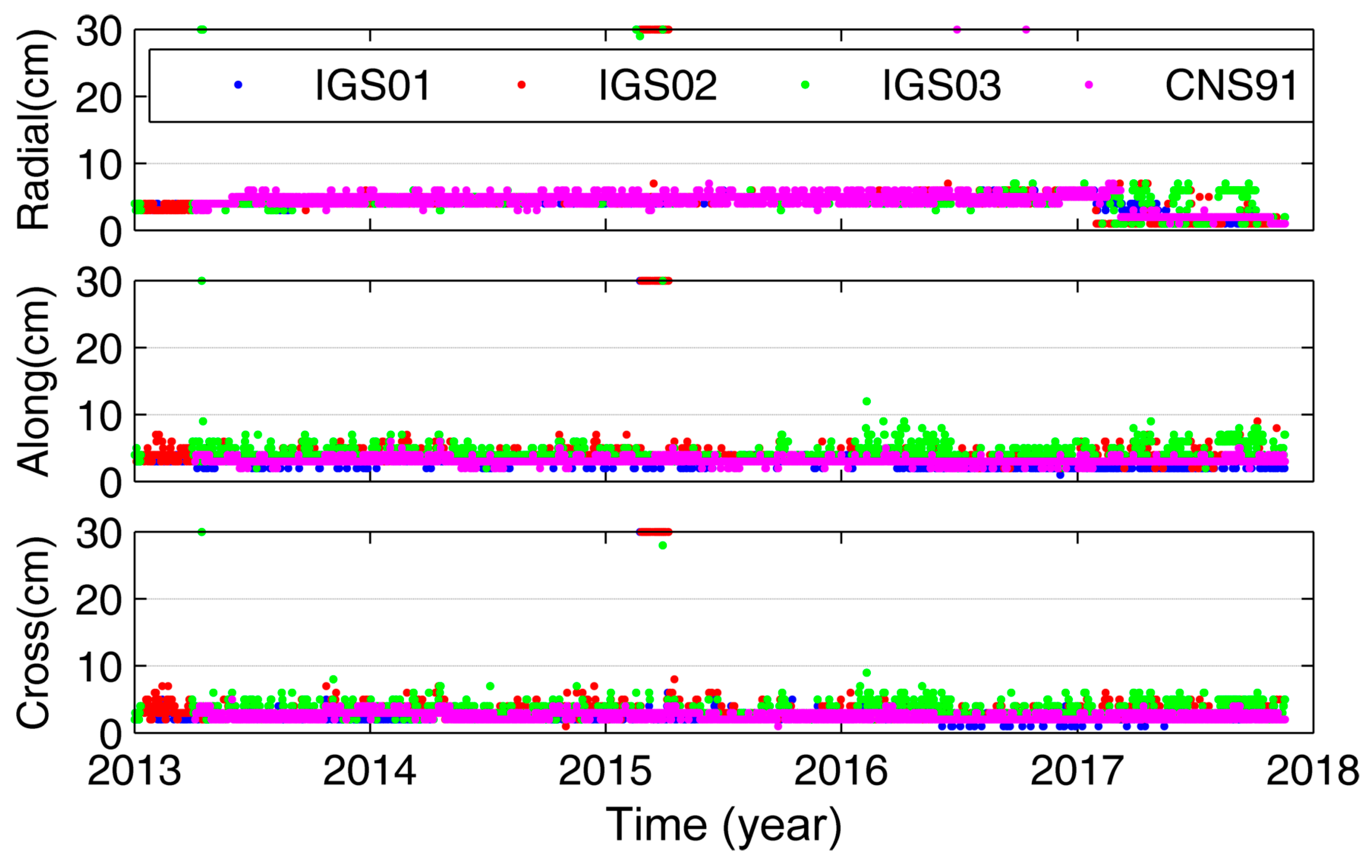
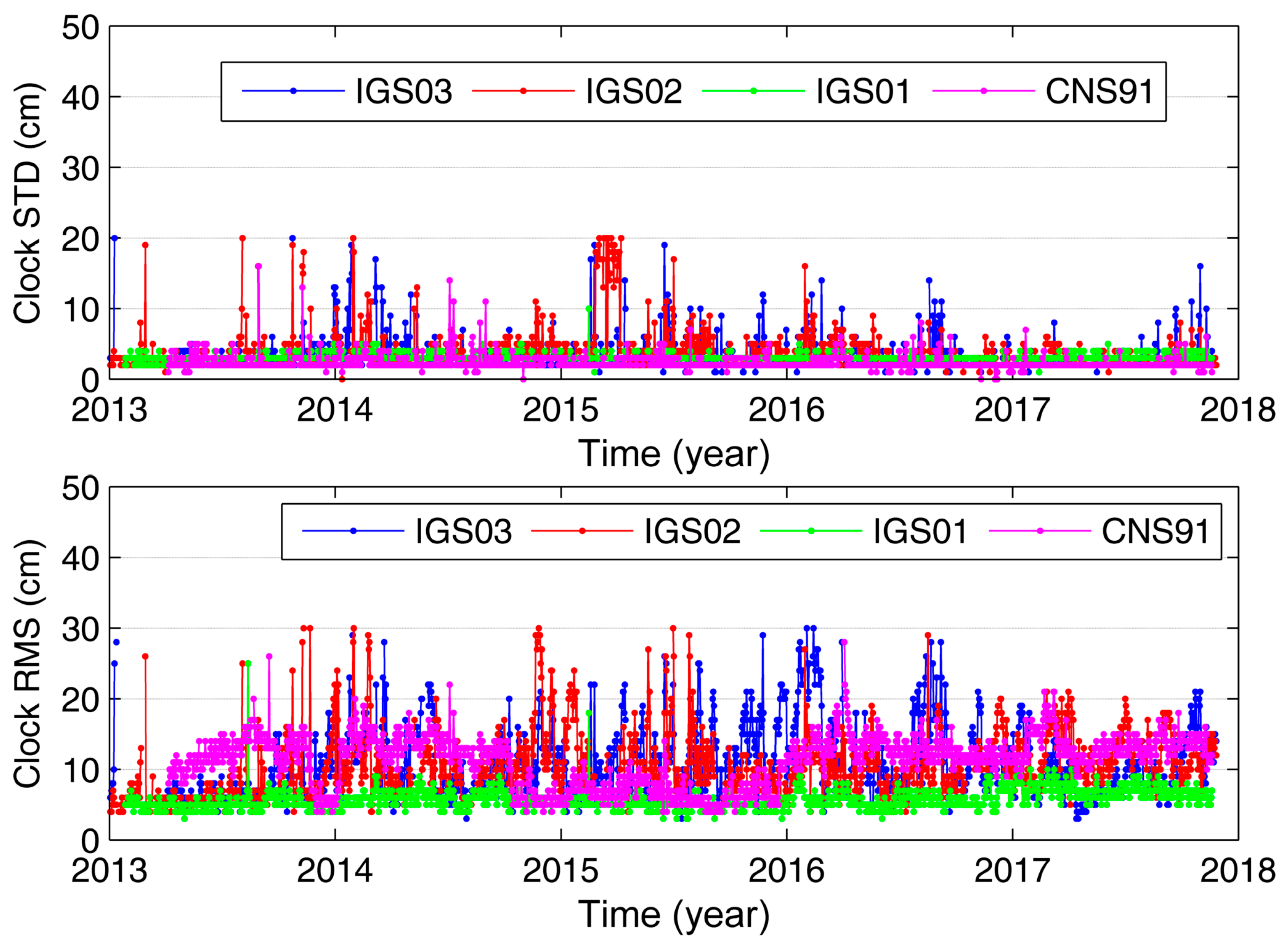
| RMSE | SDEV | |||||
|---|---|---|---|---|---|---|
| Radial | Along | Cross | 3D | Clock | Clock | |
| IGS01 | 1.84 | 2.83 | 2.38 | 4.34 | 5.72 | 2.95 |
| IGS02 | 2.35 | 3.71 | 3.04 | 5.63 | 10.08 | 3.52 |
| IGS03 | 2.41 | 3.82 | 3.10 | 5.70 | 10.28 | 3.03 |
| CNS91 | 2.68 | 3.07 | 2.47 | 5.01 | 11.16 | 2.29 |
| G-Nut/Tefnut PPP Input Precise Products | ZTD Reference Product | Bias (mm] | STD (mm) | RMS (mm] |
|---|---|---|---|---|
| IGS final (SP3 files) | GOP final (Bernese/DD) | +0.9 | 5.1 | 5.2 |
| IGS01 RT corrections | GOP final (Bernese/DD) | +2.4 | 5.8 | 6.4 |
| IGS final (SP3 files) | GFZ final (EPOS/PPP) | +0.4 | 4.1 | 4.2 |
| IGS01 RT corrections | GFZ final (EPOS/PPP) | +2.8 | 4.9 | 5.7 |
| Solution Description | BIAS (mm) mean ± sdev | SDEV (mm) mean ± sdev | RMSE (mm) mean ± sdev |
|---|---|---|---|
| GOPQ—GPS+GLO | 1.8 ± 2.9 | 6.7 ± 1.2 | 7.5 ± 2.5 |
| GOPR—GPS | 2.0 ± 2.8 | 7.2 ± 1.0 | 7.9 ± 1.5 |
| Solution | Software | Strategy Description | Latency | Mean BIAS | Mean SDEV |
|---|---|---|---|---|---|
| RT PPP (HR:59) | G-Nut/Tefnut | Kalman filter in simulated real-time solution | <5 min | 2.4 mm | 5.7 mm |
| NRT PPP (HR:00) | G-Nut/Tefnut | Hourly backward smoothing in real time | ~60 min | 2.5 mm | 4.6 mm |
| PP PPP (HR:59) | G-Nut/Tefnut | Kalman filter in offline processing, IGS final | <5 min | 0.1 mm | 4.7 mm |
| PP PPP (HR:00) | G-Nut/Tefnut | Hourly backward smoothing with IGS final | ~60 min | −0.2 mm | 3.6 mm |
| NRT DD (HR:59) | Bernese V52 | Last ZTD of hourly PW linear LSQ | ~90 min | 0.4 mm | 4.9 mm |
| NRT DD (HR:00) | Bernese V52 | First ZTD of hourly PW linear LSQ | ~30 min | 0.2 mm | 3.7 mm |
| Station Pair | GNSS | BIAS ± SDEV ZTD (mm) | BIAS ± SDEV N-GRD (mm) | BIAS ± SDEV E-GRD (mm) |
|---|---|---|---|---|
| ZIM2-ZIMJ | G | +2.8 ± 1.4 | +0.08 ± 0.17 | −0.02 ± 0.14 |
| ZIM2-ZIMJ | GR | +2.4 ± 1.3 | +0.02 ± 0.14 | −0.02 ± 0.12 |
| ZIM2-ZIMJ | GRE | +2.0 ± 1.3 | +0.03 ± 0.14 | −0.04 ± 0.13 |
| MAT1-MATE | G | −0.5 ± 2.4 | −0.03 ± 0.18 | +0.18 ± 0.25 |
| MAT1-MATE | GR | +0.1 ± 2.3 | +0.01 ± 0.15 | +0.14 ± 0.22 |
| MAT1-MATE | GRE | +0.1 ± 2.2 | +0.00 ± 0.15 | +0.13 ± 0.21 |
| Station Pair | GNSS | BIAS ± SDEV ZTD (mm) | BIAS ± SDEV N-GRD (mm) | BIAS ± SDEV E-GRD (mm) |
|---|---|---|---|---|
| ZIM2-ZIMJ | G | +2.7 ± 1.1 | +0.11 ± 0.12 | −0.02 ± 0.10 |
| ZIM2-ZIMJ | GR | +2.3 ± 1.0 | +0.06 ± 0.11 | −0.02 ± 0.09 |
| ZIM2-ZIMJ | GRE | +1.9 ± 1.0 | +0.07 ± 0.12 | −0.04 ± 0.09 |
| MAT1-MATE | G | −1.3 ± 1.6 | −0.04 ± 0.15 | +0.22 ± 0.19 |
| MAT1-MATE | GR | +0.6 ± 1.4 | +0.00 ± 0.12 | +0.16 ± 0.17 |
| MAT1-MATE | GRE | +0.5 ± 1.4 | -0.01 ± 0.11 | +0.16 ± 0.16 |
| Station Pair | Products | Kalman/Smoother ZTD SDEV (mm) | Kalman/Smoother N-GRD SDEV (mm) | Kalman/Smoother E-GRD SDEV (mm) |
|---|---|---|---|---|
| ZIM2-ZIMJ | IGS01 | 3.3/2.7 | 0.34/0.26 | 0.32/0.25 |
| ZIM2-ZIMJ | IGS03 | 2.3/1.9 | 0.25/0.23 | 0.25/0.21 |
| ZIM2-ZIMJ | COM MGEX | 1.4/1.1 | 0.17/0.12 | 0.14/0.10 |
| ZIM2-ZIMJ | GFZ MGEX | 1.4/1.1 | 0.18/0.12 | 0.14/0.10 |
| MAT1-MATE | IGS01 | 4.8/3.6 | 0.41/0.36 | 0.42/0.33 |
| MAT1-MATE | IGS03 | 3.4/2.6 | 0.31/0.33 | 0.39/0.32 |
| MAT1-MATE | COM MGEX | 2.5/1.6 | 0.18/0.15 | 0.25/0.19 |
| MAT1-MATE | GFZ MGEX | 2.5/1.6 | 0.19/0.15 | 0.24/0.19 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Douša, J.; Václavovic, P.; Zhao, L.; Kačmařík, M. New Adaptable All-in-One Strategy for Estimating Advanced Tropospheric Parameters and Using Real-Time Orbits and Clocks. Remote Sens. 2018, 10, 232. https://doi.org/10.3390/rs10020232
Douša J, Václavovic P, Zhao L, Kačmařík M. New Adaptable All-in-One Strategy for Estimating Advanced Tropospheric Parameters and Using Real-Time Orbits and Clocks. Remote Sensing. 2018; 10(2):232. https://doi.org/10.3390/rs10020232
Chicago/Turabian StyleDouša, Jan, Pavel Václavovic, Lewen Zhao, and Michal Kačmařík. 2018. "New Adaptable All-in-One Strategy for Estimating Advanced Tropospheric Parameters and Using Real-Time Orbits and Clocks" Remote Sensing 10, no. 2: 232. https://doi.org/10.3390/rs10020232
APA StyleDouša, J., Václavovic, P., Zhao, L., & Kačmařík, M. (2018). New Adaptable All-in-One Strategy for Estimating Advanced Tropospheric Parameters and Using Real-Time Orbits and Clocks. Remote Sensing, 10(2), 232. https://doi.org/10.3390/rs10020232





