Efficiency of Individual Tree Detection Approaches Based on Light-Weight and Low-Cost UAS Imagery in Australian Savannas
Abstract
1. Introduction
2. Materials
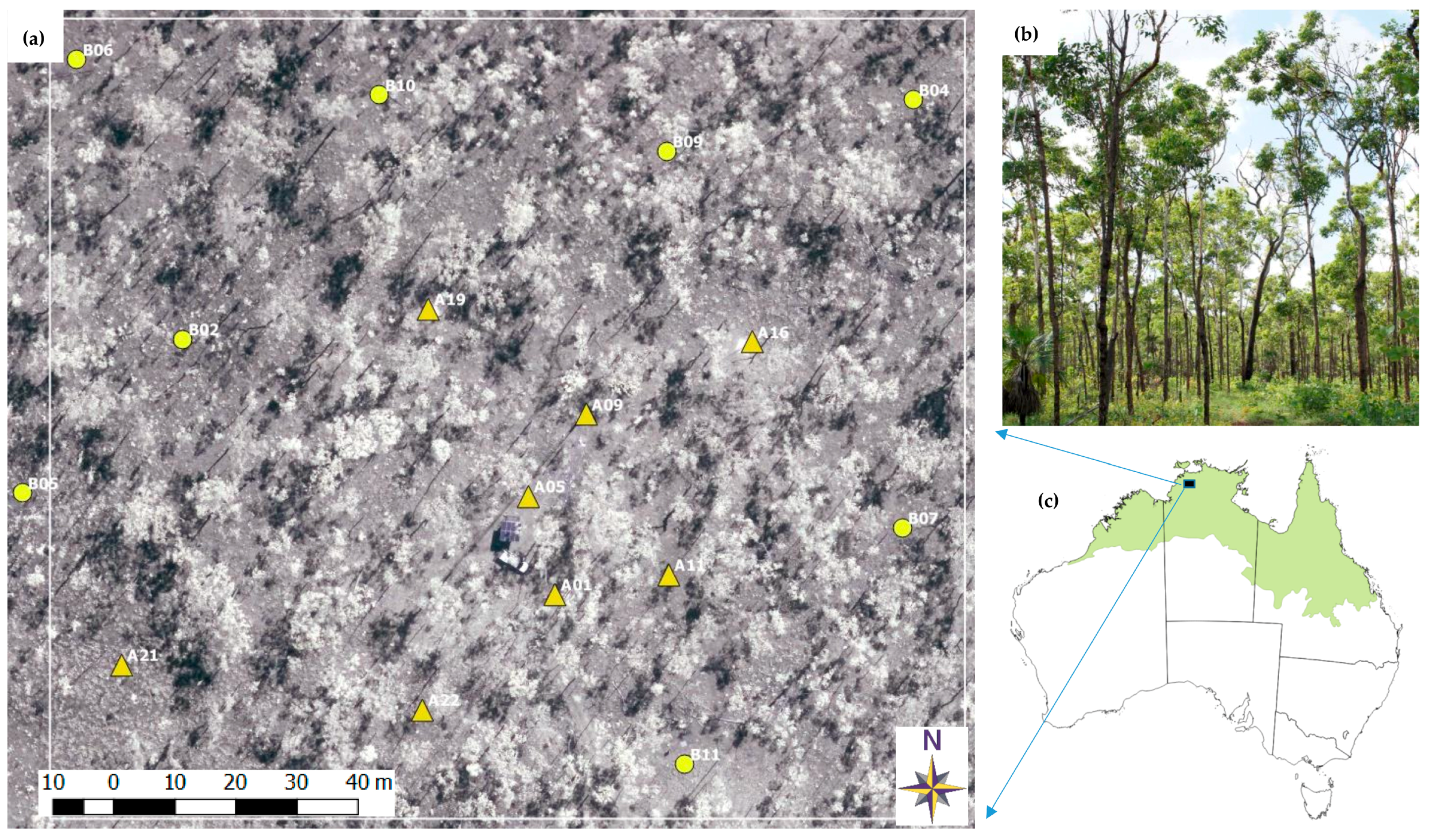
2.1. Study Area
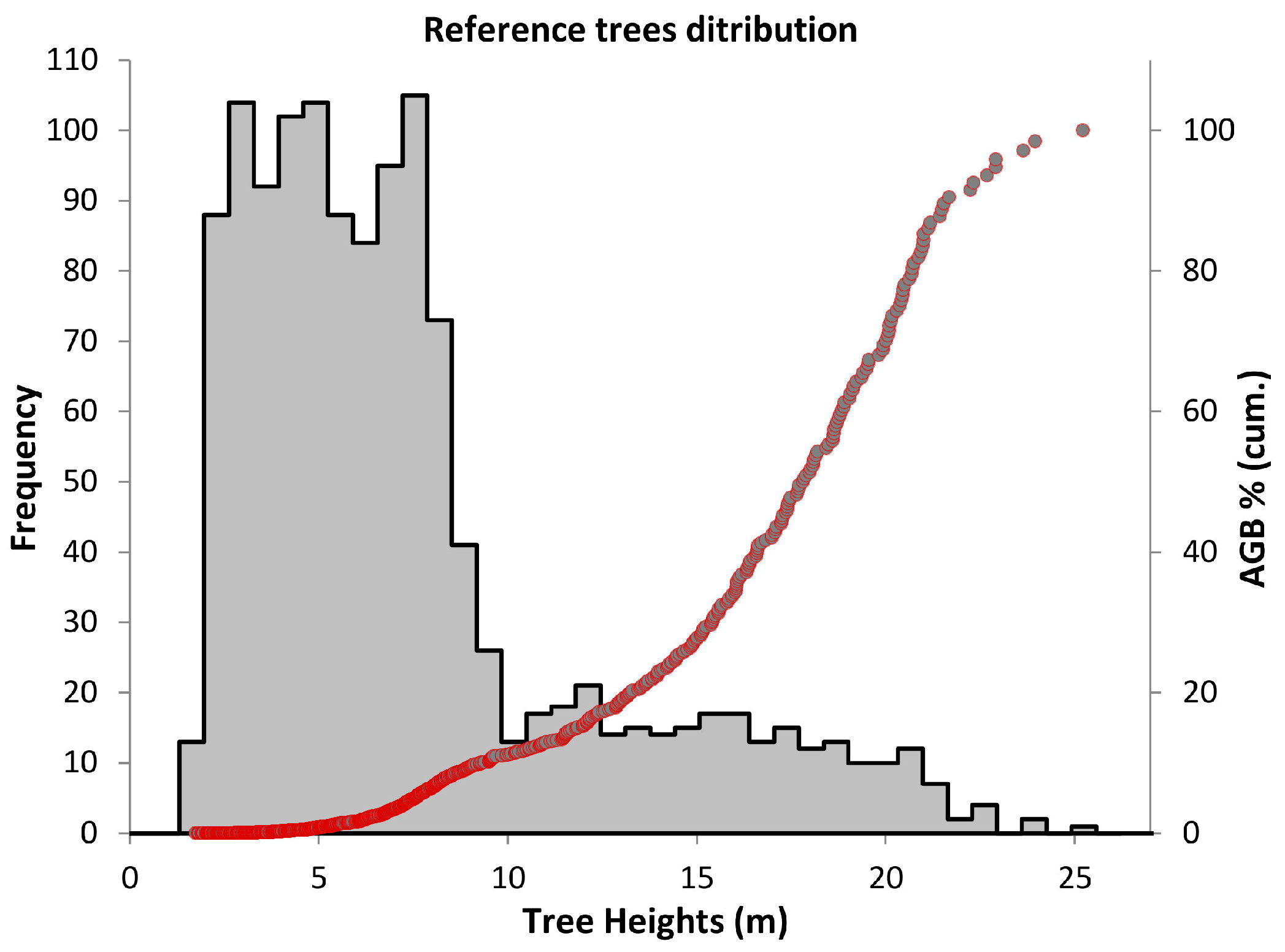
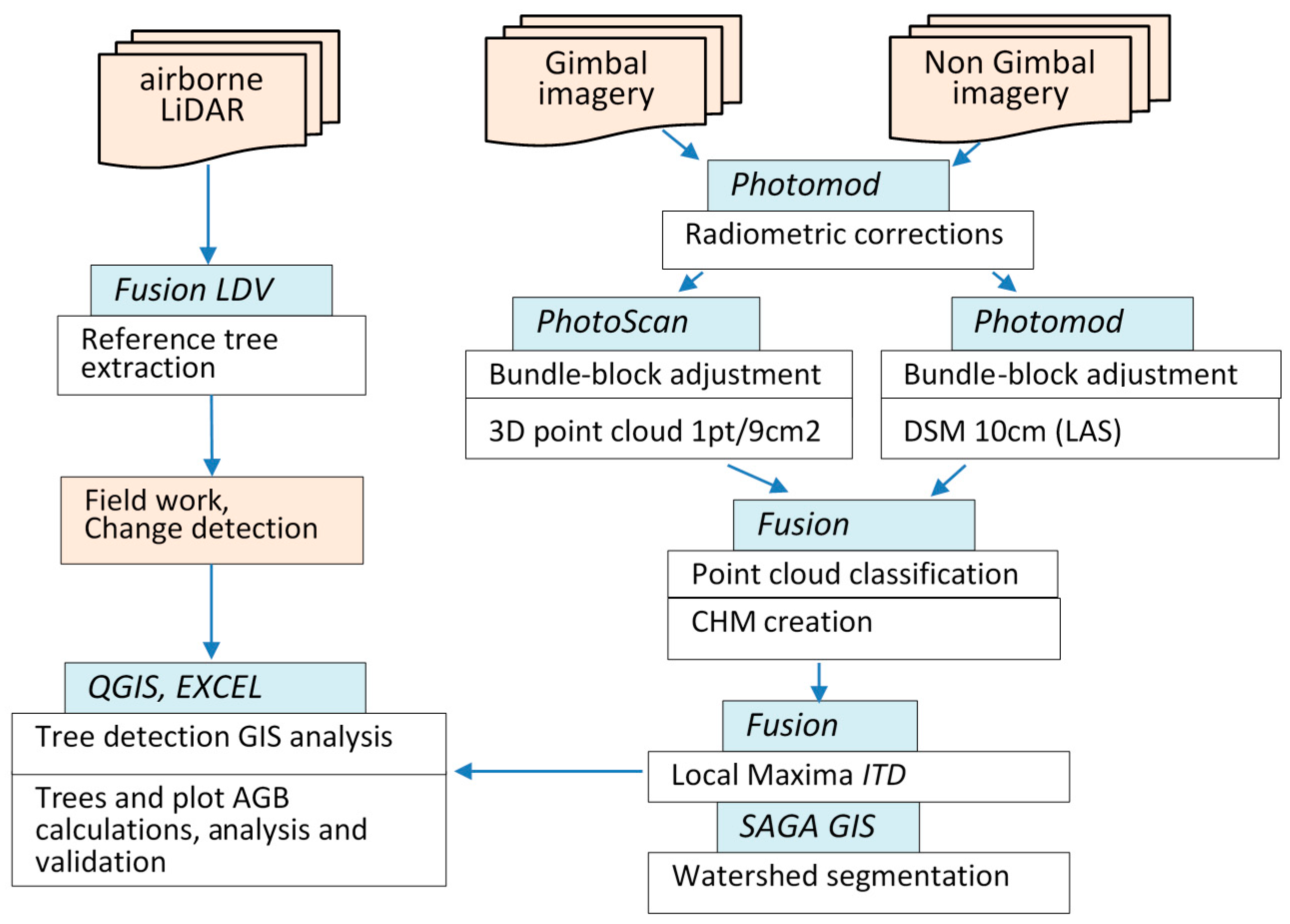
2.2. Airborne LiDAR and Reference Trees Extraction
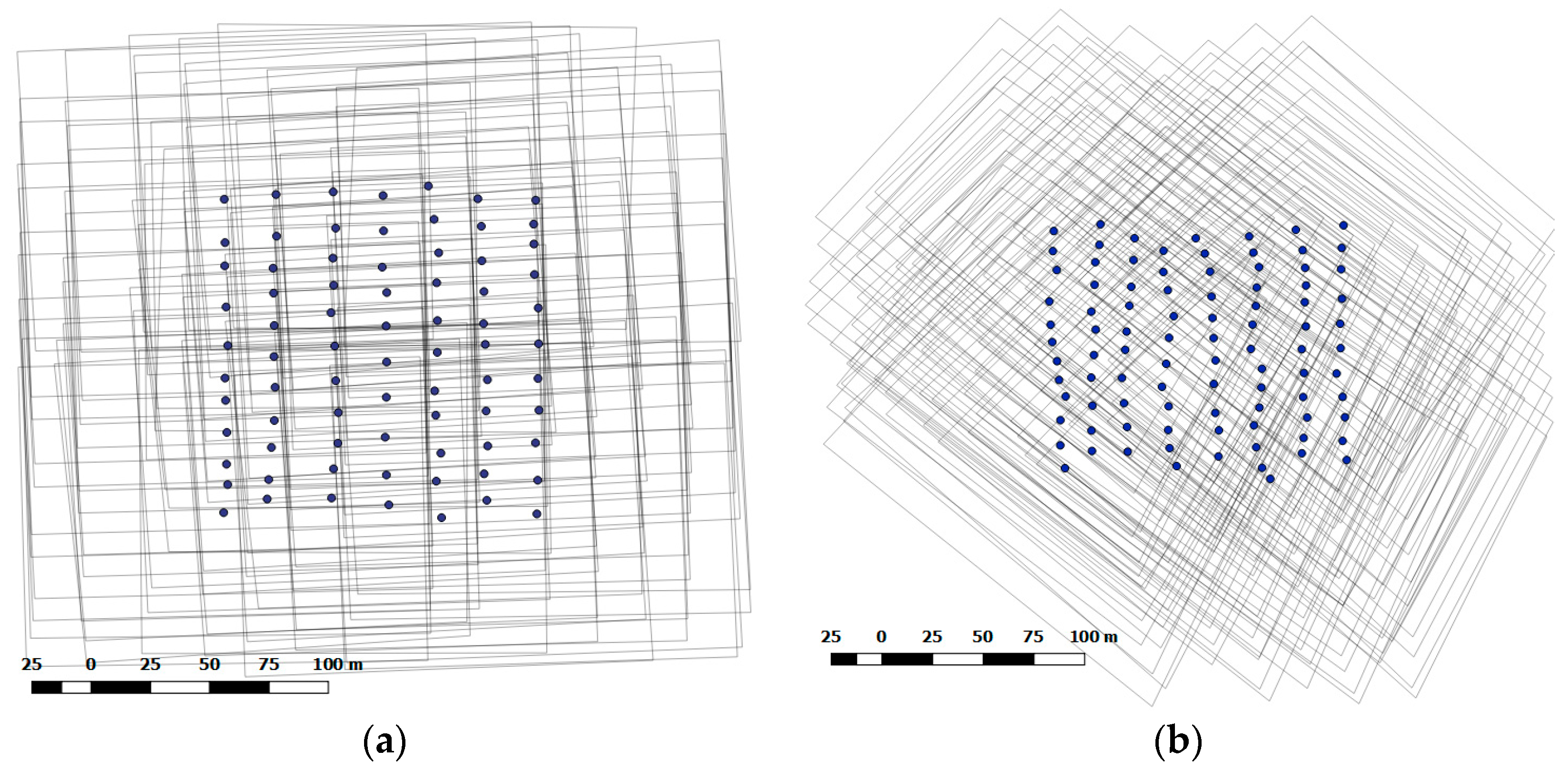
2.3. UAS Platform and Image Data Acquisition
2.4. Image Data Processing and Point Cloud Generation
2.5. Local Maxima Tree Detection Approach and CHM Resolution Choice
2.6. Individual Tree Detection Processing
2.7. AGB Estimation and Data Validation
3. Results
3.1. Bundle-Block Adjustments
3.2. Accuracy of the SfM Based Ground Surfaces
3.3. Optimal CHMs Resolution Choice
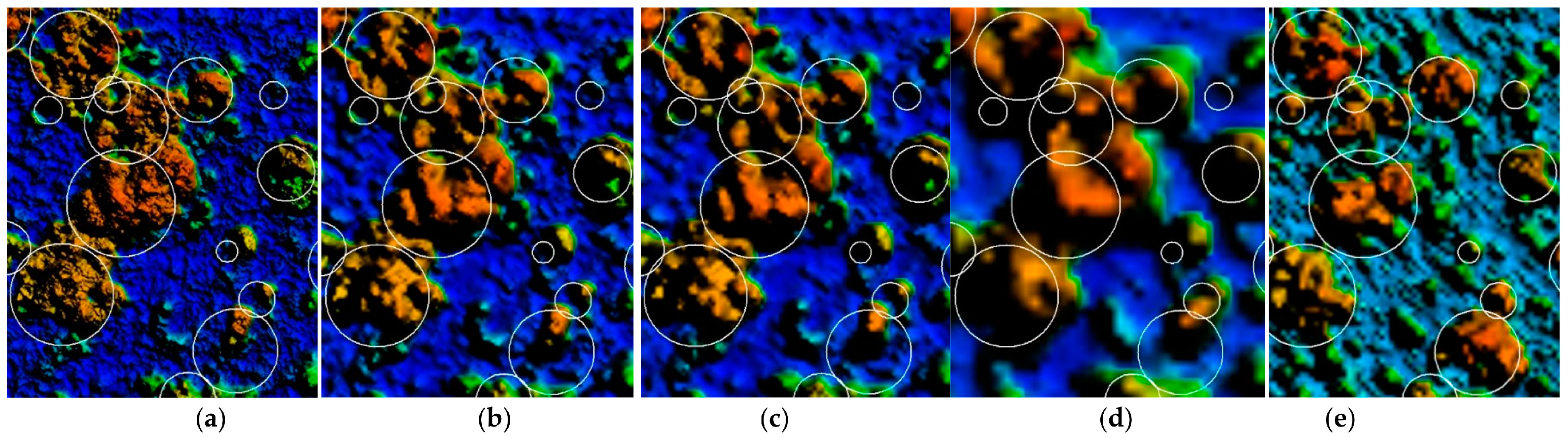
3.4. Local Maxima Individual Tree Detection and Watershed Segmentation Results
3.5. AGB Estimation
4. Discussion
4.1. Accuracy of Individual Tree Detection Based on Canopy Maxima and Watershed Segmentation Approaches
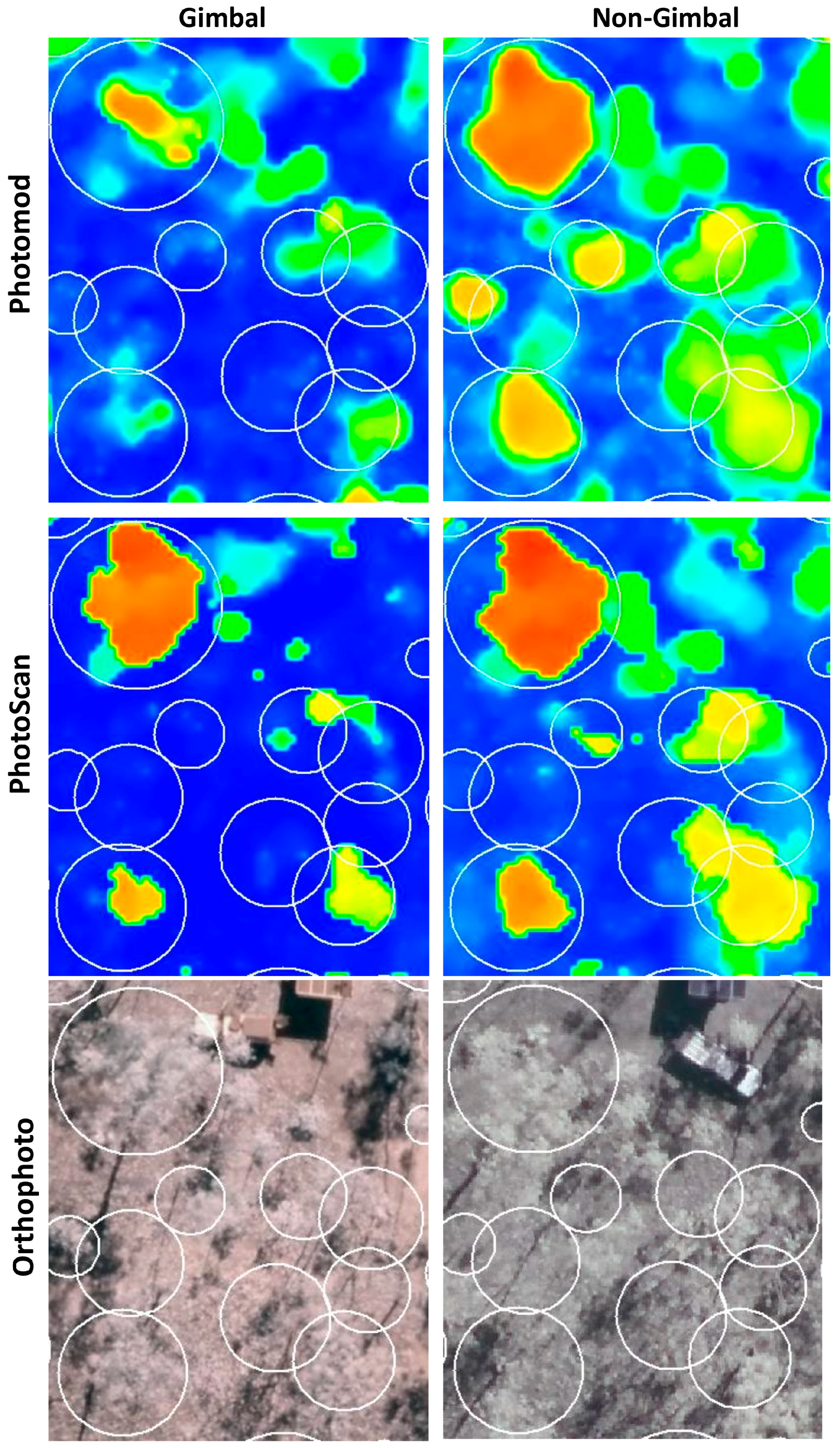
4.2. The Effect of Camera Calibration Precision on the Accuracy of Tree Height and Biomass Estimation
4.3. Aspects and Limitations of Data Acquisition by GoPro HERO4 Camera
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Trumbore, S.; Brando, P.; Hartmann, H. Forest health and global change. Science 2015, 349, 814–818. [Google Scholar] [CrossRef] [PubMed]
- Maltamo, M.; Næsset, E.; Vauhkonen, J. Forestry Applications of Airborne Laser Scanning Concepts and Case Studies; Springer: Berlin/Heidelberg, Germany, 2014; Volume 27. [Google Scholar]
- Lefsky, M.A.; Cohen, W.B.; Harding, D.J.; Parker, G.G.; Acker, S.A.; Gower, S.T. Lidar remote sensing of above-ground biomass in three biomes. Glob. Ecol. Biogeogr. 2002, 11, 393–399. [Google Scholar] [CrossRef]
- Asner, G.P.; Mascaro, J. Mapping tropical forest carbon: Calibrating plot estimates to a simple LiDAR metric. Remote Sens. Environ. 2014, 140, 614–624. [Google Scholar] [CrossRef]
- Goldbergs, G.; Levick, S.R.; Lawes, M.; Edwards, A. Hierarchical integration of individual tree and area-based approaches for savanna biomass uncertainty estimation from airborne LiDAR. Remote Sens. Environ. 2018, 205, 141–150. [Google Scholar] [CrossRef]
- Colomina, I.; Molina, P. Unmanned aerial systems for photogrammetry and remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2014, 92, 79–97. [Google Scholar] [CrossRef]
- Westoby, M.J.; Brasington, J.; Glasser, N.F.; Hambrey, M.J.; Reynolds, J.M. ‘Structure-from-Motion’ photogrammetry: A low-cost, effective tool for geoscience applications. Geomorphology 2012, 179, 300–314. [Google Scholar] [CrossRef]
- Torresan, C.; Berton, A.; Carotenuto, F.; Di Gennaro, S.F.; Gioli, B.; Matese, A.; Miglietta, F.; Vagnoli, C.; Zaldei, A.; Wallace, L. Forestry applications of UAVs in Europe: A review. Int. J. Remote Sens. 2017, 38, 2427–2447. [Google Scholar] [CrossRef]
- Tang, L.; Shao, G. Drone remote sensing for forestry research and practices. J. For. Res. 2015, 26, 791–797. [Google Scholar] [CrossRef]
- Paneque-Gálvez, J.; McCall, M.; Napoletano, B.; Wich, S.; Koh, L. Small Drones for Community-Based Forest Monitoring: An Assessment of Their Feasibility and Potential in Tropical Areas. Forests 2014, 5, 1481. [Google Scholar] [CrossRef]
- Beringer, J.; Hutley, L.B.; Abramson, D.; Arndt, S.K.; Briggs, P.; Bristow, M.; Canadell, J.G.; Cernusak, L.A.; Eamus, D.; Edwards, A.C.; et al. Fire in Australian savannas: From leaf to landscape. Glob. Chang. Biol. 2015, 21, 62–81. [Google Scholar] [CrossRef] [PubMed]
- Williams, R.; Hutley, L.B.; Cook, G.D.; Russell-Smith, J.; Edwards, A.; Chen, X. Assessing the carbon sequestration potential of mesic savannas in the Northern Territory, Australia: Approaches, uncertainties and potential impacts of fire. Funct. Plant Biol. 2004, 31, 415–422. [Google Scholar] [CrossRef]
- Russell-Smith, J.; Murphy, B.P.; Meyer, C.P.; Cooka, G.D.; Maier, S.; Edwards, A.C.; Schatz, J.; Brocklehurst, P. Improving estimates of savanna burning emissions for greenhouse accounting in northern Australia: Limitations, challenges, applications. Int. J. Wildland Fire 2009, 18, 1–18. [Google Scholar] [CrossRef]
- Hung, C.; Bryson, M.; Sukkarieh, S. Multi-class predictive template for tree crown detection. ISPRS J. Photogramm. Remote Sens. 2012, 68, 170–183. [Google Scholar] [CrossRef]
- Wallace, L.; Lucieer, A.; Malenovský, Z.; Turner, D.; Vopěnka, P. Assessment of Forest Structure Using Two UAV Techniques: A Comparison of Airborne Laser Scanning and Structure from Motion (SfM) Point Clouds. Forests 2016, 7, 62. [Google Scholar] [CrossRef]
- Wallace, L.; Lucieer, A.; Watson, C.; Turner, D. Development of a UAV-LiDAR System with Application to Forest Inventory. Remote Sens. 2012, 4, 1519. [Google Scholar] [CrossRef]
- Whiteside, T.G.; Bartolo, R.E. Robust and Repeatable Ruleset Development for Hierarchical Object-Based Monitoring of Revegetation Using High Spatial and Temporal Resolution UAS Data. In Proceedings of the GEOBIA 2016: Solutions and Synergies, Enschede, The Netherlands, 14–16 September 2016. [Google Scholar]
- TERN. Litchfield Savanna SuperSite. Available online: http://www.tern-supersites.net.au/supersites/lfld (accessed on 30 March 2015).
- Beringer, J.; Hacker, J.; Hutley, L.B.; Leuning, R.; Arndt, S.K.; Amiri, R.; Bannehr, L.; Cernusak, L.A.; Grover, S.; Hensley, C.; et al. SPECIAL—Savanna Patterns of Energy and Carbon Integrated across the Landscape. Bull. Am. Meteorol. Soc. 2011, 92, 1467–1485. [Google Scholar] [CrossRef]
- O’Grady, A.P.; Chen, X.; Eamus, D.; Hutley, L.B. Composition, leaf area index and standing biomass of eucalypt open forests near Darwin in the Northern Territory, Australia. Aust. J. Bot. 2000, 48, 629–638. [Google Scholar] [CrossRef]
- Isenburg, M. LAStools—Efficient LiDAR Processing Software (Version 141017, Unlicensed). Available online: https://rapidlasso.com/lastools/ (accessed on 30 May 2015).
- McGaughey, R.J. FUSION/LDV: Software for LIDAR Data Analysis and Visualization; Version 3.50; US Department of Agriculture, Forest Service, Pacific Northwest Research Station: Seattle, WA, USA, 2015.
- Hirschmüller, H. Semi-global matching-motivation, developments and applications. In Proceedings of the Photogrammetric Week 11, Stuttgart, Germany, 9–13 September 2011; pp. 173–184. [Google Scholar]
- Agisoft. PhotoScan Community Forum Topic: Algorithms Used in Photoscan. Available online: http://www.agisoft.com/forum/index.php?topic=89.msg13780;topicseen#msg13780 (accessed on 27 February 2017).
- Kaartinen, H.; Hyyppä, J.; Yu, X.; Vastaranta, M.; Hyyppä, H.; Kukko, A.; Holopainen, M.; Heipke, C.; Hirschmugl, M.; Morsdorf, F. An international comparison of individual tree detection and extraction using airborne laser scanning. Remote Sens. 2012, 4, 950–974. [Google Scholar] [CrossRef]
- Popescu, S.C.; Wynne, R.H.; Nelson, R.F. Estimating plot-level tree heights with lidar: Local filtering with a canopy-height based variable window size. Comput. Electron. Agric. 2002, 37, 71–95. [Google Scholar] [CrossRef]
- Li, W.; Guo, Q.; Jakubowski, M.K.; Kelly, M. A new method for segmenting individual trees from the lidar point cloud. Photogramm. Eng. Remote Sens. 2012, 78, 75–84. [Google Scholar] [CrossRef]
- Goutte, C.; Gaussier, E. A probabilistic interpretation of precision, recall and F-score, with implication for evaluation. In Proceedings of the 27th European conference on Advances in Information Retrieval Research (ECIR), Santiago de Compostela, Spain, 21–23 March 2005; pp. 345–359. [Google Scholar]
- Conrad, O.; Bechtel, B.; Bock, M.; Dietrich, H.; Fischer, E.; Gerlitz, L.; Wehberg, J.; Wichmann, V.; Böhner, J. System for Automated Geoscientific Analyses (SAGA) v. 2.1.4. Geosci. Model Dev. 2015, 8, 1991–2007. [Google Scholar] [CrossRef]
- QGIS. QGIS Geographic Information System. Open Source Geospatial Foundation Project. Available online: http://www.qgis.org (accessed on 30 May 2015).
- Agüera-Vega, F.; Carvajal-Ramírez, F.; Martínez-Carricondo, P. Assessment of photogrammetric mapping accuracy based on variation ground control points number using unmanned aerial vehicle. Measurement 2017, 98, 221–227. [Google Scholar] [CrossRef]
- Goldstein, E.B.; Oliver, A.R.; de Vries, E.; Moore, L.J.; Jass, T. Ground control point requirements for structure-from-motion derived topography in low-slope coastal environments. PeerJ PrePrints 2015, 3, e1444v1441. [Google Scholar] [CrossRef]
- Russell-Smith, J.; Murphy, B.; Edwards, A.; Meyer, C.P. Carbon Accounting and Savanna Fire Management; CSIRO Publishing: Clayton, Australia, 2015. [Google Scholar]
- Ferraz, A.; Bretar, F.; Jacquemoud, S.; Gonçalves, G.; Pereira, L.; Tomé, M.; Soares, P. 3-D mapping of a multi-layered Mediterranean forest using ALS data. Remote Sens. Environ. 2012, 121, 210–223. [Google Scholar] [CrossRef]
- Reitberger, J.; Schnörr, C.; Krzystek, P.; Stilla, U. 3D segmentation of single trees exploiting full waveform LIDAR data. ISPRS J. Photogramm. Remote Sens. 2009, 64, 561–574. [Google Scholar] [CrossRef]
- Duncanson, L.I.; Cook, B.D.; Hurtt, G.C.; Dubayah, R.O. An efficient, multi-layered crown delineation algorithm for mapping individual tree structure across multiple ecosystems. Remote Sens. Environ. 2014, 154, 378–386. [Google Scholar] [CrossRef]
- Edson, C.; Wing, M.G. Airborne Light Detection and Ranging (LiDAR) for Individual Tree Stem Location, Height, and Biomass Measurements. Remote Sens. 2011, 3, 2494–2528. [Google Scholar] [CrossRef]
- Turner, R.S. An Airborne Lidar Canopy Segmentation Approach for Estimating Above-Ground Biomass in Coastal Eucalypt Forests. Ph.D. Thesis, University of New South Wales, Sydney, Australia, 2006. [Google Scholar]
- James, M.R.; Robson, S. Mitigating systematic error in topographic models derived from UAV and ground-based image networks. Earth Surf. Process. Landf. 2014, 39, 1413–1420. [Google Scholar] [CrossRef]
- Luhmann, T.; Fraser, C.; Maas, H.-G. Sensor modelling and camera calibration for close-range photogrammetry. ISPRS J. Photogramm. Remote Sens. 2016, 115, 37–46. [Google Scholar] [CrossRef]
- Bosak, K. Secrets of UAV Photomapping. Pteryx: Poland, 2011. Available online: http://www.academia.edu/download/32814759/pteryx-mapping-secrets.pdf (accessed on 30 September 2014).

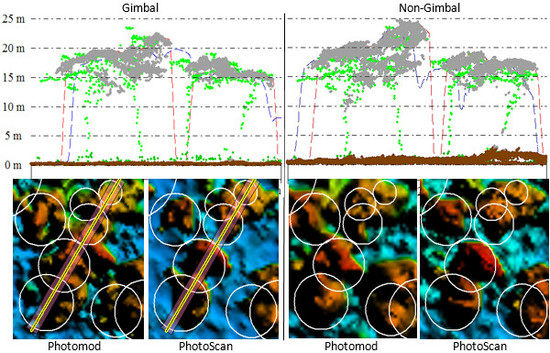
| Ϭo (pix) | RMSE (X) (m) | RMSE (Y) (m) | RMSE (Z) (m) | Pitch (deg) | Roll (deg) | Yaw (deg) | ||
|---|---|---|---|---|---|---|---|---|
| Gimbal | Photomod | 0.38 | 0.17 | 0.13 | 0.31 | 0.02 | 0.04 | 2.8 |
| PhotoScan | n/a | 0.19 | 0.16 | 0.36 | −0.05 | 0.28 | 2.8 | |
| Non-Gimbal | Photomod | 0.97 | 0.33 | 0.29 | 0.33 | −12.5 | 10.6 | −37 |
| PhotoScan | n/a | 0.25 | 0.28 | 0.44 | −12.7 | 8.2 | −37 |
| DTMSfM–DTMLiDAR | Photomod | PhotoScan | ||
|---|---|---|---|---|
| Gimbal | Non-Gimbal | Gimbal | Non-Gimbal | |
| Mean Error (m) | 0.12 | 0.27 | 0.08 | 0.41 |
| RMSE (m) | 0.22 | 0.43 | 0.19 | 0.54 |
| SD (m) | 0.19 | 0.34 | 0.17 | 0.35 |
| CHM Resolutions | ||||
|---|---|---|---|---|
| Rates | 30 cm | 40 cm | 50 cm | 100 cm |
| r | 69% | 70% | 66% | 64% |
| p | 59% | 71% | 72% | 77% |
| Fscore | 64% | 71% | 69% | 69% |
| Local Maxima | Watershed Segmentation | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Photomod | PhotoScan | LiDAR | Photomod | PhotoScan | LiDAR | |||||
| Rates | Gimbal | Non-gimbal | Gimbal | Non-gimbal | Gimbal | Non-gimbal | Gimbal | Non-gimbal | ||
| r | 42% | 43% | 41% | 43% | 61% | 32% | 34% | 35% | 36% | 43% |
| p | 74% | 68% | 76% | 60% | 69% | 76% | 79% | 81% | 71% | 83% |
| Fscore | 53% | 53% | 54% | 50% | 65% | 45% | 48% | 49% | 48% | 57% |
| Local Maxima | Watershed Segmentation | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Photomod | PhotoScan | LiDAR | Photomod | PhotoScan | LiDAR | |||||
| Rates | Gimbal | Non-gimbal | Gimbal | Non-gimbal | Gimbal | Non-gimbal | Gimbal | Non-gimbal | ||
| r | 70% | 71% | 71% | 70% | 80% | 67% | 68% | 69% | 71% | 81% |
| p | 71% | 72% | 72% | 57% | 78% | 68% | 69% | 72% | 56% | 72% |
| Fscore | 71% | 71% | 71% | 63% | 79% | 68% | 69% | 71% | 63% | 76% |
| Local Maxima | Watershed Segmentation | |||||||
|---|---|---|---|---|---|---|---|---|
| Photomod | PhotoScan | Photomod | PhotoScan | |||||
| Gimbal | Non-gimbal | Gimbal | Non-gimbal | Gimbal | Non-gimbal | Gimbal | Non-gimbal | |
| Mean Error (m) | −0.28 | −0.04 | 0.09 | 0.55 | −0.25 | −0.08 | 0.12 | 0.68 |
| SD (m) | 1.22 | 1.36 | 1.18 | 1.42 | 1.27 | 1.39 | 1.21 | 1.50 |
| AGB plot diff (%) | −11% | 7% | 12% | 46% | −4% | 14% | 15% | 57% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goldbergs, G.; Maier, S.W.; Levick, S.R.; Edwards, A. Efficiency of Individual Tree Detection Approaches Based on Light-Weight and Low-Cost UAS Imagery in Australian Savannas. Remote Sens. 2018, 10, 161. https://doi.org/10.3390/rs10020161
Goldbergs G, Maier SW, Levick SR, Edwards A. Efficiency of Individual Tree Detection Approaches Based on Light-Weight and Low-Cost UAS Imagery in Australian Savannas. Remote Sensing. 2018; 10(2):161. https://doi.org/10.3390/rs10020161
Chicago/Turabian StyleGoldbergs, Grigorijs, Stefan W. Maier, Shaun R. Levick, and Andrew Edwards. 2018. "Efficiency of Individual Tree Detection Approaches Based on Light-Weight and Low-Cost UAS Imagery in Australian Savannas" Remote Sensing 10, no. 2: 161. https://doi.org/10.3390/rs10020161
APA StyleGoldbergs, G., Maier, S. W., Levick, S. R., & Edwards, A. (2018). Efficiency of Individual Tree Detection Approaches Based on Light-Weight and Low-Cost UAS Imagery in Australian Savannas. Remote Sensing, 10(2), 161. https://doi.org/10.3390/rs10020161