1. Introduction
The all-weather capability of radar makes it the natural instrument for real-time monitoring in geosciences for potential life-threatening natural events like rock and mountain slides; clay and snow avalanches; volcanoes; open pit mines [
1]; and structural monitoring of dam fronts [
2], buildings and bridges [
3,
4,
5]. The use of ground-based interferometric real aperture radar to measure unstable mountains [
6,
7,
8,
9], landslides [
10], glacier movements, and calving events [
11,
12,
13] gives good results. Experience from radar measurements shows that environmental and geometrical effects limit or have a great influence on the accuracy of the measurements. In a recent 8-year study of monitoring an unstable mountainside [
6], it was found that atmospheric decorrelation was the major factor limiting the measurement accuracy when monitoring submillimeter motion at distances of 3 to 4 km. In this study and in Reference [
8], it was shown that by introducing a reference reflector and by performing differential interferometry, most of the variations caused by atmospheric decorrelation were removed. However, it is not always possible to introduce radar reflectors due to the nature of the monitored area or from a safety point of view, typically for an unstable mountain with a lot of motion and occasional rock falls. In cases with unexpected geological hazards, it may not be possible to establish a set of corner reflectors. There is, therefore, a need for a thorough assessment of GB-InRAR systems, including radar hardware, measurement geometry and environmental effects, to find ways to compensate for the interferometric measurements for the environmental and geometrical effects in order to achieve accuracies comparable to differential interferometry.
Published literature on environmental variations on longtime geological monitoring with real-aperture radar are scarce as the main focus is on space-borne and ground-based Synthetic Aperture Radar (SAR); however, the environmental effects discussed in the literature are also for the use of Frequency Modulated Continuous Wave (FMCW) GB-InRAR systems. Atmospheric decorrelation was first observed in space-born SAR data when assessing slow subsidence rates [
14]. To overcome the problem of atmospheric decorrelation, the Permanent Scatter (PS) Technique was developed [
15], and a thorough analysis of the technique is given in Reference [
16]. The technique utilizes time-coherent pixels to help bypass the geometrical and temporal decorrelation. Efficient techniques for compensation of GB-SAR based on statistical analysis of local meteorological data in combination with PS is reported in References [
17,
18,
19,
20]. In Reference [
20] it was noted that compensating for atmospheric decorrelation due to temperature-induced turbulence and long distances is still a challenge. A recent study of Alpine glaciers in Italy and Spain reports an accuracy of a few millimeters/day when applying atmospheric phase screening (APS) corrections under challenging atmospheric conditions [
13]. Accuracy improvements for real-aperture differential interferometric radar based on local meteorological data are reported in Reference [
8].
One of the main differences between GB-SAR and real-aperture radar is the two-dimensional mapping capability of the GB-SAR system. The cost of 2D mapping is longer data acquisition time due to the mechanical motion of the antenna, which makes the GB-SAR system more sensitive to atmospheric and geometric decorrelation both during and between data acquisition. As stated in Reference [
19], the time between data acquisition should be reduced as much as possible to avoid significant variation in the atmospheric conditions between measurements. Typical acquisition times of a GB-SAR-system are in the order of minutes while a typical real-aperture radar has a pulse repetition frequency (PRF) of a few thousand measurements per second. The high PRF of the real-aperture radar makes it easier to track and correct for atmospheric decorrelation due to the temporal variation in temperature, humidity and the pressure between measurements.
The geometry of the system must be considered carefully when deploying a GB-InRAR. When deploying an on-demand remote sensing system it is often time-critical to get the system operational and on-line. The choices of where to locate the radar are often restricted and the measurement geometry may deviate from an optimum radar measurement setup. If the radar is not radially directed against the anticipated motional direction of the monitored objects, the motion will be underestimated and must be corrected for. Another geometrical effect that may affect the measurement accuracy is multipath interference [
21]. Multipath interference can occur when the energy radiated from the radar antenna hits a reflective surface, usually the ground, and is reflected towards the target. This additional signal adds coherently to the direct path signal and deteriorates the phase and magnitude of the data. It is stated in Reference ([
22]; p. 2.31) that multipath interference is the most important non-free-space effect. A ripple in the amplitude of the backscatter from both stationary and moving objects is another geometric effect observed in high-resolution radar measurements of moving objects, where the data acquisition time is substantially faster than the velocity of the tracked object. This effect is probably coupled to the relative radar cross-section (RCS) value of the objects in the measurement area.
Environmental effects affect all radar system hardware, however, unlike a permanently installed remote sensing system an on-demand deployed system is more likely to be exposed to environmental variations as no infrastructure or environmental shielding can be expected to be present. The frequency and phase stability of microwave hardware is sensitive to variation in temperature, and this applies especially to oscillators and microwave cables. Uncorrected, this may lead to variations in the measured interferometric distance and a decrease in measurement accuracy. In Reference [
23] it is stated that the temperature-induced phase shift in microwave cables is critical in high performance measurements. The magnitude of the phase-shift depends on the length of the cable and the operational temperature range of the radar system. The temperature-induced variation in the radar hardware should be separated from the temperature-induced environmental effects to avoid overcompensation of either effect.
A concern when measuring displacements without the use of reflectors is strong scatterers on the surface illuminated by the radar. Strong scatterers may be natural, e.g., stone blocks, or artificial, e.g., rockfall catch fences. Their presence may negatively affect the accuracy of the measurements as the strong back scatterers may interfere or shadow the backscatter from the other objects in the monitoring area. In Reference [
24] it is stated that when monitoring in the presence of rockfall catch fences the interferometric phase information is not reliable. This is likely due to multiple effects like strong backscatter, shadowing and interference. In Reference [
25] it is stated that GB-SAR is less suited for single-point monitoring than GB-InRAR in the presence of spatially-concentrated backscatter. This may be due to the azimuth width of the antennas, which for GB-SAR usually is much wider than for GB-InRAR, resulting in a larger illuminated area, hence, making the GB-SAR more vulnerable to cross-range interference. It is therefore of interest to assess the effect experimentally by tracking objects in the presence of stationary strong scatterers.
In this paper, we have investigated the effects influencing interferometric measurements of moving targets using a GB-InRAR, with a focus on applications in geosciences. Both controlled field and laboratory measurement experiments were set up to assess the effects influencing the measurement accuracy. In addition, a software model was developed to verify these effects. A series of experimental interferometric radar measurements were conducted on both stationary and moving targets. The purpose of the measurements was to gather information on how various environmental and geometric effects influenced the accuracy of the measurements, and to find a way to predict and correct for the effects, so that a relatively simple GB-InRAR system can be readily and optimally employed on site for field measurements.
This paper deals with five major effects influencing the accuracy of interferometric and differential interferometric radar measurements:
The geometry of the measurement setup
Atmospheric effects i.e., radio refractivity
Effect of ground reflections i.e., multipath interference
Radar target interference
The radar hardware
The presented field results are utilizing the measured phase information registered by the GB-InRAR from the company ISPAS AS, and movements are calculated from phase differences based on the principle of interferometry. To exclude any systematic artifacts of the GB-InRAR, the laboratory measurements were all made using a Rhode & Schwarz Vector Network Analyzer (VNA).
In this paper, we start by outlining the radar theory necessary to analyze the measured data and to develop the numerical simulation model. We then describe the measurement setup and compare the field measurements with the results from the numeric model. Finally, we discuss the error sources and the factors limiting the accuracy of interferometric measurements and give some advice regarding setup and operational measurements.
4. Experiment Results
In this chapter, we first present and compare the measurements with the theoretical calculations. The analysis of the differences is divided into the following subsections: amplitude analysis, radio refractivity, multipath interference, reflector interference, and electrical length of microwave cables. We then assess the geometric, environmental and hardware influence on interferometric and differential interferometric measurements. Finally, we summarize all measurement results. The range to the targets is given as the radar range cell number rather than the actual distance in meters.
4.1. Amplitude Analysis
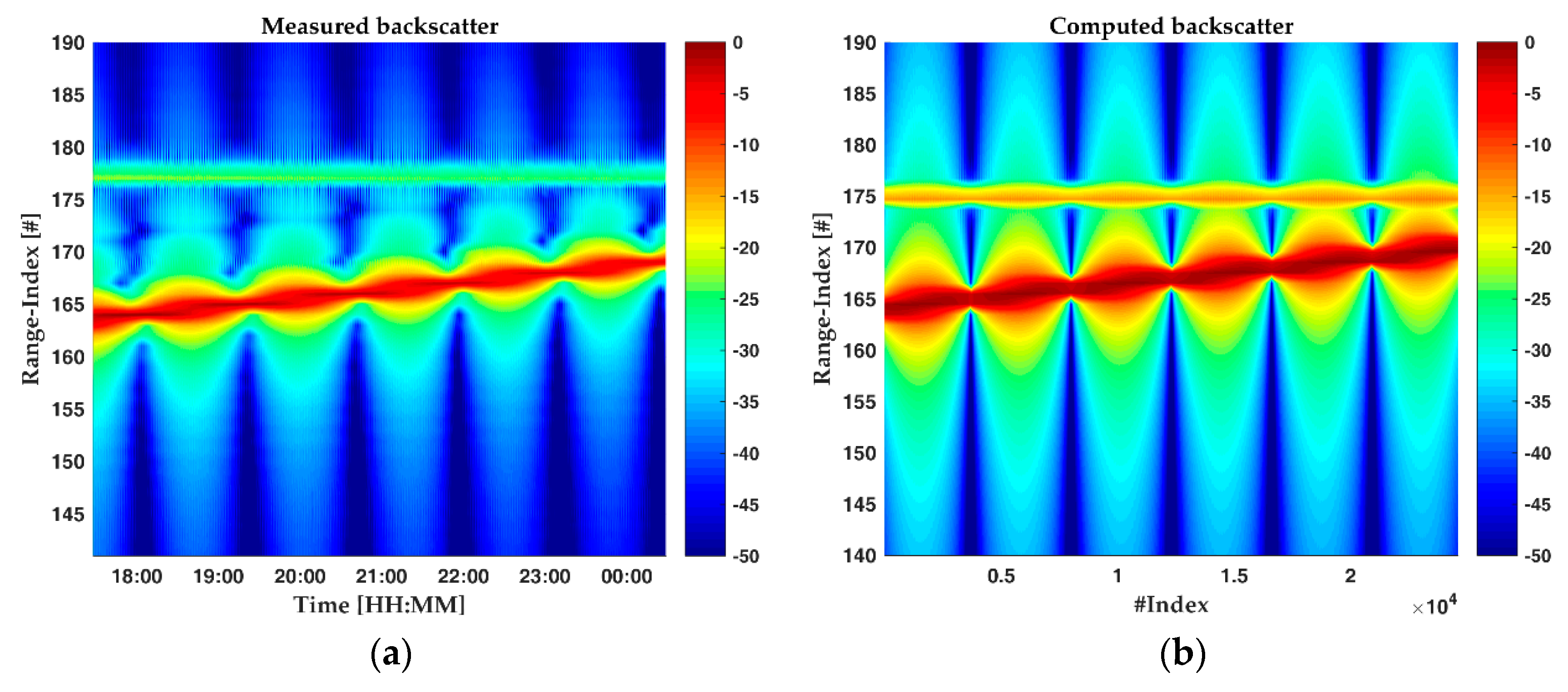
We start by comparing the amplitude of measured backscatter with the computed values to highlight the differences. The resulting normalized High-Resolution Range (HRR) plot from the towed reflector experiment is shown in
Figure 5a. The results from the numerical model based on Equations (2) and (5) are shown in
Figure 5b.
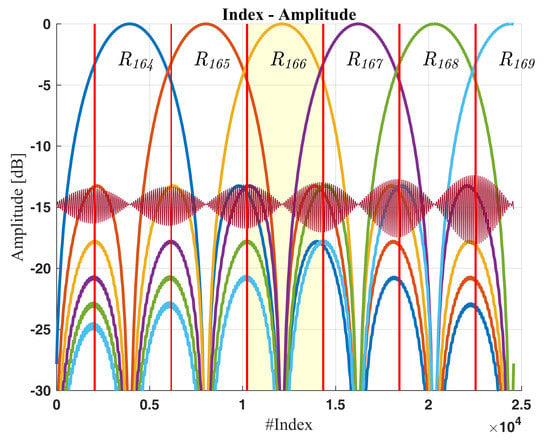
Figure 5a shows how the amplitude of the reflected energy from the towed reflector changes as it is moved away from the radar. The reflector starts in range index 164 and ends in range index 169. The reference reflector remains stationary in range index 177. The amplitude of the stationary reflector is approximately five times lower than the towed reflector due to its smaller size; see
Table 1.
Figure 5b shows the computed backscatter from the numerical model.
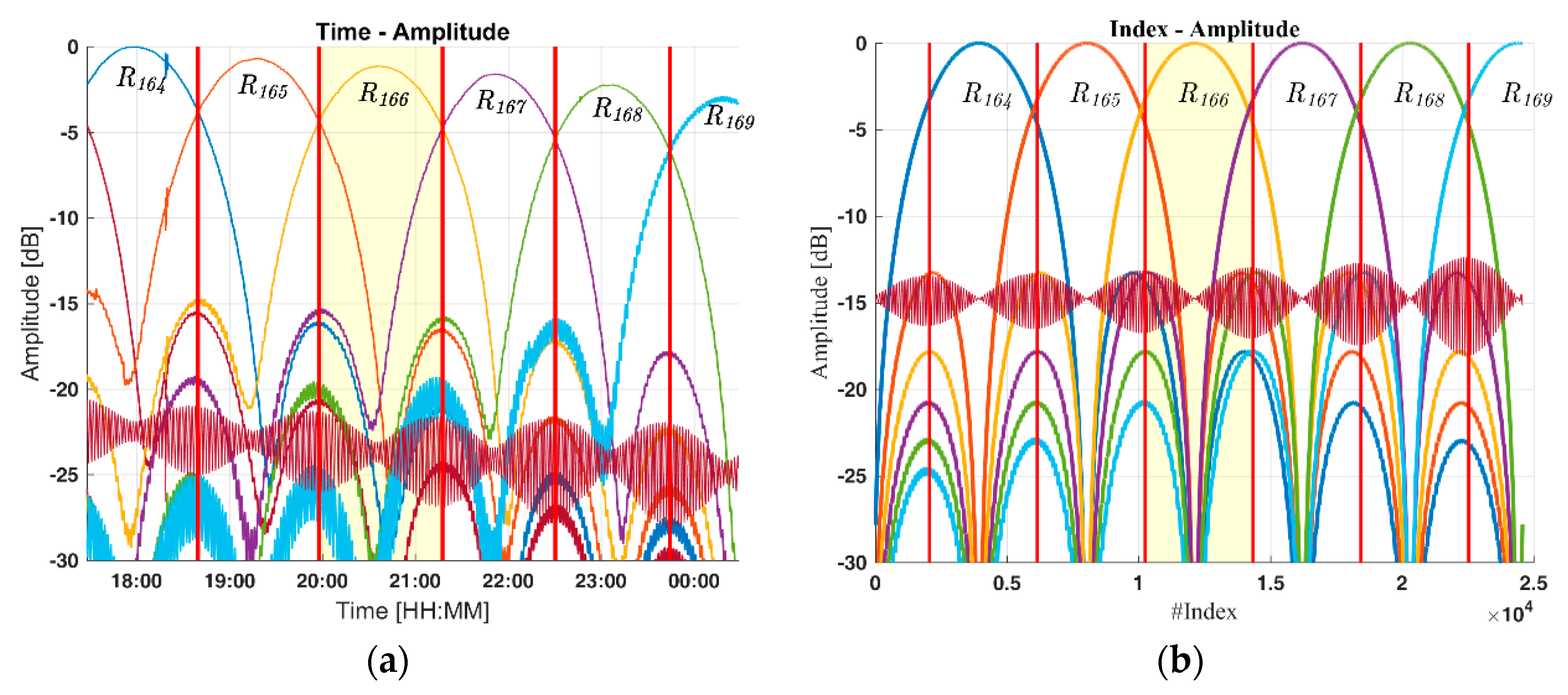
Figure 6a,b shows a cut through
Figure 5a,b following the maximum amplitude of the backscattered energy.
The measurements and the computed results correlate to some extent, but major differences are observed, like the reduction in amplitude as the towed reflector is moved away from the radar. The theoretical attenuation from the FSPL, see Equation (16), is approximately 0.33 dB while we observe a close to 3 dB attenuation. This missing 2.7 dB is, as discussed in the next section, believed to be caused by ground reflection or multipath interference. Another difference is the amplitude level of the stationary reflector, which starts 7 dB below the theoretic value and drops in amplitude as the towed reflector gets closer. This is partly believed to be caused by shadowing which will be addressed in
Appendix A. The oscillations in the amplitude of the backscatter from the reference reflector are observed in both
Figure 6a,b. This oscillation is believed to be caused by constructive and destructive interference between the two reflectors which is discussed in
Section 4.3.
4.2. Multipath Interference
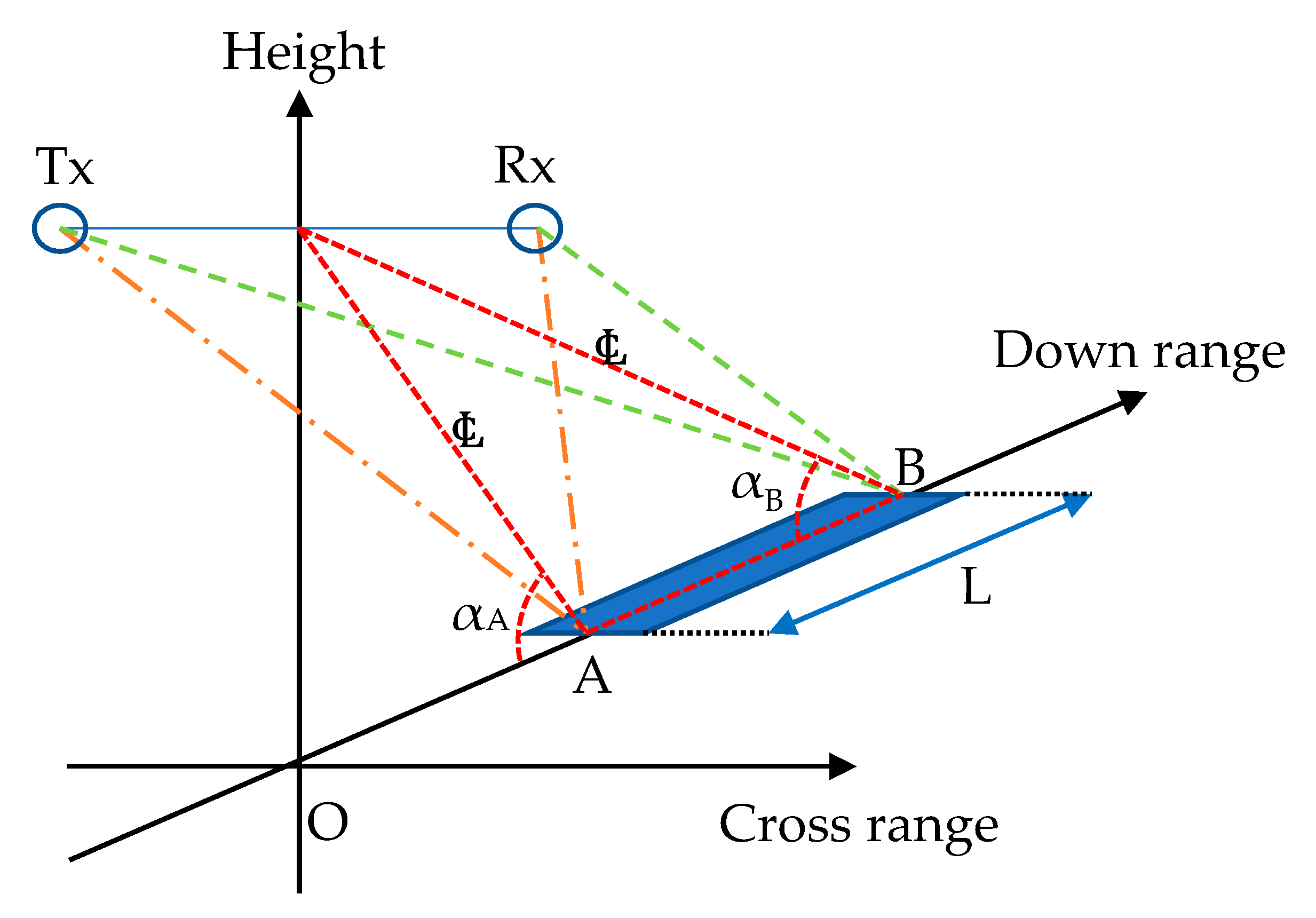
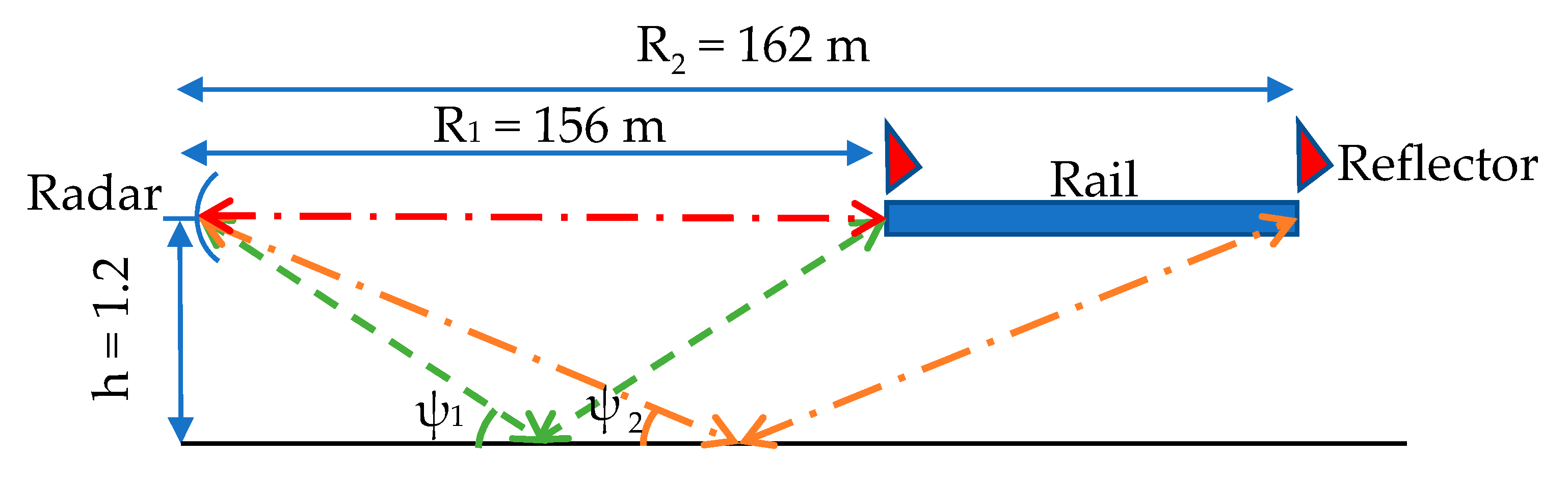
To assess whether the excess damping of the amplitude of the towed reflector was caused by multipath interference, the geometry of the measurement setup was analyzed. During the measurements, the ground was covered by windswept compact snow, which provided a smooth reflecting surface. The difference between the direct path and the indirect path of the backscatter varies with the grazing angle
. In the measurements, the change in grazing angle comes from the towing of the reflector as illustrated in
Figure 7.
The geometrical change in range and angle, when towing the reflector, will produce an alternating constructive and destructive pattern according to Equation (13). This pattern is proportional to the wavelength and is inversely proportional to the height of the radar above the ground. In this measurement setup, the first four maxima will occur for a grazing angle of ψ = 0.63°, 1.89°, 3.15°, and 4.41° likewise the four first minima will occur at ψ = 0°, 1.26°, 2.52°, and 3.78°.
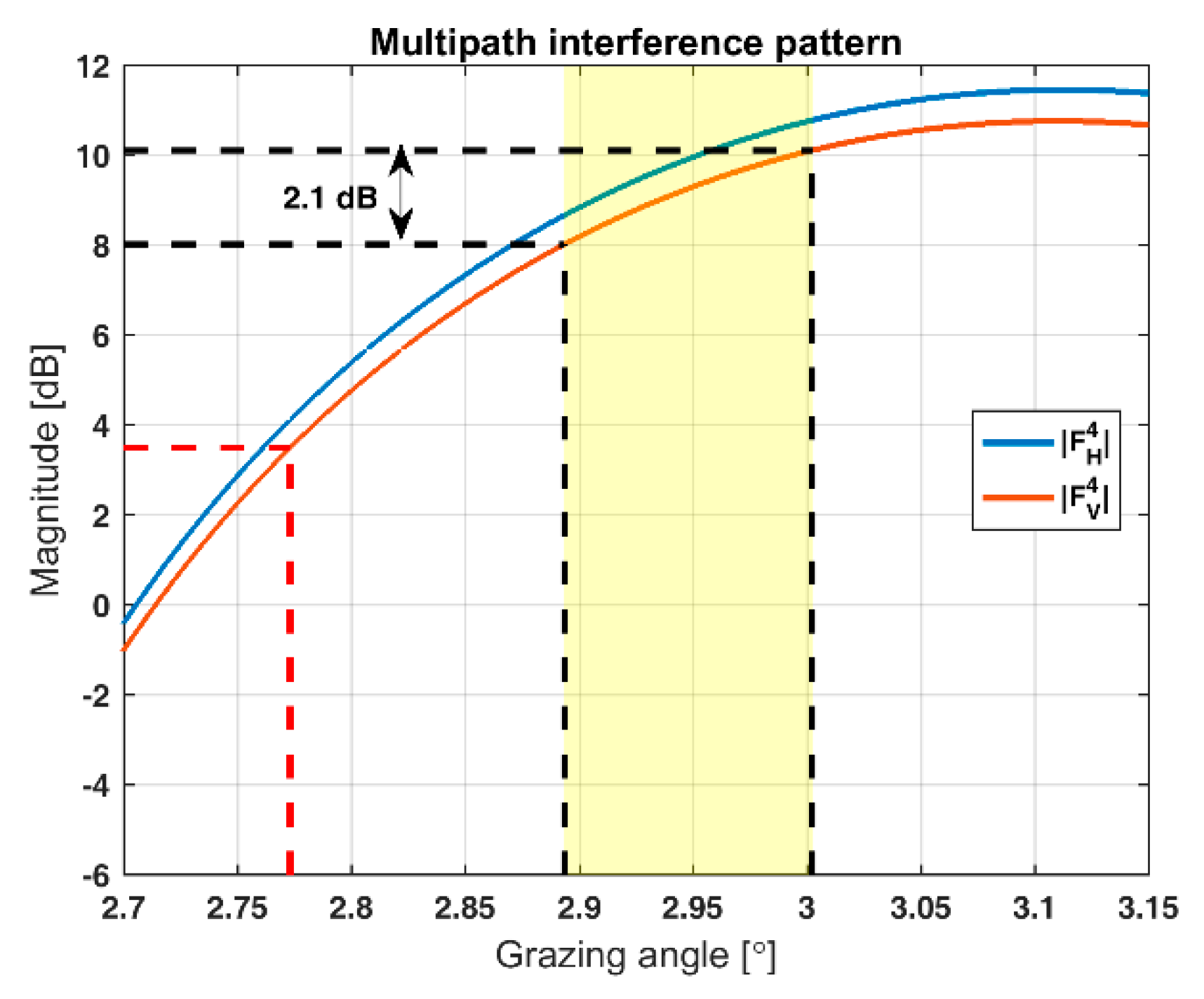
Figure 8 shows the variation in amplitude as a function of the grazing angle relevant for the measurement geometry.
Figure 8 shows that a 2.1 dB attenuation of the backscattered energy from the towed reflector due to the change in measurement geometry. By adding the multipath interference loss to the FSPL of 0.3 dB, the total loss is 2.4 dB, which correlates well with the measured 2.7 dB attenuation of the towed reflector. Based on this analysis it is believed that multipath interference is the main cause of the damping of the reflected energy from the towed reflector.
4.3. Constructive and Destructive Interference between Reflectors in the Measurement Scene
The amplitude oscillations in the backscatter from the stationary reflector in
Figure 6 are believed to be caused by inter-reflector interference. The distance to the stationary reflector is constant, hence the frequency of its demodulated signal is constant. The distance to the towed reflector changes proportionally with the tow-speed and the demodulated signal will produce a time-varying increasing frequency. To verify the inter-reflector interference, a laboratory experiment was undertaken, and the measurements are presented in
Figure 9.
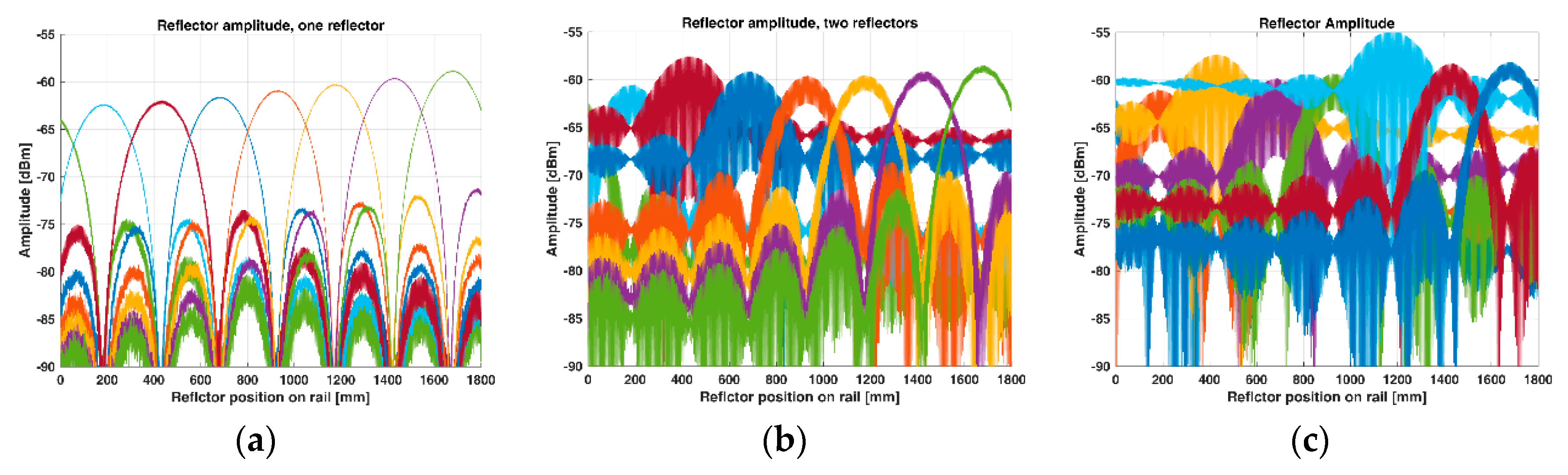
Figure 9a shows little variation in amplitude of the backscatter from the towed reflector apart from the 3 dB variation which is a function of the reflector’s position within the range cell and the FSPL attenuation of approximately 2 dB. When a second and third reflector are introduced, as shown in
Figure 9b,c, there is a noticeable increase in the amplitude variation of the moved reflector. The amplitude decreases with the distance to the stationary reflector, and the peak occurs when they are in the same range cell. In
Figure 9b, the stationary reflector is located 0.4 times the distance from the center of the range cell, while in
Figure 9c it is located at the center. Based on this experiment, the amplitude variations observed in
Figure 6a are believed to be caused by inter-reflector interference.
4.4. Comparison of Measured and Numerically Calculated Inerferometric and Differentail Interferometric Motion
During the outdoor experiment, the actual position of the towed reflector was not recorded. To find the extent of the range cells, the point where the maximum amplitude has fallen by
or the 3 dB-point is used. However, since there are several environmental effects affecting the amplitude it was simply recorded when the maximum returned energy was shifted from one range cell to the next. The distance between the two amplitude intersections is the range cell resolution, as indicated by the vertical red lines in
Figure 6. The measured motion from the outdoor measurement is shown in
Figure 10a and the computed motion is show in
Figure 10b.
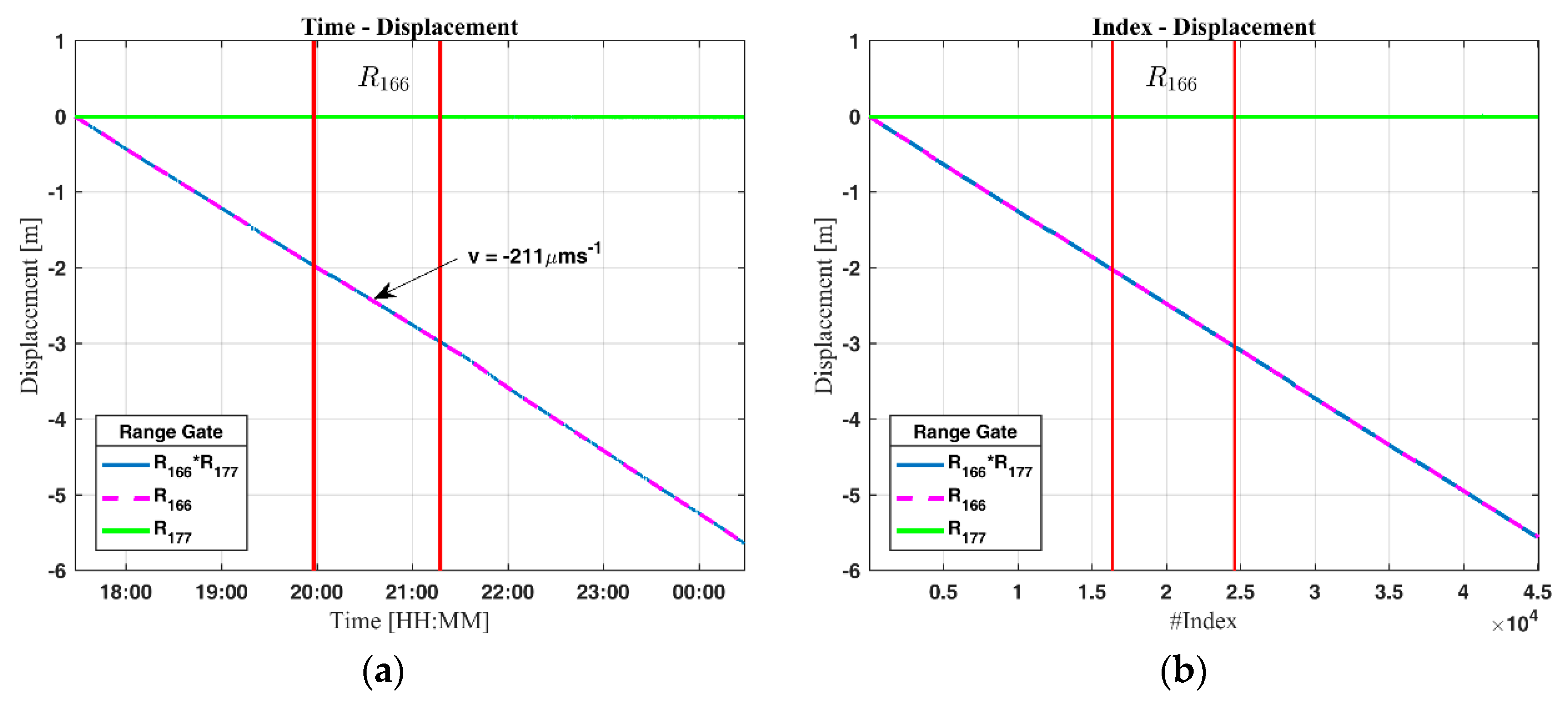
Figure 10a shows the measured displacement of the towed reflector, and
Figure 10b shows the computed displacement. As expected, the reference reflector remains stationary while the towed reflector shows a displacement of approximately 5.61 m. The calculated velocity of the motion is −211 µm/s, which corresponds well with the theoretical speed of the winch, which is 220 µm/s. The measured displacement from the second laboratory experiment is presented for two different step increments in
Figure 11.
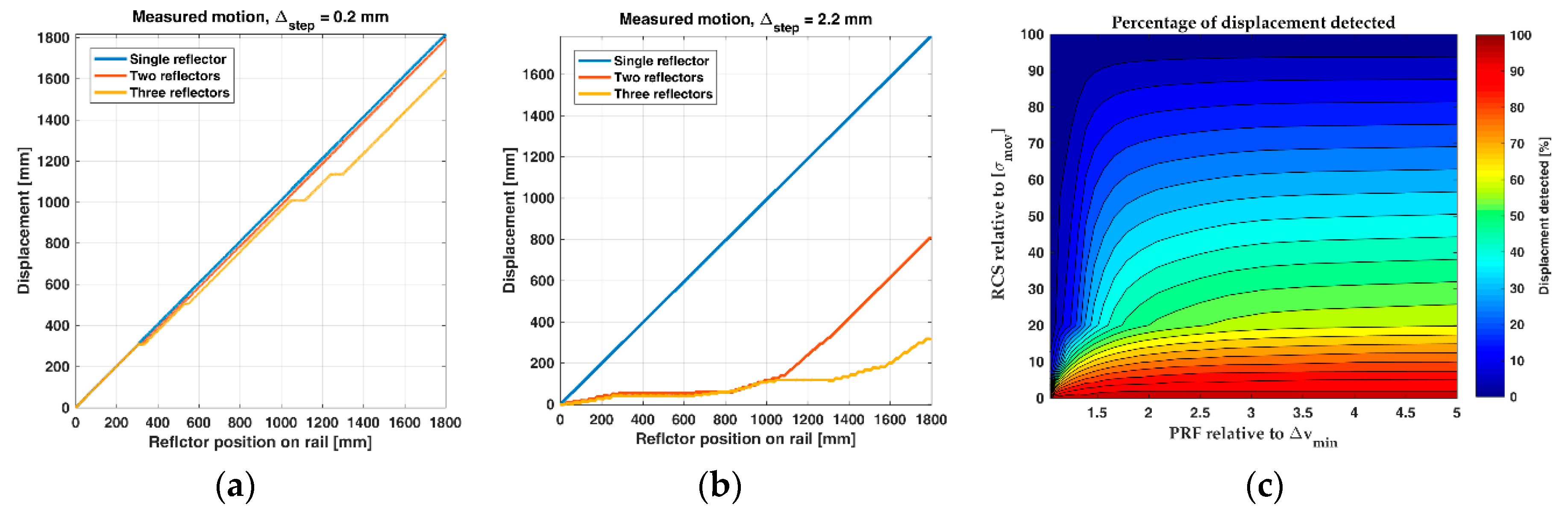
Figure 11 shows the measured motion from the three laboratory experiments for two different sampling intervals. In both experiments, the reflector was moved 1800 mm. The blue line shows the single reflector displacement, and the red and yellow lines show the displacement when one and two stationary reflectors are added to the measurement scene. The data is from the same measurement, the only difference is the step-size between the measurements which is equal to a radar setup with three different PRFs. Both measurements fulfill the maximum unambiguous velocity (
) as can be seen from the single-reflector displacement (the blue line in
Figure 11a,b). When stationary reflectors are introduced, the displacement is partly masked.
Figure 11c shows the result of a simulation where a reflector is moved past a stationary reflector. The RCS of the stationary reflector is varied from 0 to 100 times the RCS of the moved reflector, and the PRF is varied from λ/4 to λ/20. The total motion is collected in 20 range cells from the stationary reflector, and the displacement is presented as a percent of the total motion.
In
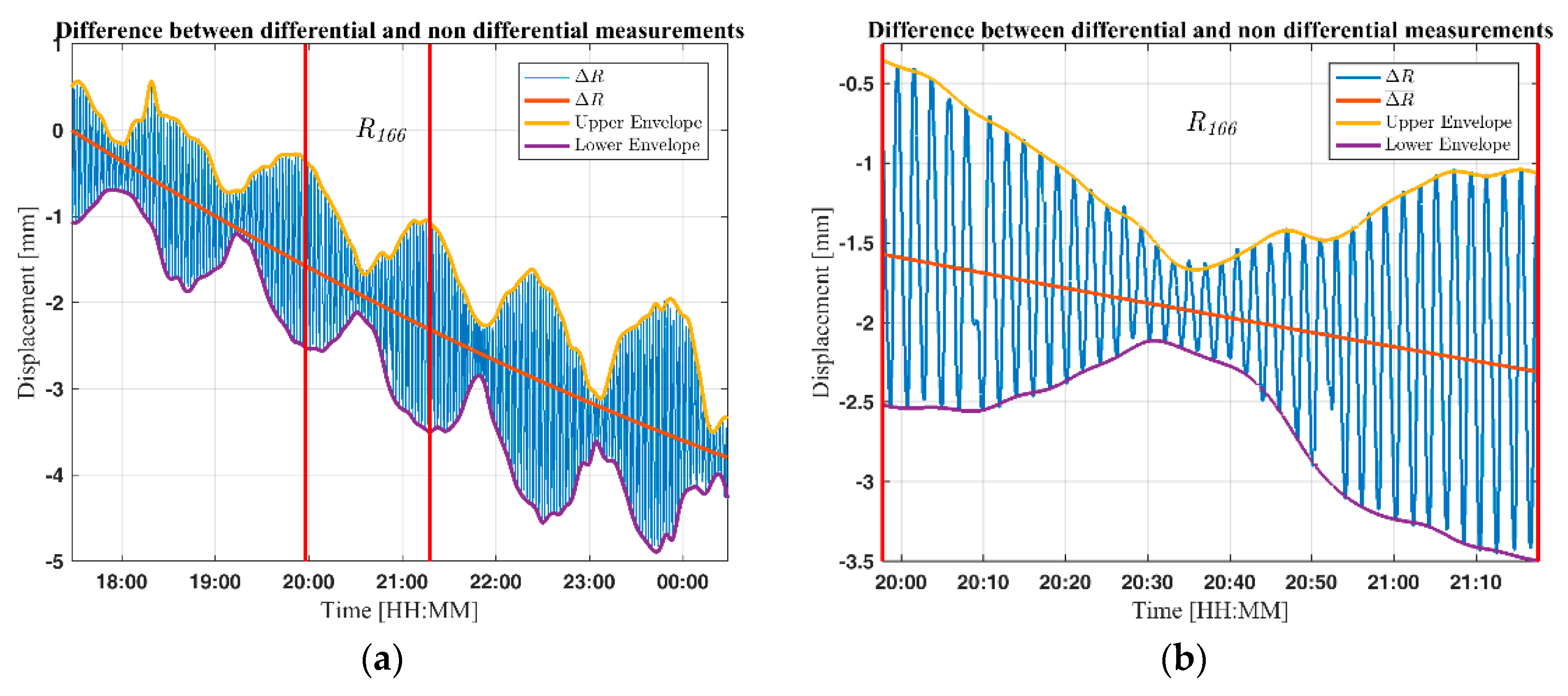
Figure 12, the determined displacements from the outdoor experiment based on interferometric and differential interferometric measurements are compared.
Figure 12a highlights the difference between the interferometric and differential interferometric measured displacement. Most noticeable are the oscillations in the differential measurements, which reach an amplitude of approximately ±1.5 mm, this oscillation is due to inter-reflector interference. The difference between the two methods is approximately 3.9 mm, which corresponds to 0.7‰ of the total motion.
Figure 12b highlights the oscillations in the differential displacement for range index 166. The number of wavelengths per range cell corresponds to the range resolution divided by the wavelength, see Equation (13), which in this setup is 38 wavelengths per range cell.
4.5. Geometric, Environmental and Hardware Influence on Interferometric and Differential Interferometric Measurements
In this section, we assess the deviations in the interferometric and differential interferometric displacements. We analyze the effect the environment, measurement geometry and radar hardware have on the measurement accuracy.
4.6. Radio Refractivity
To compensate for the variations in the radio refractivity, an empirical model based on temperature, humidity and pressure may be used ([
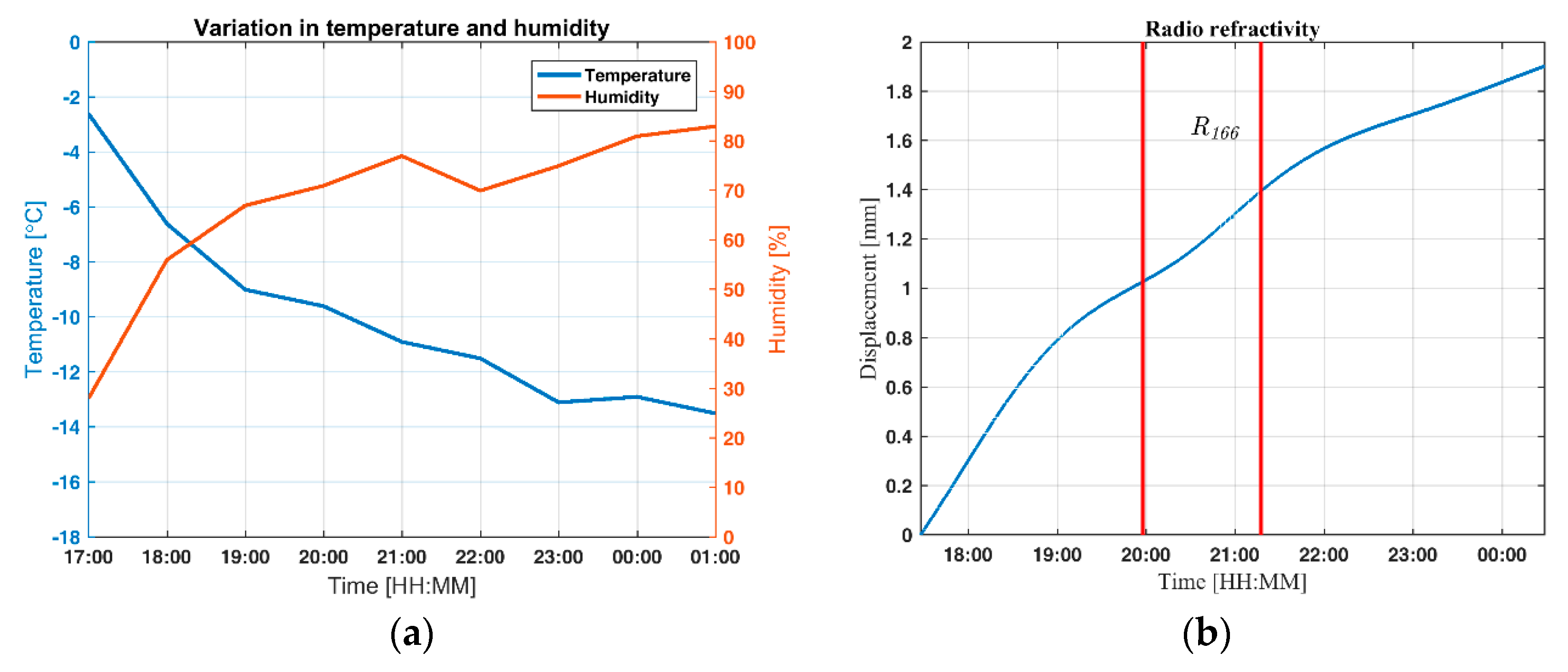
33]; p. 304). To compensate for atmospheric decorrelation, metrological data was downloaded from the Norwegian Metrological Institutes Station in Ås, located 2.7 km from the measurement site. During the measurements, the temperature dropped from −1.9 °C at 17:00 to −13.1 °C at 01:00 at the same time the relative air humidity increased from 26 to 81%, see
Figure 13a. The pressure was not recorded but the mean air pressure was 990 mbar. This gives a change in the refractivity index from n = 298 to n = 314 resulting in an apparent motion of approximately 1.9 mm, see
Figure 13b.
By adjusting the displacement for the estimated variation in refractivity the deviation is reduced by 1.9 mm. This is an improvement of nearly 50%, even when the metrological data is not acquired locally.
4.7. Multipath Interference
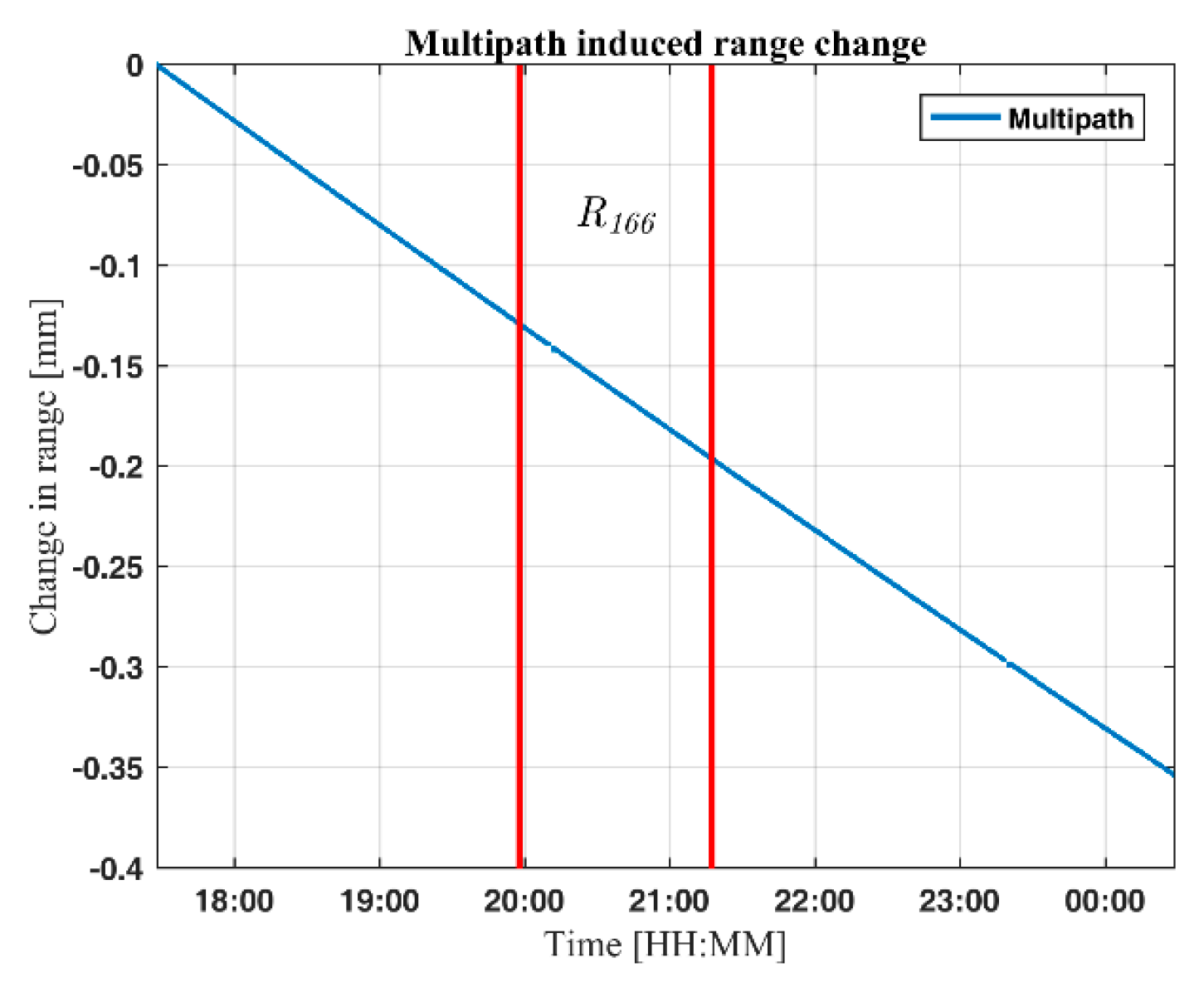
In
Section 4.2, multipath interference was found to affect the amplitude of the backscatter from the reflectors. Multipath interference will also affect the phase of the received signal as shown in
Figure 14.
The change in distance due to multipath interference during the measurement is estimated to be 0.35 mm.
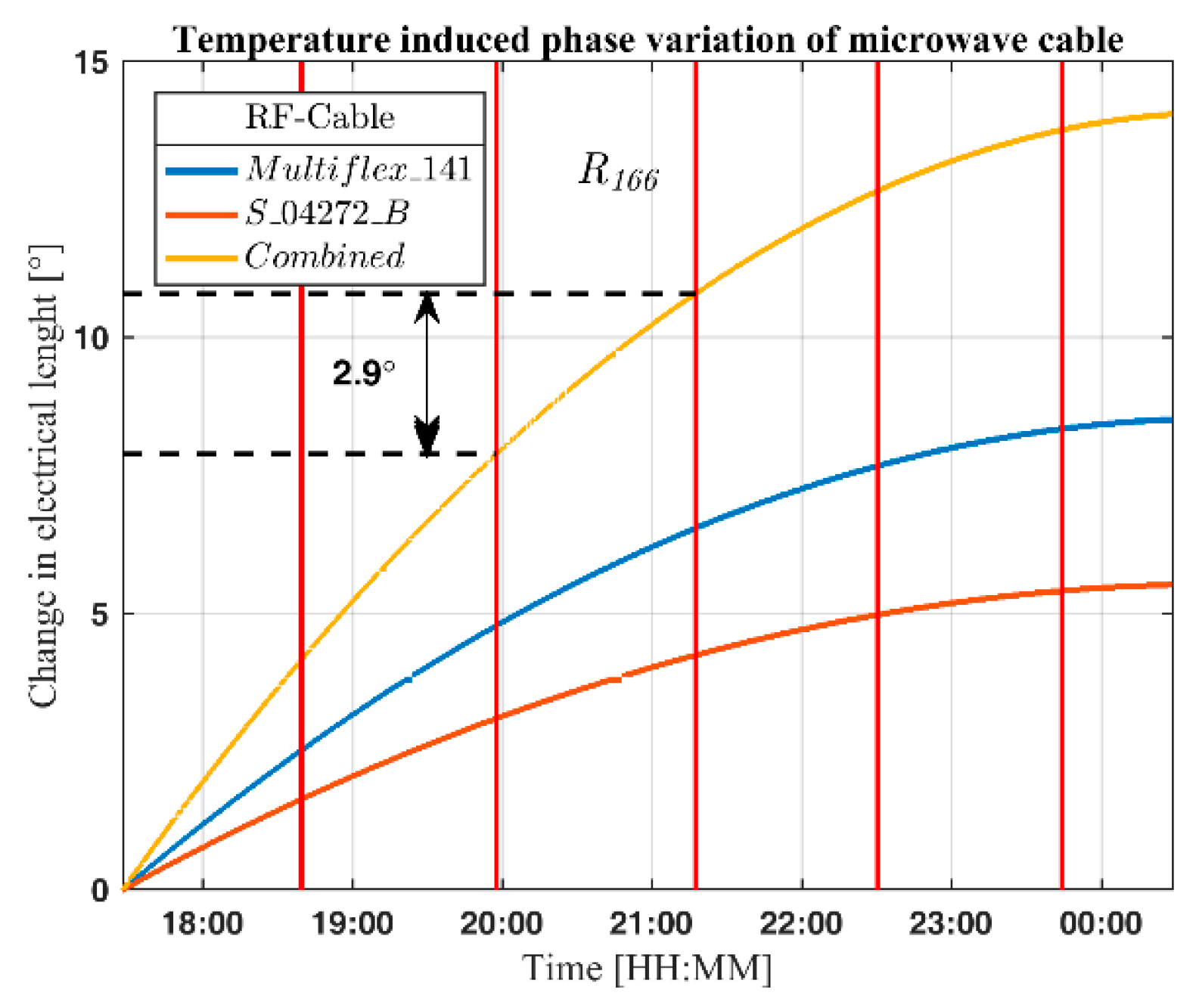
4.8. Electrical Length of the Microwave Cables and Velocity Factor
Varying temperature and/or any change in the path of the electromagnetic waves will affect the accuracy of high precision radar measurements. Two types of microwave cables were used, Huber & Suhner Multiflex_141 and S_04272_B. The total length of the cables was 10.5 m, 4.5 m of Multiflex_141 and 6 m of S_04272_B. The temperature phase variation used for the two cables is Multiflex_141 = 1500 ppm and S_04272_B = 400 ppm [
34]. Estimated change in electrical length of the cables used during the measurement based on the same temperature data as used in
Section 4.6 is shown in
Figure 15.
Applying the estimated change in electrical length of the microwave cable further reduces the difference by approximately 2 mm.
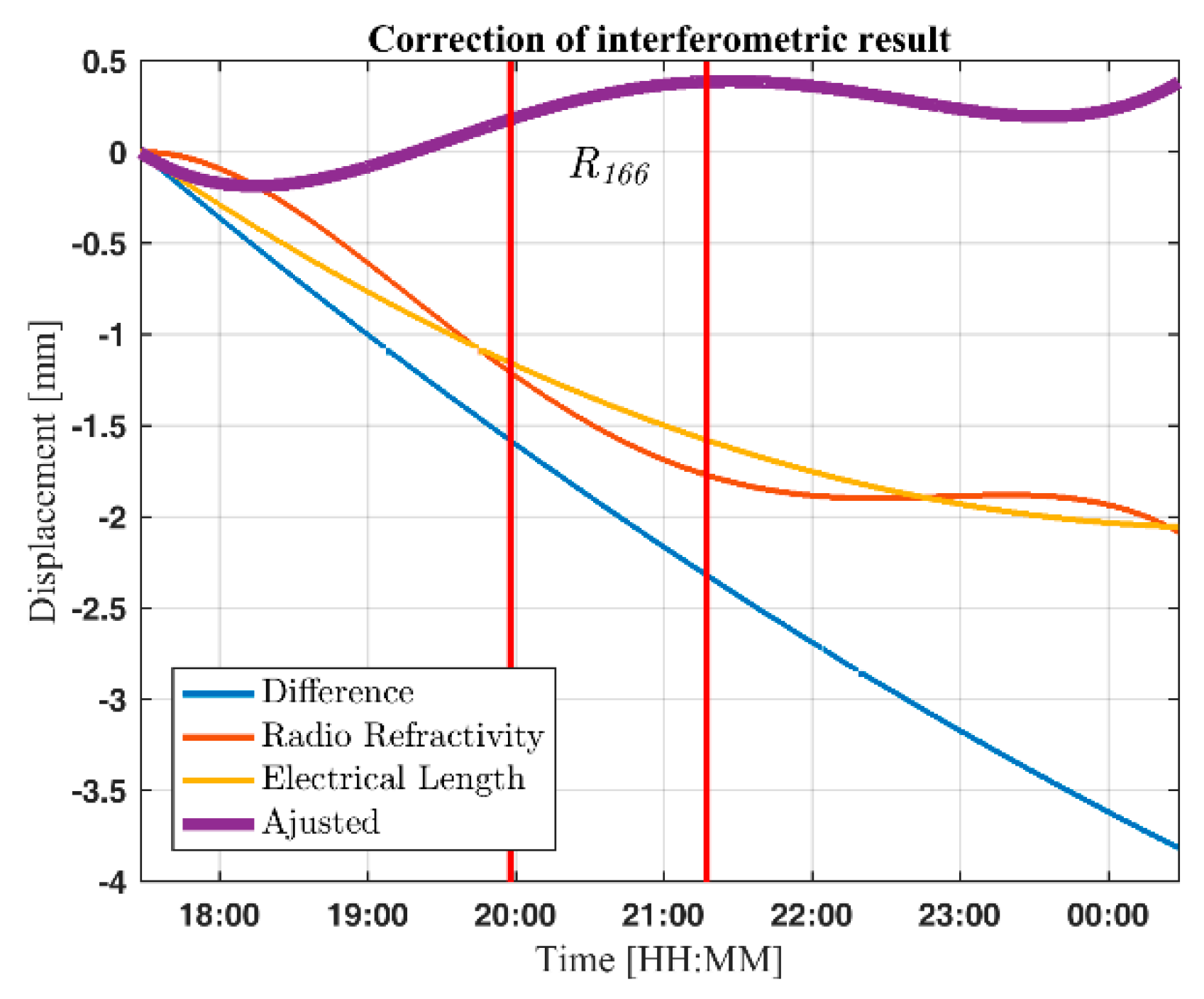
4.9. Result of Compensation
Figure 16 sums up the combined effect of radio refractivity and change in electrical length of the microwave cable. To avoid the effect of inter-reflector interference, the moving mean of the differential displacement is used for comparison.
In
Figure 16 the blue line is the difference between the mean differential displacement and the interferometric displacement. The red line is the estimated displacement due to variation in the radio refractivity, the yellow line is the variation in distance due to the change in electrical length of the microwave cables, and the purple line shows the resulting interferometric displacement when the corrections are applied.
4.10. Summary of the Interferometric Experiment
Table 3 summarizes geometrical, environmental and electrical effects on the measurement accuracy.
Note that the change in electrical length of the microwave cable only applies to the interferometric computation while shadowing only applies to the differential interferometry. The radio refractivity applies to all computations but for the differential interferometry only by a fraction varying from 13/157 to 7/162. Multipath interference and the measurement geometry applies to both methods. The average range cell length measured is 1004.69 mm for interferometry and 1001.13 mm for differential interferometry.
5. Discussion
The experiment shows that the accuracy of both interferometry and differential interferometry depends on the measurement geometry, variations in radio refractivity, multipath interference, interference between scatterers, and the radar hardware. In this chapter, the influence of these effects are discussed. The discussion is divided into three sections: Amplitude, phase and radar hardware. Some general advice is then given on how to minimize the impact of these effects in an operational system.
5.1. Amplitude
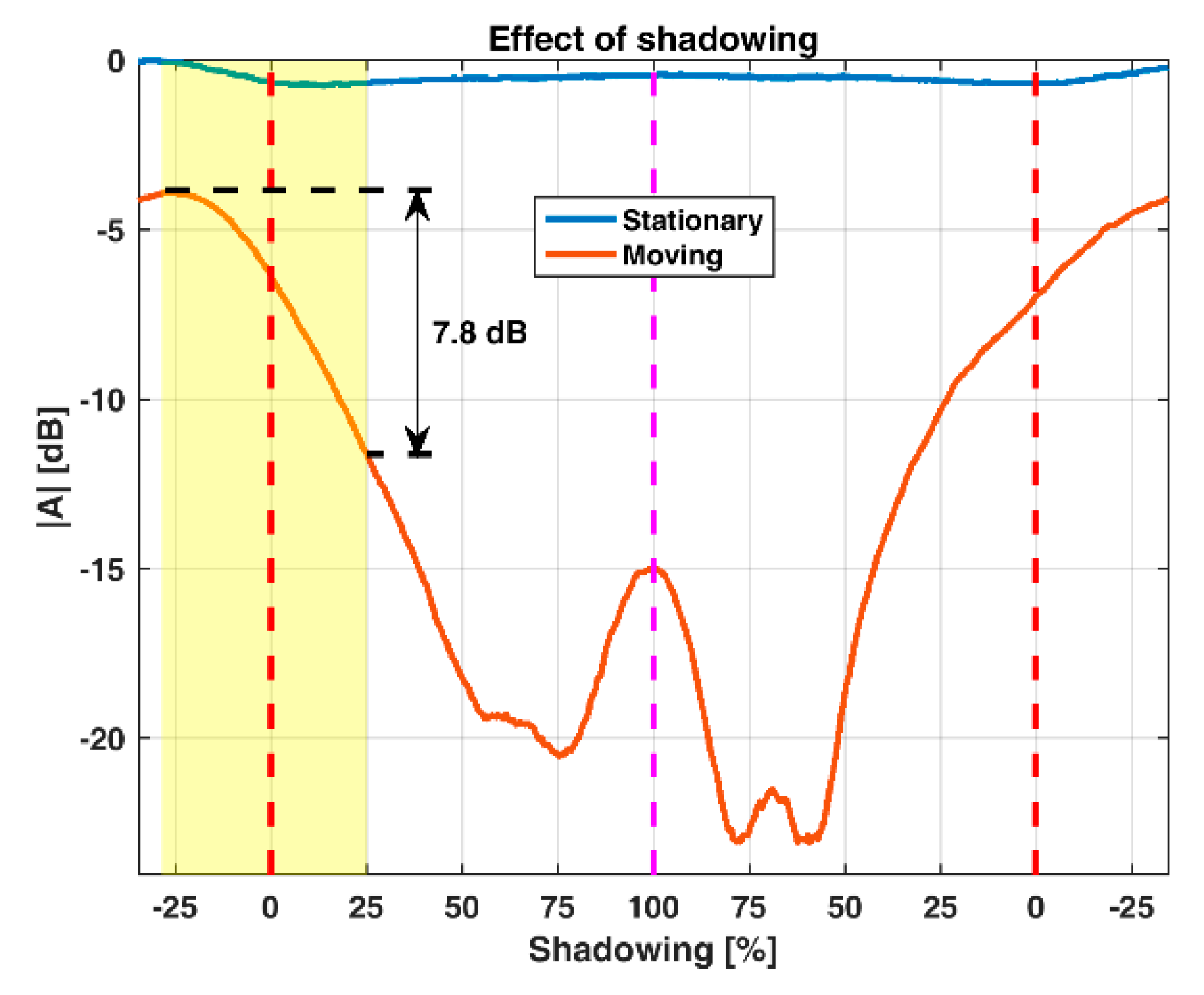
The amplitude data is often the first information to assess when analyzing radar measurements. Any deviations in backscattered energy from reflectors compared to what is expected from theoretical values are easily detectable. Two effects were observed, damping and oscillations. The theoretical RCS of the towed reflector is 20.4 dBsm and the theoretical RCS of the stationary reflector is 13.1 dBsm. This gives a difference in backscatter between the two reflectors of 7.3 dB, while the measured difference was approximately 21.7 dB when the towed reflector was at the far end of the rail. Three major effects may explain this difference: Multipath interference, shadowing (for details see
Appendix A) and propagation loss. First, the multipath interference-induced gain of the towed reflector, which is estimated to 8 dB when the towed reflector is at the end of the rail, and the multipath interference-induced gain of the stationary reflector, which is estimated to be 3.5 dB, see
Figure 8. This gives a 4.5 dB multipath interference gain. Second, the contribution from shadowing which is estimated to be 7.8 dB (see
Appendix A). Third, the FSPL that is 0.7 dB. The combined total of these three effects are 13 dB. Subtracting the combined contribution from the measured value gives a difference of 8.9 dB, which agrees with the theoretical difference of 7.3 dB. The deviation of 1.6 dB might come from using uncalibrated corner reflectors, by misalignment of one or both reflectors, and inaccurate measuring of reflector and radar antenna height. The results show that the combined effect of measurement geometry, multipath interference and shadowing may give large time variations in the backscattered energy from scatterers in the measurement scene. In a measurement scene with many moving scatterers, tracking of natural scatterers can be challenging as they may disappear and reappear depending on geometry, shadowing and motion.
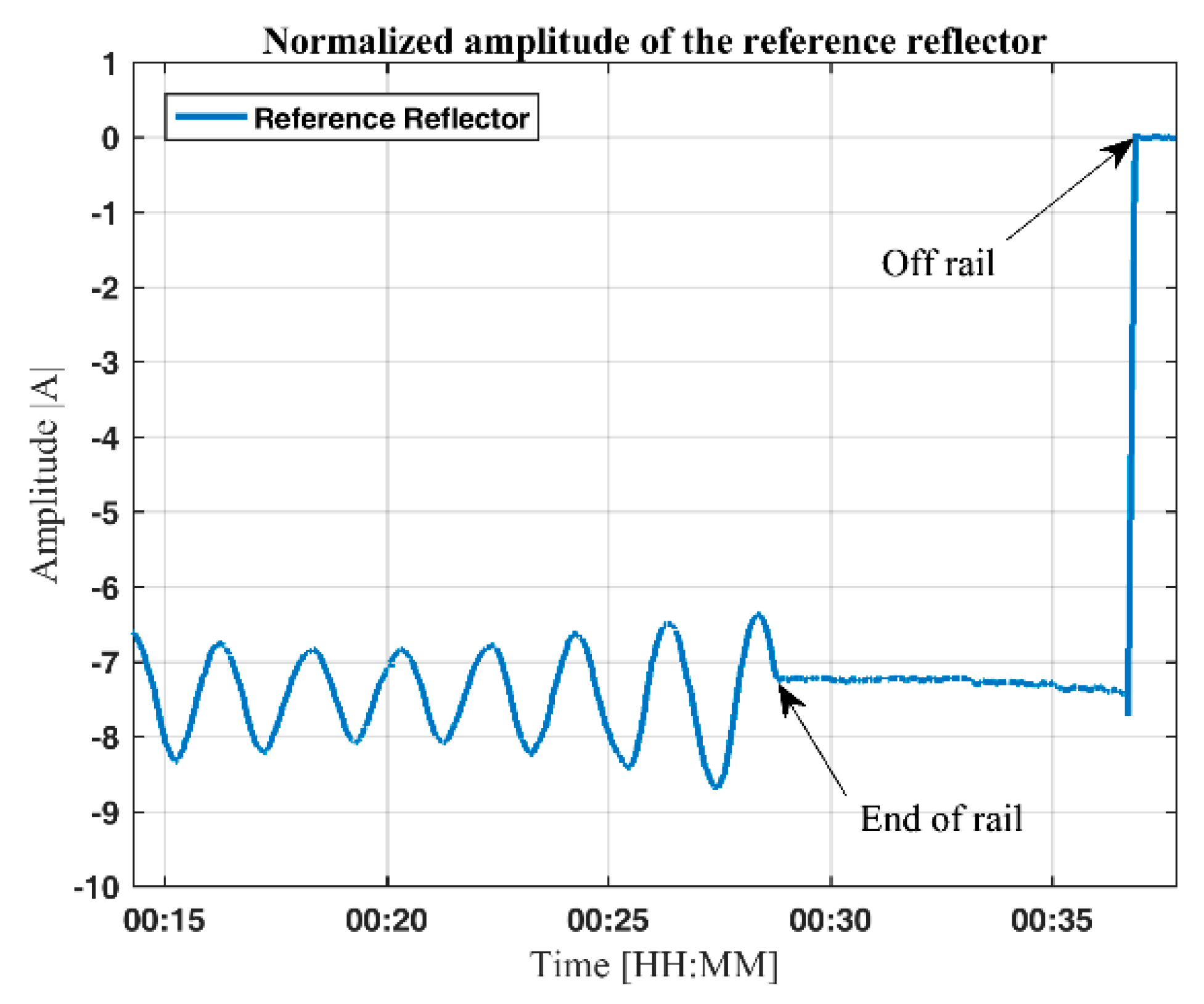
The shadowing of the stationary reflector was found to be the main cause of the damping of the reflected energy. This is supported both by observing the increase in reflected energy backscattered from the reference reflector as the towed reflector was towed beyond the end of the rail, see
Figure A1, and by the reflector shadowing experiment in the laboratory, see
Figure A3.
The oscillations observed in the amplitude of the backscatter from the reference reflector are caused by inter-reflector interference between the two reflectors in the measurement scene. The oscillation increase as the towed reflector gets closer to the stationary reflector, see
Figure 9a. The interference is visible in both
Figure 9a,b, however, the amplitude of the oscillations is higher for the stationary reflector than for the towed reflector. This is due to the mutual size difference, i.e., the largest reflector has a greater influence on the small reflector than the small reflector on the large reflector. Maximum constructive interference between two reflectors occurs when the mutual distance, ΔR, is equal to integer multiples of the wavelength of the transmitted signal and maximum destructive interference that occurs when the mutual distance is equal to integer multiples of half the wavelength. The amplitude of the interference will follow a sine cardinal pattern due to the Fourier transform when going from the time domain to frequency domain. The maximum and minimum amplitude will occur when the two reflectors are in the same range cell, see
Figure 9. This shows that all scatterers within the measurement scene may affect each other and the magnitude of the interference depends on the reflected energy of the scatterers according to the exponent in Equation (13).
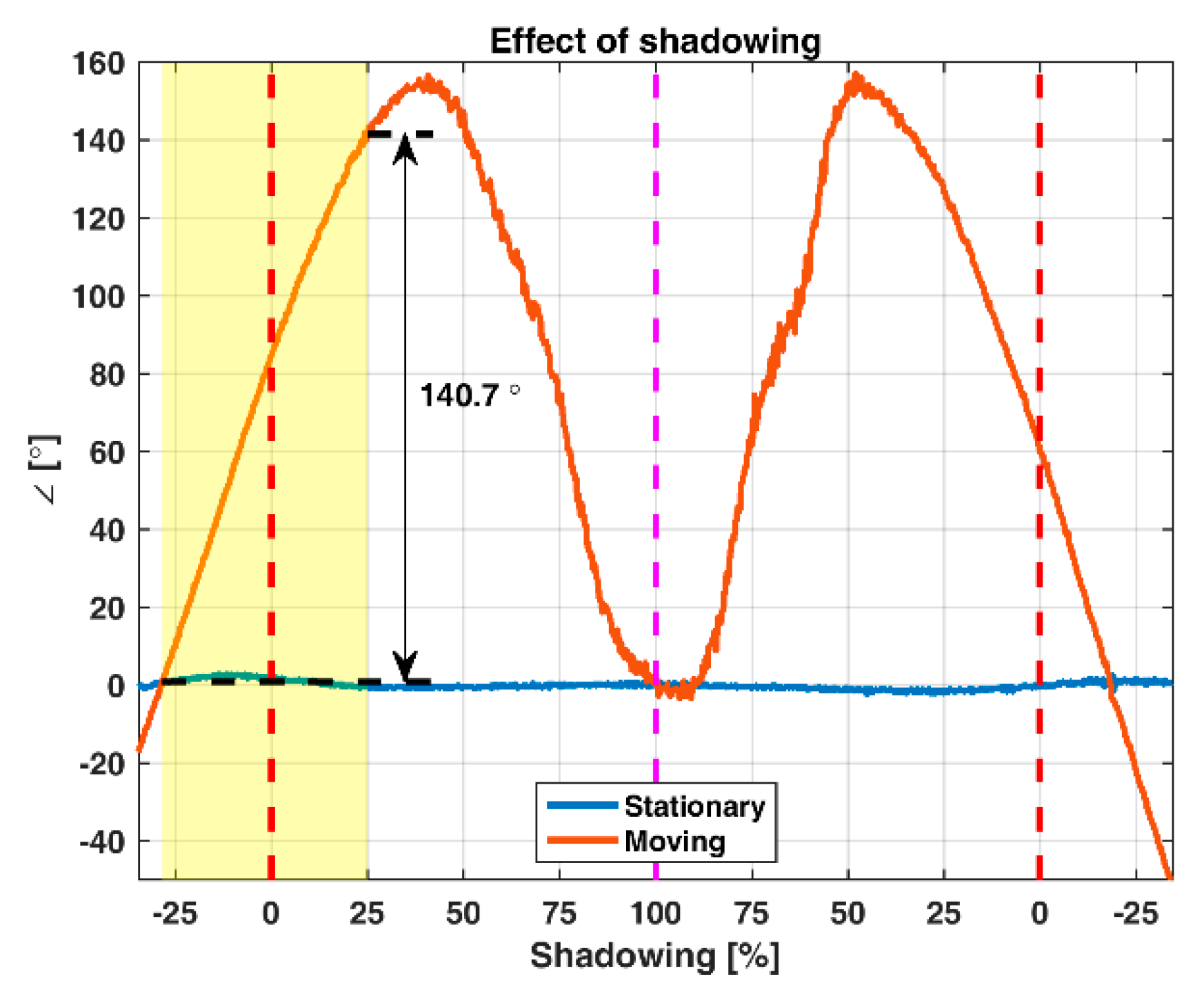
5.2. Phase
As discussed in the previous section, the effect of radio refractivity, multipath interference, inter-reflector interference, and shadowing affects the amplitude. In addition, it affects the phase of the reflections, see
Figure 13,
Figure 14 and
Figure 15.
The variation in radio refractivity during the measurements was estimated based on meteorological data and was found to contribute to almost 50% of the deviation between the interferometric and the differential interferometric displacement. The temporal sampling rate of the meteorological data was 1 h. This gives a relatively large uncertainty in the computations. Another factor adding to the uncertainty is the distance between the radar site and the meteorological station that is 2.7 km. However, we show that the corrections of radio refractivity improve the results. The influence of the variation in radio refractivity increases with distance; hence, in real-life setups the contribution may be substantially higher.
The effect of multipath interference depends on the geometry of the measurement setup and since the height of the antennas and reflectors were recorded manually, a fair amount of tolerance in the result is to be expected. The change of 0.35 mm for the 6 m tow of the reflector in this setup might seem to be insignificant, but given another setup geometry, the effect might be significantly higher. The effect of multipath interference should therefore always be considered as a source of measurement error in high-precision measurements. The estimation of multipath interference is a challenging task in real-life measurements due to temporal variation in the reflection coefficient as the backscatter depends on surface roughness, moisture and texture [
35].
The effect of shadowing was, based on the laboratory measurements, found to contribute to 14.2 mm of the measured displacement of the differential result. The laboratory experiment was based on the measured geometry of the field experiment and some uncertainty is expected in the result. The effect of shadowing was an unintended result of an unfortunate measurement setup and is only added to explain the measured deviations. In some remote sensing scenarios, shadowing might be unavoidable, leading to low coherence and consequently, could be detrimental for the monitoring [
24].
The laboratory experiment shows that inter-reflector interference can mask the motion. To avoid this, the backscatter of the moving object should be higher than the backscatter of the stationary object, see
Figure 11c. This follows directly from Equation (13), which states that the energy backscatter of a range cell is the coherent sum of all the scatterers within the range cell. In GB-SAR, this applies both in the down and cross range [
24] (
Figure 7b). This result indicates that it is beneficial to introduce reflectors to the measurement scene to follow the motion of point objects. The introduction of a reflector is artificial, but it can be viewed without loss of generality as natural stationary clutter or infrastructure like rockfall catch fences in a real-life measurement scene either in the mainlobe or in the sidelobe. This indicated that in a measurement scene without a distinct scatterer, care should be exercised when analyzing the displacement.
The variation in radio refractivity applies to both interferometry and differential interferometry, but for differential interferometry only by a fraction equal to the length between the reflectors. The multipath interference applies to both interferometry and differential interferometry.
5.3. Radar Hardware
A part of the difference between the interferometric and differential interferometric results may be explained by variations in the radar hardware. If the variations due to the radar hardware can be measured or predicted, the measurements can be corrected. The main source affecting the modulation bandwidth is the accuracy of the reference clock of the signal generator. Inside the radar used during this experiment there are two oscillators, one for the local oscillator, one for the sweep generator (DDS). Fluctuations in any of these oscillators will affect the measurements. The total uncertainty of the DDS reference oscillator is used in the GB-InRAR ±23 ppm, disregarding any aging effects. This may lead to variations in the transmitted bandwidth. Due to programming technicalities, the effective bandwidth from the DDS multiplier chain was 149,912,000 MHz. This will give a maximum decrease in range cell length by approximately 0.6 mm, giving a total of 3.5 mm for the 6 m tow of the reflector further reducing the deviation between the measured and computed movement. This effect is independent of distance and applies to all range cells.
The temperature-induced change in electrical length of the microwave cables contributed to a variation in range, which is visible in the measurements. The total effect of this change was approximately 2 mm. This estimate is based on meteorological data from a station 2.7 km away from the radar, leading to uncertainties in the calculations. The estimated change in electrical length of the microwave cables are based on coarse values from data sheets; a fair amount of tolerance in the calculations are expected. The temperature–phase relationship of a microwave cable is complex, and it is usually measured and not numerically modelled. To minimize error, the microwave cables used should be temperature cycled to get the correct temperature–phase variation.
5.4. Measured Displacement
The measured difference in displacement between interferometry and the mean differential motion is approximately 3.9 mm, see
Figure 12a. The mean displacement was used for the differential interferometric displacement to avoid the inter-reflector interference to influence the interferometric result. The average range cell size was estimated to be 1007.3 mm for interferometry and 1006.8 mm for differential interferometry. After adjusting the interferometric displacement for measurement geometry, variation in radio refractivity, multipath interference, change in electric length of the microwave cable, and actual bandwidth, the average range-cell size was reduced to 1004.1 mm. The differential displacement was adjusted for measurement geometry, multipath interference, shadowing, and actual bandwidth, resulting in an average range cell size of 1000.5 mm. The major part of the difference between the two methods are believed to come from inaccuracy in the data used to calculate the variation in radio refractivity and change in electric length of the microwave cable as the temperature and humidity data was not recorded locally. There is some measurement uncertainty with the geometry of the measurement setup, but this will affect both methods equally except for the shadowing, which only applies to the differential method.
The differential displacement is closer to the theoretical range cell length of 1 m, but this is the mean motion. The inter-reflector interference displayed in
Figure 12a shows a range variation of approximately ±1.5 mm, which is a product of the measurement setup and not a physical motion. This effect will diminish by increasing the distance between the reflectors, but care should be exercised when placing a reference reflector.
5.5. Minimizing the Influence of Geometic, Environmental, and Radar Hardware Effects in Operational Monitoring
In this section, we summarize the findings and give general advice on how to avoid or reduce the impact of the effects presented in this chapter.
The impact of radio refractivity is frequency dependent and it is stated in Reference [
14] that the longest radar waves possible should be used to minimize the effect of atmospheric variations. Using a lower frequency has the inherent consequence of a larger antenna to achieve the same beamwidth as the beamwidth is approximately given as λ/L, where L is the physical size of the antenna ([
22]; p. 6.8). Applying meteorological data collected locally has been shown in a number of studies to be an efficient way to compensate for atmospheric decorrelation [
8,
13,
17,
18,
19,
20].
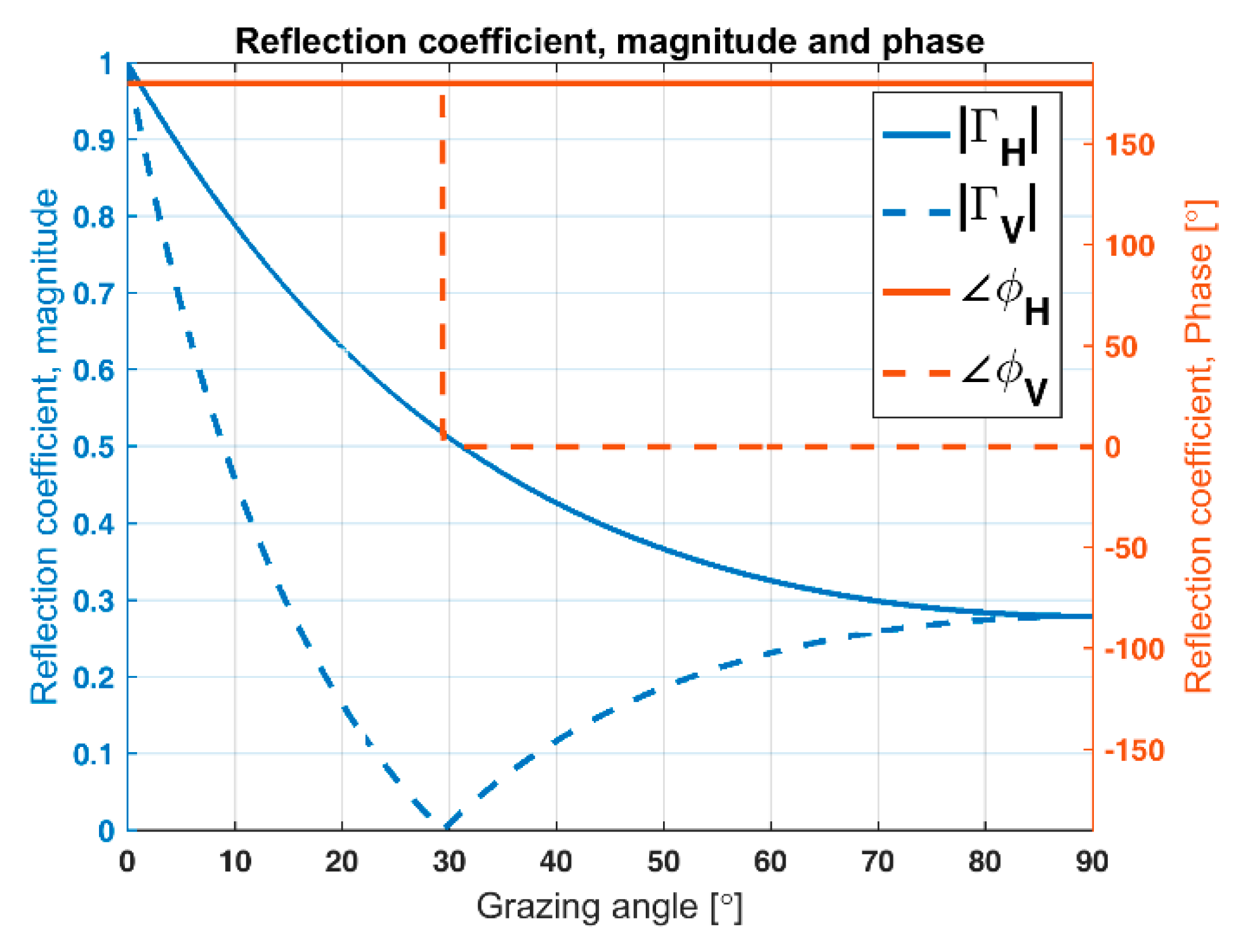
To minimize the effect of multipath interference, the vertical part of the antenna lobe should not illuminate the ground. This can be controlled by adjusting the elevation angle of the antenna and by using an antenna with a narrow elevation beam. If the installation geometry prohibits this, vertical polarization is preferable as it generates less multipath interference than horizontal polarization. This can be seen from
Figure 1 where the magnitude of the reflection coefficient for VV-polarization is significantly lower than for HH-polarization. Hence, multipath interference is less at VV-polarization than at HH-polarization. This was also one of the main findings in Reference [
21]. Another way of reducing multipath interference is by adding shielding of the antennas, preventing the radar waves from illuminating the reflective surface as presented in Reference [
21]. They state in their experiment that this greatly reduced the problem, but it did not eliminate the interference. They also recommend installing the radar at an elevated area if possible. If none of the above measures is possible, this study has shown that the effect of multipath interference can be reduced by applying corrections based on analysis of the measurement geometry and the reflective surface.
Unless the backscatter from the object or surface in motion is stronger than the backscatter from the surroundings, inter-reflector interference can mask the motion as shown in
Figure 11. One way to avoid this effect is by introducing an artificial reflector. The laboratory experiment also showed that a high PRF partly helps to resolve the problem. Both the outdoor and laboratory experiments showed that the interference between strong reflections where one object is in motion results in oscillations in the amplitude of the backscatter. This indicated that care should be taken when measuring objects in strong clutter, so that the motion of the monitored object or area is not suppressed by backscatter from stationary clutter. The general solution is to use a large antenna with a narrow beam to reduce the illuminated area and reduce the range cell size i.e., use a wideband radar.
The reference oscillator should be of high quality and preferably both temperature and voltage compensated.
The temperature-induced phase shift in the microwave cables may be reduced by keeping the cables as short as possible and by using high performance cables with low a temperature–phase coefficient. In Reference [
23] it is suggested to use active temperature stabilization of the cables to minimize the phase–temperature variation. They also recommend using PTFE-free cables for operating temperatures below 22 °C. One solution to monitor the major variations in phase due to radar hardware is to measure the phase of the antenna cross-talk and to adjust the measurements accordingly.
6. Conclusions
A GB-InRAR system is used for experimental interferometric and differential interferometric measurement experiments in the field and laboratory with a moving trihedral corner reflector. A theoretical model is developed to asses measurement uncertainties for the geometry of the measurement setup, atmospheric effects i.e., radio refractivity and the effect of ground reflections i.e., multipath interference, radar target interference and the radar hardware.
It is shown that major deviations between interferometric and differential interferometric calculated displacement can be explained by variations in environmental and geometrical effects. The accuracy of interferometry can be comparable to the differential accuracy when adjusted for environmental variations. For the analyzed experiment, the major contributing environmental effects are radio refractivity and temperature-induced change in electrical length of the microwave cables. The major geometrical effects are multipath interference and inter-reflector interference.
The experiments show inter-reflector interference, which for the differential method resulted in oscillations in measured displacement. The amplitude of these oscillations increased inversely with distance peaking when they were in the same range cell. It is shown that the motion can be masked when the backscatter from the stationary object is equal or higher than the backscatter from the moving object. It was also shown that the effect of inter-reflector interference could be reduced by using a high PRF.
The accuracy of both methods can be improved by adjusting for offsets in the radar hardware. The temperature-induced change in the electrical length of the microwave cables can be significant, and it should be considered separately to avoid mixing the effect with the radio refractivity, which is also influenced by variation in temperature.
The results derived from the experiment verify that the GB-InRAR can detect and monitor small displacements. The analysis suggests that differential interferometry is close to unaffected by radio refractivity but vulnerable to inter-reflector interference.
The compensated average interferometric displacement is within 4‰ of the theoretical range cell size while the compensated average differential displacement is within 1‰ of the theoretical range cell size. Validation of the experiments is based on general radar theory, and the calculations and results should be valid for other radar systems.