Model-Based Optimization of Spectral Sampling for the Retrieval of Crop Variables with the PROSAIL Model
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Collection and Preparation
2.2. Spectral Feature Selection
2.3. Constrained LUT Inversion
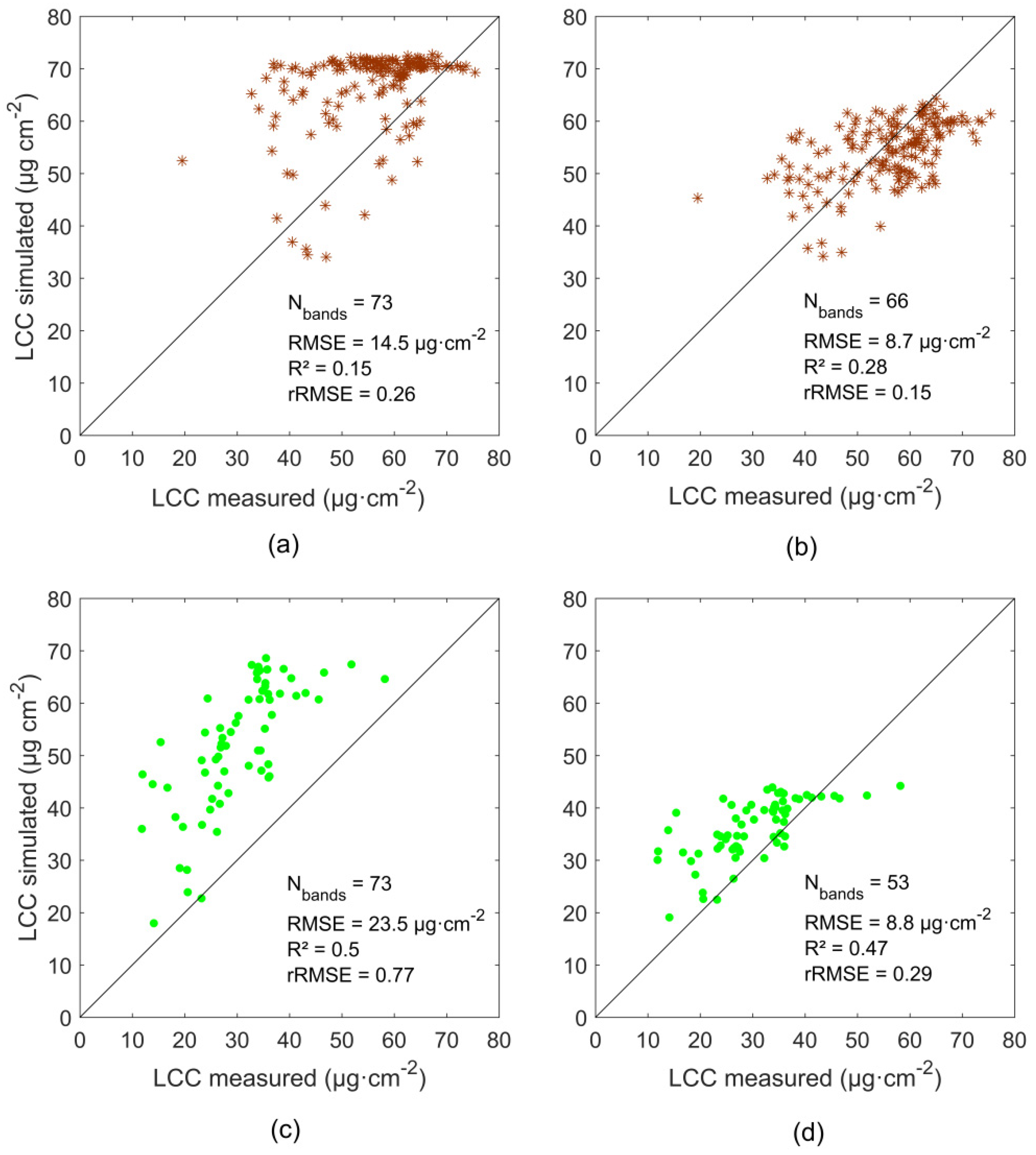
3. Results and Discussion
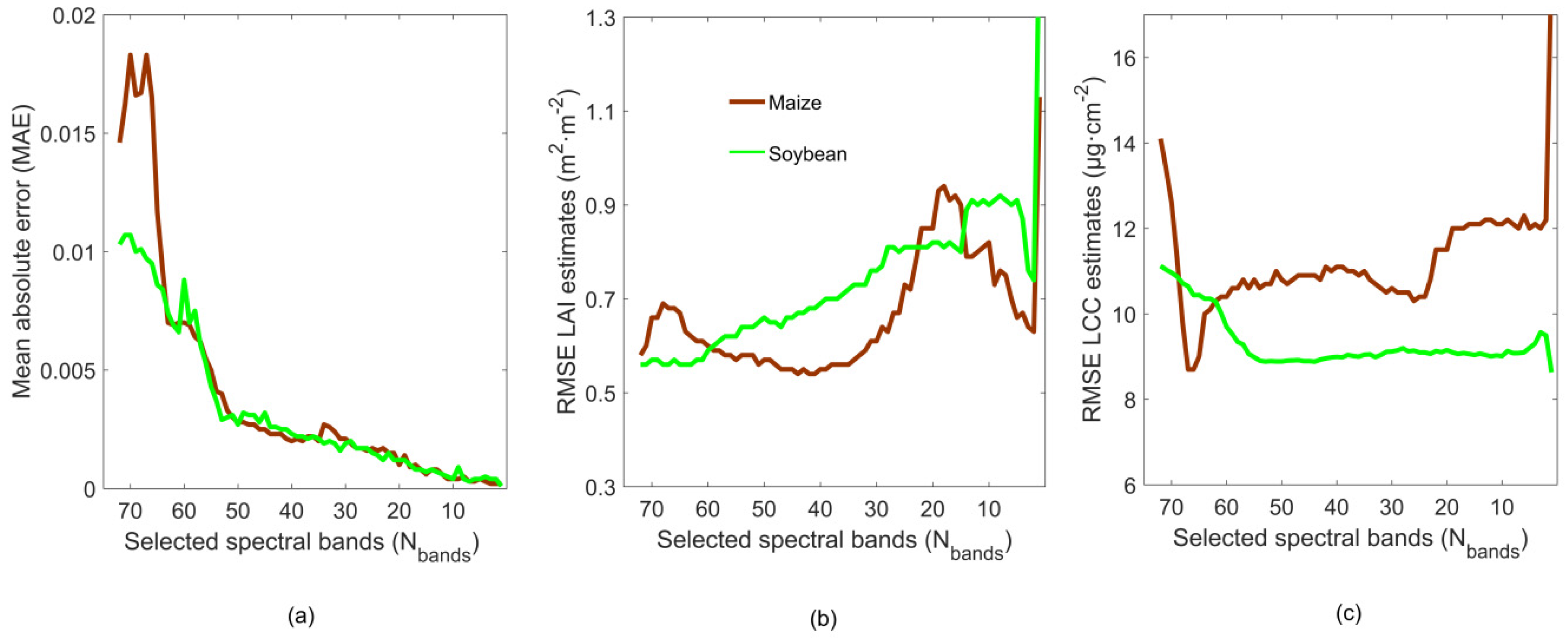
3.1. Model Suitability Test and Feature Selection
3.2. Biophysical and Biochemical Variable Estimations
4. Conclusions
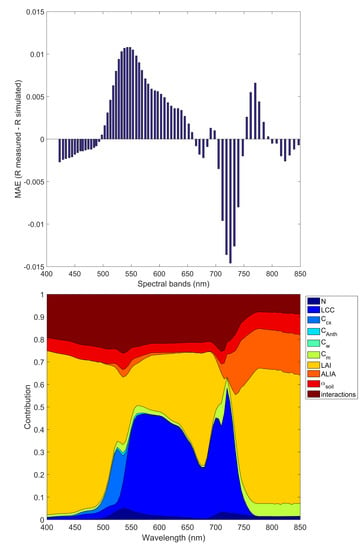
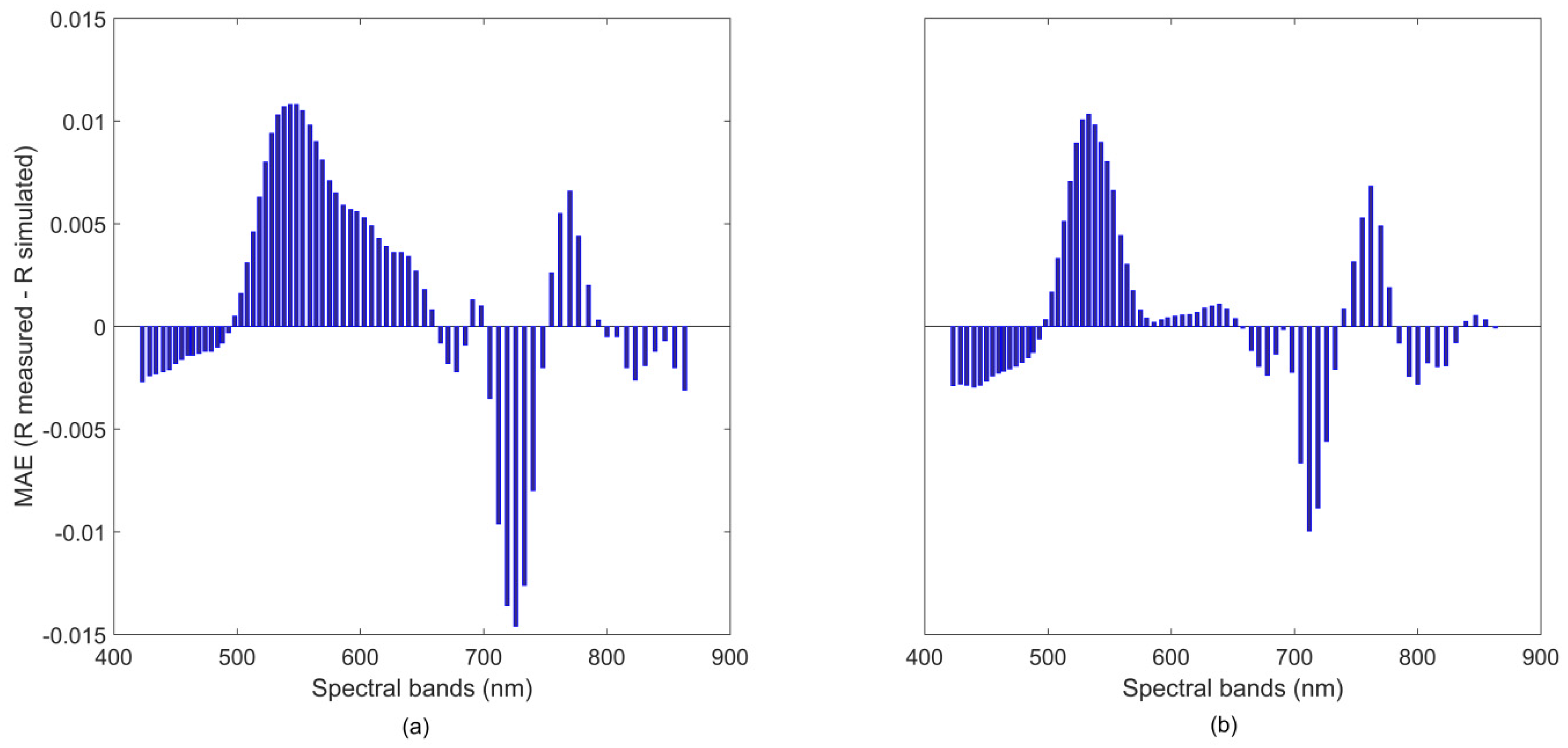
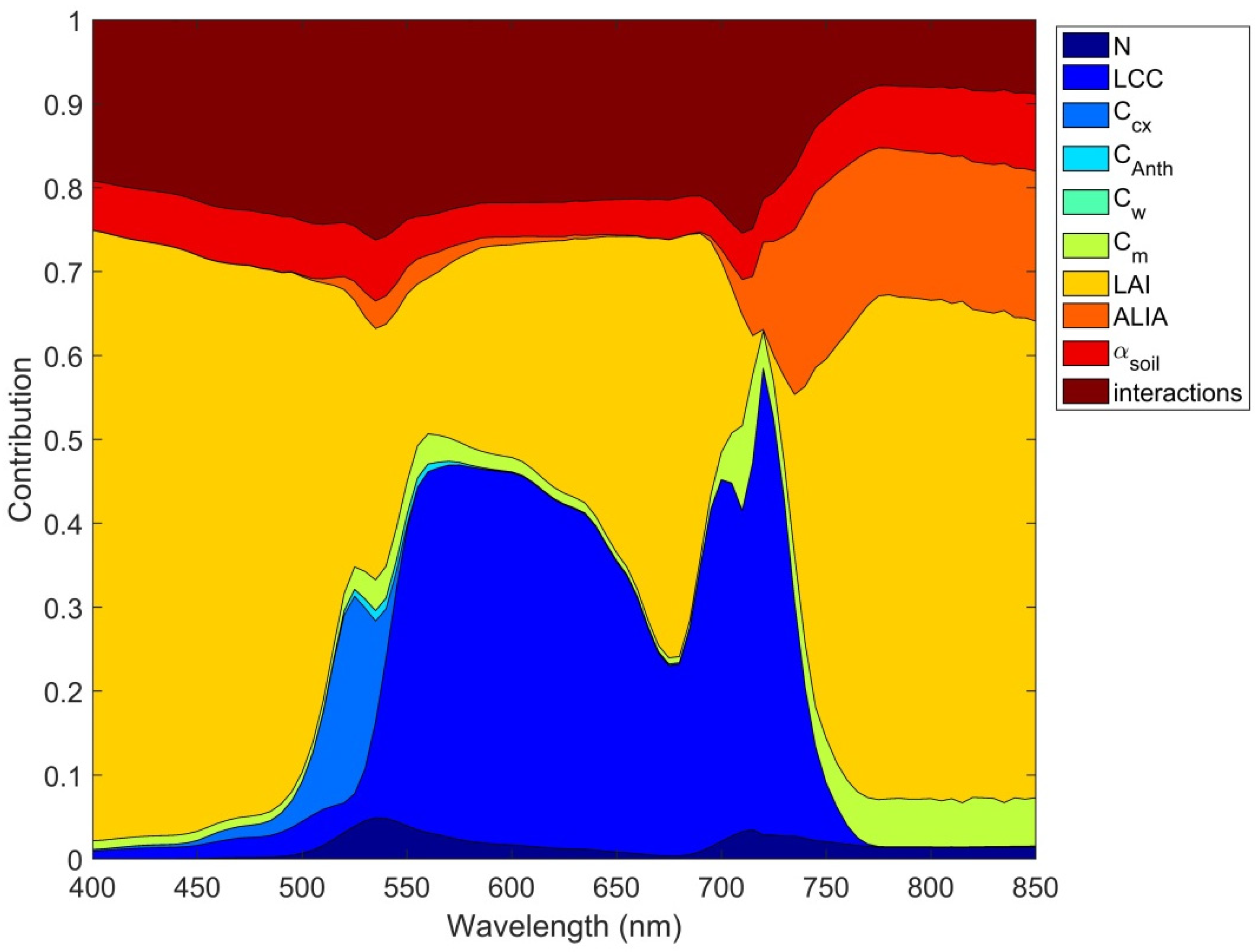
- There are two spectral regions in the VNIR region which are less well-modelled by PROSAIL independently of crop type: the green visible and the red edge. This can be explained by complex interactions of several biochemical and structural variables in these specific spectral regions. The green visible wavelength region is characterized by the influence of several pigments, in particular, carotenoids, chlorophylls, and anthocyanins. Moreover, there is an influence of leaf dry matter content, LAI, ALIA, and soil background. Regarding the red edge region, there is also a high variability with two strong peaks of chlorophyll content interacting with structural LAI and ALIA parameters.
- Discarding those wavelengths with a spectral mismatch of MAE > 0.01 leads to improvements of the leaf chlorophyll content retrieval. Such model-based analysis should therefore be carried out before applying any retrieval or data reduction algorithm.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Godfray, H.C.J.; Beddington, J.R.; Crute, I.R.; Haddad, L.; Lawrence, D.; Muir, J.F.; Pretty, J.; Robinson, S.; Thomas, S.M.; Toulmin, C. Food security: The challenge of feeding 9 billion people. Science 2010, 327, 812–818. [Google Scholar] [CrossRef] [PubMed]
- D’Urso, G.; Richter, K.; Calera, A.; Osann, M.A.; Escadafal, R.; Garatuza-Pajan, J.; Hanich, L.; Perdigao, A.; Tapia, J.B.; Vuolo, F. Earth observation products for operational irrigation management in the context of the pleiades project. Agric. Water Manag. 2010, 98, 271–282. [Google Scholar] [CrossRef]
- Hank, T.B.; Berger, K.; Bach, H.; Clevers, J.G.P.W.; Gitelson, A.; Zarco-Tejada, P.; Mauser, W. Spaceborne imaging spectroscopy for sustainable agriculture: Contributions and challenges. Surv. Geophys. 2018, 1–37. [Google Scholar] [CrossRef]
- Labate, D.; Ceccherini, M.; Cisbani, A.; De Cosmo, V.; Galeazzi, C.; Giunti, L.; Melozzi, M.; Pieraccini, S.; Stagi, M. The prisma payload optomechanical design, a high performance instrument for a new hyperspectral mission. Acta Astronaut. 2009, 65, 1429–1436. [Google Scholar] [CrossRef]
- Lee, C.M.; Cable, M.L.; Hook, S.J.; Green, R.O.; Ustin, S.L.; Mandl, D.J.; Middleton, E.M. An introduction to the nasa hyperspectral infrared imager (hyspiri) mission and preparatory activities. Remote Sens. Environ. 2015, 167, 6–19. [Google Scholar] [CrossRef]
- Eckardt, A.; Horack, J.; Lehmann, F.; Krutz, D.; Drescher, J.; Whorton, M.; Soutullo, M. Desis (dlr earth sensing imaging spectrometer for the iss-muses platform). In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 1457–1459. [Google Scholar]
- Guanter, L.; Kaufmann, H.; Segl, K.; Foerster, S.; Rogass, C.; Chabrillat, S.; Kuester, T.; Hollstein, A.; Rossner, G.; Chlebek, C.; et al. The enmap spaceborne imaging spectroscopy mission for earth observation. Remote Sens. 2015, 7, 8830–8857. [Google Scholar] [CrossRef]
- Rivera-Caicedo, J.P.; Verrelst, J.; Muñoz-Marí, J.; Camps-Valls, G.; Moreno, J. Hyperspectral dimensionality reduction for biophysical variable statistical retrieval. Isprs J. Photogramm. 2017, 132, 88–101. [Google Scholar] [CrossRef]
- Verrelst, J.; Malenovský, Z.; Van der Tol, C.; Camps-Valls, G.; Gastellu-Etchegorry, J.-P.; Lewis, P.; North, P.; Moreno, J. Quantifying vegetation biophysical variables from imaging spectroscopy data: A review on retrieval methods. Surv. Geophys. 2018, 1–41. [Google Scholar] [CrossRef]
- Verhoef, W.; Jia, L.; Xiao, Q.; Su, Z. Unified optical-thermal four-stream radiative transfer theory for homogeneous vegetation canopies. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1808–1822. [Google Scholar] [CrossRef]
- Féret, J.B.; Gitelson, A.A.; Noble, S.D.; Jacquemoud, S. Prospect-d: Towards modeling leaf optical properties through a complete lifecycle. Remote Sens. Environ. 2017, 193, 204–215. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; François, C.; Ustin, S.L. Prospect + sail models: A review of use for vegetation characterization. Remote Sens. Environ. 2009, 113 (Suppl. 1), S56–S66. [Google Scholar] [CrossRef]
- Berger, K.; Atzberger, C.; Danner, M.; D’Urso, G.; Mauser, W.; Vuolo, F.; Hank, T. Evaluation of the prosail model capabilities for future hyperspectral model environments: A review study. Remote Sens. 2018, 10, 85. [Google Scholar] [CrossRef]
- Kimes, D.S.; Knyazikhin, Y.; Privette, J.L.; Abuelgasim, A.A.; Gao, F. Inversion methods for physically-based models. Remote Sens. Rev. 2000, 18, 381–439. [Google Scholar] [CrossRef]
- Locherer, M.; Hank, T.; Danner, M.; Mauser, W. Retrieval of seasonal leaf area index from simulated enmap data through optimized lut-based inversion of the prosail model. Remote Sens. 2015, 7, 10321–10346. [Google Scholar] [CrossRef]
- Weiss, M.; Baret, F.; Myneni, R.B.; Pragnere, A.; Knyazikhin, Y. Investigation of a model inversion technique to estimate canopy biophysical variables from spectral and directional reflectance data. Agronomie 2000, 20, 3–22. [Google Scholar] [CrossRef]
- Koetz, B.; Baret, F.; Poilvé, H.; Hill, J. Use of coupled canopy structure dynamic and radiative transfer models to estimate biophysical canopy characteristics. Remote Sens. Environ. 2005, 95, 115–124. [Google Scholar] [CrossRef]
- Botha, E.J.; Leblon, B.; Zebarth, B.J.; Watmough, J. Non-destructive estimation of wheat leaf chlorophyll content from hyperspectral measurements through analytical model inversion. Int. J. Remote Sens. 2010, 31, 1679–1697. [Google Scholar] [CrossRef]
- Darvishzadeh, R.; Skidmore, A.; Schlerf, M.; Atzberger, C. Inversion of a radiative transfer model for estimating vegetation lai and chlorophyll in a heterogeneous grassland. Remote Sens. Environ. 2008, 112, 2592–2604. [Google Scholar] [CrossRef]
- Baret, F.; Buis, S. Estimating canopy characteristics from remote sensing observations: Review of methods and associated problems. In Advances in land remote sensing; Springer: Dordrecht, The Netherlands, 2008; pp. 173–201. [Google Scholar]
- Dorigo, W.; Richter, R.; Baret, F.; Bamler, R.; Wagner, W. Enhanced automated canopy characterization from hyperspectral data by a novel two step radiative transfer model inversion approach. Remote Sens. 2009, 1, 1139–1170. [Google Scholar] [CrossRef]
- Verger, A.; Baret, F.; Camacho, F. Optimal modalities for radiative transfer-neural network estimation of canopy biophysical characteristics: Evaluation over an agricultural area with chris/proba observations. Remote Sens. Environ. 2011, 115, 415–426. [Google Scholar] [CrossRef]
- Atzberger, C.; Richter, K. Spatially constrained inversion of radiative transfer models for improved lai mapping from future sentinel-2 imagery. Remote Sens. Environ. 2012, 120, 208–218. [Google Scholar] [CrossRef]
- Atzberger, C.; Darvishzadeh, R.; Schlerf, M.; Le Maire, G. Suitability and adaptation of prosail radiative transfer model for hyperspectral grassland studies. Remote Sens. Lett. 2013, 4, 56–65. [Google Scholar] [CrossRef]
- Meroni, M.; Colombo, R.; Panigada, C. Inversion of a radiative transfer model with hyperspectral observations for lai mapping in poplar plantations. Remote Sens. Environ. 2004, 92, 195–206. [Google Scholar] [CrossRef]
- Ciganda, V.; Gitelson, A.; Schepers, J. Vertical profile and temporal variation of chlorophyll in maize canopy: Quantitative “crop vigor” indicator by means of reflectance-based techniques. Agron. J. 2008, 100, 1409–1417. [Google Scholar] [CrossRef]
- Viña, A.; Gitelson, A.A.; Nguy-Robertson, A.L.; Peng, Y. Comparison of different vegetation indices for the remote assessment of green leaf area index of crops. Remote Sens. Environ. 2011, 115, 3468–3478. [Google Scholar] [CrossRef]
- Laurent, V.C.E.; Verhoef, W.; Damm, A.; Schaepman, M.E.; Clevers, J.G.P.W. A bayesian object-based approach for estimating vegetation biophysical and biochemical variables from apex at-sensor radiance data. Remote Sens. Environ. 2013, 139, 6–17. [Google Scholar] [CrossRef]
- Verrelst, J.; Rivera, J.P.; Gitelson, A.; Delegido, J.; Moreno, J.; Camps-Valls, G. Spectral band selection for vegetation properties retrieval using gaussian processes regression. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 554–567. [Google Scholar] [CrossRef]
- Richter, K.; Atzberger, C.; Vuolo, F.; Weihs, P.; D’Urso, G. Experimental assessment of the sentinel-2 band setting for rtm-based lai retrieval of sugar beet and maize. Can. J. Remote Sens. 2009, 35, 230–247. [Google Scholar] [CrossRef]
- España, M.a.L.; Baret, F.; Aries, F.; Chelle, M.; Andrieu, B.; Prévot, L. Modeling maize canopy 3d architecture: Application to reflectance simulation. Ecol. Model. 1999, 122, 25–43. [Google Scholar] [CrossRef]
- Asner, G.P. Biophysical and biochemical sources of variability in canopy reflectance. Remote Sens. Environ. 1998, 64, 234–253. [Google Scholar] [CrossRef]
- Wang, Z.; Skidmore, A.K.; Wang, T.; Darvishzadeh, R.; Hearne, J. Applicability of the prospect model for estimating protein and cellulose+lignin in fresh leaves. Remote Sens. Environ. 2015, 168, 205–218. [Google Scholar] [CrossRef]
- Cannavó, F. Sensitivity analysis for volcanic source modeling quality assessment and model selection. Comput. Geosci. 2012, 44, 52–59. [Google Scholar]
- Danner, M.; Berger, K.; Wocher, M.; Mauser, W.; Hank, T. Retrieval of biophysical crop variables from multi-angular canopy spectroscopy. Remote Sens. 2017, 9, 726. [Google Scholar] [CrossRef]
- Dawson, T.; Curran, P. Technical note a new technique for interpolating the reflectance red edge position. Int. J. Remote Sens. 1998, 19, 2133–2139. [Google Scholar] [CrossRef]
- Danner, M.; Berger, K.; Wocher, M.; Mauser, W.; Hank, T. Optimized parameterization of winter wheat and maize canopies for efficient prosail model inversion. Remote Sens. 2019. in preparation. [Google Scholar]
- Doktor, D.; Lausch, A.; Spengler, D.; Thurner, M. Extraction of plant physiological status from hyperspectral signatures using machine learning methods. Remote Sens. 2014, 6, 12247–12274. [Google Scholar] [CrossRef]
- Duan, S.B.; Li, Z.L.; Wu, H.; Tang, B.H.; Ma, L.L.; Zhao, E.Y.; Li, C.R. Inversion of the prosail model to estimate leaf area index of maize, potato, and sunflower fields from unmanned aerial vehicle hyperspectral data. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 12–20. [Google Scholar] [CrossRef]
- Verrelst, J.; Rivera, J.P.; Leonenko, G.; Alonso, L.; Moreno, J. Optimizing lut-based rtm inversion for semiautomatic mapping of crop biophysical parameters from sentinel-2 and-3 data: Role of cost functions. IEEE Trans. Geosci. Remote Sens. 2013, 52, 257–269. [Google Scholar] [CrossRef]
- Bacour, C.; Jacquemoud, S.; Tourbier, Y.; Dechambre, M.; Frangi, J.P. Design and analysis of numerical experiments to compare four canopy reflectance models. Remote Sens. Environ. 2002, 79, 72–83. [Google Scholar] [CrossRef]
- Botha, E.J.; Leblon, B.; Zebarth, B.; Watmough, J. Non-destructive estimation of potato leaf chlorophyll from canopy hyperspectral reflectance using the inverted prosail model. Int. J. Appl. Earth Obs. Geoinf. 2007, 9, 360–374. [Google Scholar] [CrossRef]
- Bsaibes, A.; Courault, D.; Baret, F.; Weiss, M.; Olioso, A.; Jacob, F.; Hagolle, O.; Marloie, O.; Bertrand, N.; Desfond, V.; et al. Albedo and lai estimates from formosat-2 data for crop monitoring. Remote Sens. Environ. 2009, 113, 716–729. [Google Scholar] [CrossRef]
- Clevers, J.; Kooistra, L. Using hyperspectral remote sensing data for retrieving canopy chlorophyll and nitrogen content. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 574–583. [Google Scholar] [CrossRef]
- Lee, K.-S.; Cohen, W.B.; Kennedy, R.E.; Maiersperger, T.K.; Gower, S.T. Hyperspectral versus multispectral data for estimating leaf area index in four different biomes. Remote Sens. Environ. 2004, 91, 508–520. [Google Scholar] [CrossRef]
- Thorp, K.R.; Gore, M.A.; Andrade-Sanchez, P.; Carmo-Silva, A.E.; Welch, S.M.; White, J.W.; French, A.N. Proximal hyperspectral sensing and data analysis approaches for field-based plant phenomics. Comput. Electron. Agric. 2015, 118, 225–236. [Google Scholar] [CrossRef]
- Kaminski, T.; Pinty, B.; Voßbeck, M.; Lopatka, M.; Gobron, N.; Robustelli, M. Consistent retrieval of land surface radiation products from eo, including traceable uncertainty estimates. Biogeosciences 2017, 14, 2527–2541. [Google Scholar] [CrossRef]
- Widlowski, J.-L.; Mio, C.; Disney, M.; Adams, J.; Andredakis, I.; Atzberger, C.; Brennan, J.; Busetto, L.; Chelle, M.; Ceccherini, G.; et al. The fourth phase of the radiative transfer model intercomparison (rami) exercise: Actual canopy scenarios and conformity testing. Remote Sens. Environ. 2015, 169, 418–437. [Google Scholar] [CrossRef]
| Measured variable | N | Min–Max | Mean | SD | CV |
|---|---|---|---|---|---|
| Maize: | |||||
| Leaf area index, LAI (m2·m−2) | 169 | 0.07–6.08 | 3.9 | 1.7 | 0.44 |
| Leaf chlorophyll content, LCC (µg·cm−2) | 169 | 19.5–83 | 56.1 | 9.9 | 0.18 |
| Soybean: | |||||
| Leaf area index, LAI (m2·m−2) | 68 | 0.1–5.5 | 2.6 | 1.6 | 0.59 |
| Leaf chlorophyll content, LCC (µg·cm−2) | 68 | 11.8–58.2 | 30.3 | 8.9 | 0.3 |
| Parameter | Notation (Unit) | Range | Source (also used by) |
|---|---|---|---|
| Leaf optical properties model (PROSPECT-D): | |||
| Leaf chlorophyll content | LCC (µg·cm−2) | 0–85 | as measured |
| Leaf structural parameter | N, no dimension | 1.2–2.6 | [29] |
| Leaf dry matter content | Cm (g·cm−2) | 0.001–0.02 | [29] |
| Leaf equivalent water thickness | Cw /EWT (cm) | 0.001–0.05 | [29] |
| Leaf carotenoid content | Ccx (µg·cm−2) | 0–20 | derived according to [11] |
| Leaf anthocyanin content | CAnth (µg·cm−2) | 0–2 | (pers. communication with J.-B. Féret) |
| Canopy reflectance model (SAIL): | |||
| Leaf area index | LAI (m2·m−2) | 0–6.1 | as measured |
| Average leaf inclination angle | ALIA (°) | 40–70 (maize), 30–60 (soybean) | [29,30] |
| Hot spot parameter | hot (m·m−1) | 0.01–0.03 | [31] |
| Soil reflectance | ρsoil (%) | as measured in the field | |
| Soil brightness | αsoil, no dim. | 0.5–1.5 | [24] |
| Measurement geometry | θv/θs/øSV | according to measurement conditions | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Berger, K.; Atzberger, C.; Danner, M.; Wocher, M.; Mauser, W.; Hank, T. Model-Based Optimization of Spectral Sampling for the Retrieval of Crop Variables with the PROSAIL Model. Remote Sens. 2018, 10, 2063. https://doi.org/10.3390/rs10122063
Berger K, Atzberger C, Danner M, Wocher M, Mauser W, Hank T. Model-Based Optimization of Spectral Sampling for the Retrieval of Crop Variables with the PROSAIL Model. Remote Sensing. 2018; 10(12):2063. https://doi.org/10.3390/rs10122063
Chicago/Turabian StyleBerger, Katja, Clement Atzberger, Martin Danner, Matthias Wocher, Wolfram Mauser, and Tobias Hank. 2018. "Model-Based Optimization of Spectral Sampling for the Retrieval of Crop Variables with the PROSAIL Model" Remote Sensing 10, no. 12: 2063. https://doi.org/10.3390/rs10122063
APA StyleBerger, K., Atzberger, C., Danner, M., Wocher, M., Mauser, W., & Hank, T. (2018). Model-Based Optimization of Spectral Sampling for the Retrieval of Crop Variables with the PROSAIL Model. Remote Sensing, 10(12), 2063. https://doi.org/10.3390/rs10122063