Hyperspectral Mixed Denoising via Spectral Difference-Induced Total Variation and Low-Rank Approximation †
Abstract
1. Introduction
- The proposed method takes full consideration of three kinds of noises that exist in HSI, i.e., random sparse noise, Gaussian noise, and structured sparse noises. To completely remove all of them, multiple priors (TV, LRR and SDS) are fused into a unified framework to accurately reconstruct the underlying clean HSI.
- The combination of TV and SDS can be treated as a novel cross TV (CTV) which is defined as the conventional 2-d TV across one-dimensional spectral TV, and CTV has been validated to be effective for dealing with both Gaussian noise and structured stripes.
- The SDTVLA model with all convex terms is easy to be separately solved by alternating direction method of multipliers (ADMM).
- Extensive experiments on three simulated and two real HSI datasets demonstrate the superiority of SDTVLA algorithm in terms of visual effect and quantitative assessment.
2. Background Formulation
2.1. Observation Model
2.2. LRMR Model
2.3. LRTV Model
3. Proposed SDTVLA Method
3.1. Spectral Difference Transformation
3.2. SDTVLA Model
- Different from the conventional TV constraint in each band, here the TV regularization is defined in SDS, and it can be seen as a cross TV that explores both spatial and spectral information. Meanwhile, it could effectively help low-rank tools to reduce the severe Gaussian noise and structured stripes.
- Spectral difference transform can effectively change the structures of the noises in the original HSI, thus enabling the TVLA regularization to further improve the denoising accuracy of the structured stripes.
- With all convex regularizations, the model (7) can be effectively and easily solved by ADMM.
3.3. Optimization
| Algorithm 1 The pseudo-code for SDTVLA solver via ADMM. |
|
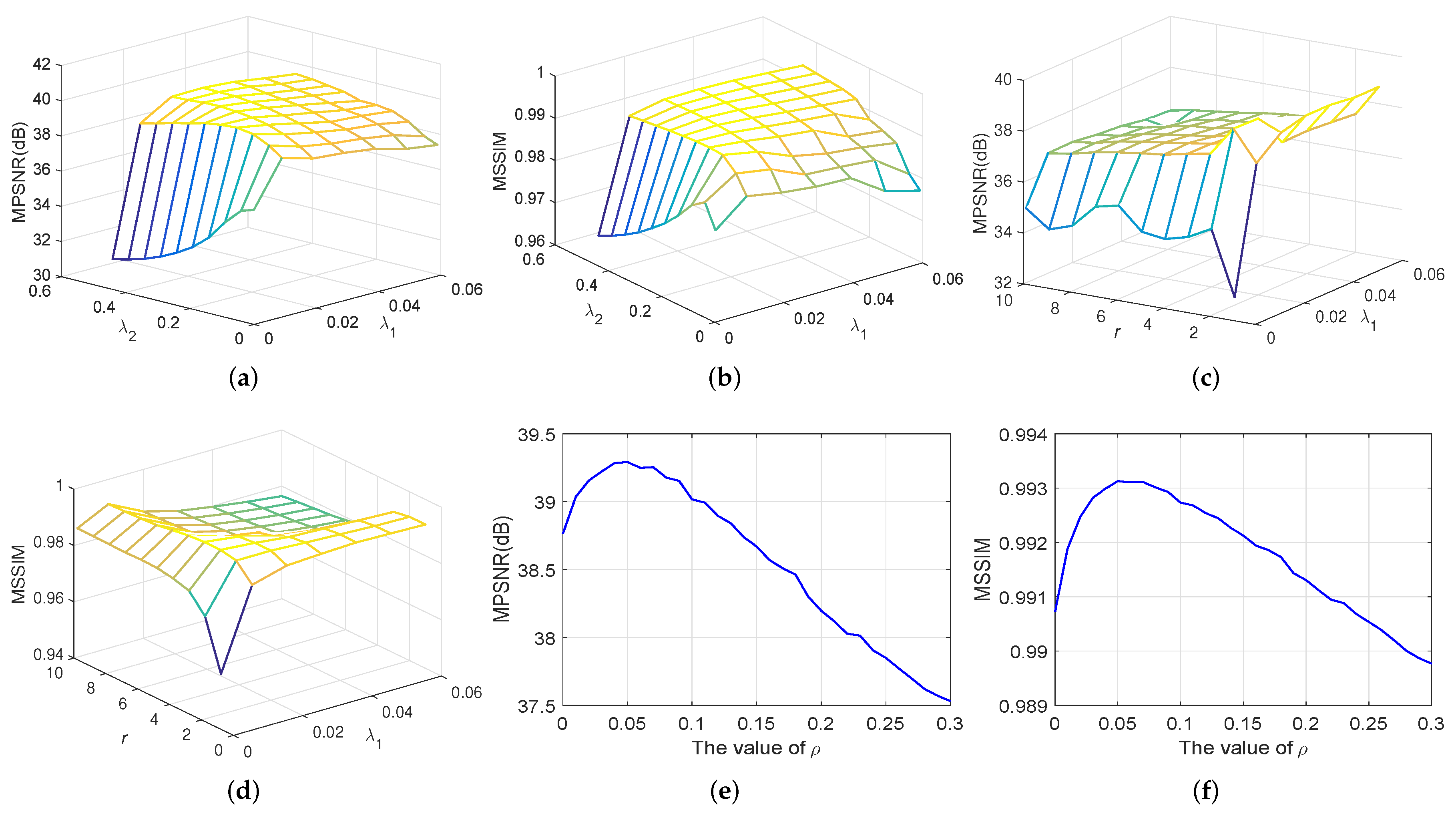
3.4. Parameters Determination and Convergence Analysis
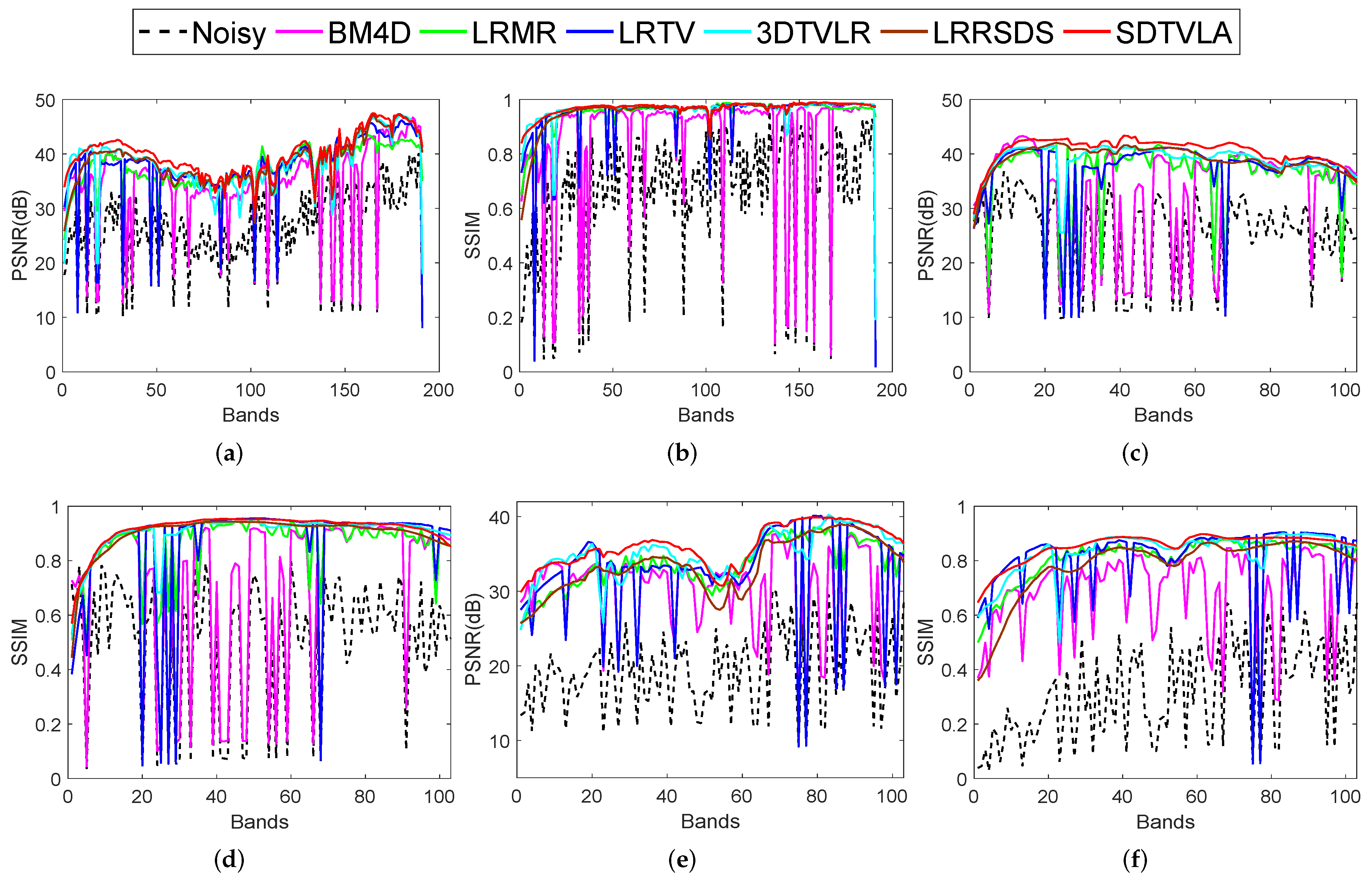
4. Experimental Results and Discussions
4.1. Datasets Description
- Washington DC (WDC): This dataset was collected by the hyperspectral digital imagery collection experiment (HYDICE) sensor over the Washington DC Mall. The scene originally contains 210 bands in the range of 0.4 to 2.4 m, with the spatial size of and spatial resolution of 2.0 m/pixel. Due to the atmospheric effect, bands in the 0.9 and 1.4 m region have been omitted from the dataset, leaving 191 usable bands. In the experiment, we use a subimage with cropped from the original dataset. The falsecolor image of it is shown in Figure 4a.
- Pavia University (Pavia): This dataset was acquired by the ROSIS sensor during a flight campaign over Pavia, northern Italy. This scene has 103 bands and there are totally pixels in the original dataset with the geometric resolution of 1.3 m/pixel. In the experiment, we use a subimage with cropped from the original dataset. The falsecolor image of it is shown in Figure 4b.
- Suwanee Gulf (Gulf): This dataset was collected by the AVIRIS instrument over the multiple National Wildlife Reserves in the Gulf of Mexico during the period of May–June 2010. This sample is from the Lower Suwanee NWR, with a spatial resolution of 2 m/pixel and spectral resolution of 5 nm. The wavelength of the scene covers the range of 0.395–2.45 m. In the experiment, we use a subimage with cropped from the original dataset. The falsecolor image of it is shown in Figure 4c.
- HYDICE Urban (Urban): This dataset was captured by the HYDICE sensor over the Copperas Cove, near Fort Hood, TX, USA, in October 1995. This scene has pixels and 210 bands ranging from 0.4–2.5 m. The spatial resolution is 2 m/pixel and spectral resolution is 10 nm. Due to atmospheric effects and water absorption, the channels 1–4, 76, 87, 101–111, 136–153 and 198–210 are heavily corrupted. In the experiment, we employ the Urban dataset with all bands to demonstrate the superiority of SDTVLA solver for removing the most complex mixed noise. The falsecolor image of it is shown in Figure 4d.
- AVIRIS Indian Pines (Indian Pines): This dataset was acquired by the AVIRIS instrument over the Indian Pines test site in Northwestern Indiana in 1992. This scene has pixels and 220 bands. It is mainly contaminated by severe Gaussian noise, stripes, and dead lines. The falsecolor image of it is shown in Figure 4e.
4.2. Competitive Methods and Assessment Indexes
- BM4D [53]: one of the representative wavelet denoisers which explores the nonlocal self-similarities in a tensor manner and achieves great success in nature image denoising.
- LRMR [34]: one of the outstanding HSI mixed denoising methods by using so-called “GoDec” algorithm to solve the patch-based low-rank matrix recovery problem.
- LRTV [43]: a novel band-by-band TV regularized LRR method for mixed noise reduction of HSI.
- 3DTVLR [45]: a novel mixed noise removal method combining three-dimensional TV (spatial TV and spectral TV) and LRR for HSI.
- LRRSDS [48]: one of the state-of-the-art mixed noise reduction methods by enforcing the low-rank constraint in the SDS.
4.3. Experiments on Simulated Datasets
- To generate the noisy HSI with difference noise intensity, we add zero-mean Gaussian noise to all bands. However, for each band, the noise variance is randomly generated from 0.049 to 0.098. It means the signal-to-noise-ratio (SNR) of noise lies in [10–20] dB.
- Since the impulse noise is usually generated by the water absorption or atmosphere effect and is often present in continuous bands, we add the impulse noise to the bands from 90 to 110 with the density of 20% pixels being contaminated;
- Caused by the sensors, dead lines or stripes always exist in the HSI. Therefore, we add dead lines to 10 bands, and the width of each dead line is randomly set from 1 to 3.
4.4. Experiments on Real Datasets
4.5. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bioucas-Dias, J.M.; Plaza, A.; Camps-Valls, G.; Scheunders, P.; Nasrabadi, N.; Chanussot, J. Hyperspectral remote sensing data analysis and future challenges. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–36. [Google Scholar] [CrossRef]
- Sun, L.; Wu, Z.; Liu, J.; Xiao, L.; Wei, Z. Supervised spectral–spatial hyperspectral image classification with weighted Markov random fields. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1490–1503. [Google Scholar] [CrossRef]
- Sun, L.; Wang, S.; Wang, J.; Zheng, Y.; Jeon, B. Hyperspectral classification employing spatial-spectral low rank representation in hidden fields. J. Ambient Intell. Humaniz. Comput. 2017, 1–12. [Google Scholar] [CrossRef]
- Wu, Z.; Shi, L.; Li, J.; Wang, Q.; Sun, L.; Wei, Z.; Plaza, J.; Plaza, A. GPU parallel implementation of spatially adaptive hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1131–1143. [Google Scholar] [CrossRef]
- Zhang, L.; Zhao, C. A spectral-spatial method based on low-rank and sparse matrix decomposition for hyperspectral anomaly detection. Int. J. Remote Sens. 2017, 38, 4047–4068. [Google Scholar] [CrossRef]
- Sun, L.; Wu, Z.; Xiao, L.; Liu, J.; Wei, Z.; Dang, F. A novel l 1/2 sparse regression method for hyperspectral unmixing. Int. J. Remote Sens. 2013, 34, 6983–7001. [Google Scholar] [CrossRef]
- Sun, L.; Ge, W.; Chen, Y.; Zhang, J.; Jeon, B. Hyperspectral unmixing employing l1-l2 sparsity and total variation regularization. Int. J. Remote Sens. 2018, 39, 6037–6060. [Google Scholar] [CrossRef]
- Lee, J.B.; Woodyatt, A.S.; Berman, M. Enhancement of high spectral resolution remote-sensing data by a noise-adjusted principal components transform. IEEE Trans. Geosci. Remote Sens. 1990, 28, 295–304. [Google Scholar] [CrossRef]
- Green, A.A.; Berman, M.; Switzer, P.; Craig, M.D. A transformation for ordering multispectral data in terms of image quality with implications for noise removal. IEEE Trans. Geosci. Remote Sens. 1988, 26, 65–74. [Google Scholar] [CrossRef]
- Zhang, M.; Gunturk, B.K. Multiresolution bilateral filtering for image denoising. IEEE Trans. Image Process. 2008, 17, 2324–2333. [Google Scholar] [CrossRef]
- Vese, L.A.; Osher, S.J. Image denoising and decomposition with total variation minimization and oscillatory functions. J. Math. Imaging Vis. 2004, 20, 7–18. [Google Scholar] [CrossRef]
- Buades, A.; Coll, B.; Morel, J.M. A non-local algorithm for image denoising. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2005; Volume 2, pp. 60–65. [Google Scholar]
- Jain, V.; Seung, S. Natural image denoising with convolutional networks. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 7–10 December 2009; pp. 769–776. [Google Scholar]
- Tang, Z.; Ling, M.; Yao, H.; Qian, Z.; Zhang, X.; Zhang, J.; Xu, S. Robust image hashing via random Gabor filtering and DWT. Comput. Mater. Contin. 2018, 55, 331–344. [Google Scholar]
- Rasti, B.; Sveinsson, J.R.; Ulfarsson, M.O.; Benediktsson, J.A. Hyperspectral image denoising using 3D wavelets. In Proceedings of the IEEE International Conference on Geoscience and Remote Sensing Symposium (IGARSS 2012), Munich, Germany, 22–27 July 2012; pp. 1349–1352. [Google Scholar]
- Zelinski, A.; Goyal, V. Denoising hyperspectral imagery and recovering junk bands using wavelets and sparse approximation. In Proceedings of the IEEE International Conference on Geoscience and Remote Sensing Symposium, Denver, CO, USA, 31 July–4 August 2006; pp. 387–390. [Google Scholar]
- Chen, G.; Qian, S.E. Denoising of hyperspectral imagery using principal component analysis and wavelet shrinkage. IEEE Trans. Geosci. Remote Sens. 2011, 49, 973–980. [Google Scholar] [CrossRef]
- Chen, G.; Bui, T.D.; Quach, K.G.; Qian, S.E. Denoising hyperspectral imagery using principal component analysis and block-matching 4D filtering. Can. J. Remote Sens. 2014, 40, 60–66. [Google Scholar] [CrossRef]
- Rasti, B.; Sveinsson, J.R.; Ulfarsson, M.O. Wavelet-based sparse reduced-rank regression for hyperspectral image restoration. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6688–6698. [Google Scholar] [CrossRef]
- Rasti, B.; Ulfarsson, M.O.; Ghamisi, P. Automatic hyperspectral image restoration using sparse and low-rank modeling. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2335–2339. [Google Scholar] [CrossRef]
- Wang, R.; Shen, M.; Li, Y.; Gomes, S. Multi-task joint sparse representation classification based on fisher discrimination dictionary learning. Comput. Mater. Contin. 2018, 57, 25–48. [Google Scholar] [CrossRef]
- Zhao, Y.Q.; Yang, J. Hyperspectral image denoising via sparse representation and low-rank constraint. IEEE Trans. Geosci. Remote Sens. 2015, 53, 296–308. [Google Scholar] [CrossRef]
- Li, J.; Yuan, Q.; Shen, H.; Zhang, L. Noise removal from hyperspectral image with joint spectral-spatial distributed sparse representation. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5425–5439. [Google Scholar] [CrossRef]
- Lu, T.; Li, S.; Fang, L.; Ma, Y.; Benediktsson, J.A. Spectral–spatial adaptive sparse representation for hyperspectral image denoising. IEEE Trans. Geosci. Remote Sens. 2016, 54, 373–385. [Google Scholar] [CrossRef]
- Fu, Y.; Lam, A.; Sato, I.; Sato, Y. Adaptive spatial-spectral dictionary learning for hyperspectral image restoration. Int. J. Comput. Vis. 2017, 122, 228–245. [Google Scholar] [CrossRef]
- Zhuang, L.; Bioucas-Dias, J.M. Fast hyperspectral image denoising and inpainting based on low-rank and sparse representations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 730–742. [Google Scholar] [CrossRef]
- Rasti, B.; Scheunders, P.; Ghamisi, P.; Licciardi, G.; Chanussot, J. Noise reduction in hyperspectral imagery: Overview and application. Remote Sens. 2018, 10, 482. [Google Scholar] [CrossRef]
- Fang, W.; Zhang, F.; Sheng, V.S.; Ding, Y. A method for improving CNN-based image recognition using DCGAN. Comput. Mater. Contin. 2018, 57, 167–178. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Q.; Li, Y.; Wu, X. Sentiment classification based on piecewise pooling convolutional neural network. Comput. Mater. Contin. 2018, 56, 285–297. [Google Scholar]
- Meng, R.; Rice, S.G.; Wang, J.; Sun, X. A fusion steganographic algorithm based on faster R-CNN. Comput. Mater. Contin. 2018, 55, 1–16. [Google Scholar]
- Li, Y.; Xie, W.; Li, H. Hyperspectral image reconstruction by deep convolutional neural network for classification. Pattern Recognit. 2017, 63, 371–383. [Google Scholar] [CrossRef]
- Xie, W.; Li, Y. Hyperspectral imagery denoising by deep learning with trainable nonlinearity function. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1963–1967. [Google Scholar] [CrossRef]
- Lu, X.; Wang, Y.; Yuan, Y. Graph-regularized low-rank representation for destriping of hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4009–4018. [Google Scholar] [CrossRef]
- Zhang, H.; He, W.; Zhang, L.; Shen, H.; Yuan, Q. Hyperspectral image restoration using low-rank matrix recovery. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4729–4743. [Google Scholar] [CrossRef]
- Zhou, T.; Tao, D. Godec: Randomized low-rank & sparse matrix decomposition in noisy case. In Proceedings of the International Conference on Machine Learning, Bellevue, WA, USA, 28 June–2 July 2011; pp. 1–8. [Google Scholar]
- Zhu, R.; Dong, M.; Xue, J.H. Spectral nonlocal restoration of hyperspectral images with low-rank property. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3062–3067. [Google Scholar]
- Wang, M.; Yu, J.; Xue, J.H.; Sun, W. Denoising of hyperspectral images using group low-rank representation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4420–4427. [Google Scholar] [CrossRef]
- He, W.; Zhang, H.; Zhang, L.; Shen, H. Hyperspectral image denoising via noise-adjusted iterative low-rank matrix approximation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3050–3061. [Google Scholar] [CrossRef]
- Sun, L.; Jeon, B.; Soomro, B.N.; Zheng, Y.; Wu, Z.; Xiao, L. Fast superpixel based subspace low rank learning method for hyperspectral denoising. IEEE Access 2018, 6, 12031–12043. [Google Scholar] [CrossRef]
- Fan, H.; Chen, Y.; Guo, Y.; Zhang, H.; Kuang, G. Hyperspectral image restoration using low-rank tensor recovery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 4589–4604. [Google Scholar] [CrossRef]
- Chang, Y.; Yan, L.; Fang, H.; Zhong, S.; Zhang, Z. Weighted low-rank tensor recovery for hyperspectral image restoration. arXiv, 2017; arXiv:1709.00192v1. [Google Scholar]
- Huang, Z.; Li, S.; Fang, L.; Li, H.; Atli, B.J. Hyperspectral image denoising with group sparse and low-rank tensor decomposition. IEEE Access 2018, 6, 1380–1390. [Google Scholar] [CrossRef]
- He, W.; Zhang, H.; Zhang, L.; Shen, H. Total-variation-regularized low-rank matrix factorization for hyperspectral image restoration. IEEE Trans. Geosci. Remote Sens. 2016, 54, 178–188. [Google Scholar] [CrossRef]
- Sun, L.; Zheng, Y.; Jeon, B. Hyperspectral restoration employing low rank and 3D total variation regularization. In Proceedings of the International Conference on Progress in Informatics and Computing (PIC), Shanghai, China, 23–25 December 2016; pp. 326–329. [Google Scholar]
- Sun, L.; Zhan, T.; Wu, Z.; Jeon, B. A novel 3d anisotropic total variation regularized low rank method for hyperspectral image mixed denoising. ISPRS Int. J. Geo-inf. 2018, 7, 412. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, Q.; Jin, J.; Shen, Y. Structure tensor total variation-regularized weighted nuclear norm minimization for hyperspectral image mixed denoising. Signal Process. 2017, 131, 202–219. [Google Scholar] [CrossRef]
- Wang, Y.; Peng, J.; Zhao, Q.; Leung, Y.; Zhao, X.L.; Meng, D. Hyperspectral image restoration via total variation regularized low-rank tensor decomposition. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1227–1243. [Google Scholar] [CrossRef]
- Sun, L.; Jeon, B.; Zheng, Y.; Wu, Z. Hyperspectral image restoration using low-rank representation on spectral difference image. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1151–1155. [Google Scholar] [CrossRef]
- Sun, L.; Jeon, B.; Zheng, Y. Hyperspectral restoration based on total variation regularized low rank decomposition in spectral difference space. In Proceedings of the IEEE International Workshop on Advanced Image Technology (IWAIT), Chiang Mai, Thailand, 7–9 January 2018; pp. 1–4. [Google Scholar]
- Lin, Z.; Chen, M.; Ma, Y. The augmented lagrange multiplier method for exact recovery of corrupted low-rank matrices. arXiv, 2010; arXiv:1009.5055. [Google Scholar]
- Sun, L.; Jeon, B.; Zheng, Y.; Wu, Z. A novel weighted cross total variation method for hyperspectral image mixed denoising. IEEE Access 2017, 5, 27172–27188. [Google Scholar] [CrossRef]
- Eckstein, J.; Yao, W. Understanding the convergence of the alternating direction method of multipliers: Theoretical and computational perspectives. Pac. J. Optim. 2015, 11, 619–644. [Google Scholar]
- Maggioni, M.; Katkovnik, V.; Egiazarian, K.; Foi, A. Nonlocal transform-domain filter for volumetric data denoising and reconstruction. IEEE Trans. Image Process. 2013, 22, 119–133. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, L.; Mou, X.; Zhang, D. FSIM: A feature similarity index for image quality assessment. IEEE Trans. Image Process. 2011, 20, 2378–2386. [Google Scholar] [CrossRef]
- Wald, L. Quality of high resolution synthesised images: Is there a simple criterion? In Proceedings of the International Conference on Fusion of Earth Data: Merging Point Measurements, Raster Maps and Remotely Sensed Images, SEE/URISCA, Nice, France, 11–14 January 2000; 99–103. [Google Scholar]












| Methods | WDC | Pavia | Gulf |
|---|---|---|---|
| BM4D [53] | - | - | - |
| LRMR [34] | |||
| LRTV [43] | |||
| 3DTVLR [45] | |||
| LRRSDS [48] | |||
| SDTVLA |
| Datasets | Metrics | Noisy | BM4D [53] | LRMR [34] | LRTV [43] | 3DTVLR [45] | LRRSDS [48] | SDTVLA |
|---|---|---|---|---|---|---|---|---|
| WDC | MPSNR(dB) | 26.13 | 34.14 | 37.40 | 37.60 | 38.43 | 38.76 | 40.10 |
| MSSIM | 0.6957 | 0.8818 | 0.9699 | 0.9575 | 0.9723 | 0.9716 | 0.9819 | |
| FSSIM | 0.8526 | 0.9388 | 0.9801 | 0.9727 | 0.9837 | 0.9852 | 0.9894 | |
| ERGAS | 404.01 | 307.34 | 56.39 | 211.05 | 81.61 | 48.19 | 40.58 | |
| MSA | 0.4434 | 0.2998 | 0.0693 | 0.1473 | 0.0896 | 0.0660 | 0.0534 | |
| Pavia | MPSNR(dB) | 25.11 | 32.26 | 36.09 | 36.86 | 38.94 | 39.13 | 40.57 |
| MSSIM | 0.5928 | 0.7831 | 0.9300 | 0.9125 | 0.9620 | 0.9614 | 0.9693 | |
| FSSIM | 0.8082 | 0.8921 | 0.9680 | 0.9546 | 0.9817 | 0.9852 | 0.9877 | |
| ERGAS | 556.77 | 410.97 | 204.60 | 297.89 | 55.77 | 48.88 | 40.78 | |
| MSA | 0.5711 | 0.4254 | 0.1012 | 0.2725 | 0.0697 | 0.0715 | 0.0584 | |
| Gulf | MPSNR(dB) | 19.45 | 30.45 | 33.65 | 32.87 | 35.08 | 33.54 | 36.12 |
| MSSIM | 0.3683 | 0.8127 | 0.9071 | 0.9005 | 0.9313 | 0.8812 | 0.9399 | |
| FSSIM | 0.6488 | 0.9047 | 0.9497 | 0.9457 | 0.9660 | 0.9437 | 0.9689 | |
| ERGAS | 365.70 | 155.63 | 53.18 | 177.27 | 46.42 | 55.39 | 39.44 | |
| MSA | 0.2955 | 0.0969 | 0.0380 | 0.0979 | 0.0365 | 0.0416 | 0.0259 | |
| Runtime (s) | - | - | 974.9 | 839.9 | 762.9 | 712.9 | 786.6 | 1017.1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, L.; Zhan, T.; Wu, Z.; Xiao, L.; Jeon, B. Hyperspectral Mixed Denoising via Spectral Difference-Induced Total Variation and Low-Rank Approximation. Remote Sens. 2018, 10, 1956. https://doi.org/10.3390/rs10121956
Sun L, Zhan T, Wu Z, Xiao L, Jeon B. Hyperspectral Mixed Denoising via Spectral Difference-Induced Total Variation and Low-Rank Approximation. Remote Sensing. 2018; 10(12):1956. https://doi.org/10.3390/rs10121956
Chicago/Turabian StyleSun, Le, Tianming Zhan, Zebin Wu, Liang Xiao, and Byeungwoo Jeon. 2018. "Hyperspectral Mixed Denoising via Spectral Difference-Induced Total Variation and Low-Rank Approximation" Remote Sensing 10, no. 12: 1956. https://doi.org/10.3390/rs10121956
APA StyleSun, L., Zhan, T., Wu, Z., Xiao, L., & Jeon, B. (2018). Hyperspectral Mixed Denoising via Spectral Difference-Induced Total Variation and Low-Rank Approximation. Remote Sensing, 10(12), 1956. https://doi.org/10.3390/rs10121956








