An Unsupervised Classification Algorithm for Multi-Temporal Irrigated Area Mapping in Central Asia
Abstract
1. Introduction
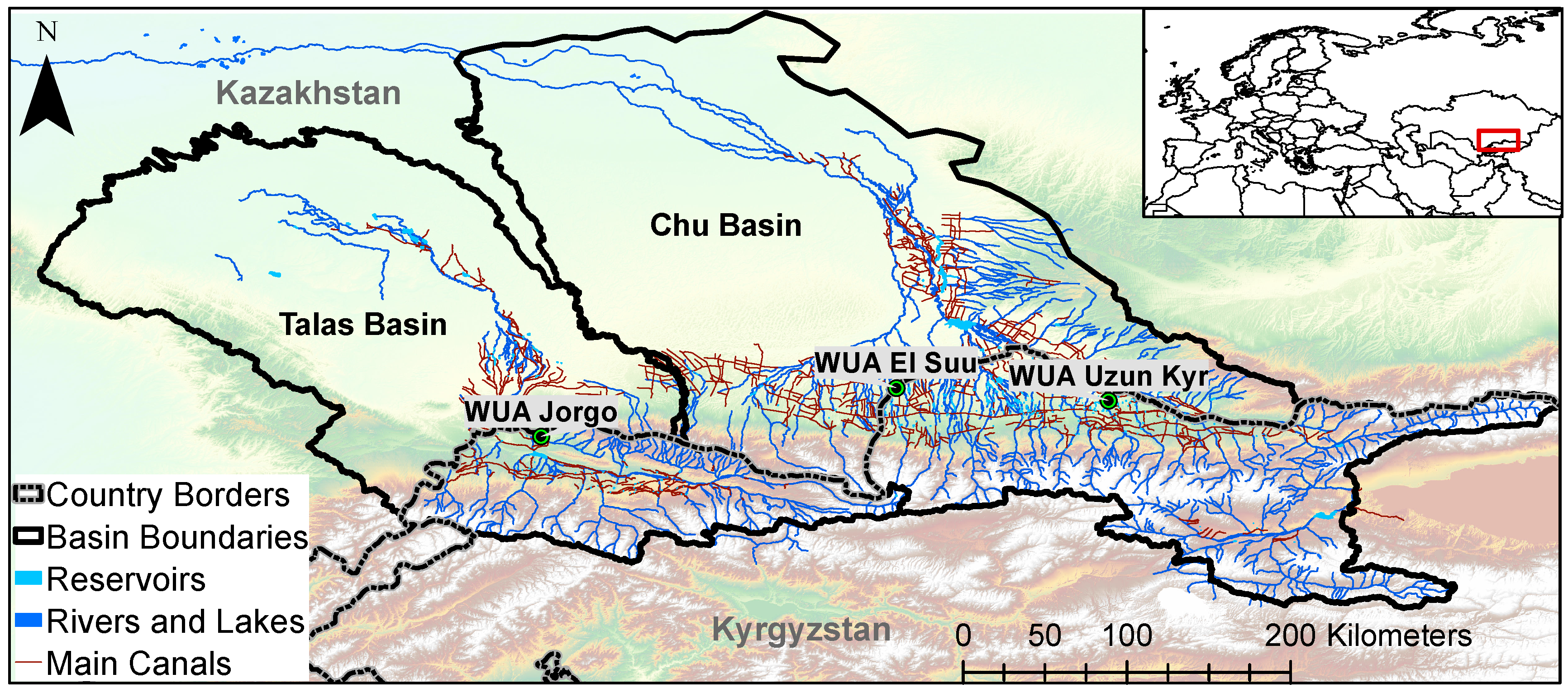
2. Study Site
3. Data
3.1. Satellite Data
- Landsat 7 imagery: Landsat 7 is in near-polar orbit with repeat cover every 16 days. The resolution of the imagery is 30 m per pixel for the bands used in this study. Data from the USGS Landsat 7 Collection are available in GEE for the period since 1 Jan 1999. However, due to the low number of scenes available for our study region from the year 1999 we only use Landsat 7 imagery from the year 2000 onward. A scan line corrector failure on Landsat 7 after 31 May 2003 causes around 22 percent of each scene to be lost after that date [30,31]. Most studies therefore use multiple images to fill in data gaps (e.g., [32]) or the data is fused with observations from other remote sensing systems [6,33].
- Landsat 8 imagery: The Landsat 8 satellite was launched on 11 February 2013 and images the entire Earth every 16 days in an 8-day offset from Landsat 7. The spatial resolution of the images is 30 m. Landsat 8 data has been used previously for detecting irrigation extent by Chen et al. [34].
- SENTINEL 2 imagery: Sentinel 2 is a high-resolution, multi-spectral imaging mission supporting Land Monitoring studies. Sentinel 2A was launched on 23 June 2015 and revisits our study region every 10 days. The spatial resolution of the imagery is 10 m (Red, NIR) and 20 m (MIR). Sentinel 2 data have been used previously for mapping croplands by Belgiu and Csillik [35].
- MODIS Terra and MODIS Aqua imagery: The two MODIS satellites image the entire Earth every 1 to 2 days. We use the 8-day composite MODIS Surface Reflectance products available in GEE. Surface spectral reflectance of bands 1 (Red) and 2 (NIR) are available at 250 m resolution (MOD09Q1 and MYD09Q1 products) and the MOD09A1 and the MYD09A1 products provide the surface spectral reflectance of band 7 (MIR) at 500m resolution. The MOD09A1 and the MYD09A1 file include quality control flags for clouds that are used to mask clouds in each MODIS tile. MODIS Terra data are available for our study region for the time since the year 2000, and MODIS Aqua data since the year 2003. MODIS surface reflectance data have been used abundantly for irrigation area mapping (e.g., [14,21,22,34,36]).
3.2. Other Data Sets
4. Methods
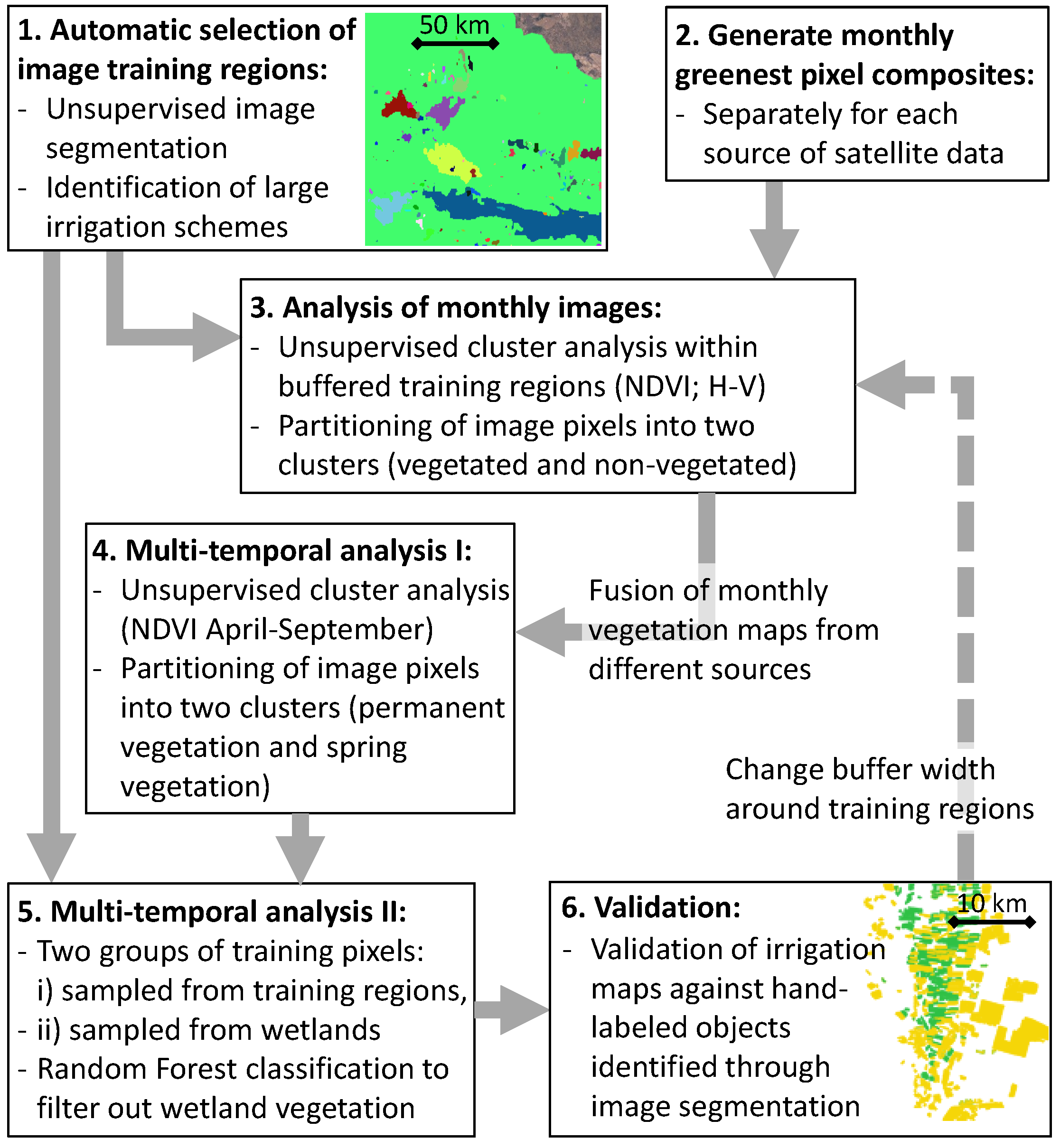
4.1. Method Overview
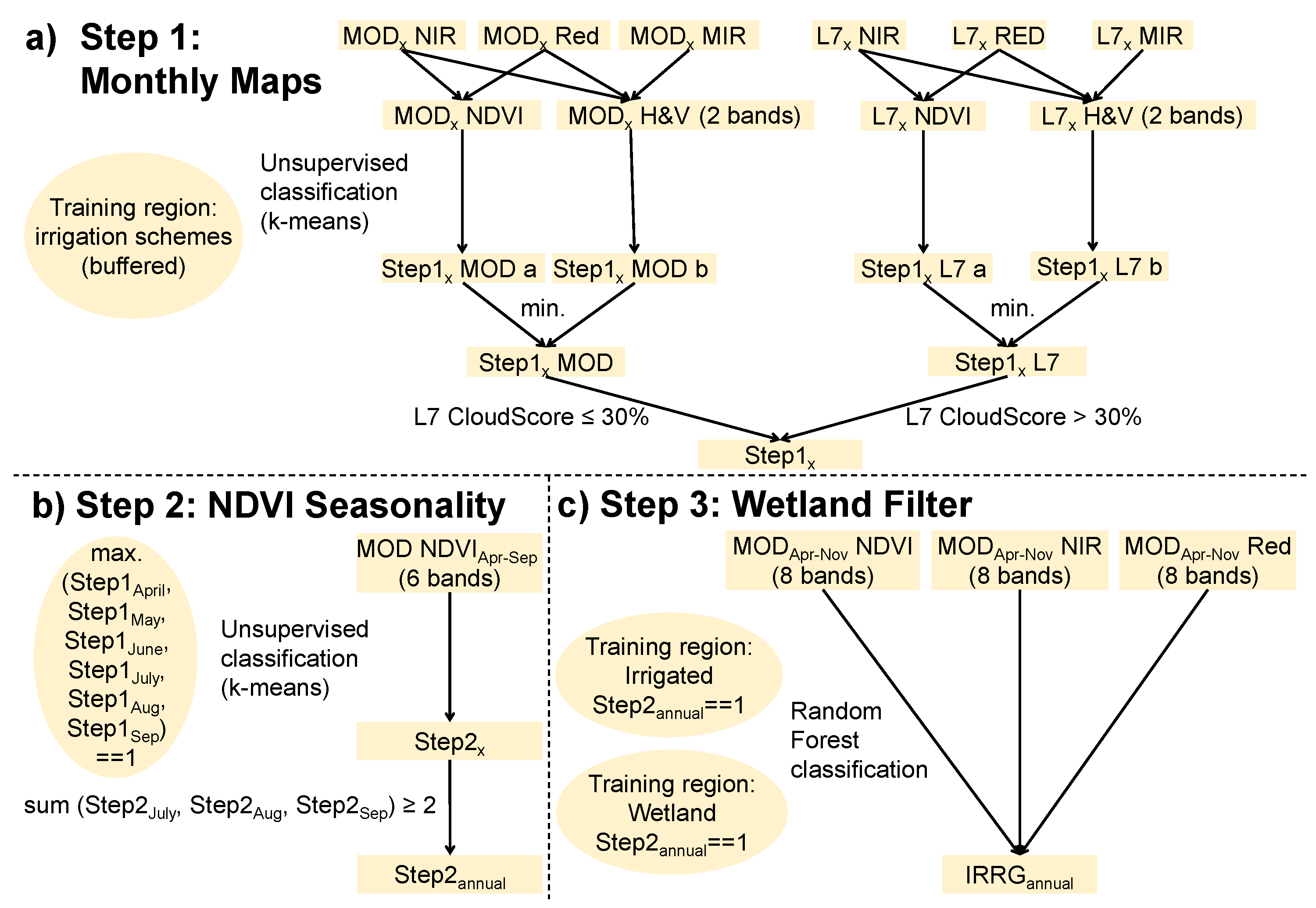
4.2. Identification of Training Sites for Unsupervised Classification
4.3. Monthly Vegetation Maps
4.4. Multi-Temporal Analysis
4.4.1. NDVI Time-Series
4.4.2. Summer Vegetation Filter
4.5. Compositing and Data Fusion
4.6. Classification Validation
4.6.1. Generation of Hand-Labeled Validation Data
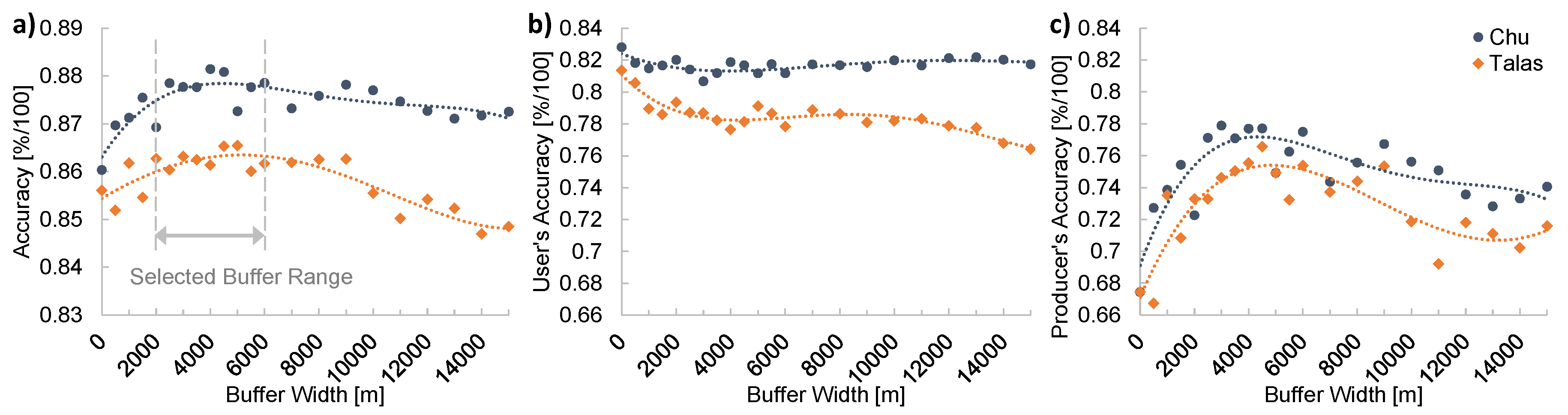
4.6.2. Accuracy Assessment
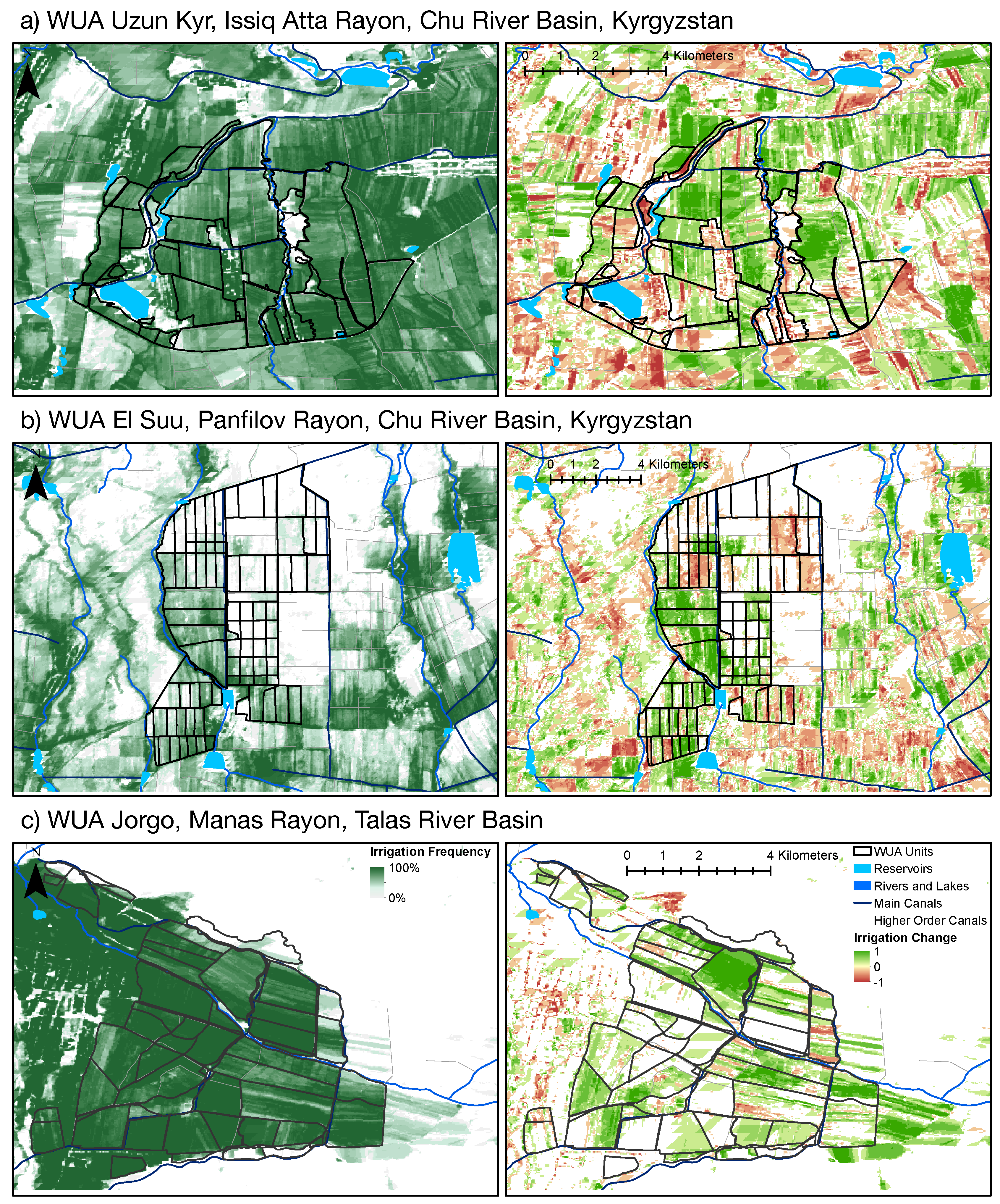
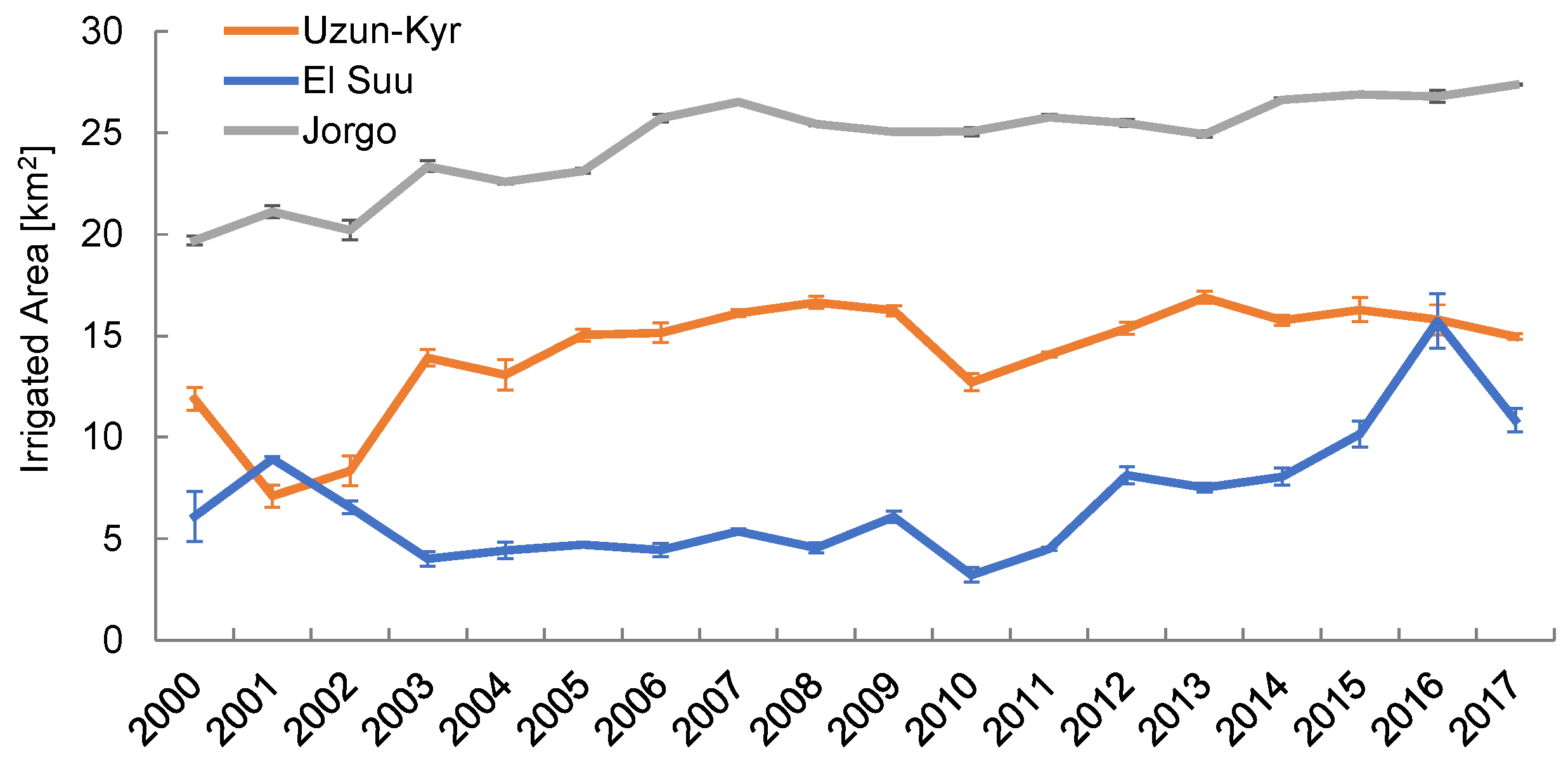
4.7. Analysis of Spatial and Temporal Trends
5. Results
5.1. Accuracy and Uncertainty Assessment of Classification Results
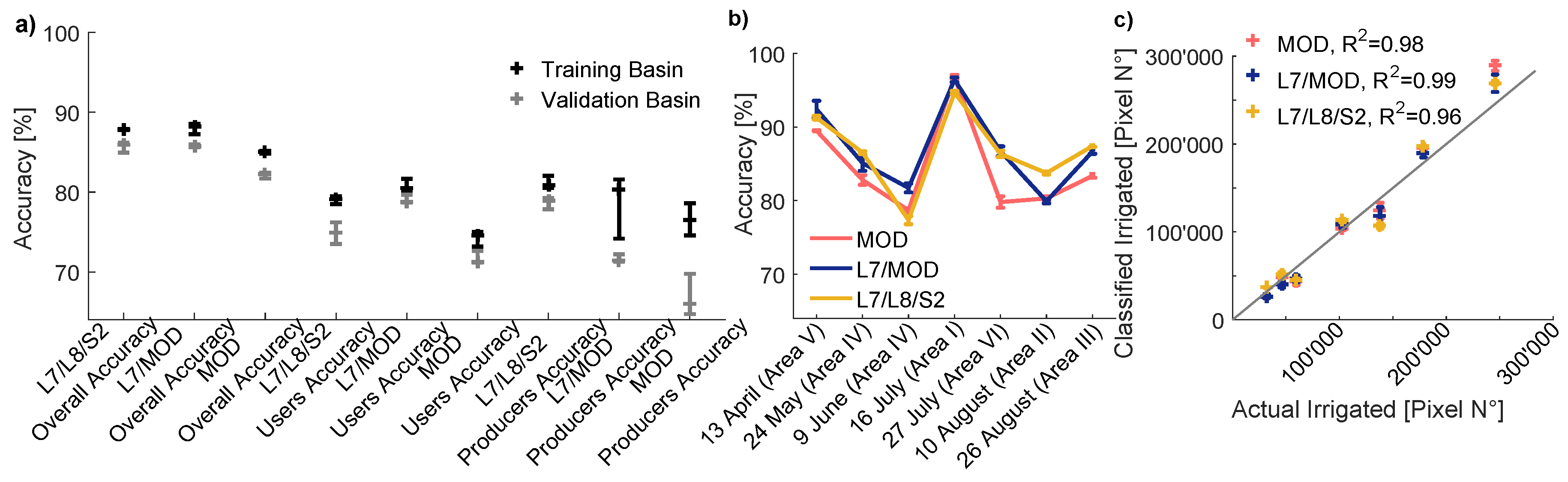
5.1.1. Validation Against Hand-Labeled Data
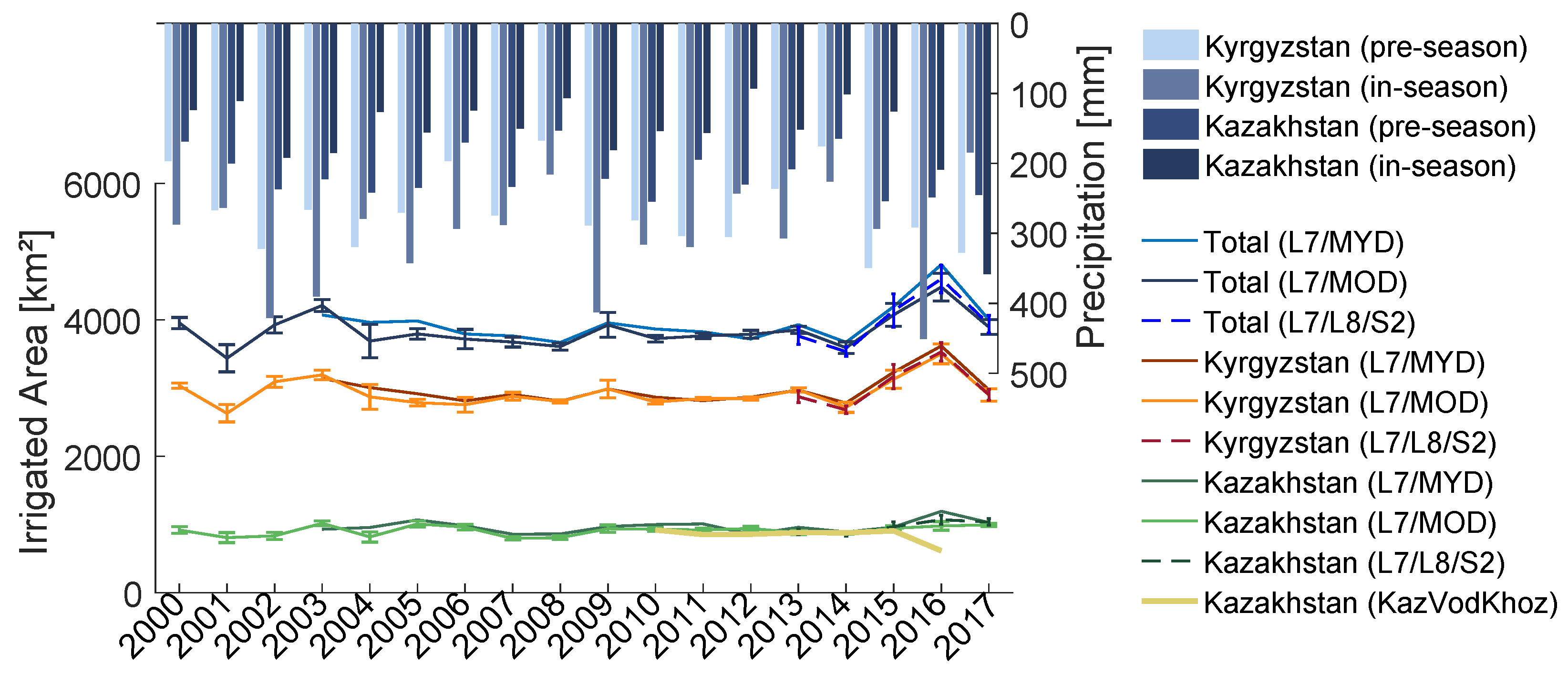
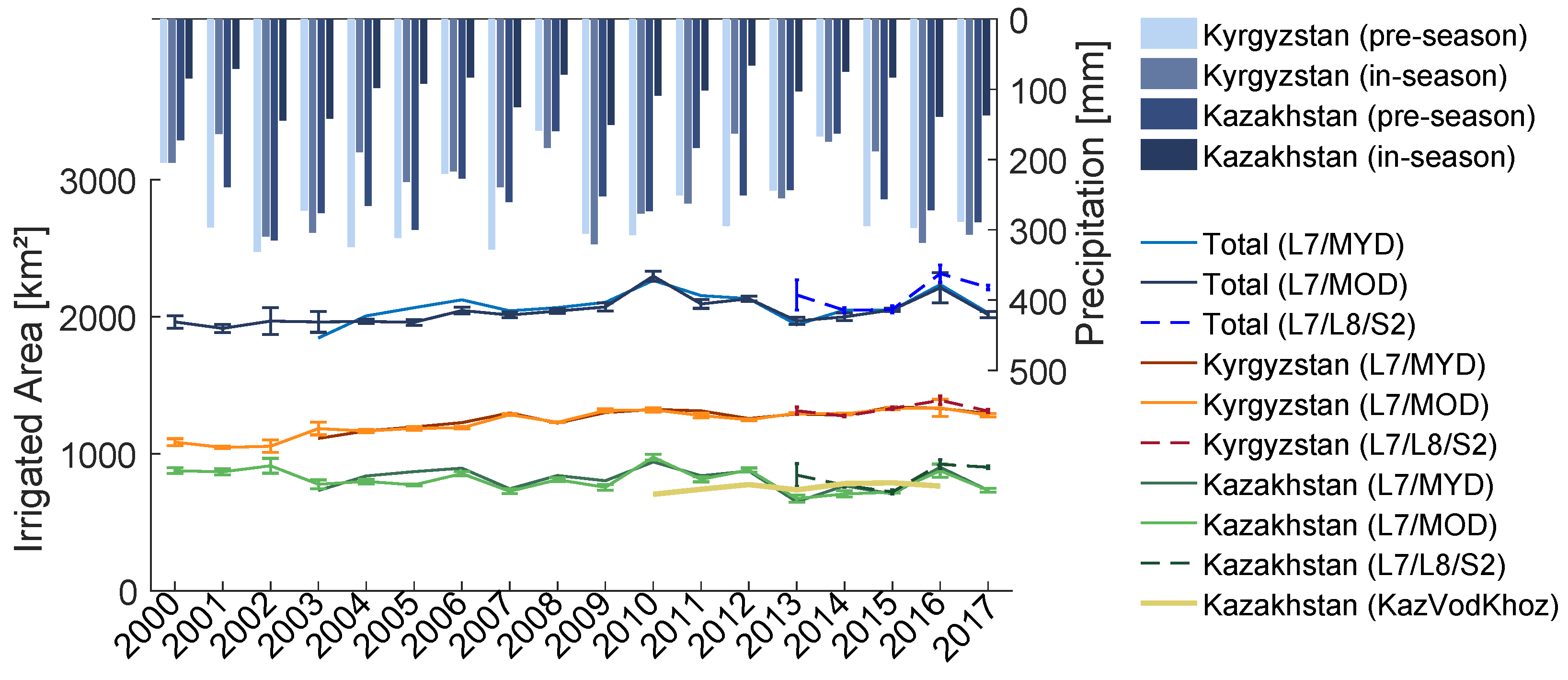
5.1.2. Uncertainty and Accuracy of Multi-Annual Irrigated Areas
5.2. Classification of Irrigated Areas
6. Discussion
6.1. Uncertainty and Accuracy Assessment
6.2. Monitoring of Agricultural Systems
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bastiaanssen, W.G.M.; Molden, D.J.; Makin, I.W. Remote sensing for irrigated agriculture: Examples from research and possible applications. Agric. Water Manag. 2000, 46, 137–155. [Google Scholar] [CrossRef]
- Seckler, D.W. World Water Demand and Supply, 1990 to 2025: Scenarios and Issues; IWMI: Colombo, Sri Lanka, 1998; Volume 19. [Google Scholar]
- Thenkabail, P.S.; Schull, M.; Turral, H. Ganges and Indus river basin land use/land cover (LULC) and irrigated area mapping using continuous streams of MODIS data. Remote Sens. Environ. 2005, 95, 317–341. [Google Scholar] [CrossRef]
- Bruinsma, J. World Agriculture: Towards 2015/2030: An FAO Perspective; Earthscan: London, UK, 2003; p. 432. [Google Scholar]
- Meier, J.; Zabel, F.; Mauser, W. A global approach to estimate irrigated areas—A comparison between different data and statistics. Hydrol. Earth Syst. Sci. 2018, 22, 1119–1133. [Google Scholar] [CrossRef]
- Thenkabail, P.S.; Wu, Z. An automated cropland classification algorithm (ACCA) for Tajikistan by combining landsat, MODIS, and secondary data. Remote Sens. 2012, 4, 2890–2918. [Google Scholar] [CrossRef]
- Xiong, J.; Thenkabail, P.S.; Gumma, M.K.; Teluguntla, P.; Poehnelt, J.; Congalton, R.G.; Yadav, K.; Thau, D. Automated cropland mapping of continental Africa using Google Earth Engine cloud computing. ISPRS J. Photogramm. Remote Sens. 2017, 126, 225–244. [Google Scholar] [CrossRef]
- Gao, Q.; Zribi, M.; Escorihuela, M.; Baghdadi, N.; Segui, P. Irrigation Mapping Using Sentinel-1 Time Series at Field Scale. Remote Sens. 2018, 10, 1495. [Google Scholar] [CrossRef]
- Estel, S.; Kuemmerle, T.; Alcántara, C.; Levers, C.; Prishchepov, A.; Hostert, P. Mapping farmland abandonment and recultivation across Europe using MODIS NDVI time series. Remote Sens. Environ. 2015, 163, 312–325. [Google Scholar] [CrossRef]
- Sharma, A.K.; Hubert-Moy, L.; Buvaneshwari, S.; Sekhar, M.; Ruiz, L.; Bandyopadhyay, S.; Corgne, S. Irrigation history estimation using multitemporal landsat satellite images: Application to an intensive groundwater irrigated agricultural watershed in India. Remote Sens. 2018, 10. [Google Scholar] [CrossRef]
- Ambika, A.K.; Wardlow, B.; Mishra, V. Remotely sensed high resolution irrigated area mapping in India for 2000 to 2015. Sci. Data 2016, 3, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Conrad, C.; Schönbrodt-Stitt, S.; Löw, F.; Sorokin, D.; Paeth, H. Cropping intensity in the Aral Sea Basin and its dependency from the runoffformation 2000–2012. Remote Sens. 2016, 8. [Google Scholar] [CrossRef]
- Alexandridis, T.K.; Zalidis, G.C.; Silleos, N.G. Mapping irrigated area in Mediterranean basins using low cost satellite Earth Observation. Comput. Electron. Agric. 2008, 64, 93–103. [Google Scholar] [CrossRef]
- Biggs, T.W.; Thenkabail, P.S.; Gumma, M.K.; Scott, C.A.; Parthasaradhi, G.R.; Turral, H.N. Irrigated area mapping in heterogeneous landscapes with MODIS time series, ground truth and census data, Krishna Basin, India. Int. J. Remote Sens. 2006, 27, 4245–4266. [Google Scholar] [CrossRef]
- Thenkabail, P.S.; Biradar, C.M.; Noojipady, P.; Dheeravath, V.; Li, Y.; Velpuri, M.; Gumma, M.; Gangalakunta, O.R.P.; Turral, H.; Cai, X.; et al. Global irrigated area map (GIAM), derived from remote sensing, for the end of the last millennium. Int. J. Remote Sens. 2009, 30, 3679–3733. [Google Scholar] [CrossRef]
- Jin, N.; Tao, B.; Ren, W.; Feng, M.; Sun, R.; He, L.; Zhuang, W.; Yu, Q. Mapping irrigated and rainfed wheat areas using multi-temporal satellite data. Remote Sens. 2016, 8, 1–19. [Google Scholar] [CrossRef]
- Bisquert, M.; Bégué, A.; Deshayes, M. Object-based delineation of homogeneous landscape units at regional scale based on modis time series. Int. J. Appl. Earth Obs. Geoinf. 2015, 37, 72–82. [Google Scholar] [CrossRef]
- Costa, H.; Carrão, H.; Bação, F.; Caetano, M. Combining per-pixel and object-based classifications for mapping land cover over large areas. Int. J. Remote Sens. 2014, 35, 738–753. [Google Scholar] [CrossRef]
- Xiong, J.; Thenkabail, P.S.; Tilton, J.C.; Gumma, M.K.; Teluguntla, P.; Oliphant, A.; Congalton, R.G.; Yadav, K.; Gorelick, N. Nominal 30-m Cropland Extent Map of Continental Africa by Integrating Pixel-Based and Object-Based Algorithms Using Sentinel-2 and Landsat-8 Data on Google Earth Engine. Remote Sens. 2017, 9, 65. [Google Scholar] [CrossRef]
- Ozdogan, M.; Yang, Y.; Allez, G.; Cervantes, C. Remote sensing of irrigated agriculture: Opportunities and challenges. Remote Sens. 2010, 2, 2274–2304. [Google Scholar] [CrossRef]
- Ozdogan, M.; Gutman, G. A new methodology to map irrigated areas using multi-temporal MODIS and ancillary data: An application example in the continental US. Remote Sens. Environ. 2008, 112, 3520–3537. [Google Scholar] [CrossRef]
- Xiao, X.; Boles, S.; Liu, J.; Zhuang, D.; Frolking, S.; Li, C.; Salas, W.; Moore, B. Mapping paddy rice agriculture in southern China using multi-temporal MODIS images. Remote Sens. Environ. 2005, 95, 480–492. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Siebert, S.; Döll, P.; Hoogeveen, J.; Faures, J.M.; Frenken, K.; Feick, S. Development and validation of the global map of irrigation areas. Hydrol. Earth Syst. Sci. 2005, 9, 535–547. [Google Scholar] [CrossRef]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World map of the Köppen-Geiger climate classification updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef]
- Funk, C.C.; Peterson, P.J.; Landsfeld, M.F.; Pedreros, D.H.; Verdin, J.P.; Rowland, J.D.; Romero, B.E.; Husak, G.J.; Michaelsen, J.C.; Verdin, A.P. A Quasi-Global Precipitation Time Series for Drought Monitoring; Technical Report, US Geological Survey; Earth Resources Observation and Science (EROS) Center: Sioux Falls, South Dakota, 2014. [Google Scholar]
- Demydenko, A. The evolution of bilateral agreements in the face of changing geo-politics in the Chu-Talas basin. In Proceedings of the International Conference ‘WATER: A Catalyst for Peace’, Zaragoza, Spain, 6–8 October 2005. [Google Scholar]
- Alekseevskii, N.; Osmonbetova, D. Similarities and Differences in Reservoirs of Kyrgyzstan. Power Technol. Eng. (Former. Hydrotech. Construct.) 2001, 35, 40–45. [Google Scholar] [CrossRef]
- Bucknall, J.; Klytchnikova, I.; Lampietti, J.; Lundell, M.; Scatasta, M.; Thurman, M. Irrigation in Central Asia. Social, Economic and Environmental Considerations; Technical Report February; The World Bank: Washington, DC, USA, 2003. [Google Scholar]
- Chen, J.; Zhu, X.; Vogelmann, J.E.; Gao, F.; Jin, S. A simple and effective method for filling gaps in Landsat ETM+ SLC-off images. Remote Sens. Environ. 2011, 115, 1053–1064. [Google Scholar] [CrossRef]
- Markham, B.L.; Storey, J.C.; Williams, D.L.; Irons, J.R. Landsat sensor performance: History and current status. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2691–2694. [Google Scholar] [CrossRef]
- Abuzar, M.; McAllister, A.; Whitfield, D. Mapping irrigated farmlands using vegetation and thermal thresholds derived from Landsat and ASTER data in an irrigation district of Australia. Photogramm. Eng. Remote. Sens. 2015, 81, 229–238. [Google Scholar] [CrossRef]
- Roy, D.P.; Ju, J.; Lewis, P.; Schaaf, C.; Gao, F.; Hansen, M.; Lindquist, E. Multi-temporal MODIS-Landsat data fusion for relative radiometric normalization, gap filling, and prediction of Landsat data. Remote Sens. Environ. 2008, 112, 3112–3130. [Google Scholar] [CrossRef]
- Chen, Y.; Lu, D.; Luo, L.; Pokhrel, Y.; Deb, K.; Huang, J.; Ran, Y. Detecting irrigation extent, frequency, and timing in a heterogeneous arid agricultural region using MODIS time series, Landsat imagery, and ancillary data. Remote Sens. Environ. 2018, 204, 197–211. [Google Scholar] [CrossRef]
- Belgiu, M.; Csillik, O. Sentinel-2 cropland mapping using pixel-based and object-based time-weighted dynamic time warping analysis. Remote Sens. Environ. 2018, 204, 509–523. [Google Scholar] [CrossRef]
- Pervez, M.S.; Brown, J.F. Mapping irrigated lands at 250-m scale by merging MODIS data and National Agricultural Statistics. Remote Sens. 2010, 2, 2388–2412. [Google Scholar] [CrossRef]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The shuttle radar topography mission. Rev. Geophys. 2007, 45, 1–33. [Google Scholar] [CrossRef]
- Jarvis, A.; Reuter, H.I.; Nelson, A.; Guevara, E. Hole-Filled SRTM for the Globe Version 4. Available online: http://srtm.csi.cgiar.org (accessed on 1 June 2018).
- Hojjatoleslami, S.A.; Kittler, J. Region growing: A new approach. IEEE Trans. Image Process. 1998, 7, 1079–1084. [Google Scholar] [CrossRef] [PubMed]
- Sathya, B.; Manavalan, R. Image Segmentation by Clustering Methods: Performance Analysis. Int. J. Comput. Appl. 2011, 29, 27–32. [Google Scholar] [CrossRef]
- Clark, B.; Pellikka, P. Landscape analysis using multiscale segmentation and object orientated classification. Recent Adv. Remote Sens. Geoinf. Process. Land Degrad. Assess. 2009, 8, 323–341. [Google Scholar]
- McGuire, R.G. Reporting of objective color measurements. HortScience 1992, 27, 1254–1255. [Google Scholar]
- Nicholson, S.E.; Davenport, M.L.; Malo, A.R. A comparison of the vegetation response to rainfall in the Sahel and East Africa, using normalized difference vegetation index from NOAA AVHRR. Clim. Chang. 1990, 17, 209–241. [Google Scholar] [CrossRef]
- Xiao, X.; He, L.; Salas, W.; Li, C.; Moore Iii, B.; Zhao, R.; Frolking, S.; Boles, S. Quantitative relationships between field-measured leaf area index and vegetation index derived from VEGETATION images for paddy rice fields. Int. J. Remote Sens. 2002, 23, 3595–3604. [Google Scholar] [CrossRef]
- Prince, S. Satellite remote sensing of primary production: Comparison of results for Sahelian grasslands 1981–1988. Int. J. Remote Sens. 1991, 12, 1301–1311. [Google Scholar] [CrossRef]
- Gutman, G.; Ignatov, A. The derivation of the green vegetation fraction from NOAA/AVHRR data for use in numerical weather prediction models. Int. J. Remote Sens. 1998, 19, 1533–1543. [Google Scholar] [CrossRef]
- Pekel, J.F.; Vancutsem, C.; Bastin, L.; Clerici, M.; Vanbogaert, E.; Bartholomé, E.; Defourny, P. A near real-time water surface detection method based on HSV transformation of MODIS multi-Spectral time series data. Remote Sens. Environ. 2014, 140, 704–716. [Google Scholar] [CrossRef]
- Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A k-means clustering algorithm. J. R. Stat. Soc. Ser. C 1979, 28, 100–108. [Google Scholar] [CrossRef]
- MacQueen, J. Some methods for classification and analysis of multivariate observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Oakland, CA, USA, 21 June–18 July 1965; Volume 1, pp. 281–297. [Google Scholar]
- Portmann, F.T.; Siebert, S.; Döll, P. MIRCA2000-Global monthly irrigated and rainfed crop areas around the year 2000: A new high-resolution data set for agricultural and hydrological modeling. Glob. Biogeochem. Cycles 2010, 24. [Google Scholar] [CrossRef]
- Zhao, H.; Yang, Z.; Di, L.; Li, L.; Zhu, H. Crop phenology date estimation based on NDVI derived from the reconstructed MODIS daily surface reflectance data. In Proceedings of the 17th International Conference on Geoinformatics, Fairfax, VA, USA, 12–14 August 2009; pp. 1–6. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.F.; Ghimire, B.; Rogan, J.; Chica-Olmo, M.; Rigol-Sanchez, J.P. An assessment of the effectiveness of a random forest classifier for land-cover classification. ISPRS J. Photogramm. Remote Sens. 2012, 67, 93–104. [Google Scholar] [CrossRef]
- Oshiro, T.M.; Perez, P.S.; Baranauskas, J.A. How Many Trees in a Random Forest. In Machine Learning and Data Mining in Pattern Recognition; Perner, P., Ed.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 154–168. [Google Scholar]
- Pelletier, C.; Valero, S.; Inglada, J.; Champion, N.; Sicre, C.M.; Dedieu, G. Effect of training class label noise on classification performances for land cover mapping with satellite image time series. Remote Sens. 2017, 9, 173. [Google Scholar] [CrossRef]
- Shrestha, B.; O’Hara, C.; Mali, P. Multi-Sensor & Temporal Data Fusion for Cloud-Free Vegetation Index Composites. In Sensor and Data Fusion; Milisavljevic, N., Ed.; InTech: Rijeka, Croatia, 2009; pp. 263–276. [Google Scholar] [CrossRef]
- Gao, Q.; Zribi, M.; Escorihuela, M.J.; Baghdadi, N. Synergetic use of sentinel-1 and sentinel-2 data for soil moisture mapping at 100 m resolution. Sensors 2017, 17, 1966. [Google Scholar] [CrossRef] [PubMed]
- Google Inc. Google Earth Engine API; Google Inc.: Mountain View, CA, USA, 2018. [Google Scholar]
- Foody, G.M. Status of land cover classification accuracy assessment. Remote Sens. Environ. 2002, 80, 185–201. [Google Scholar] [CrossRef]
- Olofsson, P.; Foody, G.M.; Herold, M.; Stehman, S.V.; Woodcock, C.E.; Wulder, M.A. Good practices for estimating area and assessing accuracy of land change. Remote Sens. Environ. 2014, 148, 42–57. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Wegerich, K. Passing over the conflict. The Chu Talas basin agreement as a model for Central Asia. In Central Asian Waters: Social, Economic, Environmental and Governance Puzzle; Rahaman, M., Varis, O., Eds.; Water & Development Publications-Helsinki University of Technology: Helsinki, Finland, 2008; pp. 117–131. [Google Scholar]
- Kireycheva, L.; Mustafaev, J.; Tursynbayev, N. Transboundary Issues of Wildlife Management in the Talas River Basin. Int. Res. J. 2015, 11, 107–109. [Google Scholar] [CrossRef]
- El-Magd, I.A.; Tanton, T. Remote sensing and GIS for estimation of irrigation crop water demand. Int. J. Remote Sens. 2005, 26, 2359–2370. [Google Scholar] [CrossRef]

| Satellite | Code | GEE ImageCollection ID | Available Since | Used Bands | Spatial/Temporal Resolution |
|---|---|---|---|---|---|
| Landsat 7 | L7 | LANDSAT/LE07/C01/T1_TOA | 1999 | B1, B2, B3 | 30 m/16 days |
| Landsat 8 | L8 | LANDSAT/LC08/C01/T1_TOA | 2013 | B2, B3, B4 | 30 m/16 days |
| Sentinel 2 | S2 | COPERNICUS/S2 | 2015 | B4, B8A, B12 | 10–20 m/10 days |
| MODIS Terra | MOD | MOD09Q1 | 2000 | B1, B2 | 250 m/Daily |
| MODIS Terra | MOD | MOD09A1 | 2000 | B7 | 500 m/Daily |
| MODIS Aqua | MYD | MYD09Q1 | 2003 | B1, B2 | 250 m/Daily |
| MODIS Aqua | MYD | MYD09A1 | 2003 | B7 | 500 m/Daily |
| Buffer 2000–2017 | L7/MYD 2003–2017 | L7/L8/S2 2013–2017 | KazVodKhoz 2010–2016 | |
|---|---|---|---|---|
| Talas (KYG) | 1.4% | 1.8% | 2.3% | - |
| Talas (KAZ) | 2.7% | 4.5% | 15.2% | 16.0% |
| Talas | 1.8% | 2.6% | 4.2% | - |
| Chu (KYG) | 2.7% | 1.5% | 1.7% | - |
| Chu (KAZ) | 4.5% | 8.2% | 5.0% | 16.9% * |
| Chu | 2.9% | 3.7% | 2.0% | - |
| Irr. Area | mean (km2) | min (km2) | max (km2) | bsen (km2/year) | 95% CI (km2/year) | ΔA2000–2017 | Cor P (pre-seas.) | Cor P (in-seas.) |
|---|---|---|---|---|---|---|---|---|
| Talas | 2038 | 1916 | 2297 | 11.0 ** | [3.1 18.8] | 9.5% | 0.07 | 0.18 |
| Talas (KYG) | 1230 | 1047 | 1335 | 14.5 *** | [9.8 19.6] | 22.8% | −0.04 | 0.24 |
| Talas (KAZ) | 808 | 673 | 976 | −6.4 | [−13.5 2.1] | −12.3% | 0.13 | −0.02 |
| Chu | 3840 | 3437 | 4481 | 11.5 | [−13.9 32.9] | 4.9% | 0.39 | 0.71 *** |
| Chu (KYG) | 2931 | 2630 | 3502 | 6.9 | [−14.9 24.6] | 3.9% | 0.33 | 0.67 ** |
| Chu (KAZ) | 909 | 796 | 1018 | 4.4 | [−3.5 11.7] | 8.2% | 0.24 | 0.47 * |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ragettli, S.; Herberz, T.; Siegfried, T. An Unsupervised Classification Algorithm for Multi-Temporal Irrigated Area Mapping in Central Asia. Remote Sens. 2018, 10, 1823. https://doi.org/10.3390/rs10111823
Ragettli S, Herberz T, Siegfried T. An Unsupervised Classification Algorithm for Multi-Temporal Irrigated Area Mapping in Central Asia. Remote Sensing. 2018; 10(11):1823. https://doi.org/10.3390/rs10111823
Chicago/Turabian StyleRagettli, Silvan, Timo Herberz, and Tobias Siegfried. 2018. "An Unsupervised Classification Algorithm for Multi-Temporal Irrigated Area Mapping in Central Asia" Remote Sensing 10, no. 11: 1823. https://doi.org/10.3390/rs10111823
APA StyleRagettli, S., Herberz, T., & Siegfried, T. (2018). An Unsupervised Classification Algorithm for Multi-Temporal Irrigated Area Mapping in Central Asia. Remote Sensing, 10(11), 1823. https://doi.org/10.3390/rs10111823





