1. Introduction
Solar radiation intercepted by vegetation canopies undergoes various physical and biological processes until it is either absorbed or escapes from the canopy boundaries. Monitoring these processes has been one of the biggest objectives of vegetation remote sensing. Radiative transfer (RT) theory bridges remote sensing observations and these processes that generate signals and, thus, is important for research regarding vegetation remote sensing [
1,
2,
3,
4].
Numerous radiative transfer models have been developed based on the RT theory. They can be broadly categorized as 1D [
5,
6,
7], 3D [
8,
9,
10], and stochastic [
11,
12] models. The 1D model is simple but less realistic, whereas the 3D model is realistic but complicated. Given this, the stochastic radiative transfer model (SRTM) was developed. In the SRTM, 3D canopy structure is considered using canopy pair-correlation function, which is defined as the probability of simultaneously finding phytoelements at two points [
11]. It has been shown that the SRTM integrates advantages of 3D and 1D RT models; it is as realistic as the 3D RT model and as simple as the 1D RT model [
11]. It has also been successfully adopted in generating leaf area index (LAI) and its sunlit portion from data collected from the EPIC instrument in the Deep Space Climate Observatory (DSCOVR) mission [
13].
Like the majority of the widely used RT models (e.g., the SAIL model [
14]), the SRTM assumes that leaves are ideal bi-Lambertian scatters [
11,
12], i.e., the incident radiation scattered by a leaf follows a cosine distribution about the leaf normal. Such assumption can reduce the number of model parameters and, consequently, simplify the photon-vegetation interactions. However, this is not the case in reality. Scattering from a leaf consists of two parts, diffuse and specular [
15,
16]. The former is primarily generated from photon interactions with the leaf interior. This part follows a near bi-Lambertian distribution [
17]. The latter results from radiation speculary reflected at the air-cuticle boundary. Unlike the diffuse part, the specular part exhibits a strong dependence on sun-sensor geometry. It varies with species and can be up to 50% in the visible bands [
18]. Individual leaves are, thus, non-Lambertian scatters.
There are certain attempts to incorporate leaf specular reflection into RT modeling. The general idea is to modify the leaf scattering phase function by accounting for leaf specular reflection, i.e., both diffuse and specular parts are considered [
17,
19,
20,
21]. By doing so, the specularly reflected radiation was shown to change the amount of radiation registered by the sensor, which is usually normalized and parameterized as the canopy bidirectional reflectance factor (
BRF, the ratio of surface leaving radiance and radiance from an ideal Lambertian surface under identical illumination conditions [
22]), especially at strongly absorbing bands. Additionally, few efforts have been devoted to fully exploring the influence of leaf specular reflection on canopy radiative regime. Compared to
BRF, the canopy radiative regime provides more comprehensive information about leaf specular reflection and its influences. Knowledge of leaf specular reflection and the canopy radiative regime will substantially help to improve forward canopy reflectance simulations, as well as backward inversions.
The goal of this paper is to propose an improved version of the SRTM by accounting for leaf specular reflection and exploring the influence of leaf specular reflection on the canopy radiative regime. In particular, we investigate its influences on vertical profiles of mean radiation flux density, canopy absorptance, BRF, and normalized difference vegetation index (NDVI, the ratio between the difference and sum of the canopy BRF in NIR and red bands).
The paper is organized as follows. A description of the improved version of the SRTM is presented in
Section 2. The evaluation of the model is presented in
Section 3. The analyses and discussion of the improved SRTM and influence of leaf specular reflection on the canopy radiative regime are given in
Section 4 and
Section 5, respectively. Finally,
Section 6 summarizes the results.
2. Methods
2.1. Stochastic Radiative Transfer Model
The stochastic radiative transfer model provides the most linkage among remotely measured mean intensity, leaf optical property, and canopy 3D structure. For a stochastic canopy medium that is confined to
, the horizontal mean intensity
for downward (
) and upward (
) directions at depth
can be descripted as the following equations [
11,
12]:
Here,
and
is the polar angle of direction
.
is the extinction coefficient.
is the probability of finding a foliated point at depth
. The second moment
represents the mean intensity that incidents on the leaf surface at depth
along direction
. The term
denotes the spherical integration of scattering as:
where,
is the differential scattering coefficient, which can be represented as
.
is the leaf area volume density.
is the area scattering phase function (or
-function).
and
describe the upper and lower boundary conditions.
Note that in the classical version of the SRTM,
is parametrized under the assumption that leaves are ideal bi-Lambertian scatters, i.e., leaf specular reflection is neglected [
11,
13]. In this case, the
-function can be expressed as:
Here, represents the leaf normal distribution function; denotes leaf scattering phase function; , , and are directions of the leaf normal, incident, and scattered radiation, respectively.
Equations (1)–(4) describe the key idea of the classical version of the SRTM. It should be noted that the most straightforward variable wherein leaf specular reflection matters is the leaf scattering phase function. Our next step is to modify this variable by accounting for leaf specular reflection.
2.2. Improvement of the SRTM by Accounting for Leaf Specular Reflection
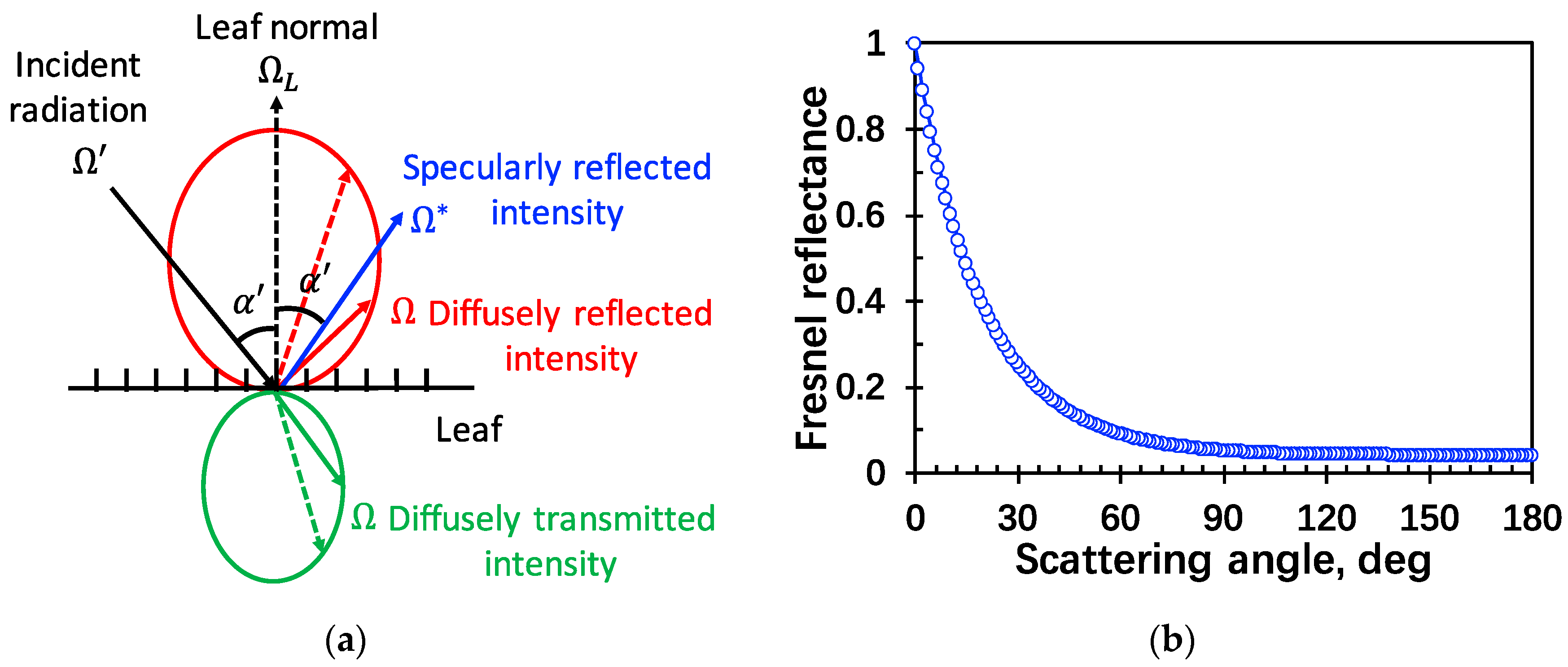
Accounting for leaf specular reflection in the SRTM needs parameterization of the scattering process that appears at the leaf scale. Radiation scattered from a leaf consists of two parts, diffuse (
) and specular (
), as
Figure 1a shows. Leaf scattering phase function (
) can be expressed as:
Spherical integration of Equation (5) results in leaf albedo , where is the scattering part for leaf specular reflection, and is the scattering part for leaf diffuse scattering, given that photons interact with leaf internal constituents.
It follows from Equation (5), one gets the total
-function as:
Here and are the -functions for the diffuse and specular part, respectively.
The specular area scattering phase function,
, describes the specularly reflected radiation resulting from photon interactions on the leaf surface. It can be evaluated as [
23]:
where
is a reduction factor;
is Fresnel reflectance describing the magnitude of specularly reflected radiation. In this model,
depends on the index of refraction,
n, a parameter
that quantifies the hairy cuticular structures (
) [
23], and the incident angle
The reduction factor proposed by Nilson and Kuusk is incorporated [
24], i.e.:
It has the desirable property as for small incident angles and for oblique incident angles. For small incident angles, the leaf surface roughness is smaller and, therefore, specularly reflected radiation is less reduced (i.e., ). However, for oblique incident angles, the roughness is greater and consequently lowers specularly reflected radiation (i.e., ).
The Fresnel reflectance is given by [
15]:
where the refractive angle,
i, is determined by the Snell’s law, i.e.,
.
varies with the incidence-view geometry. Variation of
as a function of scattering angle is illustrated in
Figure 1b. Note that when the incident radiation goes along the leaf normal, i.e.,
, Equation (9) becomes meaningless. In this special case, the Fresnel reflectance is defined as:
The leaf normal distribution function,
, is expressed as [
25]:
Here, is the polar angle of the leaf normal . Variables a and b represent planophile (a = 1, b = 2), erectophile (a = −1, b = 2), plagiophile (a = −1, b = 4), extremophile (a = 1, b = 4), and uniform (a = 0) distributions. For the spherical distribution, . Note that foliage is assumed to be azimuthally randomly oriented in this paper.
The diffuse area scattering phase function,
, describes the scattered radiation resulting from photon interactions within the leaf interior. The fraction of radiation that enters the leaf interior is
. It can be described by the following equation:
The leaf specular reflection is thus incorporated into the SRTM via Equations (5)–(12). Note that the improved version of the SRTM suggests that all photons that have not been specularly reflected enter the leaf interior. We will evaluate the model using field-measured data in the following section.
3. Evaluation of the Improved Version of the SRTM
The
BRF dataset collected from summer maize at Luancheng Agricultural Ecosystems Experimental Station, Chinese Academy of Sciences, Hebei province, China (37°52′N, 114°39′E) [
17] is used to evaluate the improved version of the SRTM. Summer maize represents one of the most typical food and forage crops in Northern China. It was also the subject of several completed sets of field campaigns carried out in July 2002, as part of a “Spectral Knowledge Library of Typical Land Surface Objects in China”. The field dataset includes (1) maize structural parameters, such as average maize height, LAI, average row-width, plant-to-plant interval, etc., and (2) optical properties of leaves, soil background and maize canopy [
17]. Characteristics of the maize canopy are presented in
Table 1. Note that the dataset has been used for an evaluation of a 3D Scene BRDF model, the radiosity-graphics combined model (RGM) [
17]. A detailed description on this station and the dataset is in [
17].
Nadir hemispherical reflectance (NHR) and transmittance (NHT) of ~10 pieces of summer maize leaves, ranging from new to mature, were measured on 21 July 2002 under laboratory conditions using a spectrophotometer (SE590, Spectron Engineering, Denver, USA) and an integrating sphere (Analytical Spectral Devices, Inc., Boulder, USA) in the spectral interval from 375 to 1100 nm with a spectral resolution of about 12 nm and a 3 nm sampling interval. Their averages denote the representatives of the maize leaf’s NHR and NHT.
The maize canopy
BRF was measured in the near principal plane using the SE590 spectrophotometer at local time 4:00 p.m., on 23 July 2002. The sensor was mounted on the arm of an automatic bracket device (Beijing Normal University, Beijing, China) at a height of 1.88 m, which ensured the maize canopy in the sensor’s field of view (
). The solar zenith angle (SZA) and solar azimuth angles (SAA) were
and
, respectively. For a given view zenith angle (VZA), the
BRF measurement could be done in 15 s. As a result, the
BRF were collected in the near principal plane in about 6 min. In addition, the ratios of direct to total incident radiation was measured simultaneously. Their values are shown in
Table 1. The nadir reflectance of soil background was measured using the SE590 right after the maize canopy
BRF measurements.
We selected four bands, blue (436 nm), green (547 nm), red (700 nm) and NIR (804 nm) as representatives for the evaluation. Optical properties of the leaf and soil background are listed in
Table 2. The Poisson germ-grain model with an identical ellipsoidal shape is used to parameterize the maize structure. The maize stem density,
d, is estimated with the ratio of unity to the product of row-width and plant-to-plant interval, i.e.,
. The maximum maize crown radius,
r, is assumed to be identical to the plant-to-plant interval, i.e.,
. Given stem density and crown radius, ground cover is calculated as
. Leaf angles are assumed to follow the uniform distribution function [
17]. The refractive index of the leaf wax,
n, and
are set to 1.5 and 0.3, respectively. The ratio of maize height to radius is adopted in the improved version of the SRTM to simulate the hot spot effect [
12].
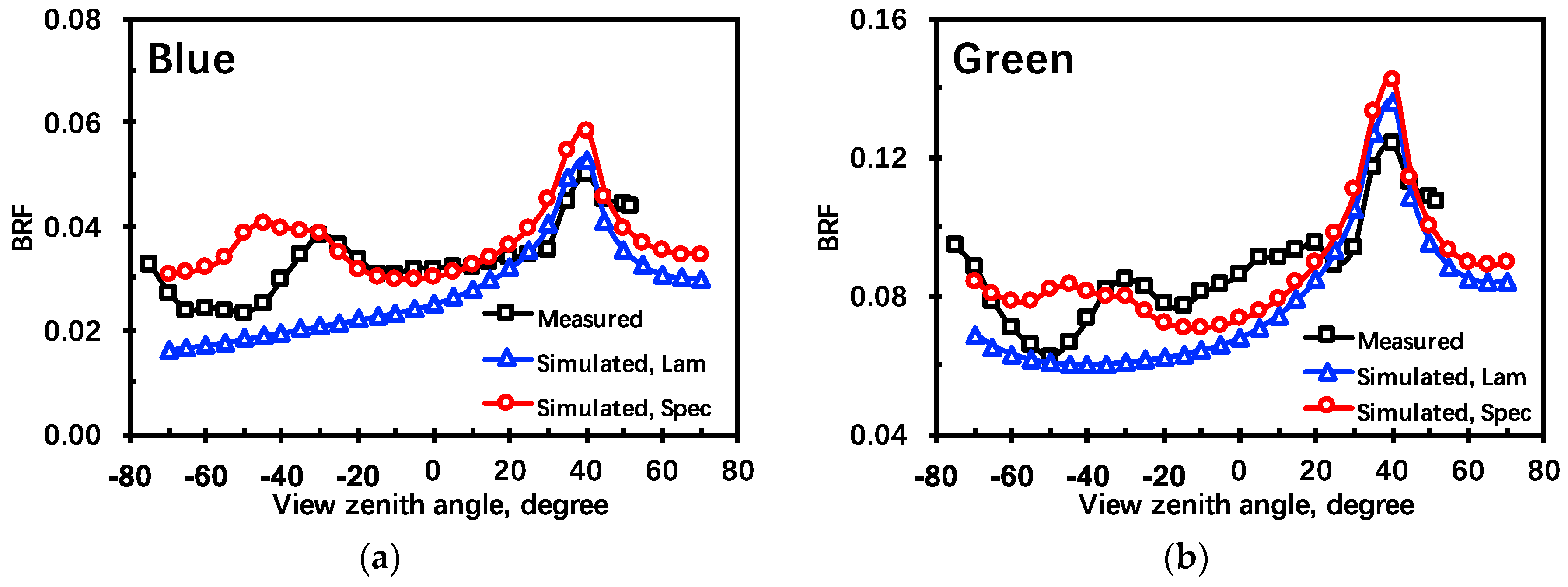
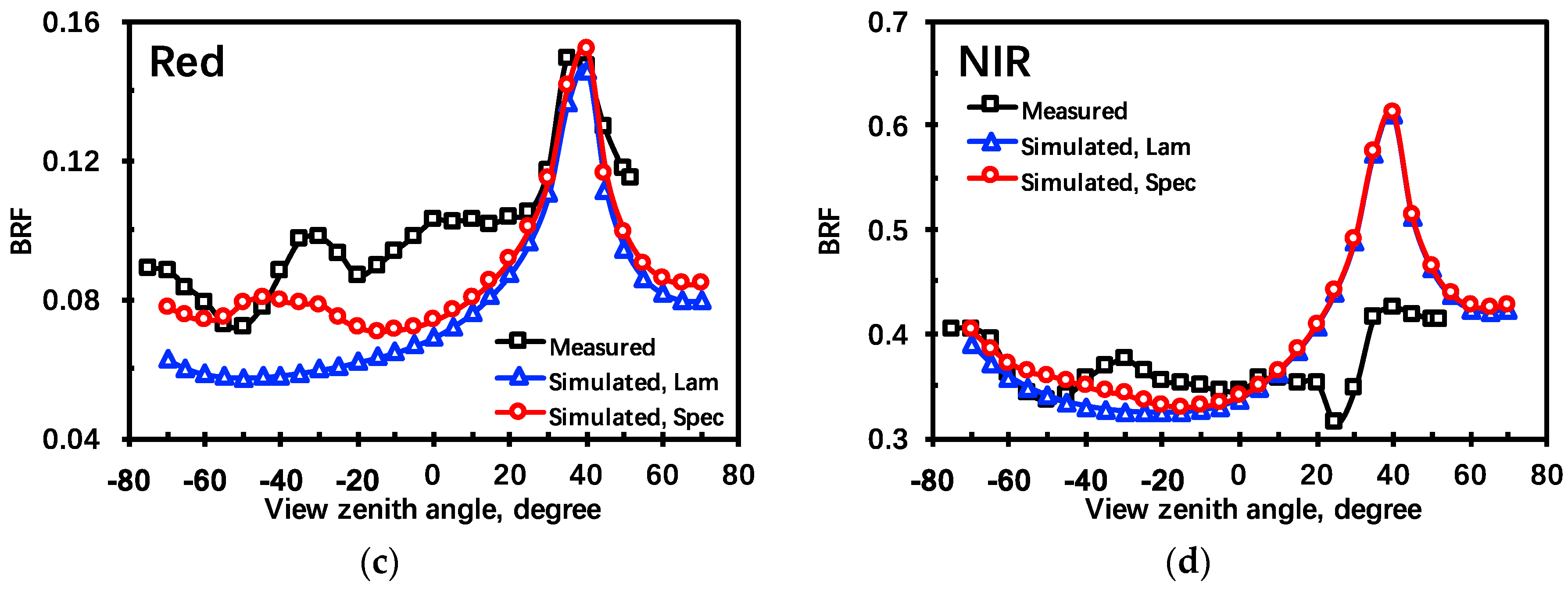
BRFs are firstly simulated with bi-Lambertian leaves using the classical version of the SRTM and then with non-Lambertian leaves using the improved version of the SRTM. Given that the illumination condition was a mixture of direct solar radiation and diffuse sky radiation (
Table 1), each version of the SRTM is executed twice under purely direct solar radiation and purely diffuse sky radiation. The final modeled
BRF is a weighted sum of the
BRF calculated from both illumination conditions using the ratios of direct to total incident radiation. The modeled
BRF is then compared with the field-measured
BRF. Their values at blue, green, red, and NIR bands in the principal plane as a function of the view zenith angle is illustrated in
Figure 2.
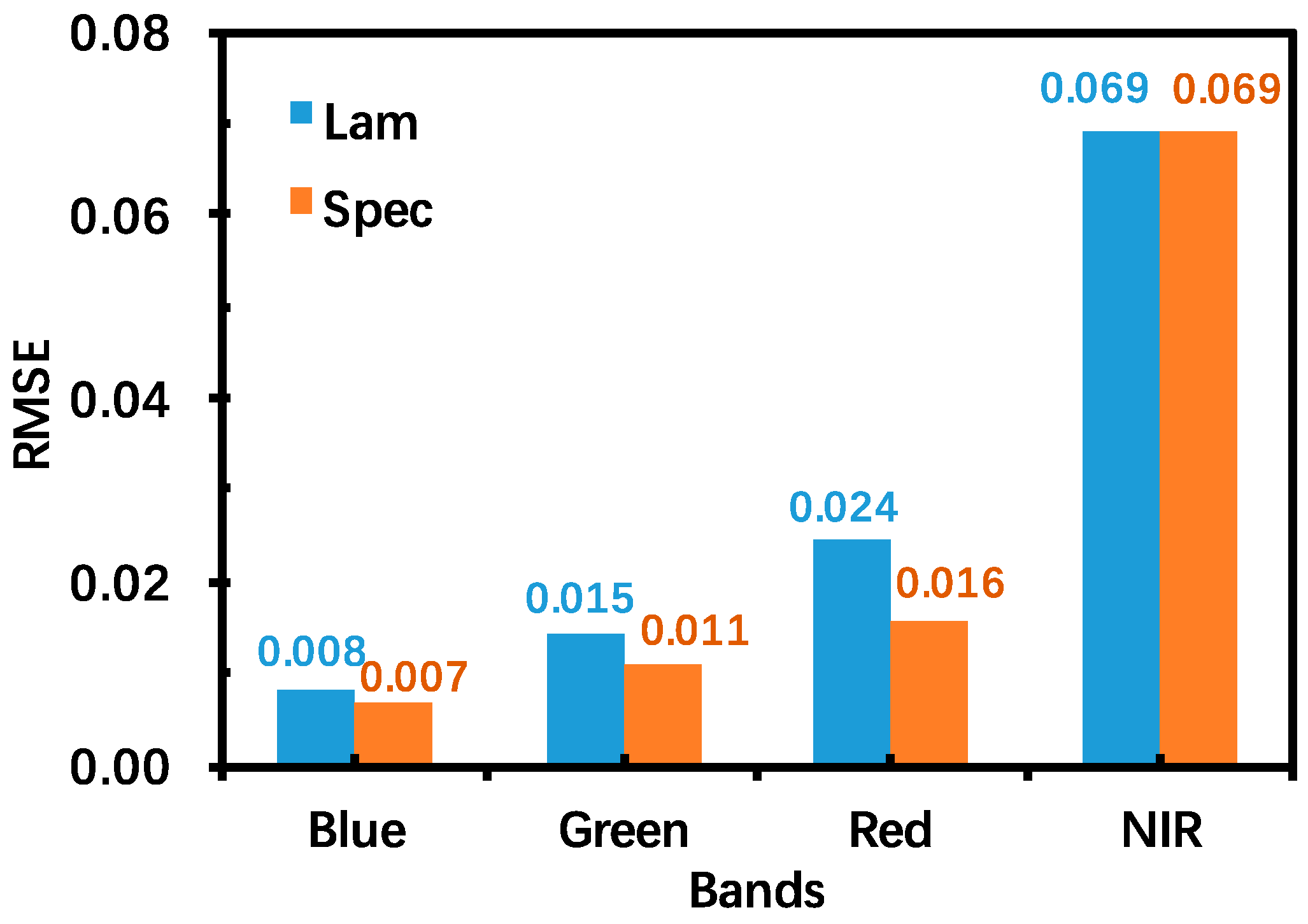
We use the root mean squared error (
RMSE) to quantify the proximity between field-measured
BRF,
, and modeled
BRF,
, i.e.:
Here,
and
represent components of
and
, respectively.
M is the number of view directions in the near principal plane. The
RMSEs between field-measured and modeled
BRF at blue, green, red, and NIR bands are shown in
Figure 3.
As shown in
Figure 2, the modeled
BRF using the improved version of the SRTM fits better with the field-measured data than that using the classical version, indicating that accounting for leaf specular reflection in the SRTM provides more realistic results than when this specular part is neglected. The
RMSE is decreased by 16.5%, 24.2%, 35.8%, and 0.15% at blue, green, red, and NIR bands, respectively. One may see the drop of
BRF at NIR band around
. It is caused by the detector’s or device shelf’s shadow [
17]. This effect significantly increases the
RMSE at the NIR band, as
Figure 3 illustrates. In addition, the heterogeneity of the maize canopy, measurement uncertainty and small environment changes may also attribute to the variations of maize
BRF.
Figure 2 and
Figure 3 thus support the improved version of the SRTM. Our next step is to explore the influence of leaf specular reflection on canopy radiative regime using the improved version of the SRTM.
4. Influence of Leaf Specular Reflection on Canopy Radiative Regime
The modification of the leaf scattering phase function by accounting for leaf specular reflection allows for a more realistic modeling of the canopy radiative regime, which definitely is different from that using the classical version of the SRTM. The goal of this section is to illustrate their differences and show how leaf specular reflection can influence the canopy radiative regime.
In our calculations, the stochastic canopy consists of identical cylindrical vegetation with crown height equal to canopy depth,
, i.e., the stochastic medium is confined to
. The crown base diameter (
) of the cylindrical-shaped vegetation is assumed to be equal to half of the canopy depth,
. Leaves are randomly distributed (i.e., turbid medium) within the crowns. In this case, the probability of finding a vegetated point at depth
is a constant and coincides with ground cover,
gc. To specify the relationship between canopy LAI and ground cover, plant LAI,
, which is defined as the amount of leaf area within canopy crowns (i.e.,
), is introduced. The following equation is thus derived:
. A detailed description on the above canopy structural parameters is documented in [
11].
Leaf angles are assumed to follow the spherical distribution function. The bi-Lambertian model is adopted to describe the leaf diffuse scattering part. Leaf diffuse hemispherical reflectance and transmittance are assumed to be identical and set to 0.07 at red and 0.38 at NIR bands. The leaf specular scattering part is parameterized using Fresnel reflectance with a constant refractive index, , at both bands. The reduction factor is set to . The vegetation canopy is illuminated by a parallel beam of unity intensity with a SZA and SAA of and , respectively.
The calculation includes two steps. Firstly, the improved version of SRTM is solved for mean intensity with leaf specular reflection accounted for in the leaf scattering phase function. Secondly, the first step is repeated using the classical version of SRTM, i.e., leaf specular reflection is neglected. In order to distinguish the mean intensity calculated from the two steps, we use subscripts “s” and “ns”, i.e., and , to represent the mean intensities calculated from Step 1 and Step 2, respectively. The differences between and will be utilized as measures to quantify the influence of leaf specular reflection on the canopy radiative regime.
4.1. Vertical Profiles of Mean Radiation Flux Density
In this subsection, we investigate the influence of leaf specular reflection on the canopy radiative regime by comparing the vertical profiles of mean radiation flux densities. The mean downward and upward flux densities from calculations using the improved version of the SRTM,
, and the classical version of the SRTM,
, are defined as follows [
11]:
Here, denotes either or . is the intensity of the incident radiation, which is unity in our calculation. and are cosine values of the SZA and the polar angle of direction . and represent integrations over downward and upward hemispherical spaces, respectively.
Figure 4 illustrates the vertical profiles of mean downward and upward radiation flux densities (
and
, respectively) at red and NIR bands for four types of ground cover conditions. In the former case when leaf specular reflection is accounted for, leaf albedo,
, is specified as the sum of leaf specular reflection and bi-Lambertian scattering, i.e.,
, where
is the leaf specular part and
is the leaf diffuse scattering part, given that photons interact with leaf internal constituents. However, in the latter case when leaf specular reflection is neglected (
), leaf albedo,
. The value of
is always greater than
because of the difference
. Thus, the leaf scattering is stronger in the case when leaf specular reflection is accounted for. In this example, the flux density can either be scattered downward or upward, indicating that accounting for leaf specular radiation increases both mean downward and upward radiation flux densities, i.e.,
, as
Figure 4 illustrates. The difference,
, is thus
, as
Figure 5 shows.
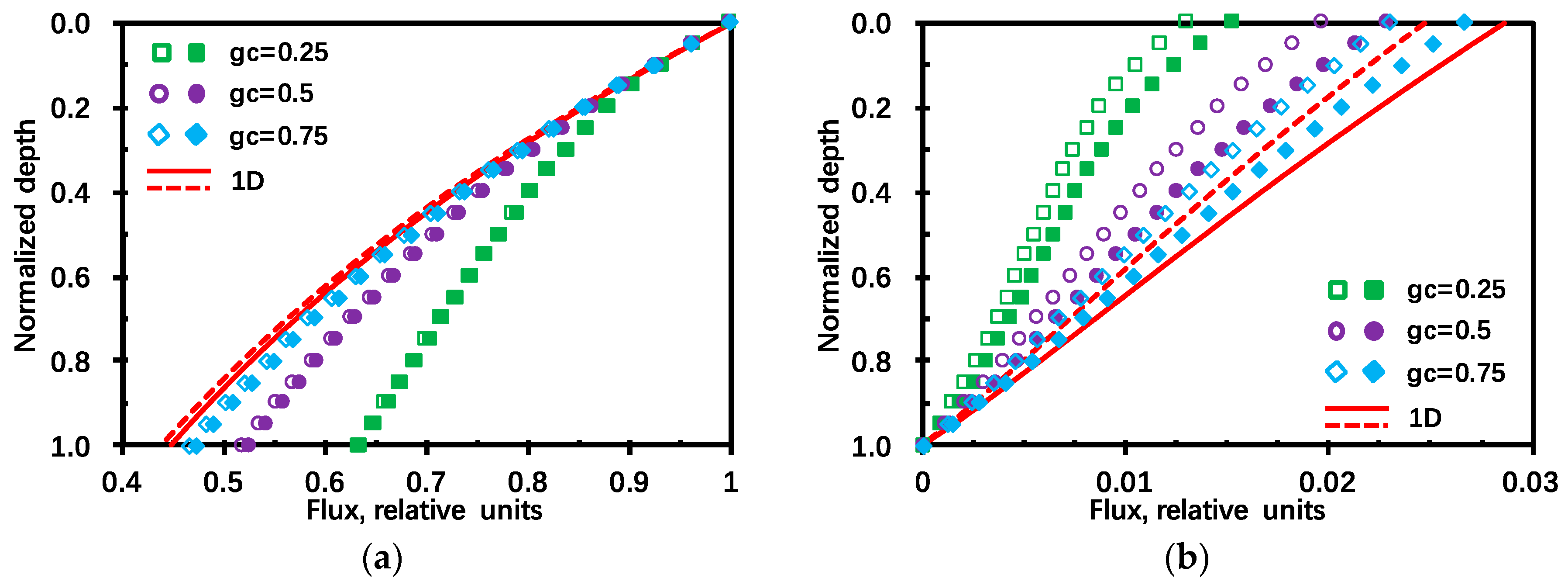
For the mean downward radiation flux density, a smaller ground cover results in less incident radiation being intercepted by the vegetation canopy. Since the intercepted radiation triggers future leaf specular reflection and consequently generates the difference (
), the smaller ground cover is, the smaller difference will be, as
Figure 5a,c illustrates. The intercepted radiation is thus primarily responsible for propagation of leaf surface reflection in the downward direction. It follows that the difference also increases with depth,
z. It reaches its maximum at the bottom of the vegetation canopy where the normalized depth,
z/H = 1. However, for a given canopy LAI (LAI = 1.5 in this example), the difference can be saturated. In such a case, the leaf area volume density within the crowns is dense and the intercepted radiation saturates with the increase of depth
z, as the green rectangles (
gc = 0.25 and
) in
Figure 5a,c illustrates.
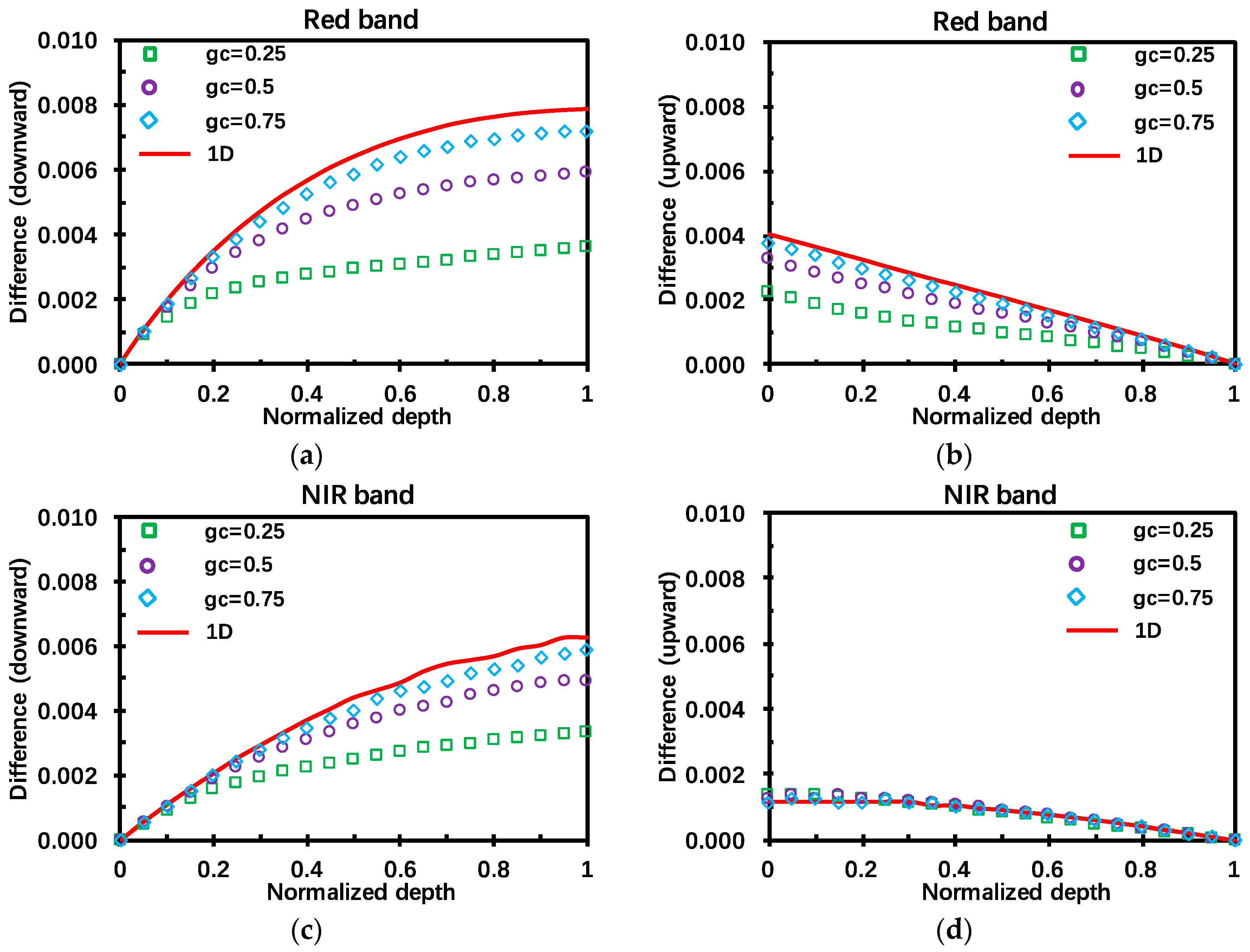
As for the difference in mean upward radiation flux density, it has the opposite tendency, i.e., the difference decreases with normalized depth. The deeper the depth is, the lower probability of the leaf specular reflection being generated. This consequently involves a decrease in the difference,
, as one can see from
Figure 5b,d. The difference also varies with ground cover, especially at strong absorbing band, i.e., the red band in this example. At the red band, the amount of leaf specular reflection generated from single scattering determines the difference. For a given canopy LAI, such a single scattering is an increasing function with respect to ground cover. However, at the NIR band, leaves absorb little radiation. Photons can undergo even more than 10 interactions with leaves before they are either absorbed or exit the canopy [
26]. Multiple scattering is so strong that the difference under different ground cover conditions is minimized, as
Figure 5d illustrates.
Overall, values of the differences are below 1% at red and NIR bands. However, the difference at red can account for up to 1.8% (=0.0079/0.4473) and 13% (=0.0040/0.0287) of the mean radiation flux density for the downward and upward directions. As for the NIR, the influences are smaller with up to 1.1% (=0.0062/0.5769) and 0.6% (=0.0012/0.1960) for the downward and upward directions.
4.2. Canopy Absorptance
Canopy absorptance conveys information on the amount of incident radiation that is potentially utilized in the photosynthetic process. Accurate monitoring of canopy absorptance is critical for many areas of research in hydrology, ecology, and climate change. The distribution of incident radiation within the vegetation canopy is mainly determined by canopy structure, which partitions canopy absorption, transmission and reflection. Additionally, leaf specular reflection decreases the amount of radiation that can enter leaf interiors, and consequently impacts canopy absorptance. In this subsection, we show examples of the influence of leaf specular reflection on canopy absorptance.
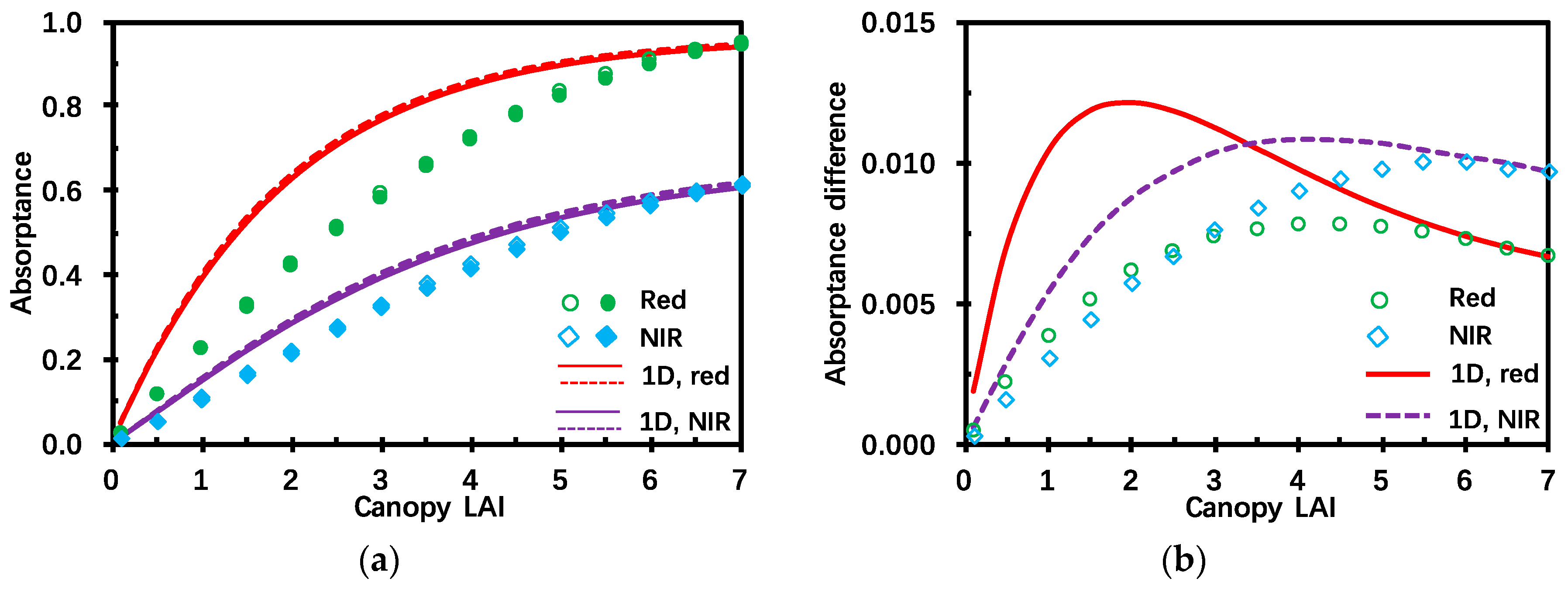
Figure 6a illustrates mean canopy absorptance for a vegetation canopy bounded from below by a non-reflecting background, which is calculated as
. Here,
represents canopy reflectance and
denotes canopy transmittance, as Equation (14) defines. Let
and
be canopy absorptances calculated with and without accounting for leaf specular reflection, respectively. Neglecting leaf specular reflection underestimates leaf albedo and, therefore, overestimates canopy absorptance when the underestimated leaf albedo is applied to the stochastic radiative transfer simulations, i.e.,
, as can be seen in
Figure 6a.
The difference,
, is given in
Figure 6b. As for the 1D canopy medium, the difference firstly increases and then decreases with canopy LAI. This is as expected because when the vegetation canopy is sparse, canopy interceptance will increase with the increase of canopy LAI, which indicates more incident radiation can be specular reflected and escapes the vegetation canopy from upper or lower boundaries. This in turn causes greater difference between
and
. However, when the vegetation canopy is dense enough, canopy interceptance does not increase rapidly with the increase of canopy LAI. Despite there still being more incident radiation which can be intercepted and specularly reflected by the vegetation canopy, a lesser amount of specular reflected radiation can exit the vegetation canopy. These two opposite features cannot compensate for each other and causes a decrease of difference,
, with the increase of canopy LAI. As for the stochastic canopy medium, we get similar tendencies, as the hollow symbols in
Figure 6b illustrate. However, the variation rate is lower than that of a 1D canopy because considering the within and between crown radiation regimes provides a more accurate saturation domain, i.e., the absorption is saturated at a slower rate for the stochastic medium than that of a 1D medium. A detailed relationship between the saturation domain and the stochastic or 1D canopy medium is discussed in [
11].
4.3. BRF and NDVI
The reflective property of the vegetated surface is widely interpreted in the remote sensing community. Such a property is usually described by
BRF.
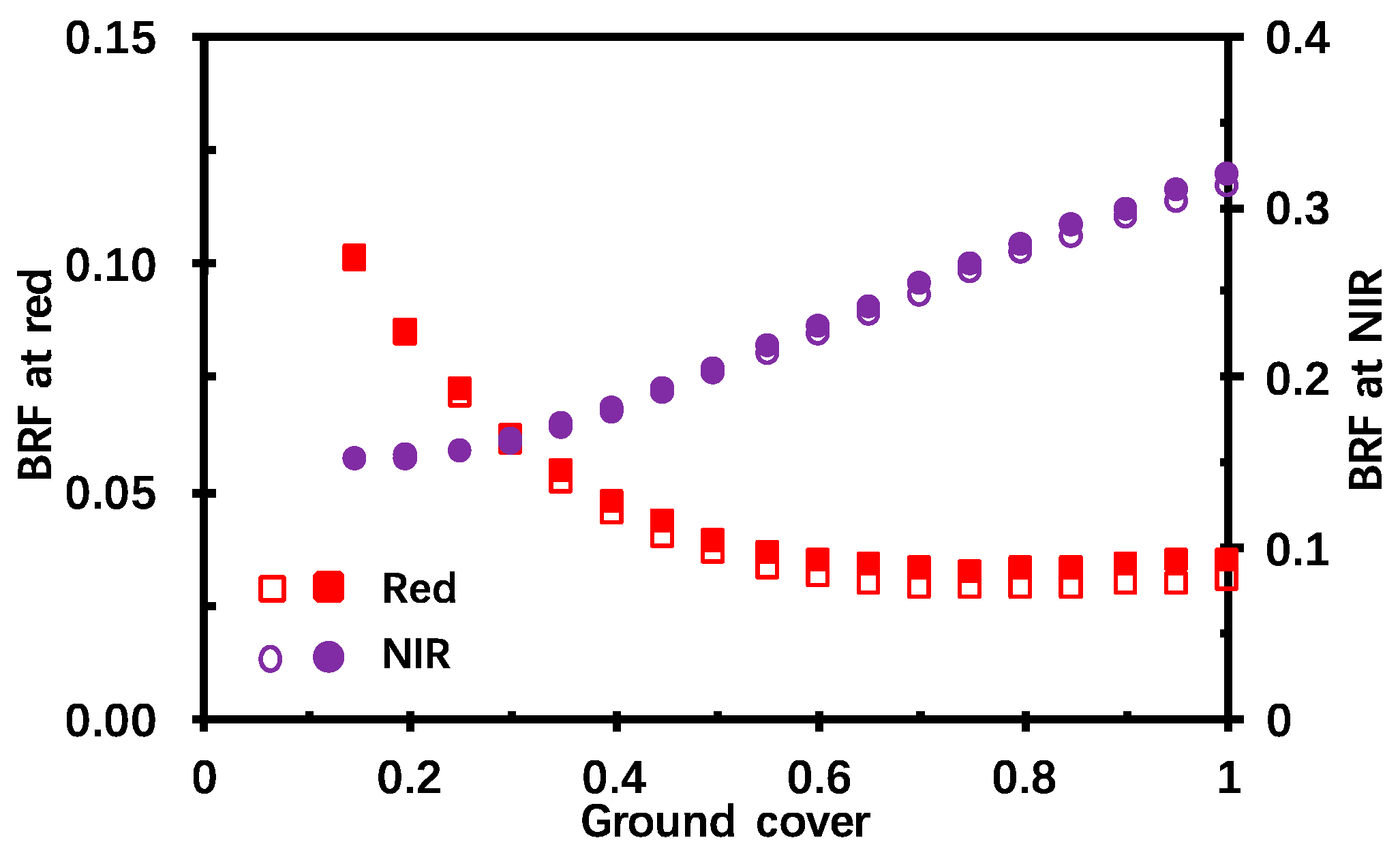
Figure 7 shows canopy
BRF at red and NIR bands in the nadir view direction. The canopy is bounded from below by a reflecting background with a surface albedo equals 0.18 at both bands. As one can see, canopy
BRFs vary with ground cover and have opposite tendencies for red and NIR bands. For the red band, canopy
BRF decreases with ground cover. At this band, little intercepted solar radiation is scattered by leaves. The contribution of background, therefore, dominates canopy
BRF. Such contribution decreases with ground cover and consequently canopy
BRF decreases. However, for the NIR band, canopy
BRF increases with ground cover. Despite the decreasing contribution of the background, the strong multiple scattering between leaves increases canopy
BRF.
As discussed earlier, accounting for leaf specular reflection increases leaf albedo, which indicates that more radiation can be scattered and escape the canopy from the upper boundary. Consequently, the canopy
BRF increases, as
Figure 7 shows. The difference can account for up to 17% (=(0.035 − 0.030)/0.030) and 2% (=(0.317 − 0.311)/0.311) of the canopy nadir
BRF at red and NIR bands when leaf specular reflection is neglected.
Canopy
BRF is often transformed to vegetation indices for the remote sensing of canopy nitrogen content, LAI, and fraction of absorbed photosynthetically active radiation (FPAR) [
27,
28,
29,
30], etc. Numerous vegetation indices are thus proposed. Among them, NDVI is quite easy to achieve and usually provides satisfactory results regarding such researches. Thus, it is one of the most popular vegetation indices. Let
and
be the NDVI calculated with and without accounting for leaf specular reflection, respectively. Here, we focus on the NDVI at the nadir direction and investigate the influence of leaf specular reflection on nadir NDVI.
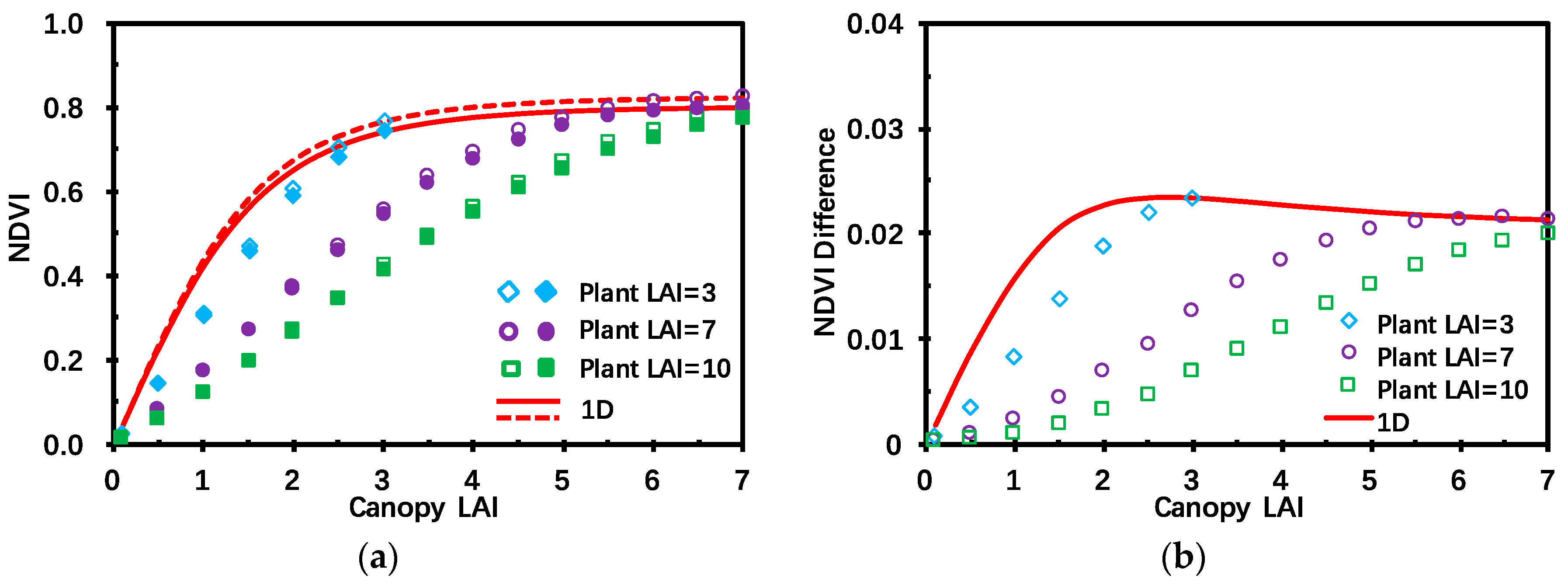
Figure 8 illustrates
,
and their difference,
, as a function of canopy LAI for four types of plant LAI. One can see that the results are quite similar to those presented in
Figure 6. The difference in the leaf scattering phase function is primarily responsible for this effect. When leaf specular reflection is accounted for, more radiation is scattered and escapes the canopy from upper or lower boundaries, which increases canopy
BRF at red and NIR bands (
Figure 7) and, consequently, decreases canopy NDVI, as
Figure 8a illustrates. It follows from
Figure 6b that the difference,
, firstly increases and then decreases with canopy LAI at difference variation rates for the 1D and stochastic canopy medium, as
Figure 8b shows.
To summarize, the classical version of the SRTM treats leaves as ideal bi-Lambertian scatters and does not account for leaf specular reflection and does not discriminate between radiation scattered from leaf surface and leaf interior. For a vegetation canopy with spherically inclined leaves, this results in, on one hand, underestimation of mean downward/upward radiation flux densities (
Figure 4 and
Figure 5) and canopy nadir
BRF (
Figure 7). On the other hand, it causes an overestimation of canopy absorptance (
Figure 6) and NDVI (
Figure 8). Accounting for leaf specular reflection in RT modeling is thus necessary for the remote sensing of vegetation because it provides a more accurate estimate of the canopy radiative regime.
5. Discussion
Solar radiation intercepted by vegetation canopies can either be scattered or absorbed. A passive optical instrument measures the amount of radiation below or/and above the canopy, which is further transferred to many variables that are linked to the vegetation functioning, such as the canopy
BRF, vegetation indices, LAI/FPAR, nitrogen content, etc. A fraction of the instrument registered radiation is caused by leaf specular reflection (
Figure 1). This fraction of radiation does not enter leaf interiors and exhibits a strong dependence on sun-sensor geometry. We use the Fresnel reflectance (Equation (9)) to parameterize the leaf specular reflection and propose an improved version of the SRTM. In this model, the leaf scattering phase function is modified accordingly (Equations (5), (7) and (12)) by assuming that all photons that have not been specularly reflected enter the leaf interior.
Canopy
BRF estimated from the improved model is evaluated through comparisons with field-measured maize
BRF. The maize in this paper is planted in rows. The structure of the maize canopy cannot be simplified as a classical 1D medium if one wants to model the maize
BRF at a high accuracy. The structure, however, is critical in the
BRF modeling because it impacts the distribution of specularly reflected and diffusely scattered radiation. Indeed, without increasing much computation cost, the row structure can be accurately parameterized using a parameter called pair correlation function in the SRTM [
11]. Our results in
Figure 2 are quite similar to those reported in [
17], which were achieved using a 3D RGM. The improved SRTM is, thus, a powerful tool for the remote sensing of vegetation because of its efficiency and accuracy. A detailed description on the pair correlation function and RGM are documented in [
11,
17], respectively. The improved model can, therefore, be used for investigating the influences of leaf specular reflection on the canopy radiative regime.
Accounting for the leaf specular reflection in the leaf scattering phase function increases leaf albedo, i.e., for a given amount of radiation incident upon a leaf, more radiation can be scattered and less radiation can be consequently absorbed (
Figure 4,
Figure 5 and
Figure 6). The distribution of canopy scattered radiation is determined by the canopy structure (e.g., LAI, leaf angles and ground cover). Despite overall canopy scattered radiation increasing, the reflectance or transmittance may increase or decrease for some directions. In our example, the nadir
BRF increases (
Figure 7). However, in other cases, it may decrease, as shown in [
17]. The variation of NDVI (
Figure 8) may also be different as it is a mathematical product of canopy
BRFs. Therefore, one should pay special attention to leaf specular reflection when it comes to remote sensing variables that are direction dependent, especially for the strongly absorbing band where the canopy specularly reflected radiation may be comparable or even greater than the canopy diffusely scattered radiation [
17,
31].
The influence is greater for downward/upward radiation flux densities and canopy nadir BRF than that for canopy absorptance and NDVI. This is mainly attributed to: (1) canopy absorptance being usually much greater than the contribution from leaf specular reflection and (2) NDVI tending to reduce (but not eliminate) the influence of leaf specular reflection. Our results suggest that the difference caused by leaf specular reflection can be up to 13% and 17% of the vertical profiles of radiation flux density and canopy nadir BRF, respectively. This may indicate that leaf specular reflection should be accounted for in the case when the error limit for modeling and measurement of vertical profiles of radiation flux density and canopy BRF is smaller than 13%.
Note that canopy
BRF at red and NIR bands and NDVI have been used in operational algorithm for generating global LAI/FPAR products from the MODIS, VIIRIS, and EPIC datasets [
13,
27,
28,
29]. Neglecting leaf specular reflection in the photon-canopy interactions causes underestimations of canopy
BRF at red and NIR bands and overestimation of canopy NDVI which, in turn, will result in overestimation of canopy LAI/FPAR [
28,
29,
32,
33,
34].
Besides the above influences, leaf specular reflection has recently been reported to decreases the accuracy of LAI estimates from LAI-2000 field measurements [
35] and remote sensing of leaf biochemical constituents [
31,
36,
37]. Determining the influence of leaf specular reflection on the canopy radiative regime is, therefore, critical because the inputs in these studies are generally related to, or determined, by the canopy radiative regime. Moreover, field measurements of vertical profiles of mean flux density are also necessary for a better understanding of the influence of leaf specular reflection, as well as for further validations and applications of the improved SRTM. It should be noted that many empirical and theoretical analyses show that leaf specular reflection is partly polarized, whereas the leaf diffuse scattering is not [
38,
39,
40,
41]. Polarization measurement can, thus, be useful for a full understanding of leaf specular reflection and its influences in the remote sensing community [
42,
43].
6. Conclusions
Leaf specular reflection is a particular feature that should be accounted for in canopy RT modeling. For this reason, an improved version of the SRTM is proposed in this paper. Compared to the classical version of the SRTM, the leaf scattering phase function is modified to include leaf specular reflection by assuming that all photons that have not been specularly reflected enter the leaf interior. The improved SRTM satisfactorily estimates maize BRF over a wide range of zenith view angles. From a practical point of view, it can efficiently and accurately provide estimates of the canopy radiative regime. It is thus desirable if one considers that leaf specular reflection lowers the sensitivity of sensor-registered signals to canopy structure, leaf biochemistry, etc.
Leaf specular reflection influences the canopy radiative regime in vertical profiles of mean radiation flux density, canopy absorptance, BRF, NDVI, etc. Analyses of the improved version of SRTM for a vegetation canopy with spherically inclined leaves shows that accounting for leaf specular reflection increases mean upward/downward radiation flux density and nadir BRF, and it decreases canopy absorptance and nadir NDVI. The influence is greater for vertical profiles of mean radiation flux density and nadir BRF than that for canopy absorptance and NDVI. Ignoring this part of specularly reflected radiation, therefore, may introduce unpredictable errors when interpreting remotely sensed data. Moreover, a small portion of incident radiation is scattered by the dust and hair on leaf surfaces. The dust and hair can somehow influence the canopy radiative regime and their influences need to be addressed in future studies.
It also should be noted that polarization measurement may be adopted for studies of leaf specular reflection. In the future, we would also expect to extend the improved version of the SRTM by accounting for canopy polarization, which can be helpful for processing remote-sensing data collected by polarization sensors, such as the POLDER, RSP, 3MI, and GF-5, etc.