LDAS-Monde Sequential Assimilation of Satellite Derived Observations Applied to the Contiguous US: An ERA-5 Driven Reanalysis of the Land Surface Variables
Abstract
:1. Introduction
2. Data and Methods
2.1. LDAS-Monde System Components
2.1.1. The SURFEX Modelling Platform
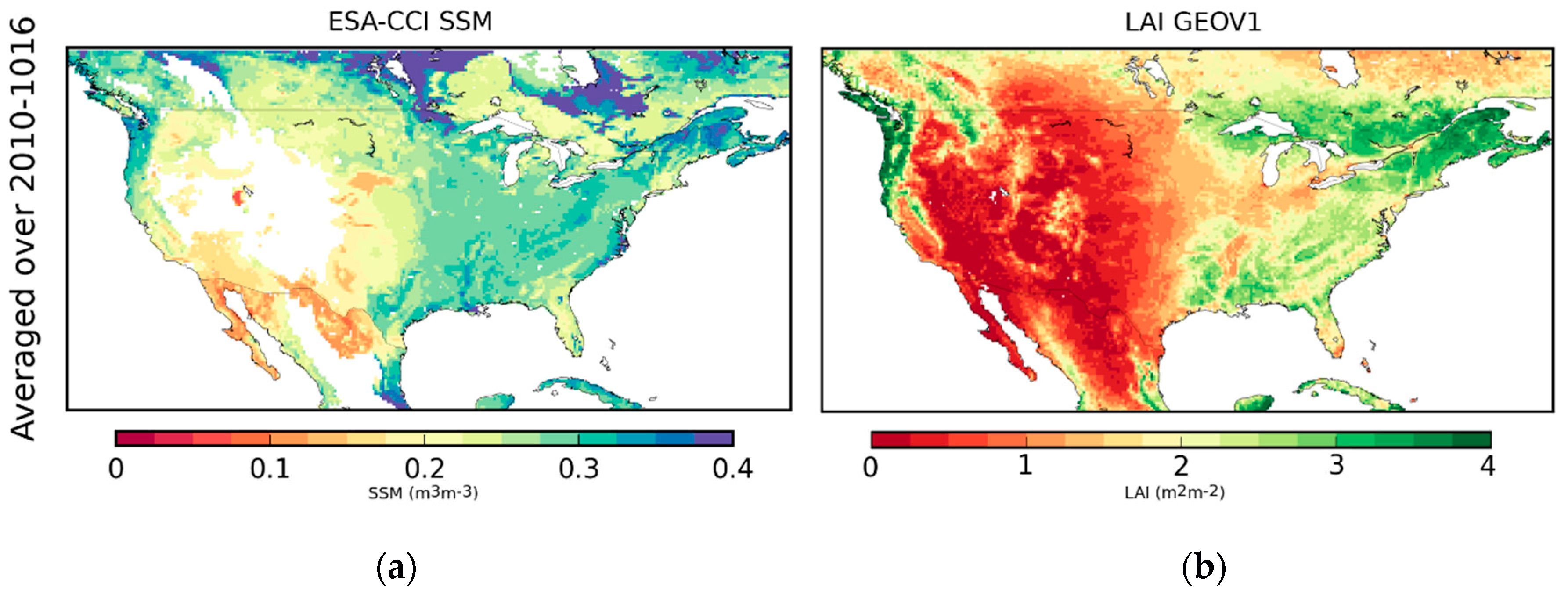
2.1.2. ESA CCI Surface Soil Moisture and CGLS Leaf Area Index
2.1.3. ERA-5 Atmospheric Reanalysis
2.2. Evaluation Datasets and Methods
3. Results
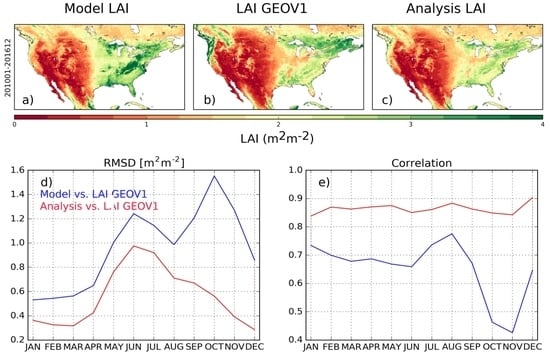
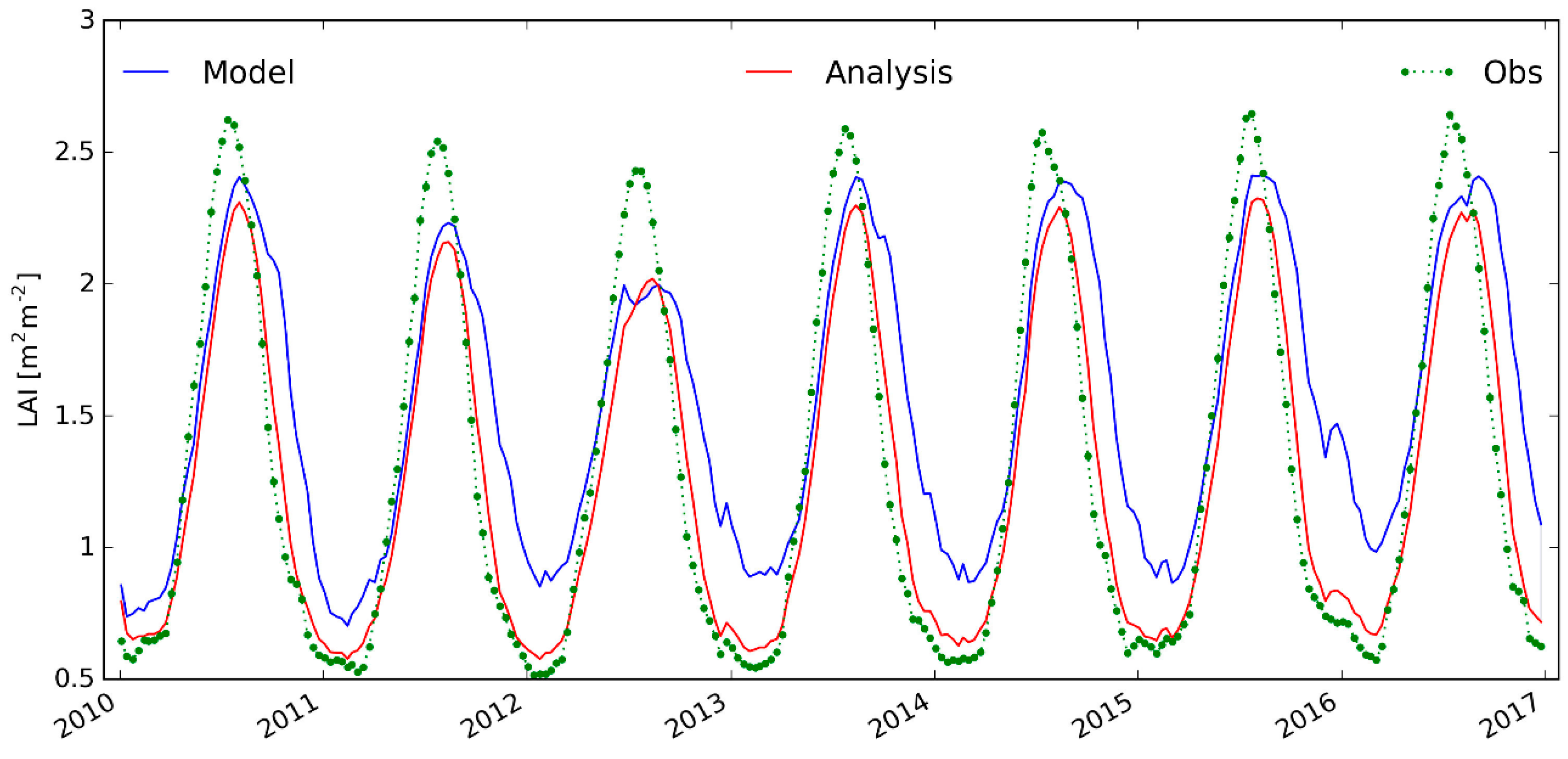
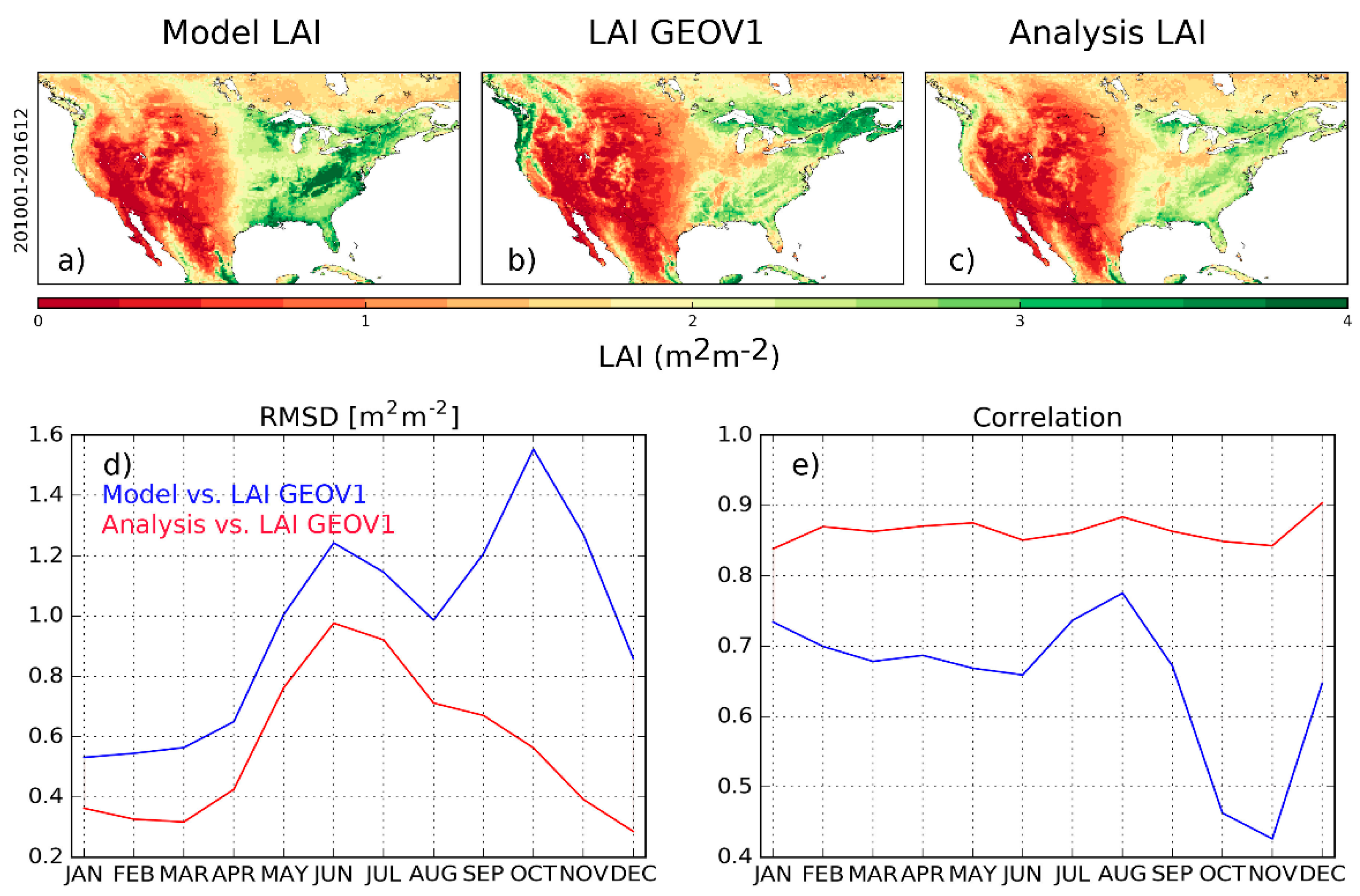
3.1. Analysis Impact on Assimilated Variables
3.2. Evaluation Using Independent Datasets
3.2.1. Evapotranspiration and GPP
3.2.2. Soil Moisture
3.2.3. Streamflow
4. Potential Applications, Discussions, and Perspectives
4.1. Could LDAS-Monde be Used to Monitor Agricultural Droughts?
4.2. Could LDAS-Monde Provide Accurate Initial Conditions for Vegetation Forecasts?
4.3. Which Alternative Data to Better Constrain LDAS-Monde?
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Code Availability
Data Availability
References
- Dirmeyer, P.A.; Gao, X.; Zhao, M.; Guo, Z.; Oki, T.; Hanasaki, N. The Second Global Soil Wetness Project (GSWP-2): Multi-model analysis and implications for our perception of the land surface. Bull. Am. Meteorol. Soc. 2006, 87, 1381–1397. [Google Scholar] [CrossRef]
- Schellekens, J.; Dutra, E.; Martínez-de la Torre, A.; Balsamo, G.; van Dijk, A.; Sperna Weiland, F.; Minvielle, M.; Calvet, J.-C.; Decharme, B.; Eisner, S.; et al. A global water resources ensemble of hydrological models: The eartH2Observe Tier-1 dataset. Earth Syst. Sci. Data 2017, 9, 389–413. [Google Scholar] [CrossRef]
- Lettenmaier, D.P.; Alsdorf, D.; Dozier, J.; Huffman, G.J.; Pan, M.; Wood, E.F. Inroads of remote sensing into hydrologic science during the WRR era. Water Resour. Res. 2015, 51, 7309–7342. [Google Scholar] [CrossRef] [Green Version]
- Reichle, R.H.; Koster, R.D.; Liu, P.; Mahanama, S.P.; Njoku, E.G.; Owe, M. Comparison and assimilation of global soil moisture retrievals from the Advanced Microwave Scanning Radiometer for the Earth Observing System (AMSR-E) and the Scanning Multichannel Microwave Radiometer (SMMR). J. Geophys. Res. 2007, 112, D09108. [Google Scholar] [CrossRef]
- Fox, A.M.; Hoar, T.J.; Anderson, J.L.; Arellano, A.F.; Smith, W.K.; Litvak, M.E.; MacBean, N.; Schimel, D.S.; Moore, D.J.P. Evaluation of a Data Assimilation System for Land Surface Models using CLM4.5. J. Adv. Model. Earth Syst. 2018. [Google Scholar] [CrossRef]
- Sawada, Y.; Koike, T. Simultaneous estimation of both hydrological and ecological parameters in an ecohydrological model by assimilating microwave signal. J. Geophys. Res. Atmos. 2014, 119. [Google Scholar] [CrossRef]
- Sawada, Y.; Koike, T.; Walker, J.P. A land data assimilation system for simultaneous simulation of soil moisture and vegetation dynamics. J. Geophys. Res. Atmos. 2015, 120. [Google Scholar] [CrossRef]
- McNally, A.; Arsenault, K.; Kumar, S.; Shukla, S.; Peterson, P.; Wang, S.; Funk, C.; Peters-Lidard, C.D.; Verdin, J.P. A land data assimilation system for sub-Saharan Africa food and water security applications. Sci. Data 2017, 4, 170012. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mitchell, K.E.; Lohmann, D.; Houser, P.R.; Wood, E.F.; Schaake, J.C.; Robock, A.; Cosgrove, B.A.; Sheffield, J.; Duan, Q.; Luo, L.; et al. The multi-institution North American Land Data Assimilation System (NLDAS): Utilizing multiple GCIP products and partners in a continental distributed hydrological modeling system. J. Geophys. Res. 2004, 109, D07S90. [Google Scholar] [CrossRef]
- Xia, Y.; Mitchell, K.; Ek, M.; Sheffield, J.; Cosgrove, B.; Wood, E.; Luo, L.; Alonge, C.; Wei, H.; Meng, J.; et al. Continental-scale water and energy flux analysis and validation for the North American Land Data Assimilation System project phase 2 (NLDAS-2): 1. Intercomparison and application of model products. J. Geophys. Res. 2012, 117, D03109. [Google Scholar] [CrossRef]
- Kumar, S.V.; Jasinski, M.; Mocko, D.; Rodell, M.; Borak, J.; Li, B.; Kato Beaudoing, H.I.R.O.K.O.; Peters-Lidard, C.D. NCA-LDAS land analysis: Development and performance of a multisensor, multivariate land data assimilation system for the National Climate Assessment. J. Hydrometeorol. 2018. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.R.; Jambor, U.E.; Gottschalck, J.; Mitchell, K.; Meng, C.J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The Global Land Data Assimilation System. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef] [Green Version]
- Albergel, C.; Munier, S.; Leroux, D.J.; Dewaele, H.; Fairbairn, D.; Barbu, A.L.; Gelati, E.; Dorigo, W.; Faroux, S.; Meurey, C.; et al. Sequential assimilation of satellite-derived vegetation and soil moisture products using SURFEX_v8.0: LDAS-Monde assessment over the Euro-Mediterranean area. Geosci. Model Dev. 2017, 10, 3889–3912. [Google Scholar] [CrossRef] [Green Version]
- Noilhan, J.; Mahfouf, J.-F. The ISBA land surface parameterisation scheme. Glob. Planet. Chang. 1996, 13, 145–159. [Google Scholar] [CrossRef]
- Calvet, J.-C.; Noilhan, J.; Roujean, J.-L.; Bessemoulin, P.; Cabelguenne, M.; Olioso, A.; Wigneron, J.-P. An interactive vegetation SVAT model tested against data from six 780 contrasting sites. Agric. For. Meteorol. 1998, 92, 73–95. [Google Scholar] [CrossRef]
- Calvet, J.-C.; Rivalland, V.; Picon-Cochard, C.; Guehl, J.-M. Modelling forest transpiration and CO2 fluxes—Response to soil moisture stress. Agric. For. Meteorol. 2004, 124, 143–156. [Google Scholar] [CrossRef]
- Gibelin, A.-L.; Calvet, J.-C.; Roujean, J.-L.; Jarlan, L.; Los, S.O. Ability of the land surface model ISBA-A-gs to simulate leaf area index at global scale: Comparison with satellite products. J. Geophys. Res. 2006, 111, 1–16. [Google Scholar] [CrossRef]
- Masson, V.; Le Moigne, P.; Martin, E.; Faroux, S.; Alias, A.; Alkama, R.; Belamari, S.; Barbu, A.; Boone, A.; Bouyssel, F.; et al. The SURFEXv7.2 land and ocean surface platform for coupled or offline simulation of earth surface variables and fluxes. Geosci. Model Dev. 2013, 6, 929–960. [Google Scholar] [CrossRef] [Green Version]
- Barbu, A.L.; Calvet, J.-C.; Mahfouf, J.-F.; Albergel, C.; Lafont, S. Assimilation of Soil Wetness Index and Leaf Area Index into the ISBA-A-gs land surface model: Grassland case study. Biogeosciences 2011, 8, 1971–1986. [Google Scholar] [CrossRef] [Green Version]
- Barbu, A.L.; Calvet, J.C.; Mahfouf, J.F.; Lafont, S. Integrating ASCAT surface soil moisture and GEOV1 leaf area index into the SURFEX modelling platform: A land data assimilation application over France. Hydrol. Earth Syst. Sci. 2014, 18, 173–192. [Google Scholar] [CrossRef] [Green Version]
- Fairbairn, D.; Barbu, A.L.; Napoly, A.; Albergel, C.; Mahfouf, J.-F.; Calvet, J.-C. The effect of satellite-derived surface soil moisture and leaf area index land data assimilation on streamflow simulations over France. Hydrol. Earth Syst. Sci. 2017, 21, 2015–2033. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Parinussa, R.M.; Dorigo, W.A.; De Jeu, R.A.; Wagner, W.; Van Dijk, A.I.; McCabe, M.F.; Evans, J.P. Developing an improved soil moisture dataset by blending passive and active microwave satellite-based retrievals. Hydrol. Earth Syst. Sci. 2011, 15, 425–436. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.Y.; Dorigo, W.A.; Parinussa, R.M.; de Jeu, R.A.; Wagner, W.; McCabe, M.F.; Evans, J.P.; Van Dijk, A.I. Trend-preserving blending of passive and active microwave soil moisture retrievals. Remote Sens. Environ. 2012, 123, 280–297. [Google Scholar] [CrossRef]
- Dorigo, W.A.; Gruber, A.; De Jeu, R.A.; Wagner, W.; Stacke, T.; Loew, A.; Albergel, C.; Brocca, L.; Chung, D.; Parinussa, R.M.; et al. Evaluation of the ESA CCI soil moisture product using ground-based observations. Remote Sens. Environ. 2015. [Google Scholar] [CrossRef]
- Dorigo, W.; Wagner, W.; Albergel, C.; Albrecht, F.; Balsamo, G.; Brocca, L.; Chung, D.; Ertl, M.; Forkel, M.; Gruber, A.; et al. ESA CCI Soil Moisture for improved Earth system understanding: State-of-the art and future directions. Remote Sens. Environ. 2017. [Google Scholar] [CrossRef]
- Weedon, G.P.; Gomes, S.; Viterbo, P.; Shuttleworth, W.J.; Blyth, E.; Österle, H.; Adam, J.C.; Bellouin, N.; Boucher, O.; Best, M. Creation of the WATCH forcing data and its use to assess global and regional reference crop evaporation over land during the twentieth century. J. Hydrometeorol. 2011, 12, 823–848. [Google Scholar] [CrossRef]
- Weedon, G.P.; Balsamo, G.; Bellouin, N.; Gomes, S.; Best, M.J.; Viterbo, P. The WFDEI meteorological forcing data set: WATCH Forcing data methodology applied to ERA- interim reanalysis data. Water Resour. Res. 2014, 50, 7505–7514. [Google Scholar] [CrossRef]
- Albergel, C.; Dutra, E.; Munier, S.; Calvet, J.-C.; Munoz-Sabater, J.; de Rosnay, P.; Balsamo, G. ERA-5 and ERA-Interim driven ISBA land surface model simulations: Which one performs better? Hydrol. Earth Syst. Sci. 2018, 22, 3515–3532. [Google Scholar] [CrossRef]
- Boone, A.; Masson, V.; Meyers, T.; Noilhan, J. The influence of the inclusion of soil freezing on simulations by a soil vegetation–atmosphere transfer scheme. J. Appl. Meteorol. 2000, 39, 1544–1569. [Google Scholar] [CrossRef]
- Decharme, B.; Martin, E.; Faroux, S. Reconciling soil thermal and hydrological lower boundary conditions in land surface models. J. Geophys. Res.-Atmos. 2013, 118, 7819–7834. [Google Scholar] [CrossRef] [Green Version]
- Voldoire, A.; Decharme, B.; Pianezze, J.; Lebeaupin Brossier, C.; Sevault, F.; Seyfried, L.; Garnier, V.; Bielli, S.; Valcke, S.; Alias, A.; et al. SURFEX v8.0 interface with OASIS3-MCT to couple atmosphere with hydrology, ocean, waves and sea-ice models, from coastal to global scales. Geosci. Model Dev. 2017, 10, 4207–4227. [Google Scholar] [CrossRef] [Green Version]
- Decharme, B.; Alkama, R.; Douville, H.; Becker, M.; Cazenave, A. Global evaluation of the ISBA-TRIP continental hydrologic system, Part 2: Uncertainties in river routing simulation related to flow velocity and groundwater storage. J. Hydrometeorol. 2010, 11, 601–617. [Google Scholar] [CrossRef]
- Decharme, B.; Alkama, R.; Papa, F.; Faroux, S.; Douville, H.; Prigent, C. Global offline evaluation of the ISBA-TRIP flood model. Clim. Dynam. 2012, 38, 1389–1412. [Google Scholar] [CrossRef]
- Vergnes, J.-P.; Decharme, B. A simple groundwater scheme in the TRIP river routing model: Global off-line evaluation against GRACE terrestrial water storage estimates and observed river discharges. Hydrol. Earth Syst. Sci. 2012, 16, 3889–3908. [Google Scholar] [CrossRef] [Green Version]
- Vergnes, J.-P.; Decharme, B.; Habets, F. Introduction of groundwater capillary rises using subgrid spatial variability of topography into the ISBA land surface model. J. Geophys. Res.-Atmos. 2014, 119, 11065–11086. [Google Scholar] [CrossRef]
- Leroux, D.J.; Calvet, J.-C.; Munier, S.; Albergel, C. Using Satellite-Derived Vegetation Products to Evaluate LDAS-Monde over the Euro-Mediterranean Area. Remote Sens. 2018, 10, 1199. [Google Scholar] [CrossRef]
- Mätzler, C.; Standley, A. Relief effects for passive microwave remote sensing. Int. J. Remote Sens. 2000, 21, 2403–2412. [Google Scholar] [CrossRef]
- Draper, C.; Mahfouf, J.-F.; Calvet, J.-C.; Martin, E.; Wagner, W. Assimilation of ASCAT near-surface soil moisture into the SIM hydrological model over France. Hydrol. Earth Syst. Sci. 2011, 15, 3829–3841. [Google Scholar] [CrossRef] [Green Version]
- Reichle, R.H.; Koster, D. Bias reduction in short records of satellite soil moisture. Geophys. Res. Lett. 2004, 31, L19501. [Google Scholar] [CrossRef]
- Drusch, M.; Wood, E.F.; Gao, H. Observations operators for the direct assimilation of TRMM microwave imager retrieved soil moisture. Geophys. Res. Lett. 2005, 32, L15403. [Google Scholar] [CrossRef]
- Scipal, K.; Drusch, M.; Wagner, W. Assimilation of a ERS scatterometer derived soil moisture index in the ECMWF numerical weather prediction system. Adv. Water Resour. 2008, 31, 1101–1112. [Google Scholar] [CrossRef]
- Boussetta, S.; Balsamo, G.; Dutra, E.; Beljaars, A.; Albergel, C. Assimilation of surface albedo and vegetation states from satellite observations and their impact on numerical weather prediction. Remote Sens. Environ. 2015, 163, 111–126. [Google Scholar] [CrossRef] [Green Version]
- Baret, F.; Weiss, M.; Lacaze, R.; Camacho, F.; Makhmared, H.; Pacholczyk, P.; Smetse, B. GEOV1: LAI and FAPAR essential climate variables and FCOVER global time series capitalizing over existing products, Part 1: Principles of development and production. Remote Sens. Environ. 2013, 137, 299–309. [Google Scholar] [CrossRef]
- Hersbach, H.; Dee, D. ERA-5 Reanalysis is in Production; ECMWF Newsletter, Number 147; ECMWF: Reading, UK, 2016; p. 7. [Google Scholar]
- Miralles, D.G.; Holmes, T.R.H.; De Jeu, R.A.M.; Gash, J.H.; Meesters, A.G.C.A.; Dolman, A.J. Global land-surface evaporation estimated from satellite-based observations. Hydrol. Earth Syst. Sci. 2011, 15, 453–469. [Google Scholar] [CrossRef] [Green Version]
- Martens, B.; Miralles, D.G.; Lievens, H.; van der Schalie, R.; de Jeu, R.A.M.; Fernández-Prieto, D.; Beck, H.E.; Dorigo, W.A.; Verhoest, N.E.C. GLEAM v3: Satellite-based land evaporation and root-zone soil moisture. Geosci. Model Dev. 2017, 10, 1903–1925. [Google Scholar] [CrossRef]
- Tramontana, G.; Jung, M.; Schwalm, C.R.; Ichii, K.; Camps-Valls, G.; Ráduly, B.; Reichstein, M.; Arain, M.A.; Cescatti, A.; Kiely, G.; et al. Predicting carbon dioxide and energy fluxes across global FLUXNET sites with regression algorithms. Biogeosciences 2016, 13, 4291–4313. [Google Scholar] [CrossRef] [Green Version]
- Jung, M.; Reichstein, M.; Schwalm, C.R.; Huntingford, C.; Sitch, S.; Ahlström, A.; Arneth, A.; Camps-Valls, G.; Ciais, P.; Friedlingstein, P.; et al. Compensatory water effects link yearly global land CO2 sink changes to temperature. Nature 2017, 541, 516–520. [Google Scholar] [CrossRef] [PubMed]
- Bell, J.E.; Palecki, M.A.; Collins, W.G.; Lawrimore, J.H.; Leeper, R.D.; Hall, M.E.; Kochendorfer, J.; Meyers, T.P.; Wilson, T.; Baker, B.; et al. U.S. Climate Reference Network soil moisture and temperature observatons. J. Hydrometeorol. 2013, 14, 977–988. [Google Scholar] [CrossRef]
- Kumar, S.; Reichle, R.H.; Koster, R.D.; Crow, W.T.; Peters-Lidard, C. Role of Subsurface Physics in the Assimilation of Surface Soil Moisture Observations. J. Hydrometeor. 2009, 10, 1534–1547. [Google Scholar] [CrossRef] [Green Version]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef] [Green Version]
- Beck, H.E.; Pan, M.; Roy, T.; Weedon, G.P.; Pappenberger, F.; van Dijk, A.I.J.M.; Huffman, G.J.; Adler, R.F.; Wood, E.F. Daily evaluation of 26 precipitation datasets using Stage-IV gauge-radar data for the CONUS, Hydrol. Earth Syst. Sci. Discuss. 2018. [Google Scholar] [CrossRef]
- Olive, W.W.; Chleborad, A.F.; Frahme, C.W.; Schlocker, J.; Schneider, R.R.; Schuster, R.L. Swelling Clays Map of the Conterminous United States; USGS: Reston, VA, USA, 1989.
- Hoerling, M.; Eischeid, J.; Kumar, A.; Leung, R.; Mariotti, A.; Mo, K.; Schubert, S.; Seager, R. Causes and Predictability of the 2012 Great Plains Drought. Bull. Am. Meteorol. Soc. 2014, 95, 269–282. [Google Scholar] [CrossRef]
- Ault, T.R.; Henebry, G.M.; De Beurs, K.M.; Schwartz, M.D.; Betancourt, J.L.; Moore, D. The False Spring of 2012, Earliest in North American Record. EOS 2013, 94, 181–182. [Google Scholar] [CrossRef] [Green Version]
- Rüdiger, C.; Albergel, C.; Mahfouf, J.-F.; Calvet, J.-C.; Walker, J.P. Evaluation of Jacobians for Leaf Area Index data assimilation with an extended Kalman filter. J. Geophys. Res. 2010, 115, D09111. [Google Scholar] [CrossRef]
- Ukkola, A.M.; De Kauwe, M.G.; Pitman, A.J.; Best, M.J.; Abramowitz, G.; Haverd, V.; Decker, M.; Haughton, N. Land surface models systematically overestimate the intensity, duration and magnitude of seasonal-scale evaporative droughts. Environ. Res. Lett. 2016, 11, 104012. [Google Scholar] [CrossRef] [Green Version]
- Carrer, D.; Meurey, C.; Ceamanos, X.; Roujean, J.-L.; Calvet, J.-C.; Liu, S. Dynamic mapping of snow-free vegetation and bare soil albedos at global 1 km scale from 10 year analysis of MODIS satellite products. Remote Sens. Environ. 2014, 140, 420–432. [Google Scholar] [CrossRef]
- Munier, S.; Carrer, D.; Planque, C.; Camacho, F.; Albergel, C.; Calvet, J.-C. Satellite Leaf Area Index: Global Scale Analysis of the Tendencies Per Vegetation Type Over the Last 17 Years. Remote Sens. 2018, 10, 424. [Google Scholar] [CrossRef]
- Bauer, P.; Thorpe, A.; Brunet, G. The quiet revolution of numerical weather prediction. Nature 2015, 525, 47–55. [Google Scholar] [CrossRef] [PubMed]
- De Rosnay, P.; Drusch, M.; Vasiljevic, D.; Balsamo, G.; Albergel, C.; Isaksen, L. A simplified extended Kalman filter for the global operational soil moisture analysis at ECMWF. Q. J. R. Meteorol. Soc. 2013, 139, 1199–1213. [Google Scholar] [CrossRef]
- Calvet, J.-C.; Lafont, S.; Cloppet, E.; Souverain, F.; Badeau, V.; Le Bas, C. Use of agricultural statistics to verify the interannual variability in land surface models: A case study over France with ISBA-A-gs. Geosci. Model Dev. 2012, 5, 37–54. [Google Scholar] [CrossRef]
- Canal, N.; Calvet, J.-C.; Decharme, B.; Carrer, D.; Lafont, S.; Pigeon, G. Evaluation of root water uptake in the ISBA-A-gs land surface model using agricultural yield statistics over France. Hydrol. Earth Syst. Sci. 2014, 18, 4979–4999. [Google Scholar] [CrossRef]
- Dewaele, H.; Munier, S.; Albergel, C.; Planque, C.; Laanaia, N.; Carrer, D.; Calvet, J.-C. Parameter optimisation for a better representation of drought by LSMs: Inverse modelling vs. sequential data assimilation. Hydrol. Earth Syst. Sci. 2017, 21, 4861–4878. [Google Scholar] [CrossRef]
- Munier, S.; Leroux, D.; Albergel, C.; Carrer, D.; Calvet, J.C. Hydrological impacts of the assimilation of satellite-derived disaggregated Leaf Area Index into the SURFEX modelling platform. Hydrol. Earth Syst. Sci. Discuss. 2018. in preparation. [Google Scholar]
- Entekhabi, D.; Nakamura, H.; Njoku, E.G. Solving the inverse problem for soil moisture and tem-perature profiles by the sequential assimilation of multifrequency remotely sensed observations. IEEE Trans. Geosci. Remote Sens. 1994, 32, 438–448. [Google Scholar] [CrossRef]
- Reichle, R.H.; Entekhabi, D.; McLaughlin, D.B. Downscaling of radio brightness measurements for soil moisture estimation: A four-dimensional variational data assimilation approach. Water Resour. Res. 2001, 37, 2353–2364. [Google Scholar] [CrossRef] [Green Version]
- Kurum, M.; Lang, R.H.; O’Neill, P.E.; Joseph, A.T.; Jackson, T.J.; Cosh, M. A first-order radiative transfer model for microwave radiometry of forest canopies at L-band. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3167–3179. [Google Scholar] [CrossRef]
- Kurum, M.; O’Neill, P.E.; Lang, R.H.; Joseph, A.T.; Cosh, M.H.; Jackson, T.J. Effective tree scattering and opacity at L-band. Remote Sens. Environ. 2012, 118, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Meesters, A.G.C.A.; Jeu, R.A.M.D.; Owe, M. Analytical derivation of the vegetation optical depth from the microwave polarization difference index. IEEE Geosci. Remote Sens. Lett. 2005, 2, 121–123. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Jeu, R.D.; McCabe, M.F.; Evans, J.P.; van Dijk, A.I.J.M. Global lon-term passive microwave satellite-based retrievals of vegetation optical depth. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Konings, A.G.; Gentine, P. Global variations in ecosystem-scale isohydricity. Glob. Chang. Biol. 2016, 23, 891–905. [Google Scholar] [CrossRef] [PubMed]
- Tian, F.; Brandt, M.; Liu, Y.Y.; Verger, A.; Tagesson, T.; Diouf, A.A.; Rasmussen, K.; Mbow, C.; Wang, Y.; Fensholt, R. Remote sensing of vegetation dynamics in drylands: Evaluating vegetation optical depth (VOD) using AVHRR NDVI and in situ green biomass data over West African Sahel. Remote Sens. Environ. 2016, 177, 265–276. [Google Scholar] [CrossRef] [Green Version]
- Fernandez-Moran, R.; Wigneron, J.-P.; De Lannoy, G.; Lopez-Baeza, E.; Parrens, M.; Mialon, A.; Mahmoodi, A.; Al-Yaari, A.; Bircher, S.; Al Bitar, A.; et al. A new calibration of the effective scattering albedo and soil roughness parameters in the SMOS SM retrieval algorithm. Int. J. Appl. Earth Obs. Geoinf. 2017, 62, 27–38. [Google Scholar] [CrossRef]
- Vreugdenhil, M.; Dorigo, W.A.; Wagner, W.; de Jeu, R.A.M.; Hahn, D.; Marle, M.J.E. Analyzing the vegetation parameterization in the TU-Wien ASCAT soil moisture retrieval. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3513–3531. [Google Scholar] [CrossRef]
- Vreugdenhil, M.; Hahn, S.; Melzer, T.; Bauer-Marschallinger, B.; Reimer, C.; Dorigo, W.A.; Wagner, W. Assessing vegetation dynamics over Mainland Australia with Metop ASCAT. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 10, 2240–2248. [Google Scholar] [CrossRef]
- Zribi, M.; Chahbi, A.; Shabou, M.; Lili-Chabaane, Z.; Duchemin, B.; Baghdadi, N.; Amri, R.; Chehbouni, A. Soil surface moisture estimation over a semi-arid region using ENVISAT ASAR radar data for soil evaporation evaluation. Hydrol. Earth Syst. Sci. Discuss. 2011, 15, 345–358. [Google Scholar] [CrossRef] [Green Version]
- Kim, Y.; Jackson, T.; Bindlish, R.; Lee, H.; Hong, S. Radar Vegetation Index for Estimating the Vegetation Water Content of Rice and Soybean. IEEE Geosci. Remote Sens. Lett. 2012, 9, 564–568. [Google Scholar] [CrossRef]
- Sawada, Y.; Tsutsui, H.; Koike, T.; Rasmy, M.; Seto, R.; Fuji, H. A Field Verification of an Algorithm for Retrieving Vegetation Water Content from Passive Microwave Observations. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2082–2095. [Google Scholar] [CrossRef]
- Momen, M.; Wood, J.D.; Novick, K.A.; Pangle, R.; Pockman, W.T.; McDowell, N.G.; Konings, A.G. Interacting effects of leaf water potential and biomass on vegetation optical depth. J. Geophys. Res. Biogeosci. 2017, 122, 3031–3046. [Google Scholar] [CrossRef]
- Rodríguez-Fernández, N.J.; Muñoz Sabater, J.; Richaume, P.; de Rosnay, P.; Kerr, Y.H.; Albergel, C.; Drusch, M.; Mecklenburg, S. SMOS near-real-time soil moisture product: Processor overview and first validation results. Hydrol. Earth Syst. Sci. 2017, 21, 5201–5216. [Google Scholar] [CrossRef]
- De Lannoy, G.J.M.; Reichle, R.H.; Pauwels, V.R.N. Global calibration of the GEOS-5 L-band microwave radiative transfer model over nonfrozen land using SMOS observations. J. Hydrometeorol. 2013, 14, 765–785. [Google Scholar] [CrossRef]
- De Lannoy, G.J.M.; Reichle, R.H. Global assimilation of multiangle and multipolarization SMOS brightness temperature observations into the GEOS-5 catchment Land Surface Model for soil moisture estimation. J. Hydrometeorol. 2016, 17, 669–691. [Google Scholar] [CrossRef]
- Han, X.; Hendricks Franssen, H.-J.; Montzka, C.; Vereecken, H. Soil moisture and soil properties estimation in the community land model with synthetic brightness temperature observations. Water Resour. Res. 2014, 50, 6081–6105. [Google Scholar] [CrossRef]
- Lievens, H.; Al Bitar, A.; Verhoest, N.E.C.; Cabot, F.; De Lannoy, G.J.M.; Drusch, M.; Dumedah, G.; Hendricks Franssen, H.J.; Kerr, Y.H.; Kumar Tomer, S.; et al. Optimization of a radiative transfer forward operator for simulating SMOS brightness temperatures over the Upper Mississippi Basin. J. Hydrometeorol. 2015, 16, 1109–1134. [Google Scholar] [CrossRef]
- Lievens, H.; Martens, B.; Verhoest, N.E.C.; Hahn, S.; Reichle, R.H.; Miralles, D.G. Assimilation of global radar backscatter and radiometer brightness temperature observations to improve soil moisture and land evaporation estimates. Remote Sens. Environ. 2016, 189, 194–210. [Google Scholar] [CrossRef]
- Zhao, L.; Yang, Z.-L.; Hoar, T.J. Global Soil Moisture Estimation by Assimilating AMSR-E Brightness Temperatures in a Coupled CLM4–RTM–DART System. J. Hydrometeorol. 2016, 17, 2431–2454. [Google Scholar] [CrossRef]
- Attema, E.; Ulaby, F. Vegetation modeled as a water cloud. Radio Sci. 1978, 13, 357–364. [Google Scholar] [CrossRef]
- Miralles, D.G.; De Jeu, R.A.M.; Gash, J.H.; Holmes, T.R.H.; Dolman, A.J. Magnitude and variability of land evaporation and its components at the global scale. Hydrol. Earth Syst. Sci. 2011, 15, 967–981. [Google Scholar] [CrossRef] [Green Version]
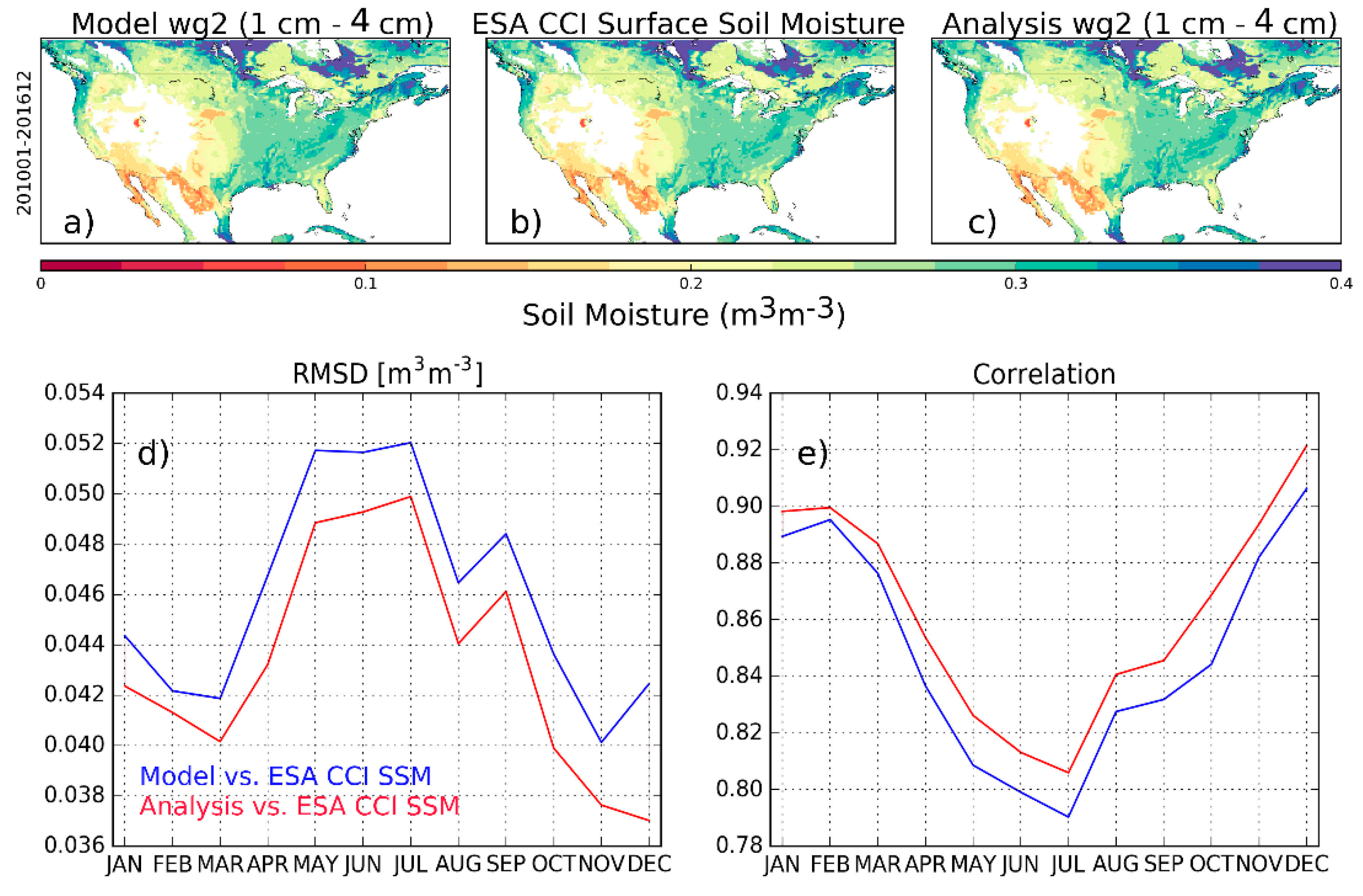

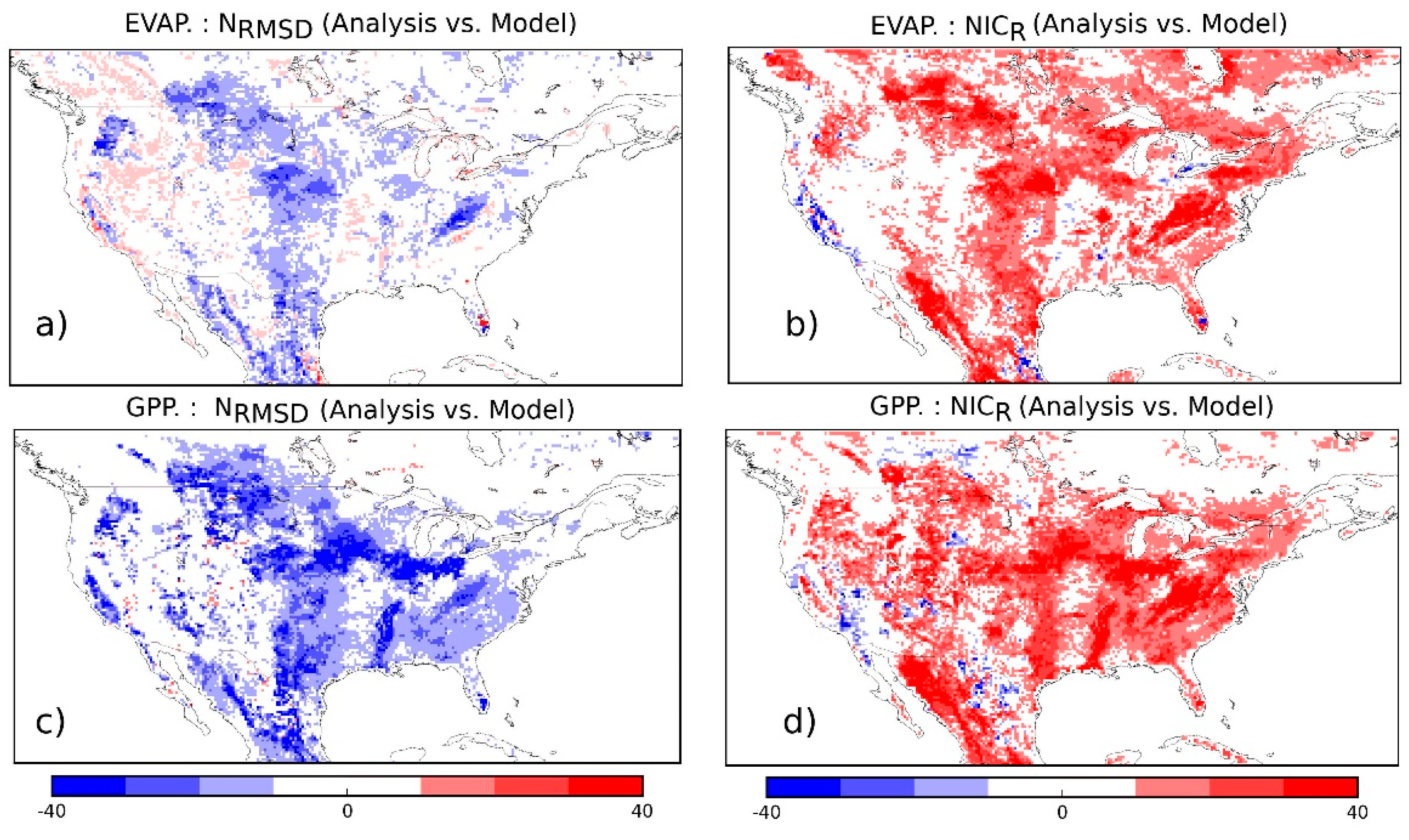
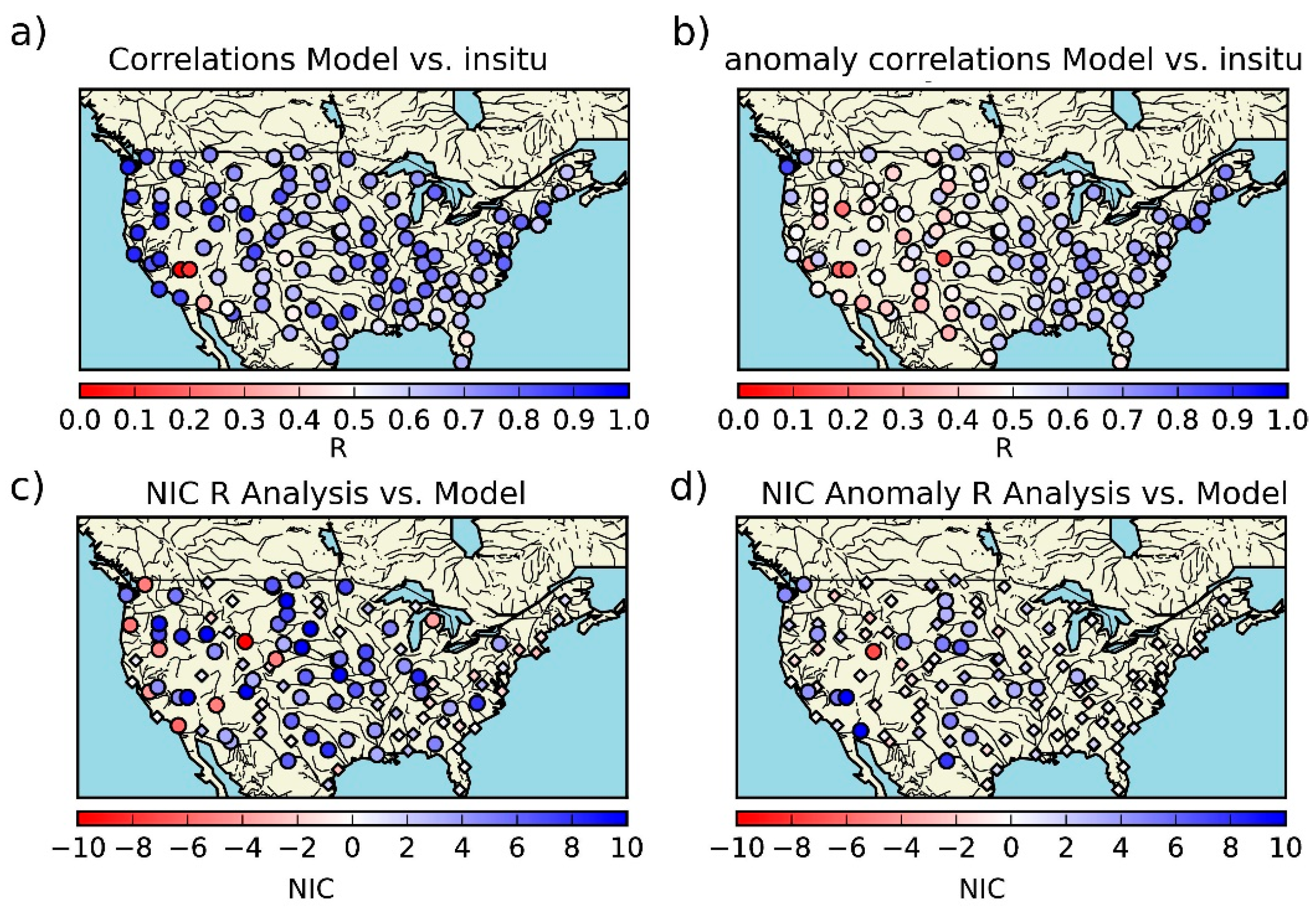
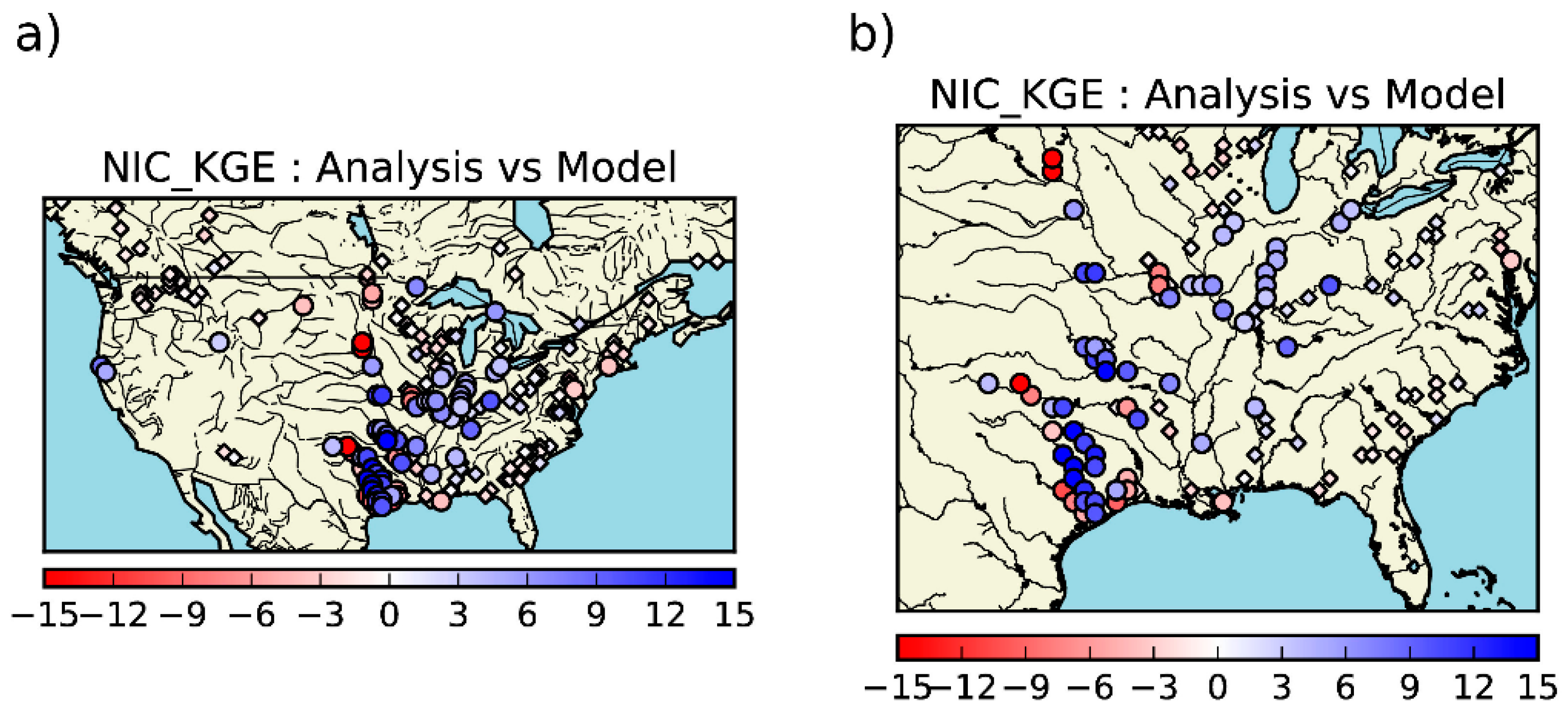
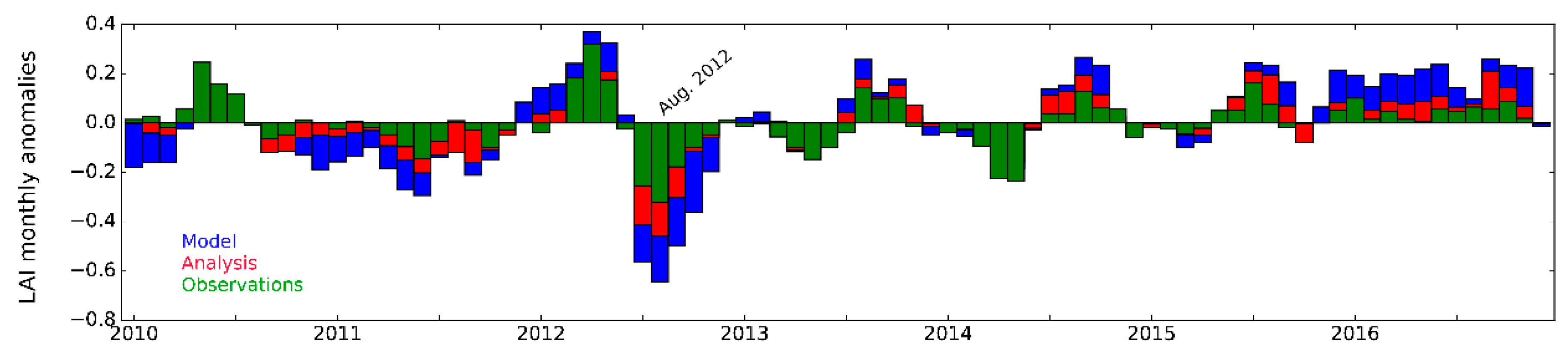
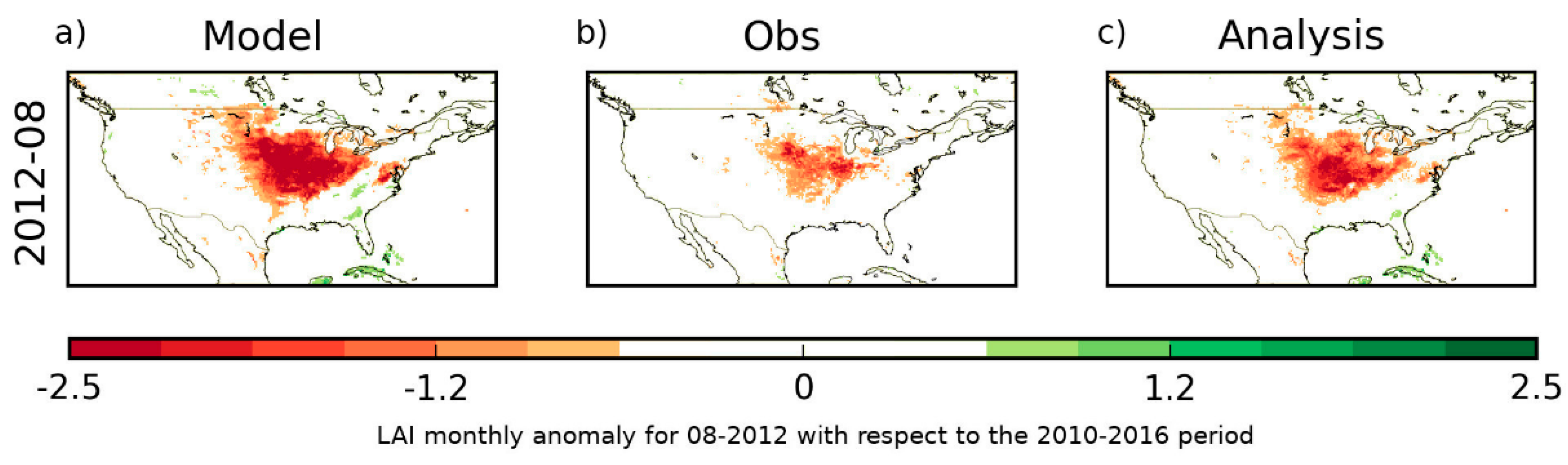
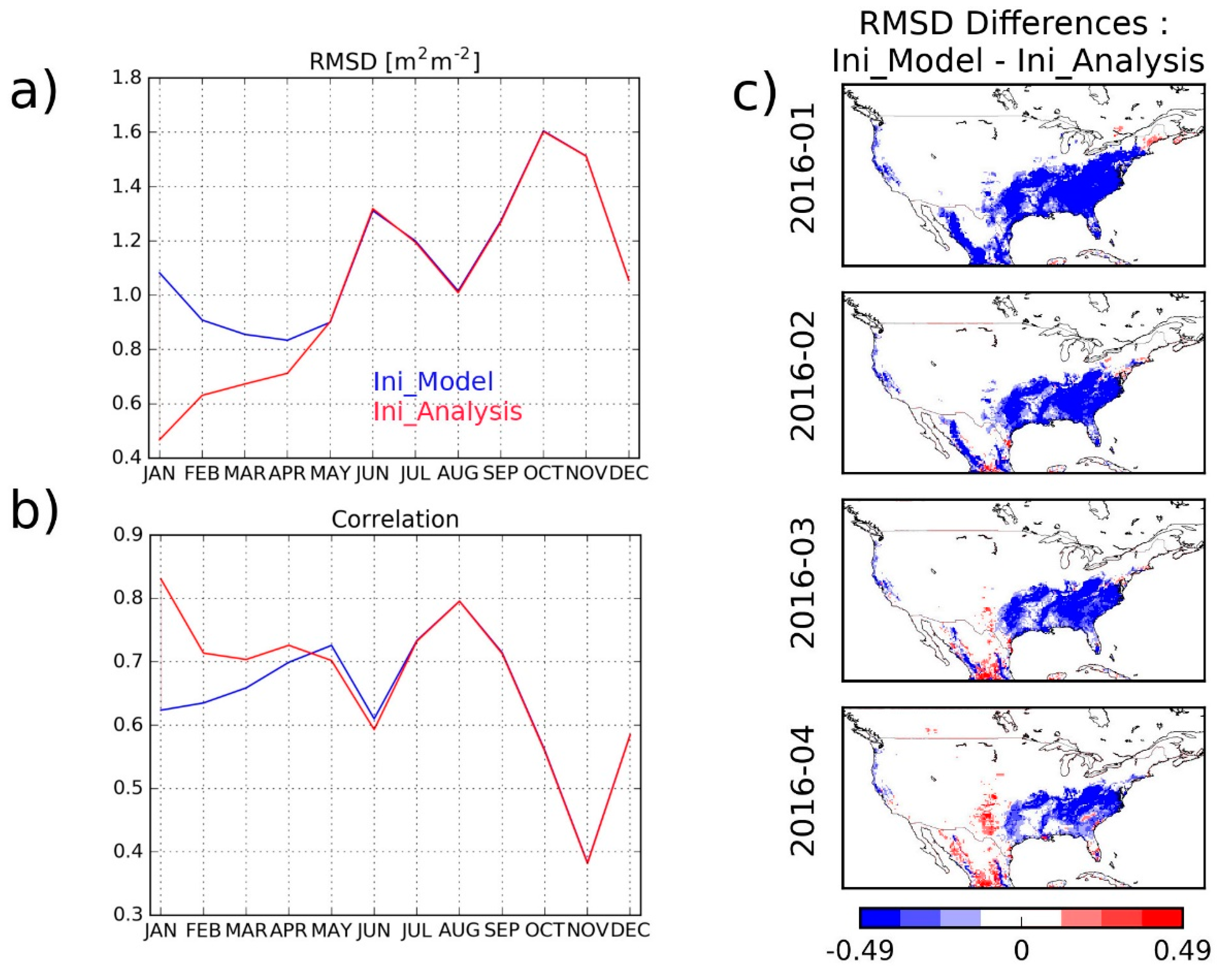
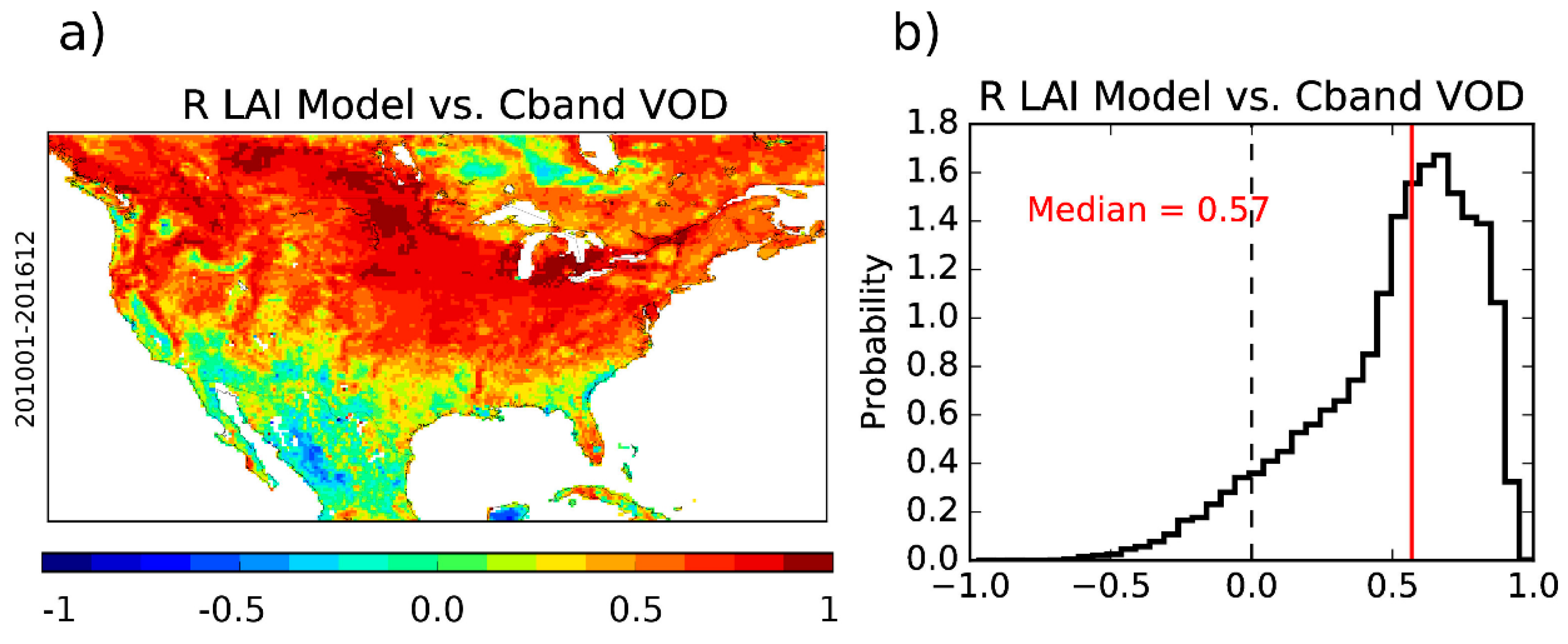
| Experiments (Time Period) | Model | Domain & Spatial Resolution | Atmospheric Forcing | DA Method | Assimilated Observations | Model Equivalents of the Observations | Control Variables | Additional Options |
|---|---|---|---|---|---|---|---|---|
| Model or Open-loop (2010–2016) | ISBA Multi-layer soil model CO2-responsive version (Interactive vegetation) | CONtiguous US (CONUS), 0.25° × 0.25° | ERA-5 | N/A | N/A | N/A | N/A | Coupling with CTRIP (0.5°) |
| Analysis (2010–2016) | ISBA Multi-layer soil model CO2-responsive version (Interactive vegetation) | CONtiguous US (CONUS), 0.25° × 0.25° | ERA-5 | SEKF | SSM (ESA CCI) LAI (GEOV1) | Rescaled WG2 (Second layer of soil (1–4 cm)) LAI | Layers of soil 2 to 8 (WG2 to WG8, 1–100 cm) LAI | Coupling with CTRIP (0.5°) |
| Ini_Model (2016) | ISBA Multi-layer soil model CO2-responsive version (Interactive vegetation) | CONtiguous US (CONUS), 0.25° × 0.25° | ERA-5 | 12-month model run starting on 1 January 2016 (initialised by the model simulation, i.e., Open-loop, run from 2010 to 2015) | Coupling with CTRIP (0.5°) | |||
| Ini_Analysis (2016) | ISBA Multi-layer soil model CO2-responsive version (Interactive vegetation) | CONtiguous US (CONUS), 0.25° × 0.25° | ERA-5 | 12-month model run starting on 1 January 2016 (initialised by the analysis run from 2010 to 2015) | Coupling with CTRIP (0.5°) | |||
| Mean of the Evaluation Data Set | Experiments | RMSD | R | |
|---|---|---|---|---|
| Evapotranspiration | 1.46 kg/m2/d | Open-loop | 0.87 kg/m2/d | 0.80 |
| Analysis | 0.85 kg/m2/d | 0.81 | ||
| Gross Primary Production | 1.76 g(C)/m2/d | Open-loop | 2.20 g(C)/m2/d | 0.74 |
| Analysis | 1.91 g(C)/m2/d | 0.78 |
| 110 (110) Stations with Significant R (Anomaly R) | Median R (Anomaly R) | Median ubRMSD | Positive Impact: >+3 | ←3 Negative Impact: <−3 | Neutral Impact [−3; +3] |
|---|---|---|---|---|---|
| Model | 0.72 ± 0.02 * (0.60 ± 0.02 *) | 0.049 ± 0.004 * | N/A | N/A | N/A |
| Analysis | 0.74 ± 0.02 * (0.60 ± 0.02 *) | 0.048 ± 0.004 * | 46% (18%) | 8% (1%) | 46% (81%) |
| 258 out of 531 Stations with KGE Greater than 0 | Positive Impact: >+3 | Negative Impact: <−3 | Neutral Impact [−3; +3] |
|---|---|---|---|
| NICKGE | 26% | 12% | 62% |
| NREσ | 22% | 1% | 77% |
| NREμ | 34% | 1% | 65% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Albergel, C.; Munier, S.; Bocher, A.; Bonan, B.; Zheng, Y.; Draper, C.; Leroux, D.J.; Calvet, J.-C. LDAS-Monde Sequential Assimilation of Satellite Derived Observations Applied to the Contiguous US: An ERA-5 Driven Reanalysis of the Land Surface Variables. Remote Sens. 2018, 10, 1627. https://doi.org/10.3390/rs10101627
Albergel C, Munier S, Bocher A, Bonan B, Zheng Y, Draper C, Leroux DJ, Calvet J-C. LDAS-Monde Sequential Assimilation of Satellite Derived Observations Applied to the Contiguous US: An ERA-5 Driven Reanalysis of the Land Surface Variables. Remote Sensing. 2018; 10(10):1627. https://doi.org/10.3390/rs10101627
Chicago/Turabian StyleAlbergel, Clement, Simon Munier, Aymeric Bocher, Bertrand Bonan, Yongjun Zheng, Clara Draper, Delphine J. Leroux, and Jean-Christophe Calvet. 2018. "LDAS-Monde Sequential Assimilation of Satellite Derived Observations Applied to the Contiguous US: An ERA-5 Driven Reanalysis of the Land Surface Variables" Remote Sensing 10, no. 10: 1627. https://doi.org/10.3390/rs10101627