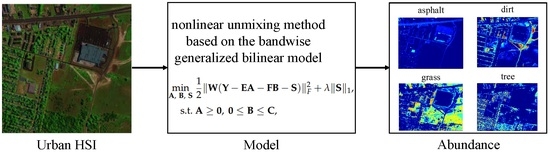
Hyperspectral Unmixing with Bandwise Generalized Bilinear Model
Abstract
1. Introduction
2. Bandwise Generalized Bilinear Model and Algorithm
2.1. The Related GBM
2.2. Formulation of the Proposed BGBM and the Corresponding Unmixing Method NU-BGBM
2.3. Solving the Proposed NU-BGBM with ADMM
| Algorithm 1: Solving the proposed NU-BGBM with ADMM. |
 |
3. Experiments
3.1. Experimental Results with Synthetic Data
- Gaussian noise: all bands of the HSI are contaminated by zero mean i.i.d. Gaussian noise, and the signal-to-noise ratio (SNR) of each band is a random number ranging from 10 dB to 50 dB.
- Impulse noise: only 11 bands (60–70) are contaminated by 30% impulse noise.
- Dead lines: only 11 bands (120–130) are contaminated by dead lines.
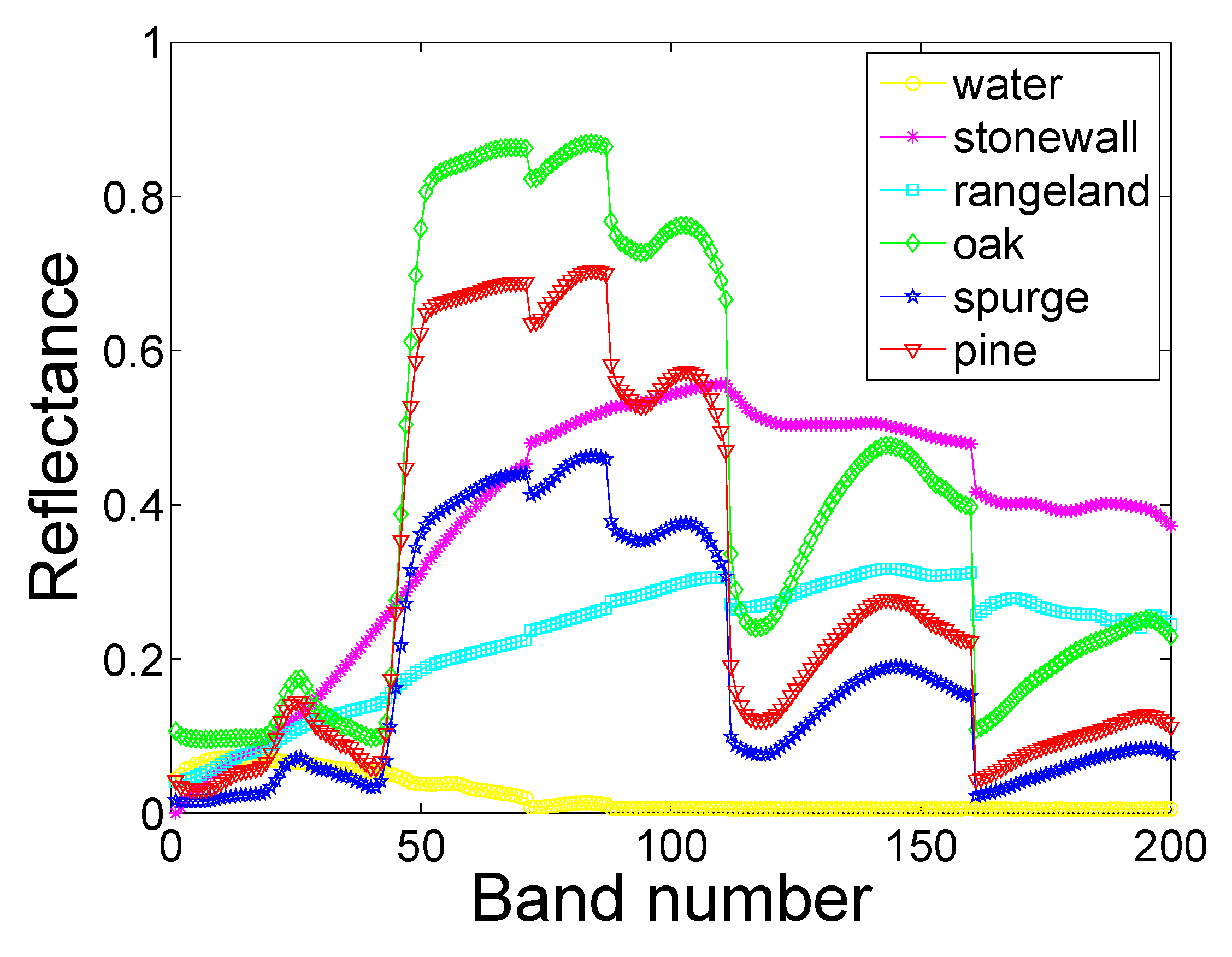
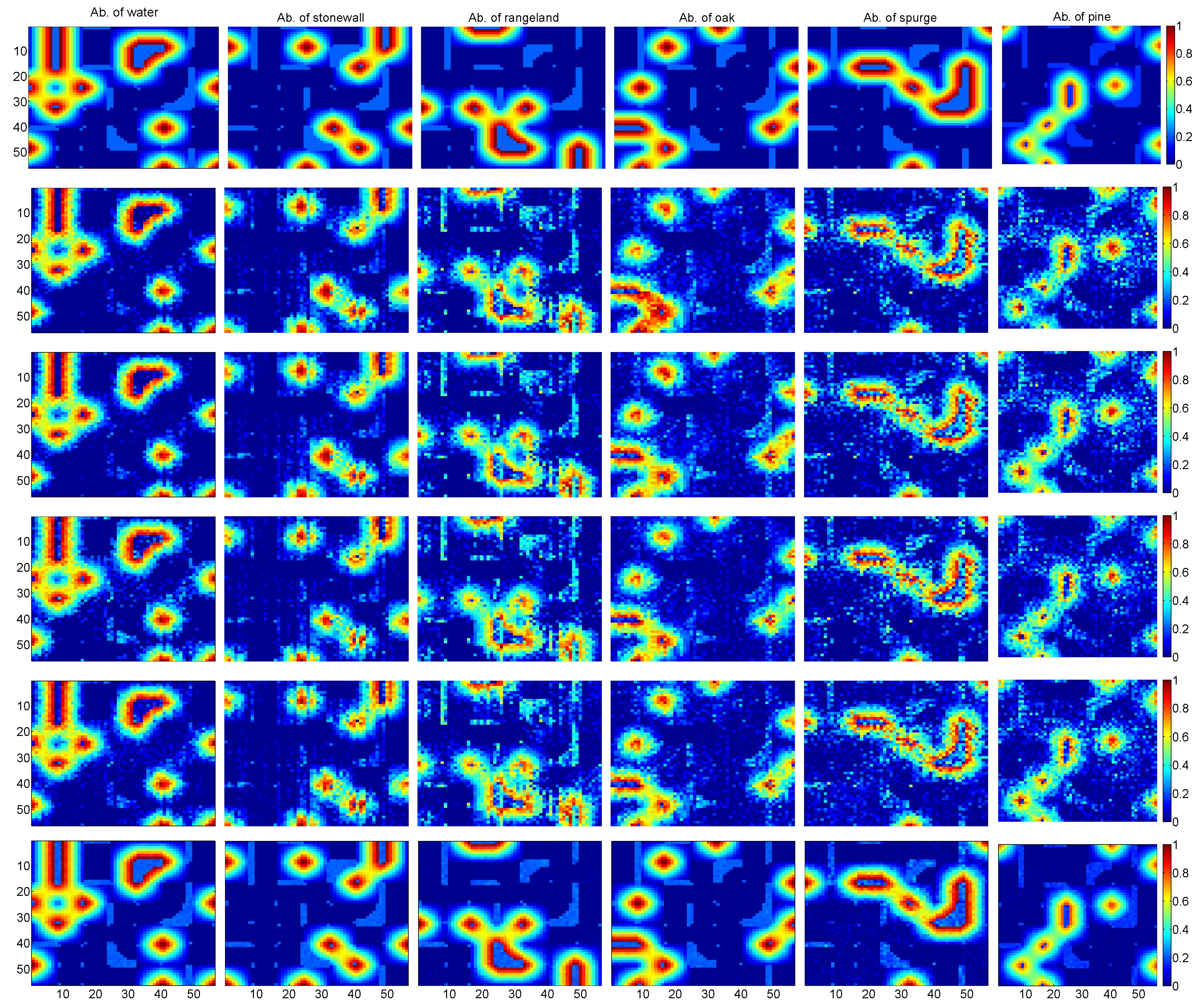
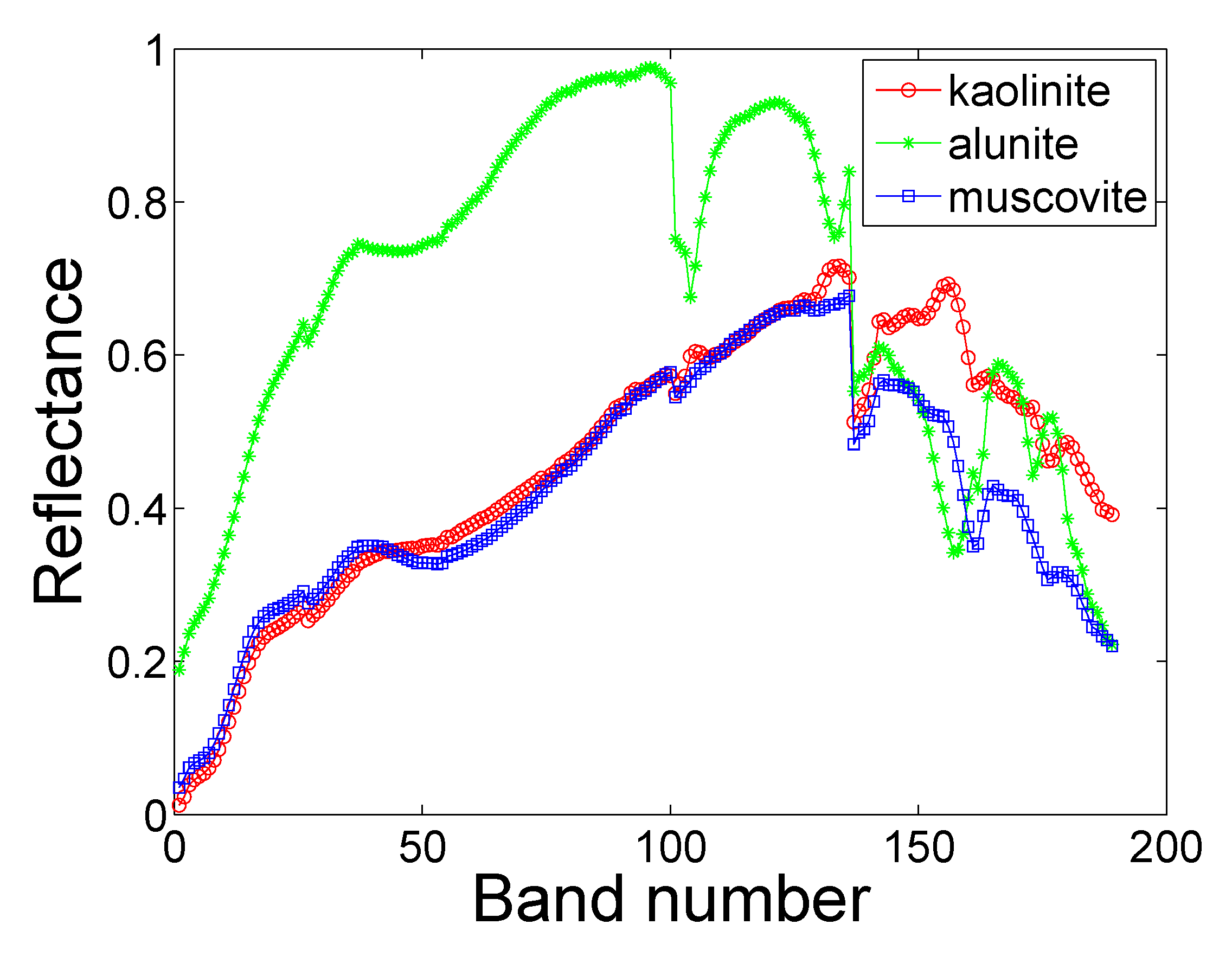
3.2. Experimental Results with Real Data
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bioucas-Dias, J.M.; Plaza, A.; Dobigeon, N.; Parente, M.; Du, Q.; Gader, P.; Chanussot, J. Hyperspectral unmixing overview: Geometrical, statistical, and sparse regression-based approaches. IEEE J. Select. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 354–379. [Google Scholar] [CrossRef]
- Zhang, X.; Li, C.; Zhang, J.; Chen, Q.; Feng, J.; Jiao, L.; Zhou, H. Hyperspectral unmixing via low-rank representation with space consistency constraint and spectral library pruning. Remote Sens. 2018, 10, 339. [Google Scholar] [CrossRef]
- Li, C.; Ma, Y.; Mei, X.; Fan, F.; Huang, J.; Ma, J. Sparse unmixing of hyperspectral data with noise level estimation. Remote Sens. 2017, 9, 1166. [Google Scholar] [CrossRef]
- Zhang, Z.; Liao, S.; Zhang, H.; Wang, S.; Wang, Y. Bilateral Filter Regularized L2 Sparse Nonnegative Matrix Factorization for Hyperspectral Unmixing. Remote Sens. 2018, 10, 816. [Google Scholar] [CrossRef]
- Yang, B.; Wang, B.; Wu, Z. Unsupervised Nonlinear Hyperspectral Unmixing Based on Bilinear Mixture Models via Geometric Projection and Constrained Nonnegative Matrix Factorization. Remote Sens. 2018, 10, 801. [Google Scholar] [CrossRef]
- Li, C.; Ma, Y.; Mei, X.; Liu, C.; Ma, J. Hyperspectral unmixing with robust collaborative sparse regression. Remote Sens. 2016, 8, 588. [Google Scholar] [CrossRef]
- Manolakis, D.; Siracusa, C.; Shaw, G. Hyperspectral subpixel target detection using the linear mixing model. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1392–1409. [Google Scholar] [CrossRef]
- Xu, X.; Zhong, Y.; Zhang, L.; Zhang, H. Sub-pixel mapping based on a MAP model with multiple shifted hyperspectral imagery. IEEE J. Select. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 580–593. [Google Scholar] [CrossRef]
- Jiang, J.; Ma, J.; Chen, C.; Wang, Z.; Wang, L. SuperPCA: A Superpixelwise Principal Component Analysis Approach for Unsupervised Feature Extraction of Hyperspectral Imagery. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4581–4593. [Google Scholar] [CrossRef]
- Ma, Y.; Li, C.; Li, H.; Mei, X.; Ma, J. Hyperspectral Image Classification with Discriminative Kernel Collaborative Representation and Tikhonov Regularization. IEEE Geosci. Remote Sens. Lett. 2018, 15, 587–591. [Google Scholar] [CrossRef]
- Liu, T.; Liu, H.; Chen, Z.; Lesgold, A.M. Fast blind instrument function estimation method for industrial infrared spectrometers. IEEE Trans. Ind. Inform. 2018. [Google Scholar] [CrossRef]
- Liu, H.; Li, Y.; Zhang, Z.; Liu, S.; Liu, T. Blind Poissonian reconstruction algorithm via curvelet regularization for an FTIR spectrometer. Opt. Express 2018, 26, 22837–22856. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Zhou, H.; Zhao, J.; Gao, Y.; Jiang, J.; Tian, J. Robust feature matching for remote sensing image registration via locally linear transforming. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6469–6481. [Google Scholar] [CrossRef]
- Ma, J.; Jiang, J.; Zhou, H.; Zhao, J.; Guo, X. Guided locality preserving feature matching for remote sensing image registration. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4435–4447. [Google Scholar] [CrossRef]
- Yan, J.; Li, C.; Li, Y.; Cao, G. Adaptive discrete hypergraph matching. IEEE Trans. Cybern. 2018, 48, 765–779. [Google Scholar] [CrossRef] [PubMed]
- Ghamisi, P.; Yokoya, N.; Li, J.; Liao, W.; Liu, S.; Plaza, J.; Rasti, B.; Plaza, A. Advances in hyperspectral image and signal processing: A comprehensive overview of the state of the art. IEEE Geosci. Remote Sens. Mag. 2017, 5, 37–78. [Google Scholar] [CrossRef]
- Ma, Y.; Li, C.; Mei, X.; Liu, C.; Ma, J. Robust Sparse Hyperspectral Unmixing with ℓ2,1 Norm. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1227–1239. [Google Scholar] [CrossRef]
- Heylen, R.; Parente, M.; Gader, P. A review of nonlinear hyperspectral unmixing methods. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2014, 7, 1844–1868. [Google Scholar] [CrossRef]
- Feng, R.; Zhong, Y.; Wang, L.; Lin, W. Rolling Guidance Based Scale-Aware Spatial Sparse Unmixing for Hyperspectral Remote Sensing Imagery. Remote Sens. 2017, 9, 1218. [Google Scholar] [CrossRef]
- Halimi, A.; Bioucas-Dias, J.M.; Dobigeon, N.; Buller, G.S.; McLaughlin, S. Fast hyperspectral unmixing in presence of nonlinearity or mismodeling effects. IEEE Trans. Comput. Imaging 2017, 3, 146–159. [Google Scholar] [CrossRef]
- Dobigeon, N.; Tourneret, J.Y.; Richard, C.; Bermudez, J.; Mclaughlin, S.; Hero, A.O. Nonlinear unmixing of hyperspectral images: Models and algorithms. IEEE. Signal Process. Mag. 2014, 31, 82–94. [Google Scholar] [CrossRef]
- Altmann, Y.; Halimi, A.; Dobigeon, N.; Tourneret, J.Y. Supervised nonlinear spectral unmixing using a postnonlinear mixing model for hyperspectral imagery. IEEE Trans. Image Process. 2012, 21, 3017–3025. [Google Scholar] [CrossRef] [PubMed]
- Licciardi, G.A.; Del Frate, F. Pixel unmixing in hyperspectral data by means of neural networks. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4163–4172. [Google Scholar] [CrossRef]
- Ammanouil, R.; Ferrari, A.; Richard, C.; Mathieu, S. Nonlinear unmixing of hyperspectral data with vector-valued kernel functions. IEEE Trans. Image Process. 2017, 26, 340–354. [Google Scholar] [CrossRef] [PubMed]
- Hapke, B. Bidirectional reflectance spectroscopy: 1. Theory. J. Geophys. Res. Solid Earth (1978–2012) 1981, 86, 3039–3054. [Google Scholar] [CrossRef]
- Nascimento, J.M.; Bioucas-Dias, J.M. Nonlinear mixture model for hyperspectral unmixing. In Proceedings of the SPIE Image and Signal Processing Remote Sensing XV, Berlin, Germany, 31 August–3 September 2009; Bruzzone, L., Notarnicola, C., Posa, F., Eds.; SPIE: Berlin, Germany, 2009; Volume 7477, p. 74770I. [Google Scholar]
- Fan, W.; Hu, B.; Miller, J.; Li, M. Comparative study between a new nonlinear model and common linear model for analysing laboratory simulated-forest hyperspectral data. Int. J. Remote Sens. 2009, 30, 2951–2962. [Google Scholar] [CrossRef]
- Halimi, A.; Altmann, Y.; Dobigeon, N.; Tourneret, J.Y. Nonlinear unmixing of hyperspectral images using a generalized bilinear model. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4153–4162. [Google Scholar] [CrossRef]
- Halimi, A.; Altmann, Y.; Dobigeon, N.; Tourneret, J.Y. Unmixing hyperspectral images using the generalized bilinear model. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Vancouver, BC, Canada, 24–29 July 2011; pp. 1886–1889. [Google Scholar]
- Yokoya, N.; Chanussot, J.; Iwasaki, A. Nonlinear unmixing of hyperspectral data using semi-nonnegative matrix factorization. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1430–1437. [Google Scholar] [CrossRef]
- Li, C.; Ma, Y.; Huang, J.; Mei, X.; Liu, C.; Ma, J. GBM-Based Unmixing of Hyperspectral Data Using Bound Projected Optimal Gradient Method. IEEE Geosci. Remote Sens. Lett. 2016, 13, 952–956. [Google Scholar] [CrossRef]
- Yang, B.; Wang, B.; Wu, Z. Nonlinear hyperspectral unmixing based on geometric characteristics of bilinear mixture models. IEEE Trans. Geosci. Remote Sens. 2018, 56, 694–714. [Google Scholar] [CrossRef]
- Mei, X.; Ma, Y.; Li, C.; Fan, F.; Huang, J.; Ma, J. Robust GBM hyperspectral image unmixing with superpixel segmentation based low rank and sparse representation. Neurocomputing 2018, 275, 2783–2797. [Google Scholar] [CrossRef]
- Heylen, R.; Scheunders, P. A multilinear mixing model for nonlinear spectral unmixing. IEEE Trans. Geosci. Remote Sens. 2016, 54, 240–251. [Google Scholar] [CrossRef]
- Wei, Q.; Chen, M.; Tourneret, J.Y.; Godsill, S. Unsupervised nonlinear spectral unmixing based on a multilinear mixing model. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4534–4544. [Google Scholar] [CrossRef]
- Yang, B.; Wang, B. Band-Wise Nonlinear Unmixing for Hyperspectral Imagery Using an Extended Multilinear Mixing Model. IEEE Trans. Geosci. Remote Sens. 2018, 99, 1–16. [Google Scholar] [CrossRef]
- Zhang, H.; He, W.; Zhang, L.; Shen, H.; Yuan, Q. Hyperspectral image restoration using low-rank matrix recovery. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4729–4743. [Google Scholar] [CrossRef]
- Li, C.; Ma, Y.; Huang, J.; Mei, X.; Ma, J. Hyperspectral image denoising using the robust low-rank tensor recovery. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2015, 32, 1604–1612. [Google Scholar] [CrossRef] [PubMed]
- Fan, F.; Ma, Y.; Li, C.; Mei, X.; Huang, J.; Ma, J. Hyperspectral image denoising with superpixel segmentation and low-rank representation. Inf. Sci. 2017, 397, 48–68. [Google Scholar] [CrossRef]
- Fan, H.; Li, C.; Guo, Y.; Kuang, G.; Ma, J. Spatial-Spectral Total Variation Regularized Low-Rank Tensor Decomposition for Hyperspectral Image Denoising. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6196–6213. [Google Scholar] [CrossRef]
- Aggarwal, H.K.; Majumdar, A. Hyperspectral unmixing in the presence of mixed noise using joint-sparsity and total variation. IEEE J. Select. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4257–4266. [Google Scholar] [CrossRef]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends Mach. Learn. 2011, 3, 1–122. [Google Scholar] [CrossRef]
- Iordache, M.D.; Bioucas-Dias, J.M.; Plaza, A. Sparse unmixing of hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2014–2039. [Google Scholar] [CrossRef]
- Qu, Q.; Nasrabadi, N.M.; Tran, T.D. Abundance estimation for bilinear mixture models via joint sparse and low-rank representation. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4404–4423. [Google Scholar]
- Zhu, F.; Halimi, A.; Honeine, P.; Chen, B.; Zheng, N. Correntropy Maximization via ADMM: Application to Robust Hyperspectral Unmixing. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4944–4955. [Google Scholar] [CrossRef]
- Donoho, D.L. De-noising by soft-thresholding. IEEE Trans. Inf. Theory 1995, 41, 613–627. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Nascimento, J.M. Hyperspectral subspace identification. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2435–2445. [Google Scholar] [CrossRef]
- Heinz, D.C.; Chang, C.I. Fully constrained least squares linear spectral mixture analysis method for material quantification in hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2001, 39, 529–545. [Google Scholar] [CrossRef]
- Miao, L.; Qi, H. Endmember extraction from highly mixed data using minimum volume constrained nonnegative matrix factorization. IEEE Trans. Geosci. Remote Sens. 2007, 45, 765–777. [Google Scholar] [CrossRef]
- Nascimento, J.M.; Dias, J.M.B. Vertex component analysis: A fast algorithm to unmix hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 898–910. [Google Scholar] [CrossRef]

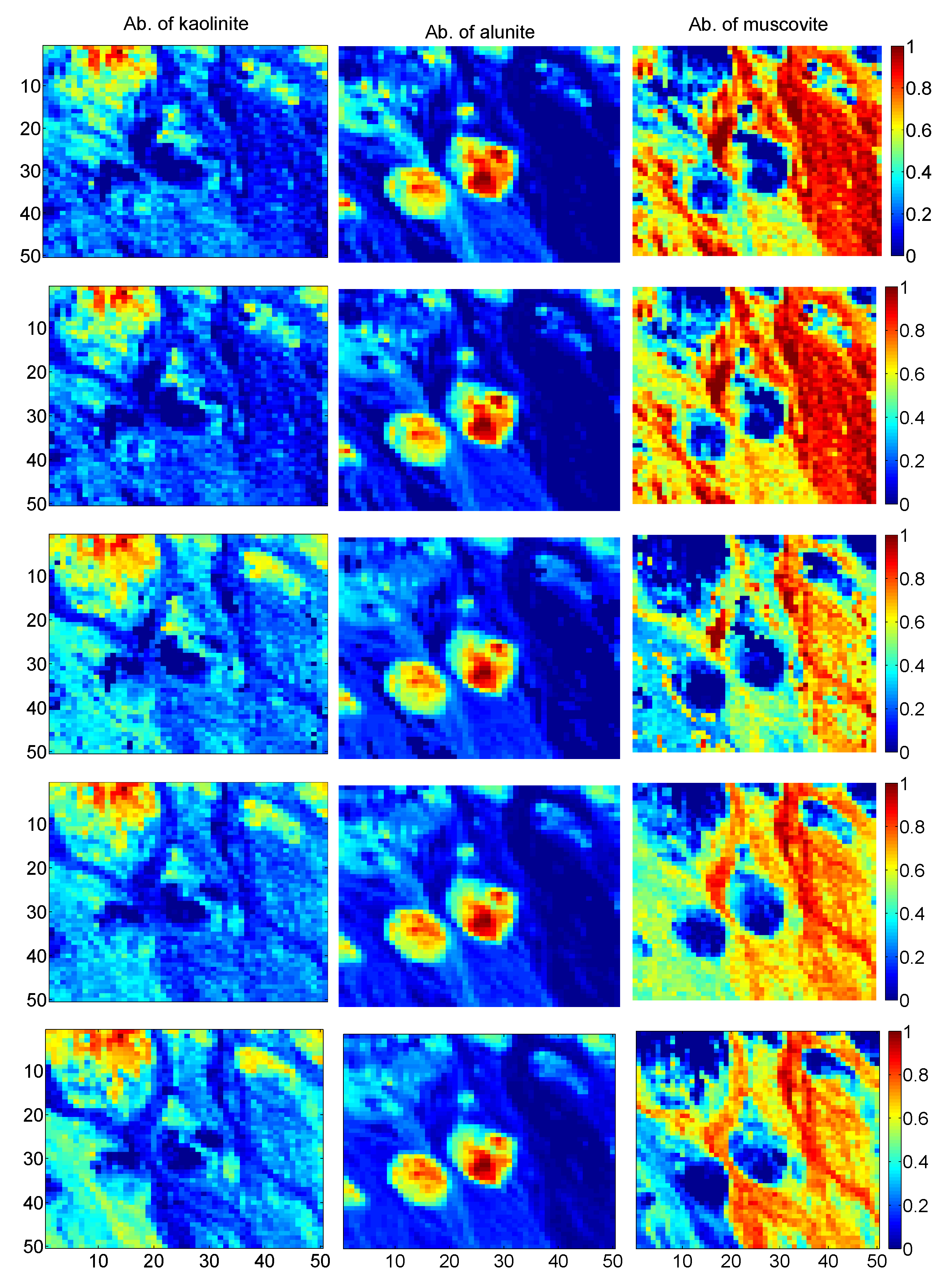

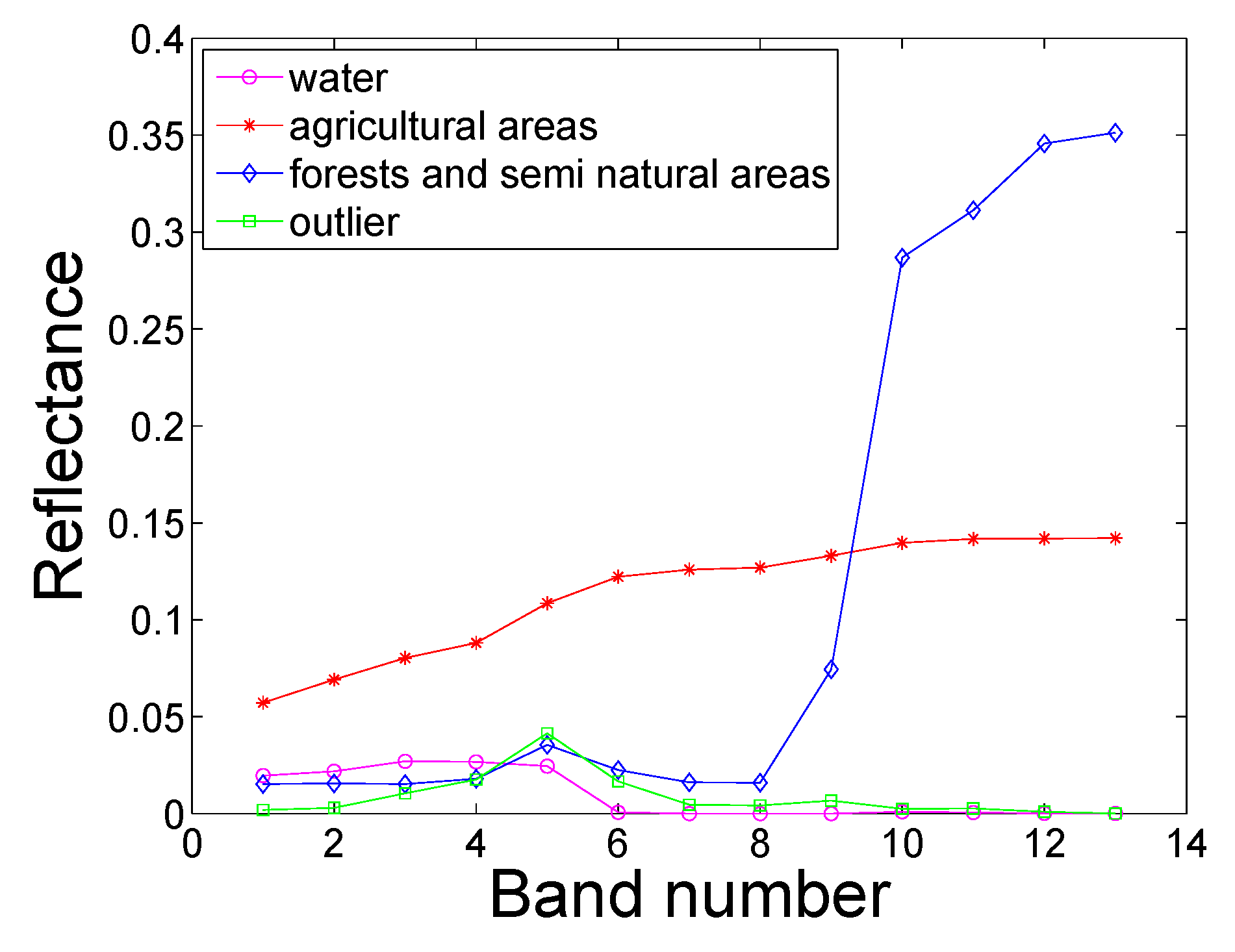

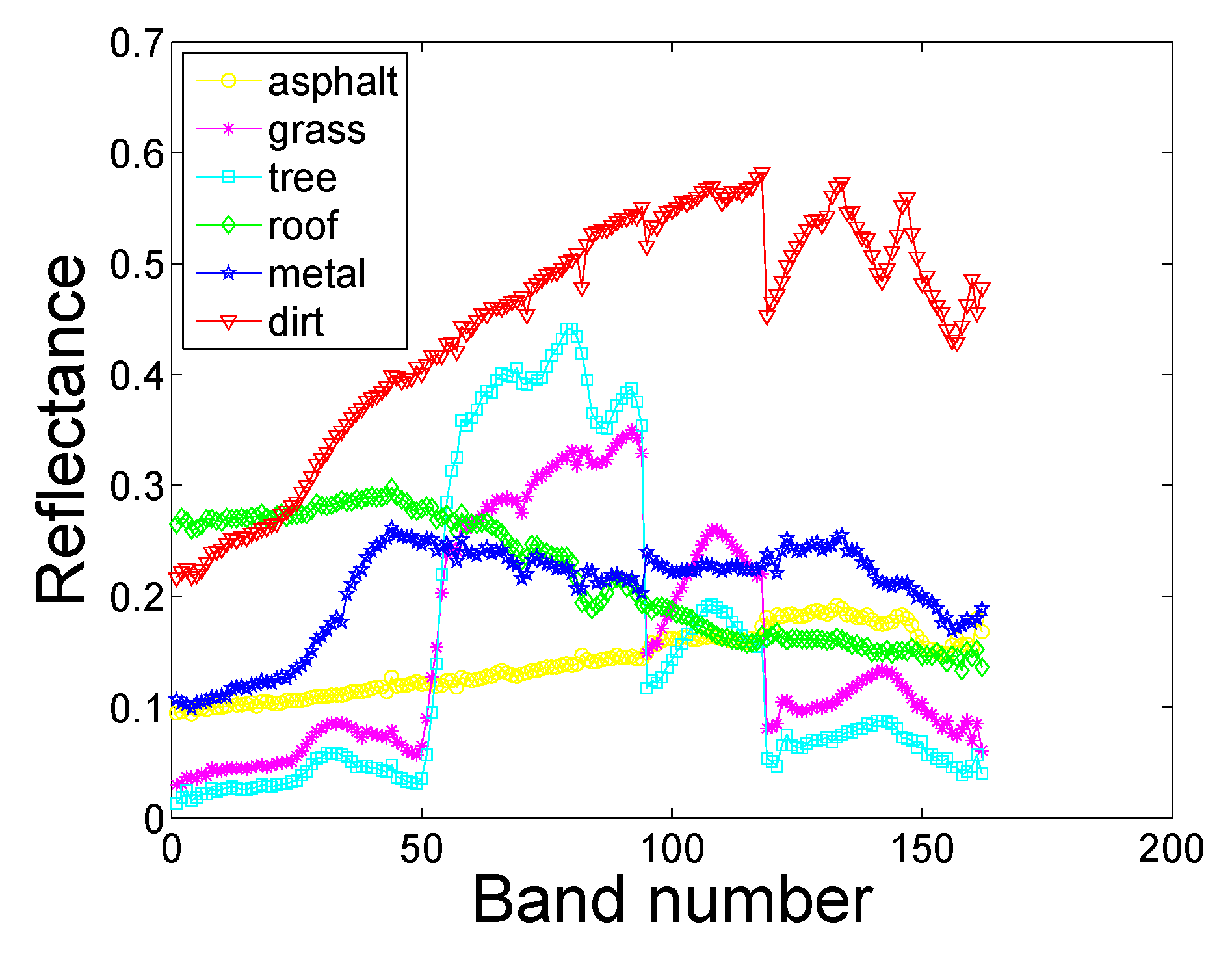

| Type of Noise | FCLS | GDA | Semi-NMF | BPOGM | NU-BGBM |
|---|---|---|---|---|---|
| Gaussian noise | 7.103 | 6.053 | 5.520 | 5.157 | 0.990 |
| Impulse noise | 7.123 | 6.395 | 6.161 | 5.403 | 0.167 |
| Dead lines | 6.812 | 5.773 | 5.796 | 5.436 | 0.171 |
| Gaussian noise & Impulse noise | 8.411 | 7.781 | 7.651 | 7.065 | 1.004 |
| Gaussian noise & Dead lines | 8.084 | 7.185 | 7.197 | 6.996 | 1.003 |
| Impulse noise & Dead lines | 7.941 | 7.254 | 7.469 | 6.962 | 0.296 |
| Gaussian noise & Impulse noise & Dead lines | 9.010 | 8.395 | 8.609 | 8.216 | 1.021 |
| FCLS | GDA | Semi-NMF | BPOGM | NU-BGBM | |
|---|---|---|---|---|---|
| RE | 2.106 | 1.980 | 1.481 | 1.117 | 1.046 |
| SMAD | 3.131 | 2.920 | 2.738 | 2.077 | 1.891 |
| FCLS | GDA | Semi-NMF | BPOGM | NU-BGBM | |
|---|---|---|---|---|---|
| RE | 1.138 | 1.044 | 0.899 | 0.898 | 0.353 |
| SMAD | 3.932 | 3.660 | 3.585 | 3.581 | 2.643 |
| FCLS | GDA | Semi-NMF | BPOGM | NU-BGBM | |
|---|---|---|---|---|---|
| RE | 4.120 | 4.057 | 1.837 | 1.721 | 1.443 |
| SMAD | 12.713 | 12.646 | 9.541 | 9.000 | 7.353 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Liu, Y.; Cheng, J.; Song, R.; Peng, H.; Chen, Q.; Chen, X. Hyperspectral Unmixing with Bandwise Generalized Bilinear Model. Remote Sens. 2018, 10, 1600. https://doi.org/10.3390/rs10101600
Li C, Liu Y, Cheng J, Song R, Peng H, Chen Q, Chen X. Hyperspectral Unmixing with Bandwise Generalized Bilinear Model. Remote Sensing. 2018; 10(10):1600. https://doi.org/10.3390/rs10101600
Chicago/Turabian StyleLi, Chang, Yu Liu, Juan Cheng, Rencheng Song, Hu Peng, Qiang Chen, and Xun Chen. 2018. "Hyperspectral Unmixing with Bandwise Generalized Bilinear Model" Remote Sensing 10, no. 10: 1600. https://doi.org/10.3390/rs10101600
APA StyleLi, C., Liu, Y., Cheng, J., Song, R., Peng, H., Chen, Q., & Chen, X. (2018). Hyperspectral Unmixing with Bandwise Generalized Bilinear Model. Remote Sensing, 10(10), 1600. https://doi.org/10.3390/rs10101600