Unsupervised Feature Selection Based on Ultrametricity and Sparse Training Data: A Case Study for the Classification of High-Dimensional Hyperspectral Data
Abstract
1. Introduction
1.1. Contribution
- the presentation of an approach for unsupervised feature selection based on the topology of given sparse training data,
- the use of different ultrametricity indices to describe the topology of given training data,
- the in-depth analysis of the potential of the proposed approach for unsupervised feature selection for the classification of high-dimensional hyperspectral data, and
- the comparison of achieved results with those of state-of-the-art feature selection and dimensionality reduction techniques.
1.2. Paper Outline
1.3. Related Work
1.3.1. Feature Extraction
1.3.2. Dimensionality Reduction (DR) vs. Feature Selection (FS)
- Filter-based methods focus on evaluating relatively simple relations between features and classes and possibly also among features. These relations are typically quantified via a score function which is directly applied to the given training data [4,6,24,29]. Such a classifier-independent scheme typically results in simplicity and efficiency. Many respective methods only focus on relations between features and classes (univariate filter-based feature selection). These relations can be quantified by comparing the values of a feature across all data points with the respective class labels, e.g., via the correlation coefficient [30], Gini index [31], Fisher score [32], or information gain [33]. This allows ranking the features with respect to their relevance. Other methods take into account both feature-class relations and feature-feature relations (multivariate filter-based feature selection) and can thus be used to remove redundancy to a certain degree. Respective examples are represented by Correlation-based Feature Selection [34] and the Fast Correlation-Based Filter [35].
- Wrapper-based methods rely on the use of a classifier in order to select features based on their suitability for classification. On the one hand, this may be achieved via Sequential Forward Selection (SFS) where, beginning with an empty feature subset, it is tested which feature can be added so that the increase in performance is as high as possible. Accordingly, classification is first performed separately for each available feature. The feature leading to the highest predictive accuracy is then added to the feature subset. The following steps consist in successively adding the feature that improves performance the most when considering the existing feature subset and the tested feature as input for classification. On the other hand, a classifier may be involved via Sequential Backward Elimination (SBE) where, beginning with the whole feature set, it is tested which feature can be discarded so that the decrease in performance is as low as possible. The following steps consist in successively removing the feature that reduces performance the least. Besides sequential selection, genetic algorithms which represent a family of stochastic optimization heuristics can be involved to select feature subsets [36].
- Embedded methods rely on the use of a classifier which provides the capability to internally select the most relevant features during the training phase of the classifier. Prominent examples in this regard are represented by the AdaBoost classifier [37] and the Random Forest classifier [38]. In contrast to wrapper-based methods, the involved classifier has to be trained only once to be able to conclude about the relevance of single features and the computational effort is therefore still acceptable, particularly for the Random Forest classifier which reveals a reasonable computational effort for both training and testing phase.
1.3.3. Classification
2. Materials and Methods
2.1. Datasets
2.1.1. Pavia Centre
2.1.2. Pavia University
2.1.3. Salinas
2.1.4. EnMAP
2.2. Feature Extraction
2.3. Dimensionality Reduction (DR) vs. Feature Selection (FS)
2.3.1. DR: Principal Component Analysis (PCA)
2.3.2. Supervised FS: Random Forest’s Mean Decrease in Permutation Accuracy (RF-MDPA)
2.3.3. Supervised FS: A General Relevance Metric (GRM)
2.3.4. Supervised FS: Correlation-Based Feature Selection (CFS)
2.3.5. Supervised FS: Fast Correlation-Based Filter (FCBF)
2.3.6. Unsupervised FS: Murtagh Ultrametricity Index (MUI)
2.3.7. Unsupervised FS: Topological Ultrametricity Index (TUI)
- The vertex set is X.
- A pair of data points is an edge if and only if .
2.3.8. Unsupervised FS: Baire-Optimal Feature Ranking (BOFR)
2.4. Classification
- The Nearest Neighbor (NN) classifier relies on instance-based learning. Thereby, a new feature vector is first compared with all feature vectors in the training data. Subsequently, the class label of the most similar feature vector in the training data is assigned to the new feature vector.
- The Linear Discriminant Analysis (LDA) classifier relies on probabilistic learning. The training of a respective classifier consists in fitting a multivariate Gaussian distribution to the training data. Thereby, the same covariance matrix is assumed for each class and only the means may vary. The testing consists in evaluating the probability of a new feature vector to belong to the different classes and assigning the class label corresponding to the highest probability.
- The Quadratic Discriminant Analysis (QDA) classifier also relies on probabilistic learning by fitting a multivariate Gaussian distribution to the training data. In contrast to the LDA classifier, both the covariance matrices and the means may vary for different classes. The testing again consists in evaluating the probability of a new feature vector to belong to the different classes and assigning the class label corresponding to the highest probability.
- The Random Forest (RF) classifier [38] relies on ensemble learning in terms of bagging. Thereby, an ensemble of decision trees is trained on randomly selected subsets of the training data. For a new feature vector, each decision tree casts a vote for one of the defined classes, and the majority vote across all decision trees is finally assigned.
3. Results
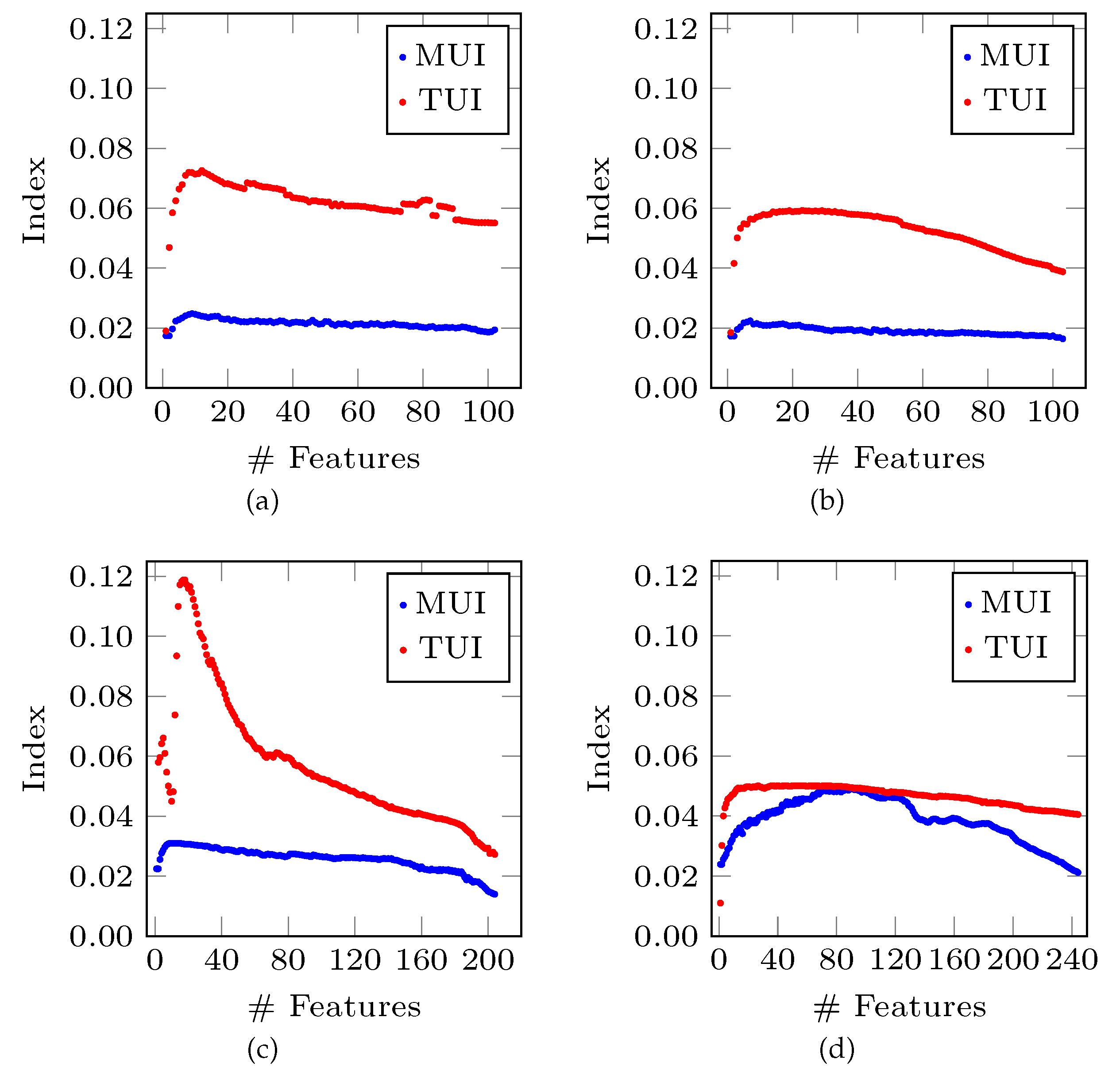
3.1. Ultrametricity Indices
3.2. Feature Ranking
3.3. Feature Subset Selection
- the complete feature set (),
- the feature set derived via PCA covering % of the variability of the given training data (),
- the feature set derived via RF-MDPA using the d best-ranked features (),
- the feature set derived via GRM using the d best-ranked features (),
- the feature set derived via CFS (),
- the feature set derived via FCBF (),
- the feature set derived via the first maximum of the MUI (),
- the feature set derived via the global maximum of the MUI (),
- the feature set derived via the first maximum of the TUI (),
- the feature set derived via the global maximum of the TUI (), and
- the feature set derived via BOFR using the d best-ranked features ().
3.4. Scene Interpretation
4. Discussion
4.1. Qualitative Discussion of the Derived Results
4.2. Quantitative Discussion of the Derived Results
4.3. Overview
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Braun, A.C.; Weinmann, M.; Keller, S.; Müller, R.; Reinartz, P.; Hinz, S. The EnMAP contest: Developing and comparing classification approaches for the Environmental Mapping and Analysis Programme—Dataset and first results. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 40, 169–175. [Google Scholar] [CrossRef]
- Dash, M.; Liu, H.; Motoda, H. Consistency based feature selection. In Proceedings of the Pacific-Asia Conference on Knowledge Discovery and Data Mining, Kyoto, Japan, 18–20 April 2000; Springer: Berlin, Germany, 2000; pp. 98–109. [Google Scholar]
- Saeys, Y.; Inza, I.; Larrañaga, P. A review of feature selection techniques in bioinformatics. Bioinformatics 2007, 23, 2507–2517. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Z.; Morstatter, F.; Sharma, S.; Alelyani, S.; Anand, A.; Liu, H. Advancing Feature Selection Research—ASU Feature Selection Repository; Technical Report; School of Computing, Informatics, and Decision Systems Engineering, Arizona State University: Tempe, AZ, USA, 2010. [Google Scholar]
- Weinmann, M.; Jutzi, B.; Hinz, S.; Mallet, C. Semantic point cloud interpretation based on optimal neighborhoods, relevant features and efficient classifiers. ISPRS J. Photogramm. Remote Sens. 2015, 105, 286–304. [Google Scholar] [CrossRef]
- Guyon, I.; Elisseeff, A. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Pesaresi, M.; Benediktsson, J.A. A new approach for the morphological segmentation of high-resolution satellite imagery. IEEE Trans. Geosci. Remote Sens. 2001, 39, 309–320. [Google Scholar] [CrossRef]
- Dalla Mura, M.; Villa, A.; Benediktsson, J.A.; Chanussot, J.; Bruzzone, L. Classification of hyperspectral images by using extended morphological attribute profiles and independent component analysis. IEEE Geosci. Remote Sens. Lett. 2011, 8, 542–546. [Google Scholar] [CrossRef]
- Ghamisi, P.; Dalla Mura, M.; Benediktsson, J.A. A survey on spectral-spatial classification techniques based on attribute profiles. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2335–2353. [Google Scholar] [CrossRef]
- Fauvel, M.; Chanussot, J.; Benediktsson, J.A. Adaptive pixel neighborhood definition for the classification of hyperspectral images with support vector machines and composite kernel. In Proceedings of the 2008 15th IEEE International Conference on Image Processing, San Diego, CA, USA, 12–15 October 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 1884–1887. [Google Scholar]
- Roscher, R.; Waske, B. Superpixel-based classification of hyperspectral data using sparse representation and conditional random fields. In Proceedings of the IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 3674–3677. [Google Scholar]
- Fang, L.; Li, S.; Kang, X.; Benediktsson, J.A. Spectral-spatial classification of hyperspectral images with a superpixel-based discriminative sparse model. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4186–4201. [Google Scholar] [CrossRef]
- Fang, L.; Li, S.; Duan, W.; Ren, J.; Benediktsson, J.A. Classification of hyperspectral images by exploiting spectral-spatial information of superpixel via multiple kernels. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6663–6674. [Google Scholar] [CrossRef]
- Li, W.; Chen, C.; Su, H.; Du, Q. Local binary patterns and extreme learning machine for hyperspectral imagery classification. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3681–3693. [Google Scholar] [CrossRef]
- Sidike, P.; Chen, C.; Asari, V.; Xu, Y.; Li, W. Classification of hyperspectral image using multiscale spatial texture features. In Proceedings of the 8th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing, Los Angeles, CA, USA, 21–24 August 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–4. [Google Scholar]
- Essa, A.; Sidike, P.; Asari, V. Volumetric directional pattern for spatial feature extraction in hyperspectral imagery. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1056–1060. [Google Scholar] [CrossRef]
- Keshava, N. A survey of spectral unmixing algorithms. Lincoln Lab. J. 2003, 14, 55–78. [Google Scholar]
- Parente, M.; Plaza, A. Survey of geometric and statistical unmixing algorithms for hyperspectral images. In Proceedings of the 2nd Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing, Reykjavik, Iceland, 14–16 June 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 1–4. [Google Scholar]
- Bioucas-Dias, J.M.; Plaza, A.; Dobigeon, N.; Parente, M.; Du, Q.; Gader, P.; Chanussot, J. Hyperspectral unmixing overview: Geometrical, statistical, and sparse regression-based approaches. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 354–379. [Google Scholar] [CrossRef]
- Dópido, I.; Villa, A.; Plaza, A.; Gamba, P. A quantitative and comparative assessment of unmixing-based feature extraction techniques for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 421–435. [Google Scholar] [CrossRef]
- Hughes, G.F. On the mean accuracy of statistical pattern recognizers. IEEE Trans. Inf. Theory 1968, 14, 55–63. [Google Scholar] [CrossRef]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef]
- Keller, S.; Braun, A.C.; Hinz, S.; Weinmann, M. Investigation of the impact of dimensionality reduction and feature selection on the classification of hyperspectral EnMAP data. In Proceedings of the 8th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing, Los Angeles, CA, USA, 21–24 August 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–5. [Google Scholar]
- Weinmann, M. Reconstruction and Analysis of 3D Scenes—From Irregularly Distributed 3D Points to Object Classes; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Licciardi, G.; Marpu, P.R.; Chanussot, J.; Benediktsson, J.A. Linear versus nonlinear PCA for the classification of hyperspectral data based on the extended morphological profiles. IEEE Geosci. Remote Sens. Lett. 2012, 9, 447–451. [Google Scholar] [CrossRef]
- Wang, J.; Chang, C.I. Independent component analysis-based dimensionality reduction with applications in hyperspectral image analysis. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1586–1600. [Google Scholar] [CrossRef]
- Villa, A.; Benediktsson, J.A.; Chanussot, J.; Jutten, C. Hyperspectral image classification with independent component discriminant analysis. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4865–4876. [Google Scholar] [CrossRef]
- Bandos, T.V.; Bruzzone, L.; Camps-Valls, G. Classification of hyperspectral images with regularized linear discriminant analysis. IEEE Trans. Geosci. Remote Sens. 2009, 47, 862–873. [Google Scholar] [CrossRef]
- Chehata, N.; Le Bris, A.; Najjar, S. Contribution of band selection and fusion for hyperspectral classification. In Proceedings of the 6th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing, Lausanne, Switzerland, 24–27 June 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1–4. [Google Scholar]
- Pearson, K. Mathematical contributions to the theory of evolution. III. Regression, heredity and panmixia. Philos. Trans. R. Soc. Lond. A 1896, 187, 253–318. [Google Scholar] [CrossRef]
- Gini, C. Variabilite e mutabilita. In Memorie di Metodologia Statistica; Libreria Eredi Virgilio Veschi: Rome, Italy, 1912. [Google Scholar]
- Fisher, R.A. The use of multiple measurements in taxonomic problems. Ann. Eugen. 1936, 7, 179–188. [Google Scholar] [CrossRef]
- Quinlan, J.R. Induction of decision trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]
- Hall, M.A. Correlation-Based Feature Subset Selection for Machine Learning. Ph.D. Thesis, Department of Computer Science, University of Waikato, Hamilton, New Zealand, 1999. [Google Scholar]
- Yu, L.; Liu, H. Feature selection for high-dimensional data: A fast correlation-based filter solution. In Proceedings of the International Conference on Machine Learning, Washington, DC, USA, 21–24 August 2003; AAAI Press: Palo Alto, CA, USA, 2003; pp. 856–863. [Google Scholar]
- Le Bris, A.; Chehata, N.; Briottet, X.; Paparoditis, N. Use intermediate results of wrapper band selection methods: A first step toward the optimization of spectral configuration for land cover classifications. In Proceedings of the 6th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing, Lausanne, Switzerland, 24–27 June 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1–4. [Google Scholar]
- Freund, Y.; Schapire, R.E. A decision-theoretic generalization of on-line learning and an application to boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Handl, J.; Knowles, J. Feature subset selection in unsupervised learning via multiobjective optimization. Int. J. Comput. Intell. Res. 2006, 2, 217–238. [Google Scholar] [CrossRef]
- Søndberg-Madsen, N.; Thomsen, C.; Peña, J.M. Unsupervised feature subset selection. In Proceedings of the Workshop on Probabilistic Graphical Models for Classification (within European Conference on Machine Learning 2003), Cavtat-Dubrovnik, Croatia, 23 September 2003; pp. 71–82. [Google Scholar]
- Handl, J.; Knowles, J.; Kell, D.B. Computational cluster validation in post-genomic data analysis. Bioinformatics 2005, 21, 3201–3212. [Google Scholar] [CrossRef] [PubMed]
- Dy, J.G.; Brodley, C.E. Feature selection for unsupervised learning. J. Mach. Learn. Res. 2004, 5, 845–889. [Google Scholar]
- Guo, D.; Gahegan, M.; Peuquet, D.; MacEachren, A. Breaking down dimensionality: An effective feature selection method for high-dimensional clustering. In Proceedings of the Third SIAM International Conference on Data Mining, Workshop on Clustering High Dimensional Data and its Applications, San Francisco, CA, USA, 3 May 2003; SIAM Press: Philadelphia, PA, USA, 2003; pp. 29–42. [Google Scholar]
- Mitra, P.; Murthy, C.A.; Pal, S.K. Unsupervised feature selection using feature similarity. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 301–312. [Google Scholar] [CrossRef]
- Du, Q.; Yang, H. Similarity-based unsupervised band selection for hyperspectral image analysis. IEEE Geosci. Remote Sens. Lett. 2008, 5, 564–568. [Google Scholar] [CrossRef]
- Cao, Y.; Zhang, J.; Zhuo, L.; Wang, C.; Zhou, Q. An unsupervised band selection based on band similarity for hyperspectral image target detection. In Proceedings of the International Conference on Internet Multimedia Computing and Service, Xiamen, China, 10–12 July 2014; ACM: New York, NY, USA, 2014; pp. 1–4. [Google Scholar]
- Datta, A.; Ghosh, S.; Ghosh, A. Combination of clustering and ranking techniques for unsupervised band selection of hyperspectral images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2814–2823. [Google Scholar] [CrossRef]
- Cariou, C.; Chehdi, K.; Le Moan, S. BandClust: An unsupervised band reduction method for hyperspectral remote sensing. IEEE Geosci. Remote Sens. Lett. 2011, 8, 565–569. [Google Scholar] [CrossRef]
- Bevilacqua, M.; Berthoumieu, Y. Unsupervised hyperspectral band selection via multi-feature information- maximization clustering. In Proceedings of the 2017 IEEE International Conference on Image Processing, Beijing, China, 17–20 September 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 540–544. [Google Scholar]
- Elghazel, H.; Aussem, A. Unsupervised feature selection with ensemble learning. Mach. Learn. 2015, 98, 157–180. [Google Scholar] [CrossRef]
- Kohonen, T. Self-Organizing Maps; Springer: Berlin, Germany, 2001. [Google Scholar]
- Köhler, A.; Ohrnberger, M.; Scherbaum, F. Unsupervised feature selection and general pattern discovery using self-organizing maps for gaining insights into the nature of seismic wavefields. Comput. Geosci. 2009, 35, 1757–1767. [Google Scholar] [CrossRef]
- Balabin, R.M.; Smirnov, S.V. Variable selection in near-infrared spectroscopy: Benchmarking of feature selection methods on biodiesel data. Anal. Chim. Acta 2011, 692, 63–72. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Usó, A.; Pla, F.; Sotoca, J.M.; García-Sevilla, P. Comparison of unsupervised band selection methods for hyperspectral imaging. In Proceedings of the Iberian Conference on Pattern Recognition and Image Analysis, Girona, Spain, 6–8 June 2007; Springer: Berlin, Germany, 2007; pp. 30–38. [Google Scholar]
- Murtagh, F. On ultrametricity, data coding, and computation. J. Classif. 2004, 21, 167–184. [Google Scholar] [CrossRef]
- Bradley, P.E. Degenerating families of dendrograms. J. Classif. 2008, 25, 27–42. [Google Scholar] [CrossRef]
- Bradley, P.E. On p-adic classification. p-Adic Numbers Ultrametr. Anal. Appl. 2009, 1, 271–285. [Google Scholar] [CrossRef]
- Murtagh, F. The remarkable simplicity of very high dimensional data: Application of model-based clustering. J. Classif. 2009, 26, 249–277. [Google Scholar] [CrossRef]
- Rammal, R.; Angles D’Auriac, J.C.; Doucot, B. On the degree of ultrametricity. J. Phys. Lett. 1985, 46, 945–952. [Google Scholar] [CrossRef]
- Benzecri, J.P. L’Analyse des Données: La Taxonomie, Tome 1, 3rd ed.; Dunod: Paris, France, 1980. [Google Scholar]
- Fouchal, S.; Ahat, M.; Ben Amor, S.; Lavallée, I.; Bui, M. Competitive clustering algorithms based on ultrametric properties. J. Comput. Sci. 2013, 4, 219–231. [Google Scholar] [CrossRef]
- Ham, J.; Chen, Y.; Crawford, M.M.; Ghosh, J. Investigation of the random forest framework for classification of hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 492–501. [Google Scholar] [CrossRef]
- Tarabalka, Y.; Chanussot, J.; Benediktsson, J.A.; Angulo, J.; Fauvel, M. Segmentation and classification of hyperspectral data using watershed. In Proceedings of the IEEE Geoscience and Remote Sensing Symposium, Boston, MA, USA, 7–11 July 2008; IEEE: Piscataway, NJ, USA, 2008; pp. III:652–III:655. [Google Scholar]
- Tarabalka, Y.; Fauvel, M.; Chanussot, J.; Benediktsson, J.A. SVM- and MRF-based method for accurate classification of hyperspectral images. IEEE Geosci. Remote Sens. Lett. 2010, 7, 736–740. [Google Scholar] [CrossRef]
- Tarabalka, Y.; Tilton, J.C. Spectral-spatial classification of hyperspectral images using hierarchical optimization. In Proceedings of the IEEE Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing, Lisbon, Portugal, 6–9 June 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 1–4. [Google Scholar]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep feature extraction and classification of hyperspectral images based on convolutional neural networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef]
- Tuia, D.; Ratle, F.; Pacifici, F.; Kanevski, M.F.; Emery, W.J. Active learning methods for remote sensing image classification. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2218–2232. [Google Scholar] [CrossRef]
- Tuia, D.; Volpi, M.; Copa, L.; Kanevski, M.; Munoz-Mari, J. A survey of active learning algorithms for supervised remote sensing image classification. IEEE J. Sel. Top. Signal Process. 2011, 5, 606–617. [Google Scholar] [CrossRef]
- Doerffer, R.; Grabl, H.; Kunkel, B.; van der Piepen, H. ROSIS—An advanced imaging spectrometer for the monitoring of water colour and chlorophyll fluorescence. Proc. SPIE 1989, 1129, 117–121. [Google Scholar]
- Guanter, L.; Segl, K.; Kaufmann, H. Simulation of optical remote-sensing scenes with application to the EnMAP hyperspectral mission. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2340–2351. [Google Scholar] [CrossRef]
- Segl, K.; Guanter, L.; Kaufmann, H.; Schubert, J.; Kaiser, S.; Sang, B.; Hofer, S. Simulation of spatial sensor characteristics in the context of the EnMAP hyperspectral mission. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3046–3054. [Google Scholar] [CrossRef]
- Benediktsson, J.A.; Ghamisi, P. Spectral-Spatial Classification of Hyperspectral Remote Sensing Images; Artech House: Boston, MA, USA, 2015. [Google Scholar]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Kononenko, I. Estimating attributes: Analysis and extensions of RELIEF. In Proceedings of the European Conference on Machine Learning, Catania, Italy, 6–8 April 1994; Springer: Berlin, Germany, 1994; pp. 171–182. [Google Scholar]
- Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. Numerical Recipes in C; Cambridge University Press: New York, NY, USA, 1988. [Google Scholar]
- Carlsson, G. Topology and data. Bull. Am. Math. Soc. 2009, 46, 255–308. [Google Scholar] [CrossRef]
- Vietoris, L. Über den höheren Zusammenhang kompakter Räume und eine Klasse von zusammenhangstreuen Abbildungen. Math. Ann. 1927, 97, 454–472. [Google Scholar] [CrossRef]
- Zomorodian, A. Fast construction of the Vietoris-Rips complex. Comput. Graph. 2010, 34, 263–271. [Google Scholar] [CrossRef]
- Bradley, P.E. Ultrametricity indices for the Euclidean and Boolean hypercubes. p-Adic Numbers Ultrametr. Anal. Appl. 2016, 8, 298–311. [Google Scholar] [CrossRef]
- Moon, J.W.; Moser, L. On cliques in graphs. Israel J. Math. 1965, 3, 23–28. [Google Scholar] [CrossRef]
- Bradley, P.E. Finding ultrametricity in data using topology. J. Classif. 2017, 34, 76–84. [Google Scholar] [CrossRef]
- Contreras, P.; Murtagh, F. Fast hierarchical clustering from the Baire distance. In Proceedings of the 11th IFCS Biennial Conference and 33rd Annual Conference of the Gesellschaft für Klassifikation e.V., Dresden, Germany, 13–18 March 2009; Springer: Berlin, Germany, 2010; pp. 235–243. [Google Scholar]
- Bradley, P.E.; Braun, A.C. Finding the asymptotically optimal Baire distance for multi-channel data. Appl. Math. 2015, 6, 484–495. [Google Scholar] [CrossRef]
- Schindler, K. An overview and comparison of smooth labeling methods for land-cover classification. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4534–4545. [Google Scholar] [CrossRef]
- Landrieu, L.; Raguet, H.; Vallet, B.; Mallet, C.; Weinmann, M. A structured regularization framework for spatially smoothing semantic labelings of 3D point clouds. ISPRS J. Photogramm. Remote Sens. 2017, 132, 102–118. [Google Scholar] [CrossRef]
- Keller, S.; Braun, A.C.; Hinz, S.; Weinmann, M. Investigation of the potential of hyperspectral EnMAP data for land cover and land use classification. In Proceedings of the 37 Wissenschaftlich-Technische Jahrestagung der DGPF, Würzburg, Germany, 8–10 March 2017; DGPF: München, Germany, 2017; pp. 110–121. [Google Scholar]
- Weinmann, M.; Weidner, U. Land-cover and land-use classification based on multitemporal Sentinel-2 data. In Proceedings of the IEEE Geoscience and Remote Sensing Symposium, Valencia, Spain, 23–27 July 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–4. [Google Scholar]














| Category | Strategy | Characteristics | Examples |
|---|---|---|---|
| Supervised | Filter-based FS | ||
| -Univariate | + Simple | Fisher score | |
| + Fast | Information gain | ||
| + Classifier-independent selection | Symm. uncertainty | ||
| − No feature dependencies | |||
| − No interaction with the classifier | |||
| -Multivariate | + Classifier-independent selection | CFS [34] | |
| + Models feature dependencies | FCBF [35] | ||
| + Faster than wrapper-based FS | |||
| − Slower than univariate techniques | |||
| − No interaction with the classifier | |||
| Wrapper-based FS | + Interaction with the classifier | SFS | |
| + Models feature dependencies | SBE | ||
| − Classifier-dependent selection | |||
| − Computationally intensive | |||
| − Risk of over-fitting | |||
| Embedded FS | + Interaction with the classifier | Random Forest | |
| + Models feature dependencies | AdaBoost | ||
| + Faster than wrapper-based FS | |||
| − Classifier-dependent selection | |||
| Unsupervised | Filter-based FS | + Classifier-independent selection | Clustering |
| + Models feature dependencies | MUI (proposed) | ||
| − No interaction with the classifier | TUI (proposed) | ||
| BOFR (proposed) | |||
| Wrapper-based FS | + Classifier-independent selection | Cluster validation | |
| + Models feature dependencies | |||
| − Computationally intensive |
| Feature Set | # Features | OA | ||||
|---|---|---|---|---|---|---|
| 102 | ||||||
| 9 | ||||||
| 20 | ||||||
| 20 | ||||||
| 13 | ||||||
| 3 | ||||||
| 9 | ||||||
| 9 | ||||||
| 8 | ||||||
| 12 | ||||||
| 20 |
| Feature Set | # Features | OA | ||||
|---|---|---|---|---|---|---|
| 103 | ||||||
| 9 | ||||||
| 20 | ||||||
| 20 | ||||||
| 21 | ||||||
| 5 | ||||||
| 7 | ||||||
| 7 | ||||||
| 5 | ||||||
| 23 | ||||||
| 20 |
| Feature Set | # Features | OA | ||||
|---|---|---|---|---|---|---|
| 204 | ||||||
| 5 | ||||||
| 40 | ||||||
| 40 | ||||||
| 30 | ||||||
| 17 | ||||||
| 11 | ||||||
| 11 | ||||||
| 5 | ||||||
| 16 | ||||||
| 40 |
| Feature Set | # Features | OA | ||||
|---|---|---|---|---|---|---|
| 244 | ||||||
| 8 | ||||||
| 40 | ||||||
| 40 | ||||||
| 24 | ||||||
| 10 | ||||||
| 12 | ||||||
| 89 | ||||||
| 13 | ||||||
| 56 | ||||||
| 40 |
| Method | Type | Strategy | Performance | Automation | Dimensionality of the New Feature Space |
|---|---|---|---|---|---|
| DR | U | − | + | ||
| FS | S | + | − | ∘ | |
| FS | S | − | − | ∘ | |
| FS | S | + | + | + | |
| FS | S | ∘ | + | + | |
| FS | U | + | + | + | |
| FS | U | + | + | ∘ | |
| FS | U | − | + | + | |
| FS | U | + | + | ∘ | |
| FS | U | − | − | ∘ |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bradley, P.E.; Keller, S.; Weinmann, M. Unsupervised Feature Selection Based on Ultrametricity and Sparse Training Data: A Case Study for the Classification of High-Dimensional Hyperspectral Data. Remote Sens. 2018, 10, 1564. https://doi.org/10.3390/rs10101564
Bradley PE, Keller S, Weinmann M. Unsupervised Feature Selection Based on Ultrametricity and Sparse Training Data: A Case Study for the Classification of High-Dimensional Hyperspectral Data. Remote Sensing. 2018; 10(10):1564. https://doi.org/10.3390/rs10101564
Chicago/Turabian StyleBradley, Patrick Erik, Sina Keller, and Martin Weinmann. 2018. "Unsupervised Feature Selection Based on Ultrametricity and Sparse Training Data: A Case Study for the Classification of High-Dimensional Hyperspectral Data" Remote Sensing 10, no. 10: 1564. https://doi.org/10.3390/rs10101564
APA StyleBradley, P. E., Keller, S., & Weinmann, M. (2018). Unsupervised Feature Selection Based on Ultrametricity and Sparse Training Data: A Case Study for the Classification of High-Dimensional Hyperspectral Data. Remote Sensing, 10(10), 1564. https://doi.org/10.3390/rs10101564