Compensation of Oxygen Transmittance Effects for Proximal Sensing Retrieval of Canopy–Leaving Sun–Induced Chlorophyll Fluorescence
Abstract
:1. Introduction
- How ignoring atmospheric effects can distinctly impact the success of the technique applied (FLD or SFM) to disentangle SIF from reflected light?
- What could be the best strategy to correct proximal sensing data for atmospheric effects?
- Is it possible to adapt atmospheric correction strategies used to process airborne data for proximal sensing measurements?
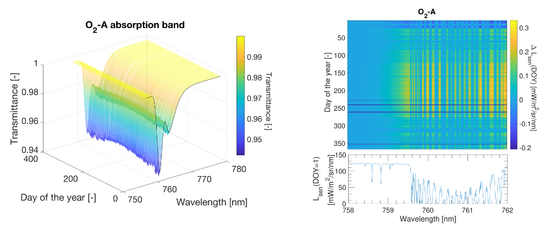
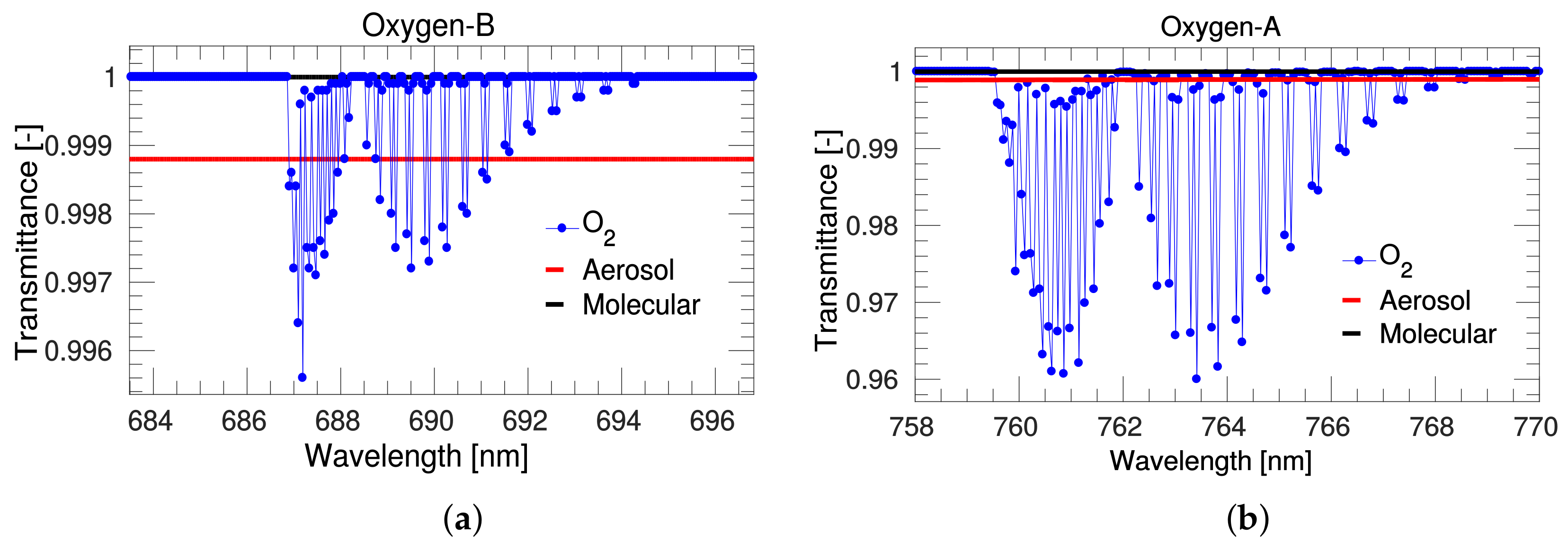
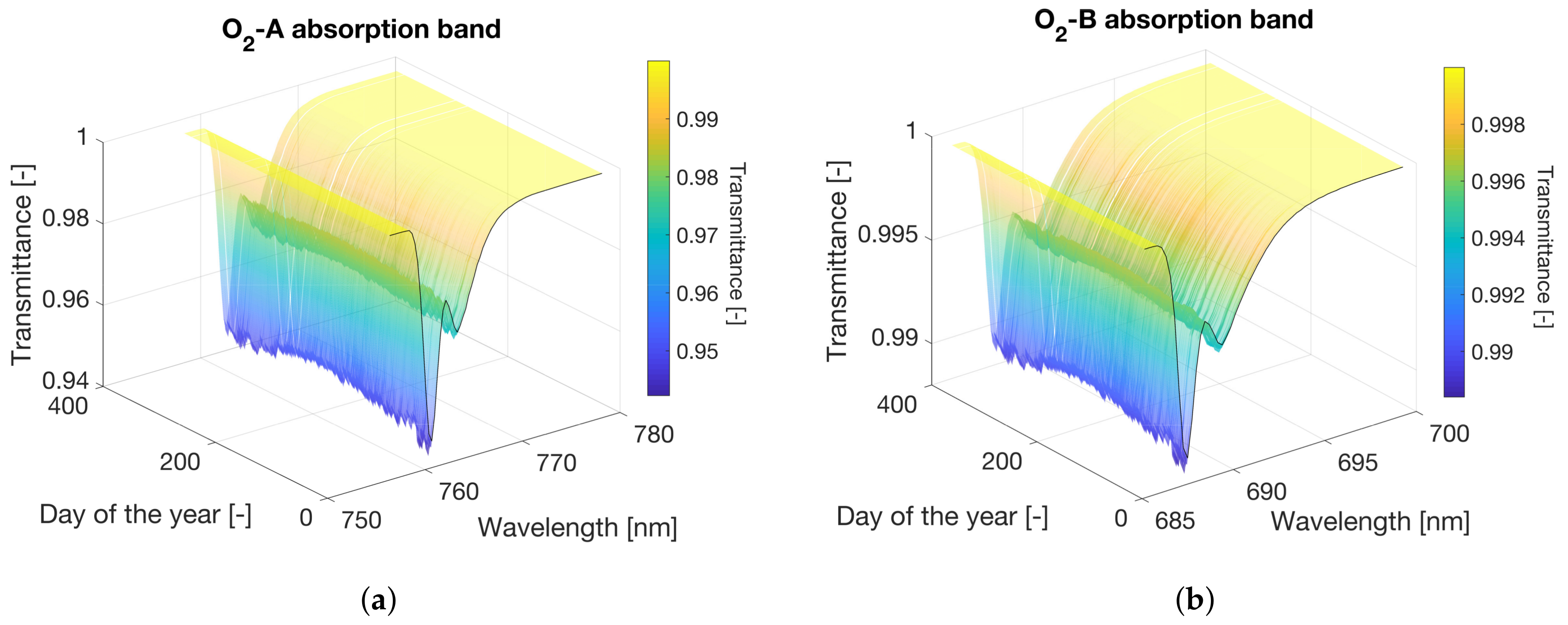
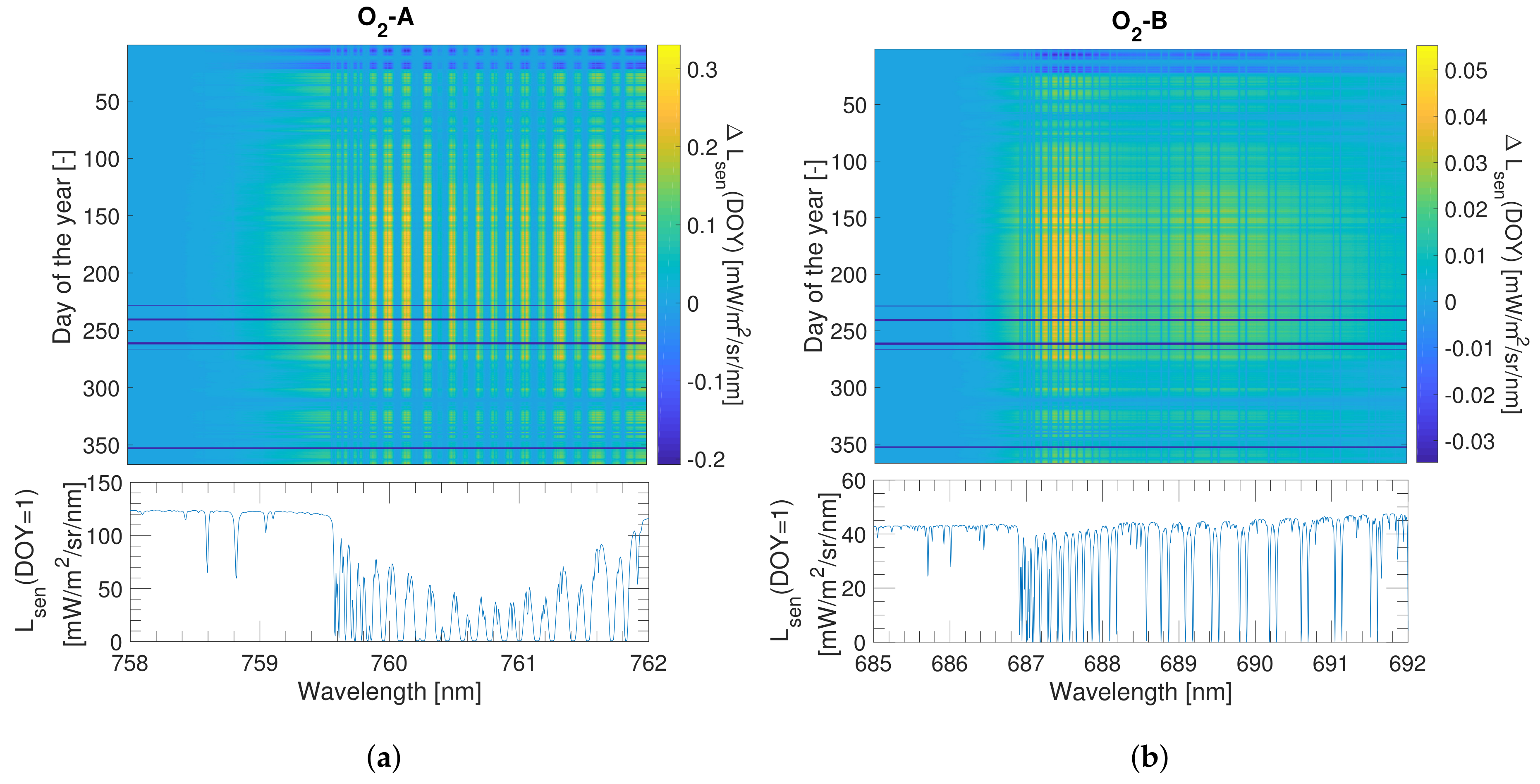
2. Atmospheric Oxygen Transmittance Effects at Tower Scale
2.1. At–Sensor and At–Canopy Solar Irradiance
2.2. Upward Atmospheric Transmittance from Surface TOC to Sensor Level
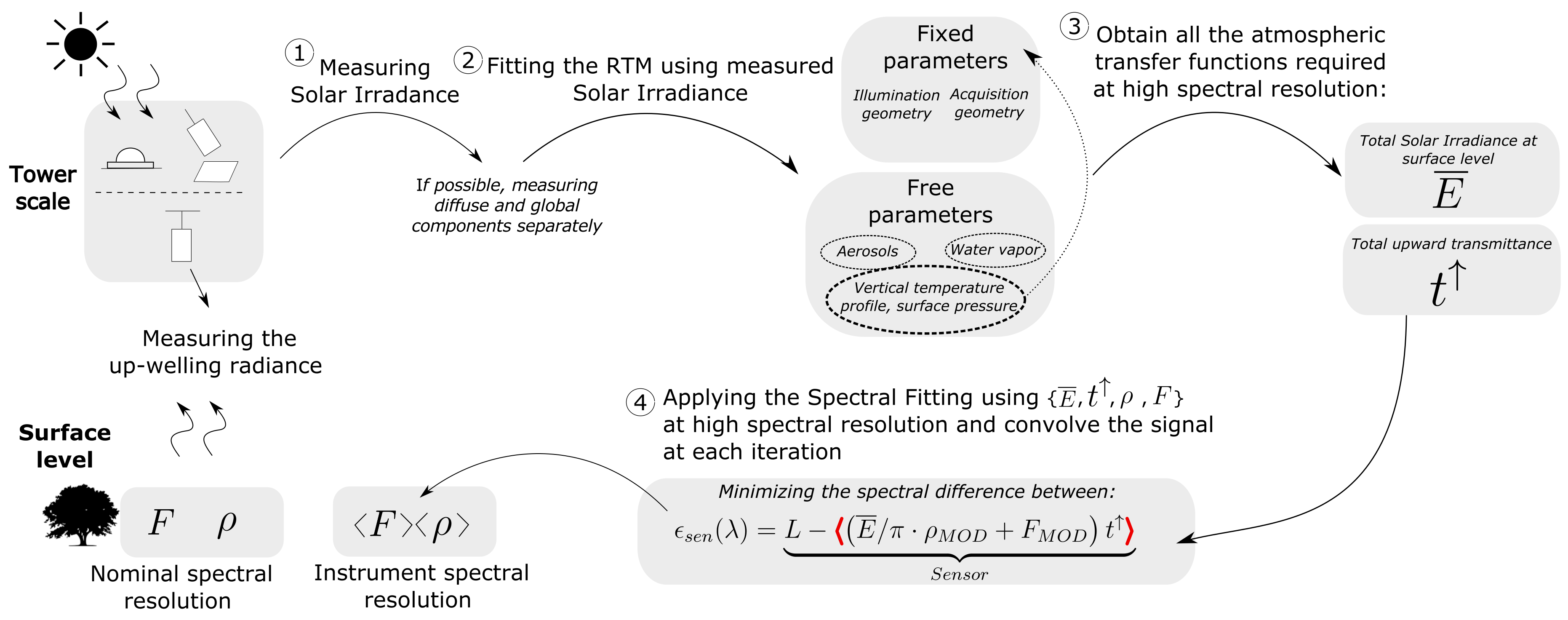
2.3. The Atmospheric Inversion Problem at High Spectral Resolution
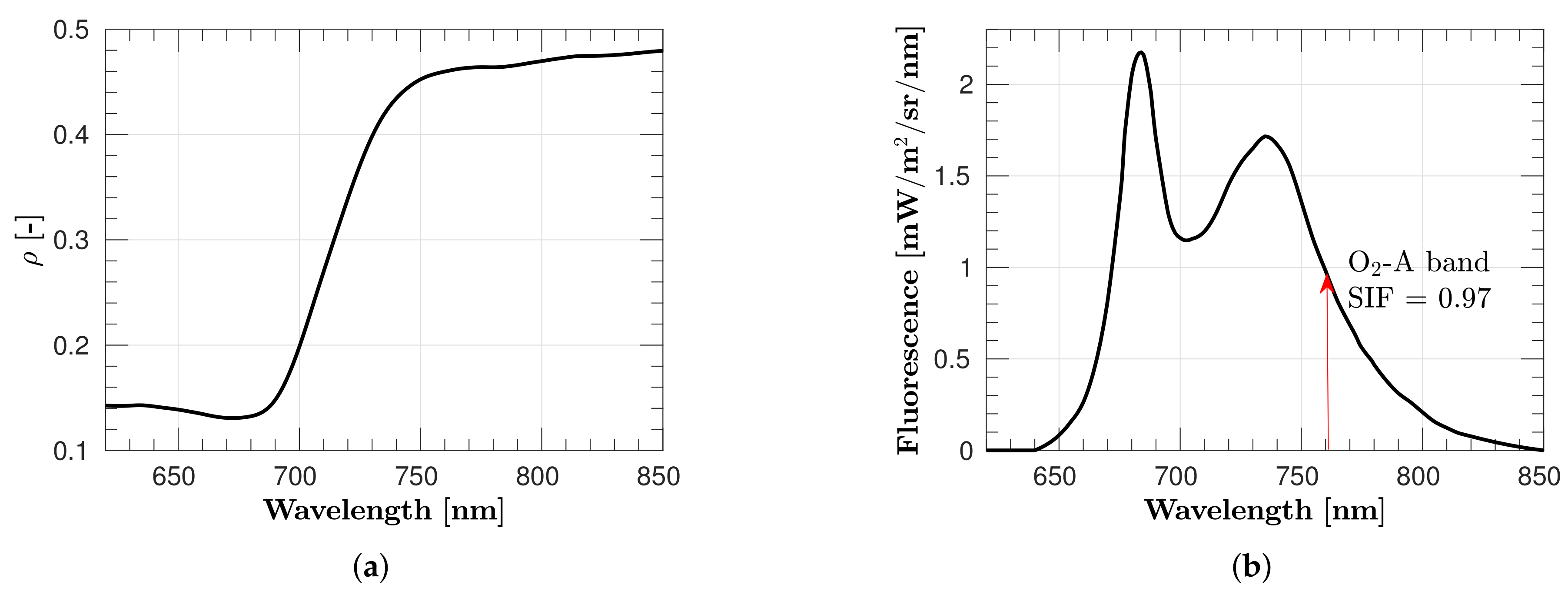
3. SIF Retrieval Methods
3.1. FLD and SFM Methods
3.2. O Transmittance Compensation on FLD and SFM
3.3. Adapting an Airborne Atmospheric Correction Scheme for Proximal Sensing Data
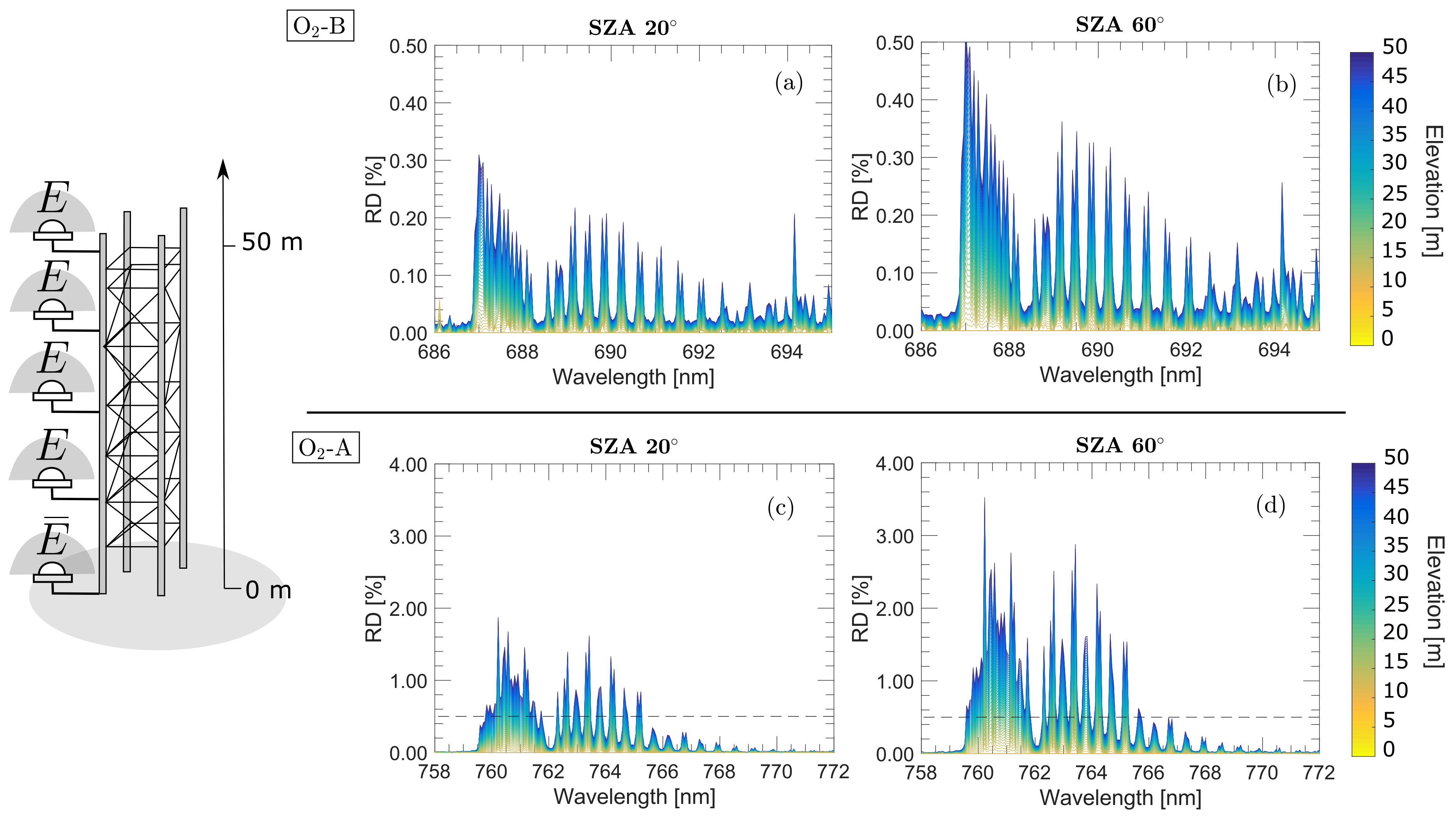
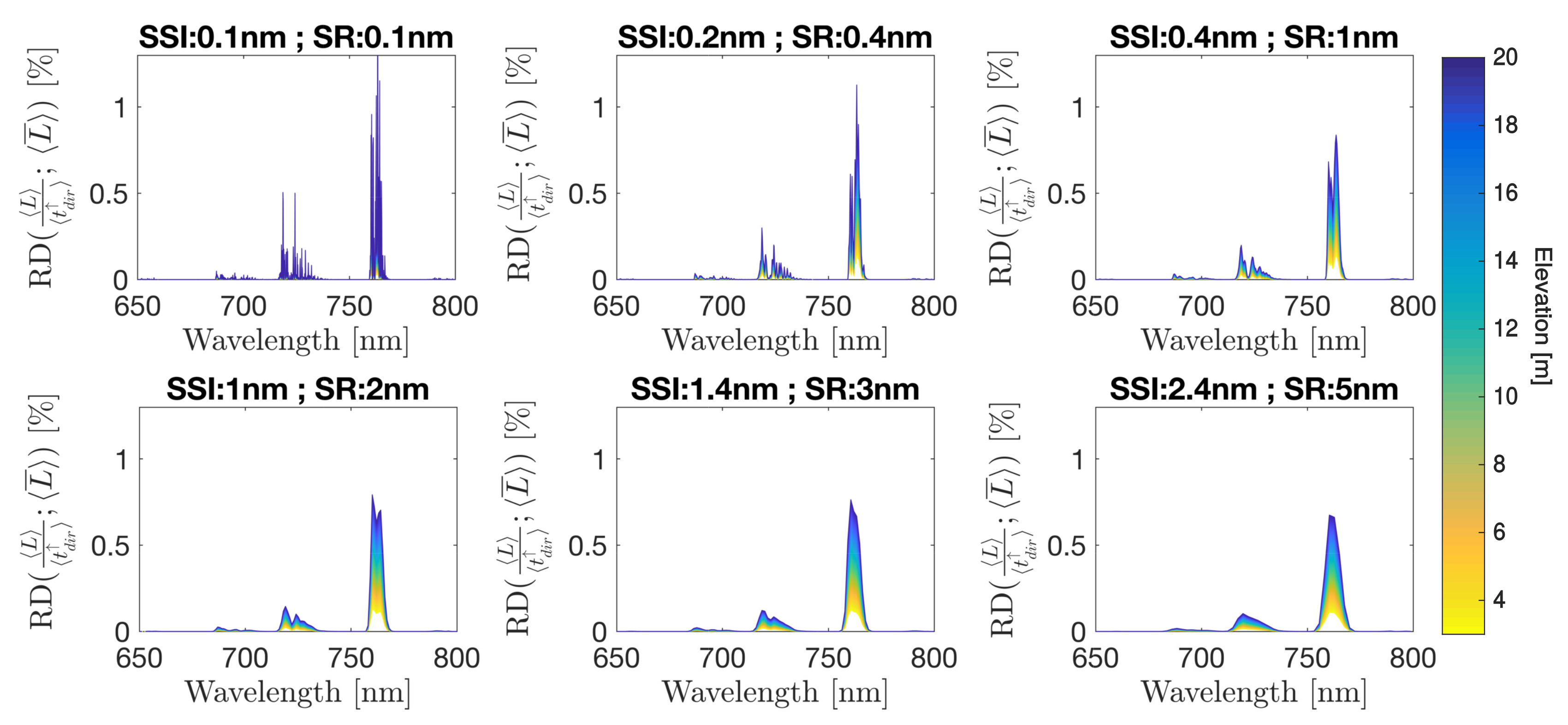
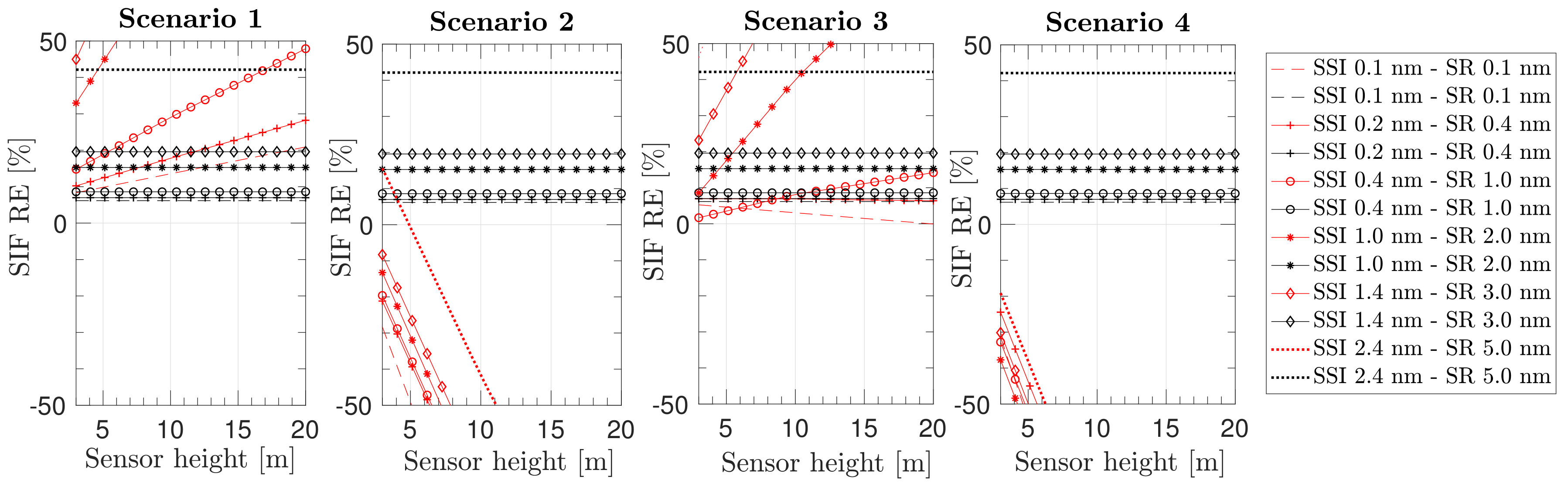
4. Impact of Oxygen Transmittance Compensation on Different SIF Retrieval Strategies
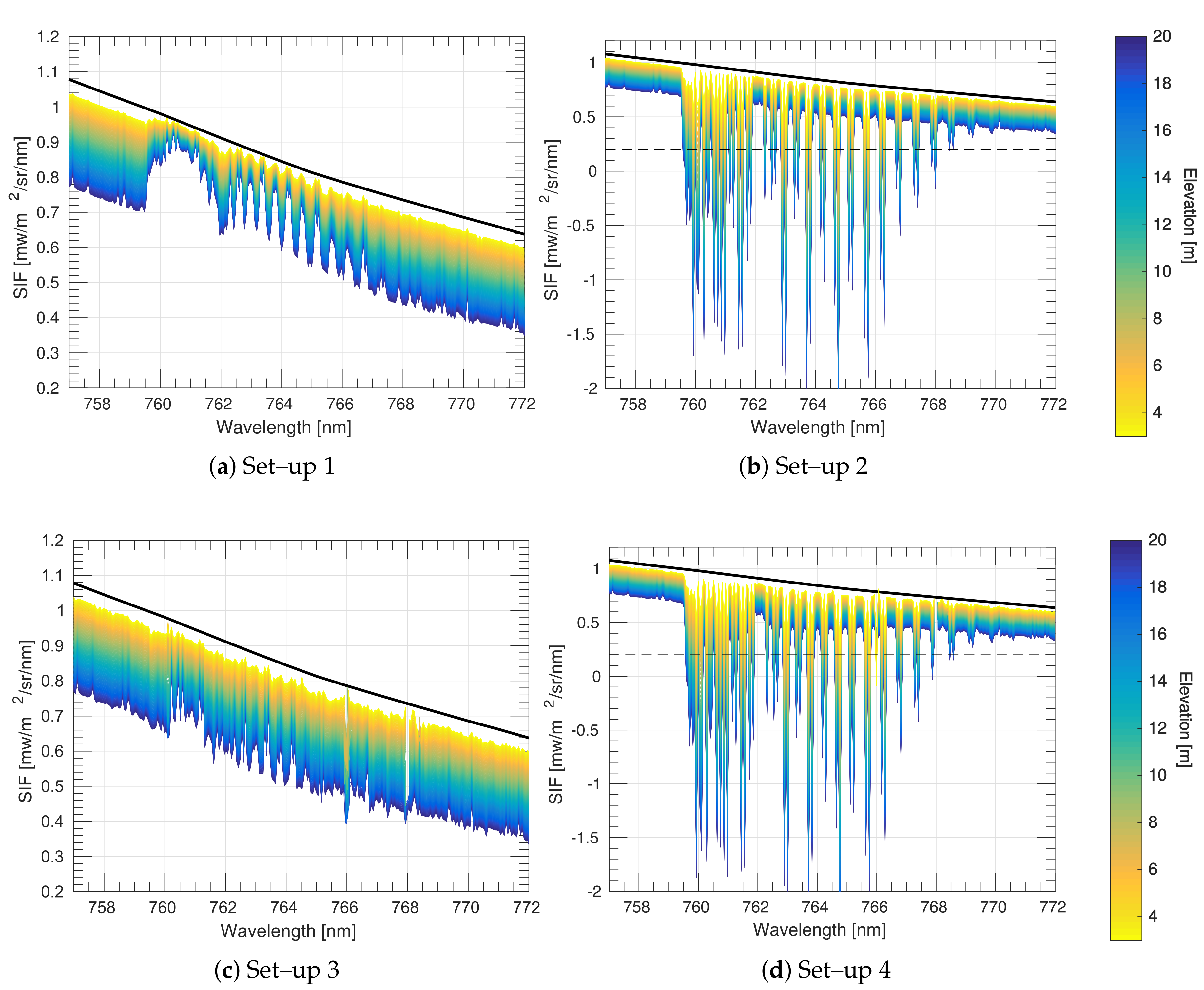
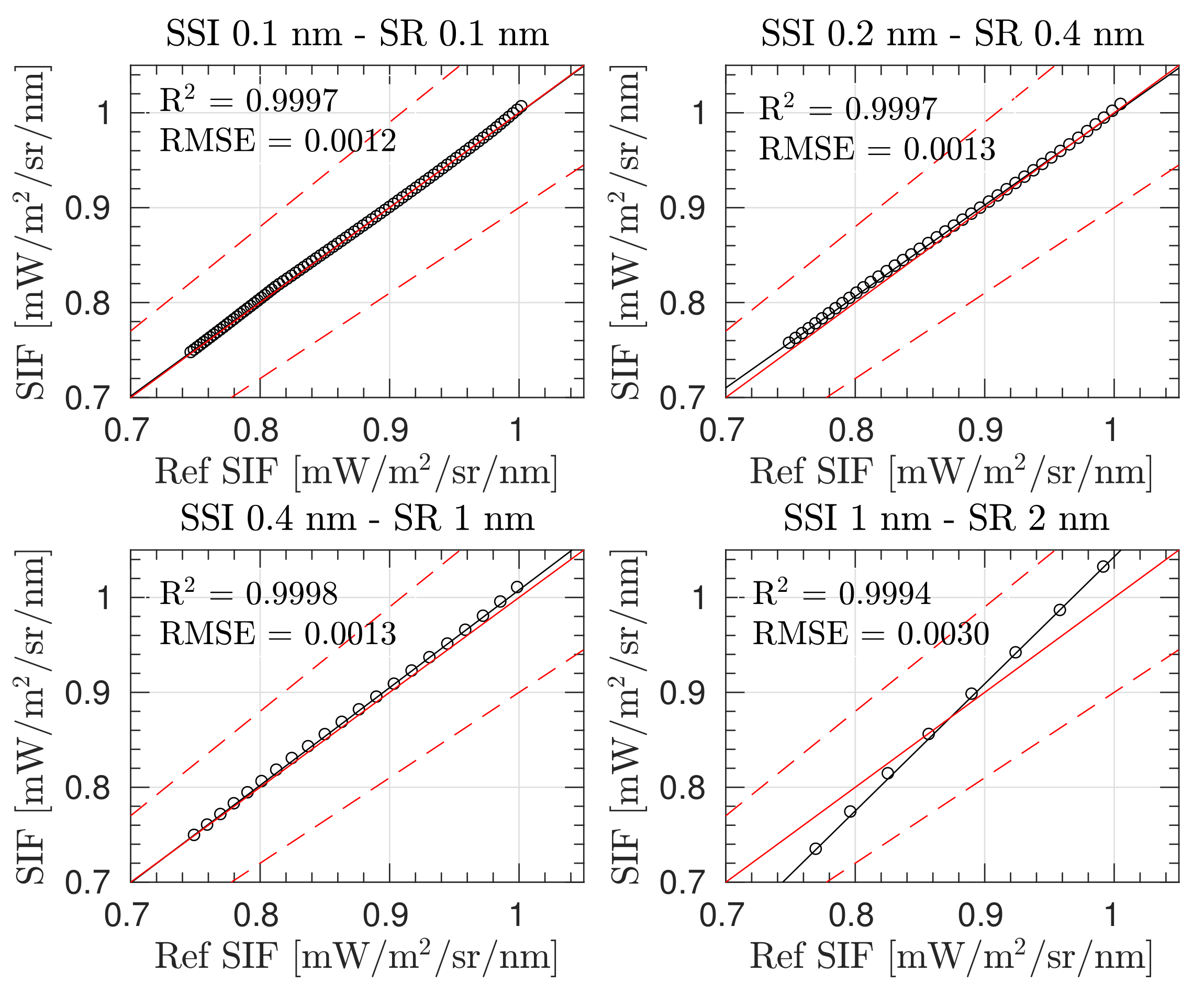
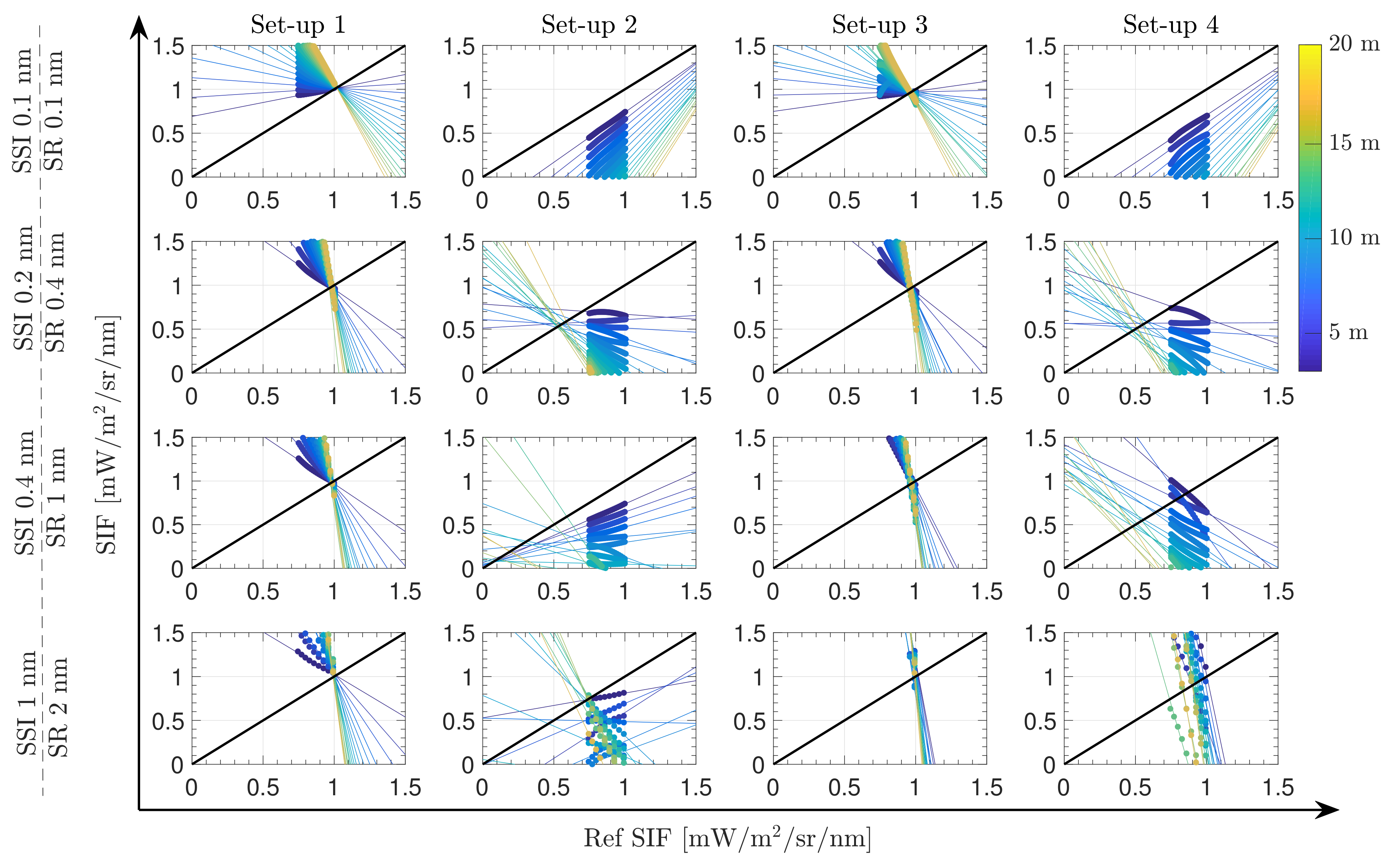
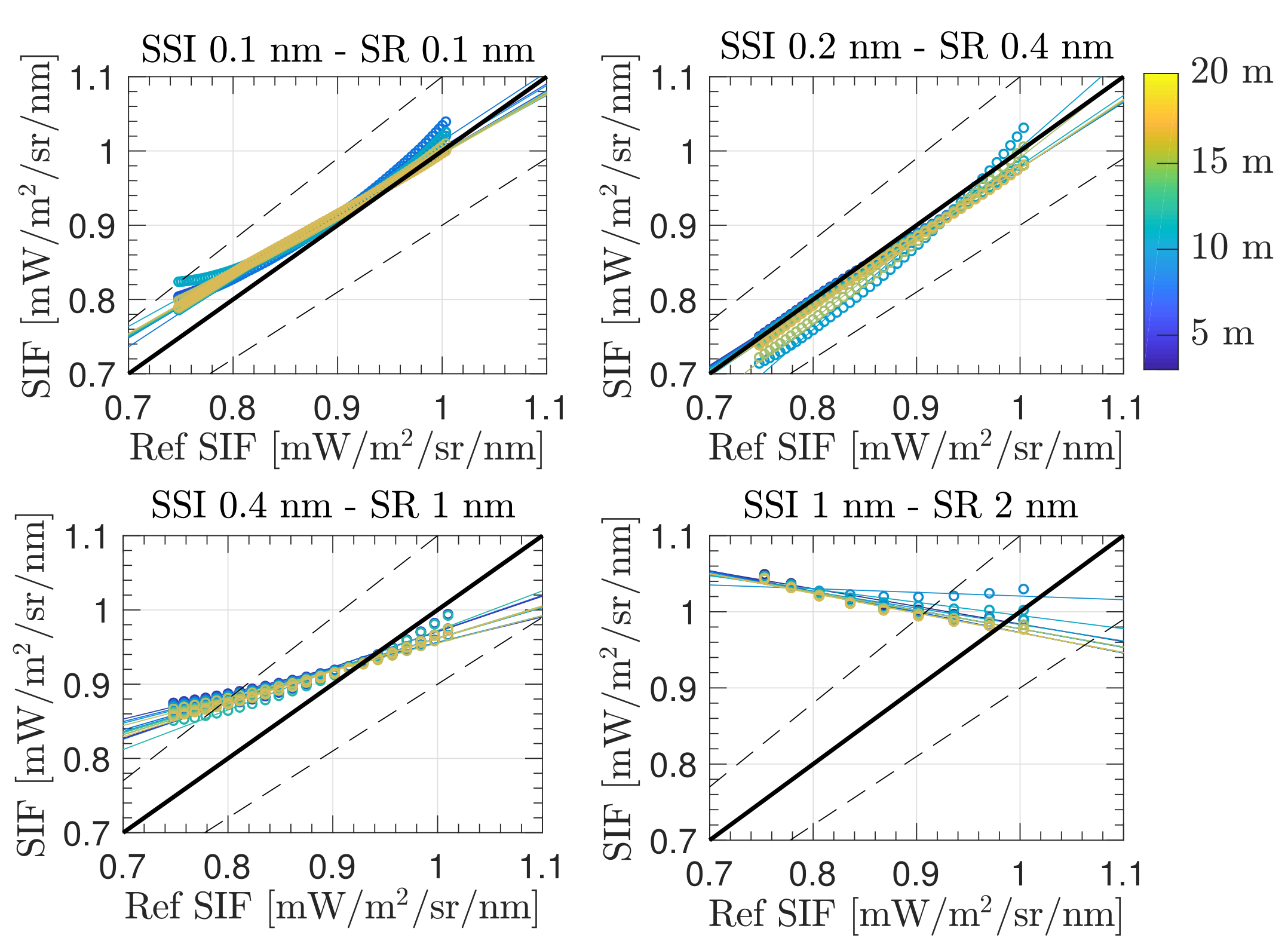
4.1. High Spectral Resolution
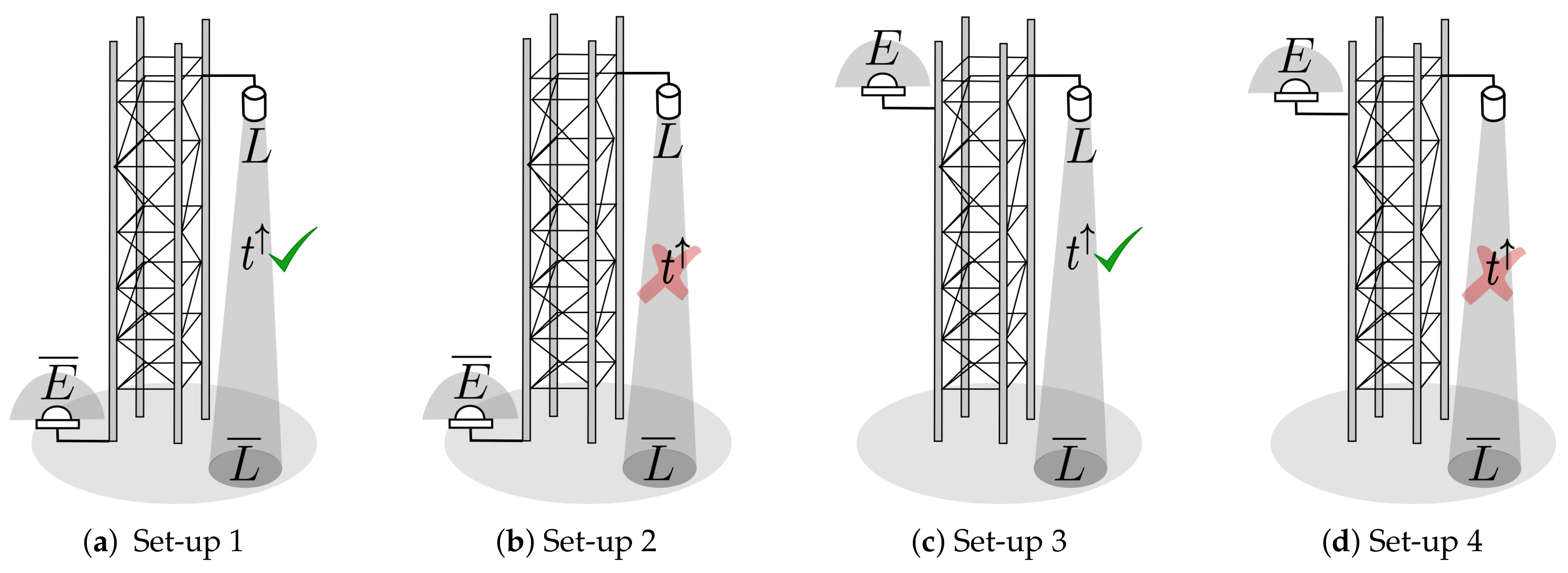
- Set–up :
- Set–up :
- Set–up :
- Set–up :
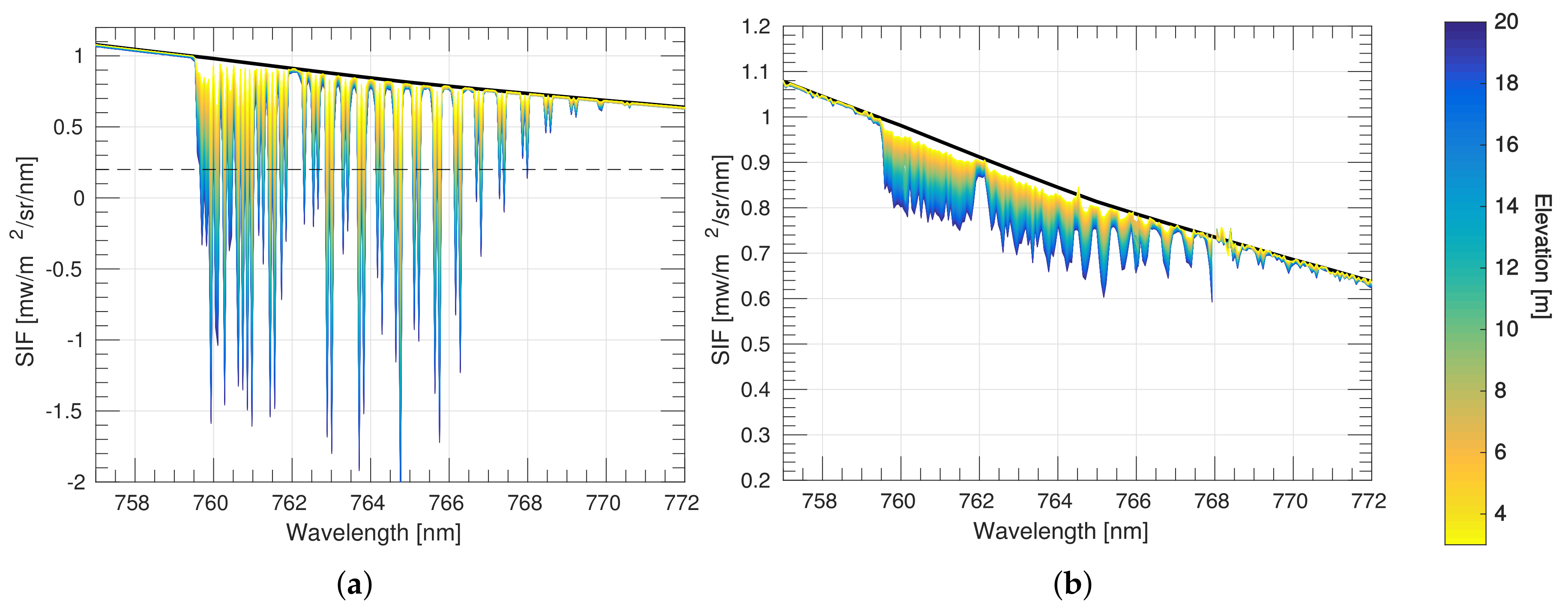
4.2. Oxygen Compensated 3FLD
4.3. Oxygen Compensated SFM
4.4. Airborne Atmospheric Correction Scheme Applied to Proximal Sensing Data: O and ISRF Compensated SFM
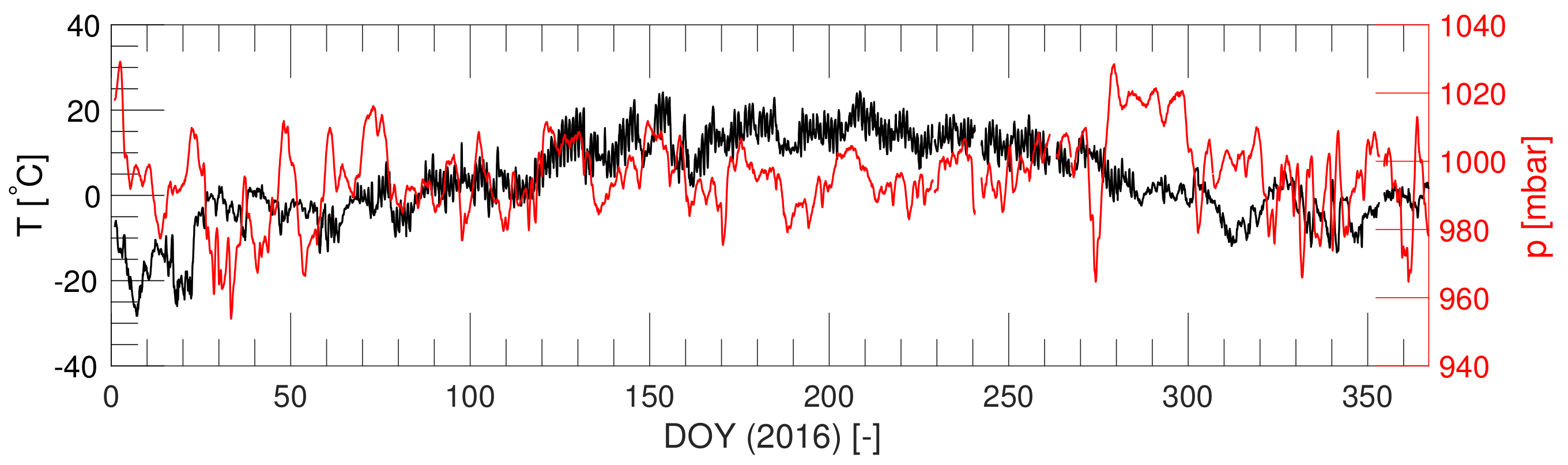
5. Temporal Analysis on Temperature and Pressure Environmental Conditions
6. Discussion
6.1. Ground–Based Validations
6.2. The Case Studies for Tower–Mounted Sensor Measurement Protocols
6.3. Utilizing an RTM
6.4. Other Factors Influencing SIF Retrievals
6.5. Environmental Factors Affecting SIF
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AOT | Aerosol Optical Thickness |
| EVI | Enhanced Vegetation Index |
| FLD | Fraunhofer Line Discriminator |
| FLEX | FLuorescence EXplorer |
| FOV | Field Of View |
| GOME–2 | Global Ozone Monitoring Mission–2 |
| GOSAT | Greenhouse Gases Observing Satellite |
| GPP | Gross Primary Productivity |
| HG | Henyey–Greenstein |
| HITRAN | HIgh–resolution TRANsmission molecular absorption database |
| ISRF | Instrumental Spectral Response Function |
| MODTRAN | MODerate TRANsmission molecular absorption database |
| NDVI | Normalized Difference Vegetation Index |
| OCO–2 | Orbiting Carbon Observatory–2 |
| RTM | Radiative Transfer Model |
| SFM | Spectral Fitting Methods |
| SIF | Solar–Induced chlorophyll Fluorescence |
| SNR | Signal To Noise Ratio |
| SPECNET | Spectral Network |
| SR | Spectral Resolution |
| SSI | Spectral Sampling Interval |
| SZA | Solar Zenith Angle |
| TOA | Top Of Atmosphere |
| TOC | Top Of Canopy |
| UAV | Unmanned Aerial Vehicle |
| VZA | Visual Zenith Angle |
Appendix A
| MODTRAN Input Parameter | Value (Units) | |
|---|---|---|
| Atmospheric parameters (total column) | Model of atmosphere | Model of atmosphere |
| AOT at 550 nm | 0.15 (-) | |
| Aerosol Type | Rural (-) | |
| Water vapour | 2.5 (g/cm2) | |
| Geometry parameters | sensor elevation | 0, 3, 10, 20, 50 (m) |
| Solar Zenith Angle | 0, 20, 40, 60 (°) | |
| Viewing Zenith Angle | 0 (°) | |
| Relative Azimuth Angle between sun and sensor | 90 (°) | |
| High Spectral Resolution | Spectral Resolution at O2–B | 1 (cm−1) ∼0.04 (nm) |
| Spectral Resolution at O2–A | 1 (cm−1) ∼0.05 (nm) |
Appendix B
References
- Porcar-Castell, A.; Tyystjarvi, E.; Atherton, J.; van der Tol, C.; Flexas, J.; Pfundel, E.E.; Moreno, J.; Frankenberg, C.; Berry, J.A. Linking chlorophyll a fluorescence to photosynthesis for remote sensing applications: Mechanisms and challenges. J. Exp. Bot. 2014, 1–31. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Fan, Y.; Zhang, Y.; Chou, S.; Ju, W.; Chen, J.M. A conjunct near-surface spectroscopy system for fix-angle and multi-angle continuous measurements of canopy reflectance and sun-induced chlorophyll fluorescence. In Proceedings of the SPIE Optical Engineering + Applications. International Society for Optics and Photonics, San Diego, CA, USA, 19 September 2016; p. 99770C. [Google Scholar]
- Balzarolo, M.; Anderson, K.; Nichol, C.; Rossini, M.; Vescovo, L.; Arriga, N.; Wohlfahrt, G.; Calvet, J.C.; Carrara, A.; Cerasoli, S.; et al. Ground-based optical measurements at European flux sites: A review of methods, instruments and current controversies. Sensors 2011, 11, 7954–7981. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mac Arthur, A.; Robinson, I.; Rossini, M.; Davis, N.; MacDonald, K. A dual-field-of-view spectrometer system for reflectance and fluorescence measurements (Piccolo Doppio) and correction of etaloning. In Proceedings of the Fifth International Workshop on Remote Sensing of Vegetation Fluorescence, Paris, France, 22–24 April 2014; pp. 22–24. [Google Scholar]
- Porcar-Castell, A.; Mac Arthur, A.; Rossini, M.; Eklundh, L.; Pacheco-Labrador, J.; Anderson, K.; Balzarolo, M.; Martín, M.; Jin, H.; Tomelleri, E.; et al. EUROSPEC. Biogeosciences 2015. [Google Scholar] [CrossRef]
- Joiner, J.; Yoshida, Y.; Vasilkov, A.; Middleton, E.; Campbell, P.; Kuze, A. Filling-in of near-infrared solar lines by terrestrial fluorescence and other geophysical effects: Simulations and space-based observations from SCIAMACHY and GOSAT. Atmos. Meas. Tech. 2012, 5, 809–829. [Google Scholar] [CrossRef]
- Guanter, L.; Zhang, Y.; Jung, M.; Joiner, J.; Voigt, M.; Berry, J.A.; Frankenberg, C.; Huete, A.R.; Zarco-Tejada, P.; Lee, J.E.; et al. Global and time-resolved monitoring of crop photosynthesis with chlorophyll fluorescence. Proc. Natl. Acad. Sci. USA 2014, 111, E1327–E1333. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sun, Y.; Frankenberg, C.; Wood, J.D.; Schimel, D.; Jung, M.; Guanter, L.; Drewry, D.; Verma, M.; Porcar-Castell, A.; Griffis, T.J.; et al. OCO-2 advances photosynthesis observation from space via solar-induced chlorophyll fluorescence. Science 2017, 358, eaam5747. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moreno, J.F.; Goulas, Y.; Huth, A.; Middleton, E.; Miglietta, F.; Mohammed, G.; Nedbal, L.; Rascher, U.; Verhoef, W.; Drusch, M. Very high spectral resolution imaging spectroscopy: The Fluorescence Explorer (FLEX) mission. Procedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 264–267. [Google Scholar]
- Daumard, F.; Champagne, S.; Fournier, A.; Goulas, Y.; Ounis, A.; Hanocq, J.F.; Moya, I. A field platform for continuous measurement of canopy fluorescence. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3358–3368. [Google Scholar] [CrossRef]
- Drolet, G.; Wade, T.; Nichol, C.J.; MacLellan, C.; Levula, J.; Porcar-Castell, A.; Nikinmaa, E.; Vesala, T. A temperature-controlled spectrometer system for continuous and unattended measurements of canopy spectral radiance and reflectance. Int. J. Remote Sens. 2014, 35, 1769–1785. [Google Scholar] [CrossRef]
- Bresciani, M.; Rossini, M.; Morabito, G.; Matta, E.; Pinardi, M.; Cogliati, S.; Julitta, T.; Colombo, R.; Braga, F.; Giardino, C. Analysis of within-and between-day chlorophyll-a dynamics in Mantua Superior Lake, with a continuous spectroradiometric measurement. Mar. Freshw. Res. 2013, 64, 303–316. [Google Scholar] [CrossRef]
- Cogliati, S.; Rossini, M.; Julitta, T.; Meroni, M.; Schickling, A.; Burkart, A.; Pinto, F.; Rascher, U.; Colombo, R. Continuous and long-term measurements of reflectance and sun-induced chlorophyll fluorescence by using novel automated field spectroscopy systems. Remote Sens. Environ. 2015, 164, 270–281. [Google Scholar] [CrossRef]
- Meroni, M.; Barducci, A.; Cogliati, S.; Castagnoli, F.; Rossini, M.; Busetto, L.; Migliavacca, M.; Cremonese, E.; Galvagno, M.; Colombo, R.; et al. The hyperspectral irradiometer, a new instrument for long-term and unattended field spectroscopy measurements. Rev. Sci. Instrum. 2011, 82, 043106. [Google Scholar] [CrossRef] [PubMed]
- Rossini, M.; Cogliati, S.; Meroni, M.; Migliavacca, M.; Galvagno, M.; Busetto, L.; Cremonese, E.; Julitta, T.; Siniscalco, C.; Morra di Cella, U.; et al. Remote sensing-based estimation of gross primary production in a subalpine grassland. Biogeosciences 2012, 9, 2565–2584. [Google Scholar] [CrossRef] [Green Version]
- Rossini, M.; Migliavacca, M.; Galvagno, M.; Meroni, M.; Cogliati, S.; Cremonese, E.; Fava, F.; Gitelson, A.; Julitta, T.; di Cella, U.M.; et al. Remote estimation of grassland gross primary production during extreme meteorological seasons. Int. J. Appl. Earth Obs. Geoinf. 2014, 29, 1–10. [Google Scholar] [CrossRef]
- Guanter, L.; Rossini, M.; Colombo, R.; Meroni, M.; Frankenberg, C.; Lee, J.E.; Joiner, J. Using field spectroscopy to assess the potential of statistical approaches for the retrieval of sun-induced chlorophyll fluorescence from ground and space. Remote Sens. Environ. 2013, 133, 52–61. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, S.; Huang, C.; Cen, Y.; Zhai, Y.; Tong, Q. Retrieval of Sun-Induced Chlorophyll Fluorescence Using Statistical Method Without Synchronous Irradiance Data. IEEE Geosci. Remote Sens. Lett. 2017, 14, 384–388. [Google Scholar] [CrossRef]
- Plascyk, J.A. The MK II Fraunhofer line discriminator (FLD-II) for airborne and orbital remote sensing of solar-stimulated luminescence. Opt. Eng. 1975, 14, 144399. [Google Scholar] [CrossRef]
- Plascyk, J.A.; Gabriel, F.C. The Fraunhofer line discriminator MKII-an airborne instrument for precise and standardized ecological luminescence measurement. IEEE Trans. Instrum. Meas. 1975, 24, 306–313. [Google Scholar] [CrossRef]
- Maier, S.W.; Günther, K.P.; Stellmes, M. Sun-induced fluorescence: A new tool for precision farming. In Digital Imaging and Spectral Techniques: Applications to Precision Agriculture and Crop Physiology; ASA; CSSA; SSSA: Madison, WI, USA, 2003; Volume 66. [Google Scholar]
- Alonso, L.; Gomez-Chova, L.; Vila-Frances, J.; Amoros-Lopez, J.; Guanter, L.; Calpe, J. Improved Fraunhofer Line Discrimination method for vegetation fluorescence quantification. IEEE Geosci. Remote Sens. Lett. 2008, 5, 620–624. [Google Scholar] [CrossRef]
- Mazzoni, M.; Falorni, P.; Verhoef, W. High-resolution methods for fluorescence retrieval from space. Opt. Express 2010, 18, 15649–15663. [Google Scholar] [CrossRef] [PubMed]
- Meroni, M.; Busetto, L.; Colombo, R.; Guanter, L.; Moreno, J.; Verhoef, W. Performance of spectral fitting methods for vegetation fluorescence quantification. Remote Sens. Environ. 2010, 114, 363–374. [Google Scholar] [CrossRef]
- Cogliati, S.; Verhoef, W.; Kraft, S.; Sabater, N.; Alonso, L.; Vicent, J.; Moreno, J.; Drusch, M.; Colombo, R. Retrieval of sun-induced fluorescence using advanced spectral fitting methods. Remote Sens. Environ. 2015, 169, 344–357. [Google Scholar] [CrossRef]
- Meroni, M.; Colombo, R. Leaf level detection of solar induced chlorophyll fluorescence by means of a subnanometer resolution spectroradiometer. Remote Sens. Environ. 2006, 103, 438–448. [Google Scholar] [CrossRef]
- Meroni, M.; Rossini, M.; Picchi, V.; Panigada, C.; Cogliati, S.; Nali, C.; Colombo, R. Assessing steady-state fluorescence and PRI from hyperspectral proximal sensing as early indicators of plant stress: The case of ozone exposure. Sensors 2008, 8, 1740–1754. [Google Scholar] [CrossRef] [PubMed]
- Middleton, E.M.; Corp, L.; Campbell, P. Comparison of measurements and FluorMOD simulations for solar-induced chlorophyll fluorescence and reflectance of a corn crop under nitrogen treatments. Int. J. Remote Sens. 2008, 29, 5193–5213. [Google Scholar] [CrossRef]
- Rascher, U.; Agati, G.; Alonso, L.; Cecchi, G.; Champagne, S.; Colombo, R.; Damm, A.; Daumard, F.; De Miguel, E.; Fernandez, G.; et al. CEFLES2: The remote sensing component to quantify photosynthetic efficiency from the leaf to the region by measuring sun-induced fluorescence in the oxygen absorption bands. Biogeosciences 2009, 6, 1181–1198. [Google Scholar] [CrossRef] [Green Version]
- Zarco-Tejada, P.J.; Berni, J.A.; Suárez, L.; Sepulcre-Cantó, G.; Morales, F.; Miller, J. Imaging chlorophyll fluorescence with an airborne narrow-band multispectral camera for vegetation stress detection. Remote Sens. Environ. 2009, 113, 1262–1275. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; González-Dugo, V.; Berni, J.A.J. Fluorescence, temperature and narrow-band indices acquired from a UAV platform for water stress detection using a micro-hyperspectral imager and a thermal camerça. Remote Sens. Environ. 2012, 117, 322–337. [Google Scholar] [CrossRef]
- Link, F. Variations lumineuses de la Lune. Bull. Astron. Inst. Czechoslov. 1951, 2, 131. [Google Scholar]
- Daumard, F.; Goulas, Y.; Ounis, A.; Pedrós, R.; Moya, I. Measurement and correction of atmospheric effects at different altitudes for remote sensing of sun-induced fluorescence in oxygen absorption bands. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5180–5196. [Google Scholar] [CrossRef]
- Damm, A.; Guanter, L.; Laurent, V.C.E.; Schaepman, M.E.; Schickling, A.; Rascher, U. FLD-based retrieval of sun-induced chlorophyll fluorescence from medium spectral resolution airborne spectroscopy data. Remote Sens. Environ. 2014, 147, 256–266. [Google Scholar] [CrossRef]
- Rascher, U.; Alonso, L.; Burkart, A.; Cilia, C.; Cogliati, S.; Colombo, R.; Damm, A.; Drusch, M.; Guanter, L.; Hanus, J.; et al. Sun-induced fluorescence–a new probe of photosynthesis: First maps from the imaging spectrometer HyPlant. Glob. Chang. Biol. 2015, 21, 4673–4684. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sabater, N.; Middleton, E.; Malenovsky, Z.; Alonso, L.; Verrelst, J.; Huemmrich, K.; Campbell, P.; Kustas, W.; Vicent, J.; Van Wittenberghe, S.; et al. Oxygen transmittance correction for solar-induced chlorophyll fluorescence measured on proximal sensing: Application to the NASA-GSFC FUSION tower. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017. [Google Scholar]
- Pierluisi, J.H.; Chang Mind, T. Molecular transmittance band model for oxygen in the visible. Appl. Opt. 1986, 25, 2458–2460. [Google Scholar] [CrossRef] [PubMed]
- Davidson, M.; Moya, I.; Ounis, A.; Louis, J.; Ducret, J.M.; Moreno, J.; Casselles, V.; Sobrino, J.; Alonso, L.; Pedros, R.; et al. Solar Induced Fluorescence Experiment (SIFLEX-2002): An overview. In Proceedings of the Remote Sensing of Solar-Induced Vegetation, Noordwijk, The Netherlands, 19–20 June 2002. [Google Scholar]
- Louis, J.; Ounis, A.; Ducruet, J.M.; Evain, S.; Laurila, T.; Thum, T.; Aurela, M.; Wingsle, G.; Alonso, L.; Pedros, R.; et al. Remote sensing of sunlight-induced chlorophyll fluorescence and reflectance of Scots pine in the boreal forest during spring recovery. Remote Sens. Environ. 2005, 96, 37–48. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Liu, L.; Hu, J.; Du, S. Modeling the Footprint and Equivalent Radiance Transfer Path Length for Tower-Based Hemispherical Observations of Chlorophyll Fluorescence. Sensors 2017, 17, 1131. [Google Scholar] [CrossRef] [PubMed]
- Sabater, N.; Vicent, J.; Alonso, L.; Cogliati, S.; Verrelst, J.; Moreno, J. Impact of Atmospheric Inversion Effects on Solar-Induced Chlorophyll Fluorescence: Exploitation of the Apparent Reflectance as a Quality Indicator. Remote Sens. 2017, 9, 622. [Google Scholar] [CrossRef]
- Berk, A.; Anderson, G.P.; Acharya, P.K.; Bernstein, L.S.; Muratov, L.; Lee, J.; Fox, M.; Adler-Golden, S.M.; Chetwynd, J.H.; Hoke, M.L.; et al. MODTRAN 5: A Reformulated Atmospheric Band Model with Auxiliary Species and Practical Multiple Scattering Options: Update; Proceedings SPIE: Orlando, FL, USA, 2005; Volume 5806, pp. 662–667. [Google Scholar]
- NASA Goddard Space Flight Center. FUSION: Canopy Tower System for Remote Sensing Observations of Terrestrial Ecosystems. 2012. Available online: ftp://fusionftp.gsfc.nasa.gov/FUSION (accessed on 28 November 2013).
- Meroni, M.; Rossini, M.; Guanter, L.; Alonso, L.; Rascher, U.; Colombo, R.; Moreno, J. Remote sensing of solar-induced chlorophyll fluorescence: Review of methods and applications. Remote Sens. Environ. 2009, 113, 2037–2051. [Google Scholar] [CrossRef]
- Rothman, L.S.; Gordon, I.E.; Barbe, A.; Benner, D.C.; Bernath, P.F.; Birk, M.; Boudon, V.; Brown, L.R.; Campargue, A.; Champion, J.P.; et al. The HITRAN 2008 molecular spectroscopic database. J. Quant. Spectrosc. Radiat. Transf. 2009, 110, 533–572. [Google Scholar] [CrossRef] [Green Version]
- Damm, A.; Erler, A.; Hillen, W.; Meroni, M.; Schaepman, M.E.; Verhoef, W.; Rascher, U. Modeling the impact of spectral sensor configurations on the FLD retrieval accuracy of sun-induced chlorophyll fluorescence. Remote Sens. Environ. 2011, 115, 1882–1892. [Google Scholar] [CrossRef]
- Frankenberg, C.; Fisher, J.B.; Worden, J.; Badgley, G.; Saatchi, S.S.; Lee, J.; Toon, G.C.; Butz, A.; Jung, M.; Kuze, A.; et al. New global observations of the terrestrial carbon cycle from GOSAT: Patterns of plant fluorescence with gross primary productivity. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef] [Green Version]
- Guanter, L.; Frankenberg, C.; Dudhia, A.; Lewis, P.E.; Gómez-Dans, J.; Kuze, A.; Suto, H.; Grainger, R.G. Retrieval and global assessment of terrestrial chlorophyll fluorescence from GOSAT space measurements. Remote Sens. Environ. 2012, 121, 236–251. [Google Scholar] [CrossRef]
- Joiner, J.; Yoshida, Y.; Vasilkov, A.; Schaefer, K.; Jung, M.; Guanter, L.; Zhang, Y.; Garrity, S.; Middleton, E.; Huemmrich, K.; et al. The seasonal cycle of satellite chlorophyll fluorescence observations and its relationship to vegetation phenology and ecosystem atmosphere carbon exchange. Remote Sens. Environ. 2014, 152, 375–391. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Guanter, L.; Berry, J.A.; Joiner, J.; Tol, C.; Huete, A.; Gitelson, A.; Voigt, M.; Köhler, P. Estimation of vegetation photosynthetic capacity from space-based measurements of chlorophyll fluorescence for terrestrial biosphere models. Glob. Chang. Biol. 2014, 20, 3727–3742. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Y.; Xiao, X.; Jin, C.; Dong, J.; Zhou, S.; Wagle, P.; Joiner, J.; Guanter, L.; Zhang, Y.; Zhang, G.; et al. Consistency between sun-induced chlorophyll fluorescence and gross primary production of vegetation in North America. Remote Sens. Environ. 2016, 183, 154–169. [Google Scholar] [CrossRef] [Green Version]
- Verma, M.; Schimel, D.; Evans, B.; Frankenberg, C.; Beringer, J.; Drewry, D.T.; Magney, T.; Marang, I.; Hutley, L.; Moore, C.; et al. Effect of environmental conditions on the relationship between solar-induced fluorescence and gross primary productivity at an OzFlux grassland site. J. Geophys. Res. Biogeosci. 2017, 122, 716–733. [Google Scholar] [CrossRef] [Green Version]
- Verrelst, J.; van der Tol, C.; Magnani, F.; Sabater, N.; Rivera, J.P.; Mohammed, G.; Moreno, J. Evaluating the predictive power of sun-induced chlorophyll fluorescence to estimate net photosynthesis of vegetation canopies: A SCOPE modeling study. Remote Sens. Environ. 2016, 176, 139–151. [Google Scholar] [CrossRef]
- Zhang, Y.; Guanter, L.; Berry, J.A.; van der Tol, C.; Yang, X.; Tang, J.; Zhang, F. Model-based analysis of the relationship between sun-induced chlorophyll fluorescence and gross primary production for remote sensing applications. Remote Sens. Environ. 2016, 187, 145–155. [Google Scholar] [CrossRef]
- Gamon, J.; Coburn, C.; Flanagan, L.; Huemmrich, K.; Kiddle, C.; Sanchez-Azofeifa, G.; Thayer, D.; Vescovo, L.; Gianelle, D.; Sims, D.; et al. SpecNet revisited: Bridging flux and remote sensing communities. Can. J. Remote Sens. 2010, 36, S376–S390. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef] [Green Version]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Porcar-Castell, A.; Atherton, J.; Rajewicz, P.A.; Riikonen, A.; Gebre, S.; Liu, W.; Aalto, J.; Bendoula, R.; Burkart, A.; Chen, H.; et al. Fluorescence Across Space and Time (2017 FAST Campaign): Investigating the multiscale links between fluorescence and photosynthesis. In Proceedings of the AGU Fall Meeting Abstracts, New Orleans, LA, USA, 11–15 December 2017. [Google Scholar]
- Drush, M. FLEX Earth Explorer 8 Mission Requirements Document (EOP-SM/2221/MRd-md); Technical Report; ESA: Paris, France, 2016. [Google Scholar]
- Guanter, L.; Richter, R.; Kaufmann, H. On the application of the MODTRAN4 atmospheric radiative transfer code to optical remote sensing. Int. J. Remote Sens. 2009, 30, 1407–1424. [Google Scholar] [CrossRef]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sabater, N.; Vicent, J.; Alonso, L.; Verrelst, J.; Middleton, E.M.; Porcar-Castell, A.; Moreno, J. Compensation of Oxygen Transmittance Effects for Proximal Sensing Retrieval of Canopy–Leaving Sun–Induced Chlorophyll Fluorescence. Remote Sens. 2018, 10, 1551. https://doi.org/10.3390/rs10101551
Sabater N, Vicent J, Alonso L, Verrelst J, Middleton EM, Porcar-Castell A, Moreno J. Compensation of Oxygen Transmittance Effects for Proximal Sensing Retrieval of Canopy–Leaving Sun–Induced Chlorophyll Fluorescence. Remote Sensing. 2018; 10(10):1551. https://doi.org/10.3390/rs10101551
Chicago/Turabian StyleSabater, Neus, Jorge Vicent, Luis Alonso, Jochem Verrelst, Elizabeth M. Middleton, Albert Porcar-Castell, and José Moreno. 2018. "Compensation of Oxygen Transmittance Effects for Proximal Sensing Retrieval of Canopy–Leaving Sun–Induced Chlorophyll Fluorescence" Remote Sensing 10, no. 10: 1551. https://doi.org/10.3390/rs10101551
APA StyleSabater, N., Vicent, J., Alonso, L., Verrelst, J., Middleton, E. M., Porcar-Castell, A., & Moreno, J. (2018). Compensation of Oxygen Transmittance Effects for Proximal Sensing Retrieval of Canopy–Leaving Sun–Induced Chlorophyll Fluorescence. Remote Sensing, 10(10), 1551. https://doi.org/10.3390/rs10101551