Performance and Requirements of GEO SAR Systems in the Presence of Radio Frequency Interferences
Abstract
1. Introduction
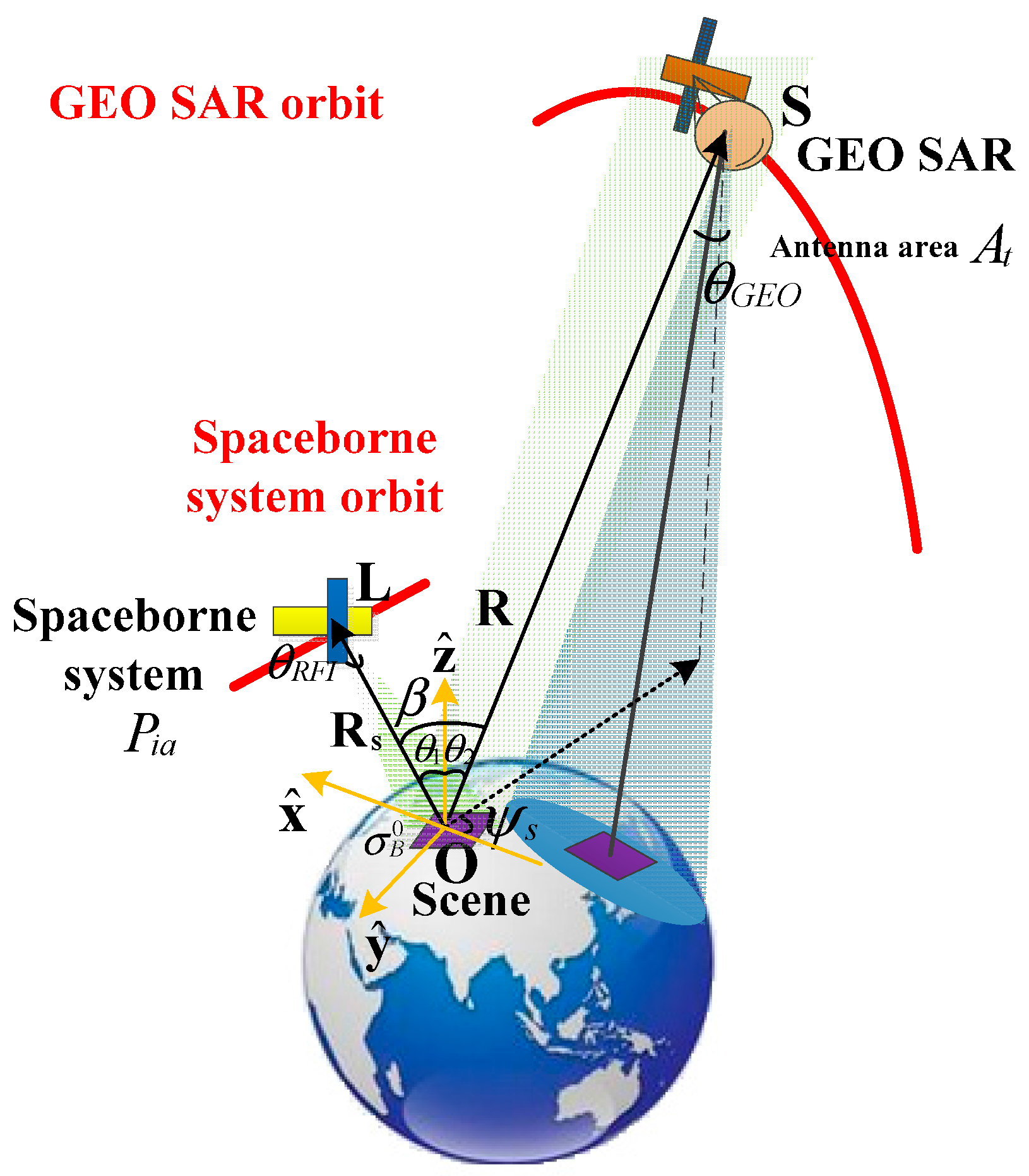
2. Ground RFI Impacts on GEO SAR Signal
2.1. Point-Like RFI Source
2.2. Distributed RFI Source
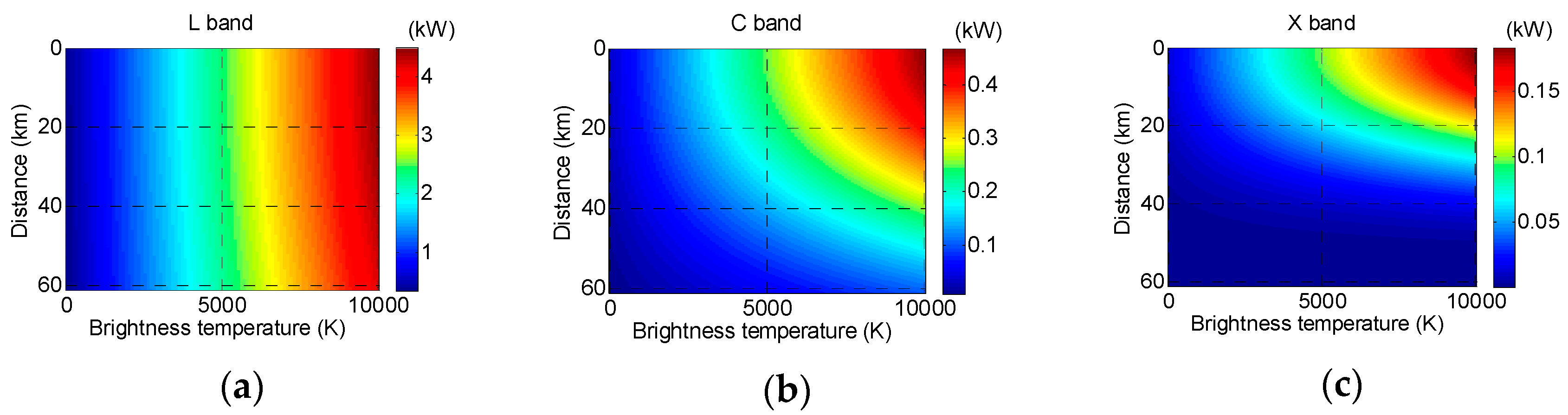
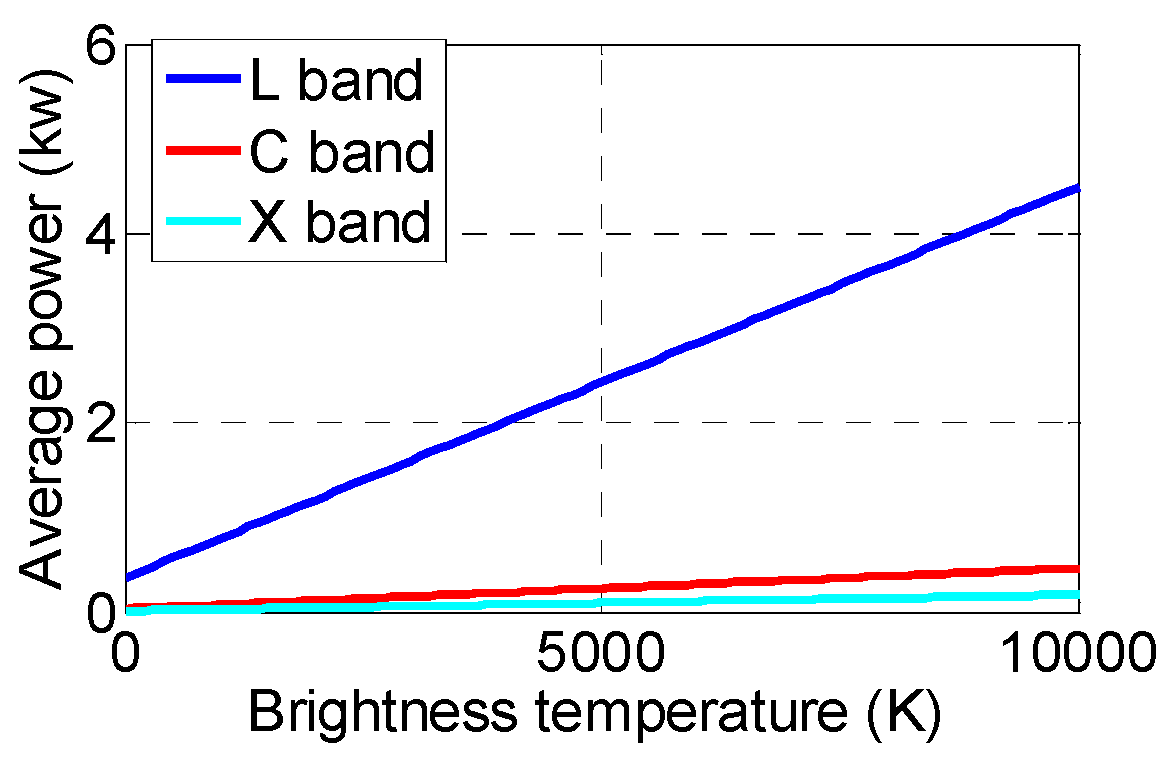
2.3. Average Transmitted Power Requirements in the Presence of RFI
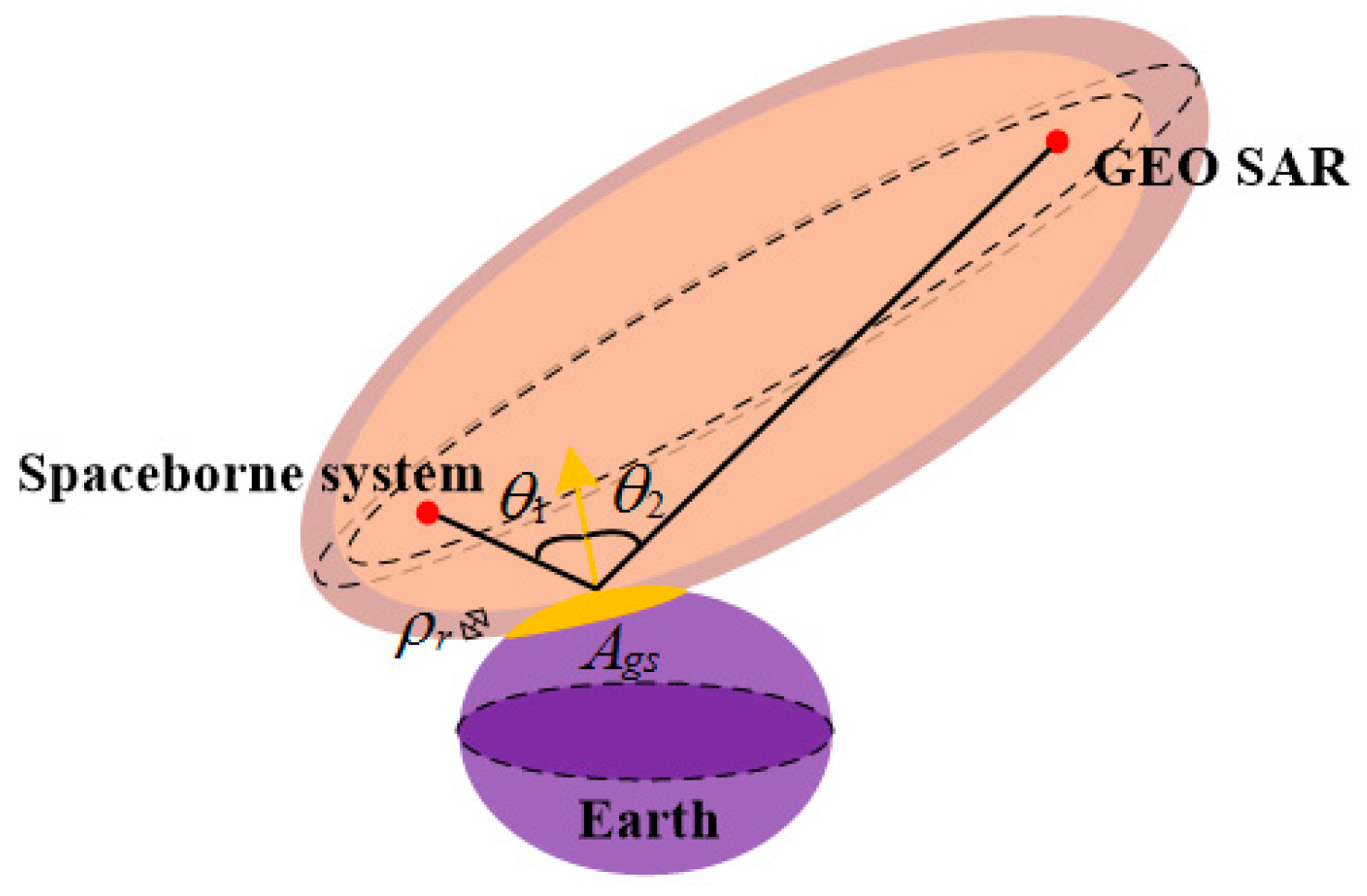
3. Bistatic Scattering RFI Impact on GEO SAR
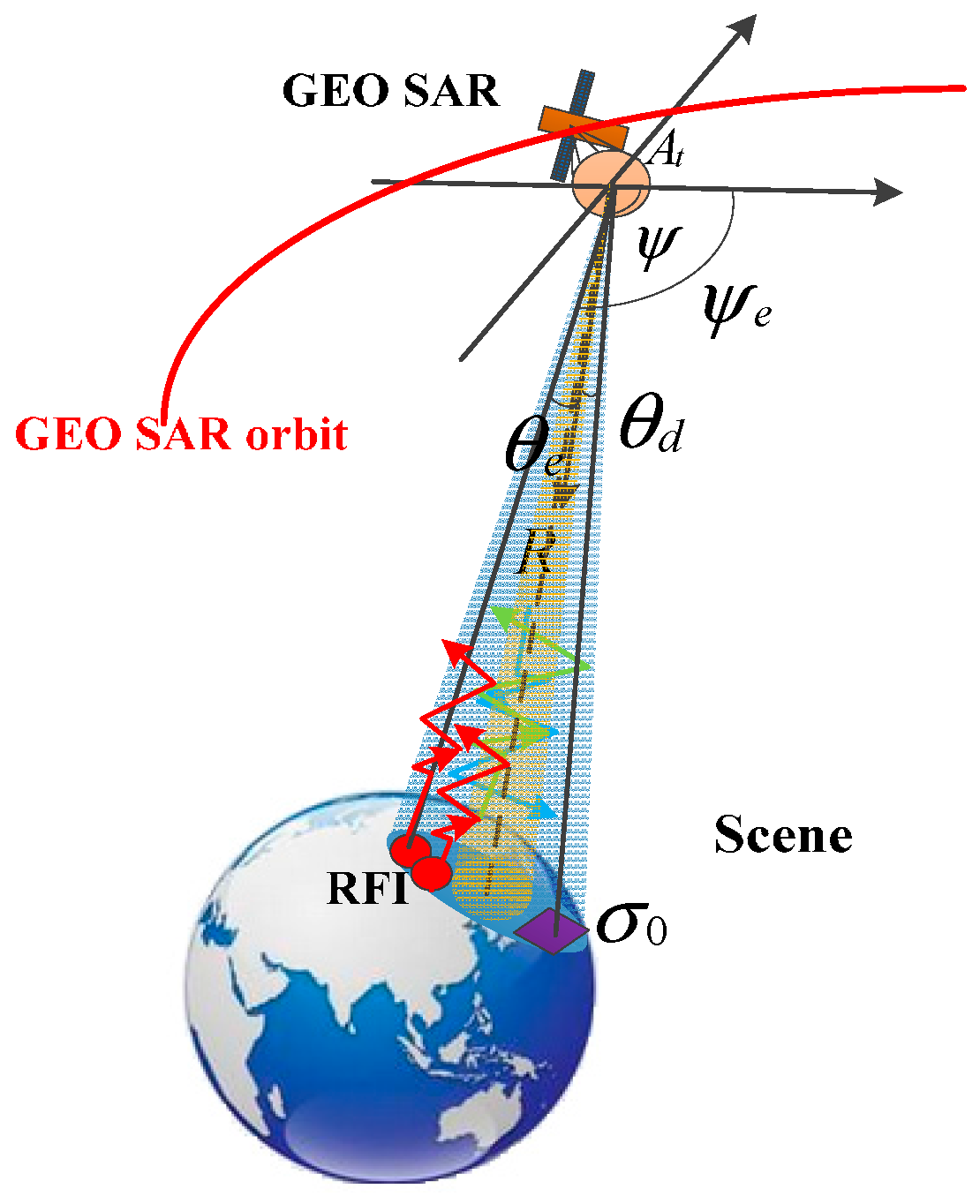
3.1. Impact of Bistatic Scattering RFI on GEO SAR
3.1.1. Non-Specular Bistatic Scattering Case
3.1.2. Specular Bistatic Scattering Case
3.1.3. SINR and Required Power Analysis
3.2. Doppler Filtering
4. Performance Evaluation and Discussion: Example of GEO SAR Design
4.1. Impact of Ground RFI
4.2. Impact of Bistatic Scattering RFI
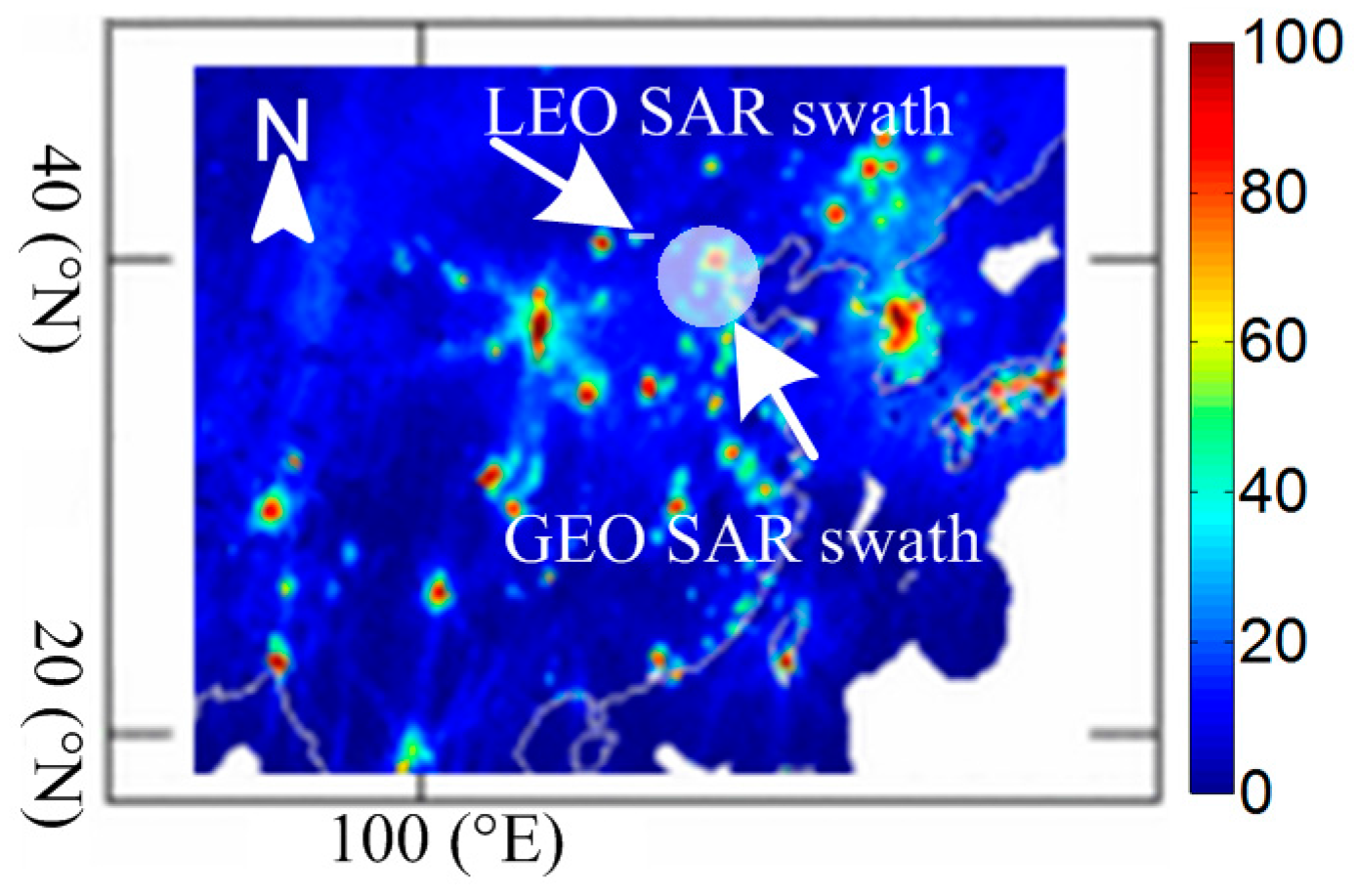
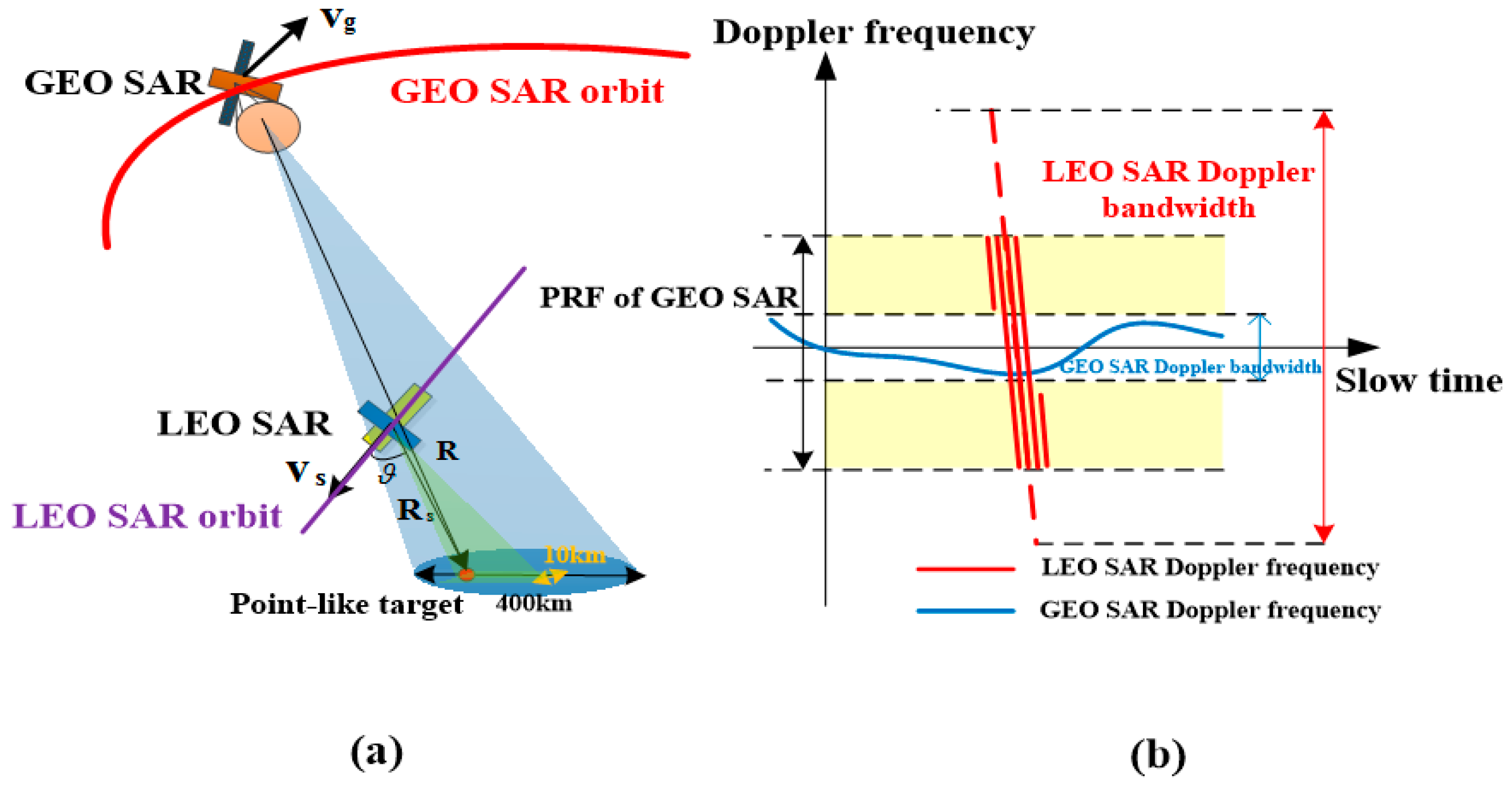
4.2.1. LEO SAR Bistatic Scattering RFI Case Analysis
4.2.2. GNSS Bistatic Scattering RFI Case Analysis
4.2.3. Doppler Filtering Analysis
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Measuring and Modelling RFI
Appendix A.1. Radio Frequency Interferences in L Band
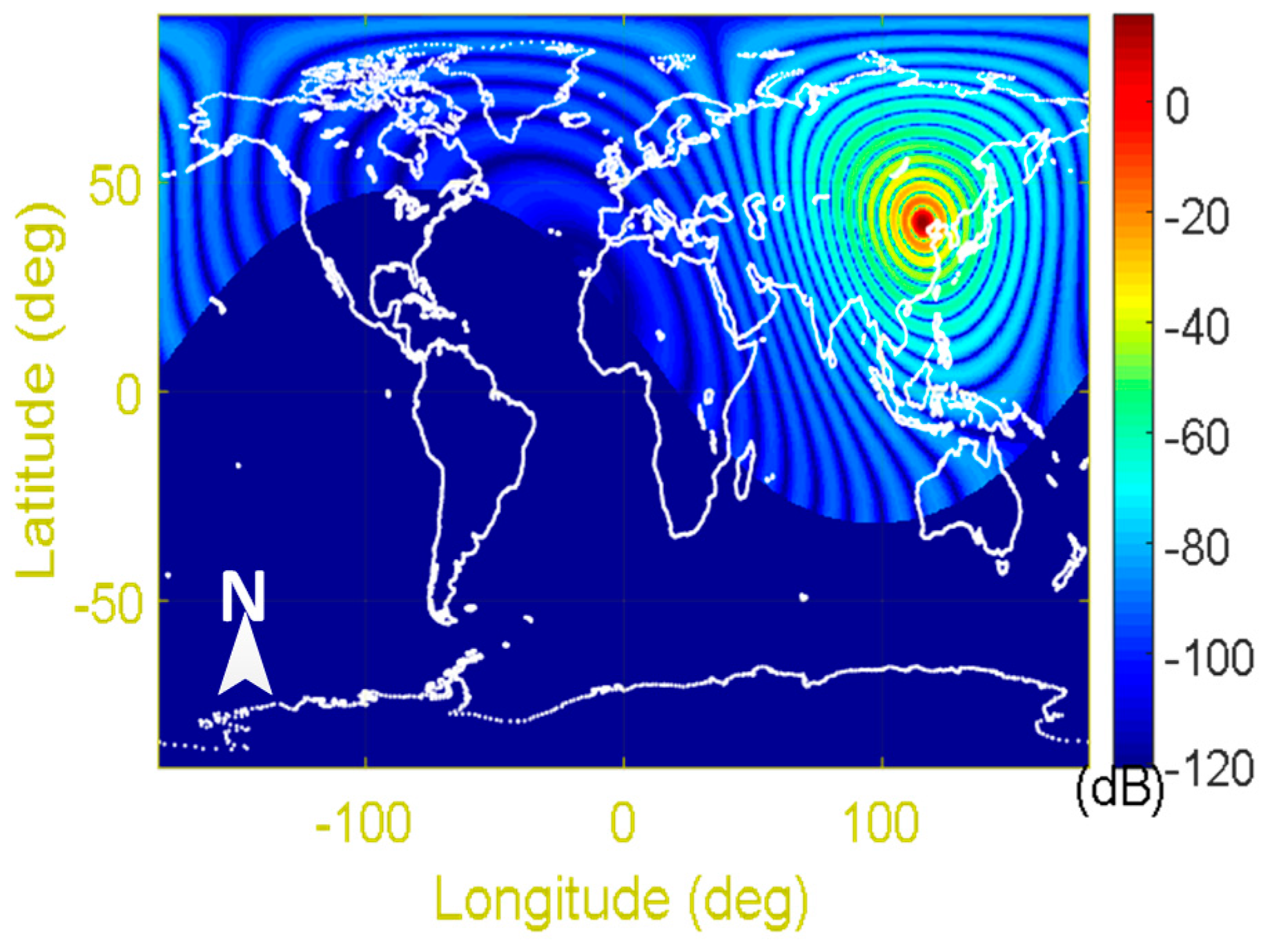
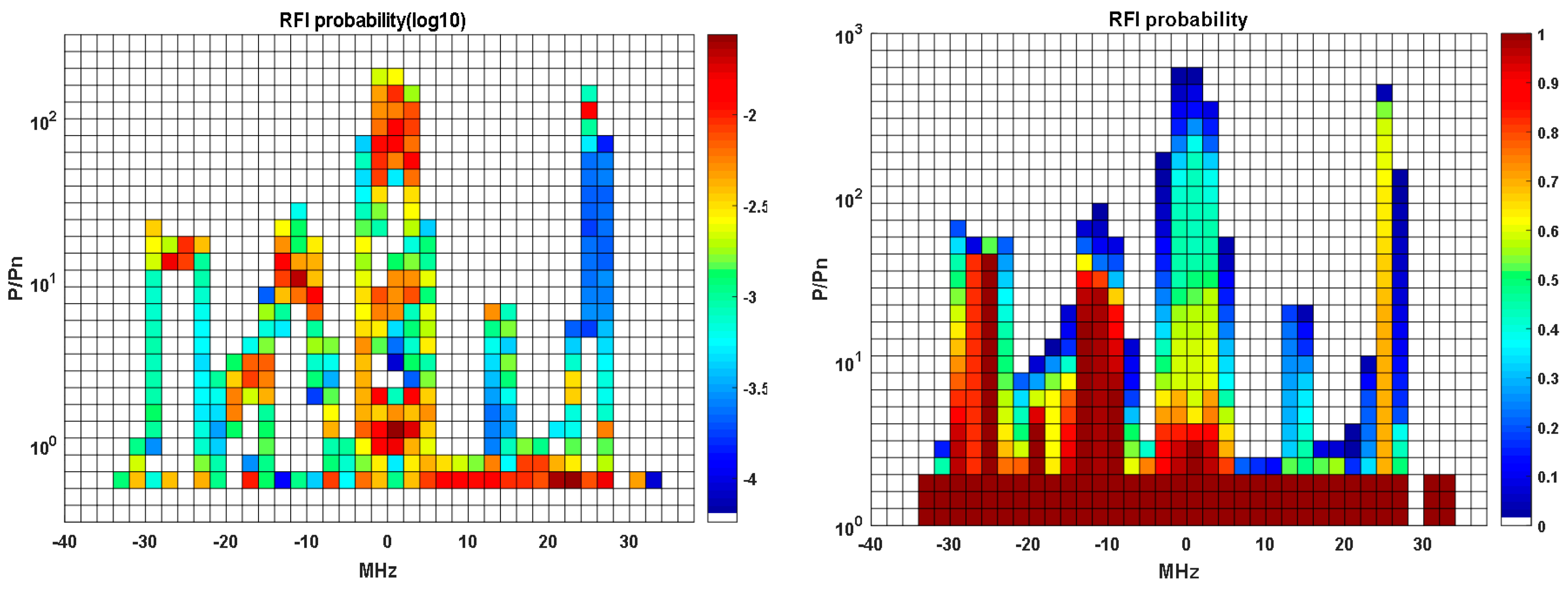
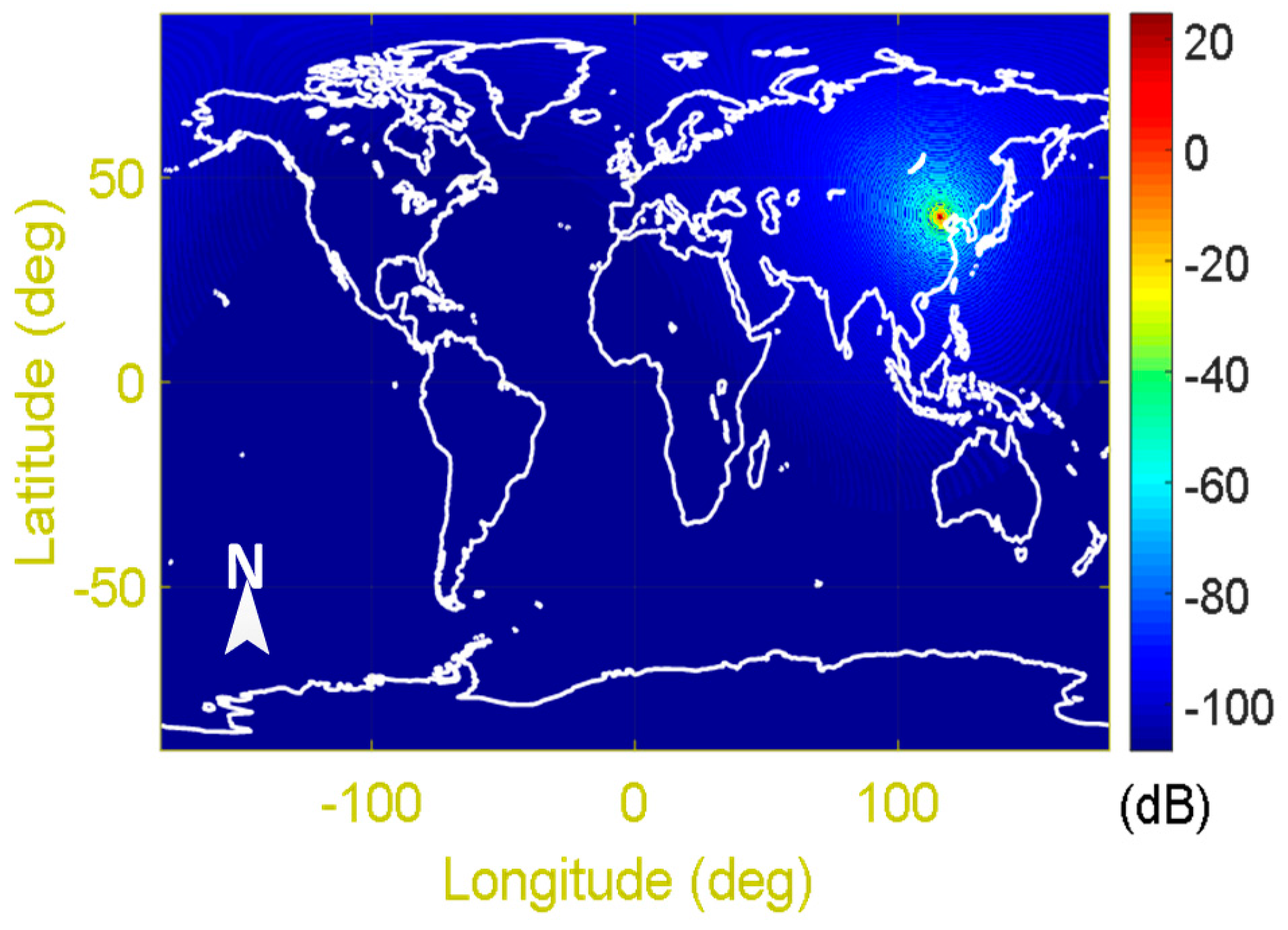
Appendix A.1.1. SMOS Satellite RFI Data

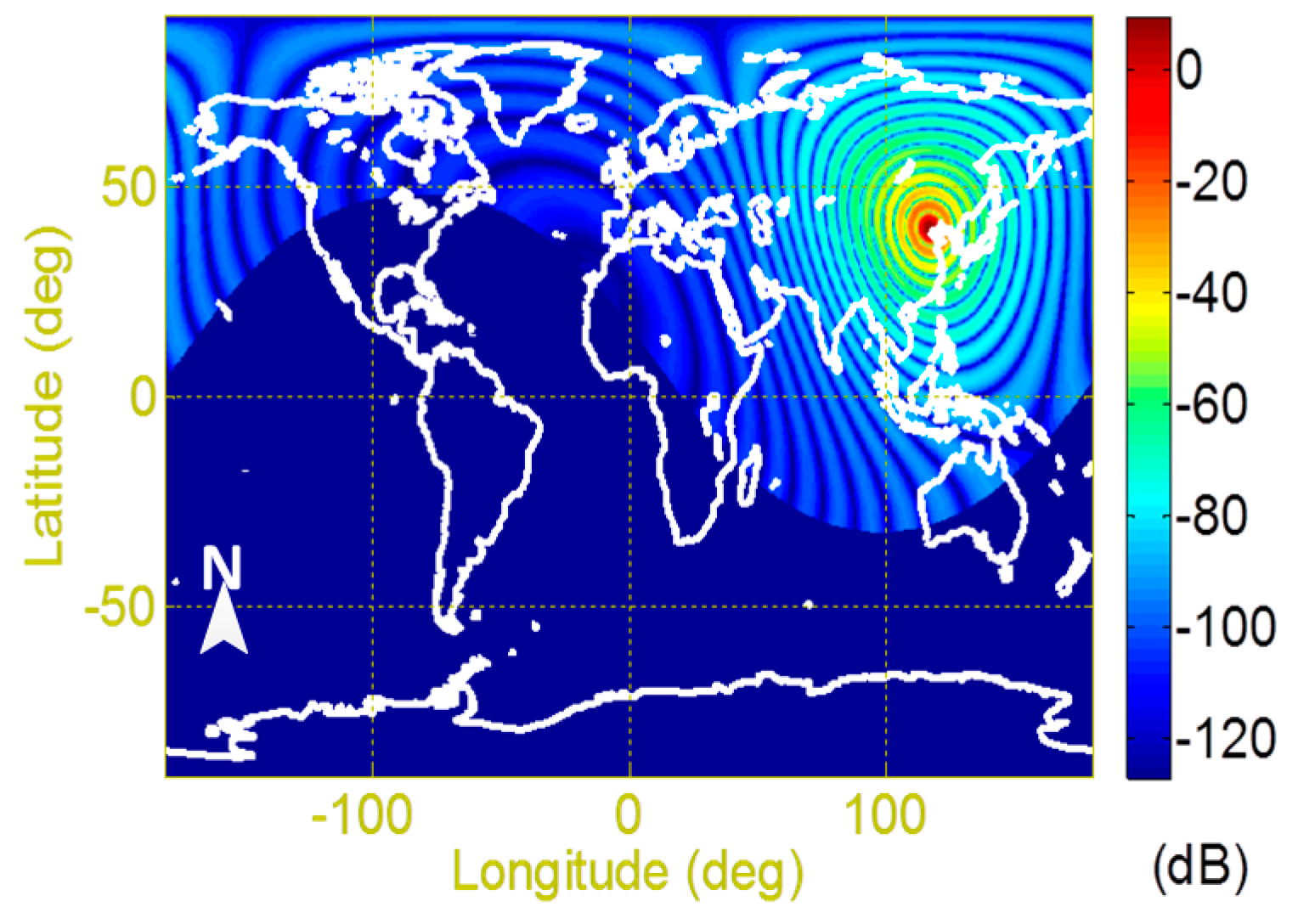
Appendix A.1.2. Beidou-2 IGSO Navigation Satellite RFI Data
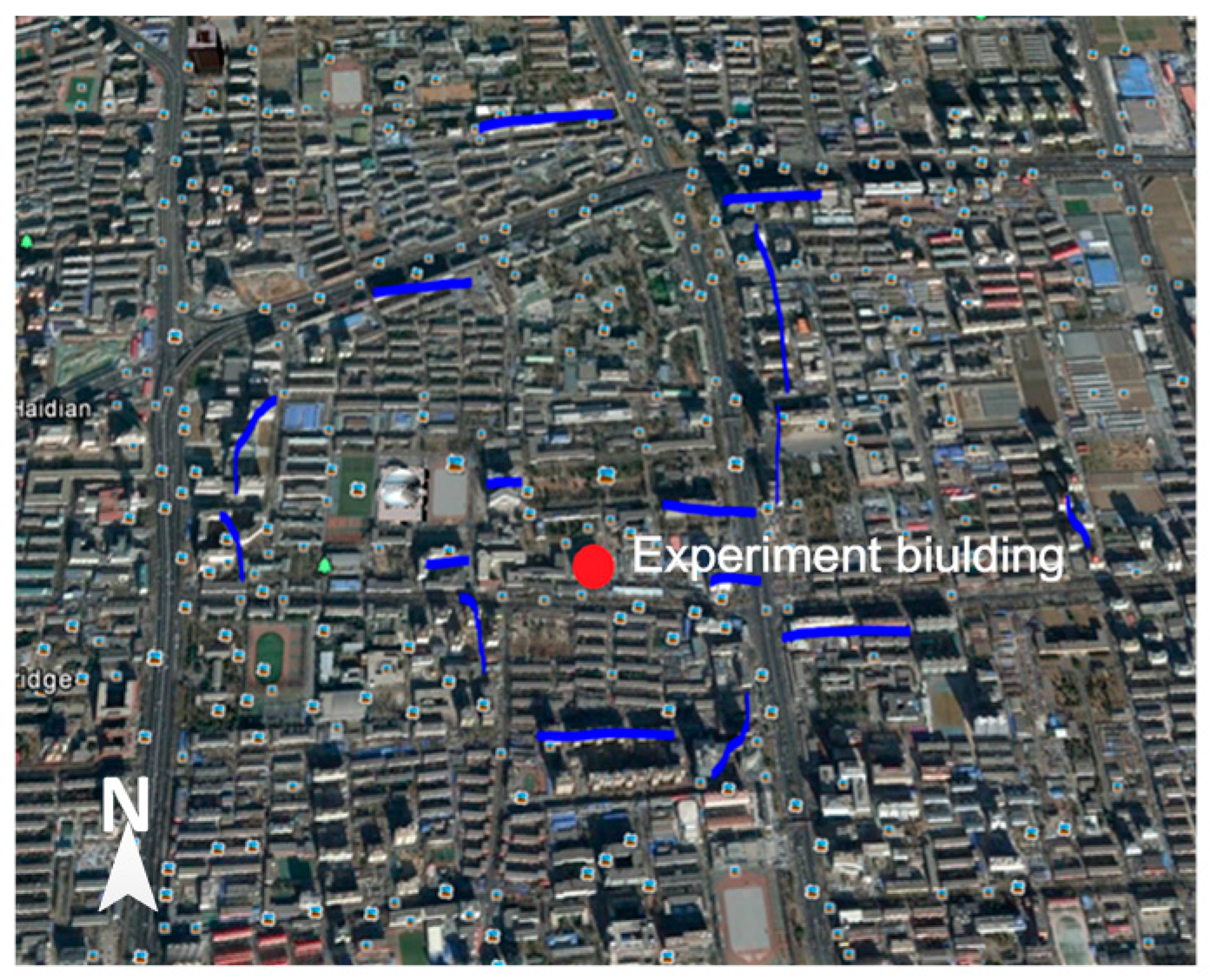

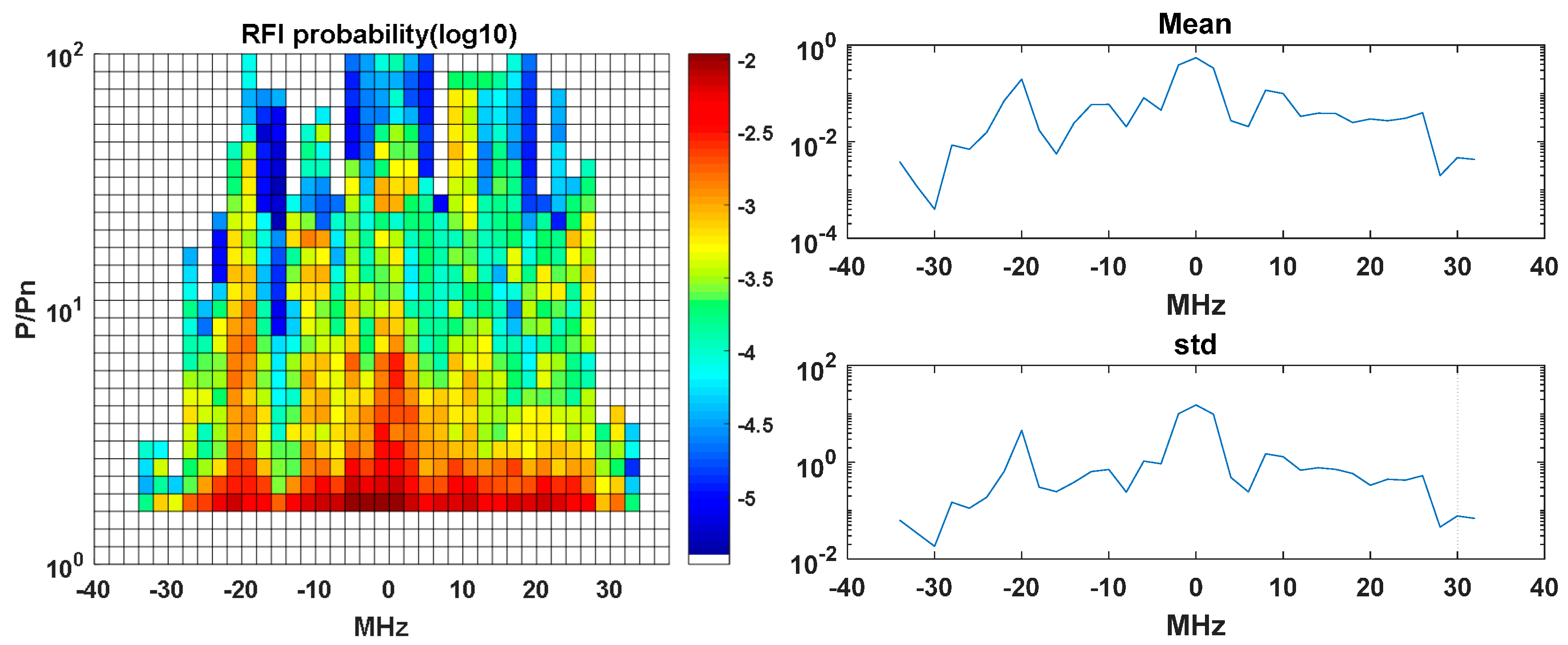
Appendix A.2. Radio Frequency Interferences in C Band

References
- Ulaby, F.; Avery, S. A Strategy for Active Remote Sensing Amid Increased Demand for Radio Spectrum; The National Academies of Sciences, Engineering and Medicines, Ed.; The National Academies Press: Washington, DC, USA, 2015. [Google Scholar]
- Oliva, R.; Nieto, S.; Félix-Redondo, F. RFI Detection Algorithm: Accurate Geolocation of the Interfering Sources in SMOS Images. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4993–4998. [Google Scholar] [CrossRef]
- Freeman, A.P.; Fischman, M.A.; McWatters, D.A.; Spencer, M.W.; Piepmeier, J.R. The Detection and Mitigation of RFI with the Aquarius L-Band Scatterometer. In Proceedings of the IEEE IGARSS, Boston, MA, USA, 7–11 July 2008. [Google Scholar]
- Oliva, R.; Daganzo, E.; Kerr, Y.H.; Mecklenburg, S.; Nieto, S.; Richaume, P.; Gruhier, C. SMOS radio frequency interference scenario: Status and actions taken to improve the RFI environment in the 1400–1427-MHz passive band. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1427–1439. [Google Scholar] [CrossRef]
- Pascual, D.; Park, H.; Onrubia, R.; Arroyo, A.A.; Querol, J.; Camps, A. Crosstalk Statistics and Impact in Interferometric GNSS-R. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4621–4630. [Google Scholar] [CrossRef]
- Musumeci, L. Advanced Signal Processing Techniques for Interference Removal in Satellite Navigation Systems. Ph.D. Thesis, Politecnico di Torino, Turin, Italy, 2014. [Google Scholar]
- Yang, L.; Zheng, H.F.; Feng, J.; Li, M.; Chen, J.Q. Detection and suppression of narrow band RFI for synthetic aperture radar imaging. Chin. J. Aeronaut. 2015, 28, 1189–1198. [Google Scholar] [CrossRef]
- Meyer, F.J.; Nicoll, J.B.; Doulgeris, A.P. Correction and Characterization of Radio Frequency Interference Signatures in L-Band Synthetic Aperture Radar Data. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4961–4972. [Google Scholar] [CrossRef]
- Brandao, A.L.; Sydor, J. 5 GHz RLAN Interference on active meteorological radars. In Proceedings of the 2005 IEEE Vehicular Technology Conference, Stockholm, Sweden, 30 May–1 June 2005. [Google Scholar]
- Tercero, M.; Sung, K.W.; Zander, J. Impact of aggregate interference on meteorological radar from secondary users. In Proceedings of the 2011 IEEE Wireless Communications and Networking Conference, Cancun, Mexico, 28–31 March 2011; pp. 2167–2172. [Google Scholar]
- Meadows, P. Sentinel-1A and -1B Annual Performance Report 2016; MPC-0366; Collecte Localisation Satellite: Ramonville Saint-Agne, France, 2016. [Google Scholar]
- Monti-Guarnieri, A.; Giudici, D.; Recchia, A. Identification of C-Band Radio Frequency Interferences from Sentinel-1 Data. Remote Sens. 2017, 9, 1183. [Google Scholar] [CrossRef]
- John, J.T.; Chen, C.C.; O’Brien, A.; Smith, G.E.; McKelvey, C.; Ball, M.A.C.; Misra, S.; Brown, S.; Kocz, J.; Jarnot, R. The CubeSat Radiometer Radio Frequency Interference Technology Validation (CubeRRT) mission. In Proceedings of the IEEE IGARSS, Beijing China, 10–15 July 2016. [Google Scholar]
- Ellingson, S.W.; Johnson, J.T. A polarimetric survey of radio-frequency interference in C- and X-bands in the continental United States using WindSat radiometry. IEEE Trans. Geosci. Remote Sens. 2006, 44, 540–548. [Google Scholar] [CrossRef]
- Hamdadou, N.; Chen, J.; Kamel, H.; Hui, K. Bidirectional notch filter for suppressing pulse modulated radio-frequency-interference in SAR data. In Proceedings of the IEEE IGARSS, Quebec, QC, Canada, 13–18 July 2014. [Google Scholar]
- Tomiyasu, K. Synthetic aperture radar in geosynchronous orbit. In Proceedings of the Digest International IEEE Antennas Propagation Symposium, College Park, MD, USA, 15–19 March 1978. [Google Scholar]
- Madsen, S.N.; Edelstein, W.; Didomenico, L.D.; LaBrecque, J. A geosynchronous synthetic aperture radar; for tectonic mapping, disaster management and measurement of vegetation and soil moisture. In Proceedings of the IEEE IGARSS, Sydney, Australia, 9–13 July 2001. [Google Scholar]
- Hobbs, S.; Mitchell, C.; Forte, B.; Holley, R.; Snapir, B.; Whittaker, P. System design for geosynchronous synthetic aperture radar missions. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7750–7763. [Google Scholar] [CrossRef]
- Bruno, D.; Hobbs, S.E.; Ottavianelli, G. Geosynchronous synthetic aperture radar: Concept design, properties and possible applications. Acta Aston. 2006, 59, 149–156. [Google Scholar] [CrossRef]
- Monti Guarnieri, A.; Hu, C. Geosynchronous and geostationary SAR: Face to face comparison. In Proceedings of the EUSAR, Hamburg, Germany, 6–9 June 2016. [Google Scholar]
- Hu, C.; Li, Y.H.; Dong, X.C.; Long, T. Optimal data acquisition and height retrieval in repeat-track geosynchronous SAR interferometry. Remote Sens. 2015, 7, 13367–13389. [Google Scholar] [CrossRef]
- Hu, C.; Li, Y.H.; Dong, X.C.; Cui, C.; Long, T. Impacts of temporal-spatial variant background ionosphere on repeat-track GEO D-InSAR system. Remote Sens. 2016, 8, 916. [Google Scholar] [CrossRef]
- Hu, C.; Li, Y.H.; Dong, X.C.; Wang, R.; Ao, D.Y. Performance Analysis of L-band Geosynchronous SAR Imaging in the Presence of Ionospheric Scintillation. IEEE Trans. Geosci. Remote Sens. 2017, 55, 159–172. [Google Scholar] [CrossRef]
- Hu, C.; Li, Y.H.; Dong, X.C.; Wang, R.; Cui, C.; Zhang, B. Three-Dimensional Deformation Retrieval in Geosynchronous SAR by Multiple-Aperture Interferometry Processing: Theory and Performance Analysis. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6150–6169. [Google Scholar] [CrossRef]
- Recchia, A.; Monti Guarnieri, A.; Broquetas, A.; Leanza, A. Impact of scene decorrelation on geosynchronous SAR data focusing. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1635–1646. [Google Scholar] [CrossRef]
- Hu, B.; Jiang, Y.; Zhang, S.; Zhang, Y.; Yeo, T. Generalized omega-K algorithm for geosynchronous SAR image formation. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2286–2290. [Google Scholar] [CrossRef]
- Wang, C.; Chen, L.; Liu, L. A New Analytical Model to Study the Ionospheric Effects on VHF/UHF Wideband SAR Imaging. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4545–4557. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, M.; Xu, Z.W.; Chen, C.; Guo, L.X. Cubic phase distortion and irregular degradation on SAR imaging due to the ionosphere. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3442–3451. [Google Scholar] [CrossRef]
- Monti-Guarnieri, A.; Broquetas, A.; Recchia, A.; Rocca, F.; Ruiz-Rodon, J. Advanced radar geosynchronous observation system: ARGOS. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1406–1410. [Google Scholar] [CrossRef]
- Ruiz-Rodon, J.; Broquetas, A.; Makhoul, E.; Monti-Guarnieri, A.; Rocca, F. Geosynchronous SAR focusing with atmospheric phase screen retrieval and compensation. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4397–4404. [Google Scholar] [CrossRef]
- SMOS Blog. Available online: http://www.cesbio.ups-tlse.fr/SMOS_blog/smos_rfi/?q=image/12894-proba-rfi-d-20170826-20170909-bb (accessed on 15 September 2017).
- Curlander, J.C.; McDonough, R.N. Synthetic Aperture Radar: Systems and Signal Processing; Wiley: New York, NY, USA, 1991. [Google Scholar]
- Meyer, F.J.; Nicoll, J.; Doulgeris, A.P. Characterization and extent of randomly-changing radio frequency interference in ALOS PALSAR data. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Vancouver, BC, Canada, 24–29 July 2011. [Google Scholar]
- Ferretti, A.; MontiGuarnieri, A.; Prati, C.; Rocca, F.; Massonnet, D. SAR Principles: Guideline for SAR Interferometry Processing and Interpretation; ESA: Noordwijk, The Netherlands, 2007; pp. 57–71. [Google Scholar]
- Rosen, P.A.; Hensley, S.; Le, C. Observations and mitigation of RFI in ALOS PALSAR SAR data: Implications for the DESDynI mission. In Proceedings of the IEEE Radar Conference, Rome, Italy, 26–30 May 2008. [Google Scholar]
- Kankaku, Y.; Osawa, Y.; Suzuki, S.; Watanabe, T. The Overview of the L-band SAR Onboard ALOS-2. In Proceedings of the Electromagnetics Research Symposium, Moscow, Russia, 18–21 August 2009. [Google Scholar]
- Huang, S.W.; Tsang, L.G. Bistatic scattering, backscattering and emissivities of randomly rough soil surfaces at L band based on numerical solutions of Maxwell equations of 3 Dimensional simulations. In Proceedings of the IEEE IGARSS, Honolulu, HI, USA, 25–30 July 2010. [Google Scholar]
- Willis, N.J. Bistatic radar, chapter 25. In Radar Handbook, 2nd ed.; Skolnik, M.I., Ed.; McGraw-Hill Education: New York, NY, USA, 1990. [Google Scholar]
- Skolnik, M. Introduction to Radar Systems; McGraw-Hill Education: New York, NY, USA, 2001. [Google Scholar]
- ESA Sentinel-1. Available online: https://sentinel.esa.int/documents/247904/349449/S1_SP-1322_1.pdf (accessed on 8 September 2017).
- EoPortal Directory. Available online: https://directory.eoportal.org/web/eoportal/satellite-missions/a/alos-2 (accessed on 8 September 2017).
- Microwave Radar and Radiometric Remote Sensing. Available online: http://mrs.eecs.umich.edu/sensors.html (accessed on 8 September 2017).
- Bordoni, F.; Younis, M.; Rodriguez-Cassola, M.; Prats-Iraola, P.; López-Dekker, P.; Krieger, G. SAOCOM-CS SAR imaging performance evaluation in large baseline bistatic configuration. In Proceedings of the IEEE IGARSS, Milan, Italy, 26–31 July 2015. [Google Scholar]
- EoPortal Directory. Available online: https://directory.eoportal.org/web/eoportal/satellite-missions/r/radarsat-2 (accessed on 8 September 2017).
- DLR. Available online: http://www.dlr.de/hr/Portaldata/32/Resources/dokumente/tdmx/Tandem-X-RADAR-2004.pdf (accessed on 8 September 2017).
- GPS Information. Available online: http://gpsinformation.net/main/gpspower.htm (accessed on 8 September 2017).
- Wikipedia. Available online: https://en.wikipedia.org/wiki/GLONASS (accessed on 8 September 2017).
- European GNSS Agency. Available online: https://www.gsa.europa.eu/galileo/programme (accessed on 8 September 2017).
- WEEBAU. Available online: http://weebau.com/satellite/B/beidou2.htm (accessed on 8 September 2017).
- Steigenberger, P.; Thoelert, S.; Montenbruck, O. GNSS satellite transmit power and its impact on orbit Determination. J. Geod. 2017. [Google Scholar] [CrossRef]
- SMOS Blog. Available online: http://www.cesbio.ups-tlse.fr/SMOS_blog/?page_id=4087 (accessed on 8 September 2017).



| Band | Frequency Range (MHz) | Services in Band |
|---|---|---|
| L | 1215–1300 | Radio Navigation Satellite System (RNSS) and radiolocation |
| C | 5250–5570 | Aeronautical RNSS and radiolocation |
| X | 9300–9900 | Radiolocation and radio navigation |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Carrier central frequency (GHz) | 1.25/5.4/9.6 | Inclination (°) | 10–60 |
| Look angle (°) | 2–7 | Argument of perigee (°) | 270 |
| Eccentricity | 0.07 | Antenna area (m2) | 531 |
| Duty cycle (%) | 15 | Incidence angle (°) | 10–60 |
| Bandwidth (MHz) | 18 | Integration time (s) | 30–250 |
| Polarization | HH | Equivalent thermal noise (K) | 879 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Number of beams | 1 (L band) 16 (C band) 64 (X band) | SINR (dB) | 10 |
| Resolution (m) | <20 × <20 (Single look) | Coverage (km) | 400 × 400 |
| Frequency | L Band | C Band | X Band | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| SAR | ALOS-2 | Tandem-L | SAOCOM-1A/B | Sentinel-1A/B | Radarsat-2 | RCM | TanDEM-X/PAZ | COSMO-SkyMed | SAR-Lupe | KOMPSAT-5 |
| Peak power (W) | 5100 | 3622 | 3100 | 4368 | 2280 | 1600 | 2260 | 7600 | 250 (total) | 1700 |
| Duty cycle of power (%) | 8 | 4 | 5 | 12 | 12 | 13.75 | 18 | 11 | 35 | |
| Orbit period (min) | 98.5 | 99.7 | 97.2 | 98.5 | 100.7 | 96.4 | 95.0 | 20% (max) | 20% (assumed) | 95.8 |
| Working time per orbit (min) | 49 | 30 | 5–20 | 25, 74 (wave mode) | 28 | 15 | 3 | 2 | ||
| Satellite number | 1 | 2 | 2 | 2 | 1 | 3 | 3 | 4 | 5 | 1 |
| Average transmitted power (W) | 203 | 44 | 32 | 394 | 76 | 34 | 13 | 167 | 50 | 13 |
| Bandwidth (MHz) | 42 (middle) | 84 | 50 | 100 | 100 | 100 | 150/300 | 400 | 300 (assumed) | 120 |
| Parameters | L | C | X | ||
|---|---|---|---|---|---|
| Occurrence probability (%) | Non-specular scattering | 44.8 | 38.1 | 39.0 | |
| Specular scattering | 5.0 × 10−2 | 1.5 × 10−2 | 2.0 × 10−3 | ||
| Mainlobe to mainlobe specular scattering | 0 | 0 | 0 | ||
| σ0 (dB) | −14.8 | −9.7 | −7.6 | ||
| Required average transmitted power (kW) | Non-specular scattering | 0 | 0.7 | 6.0 × 10−2 | 2.0 × 10−2 |
| 5000 km | 0.7 | 5.2 × 10−2 | 1.8 × 10−2 | ||
| Specular scattering | 0 | 1.1 × 109 | 3.2 × 107 | 4.7 × 105 | |
| 5000 km | 2.4 × 104 | 7.8 | 3.7 × 10−2 | ||
| Mainlobe to mainlobe specular scattering | - | - | - | ||
| Navigation System | GPS | GLONASS | Galileo | Beidou-2 |
|---|---|---|---|---|
| Transmit power (W) | 240 | 135 | 265 | 130 (MEO) 185 (IGSO/GEO) |
| Satellite number above the scene | 13 | 11 | 8 | 6 (GEO) 8 (IGSO) 5 (MEO) |
| Bandwidth (MHz) | 2 | 10 | 4 | 20 |
| Parameters | Value | ||
|---|---|---|---|
| Probability (%) | Non-specular scattering | MEO | 96.9 |
| IGSO | 100.0 | ||
| GEO stationary | 100.0 | ||
| Specular scattering | MEO | 96.9 | |
| IGSO | 100.0 | ||
| GEO stationary | 100.0 | ||
| Mainlobe to mainlobe specular scattering | MEO | 9.0 | |
| IGSO | 22.5 | ||
| GEO stationary | 48.4 | ||
| Required average transmitted power (kW) | Non-specular scattering | 0.7 | |
| Specular scattering | - | ||
| Mainlobe to mainlobe specular scattering | 2.2 × 108 ( ≈ 30 km × 30 km (maximum)) 0.8 ( = 100 m × 100 m) | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Monti Guarnieri, A.; Hu, C.; Rocca, F. Performance and Requirements of GEO SAR Systems in the Presence of Radio Frequency Interferences. Remote Sens. 2018, 10, 82. https://doi.org/10.3390/rs10010082
Li Y, Monti Guarnieri A, Hu C, Rocca F. Performance and Requirements of GEO SAR Systems in the Presence of Radio Frequency Interferences. Remote Sensing. 2018; 10(1):82. https://doi.org/10.3390/rs10010082
Chicago/Turabian StyleLi, Yuanhao, Andrea Monti Guarnieri, Cheng Hu, and Fabio Rocca. 2018. "Performance and Requirements of GEO SAR Systems in the Presence of Radio Frequency Interferences" Remote Sensing 10, no. 1: 82. https://doi.org/10.3390/rs10010082
APA StyleLi, Y., Monti Guarnieri, A., Hu, C., & Rocca, F. (2018). Performance and Requirements of GEO SAR Systems in the Presence of Radio Frequency Interferences. Remote Sensing, 10(1), 82. https://doi.org/10.3390/rs10010082









