A New Method for Automatically Tracing Englacial Layers from MCoRDS Data in NW Greenland †
Abstract
1. Introduction
2. Study Site and Datasets
2.1. NEEM Ice Drilling Core Site
2.2. MCoRDS L1B Data
2.3. Ancillary Datasets
3. Methods
3.1. MCoRDS Radio Echograms of GrIS and an Automated Tracing Strategy
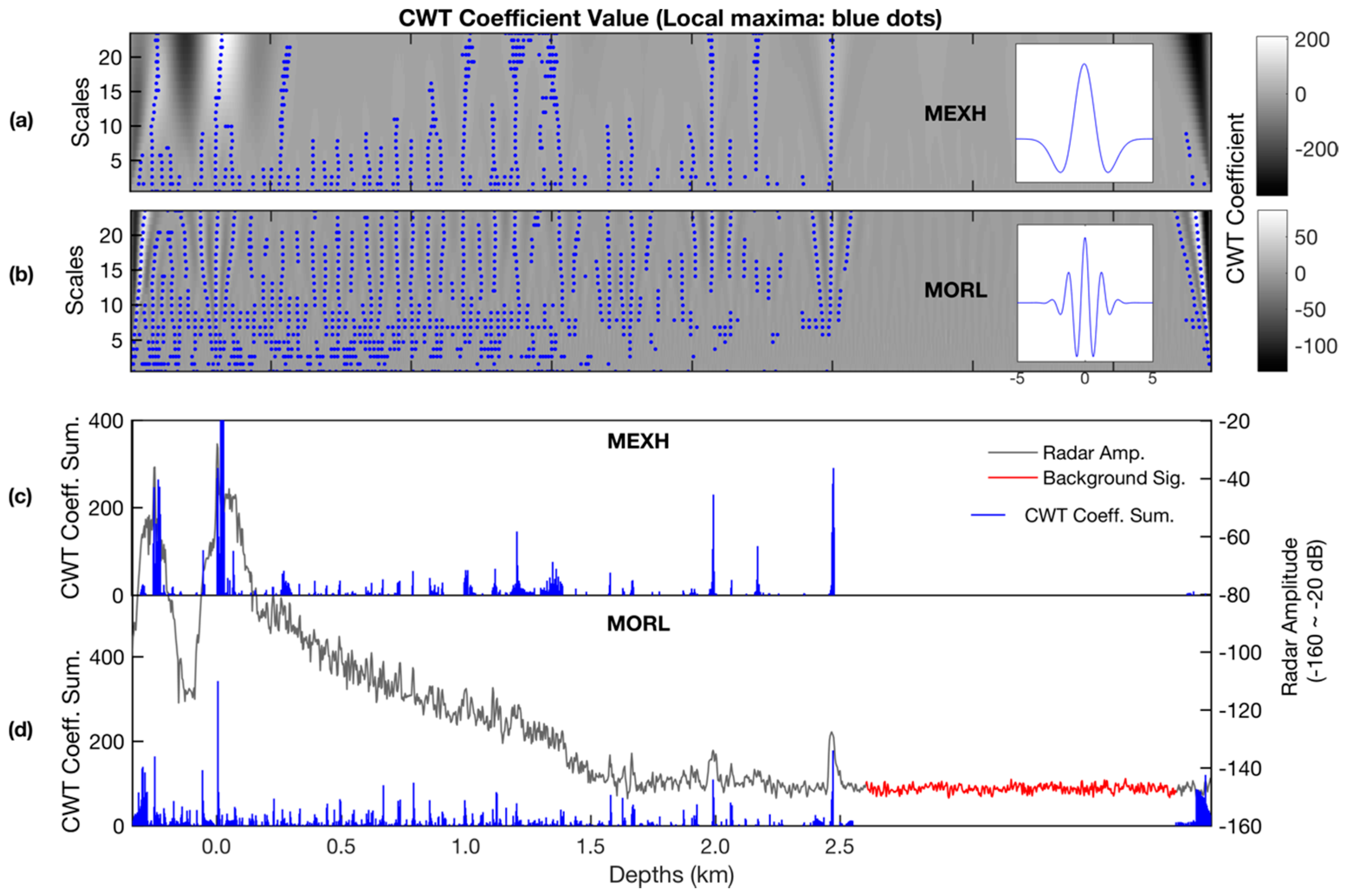
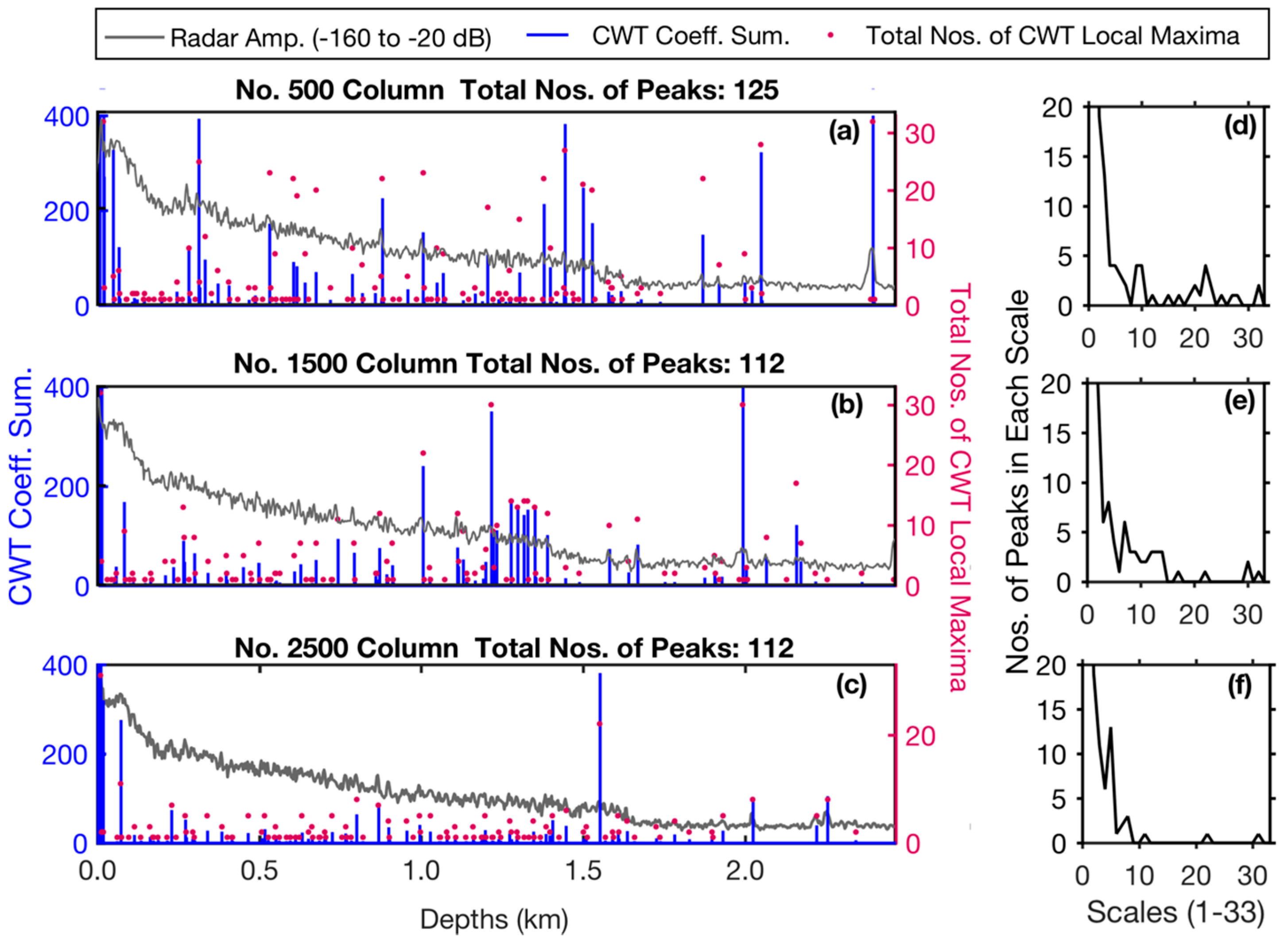
3.2. Peak Detection
3.2.1. CWT-Based Peak Detection
3.2.2. APP-Based Peak Detection
3.3. Selection of Seed Points
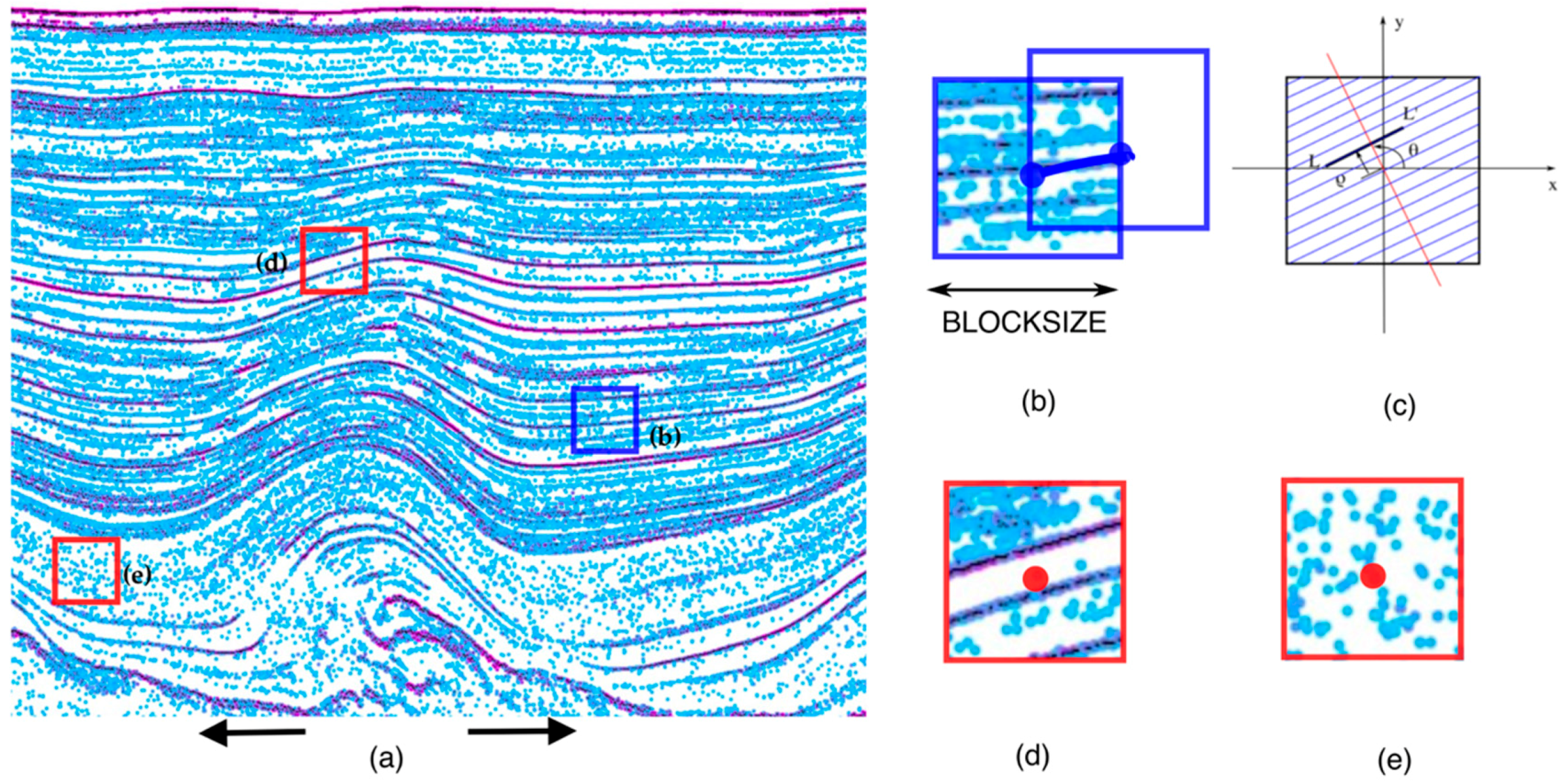
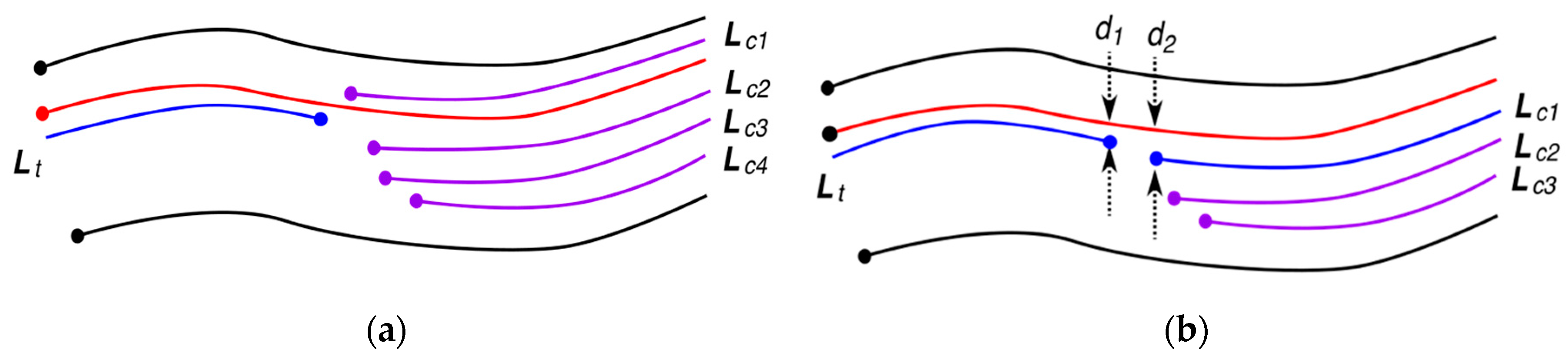
3.4. Layer-Tracing Procedure
3.5. Post-Processing of Traced Englacial Layers
4. Results
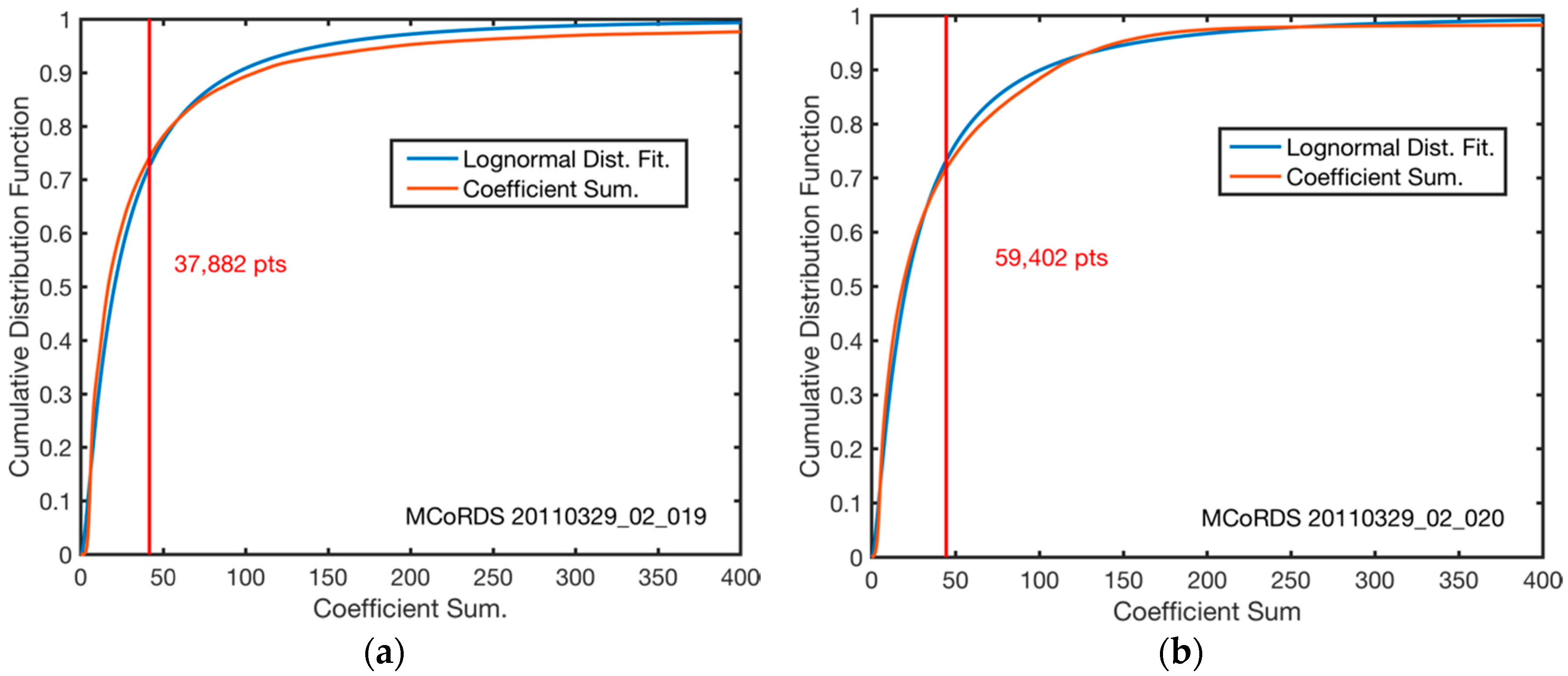
4.1. Producing the CS Image and APP Ratio Image
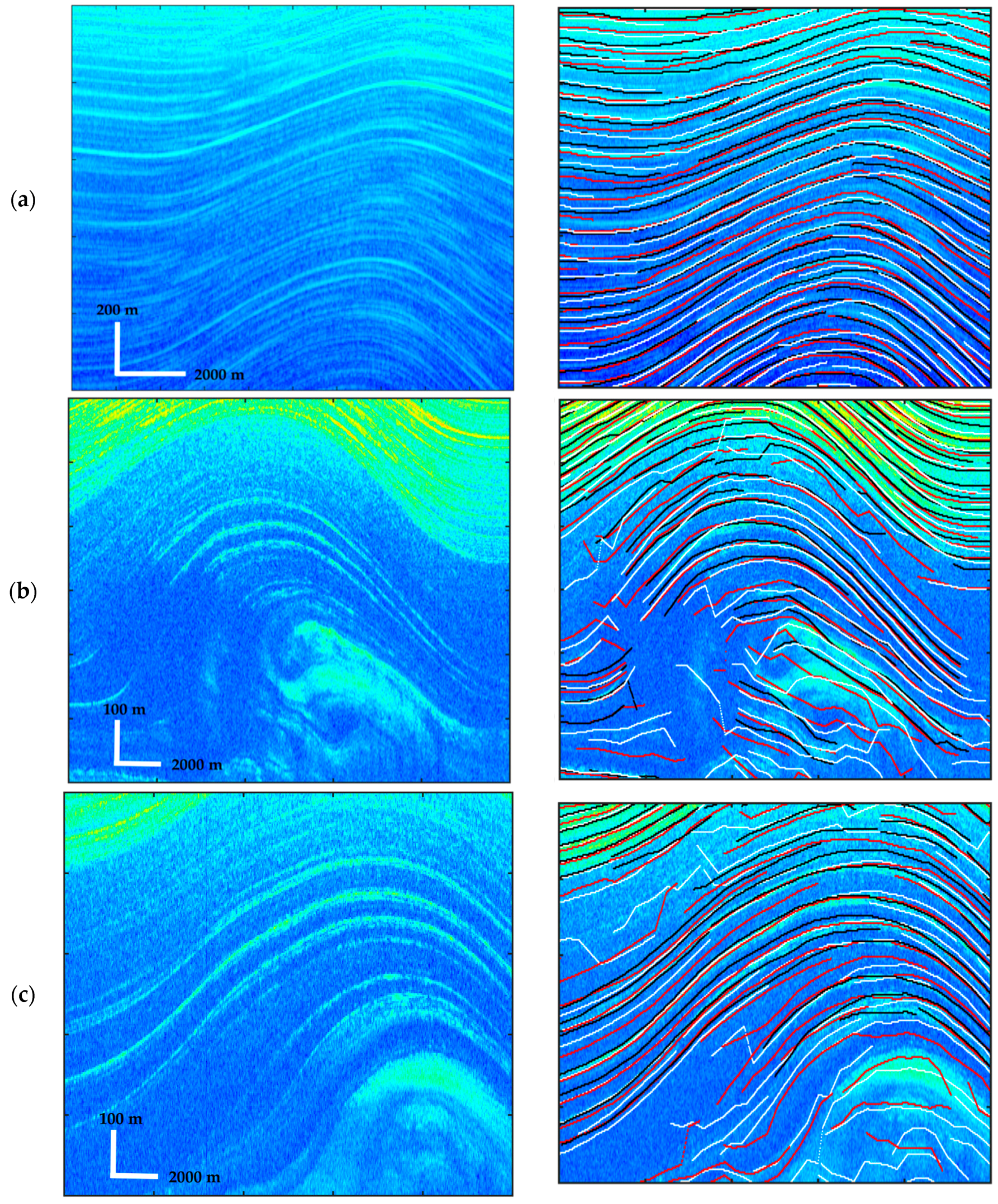
4.2. Layer-Tracing from Single Frame
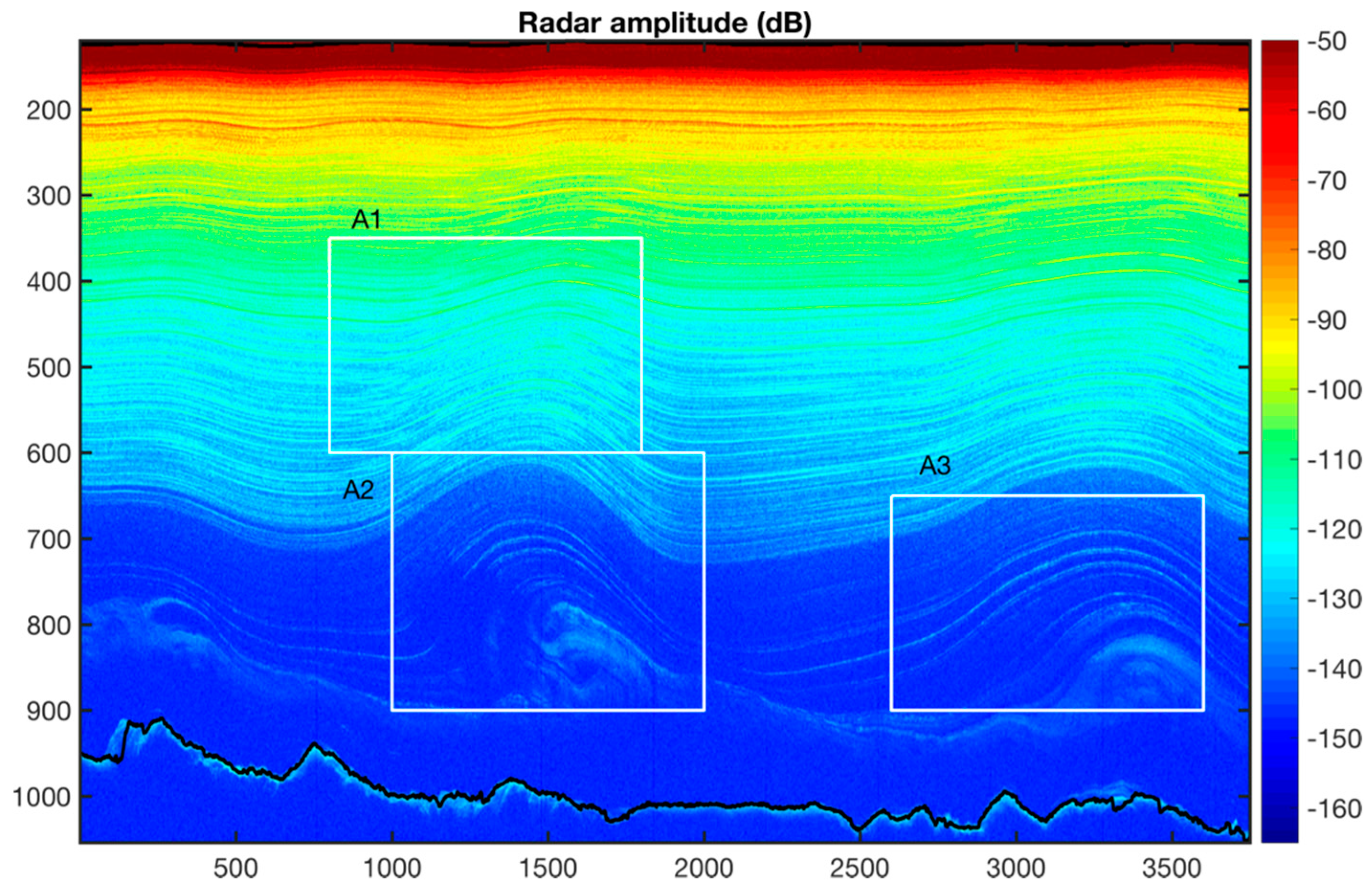
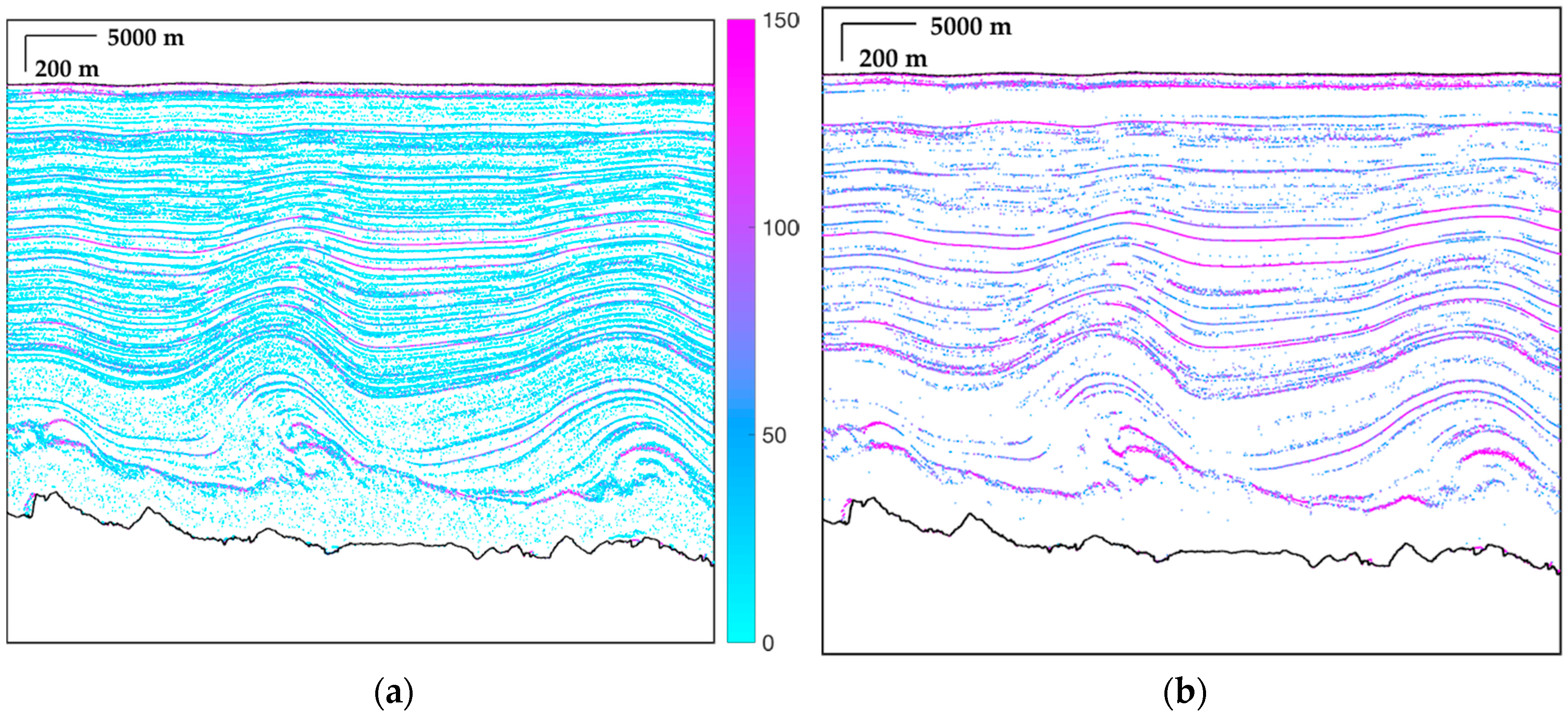
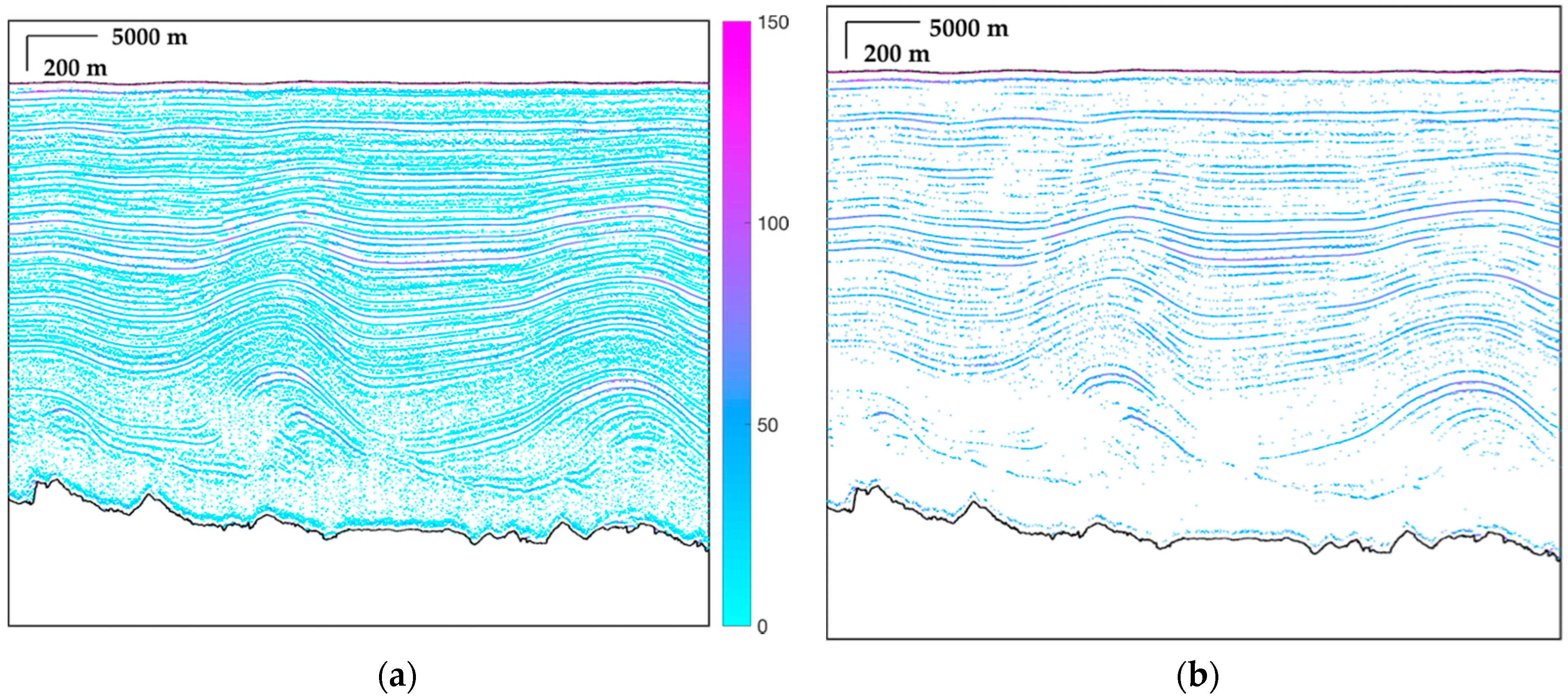
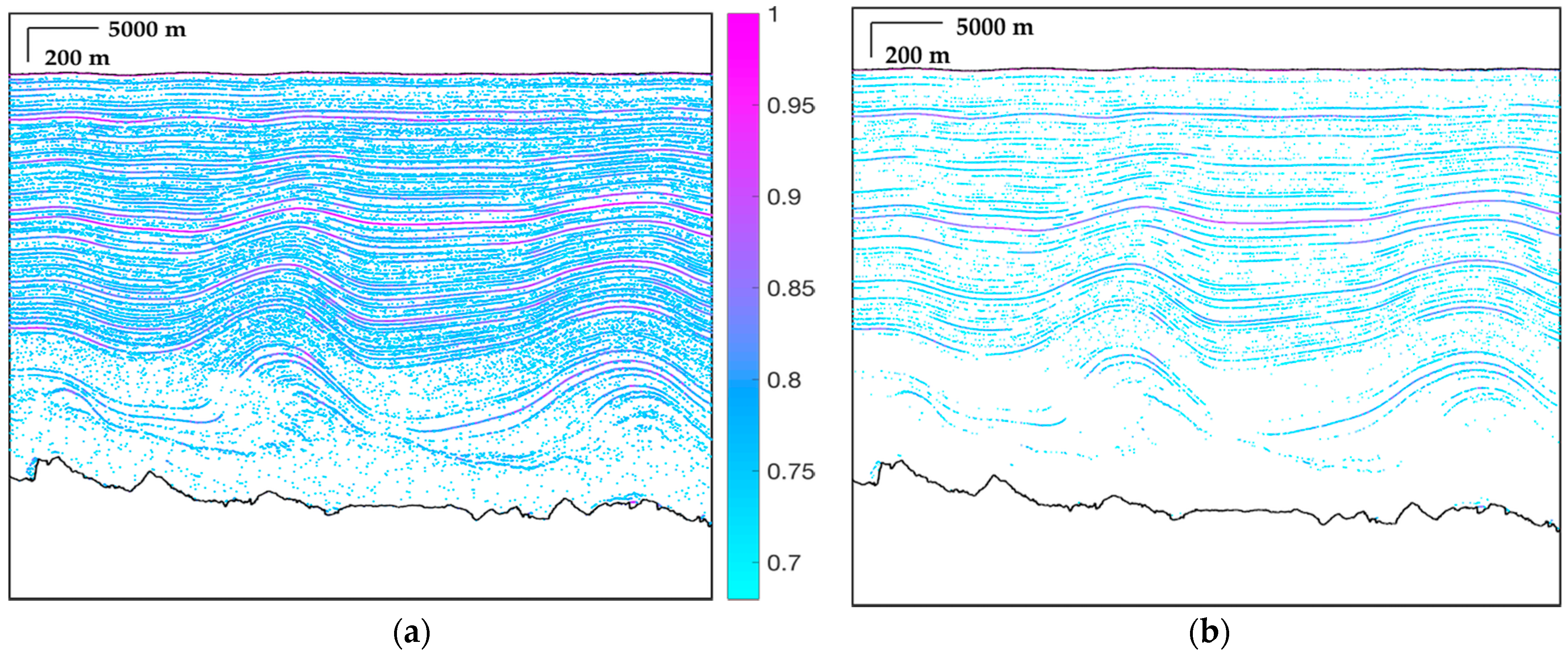
4.3. Combination of Multi-Frame and Validation
4.4. MCoRDS Data from the Pre-IceBridge Mission
5. Discussion
6. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Drewry, D.J.; Meldrum, D.T. Antarctic airborne radio echo sounding, 1977–78. Polar Rec. 1978, 19, 267–273. [Google Scholar] [CrossRef]
- Vieli, G.; Siegert, M.; Payne, A. Reconstructing ice-sheet accumulation rates at ridge B, East Antarctica. Ann. Glaciol. 2004, 39, 326–330. [Google Scholar] [CrossRef]
- Medley, B.; Ligtenberg, S.R.M.; Joughin, I.; den Broeke, M.R.; Gogineni, S.; Nowicki, S. Antarctic firn-compaction rates from repeat-track airborne radar data: I. Methods. Ann. Glaciol. 2015, 56, 155–166. [Google Scholar] [CrossRef]
- Rippin, D.M.; Siegert, M.J.; Bamber, J.L.; Vaughan, D.G.; Corr, H.F.J. Switch-off of a major enhanced ice flow unit in East Antarctica. Geophys. Res. Lett. 2006, 33, 1–6. [Google Scholar] [CrossRef]
- Bingham, R.; Rippin, D.; Karlsson, N.; Corr, H.F.J.; Ferraccioli, F.; Jordan, T.A.; Brocq, A.M.L.; Rose, K.C.; Ross, N.; Siegert, M.J. Ice-flow structure and ice dynamic changes in the Weddell Sea Sector of West Antarctica from radar-imaged internal layers. J. Geophys. Res. Earth Surf. 2014, 120, 655–670. [Google Scholar] [CrossRef]
- Drews, R.; Eisen, O.; Weikusat, I.; Kipfstuhl, S.; Lambrecht, A.; Steinhage, D.; Wilhelms, F.; Miller, H. Layer disturbances and the radio-echo free zone in ice sheets. Cryosphere 2009, 3, 195–203. [Google Scholar] [CrossRef]
- Wolovick, M.J.; Creyts, T.T. Overturned folds in ice sheets: Insights from a kinematic model of traveling sticky patches and comparisons with observations. J. Geophys. Res. Earth Surf. 2016, 121, 1065–1083. [Google Scholar] [CrossRef]
- Fretwell, P.; Pritchard, H.D.; Vaughan, D.G.; Bamber, J.; Barrand, N.; Bell, R.; Bianchi, C.; Bingham, R.; Blankenship, D.; Casassa, G.; et al. Bedmap2: Improved ice bed, surface and thickness datasets for Antarctica. Cryosphere 2013, 7, 375–393. [Google Scholar] [CrossRef]
- Bamber, J.L.; Griggs, J.A.; Hurkmans, R.T.W.L.; Dowdeswell, J.A.; Gogineni, S.P.; Howat, I.; Mouginot, J.; Paden, J.; Palmer, S.; Rignot, E.; et al. A new bed elevation dataset for Greenland. Cryosphere 2013, 7, 499–510. [Google Scholar] [CrossRef]
- Wu, C.; Zhang, X.; Shi, J.; Liu, S. Radar signal simulation on investigation of subsurface structure by radar ice depth sounder. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; pp. 4848–4851. [Google Scholar]
- Wu, X.; Jezek, K.C.; Rodriguez, E.; Gogineni, S.; Rodriguez-Morales, F.; Freeman, A. Ice Sheet Bed Mapping with Airborne SAR Tomography. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3791–3802. [Google Scholar] [CrossRef]
- Shi, L.; Allen, C.T.; Ledford, J.R.; Rodriguez-Morales, F.; Blake, W.A.; Panzer, B.G.; Prokopiack, S.C.; Leuschen, C.J.; Gogineni, S. Multichannel Coherent Radar Depth Sounder for NASA Operation Ice Bridge. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 1729–1732. [Google Scholar]
- Sime, L.C.; Hindmarsh, R.C.A.; Corr, H. Automated processing to derive dip angles of englacial radar reflectors in ice sheets. J. Glaciol. 2011, 57, 260–266. [Google Scholar] [CrossRef]
- Panton, C. Automated mapping of local layer slope and tracing of internal layers in radio echograms. Ann. Glaciol. 2014, 55, 71–77. [Google Scholar] [CrossRef]
- Holschuh, N.; Parizek, B.R.; Alley, R.B.; Anandakrishnan, S. Decoding ice sheet behavior using englacial layer slopes. Geophys. Res. Lett. 2017, 44, 5561–5570. [Google Scholar] [CrossRef]
- MacGregor, J.A.; Fahnestock, M.A.; Catania, G.A.; Paden, J.D.; Prasad Gogineni, S.; Young, S.K.; Rybarski, S.C.; Mabrey, A.N.; Wagman, B.M.; Morlighem, M. Radiostratigraphy and age structure of the Greenland Ice Sheet. J. Geophys. Res. Earth Surf. 2015, 120, 212–241. [Google Scholar] [CrossRef] [PubMed]
- Onana, V.D.P.; Koenig, L.S.; Ruth, J.; Studinger, M.; Harbeck, J.P. A Semiautomated Multilayer Picking Algorithm for Ice-Sheet Radar Echograms Applied to Ground-Based Near-Surface Data. IEEE Trans. Geosci. Remote Sens. 2015, 53, 51–69. [Google Scholar] [CrossRef]
- Xiong, S.; Muller, J.-P. Extraction of englacial layers from two intersected radar echograms near NEEM ice core in Greenland. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. ISPRS 2016, 41, 585–591. [Google Scholar] [CrossRef]
- Fahnestock, M.; Abdalati, W.; Luo, S.; Gogineni, S. Internal layer tracing and age-depth-accumulation relationships for the northern Greenland ice sheet. J. Geophys. Res. Atmos. 2011, 106, 33789–33797. [Google Scholar] [CrossRef]
- Bons, P.D.; Jansen, D.; Mundel, F.; Bauer, C.C.; Binder, T.; Eisen, O.; Jessell, M.W.; Llorens, M.G.; Steinbach, F.; Steinhage, D.; et al. Converging flow and anisotropy cause large-scale folding in Greenland’s ice sheet. Nat. Commun. 2016, 7, 11427. [Google Scholar] [CrossRef] [PubMed]
- Panton, C.; Karlsson, N.B. Automated mapping of near bed radio-echo layer disruptions in the Greenland Ice Sheet. Earth Planet. Sci. Lett. 2015, 432, 323–331. [Google Scholar] [CrossRef]
- Dahl-Jensen, D.; Albert, M.; Aldahan, A.; Azuma, N.; Balslev-Clausen, D.; Baumgartner, M.; Berggren, A.M.; Bigler, M.; Binder, T.; Blunier, T.; et al. Eemian interglacial reconstructed from a Greenland folded ice core. Nature 2013, 493, 489. [Google Scholar] [CrossRef] [PubMed]
- Morlighem, M. IceBridge BedMachine Greenland, version 2; NASA DAAC at the National Snow and Ice Data Center: Boulder, CO, USA, 2015. [Google Scholar] [CrossRef]
- Morlighem, M.; Rignot, E.; Mouginot, J.; Seroussi, H.; Larour, E. Deeply incised submarine glacial valleys beneath the Greenland ice sheet. Nat. Geosci. 2014, 7, 418–422. [Google Scholar] [CrossRef]
- Yan, J.B.; Li, J.; Rodriguez-Morales, F.; Crowe, R.; Gomez-Garcia, D.; Arnold, E.J.; Paden, J.; Leuschen, C.J.; Gogineni, S. Measurements of In-Flight Cross-Track Antenna Patterns of Radar Depth Sounder/Imager. IEEE Trans. Antennas Propag. 2012, 60, 5669–5678. [Google Scholar] [CrossRef]
- Leuschen, C. IceBridge MCoRDS L1B Geolocated Radar Echo Strength Profiles, version 1; National Snow and Ice Data Center: Boulder, CO, USA, 2011. [Google Scholar]
- Leuschen, C.; Gogineni, P.; Hale, R.; Paden, J.; Rodriguez, F.; Panzer, B.; Gomez, D. IceBridge MCoRDS L1B Geolocated Radar Echo Strength Profiles, version 2; National Snow and Ice Data Center: Boulder, CO, USA, 2014. [Google Scholar]
- MacGregor, J.A.; Fahnestock, M.; Catania, G.; Paden, J.; Gogineni, P.; Young, S.K.; Rybarski, S.C.; Mabrey, A.N.; Wagman, B.M.; Morlighem, M. Radiostratigraphy and Age Structure of the Greenland Ice Sheet, version 1; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2015. [Google Scholar]
- Du, P.; Kibbe, W.A.; Lin, S.M. Improved peak detection in mass spectrum by incorporating continuous wavelet transform-based pattern matching. Bioinformatics 2006, 22, 2059–2065. [Google Scholar] [CrossRef] [PubMed]
- Aguirre, C.; Franzese, G.; Esposito, F.; Vázquez, L.; Vilela-Mendes, R.; Carretero, R.C.; Ramírez-Nicolás, M.; Cozzolino, F.; Popa, C. Signal-adapted tomography as a tool for dust devil detection. Aeolian Res. 2017, 29, 12–22. [Google Scholar] [CrossRef]
- Duda, R.O.; Hart, P.E. Use of the Hough Transformation to Detect Lines and Curves in Pictures. Commun. ACM 1972, 15, 11–15. [Google Scholar] [CrossRef]
- Ballard, D.H. Generalizing the Hough transform to detect arbitrary shapes. Pattern Recogn. 1981, 13, 111–122. [Google Scholar] [CrossRef]
- Grossmann, A.; Kronland-Martinet, R.; Morlet, J. Reading and understanding continuous wavelet transforms. In Wavelets; Springer: Berlin/Heidelberg, Germany, 1990; pp. 2–20. [Google Scholar]
- Küperkoch, L.; Meier, T.; Lee, J.; Friederich, W.; EGELADOS Working Group. Automated determination of P-phase arrival times at regional and local distances using higher order statistics. Geophys. J. Int. 2010, 181, 1159–1170. [Google Scholar]
- Allen, R. Automatic phase pickers: Their present use and future prospects. Bull. Seismol. Soc. Am. 1982, 72, S225–S242. [Google Scholar]
- Saragiotis, C.D.; Hadjileontiadis, L.J.; Panas, S.M. PAI-S/K: A robust automatic seismic P phase arrival identification scheme. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1395–1404. [Google Scholar] [CrossRef]
- Baer, M.; Kradolfer, U. An automatic phase picker for local and teleseismic events. Bull. Seismol. Soc. Am. 1987, 77, 1437–1445. [Google Scholar]
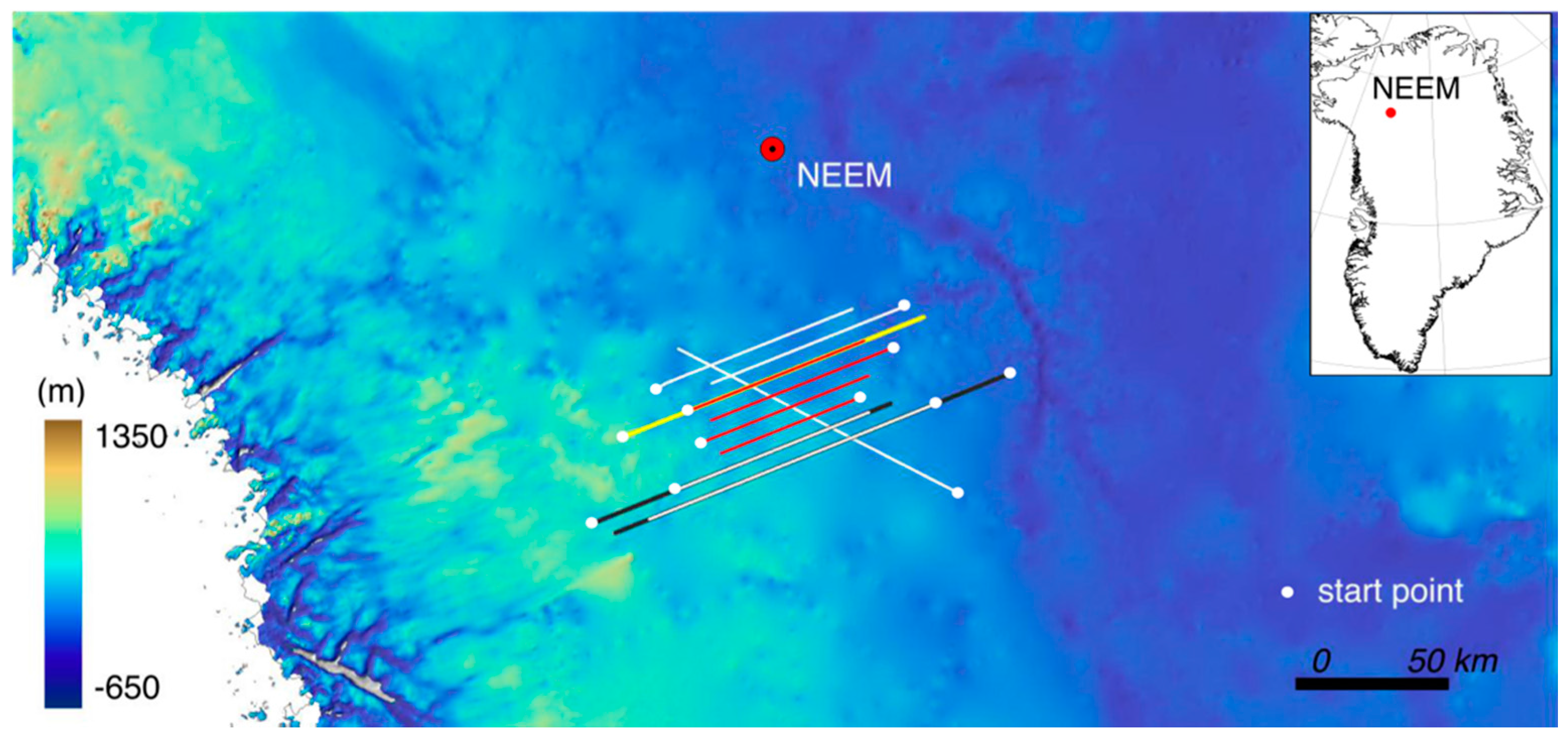


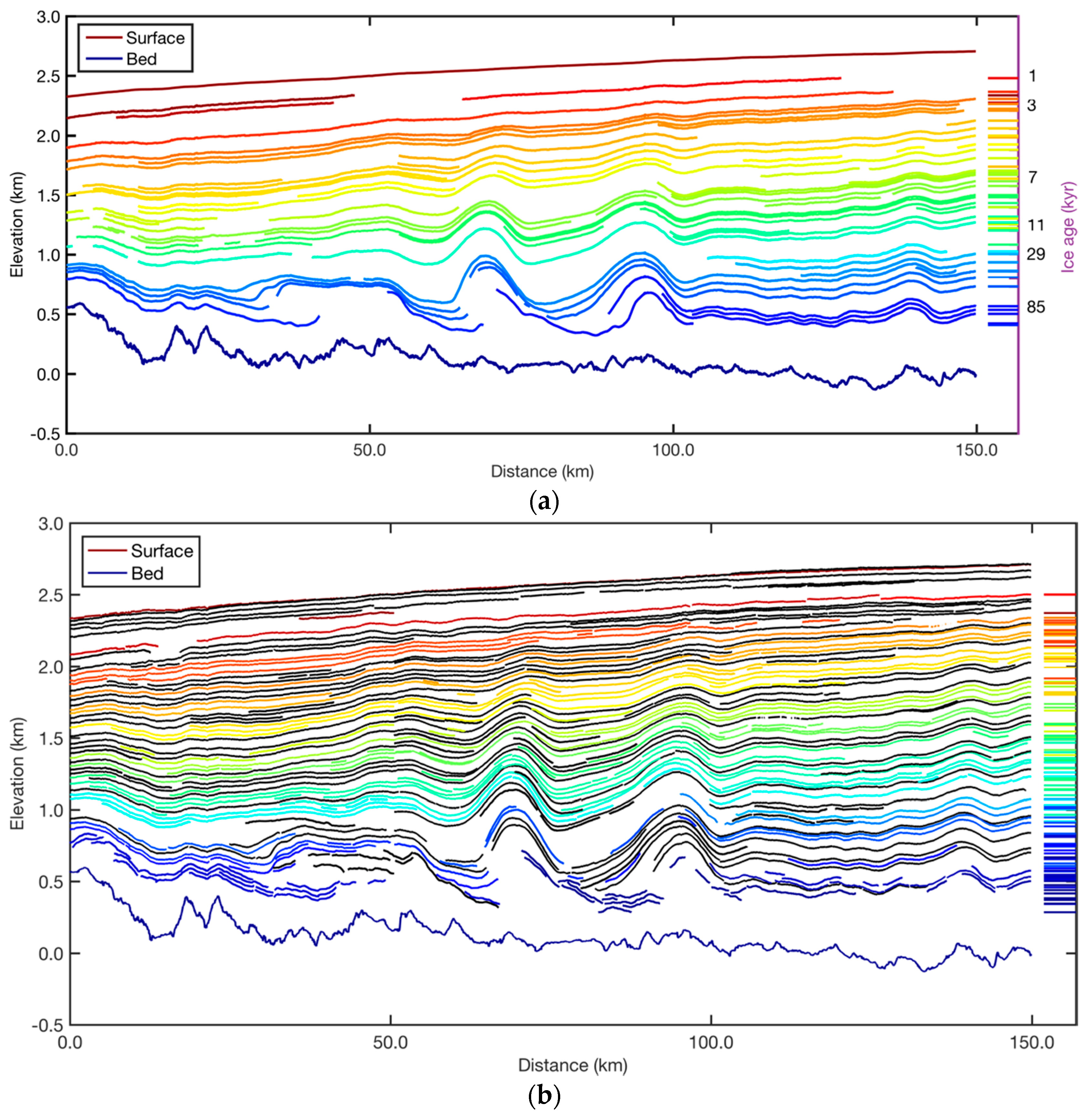
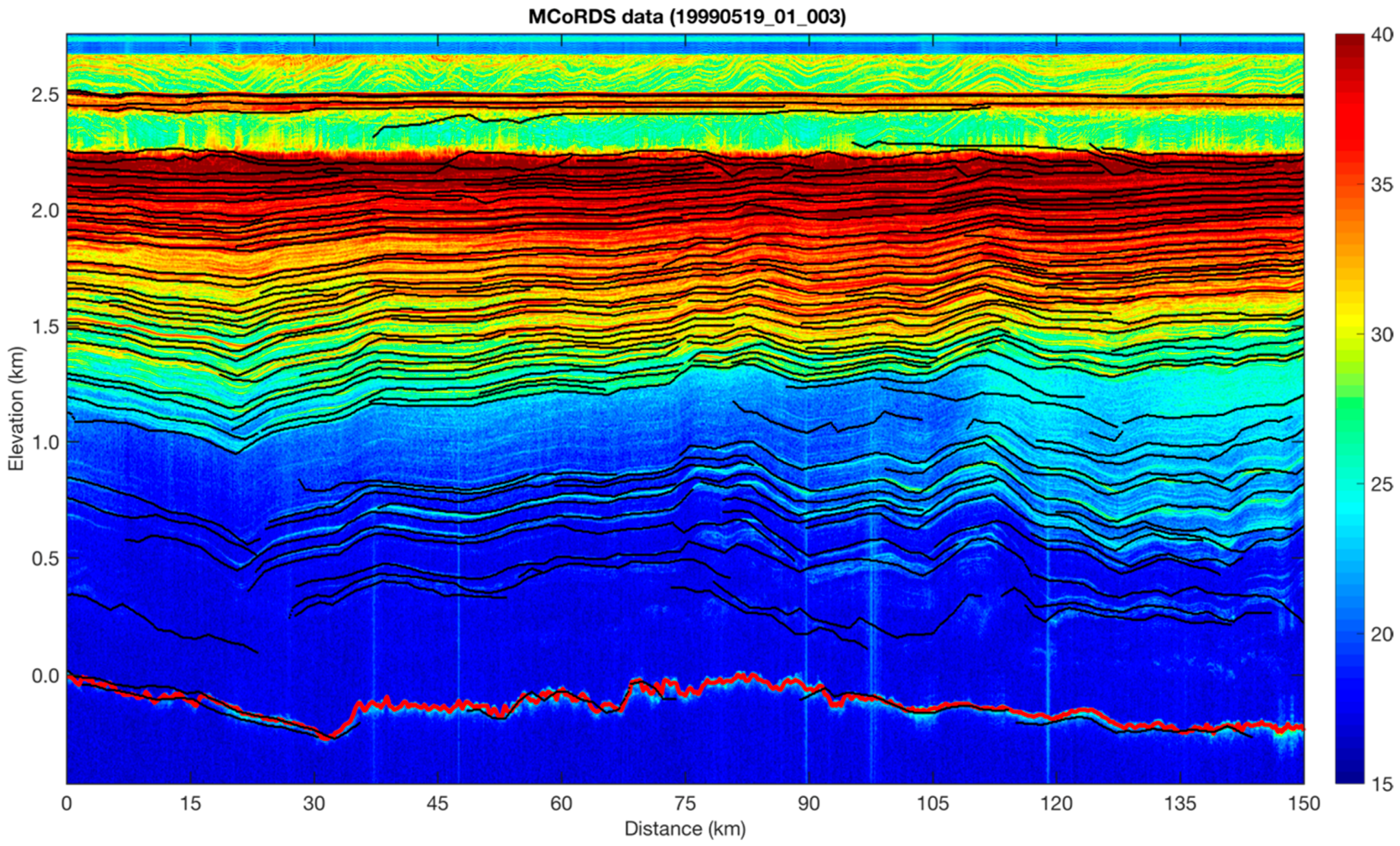

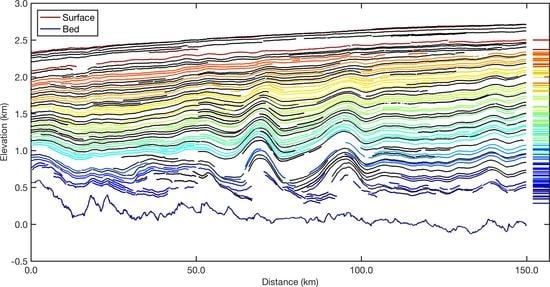
| Line No. | Date of Segment | Frames | Distance (km) | Start Lat./Lon. | End Lat./Lon. |
|---|---|---|---|---|---|
| 1 | 20110329_02 | 019–021 | 150.15 | 76.169°N, 52.197°W | 76.774°N, 46.964°W |
| 2 | 20120508_04 | 005–007 | 90.36 | 76.296°N, 51.208°W | 76.661°N, 48.054°W |
| 3 | 20120508_07 | 005–007 | 90.36 | 76.633°N, 47.567°W | 76.273°N, 50.727°W |
| 4 | 20120507_03 | 011–012 | 82.93 | 76.181°N, 50.810°W | 76.514°N, 47.939°W |
| 5 | 20120507_07 | 011–012 | 68.90 | 76.414°N, 48.125°W | 76.137°N, 50.498°W |
| 6 | 20130419_01 | 012–014 | 75.74 | 75.784°N, 52.561°W | 76.400°N, 47.514°W |
| 7 | 20130419_01 | 057–060 | 100.22 | 76.536°N, 45.387°W | 76.163°N, 48.916°W |
| 8 | 20140515_02 | 011–012 | 98.15 | 76.387°N, 51.734°W | 76.794°N, 48.303°W |
| 9 | 20140515_02 | 060–061 | 98.24 | 76.819°N, 47.304°W | 76.430°N, 50.790°W |
| 10 | 20140521_01 | 012–013 | 98.33 | 75.960°N, 51.245°W | 76.358°N, 47.896°W |
| 11 | 20140521_02 | 022–024 | 76.42 | 76.415°N, 46.602°W | 75.826°N, 51.632°W |
| 12 | 20140514_01 | 058–060 | 147.47 | 76.030°N, 46.261°W | 76.562°N, 51.467°W |
| CWT-Based Peak Detection | APP-Based Peak Detection |
|---|---|
| MEXH or MORL wavelet | Long term windows |
| Wavelet scales | Short term windows |
| weights | |
| Pixels below bed to choose noisy signals | |
| Section | Steps | Params. | Description | Default (px) |
|---|---|---|---|---|
| 3.2 | 1. CWT-based peak detection | Wavelet scales, . | ||
| Pixels below bed to obtain background noise. | 50 | |||
| 3.3 | 2. Seed point selection | N/A | N/A. | N/A |
| 3.4 | 3. Layer-tracing Procedure | Block size for estimation of slope angle. | 51 () | |
| Minimum vertical distance between two close layers. | 7 ( ) | |||
| Slope angle difference. | 90 degrees | |||
| Gap filling in HT domain. | 12 () | |||
| 3.5 | 4. post-processing | Minimum vertical distance. | 7 |
| No. Points in Image | No. of Seed Point | Time (s) | No. of Layers | No. of Layers after Post-Processing | |
|---|---|---|---|---|---|
| MEXH CS image | 210,487 | 59,402 | 342 | 227 | 121 |
| MORL CS image | 150,087 | 47,570 | 295 | 219 | 113 |
| APP ratio image | 123,544 | 51,339 | 325 | 223 | 103 |
| Time (s) | No. of Layers | Time (s) | No. of Layers | ||
|---|---|---|---|---|---|
| = 51 | before post-processing | 342 | 227 | 162 | 112 |
| after post-processing | 7 | 121 | 3 | 66 | |
| = 101 | before post-processing | 326 | 216 | 164 | 124 |
| after post-processing | 7 | 120 | 5 | 65 | |
| Line No. | RRRAG Isochrones | Restored RRRAG Isochrones | Restored Percentage | Traced Segments | Confirmed Layer Segments | Confirmed Percentage |
|---|---|---|---|---|---|---|
| 1 | 46 | 45 | 97.8% | 279 | 122 | 43.7% |
| 2 | 55 | 46 | 83.6% | 124 | 61 | 49.2% |
| 3 | 61 | 44 | 72.1% | 135 | 63 | 46.7% |
| 4 | 42 | 38 | 90.5% | 125 | 61 | 48.8% |
| 5 | 58 | 50 | 86.3% | 100 | 54 | 54.0% |
| 6 | 83 | 75 | 90.2% | 228 | 139 | 61.0% |
| 7 | 100 | 88 | 88.0% | 272 | 156 | 57.4% |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiong, S.; Muller, J.-P.; Carretero, R.C. A New Method for Automatically Tracing Englacial Layers from MCoRDS Data in NW Greenland. Remote Sens. 2018, 10, 43. https://doi.org/10.3390/rs10010043
Xiong S, Muller J-P, Carretero RC. A New Method for Automatically Tracing Englacial Layers from MCoRDS Data in NW Greenland. Remote Sensing. 2018; 10(1):43. https://doi.org/10.3390/rs10010043
Chicago/Turabian StyleXiong, Siting, Jan-Peter Muller, and Raquel Caro Carretero. 2018. "A New Method for Automatically Tracing Englacial Layers from MCoRDS Data in NW Greenland" Remote Sensing 10, no. 1: 43. https://doi.org/10.3390/rs10010043
APA StyleXiong, S., Muller, J.-P., & Carretero, R. C. (2018). A New Method for Automatically Tracing Englacial Layers from MCoRDS Data in NW Greenland. Remote Sensing, 10(1), 43. https://doi.org/10.3390/rs10010043