Time-Continuous Hemispherical Urban Surface Temperatures
Abstract
:1. Introduction
- What is the nature of the surface ‘seen’ by a thermal remote sensor?
- How does Tsurf observed by a remote sensor relate to the ‘true’ temperature governing the surface-atmosphere interface?
- Them, r samples the surface hemispherically (i.e., samples vertical, horizontal, and sloped features), providing a temperature that is more geometrically representative than one from a narrow field-of-view remote sensor in the nadir [10].
- Them, r is time-continuous and derived from measures that are often made for periods of a year or more. This allows for continuous analysis of urban Tsurf at a wide range of time scales.
- The wide spectral response of a pyrgeometer makes it potentially more susceptible to atmospheric effects compared to radiometers that operate over smaller, more transparent, spectral ranges.
- Them, r is not spatially extensive. The method yields a single value that is representative of a view factor weighted average temperature of all of the surfaces “seen” by the sensor (analogous to a single pixel of a thermal image from a satellite remote sensor).
- When measured via a pyrgeometer, longwave radiation upwelling from the urban surface is spatially variant when measured from heights below approximately 3 to 5 times mean building height. For a pyrgeometer mounted below this threshold, Them, r is potentially biased towards surfaces that are closest to the sensor.
1.1. Describing Radiation as Received by a Remote Sensor
1.2. Relating TIR and Surface Temperature
1.3. Atmospheric Correction of Near-Ground TIR Radiation Measured in Urban Environments
2. Methods
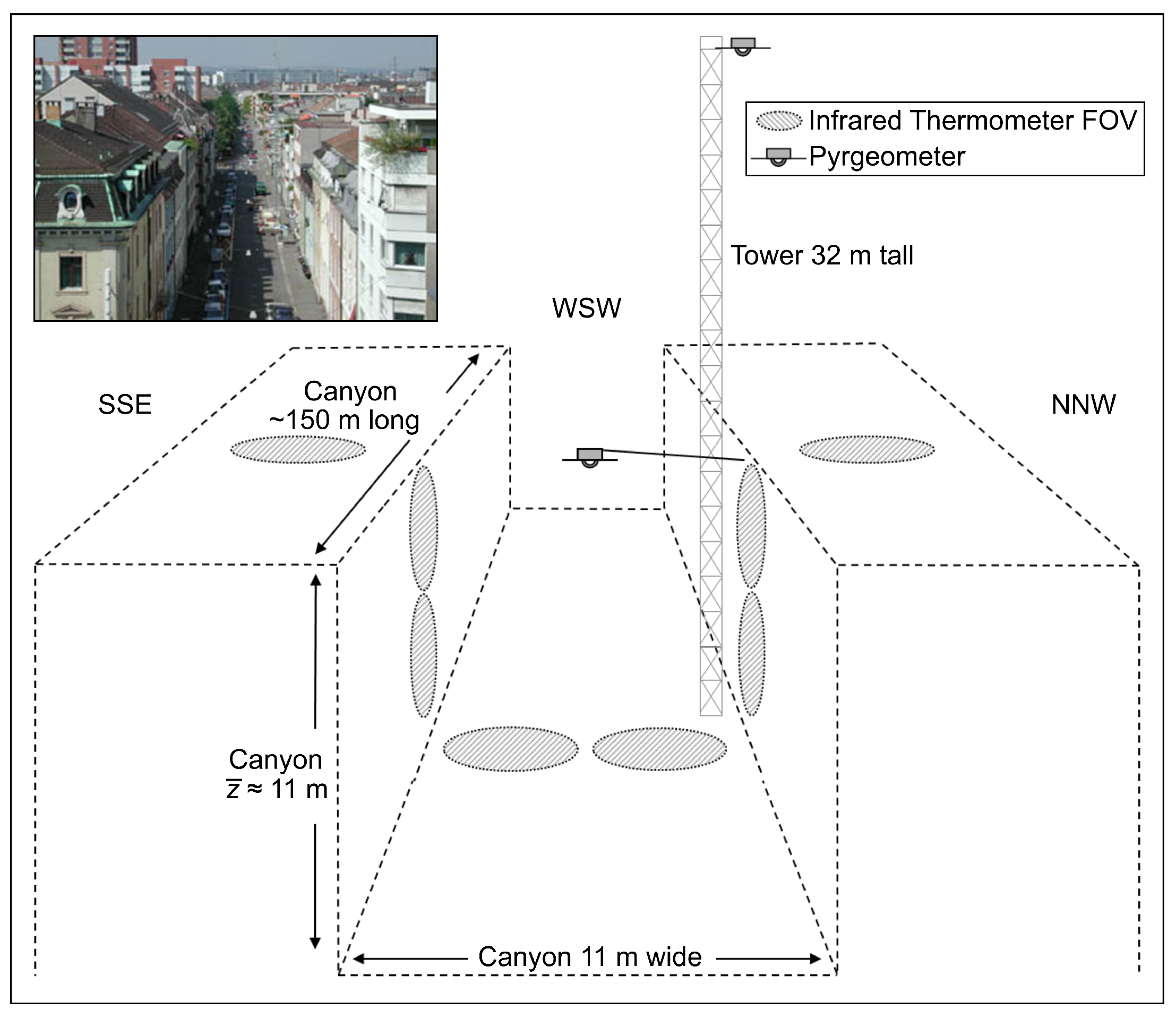
2.1. Study Area
2.2. Modeling Path Lengths of Three-Dimensional Terrain
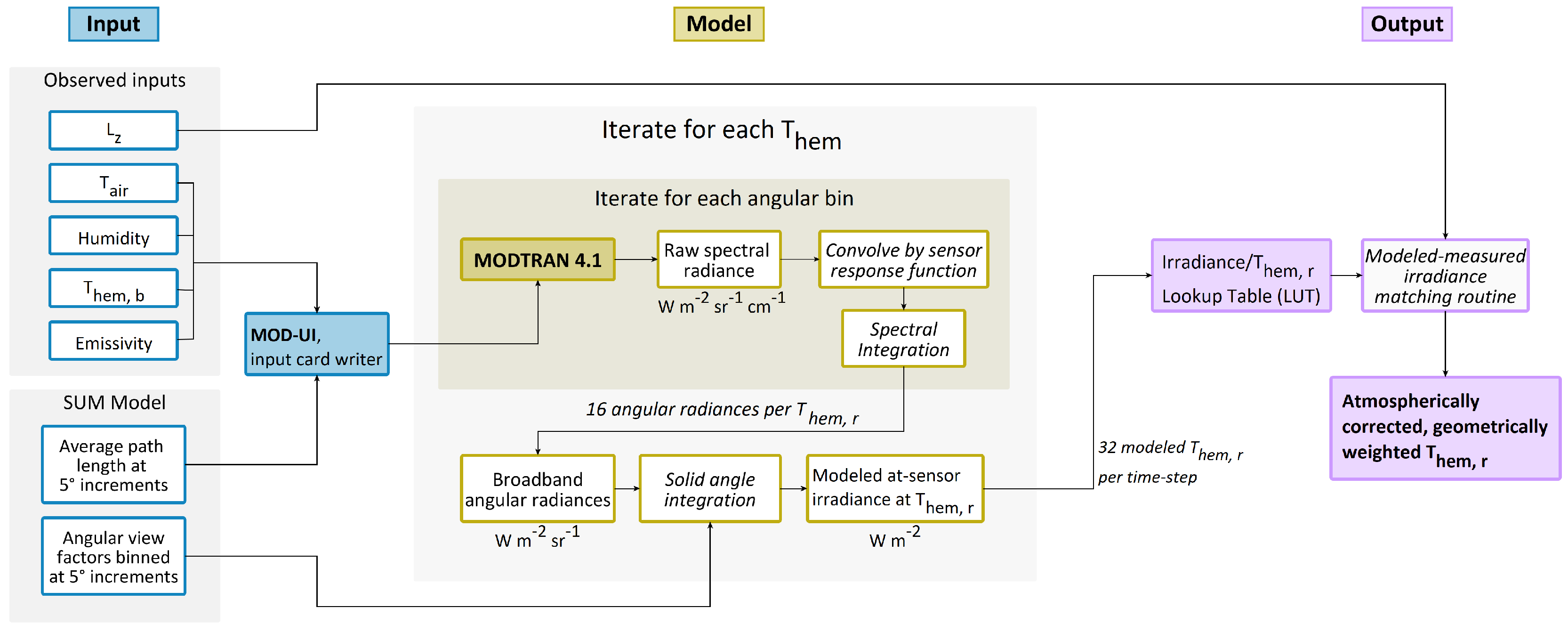
2.3. Modeling Hemispherical Irradiances
2.4. A Practical Parameterization
3. Results
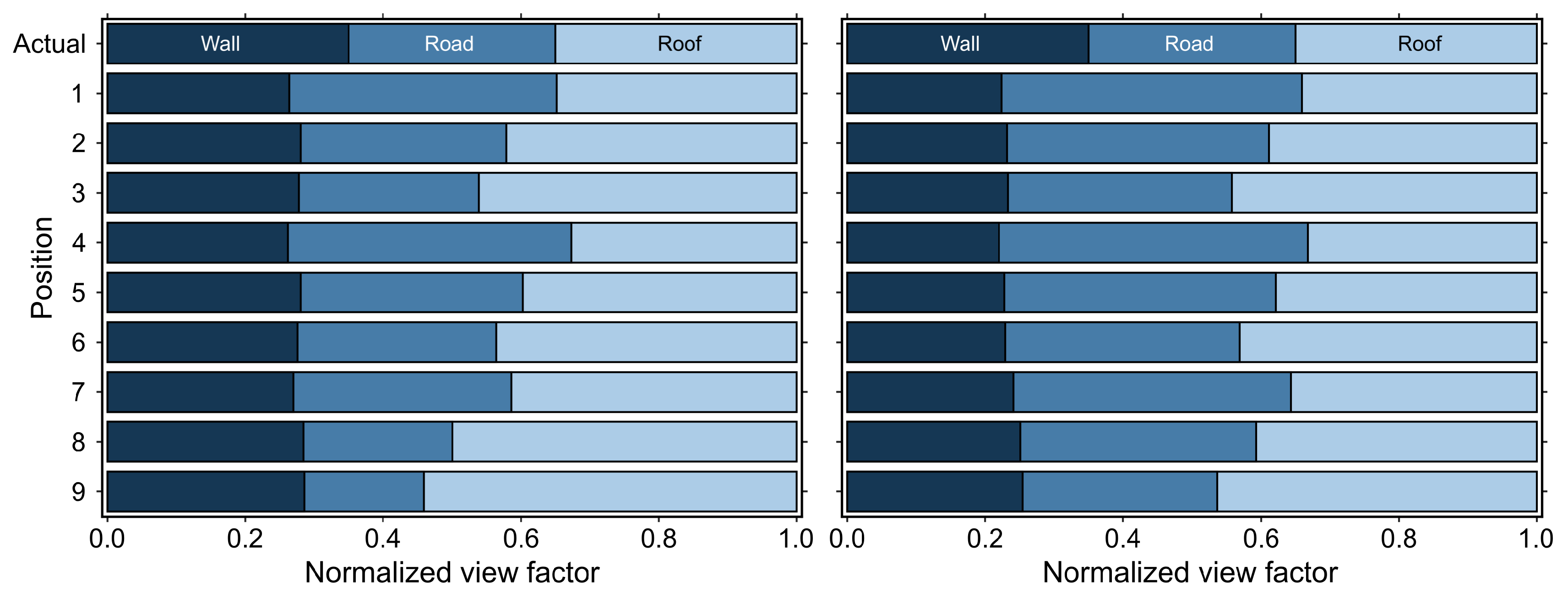
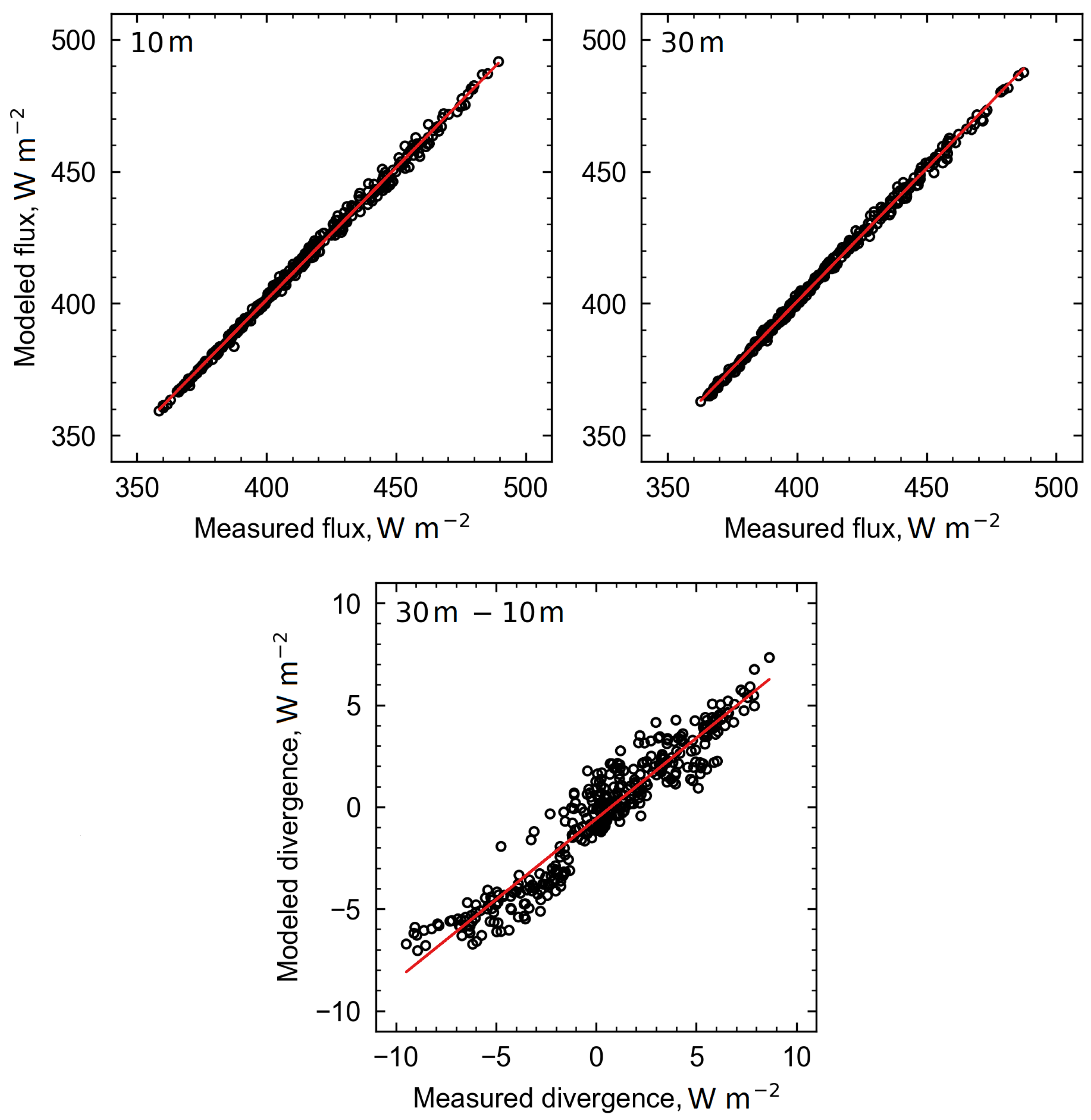
3.1. Method Evaluation
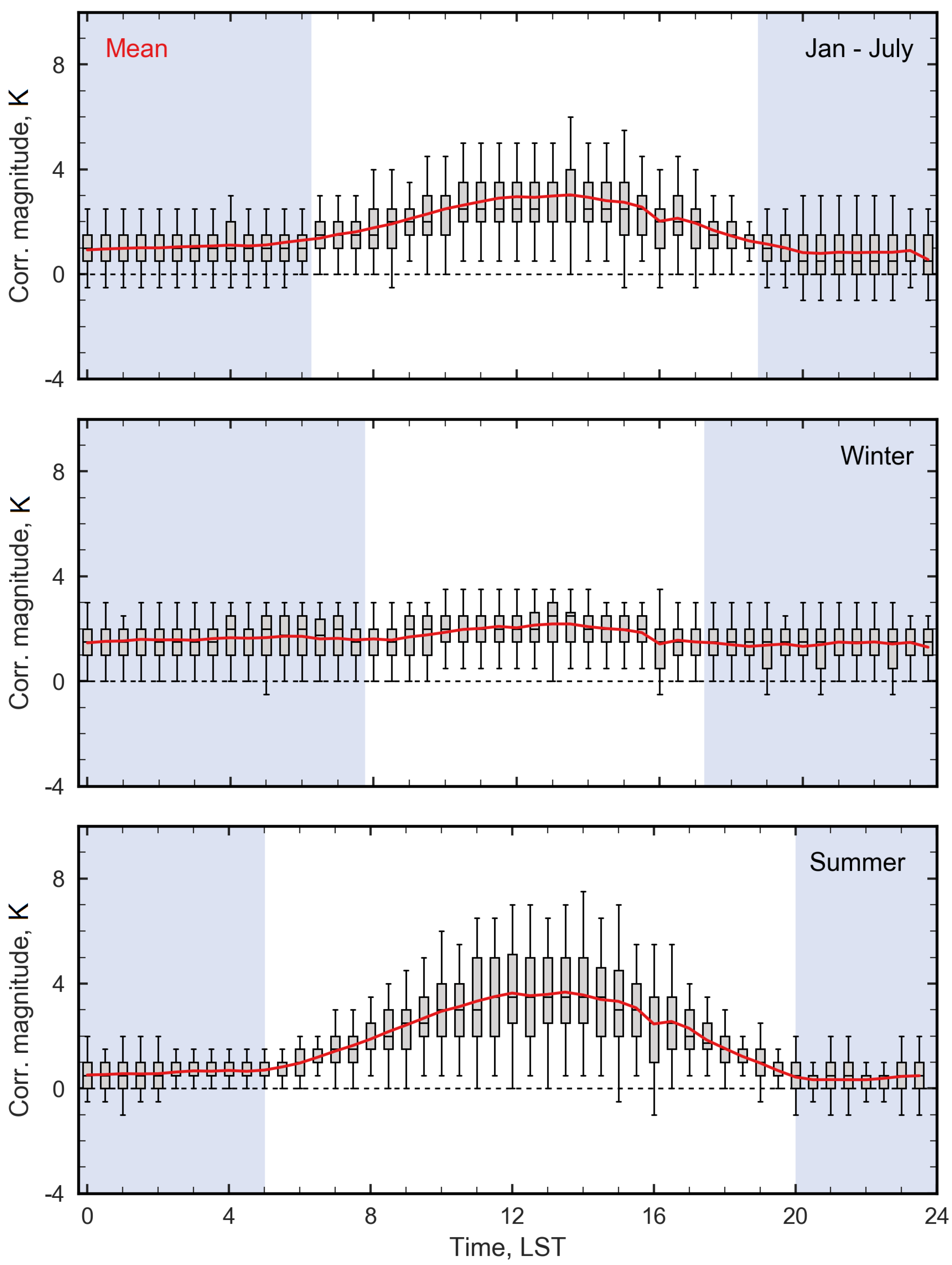
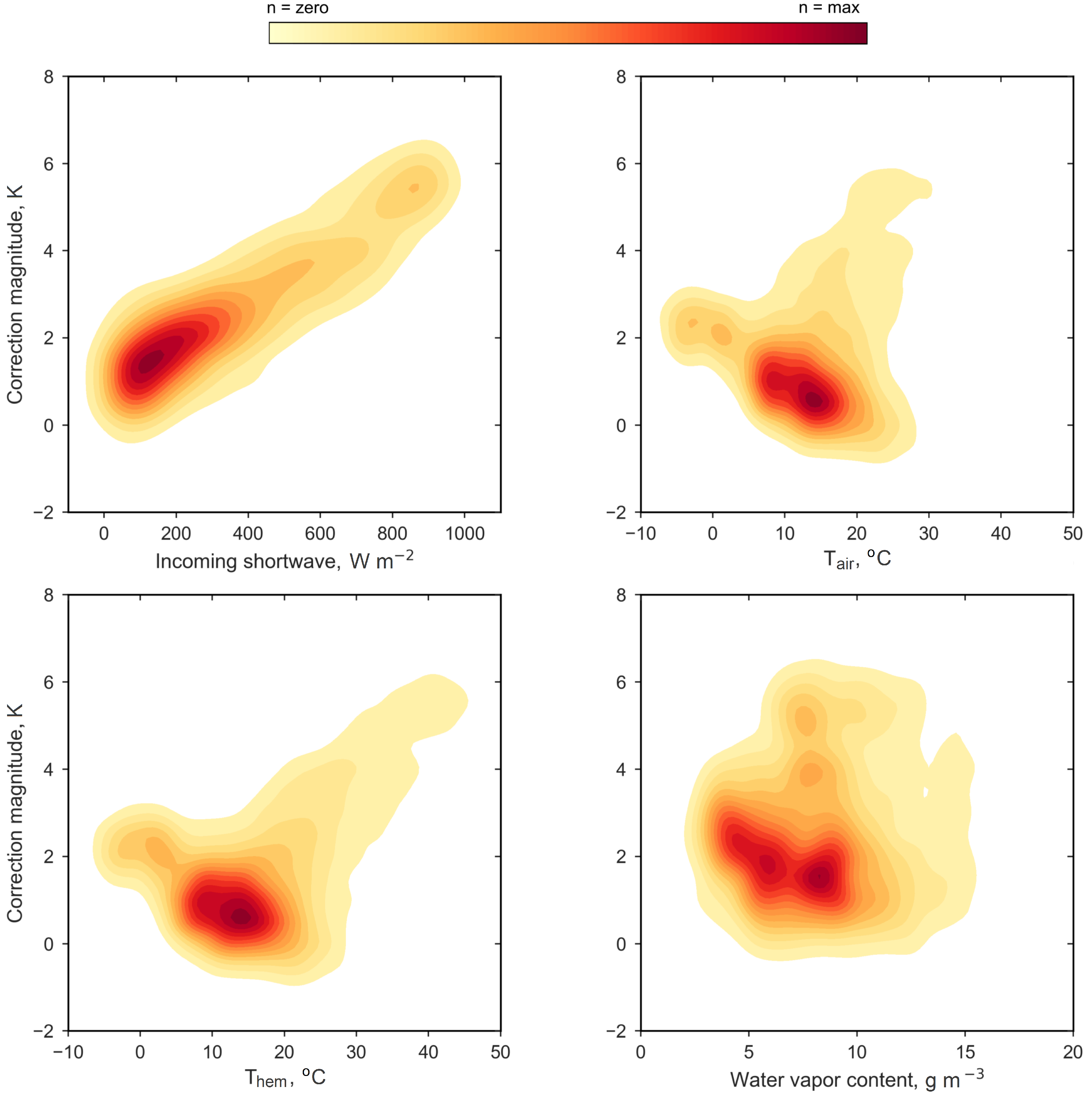
3.2. Atmospheric Correction Magnitudes
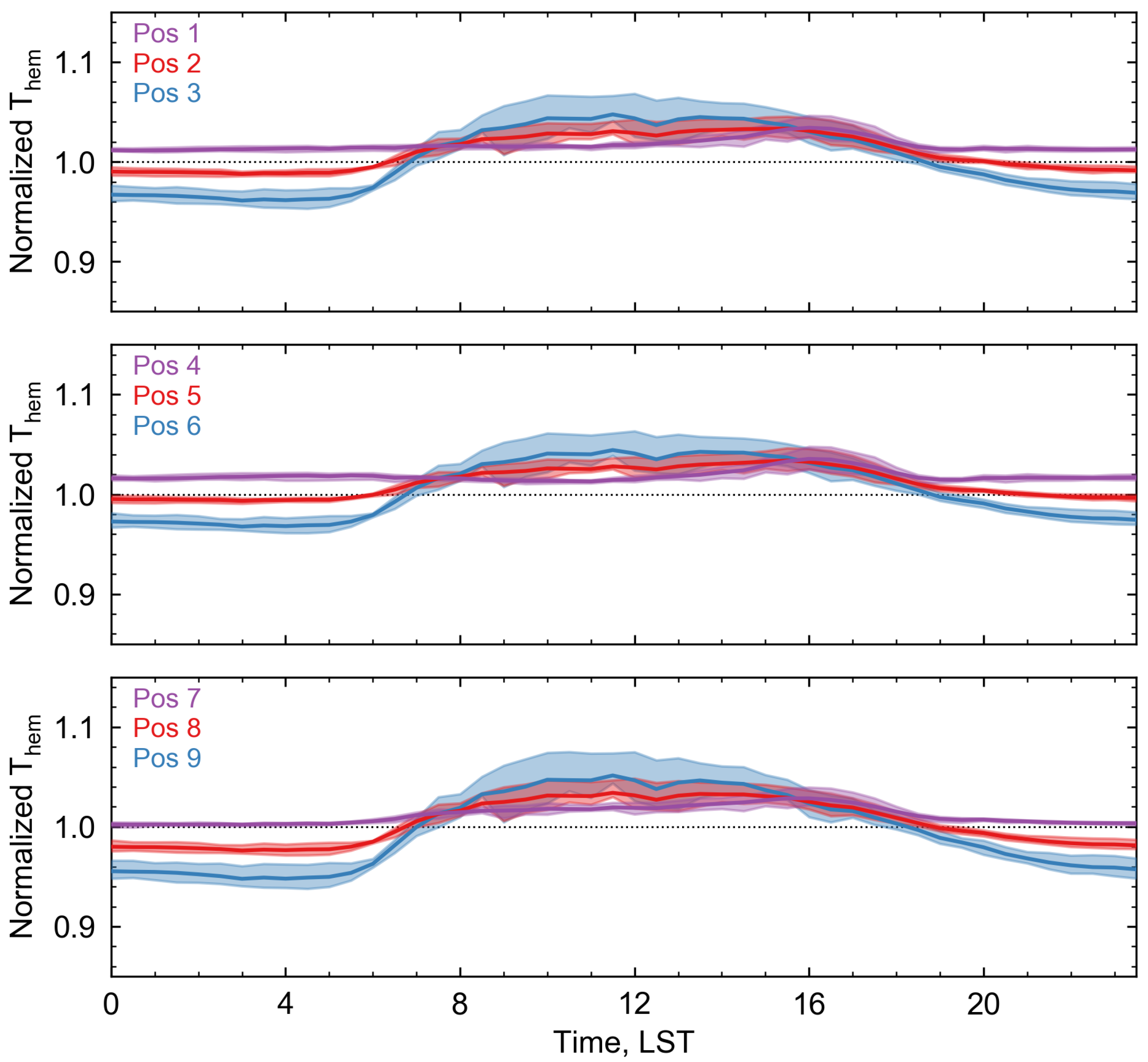
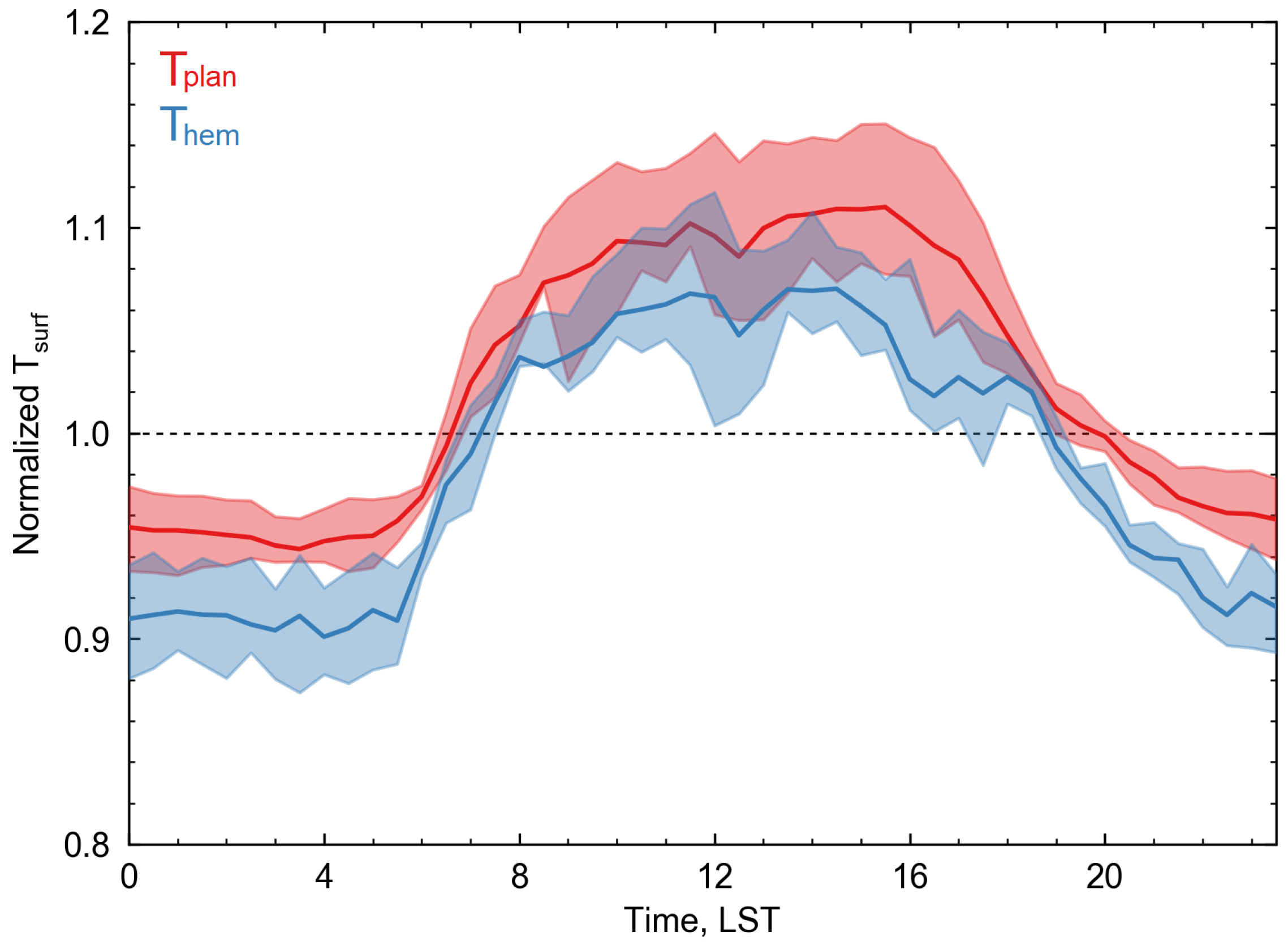
3.3. Comparing Tsurf from Different Sensor Geometries
4. Discussion
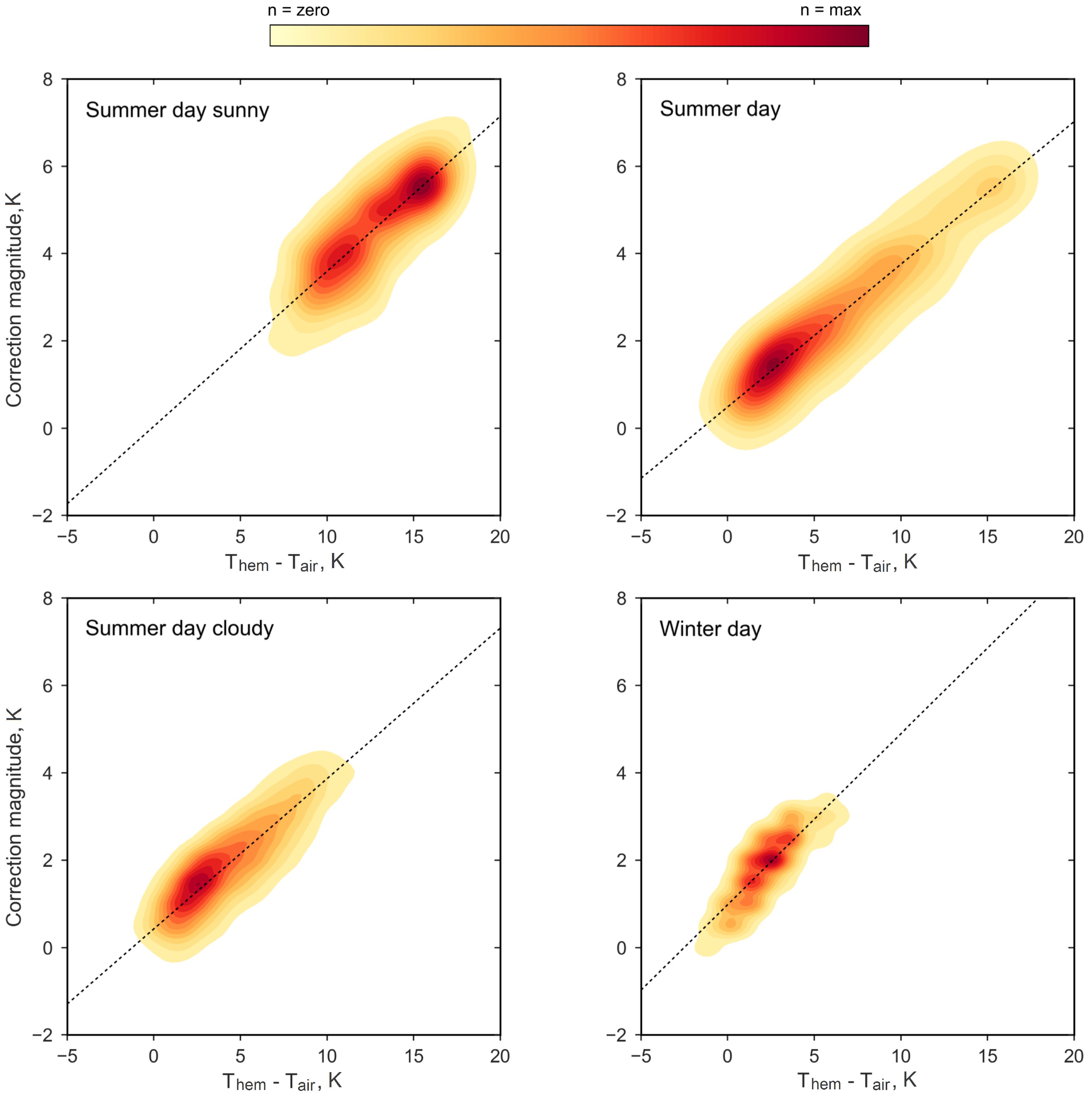
4.1. Controls on Atmospheric Correction Magnitude
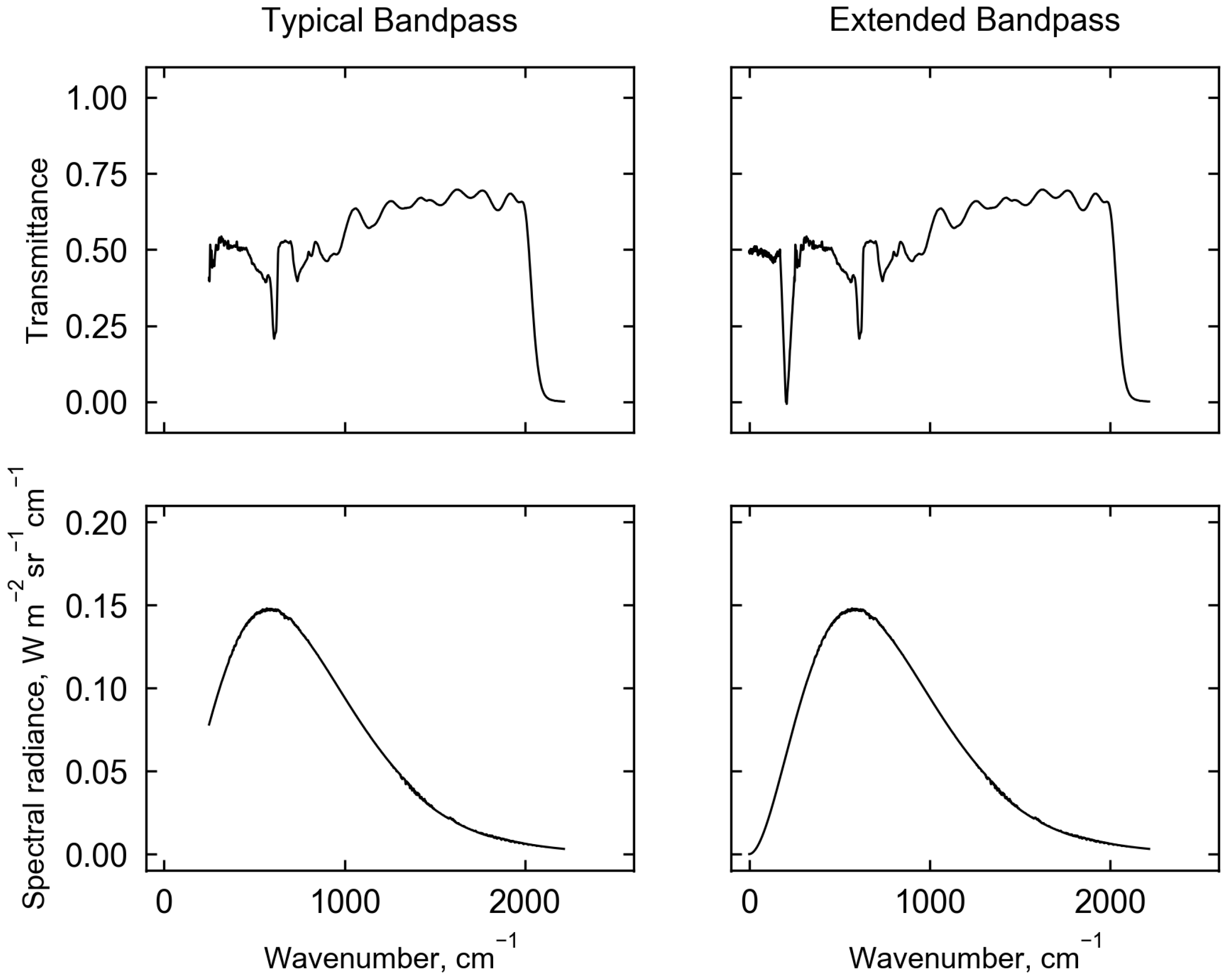
4.2. The Effect of Non-Uniform Pyrgeometer Spectral Dome Transmittance on Correction Magnitudes
4.3. The Effect of Sensor Sampling Geometry on Remote Sensed Tsurf
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Sensor Placement Sensitivity Testing


References
- Roth, M.; Oke, T.R.; Emery, W. Satellite-derived urban heat islands from three coastal cities and the utilization of such data in urban climatology. Int. J. Remote Sens. 1989, 10, 1699–1720. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, Y. Urban heat island analysis using the landsat TM data and ASTER Data: A case study in Hong Kong. Remote Sens. 2011, 3, 1535–1552. [Google Scholar] [CrossRef]
- Peng, S.; Piao, S.; Ciais, P.; Friedlingstein, P.; Ottle, C.; Bréon, F.M.; Nan, H.; Zhou, L.; Myneni, R.B. Surface urban heat island across 419 global big cities. Environ. Sci. Technol. 2012, 46, 696–703. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Zhang, Y.; Tsou, J.; Li, Y. Surface Urban Heat Island Analysis of Shanghai (China) Based on the Change of Land Use and Land Cover. Sustainability 2017, 9, 1538. [Google Scholar] [CrossRef]
- Voogt, J.A.; Oke, T.R. Complete urban surface temperatures. J. Appl. Meteorol. 1997, 36, 1117–1132. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Meneti, M.; Feddes, R.A.; Holtslag, A.A.M. A remote sensing surface energy balance algorithm for land (SEBAL): Formulation. J. Hydrol. 1998, 212–213, 198–212. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Kato, S. Analysis of urban heat-island effect using ASTER and ETM+ Data: Separation of anthropogenic heat discharge and natural heat radiation from sensible heat flux. Remote Sens. Environ. 2005, 99, 44–54. [Google Scholar]
- Frey, C.M.; Rigo, G.; Parlow, E. Urban radiation balance of two coastal cities in a hot and dry environment. Int. J. Remote Sens. 2007, 28, 2695–2712. [Google Scholar] [CrossRef]
- Stoll, M.J.; Brazel, A.J. Surface-air temperature relationship in the urban environment of Phoenix, Arizona. Phys. Geogr. 1992, 13, 160–179. [Google Scholar]
- Adderley, C.; Christen, A.; Voogt, J.A. The effect of radiometer placement and view on inferred directional and hemispheric radiometric temperatures of an urban canopy. Atmos. Meas. Tech. 2015, 8, 1891–1933. [Google Scholar] [CrossRef]
- Voogt, J.A.; Oke, T.R. Radiometric temperatures of urban canyon walls obtained from vehicle traverses. Theor. Appl. Climatol. 1998, 60, 199–217. [Google Scholar] [CrossRef]
- Voogt, J.A.; Oke, T.R. Effects of urban surface geometry on remotely-sensed surface temperature. Int. J. Remote Sens. 1998, 19, 895–920. [Google Scholar] [CrossRef]
- Rotach, M.W.; Vogt, R.; Bernhofer, C.; Batchvarova, E.; Christen, A.; Clappier, A.; Feddersen, B.; Gryning, S.E.; Martucci, G.; Mayer, H.; et al. BUBBLE—An Urban Boundary Layer Meteorology Project. Theor. Appl. Climatol. 2005, 81, 231–261. [Google Scholar] [CrossRef]
- Leroyer, S.; Bélair, S.; Mailhot, J.; Strachan, I.B. Microscale numerical prediction over Montreal with the Canadian external urban modeling system. J. Appl. Meteorol. Climatol. 2011, 50, 2410–2428. [Google Scholar] [CrossRef]
- Berk, A.; Bernstein, L.S.; Robertson, D.C. MODTRAN: A Moderate Resolution Model for LOWTRAN7; Technical Report GL-TR-89-0122; United States Air Force: Hanscom Air Force Base, Middlesex County, MA, USA, 1987. [Google Scholar]
- Norman, J.M.; Becker, F. Terminology in thermal infrared remote sensing of natural surfaces. Agric. For. Meteorol. 1995, 77, 153–166. [Google Scholar] [CrossRef]
- Meier, F.; Scherer, D.; Richters, J.; Christen, A. Atmospheric correction of thermal-infrared imagery of the 3-D urban environment acquired in oblique viewing geometry. Atmos. Meas. Tech. 2011, 4, 909–922. [Google Scholar] [CrossRef]
- Kotani, A.; Sugita, M. Concise formulae for the atmospheric correction of hemispherical thermal radiation measured near the ground surface. Water Resour. Res. 2009, 45, 1–7. [Google Scholar] [CrossRef]
- Kneizys, F.X.; Anderson, G.P.; Shettle, E.P.; Gallery, W.O.; Abreu, L.W.; Selby, J.E.A.; Chetwynd, J.H.; Clough, S.A. Users Guide to LOWTRAN 7; Technical Report AFGL-TR-88-0177; Air Force Geophysics Laboratory: Bedford, MA, USA, 1988. [Google Scholar]
- Grimmond, S.; Oke, T.R. Aerodynamic Properties of Urban Areas Derived from Analysis of Surface Form. J. Appl. Meteorol. 1999, 38, 1262–1292. [Google Scholar] [CrossRef]
- Hamdi, R.; Schayes, G. Validation of the Martilli’s Urban Boundary Layer Scheme with measurements from two mid-latitude European cities. Atmos. Chem. Phys. Discuss. 2005, 5, 4257–4289. [Google Scholar] [CrossRef]
- Mauree, D.; Blond, N.; Kohler, M.; Clappier, A. On the Coherence in the Boundary Layer: Development of a Canopy Interface Model. Front. Earth Sci. 2017, 4, 1–12. [Google Scholar] [CrossRef]
- Soux, A.; Voogt, J.A.; Oke, T.R. A model to calculate what a remote sensor ‘sees’ of an urban surface. Bound.-Layer Meteorol. 2004, 111, 109–132. [Google Scholar] [CrossRef]
- Oke, T.R. Boundary Layer Climates; Routledge Books: Abingdon, UK, 1987; pp. 1–435. [Google Scholar]
- Kantor, A.J.; Cole, A.E. Mid-latitude atmospheres, winter and summer. Geofis. Pura Appl. 1962, 53, 171–188. [Google Scholar] [CrossRef]
- Allen, M.A. A Method for Hemispherical Ground Based Remote Sensing of Urban Surface Temperatures. Master’s Thesis, University of Western Ontario, London, ON, Canada, 2017. [Google Scholar]
- Gastellu-Etchegorry, J.P.; Demarez, V.; Pinel, V.; Zagolski, F. Modeling radiative transfer in heterogeneous 3-D vegetation canopies. Remote Sens. Environ. 1996, 58, 131–156. [Google Scholar] [CrossRef]
- Buehler, S.A.; Eriksson, P.; Kuhn, T.; von Engeln, A.; Verdes, C. ARTS, the atmospheric radiative transfer simulator. J. Quant. Spectrosc. Radiat. Transf. 2005, 91, 65–93. [Google Scholar] [CrossRef]
- Willmott, C.J.; Ackleson, S.G.; Davis, R.E.; Feddema, J.J.; Klink, K.M.; Legates, D.R.; O’Donnell, J.; Rowe, C.M. Statistics for the evaluation and comparison of models. J. Geophys. Res. 1985, 90, 8995. [Google Scholar] [CrossRef]
- Willmott, C.J.; Robeson, S.M.; Matsuura, K. A refined index of model performance. Int. J. Climatol. 2012, 32, 2088–2094. [Google Scholar] [CrossRef]
- Hoch, S. Radiative Flux Divergence in the Surface Boundary Layer from Observational and Model Perspectives. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 2005. [Google Scholar]
- Hoch, S.; Calanca, P.; Philipona, R.; Ohmura, A. Year-round observation of longwave radiative flux divergence in Greenland. J. Appl. Meteorol. Climatol. 2007, 46, 1469–1479. [Google Scholar] [CrossRef]
- Nakamura, Y.; Oke, T.R. Wind, temperature and stability conditions in an east-west oriented urban canyon. Atmos. Environ. 1988, 22, 2691–2700. [Google Scholar] [CrossRef]
- Voogt, J.A.; Oke, T.R. Thermal remote sensing of urban climates. Remote Sens. Environ. 2003, 86, 370–384. [Google Scholar] [CrossRef]
- Imhoff, M.L.; Zhang, P.; Wolfe, R.E.; Bounoua, L. Remote sensing of the urban heat island effect across biomes in the continental USA. Remote Sens. Environ. 2010, 114, 504–513. [Google Scholar] [CrossRef]
- Streutker, D. Satellite-measured growth of the urban heat island of Houston, Texas. Remote Sens. Environ. 2003, 85, 282–289. [Google Scholar] [CrossRef]
- Stewart, I.D.; Oke, T.R. Local climate zones for urban temperature studies. Bull. Am. Meteorol. Soc. 2012, 93, 1879–1900. [Google Scholar] [CrossRef]
- Roberts, S. Three-Dimensional Radiation Flux Source Areas in Urban Areas. Ph.D. Thesis, University of British Columbia, Vancouver, BC, Canada, 2010. [Google Scholar]






| Site | Location | Morphological | Meteorological Variables | Radiation |
|---|---|---|---|---|
| Height | Characteristics 1 | [No of Levels] 2 | [No of Levels] 3 | |
| Basel Sperrstrasse | 47.57 N | = 14.6 | Tair [7] | Lup [3] |
| Urban street canyon | 7.60 E | = 6.9 | H [7] | Ldown [5] |
| Local Climate Zone: 2 | 255 a.s.l. | H/W = 1.0 | WV [12] | Kup [2] |
| = 1.92 | WD [1] | Kup [2] | ||
| = 0.54 | P [1] | |||
| = 11.0% |
| Road | NNW | SSE | NNW | SSE | |
|---|---|---|---|---|---|
| Roof | Roof | Wall | Wall | ||
| Complete (Tcomp) | 0.36 | 0.16 | 0.16 | 0.16 | 0.16 |
| Nadir (Tplan) | 0.46 | 0.27 | 0.27 | 0.00 | 0.00 |
| Statistic | Parameterization |
|---|---|
| Slope | 1.058 |
| Intercept, () | −1.488 |
| R2 | 0.991 |
| MAE, () | 0.607 |
| RMSE, () | 0.757 |
| RMSEs, () | 0.476 |
| RMSEu, () | 0.588 |
| d, agreement index | 0.998 |
| Statistic | 10 m Flux | 30 m Flux | Divergence |
|---|---|---|---|
| Slope | 1.002 | 1.011 | 0.792 |
| Intercept, () | 0.422 | −3.560 | −0.583 |
| R2 | 0.995 | 0.996 | 0.863 |
| MAE, () | 1.781 | 1.325 | 1.191 |
| RMSE, () | 2.204 | 1.690 | 1.423 |
| RMSEs, () | 1.444 | 0.851 | 1.028 |
| RMSEu, () | 1.666 | 1.460 | 0.985 |
| d, agreement index | 0.999 | 0.999 | 0.959 |
| Temiss, | , % | Temiss, | , % |
|---|---|---|---|
| 260 | 48.3 | 295 | 49.6 |
| 265 | 48.5 | 300 | 49.7 |
| 270 | 48.7 | 305 | 50.0 |
| 275 | 48.9 | 310 | 50.1 |
| 280 | 49.1 | 315 | 50.3 |
| 285 | 49.3 | 320 | 50.4 |
| 290 | 49.4 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Allen, M.A.; Voogt, J.A.; Christen, A. Time-Continuous Hemispherical Urban Surface Temperatures. Remote Sens. 2018, 10, 3. https://doi.org/10.3390/rs10010003
Allen MA, Voogt JA, Christen A. Time-Continuous Hemispherical Urban Surface Temperatures. Remote Sensing. 2018; 10(1):3. https://doi.org/10.3390/rs10010003
Chicago/Turabian StyleAllen, Michael A., James A. Voogt, and Andreas Christen. 2018. "Time-Continuous Hemispherical Urban Surface Temperatures" Remote Sensing 10, no. 1: 3. https://doi.org/10.3390/rs10010003
APA StyleAllen, M. A., Voogt, J. A., & Christen, A. (2018). Time-Continuous Hemispherical Urban Surface Temperatures. Remote Sensing, 10(1), 3. https://doi.org/10.3390/rs10010003





