Integrated Proactive Control Model for Energy Efficiency Processes in Facilities Management: Applying Dynamic Exponential Smoothing Optimization
Abstract
1. Introduction
2. Literature Review
2.1. Optimization Approaches for System Efficiency in Sustainable Facilities Management
2.2. Algorithms of Model Predictive Control
3. Methodology
3.1. Predicting Temperature Changes: Forecasting Model Using Exponential Smoothing Method
3.1.1. Single ESM Algorithm and Temperature Prediction
3.1.2. Double ESM Algorithm and Temperature Prediction
3.1.3. Triple ESM Algorithm and Temperature Prediction
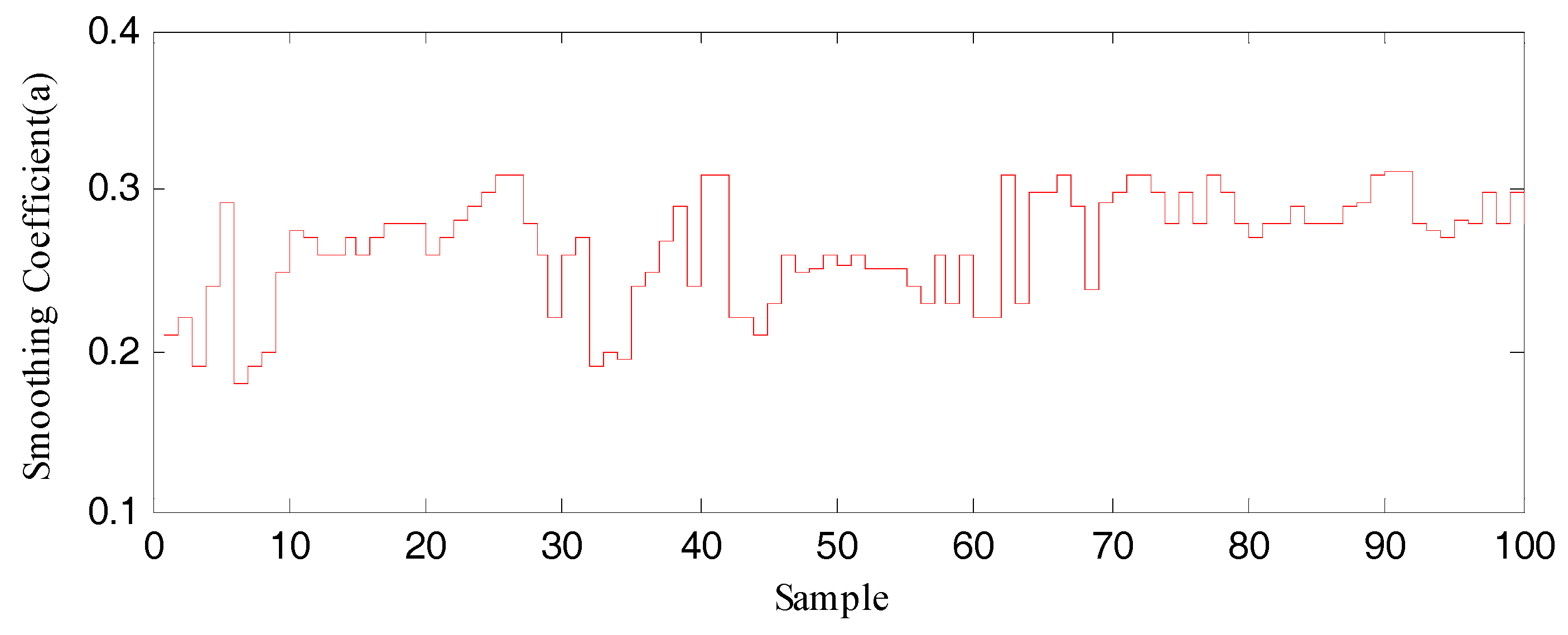
3.2. Dynamic Exponential Smoothing Optimization Algorithm
- For the values in the time series starting at a point of time , calculate the correlation coefficient of , where , and is the size of the series . The constant parameter M is the modified length of the time series for correlation calculation. It is used to define the length of the time series. The calculation of M is based on empirical experiments or observations [49,52].
- Calculate the percentages of , in the number of M.
- Depending on whether the percentage of falls within the confidence interval and distribution in the region , determine the stability of temperature time series.
- Traverse each smoothing coefficient within a specific range , to calculate the . When a value of makes , the value is selected and the iteration calculation stops.
- If for all the in the range, the algorithm finds a smoothing coefficient which minimizes the in the range. The corresponding is used as the target value.
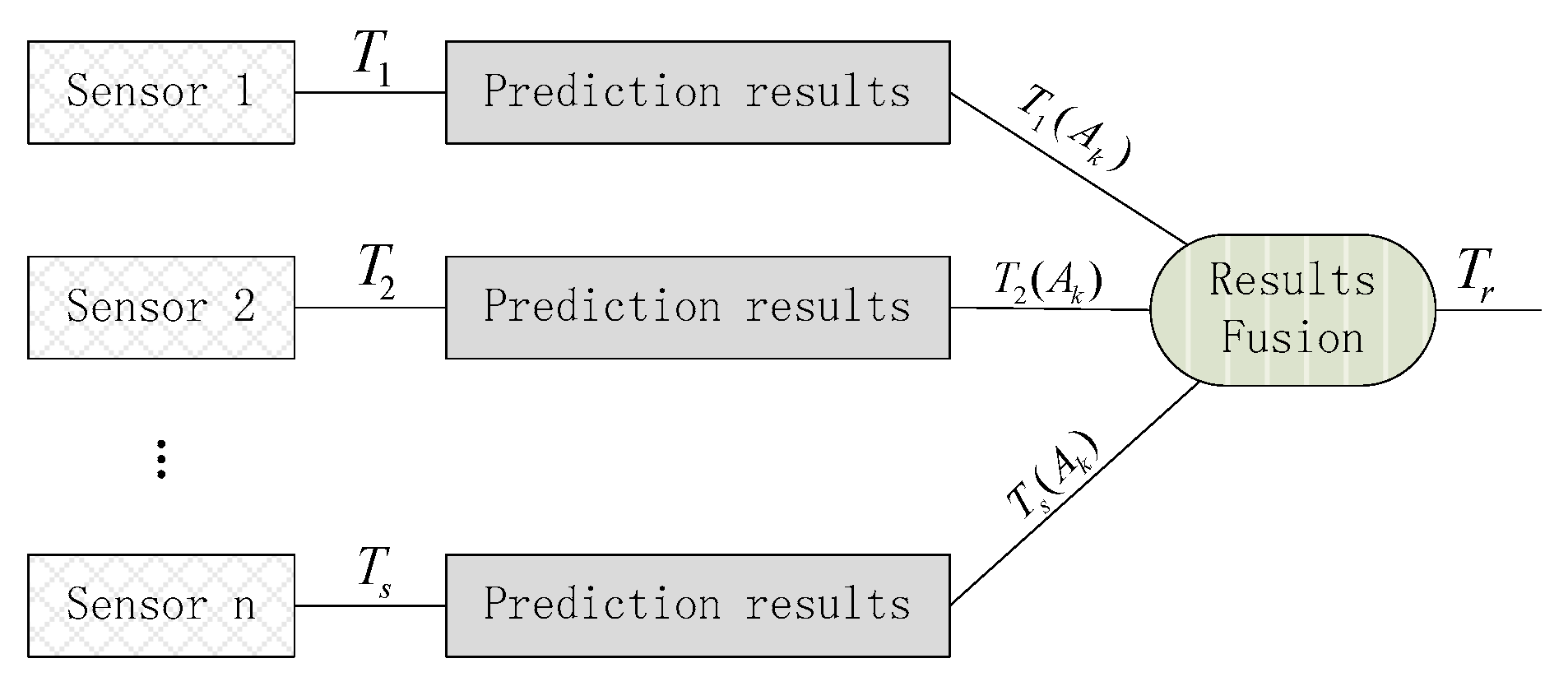
3.3. System Verification: Prediction Model Using Multi-Source Data
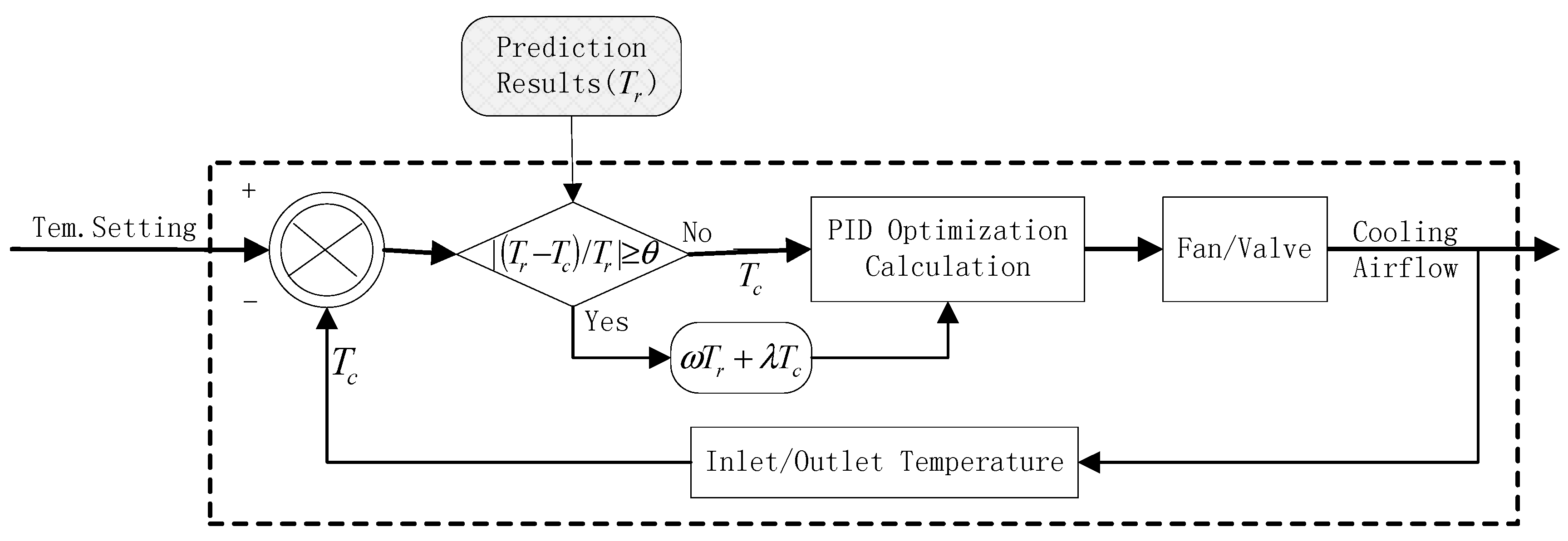
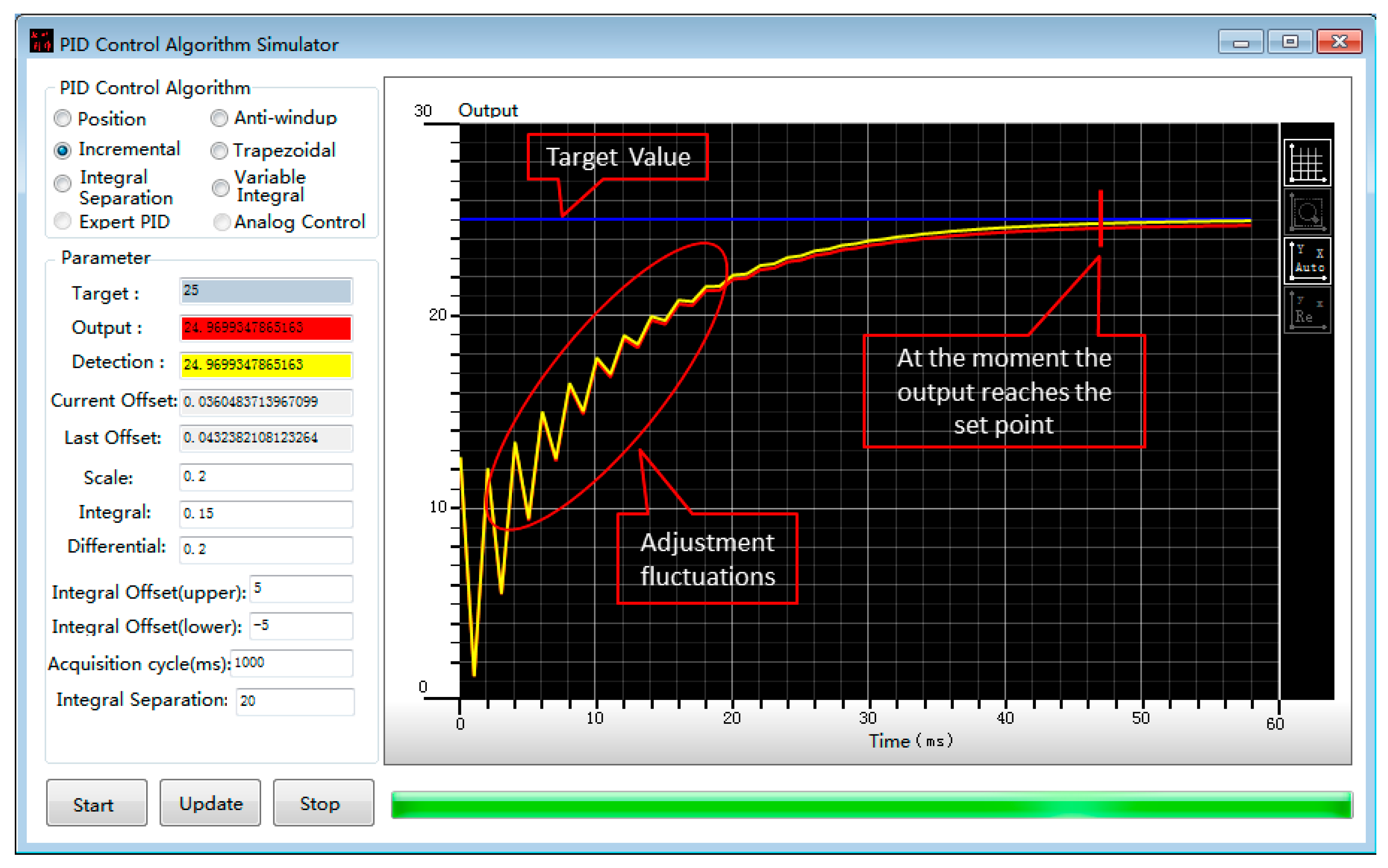
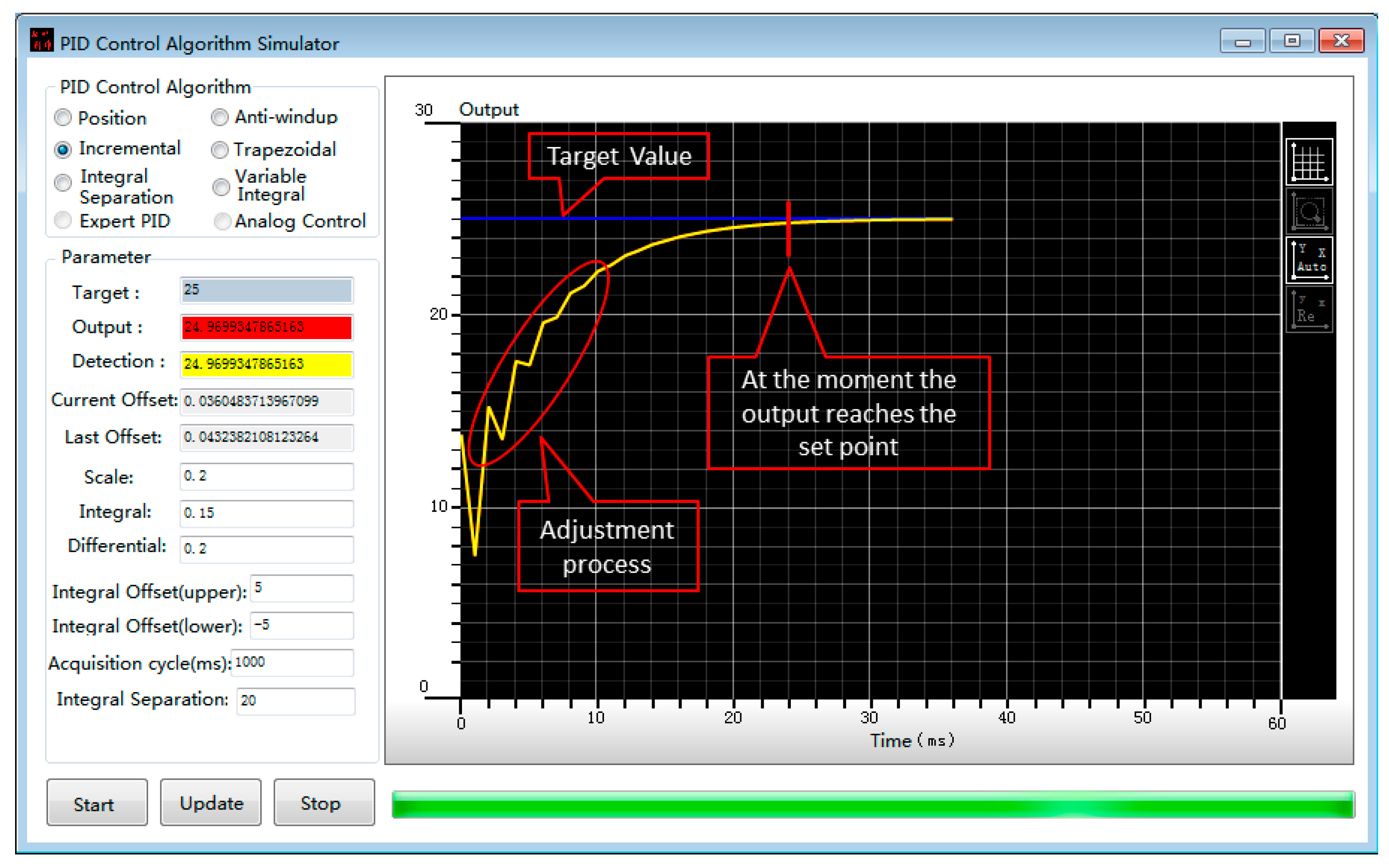
3.4. Proactive Control Method
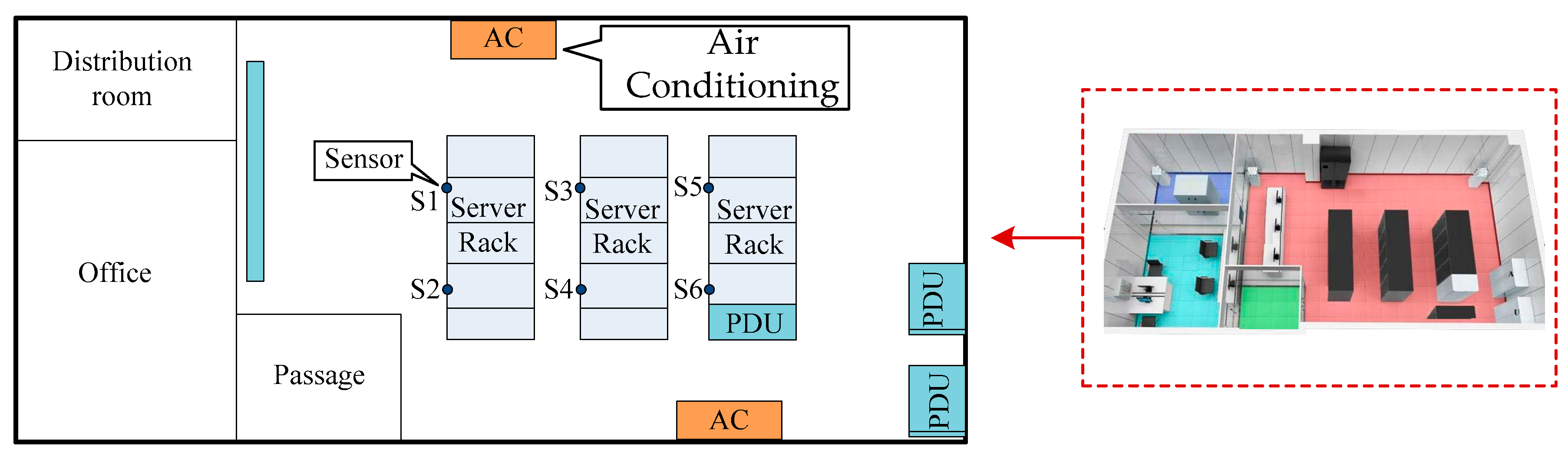
4. Experiment Design
- Use MATLAB 2014a simulation software (MathWorks, Natick, MA, USA) to analyze the effectiveness of temperature prediction algorithm.
- Analyze the effectiveness of the PCM-DTSP system for temperature simulation.
- Implement the controller program for air conditioners and use the optimized controller to test, analyze, and verify the results.
5. Result Analysis
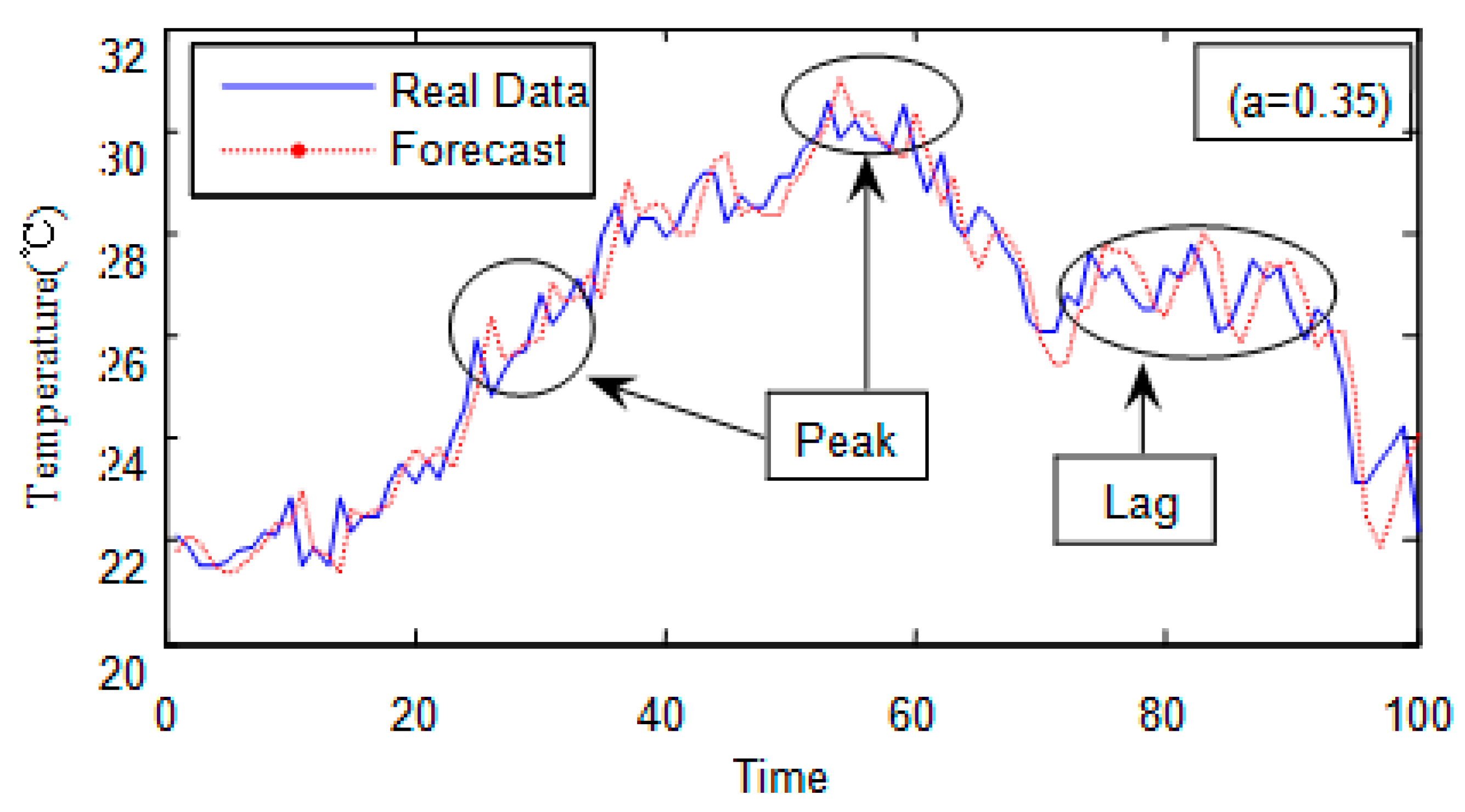
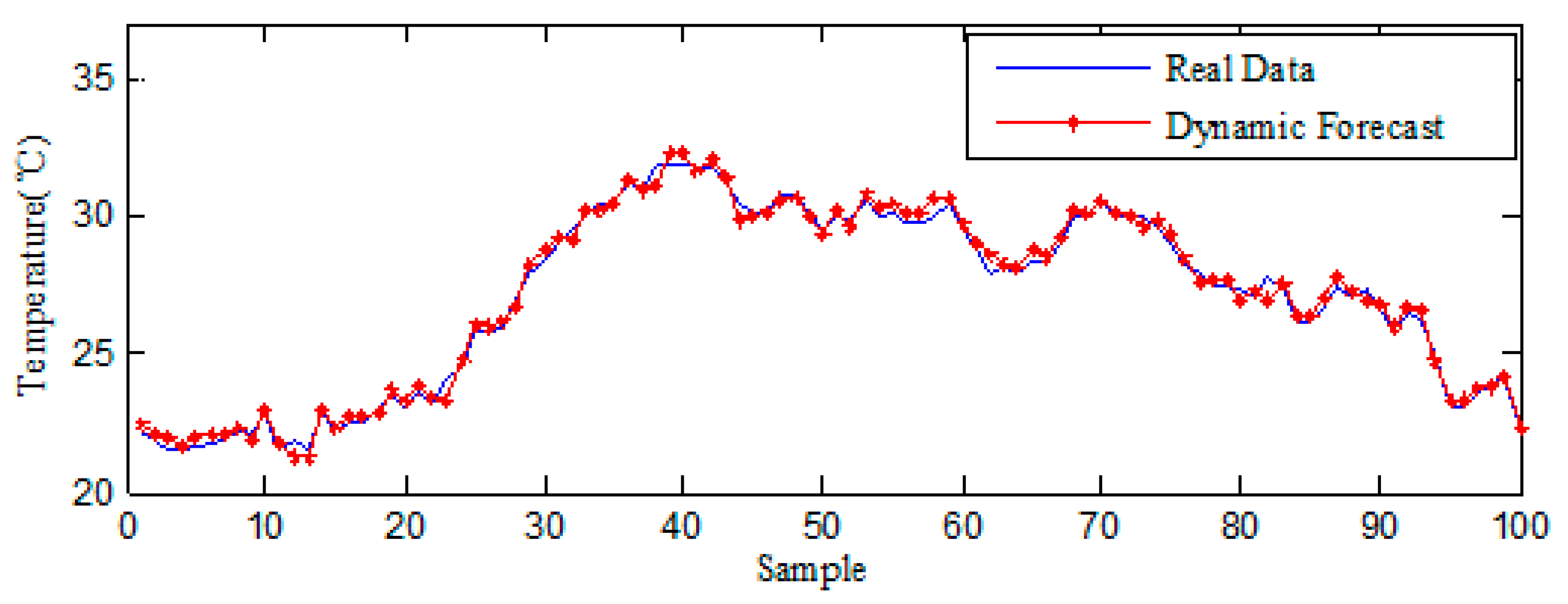
5.1. Analysis of Temperature Prediction Algorithm
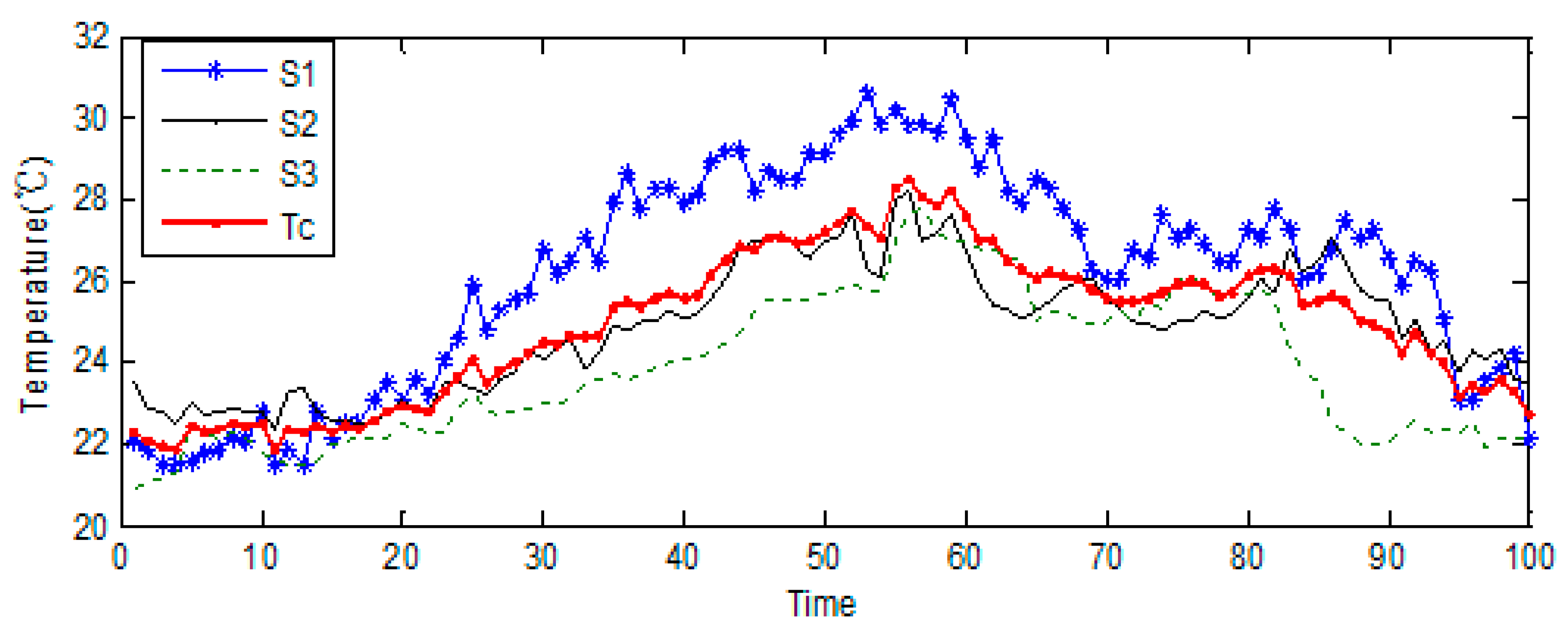
5.2. Integration of Predicted and Sensed Temperatures
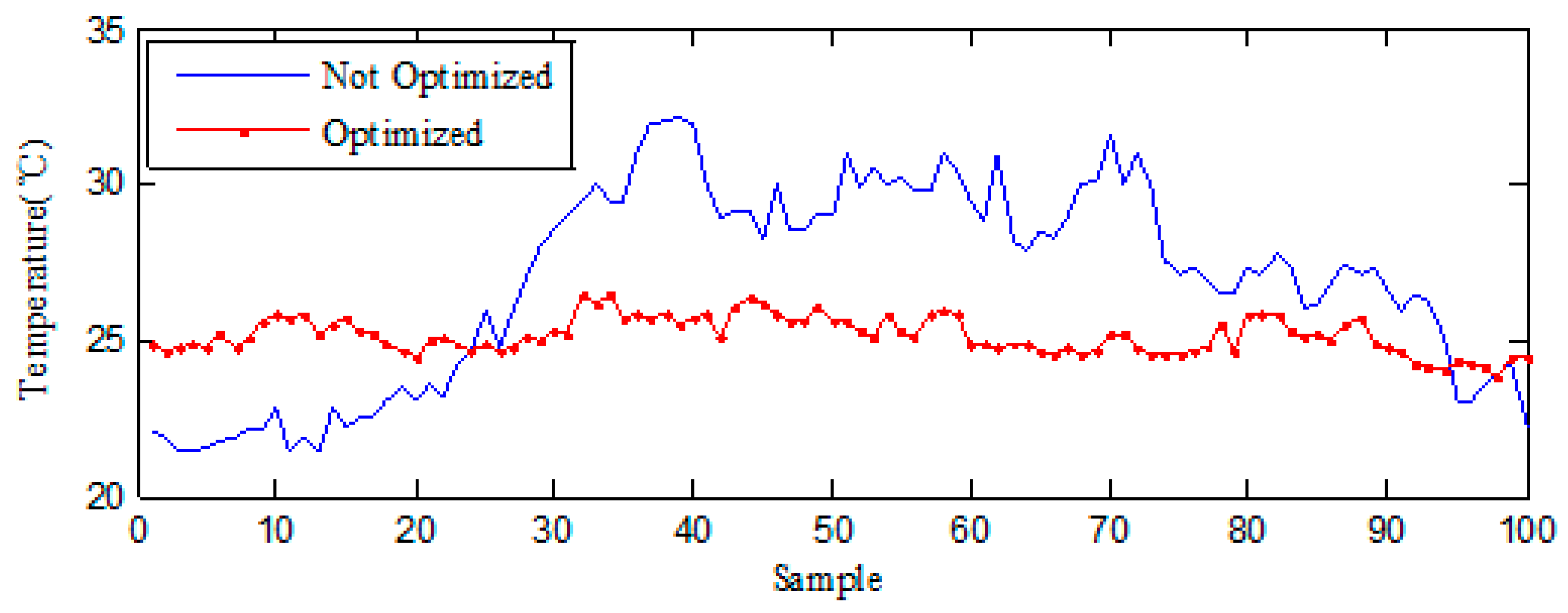
5.3. Statistical Analysis of Cooling Optimization Based on MPC
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
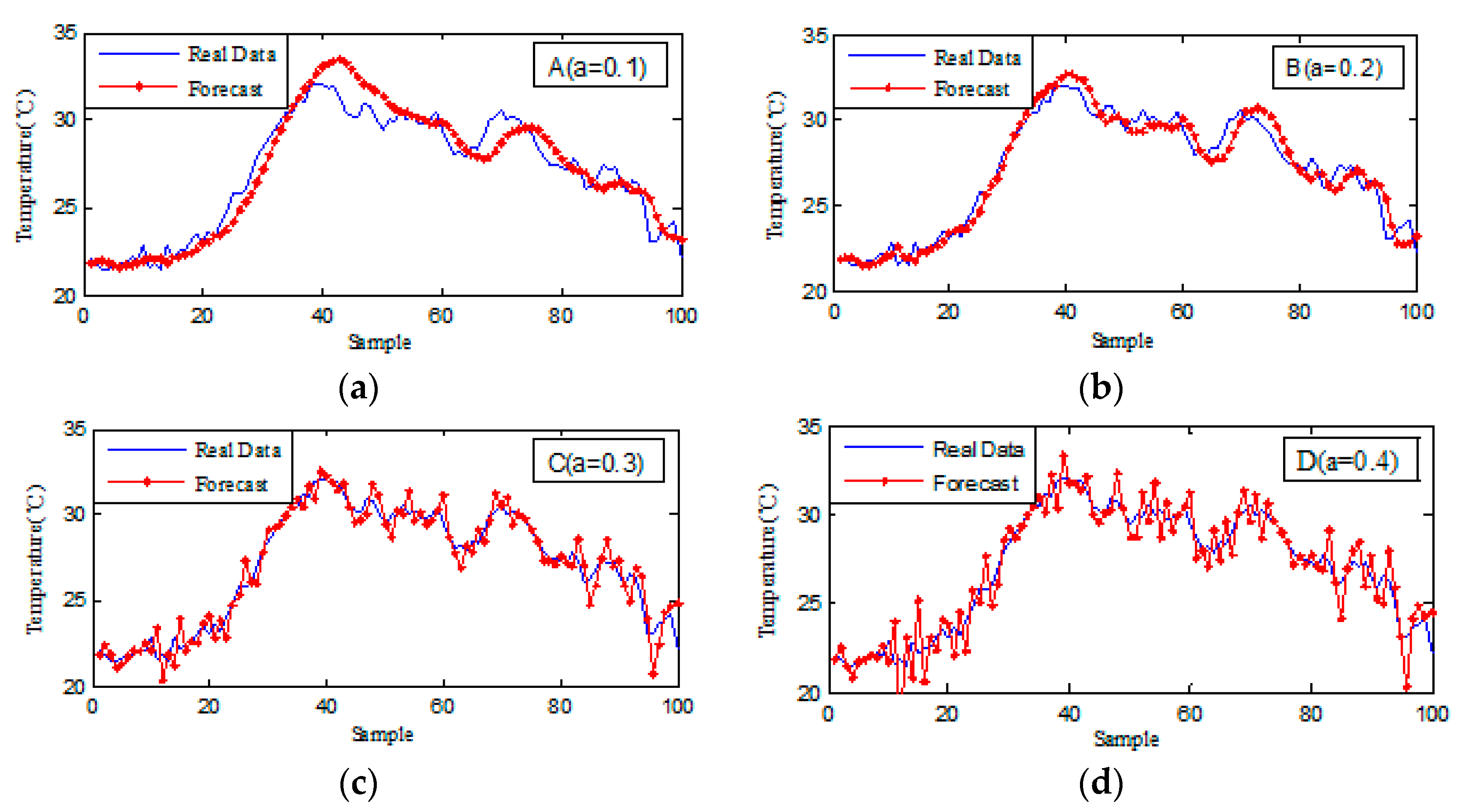
- When the smoothing coefficient , as shown in Figure A1a, the static exponential smoothing method can only predict the overall trend of the temperature changes. However, it cannot accurately predict the occurrences of sudden changes in temperatures. The deviations between the predicted results and the actual values are significant. Using the predicted results of this parameter to control cooling systems would lead to serious shortage of refrigeration or excessive cooling supply at a local area in a certain time range.
- When the smoothing coefficient , as shown in Figure A1b, relative to the situation when the smoothing coefficient , the accuracy of the forecast has greatly improved. The predicted results can reflect local variations of the temperatures. However, it has obvious lags between the predicted results and the actual data. It lacks sensitivity to temperature changes. Using this result to control cooling systems would cause local temperatures to be overheated or undercooled.
- When the smoothing coefficient , as shown in Figure A1c, the accuracy of the prediction is greatly improved. The prediction results can reflect local temperature variations. However, it has lags as well. If we use this result to control the cooling systems, it would create uneven cooling situations and waste energy consumption.
- When the smoothing coefficient , as shown in Figure A1d, the prediction results have strong jitters, where the peak values of the predicted results exceed the actual detections. If we follow these prediction results, it would exacerbate the phenomenon that the temperature is locally overheated or undercooled. It has a negative impact on the temperature stability. However, the sensitivity of the prediction algorithm is improved compared to the previous parameters.
References
- Gann, D.M.; Salter, A.J. Innovation in project-based, service-enhanced firms: The construction of complex products and systems. Res. Policy 2000, 29, 955–972. [Google Scholar] [CrossRef]
- Barrett, P. Achieving strategic facilities management through strong relationships. Facilities 2000, 18, 421–426. [Google Scholar] [CrossRef]
- Roper, K.O.; Payant, R.P. The Facility Management Handbook; AMACOM Div American Mgmt Assn: New York, NY, USA, 2014. [Google Scholar]
- Stark, J. Product lifecycle management. In Product Lifecycle Management (Volume 1); Springer: Berlin, Germany, 2015; pp. 1–29. [Google Scholar]
- Atkin, B.; Brooks, A. Total Facility Management; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Smith, L.G. Impact Assessment and Sustainable Resource Management; Routledge: Abingdon, UK, 2014. [Google Scholar]
- Higman, S. The Sustainable Forestry Handbook: A Practical Guide for Tropical Forest Managers on Implementing New Standards; Earthscan: London, UK, 2013. [Google Scholar]
- Shaikh, P.H.; Nor, N.B.M.; Nallagownden, P.; Elamvazuthi, I.; Ibrahim, T. A review on optimized control systems for building energy and comfort management of smart sustainable buildings. Renew. Sustain. Energy Rev. 2014, 34, 409–429. [Google Scholar] [CrossRef]
- Sherwin, D. A review of overall models for maintenance management. J. Qual. Maint. Eng. 2000, 6, 138–164. [Google Scholar] [CrossRef]
- Riley, D.R.; Varadan, P.; James, J.S.; Thomas, H.R. Benefit-cost metrics for design coordination of mechanical, electrical, and plumbing systems in multistory buildings. J. Constr. Eng. Manag. 2005, 131, 877–889. [Google Scholar] [CrossRef]
- Pérez-Lombard, L.; Ortiz, J.; Pout, C. A review on buildings energy consumption information. Energy Build. 2008, 40, 394–398. [Google Scholar] [CrossRef]
- Fantozzi, F.; Leccese, F.; Salvadori, G.; Rocca, M.; Garofalo, M. Led lighting for indoor sports facilities: Can its use be considered as sustainable solution from a techno-economic standpoint? Sustainability 2016, 8, 618. [Google Scholar] [CrossRef]
- Dekker, R. Applications of maintenance optimization models: A review and analysis. Reliab. Eng. Syst. Saf. 1996, 51, 229–240. [Google Scholar] [CrossRef]
- Márquez, A.C.; León, P.; Fernández, J.; Márquez, C.P.; Campos, M.L. The maintenance management framework: A practical view to maintenance management. J. Qual. Maint. Eng. 2009, 15, 167–178. [Google Scholar] [CrossRef]
- Avci, M.; Erkoc, M.; Rahmani, A.; Asfour, S. Model predictive hvac load control in buildings using real-time electricity pricing. Energy Build. 2013, 60, 199–209. [Google Scholar] [CrossRef]
- Ahuja, N.; Rego, C.; Ahuja, S.; Warner, M.; Docca, A. Data Center Efficiency with Higher Ambient Temperatures and Optimized Cooling Control. In Proceedings of the 2011 27th Annual IEEE Semiconductor Thermal Measurement and Management Symposium, Semiconductor Thermal Measurement and Management Symposium (SEMI-THERM), San Jose, CA, USA, 20–24 March 2011; p. 105. [Google Scholar]
- Durand-Estebe, B.; Le Bot, C.; Mancos, J.N.; Arquis, E. Simulation of a temperature adaptive control strategy for an iwse economizer in a data center. Appl. Energy 2014, 134, 45–56. [Google Scholar] [CrossRef]
- Ham, S.-W.; Park, J.-S.; Jeong, J.-W. Research paper: Optimum supply air temperature ranges of various air-side economizers in a modular data center. Appl. Therm. Eng. 2015, 77, 163–179. [Google Scholar] [CrossRef]
- Hiroshi, E.; Hiroyoshi, K.; Hiroyuki, F.; Toshio, S.; Takashi, H.; Masao, K. Cooperative control architecture of fan-less servers and fresh-air cooling in container servers for low power operation. ACM Oper. Syst. Rev. 2014, 48, 34. [Google Scholar]
- Huang, W.; Allen-Ware, M.; Carter, J.B.; Elnozahy, E.; Hamann, H.; Keller, T.; Lefurgy, C.; Li, J.; Rajamani, K.; Rubio, J. Tapo: Thermal-aware power optimization techniques for servers and data centers. In Proceedings of the 2011 International Green Computing Conference and Workshops Green Computing Conference and Workshops (IGCC), Orlando, FL, USA, 25–28 July 2011; p. 1. [Google Scholar]
- Nada, S.A.; Elfeky, K.E.; Attia, A.M.A. Experimental investigations of air conditioning solutions in high power density data centers using a scaled physical model. Études expérimentales des solutions de conditionnement d’air dans des centres de données à forte densité électrique en utilisant une maquette. Int. J. Refrig. 2016, 63, 87–99. [Google Scholar]
- Ogawa, M.; Endo, H.; Fukuda, H.; Kodama, H.; Sugimoto, T.; Horie, T.; Maruyama, T.; Kondo, M. Cooling control based on model predictive control using temperature information of it equipment for modular data center utilizing fresh-air. In Proceedings of the 2013 13th International Conference on Control, Automation & Systems (ICCAS 2013), Gwangju, Korea, 20–23 October 2013; p. 1815. [Google Scholar]
- Oxley, M.A. Online resource management in thermal and energy constrained heterogeneous high performance computing. In Proceedings of the 2016 IEEE 14th International Conference on Dependable, Autonomic and Secure Computing, 14th International Conference on Pervasive Intelligence and Computing, 2nd International Conference on Big Data Intelligence and Computing and Cyber Science and Technology Congress(DASC/PiCom/DataCom/CyberSciTech), Auckland, New Zealand, 8–12 August 2016; Pasricha, S., Ed.; IEEE: Piscataway, NJ, USA, 2016; p. 604. [Google Scholar]
- Smolaks, M. Research: Precision Cooling Expected to Boom in APAC; DatacenterDynamics: London, UK, 2017. [Google Scholar]
- Thota, P.K.; Dani, A.P.; Luh, P.B.; Gupta, S. Cooling load forecasting for chiller plants using similar day based wavelet neural networks. In Proceedings of the 2015 International Conference on Complex Systems Engineering (ICCSE), Storrs, CT, USA, 9–11 November 2015; p. 1. [Google Scholar]
- Zhou, R.; Bash, C.; Wang, Z.; McReynolds, A.; Christian, T.; Cader, T. Data center cooling efficiency improvement through localized and optimized cooling resources delivery. In Proceedings of the ASME 2012 International Mechanical Engineering Congress & Expositio, Houston, TX, USA, 9–15 November 2012. [Google Scholar]
- Geels, F.W. The multi-level perspective on sustainability transitions: Responses to seven criticisms. Environ. Innov. Soc. Trans. 2011, 1, 24–40. [Google Scholar] [CrossRef]
- Ioppolo, G.; Cucurachi, S.; Salomone, R.; Saija, G.; Shi, L. Sustainable local development and environmental governance: A strategic planning experience. Sustainability 2016, 8, 180. [Google Scholar] [CrossRef]
- Dounis, A.I.; Caraiscos, C. Advanced control systems engineering for energy and comfort management in a building environment—A review. Renew. Sustain. Energy Rev. 2009, 13, 1246–1261. [Google Scholar] [CrossRef]
- Wang, S.; Ma, Z. Supervisory and optimal control of building hvac systems: A review. HVAC&R Res. 2008, 14, 3–32. [Google Scholar]
- Afram, A.; Janabi-Sharifi, F. Theory and applications of hvac control systems—A review of model predictive control (MPC). Build. Environ. 2014, 72, 343–355. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, N.; Li, H.; Zhang, Y. Regression cloud models and their applications in energy consumption of data center. J. Electr. Comput. Eng. 2015, 2015, 143071. [Google Scholar] [CrossRef]
- Tarutani, Y.; Hashimoto, K.; Hasegawa, G.; Nakamura, Y.; Tamura, T.; Matsudax, K.; Matsuoka, M. Reducing power consumption in data center by predicting temperature distribution and air conditioner efficiency with machine learning. In Proceedings of the 2016 IEEE International Conference on Cloud Engineering (IC2E), Berlin, Germany, 4–8 April 2016; p. 226. [Google Scholar]
- Ahn, J.; Cho, S.; Chung, D.H. Analysis of energy and control efficiencies of fuzzy logic and artificial neural network technologies in the heating energy supply system responding to the changes of user demands. Appl. Energy 2017, 190, 222–231. [Google Scholar] [CrossRef]
- Zeigler, B.P.; Praehofer, H.; Kim, T.G. Theory of Modeling and Simulation: Integrating Discrete Event and Continuous Complex Dynamic Systems; Academic Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Pelzeter, A. Sustainability in facility management. In Proceedings of the Implementing Sustainability-Barriers and Chances, Book of Abstracts, sb13 Sustainable Building Conference, Munich, Germany, 24–16 April 2013; pp. 24–26. [Google Scholar]
- Doty, S.; Turner, W.C. Energy Management Handbook; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Dodrill, K. Demand Dispatch—Intelligent Demand for a More Efficient Grid; U.S. Department of Energy, National Energy Technology Laboratory Smart Grid Implementation Team: Morgantown, WV, USA, 2011.
- Paris, B.; Eynard, J.; Grieu, S.; Talbert, T.; Polit, M. Heating control schemes for energy management in buildings. Energy Build. 2010, 42, 1908–1917. [Google Scholar] [CrossRef]
- Arnold, M.; Andersson, G. Model predictive control of energy storage including uncertain forecasts. In Proceedings of the Power Systems Computation Conference (PSCC), Stockholm, Sweden, 22–26 August 2011; pp. 24–29. [Google Scholar]
- Li, X.; Wen, J. Review of building energy modeling for control and operation. Renew. Sustain. Energy Rev. 2014, 37, 517–537. [Google Scholar] [CrossRef]
- Li, X.; Wen, J.; Bai, E.-W. Developing a whole building cooling energy forecasting model for on-line operation optimization using proactive system identification. Appl. Energy 2016, 164, 69–88. [Google Scholar] [CrossRef]
- Ni, J.; Bai, X. A review of air conditioning energy performance in data centers. Renew. Sustain. Energy Rev. 2017, 67, 625–640. [Google Scholar] [CrossRef]
- Bilal, K.; Malik, S.U.R.; Khan, S.U.; Zomaya, A.Y. Trends and challenges in cloud datacenters. IEEE Cloud Comput. 2014, 1, 10–20. [Google Scholar] [CrossRef]
- Yin, X.; Sinopoli, B. Adaptive robust optimization for coordinated capacity and load control in data centers. In Proceedings of the 2014 IEEE 53rd Annual Conference on Decision and Control (CDC), Los Angeles, CA, USA, 15–17 December 2014; pp. 5674–5679. [Google Scholar]
- Clarke, D.W.; Mohtadi, C.; Tuffs, P. Generalized predictive control—Part I. The basic algorithm. Automatica 1987, 23, 137–148. [Google Scholar] [CrossRef]
- Kassmann, D.E.; Badgwell, T.A.; Hawkins, R.B. Robust steady-state target calculation for model predictive control. AIChE J. 2000, 46, 1007–1024. [Google Scholar] [CrossRef]
- Qin, S.J.; Badgwell, T.A. A survey of industrial model predictive control technology. Control Eng. Pract. 2003, 11, 733–764. [Google Scholar] [CrossRef]
- Montgomery, D.C.; Jennings, C.L.; Kulahci, M. Introduction to Time Series Analysis and Forecasting; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Xu, Y.; Chen, B.; Hu, Z. Research for multi-sensor data fusion based on huffman tree clustering algorithm in greenhouses. Int. J. Embed. Syst. 2016, 8, 34–38. [Google Scholar] [CrossRef]
- Ledolter, J.; Abraham, B. Some comments on the initialization of exponential smoothing. J. Forecast. 1984, 3, 79–84. [Google Scholar] [CrossRef]
- Yaffee, R.A.; McGee, M. An Introduction to Time Series Analysis and Forecasting: With Applications of Sas® and Spss®; Academic Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Levinson, N. The wiener (root mean square) error criterion in filter design and prediction. Stud. Appl. Math. 1946, 25, 261–278. [Google Scholar] [CrossRef]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Allen, D.M. Mean square error of prediction as a criterion for selecting variables. Technometrics 1971, 13, 469–475. [Google Scholar] [CrossRef]
- Cochrane, D.; Orcutt, G.H. Application of least squares regression to relationships containing auto-correlated error terms. J. Am. Stat. Assoc. 1949, 44, 32–61. [Google Scholar]

| Type | Example | Feature | Limitations |
|---|---|---|---|
| Optimize airflow organization of cooling systems | Ham et al. [18] | Modular building; closed cold/hot channels to arrange airflow. | Low efficiency. |
| Ogawa et al. [22] | Natural-air cooling systems to reduce energy consumption | Easily affected by exterior temperatures. | |
| Hiroshi et al. [19] | Cooling control method based on the predictions of the thermal management requirements at a modular building. | Depended excessively on the air temperature of external environment; Low efficiency. | |
| Reduction on redundant cooling supply | Oxley et al. [23] | Improvement of computer room air conditioners (CRAC) for heterogeneous high-performance systems under thermal and energy constraints | Static method, especially when using templates generated offline to assist the online resource manager to make thermal-aware decisions based on the incoming workload and state of the HPC facility. Not been tested by real-world data. |
| Ogawa et al. [22] and Durand-Estebe et al. [17] | Optimize the controls of fan speeds. | Only gives the optimized approximating linear manifold in the configuration space represented by the data. | |
| Thota et al. [25] | Forecast cooling loads for temperature control; Similar day selection, wavelet decomposition, and neural networks; Different sub-bands (frequency components) and training a separate neural network for each component; | Neural networks cannot be retrained. If users add data later, it is almost impossible to add to an existing network. | |
| Huang et al. [20] | Determine the set points of CRAC based on the utilization level of the building. Applied a feedback-control approach on fans to achieve a trade-off between leakage power in circuit and fan power. | Failed to minimize the overall energy consumption of the systems and fans. | |
| Zhou et al. [26] | Localized and optimized cooling resources. Adaptive vent tiles mounted on floor and control cooling provisions to reduce costs. | Did not consider the power consumption of fans. | |
| Yin and Sinopoli [45] | Coordinated service provision with thermal-load awareness in job scheduling. | Very limited consideration on the dynamic features of cooling systems. |
| Cooling Equipment | Group | Group |
|---|---|---|
| Associated Sensor | ||
| Sensor Weights | ||
| Associated Server |
| Collection Time | Sensor | The Predicted Value at Different Cycles | Sensor Prediction (from Equation (14)) | Group Prediction (from Equation (15)) | |||
|---|---|---|---|---|---|---|---|
| 12 March 2017 08:12:10 | 23.5; 0.4 | 23.7; 0.3 | 23.8; 0.2 | 23.8; 0.1 | 23.65 | 23.58 | |
| 24.1; 0.4 | 24.0; 0.3 | 23.9; 0.2 | 23.8; 0.1 | 24.0 | |||
| 22.9; 0.4 | 23.0; 0.3 | 23.0; 0.2 | 23.1; 0.1 | 22.97 | |||
| 12 March 2017 08:17:21 | 23.8; 0.4 | 23.8; 0.3 | 23.9; 0.2 | 24.0; 0.1 | 23.84 | 23.71 | |
| 24.1; 0.4 | 24.0; 0.3 | 23.8; 0.2 | 23.8; 0.1 | 23.98 | |||
| 23.2; 0.4 | 23.2; 0.3 | 23.3; 0.2 | 23.4; 0.1 | 23.24 | |||
| 12 March 2017 08:22:05 | 23.8; 0.4 | 23.9; 0.3 | 23.9; 0.2 | 24.0; 0.1 | 23.87 | 23.70 | |
| 23.9; 0.4 | 23.8; 0.3 | 23.8; 0.2 | 23.7; 0.1 | 23.83 | |||
| 23.3; 0.4 | 23.4; 0.3 | 23.5; 0.2 | 23.6; 0.1 | 23.4 | |||
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Temperature setting | 25 °C | Scale coefficient | 0.2 |
| Integral coefficient | 0.15 | Differential coefficient | 0.2 |
| Integral upper offset | 5 | Integral lower offset | −5 |
| Integral separation | 20 | Sampling period | 1000 ms |
| Optimization | Avg. Temp. (°C) | Max. Temp. (°C) | Min. Temp. (°C) |
|---|---|---|---|
| Before | 28.6 | 30.6 | 21.5 |
| After | 26.3 | 26.7 | 23.3 |
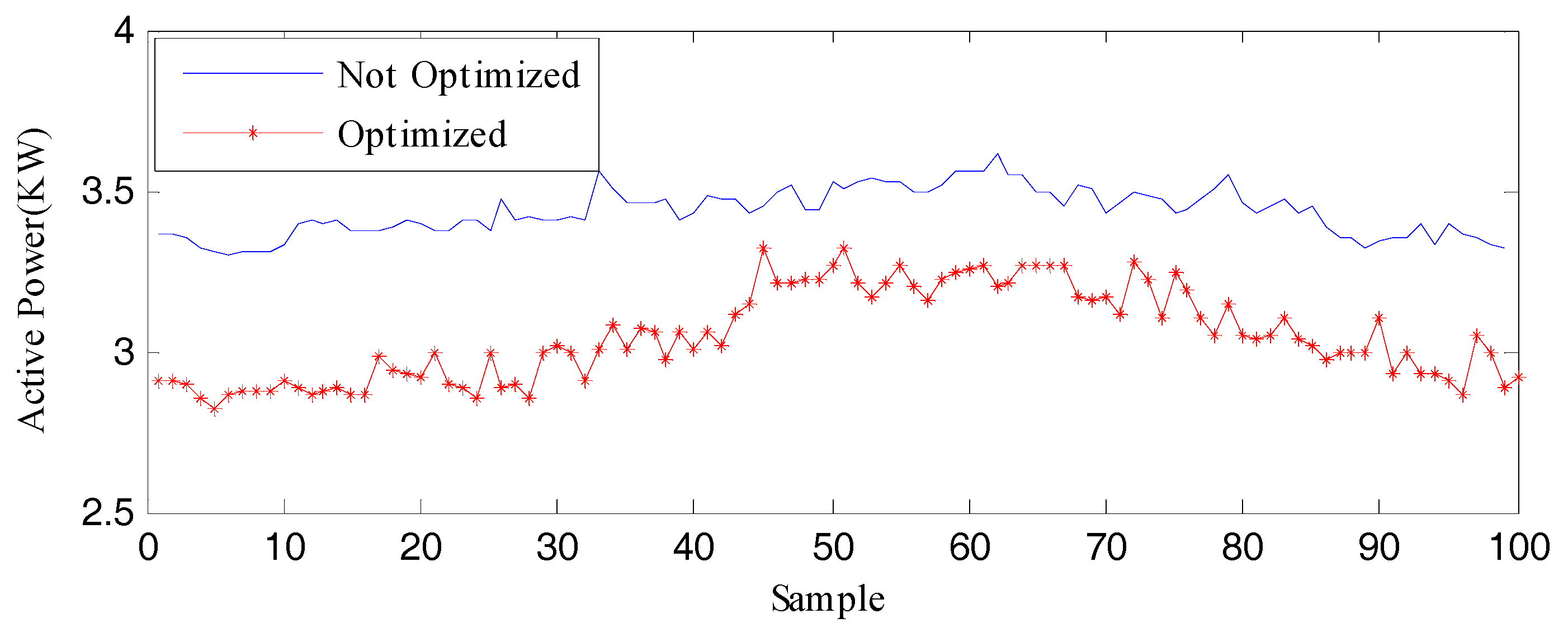
| Optimization | Rated Power (kw) | Avg. Power(kw) | Max. Power (kw) | Min. Power (kw) |
|---|---|---|---|---|
| Before | 3.56 | 3.43 | 3.48 | 3.39 |
| After | 3.56 | 3.26 | 3.31 | 2.85 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruan, S.; Xie, H.; Jiang, S. Integrated Proactive Control Model for Energy Efficiency Processes in Facilities Management: Applying Dynamic Exponential Smoothing Optimization. Sustainability 2017, 9, 1597. https://doi.org/10.3390/su9091597
Ruan S, Xie H, Jiang S. Integrated Proactive Control Model for Energy Efficiency Processes in Facilities Management: Applying Dynamic Exponential Smoothing Optimization. Sustainability. 2017; 9(9):1597. https://doi.org/10.3390/su9091597
Chicago/Turabian StyleRuan, Shunling, Haiyan Xie, and Song Jiang. 2017. "Integrated Proactive Control Model for Energy Efficiency Processes in Facilities Management: Applying Dynamic Exponential Smoothing Optimization" Sustainability 9, no. 9: 1597. https://doi.org/10.3390/su9091597
APA StyleRuan, S., Xie, H., & Jiang, S. (2017). Integrated Proactive Control Model for Energy Efficiency Processes in Facilities Management: Applying Dynamic Exponential Smoothing Optimization. Sustainability, 9(9), 1597. https://doi.org/10.3390/su9091597




