Estimating the Contribution of New Seed Cultivars to Increases in Crop Yields: A Case Study for Corn
Abstract
:1. Introduction
2. Materials and Methods
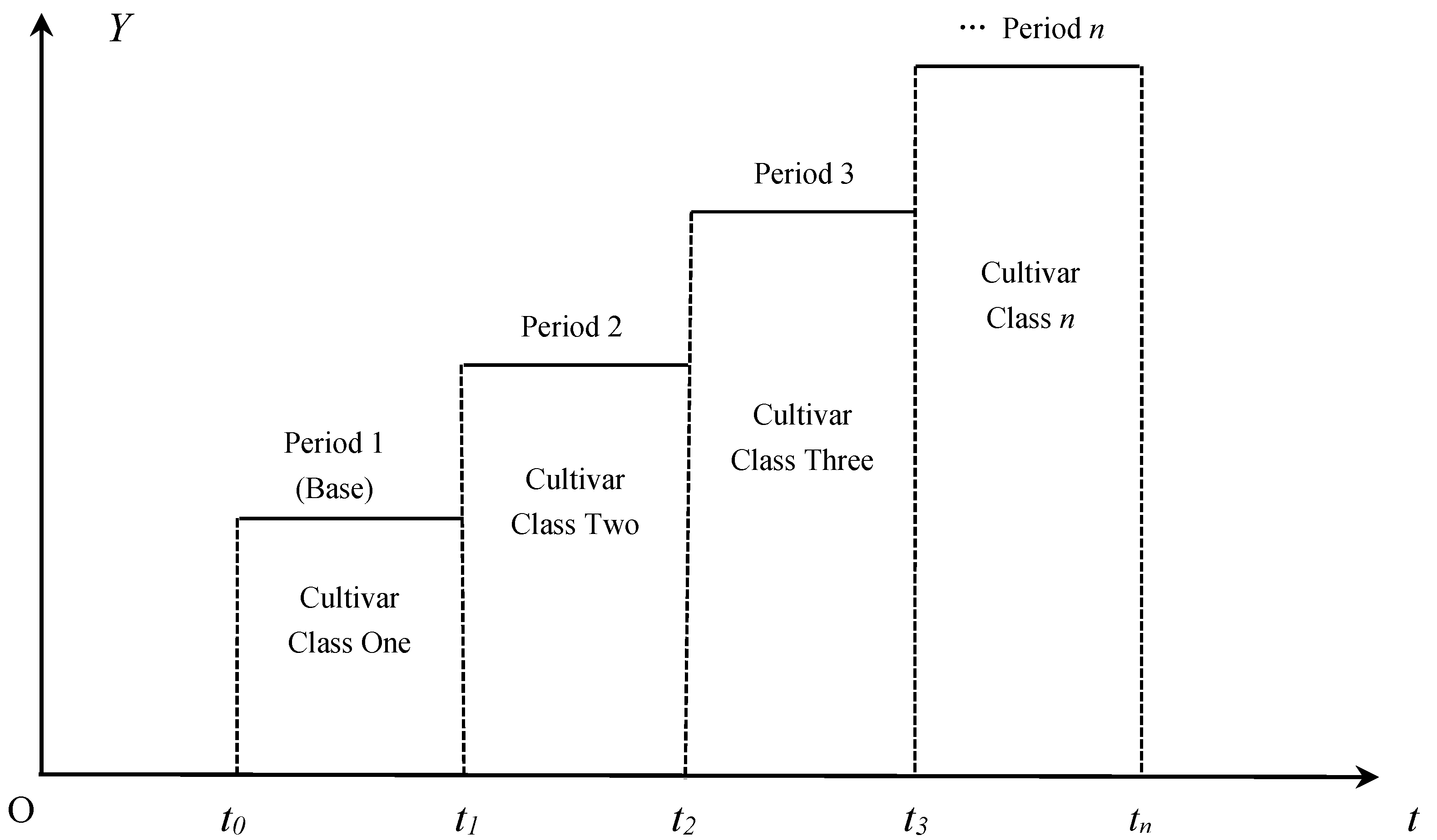
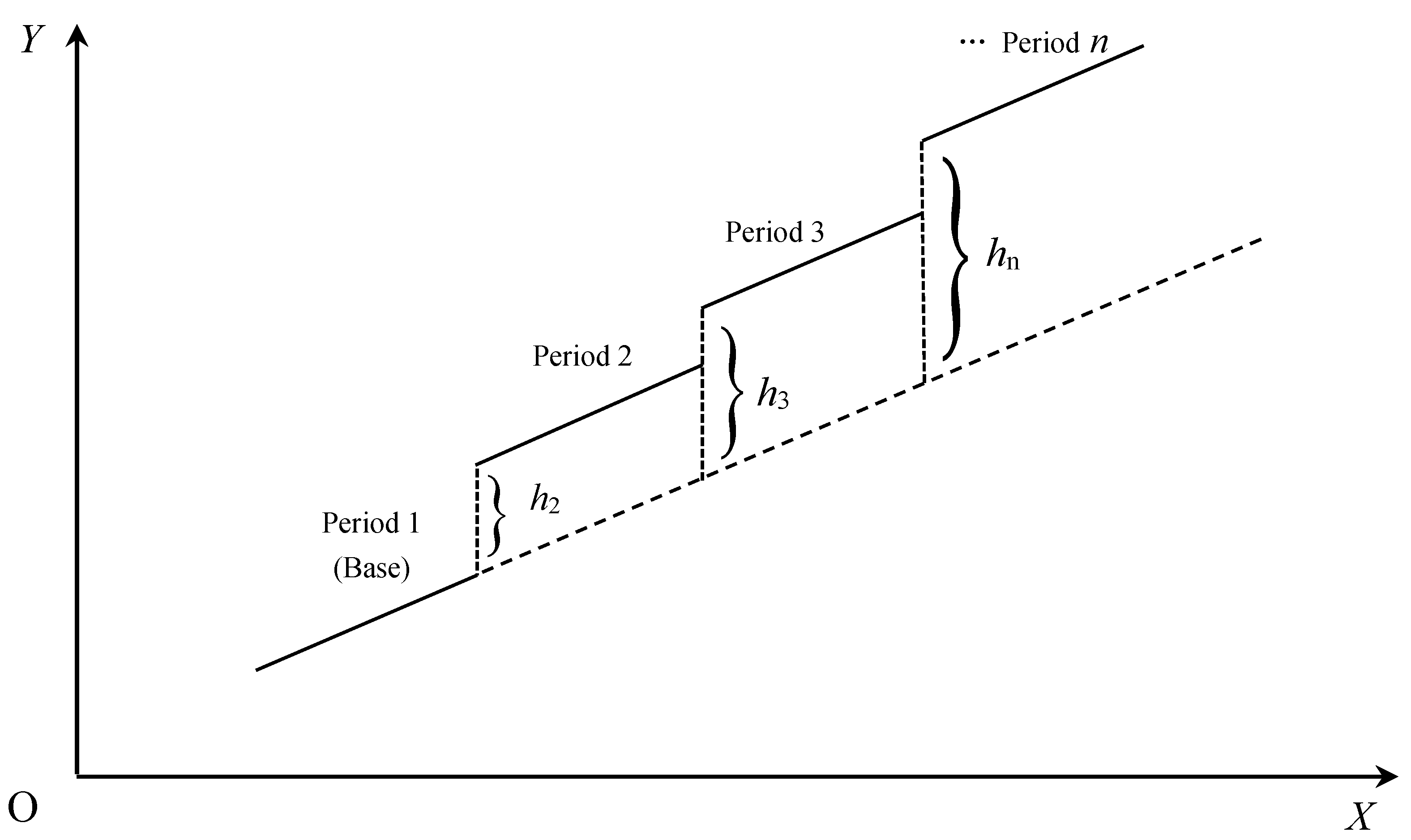
2.1. Methodology
2.2. Model Specification for Corn in China
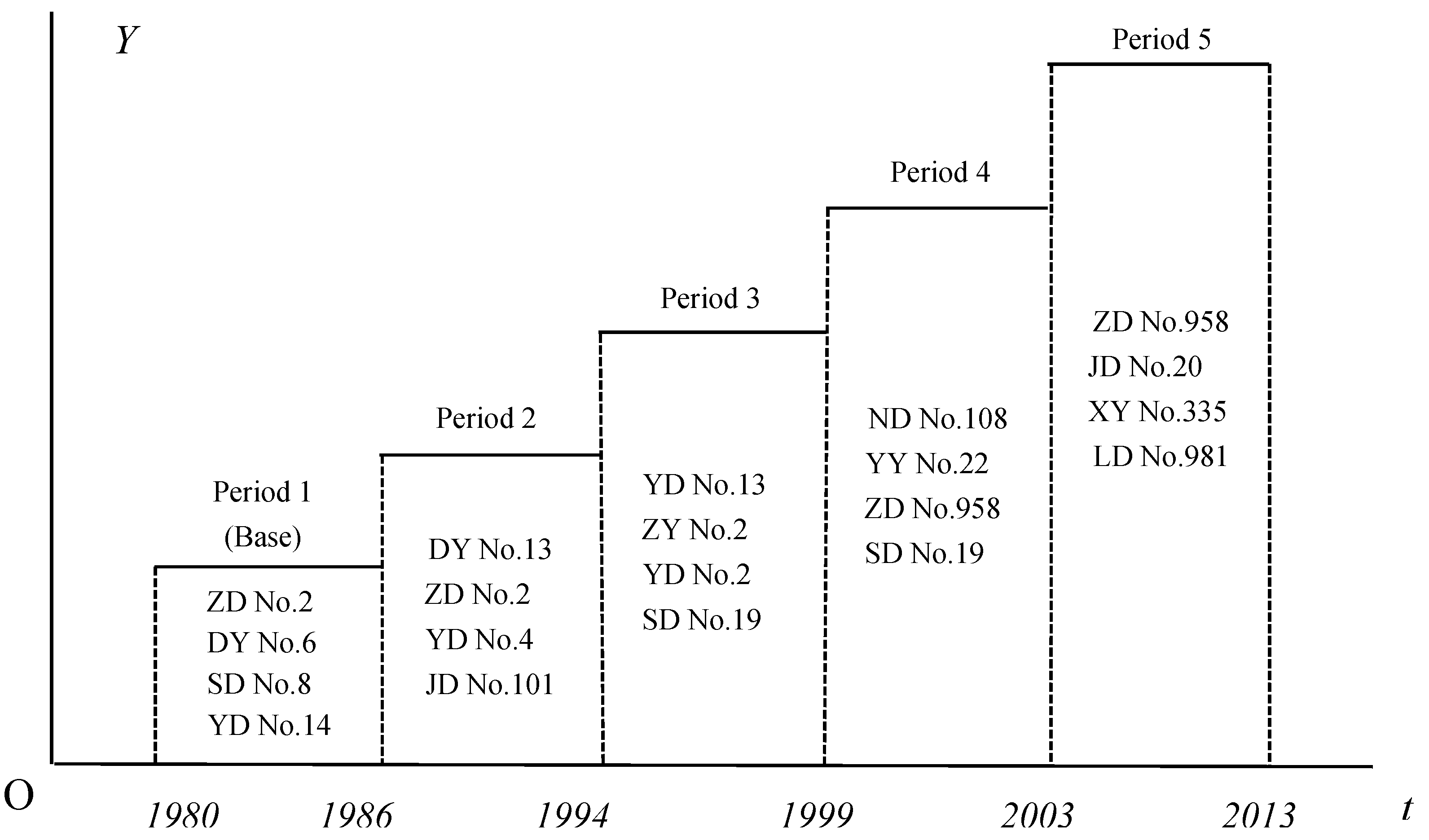
2.3. Data Sources
3. Results
3.1. Estimated Results
3.2. Contribution Calculation
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Zhao, Z.J.; Zhang, S.M. A quantitative analysis on factors driving agricultural technical progress. Issues Agric. Econ. 2005, s1, 70–75. [Google Scholar]
- Martin, K.L.; Hodgen, P.J.; Freeman, K.W.; Melchiori, R.; Arnall, D.B.; Teal, R.K.; Mullen, R.W.; Desta, K.; Phillips, S.B.; Solie, J.B.; et al. Plant-to-plant Variability in Corn Production. Agron. J. 2005, 97, 1603–1611. [Google Scholar] [CrossRef]
- Tokatlidis, I.S. Adaptation to density to optimize grain yield: Breeding implications. Euphytica 2017, 213, 92. [Google Scholar] [CrossRef]
- Wang, W.; Liao, Z. Experiment comparison for new late rice cultivars in Ningdu County in 2014. Seed World 2015, 8, 16–19. [Google Scholar]
- Liu, H.; Zhu, Y.; Feng, W. Study on the characteristics of the new maize cultivar Xinzhongyu 801 and its potentiality to increase maize yield. Seed 2015, 34, 111–114. [Google Scholar]
- Shi, Z.; Yang, Y.; Li, F.; Wang, Z.; Wang, H.; Lv, X. Study on yield increasing potential of Danyu 39. Seed 2010, 29, 72–74. [Google Scholar]
- Tian, H.; Guo, S.; Chen, L.; Zhou, T. The contribution of new cultivars to increasing rapeseed yield. Seed 2006, 25, 73–76. [Google Scholar]
- Feyerherm, A.M.; Paulsen, G.M.; Sebaugh, J.L. Contribution of genetic improvement to recent wheat yield increases in the USA. Agron. J. 1984, 76, 985–990. [Google Scholar] [CrossRef]
- Dalrymple, D.G. Development and Spread of Semidwarf Varieties of Wheat and Rice in the United States: An International Perspective; USDA Agricultural Economic Report No.455; U.S. Department of Agriculture, Economics, Statistics, and Cooperatives Service: Washington, DC, USA, 1980.
- Saaty, T.L. The Analytic Hierarchy Process; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- He, M.X.; He, C.F. Measuring technical change in agriculture: The Analytical Hierarchy Process method. J. Inn. Mong. Normal Univ. 1995, 2, 6–11. [Google Scholar]
- Tian, Z.; Jing, Q.; Dai, T.; Jiang, D.; Cao, W. Effects of genetic improvements on grain yield and agronomic traits of winter wheat in the Yangtze River Basin of China. Field Crops Res. 2011, 124, 417–425. [Google Scholar] [CrossRef]
- Cargnin, A.; Souza, M.A.D.; Fronza, V.; Fogaca, C.M. Genetic and environmental contributions to increased wheat yield in Minas Gerais, Brazil. Sci. Agric. 2009, 3, 317–322. [Google Scholar] [CrossRef]
- Duvick, D.N. Genetic progress in yield of United States maize (Zea mays L.). Maydica 2005, 50, 193–202. [Google Scholar]
- Duvick, D.N. The contribution of breeding to yield advances in maize (Zea mays L.). Adv. Agron. 2005, 86, 83–145. [Google Scholar]
- Ma, Z.Y.; Wu, Y.C. Contribution of rice genetic improvement to yield increase in China. Chin. J. Rice Sci. 2000, 14, 112–114. [Google Scholar]
- Wu, Y.C.; Ma, Z.Y.; Wang, D.Y.; Jiang, J. Contribution of maize improvement to yield increment in China. Acta Agron. Sin. 1998, 24, 595–599. [Google Scholar]
- Bell, M.A.; Fischer, R.A.; Byerlee, D.; Sayre, K. Genetic and agronomic contributions to yield gains: A case study for wheat. Field Crops Res. 1995, 44, 55–65. [Google Scholar] [CrossRef]
- Russell, W.A. Genetic improvement of maize yields. Adv. Agron. 1991, 46, 245–298. [Google Scholar]
- Feyerherm, A.M.; Kemp, K.E.; Paulsen, G.M. Genetic contribution to increased wheat yields in the USA between 1979 and 1984. Agron. J. 1989, 81, 242–245. [Google Scholar] [CrossRef]
- Feyerherm, A.M.; Paulsen, G.M. Development of a wheat yield prediction model. Agron. J. 1981, 73, 277–282. [Google Scholar] [CrossRef]
- Bell, M.A.; Fischer, R.A. Using yield prediction models to assess yield gains: A case study for wheat. Field Crops Res. 1994, 36, 161–166. [Google Scholar] [CrossRef]
- Zere, T.B.; Van Huyssteen, C.W.; Hensley, M. Development of a simple empirical model for predicting maize yields in a semi-arid area. S. Afr. J. Plant Soil 2005, 22, 22–27. [Google Scholar] [CrossRef]
- Mirschel, W.; Wieland, R.; Wenkel, K.O.; Nendel, C.; Guddat, C. YIELDSTAT—A spatial yield model for agricultural crops. Eur. J. Agron. 2014, 52, 33–46. [Google Scholar] [CrossRef]
- Qian, J.; Ito, S.; Isoda, H.; Saito, H. Yield Response to Price and High-quality Seed Subsidy Policies in China. Jpn. J. Farm Manag. 2012, 50, 118–123. [Google Scholar]
- Qian, J.; Ito, S.; Mu, Y.; Zhao, Z. Simulations on the Impact of Subsidy Policies on Grain Supply and Demand in China; China Agriculture Press: Beijing, China, 2015. [Google Scholar]
- Nerlove, M. Estimates of the elasticities of supply of selected agricultural commodities. J. Farm Econ. 1956, 38, 496–509. [Google Scholar] [CrossRef]
- Nerlove, M.; Bachman, K.L. The analysis of changes in agricultural supply: Problems and approaches. J. Farm Econ. 1960, 42, 531–554. [Google Scholar] [CrossRef]
- Jeffrey, D.; Hamady, D.; Aminata, S. Estimating the supply response of cotton and cereal crops in smallholder production systems: Recent evidence from Mali. Agric. Econ. 2009, 40, 519–533. [Google Scholar]
- French, B.C.; Mathews, J.L. A supply response model for perennial crops. Am. J. Agric. Econ. 1971, 53, 478–490. [Google Scholar] [CrossRef]
- Gafar, J. The supply response for sugar cane in Trinidad and Tobago: Some preliminary results. Appl. Econ. 1987, 19, 1221–1231. [Google Scholar] [CrossRef]
- Froster, K.A.; Mwananmo, A. Estimation of dynamic maize supply response in Zambia. Agric. Econ. 1995, 12, 99–107. [Google Scholar] [CrossRef]
- Mushtaq, K.; Dawson, P.J. Acreage response in Pakistan: A co-integration approach. Agric. Econ. 2002, 27, 111–121. [Google Scholar] [CrossRef]
- Arellano, M.; Bond, S. Some tests of specification for panel data: Monte Carlo evidence and application to employment equations. Rev. Econ. Stud. 1991, 58, 277–297. [Google Scholar] [CrossRef]
- Brennan, J.P. Measuring the contribution of new varieties to increasing wheat yields. Rev. Mark. Agric. Econ. 1984, 52, 1975–1995. [Google Scholar]
- Wooldridge, J.M. Introductory Econometrics: A Modern Approach, 5th ed.; South Western: Cincinnati, OH, USA, 2013. [Google Scholar]
- Wang, D.; Zhang, Z.; Bai, C. Size of Government, rule of law, and the development of services sector. Econ. Res. J. 2007, 6, 51–64. [Google Scholar]
| Coefficients | Estimate | Std. Error | t-Value | Prob. |
|---|---|---|---|---|
| C | 1796.95 | 309.75 | 3.92 | 0.000 |
| Yt-1 | 0.36 | 0.09 | 2.39 | 0.000 |
| Pt-1 | 18.27 | 7.66 | 5.90 | 0.017 |
| D2 | 487.27 | 82.57 | 5.01 | 0.000 |
| D3 | 782.36 | 156.08 | 6.94 | 0.000 |
| D4 | 819.25 | 118.11 | 5.62 | 0.000 |
| D5 | 1192.09 | 212.07 | 5.80 | 0.000 |
| Method = A-Bond GMM | Obs. = 988 | |||
| Diffusion Period | Average Yield | Over the Base Period | Over the Previous Period | ||||
|---|---|---|---|---|---|---|---|
| Total Increase | Increase Caused by New Cultivars | Cont. of New Cultivars | Total Increase | Increase Caused by New Cultivars | Cont. of New Cultivars | ||
| Base (80–86) | 2852.4 | -- | -- | -- | -- | -- | -- |
| 2 (87–94) | 3642.5 | 790.1 | 487.3 | 61.7 | 790.1 | 487.3 | 61.7 |
| 3 (95–99) | 4494.9 | 1642.5 | 782.4 | 47.6 | 852.4 | 295.1 | 34.6 |
| 4 (00–03) | 4633.2 | 1780.8 | 819.3 | 46.0 | 138.3 | 36.9 | 26.7 |
| 5 (04–13) | 5290.9 | 2438.5 | 1192.1 | 48.9 | 657.6 | 372.8 | 56.7 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qian, J.; Zhao, Z. Estimating the Contribution of New Seed Cultivars to Increases in Crop Yields: A Case Study for Corn. Sustainability 2017, 9, 1282. https://doi.org/10.3390/su9071282
Qian J, Zhao Z. Estimating the Contribution of New Seed Cultivars to Increases in Crop Yields: A Case Study for Corn. Sustainability. 2017; 9(7):1282. https://doi.org/10.3390/su9071282
Chicago/Turabian StyleQian, Jiarong, and Zhijun Zhao. 2017. "Estimating the Contribution of New Seed Cultivars to Increases in Crop Yields: A Case Study for Corn" Sustainability 9, no. 7: 1282. https://doi.org/10.3390/su9071282
APA StyleQian, J., & Zhao, Z. (2017). Estimating the Contribution of New Seed Cultivars to Increases in Crop Yields: A Case Study for Corn. Sustainability, 9(7), 1282. https://doi.org/10.3390/su9071282





