Hybrid Algorithm Based on an Estimation of Distribution Algorithm and Cuckoo Search for the No Idle Permutation Flow Shop Scheduling Problem with the Total Tardiness Criterion Minimization
Abstract
:1. Introduction
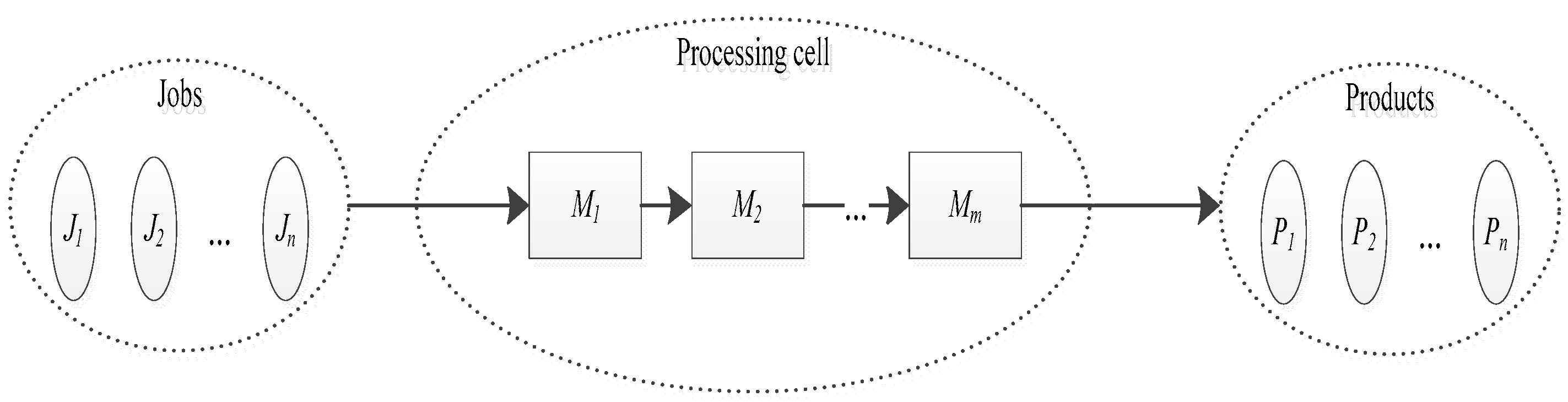
2. Problem Formulation
2.1. Notation
| i, j | normally utilized as loop variables (i.e., i represents the job number, and j represents the machine number) |
| m | machine number |
| n | job number |
| Job | {J1, J2, ….., Jn}; represents the job set to be processed |
| π | scheduling solution that is the processing sequence of the job set {J1, J2, ….., Jn} |
| Ti,j | represents the processing time of the i-th job processed on the j-th machine |
| Tsi,j | represents the starting time of the i-th processed job on the j-th machine; |
| Given that all of the jobs are prepared to be processed at time zero, then | |
| Tei,j | represents the ending time of the i-th processed job on the j-th machine |
| DifTi,j | represents the minimum difference time between the π(i)-th processed job completion time of the j-th machine and (j + 1)-th machine |
| di | represents the due date of the i-th job |
| represents the total tardiness of the schedule π |
2.2. Mathematical Model
3. HEDA_CS for NIPFSP
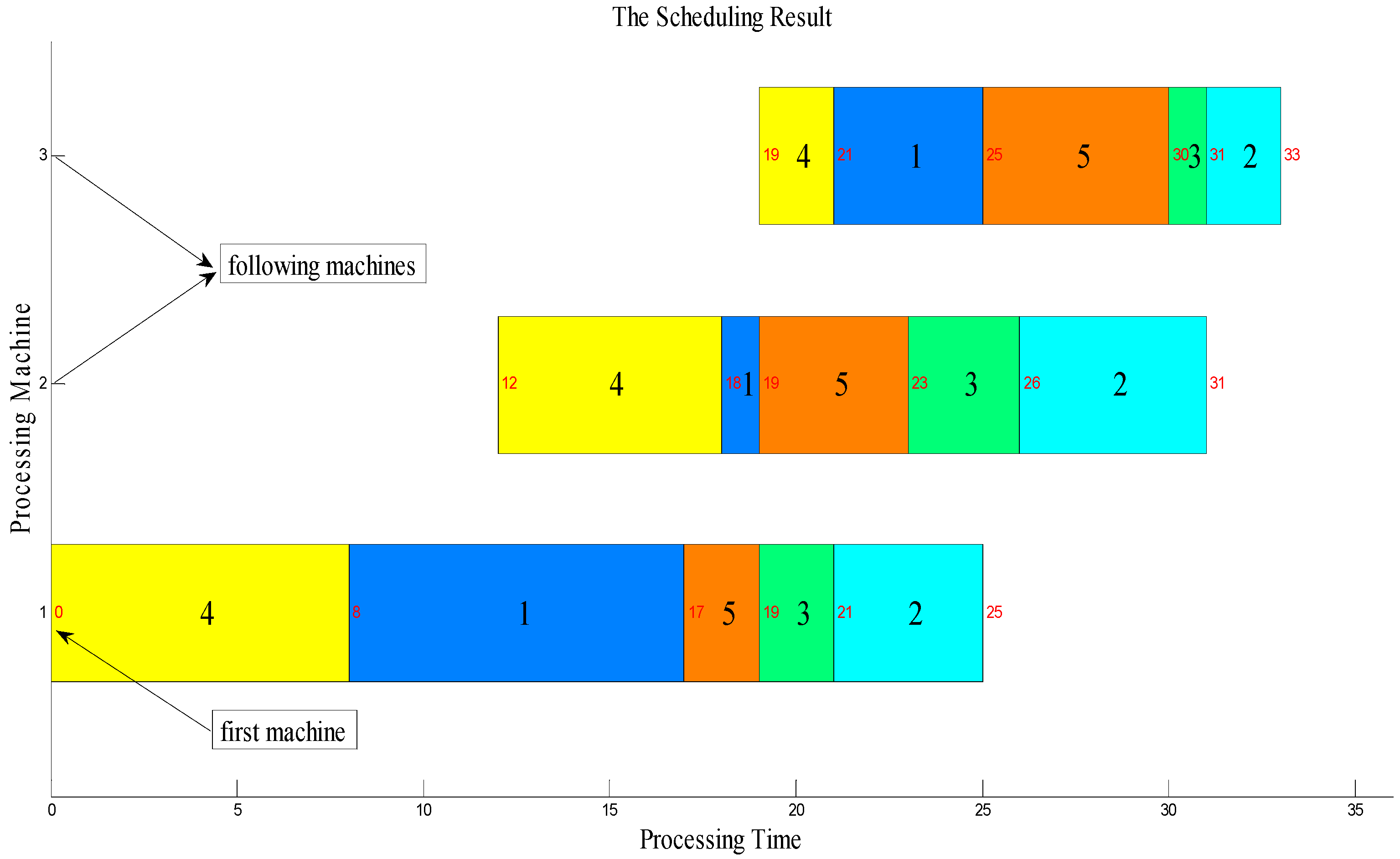
3.1. Solution Representation
3.2. Initialization and Probability Model
3.3. Lévy Flight Strategy in CS
3.4. Updating Mechanism
3.5. Knowledge-Based Local Search
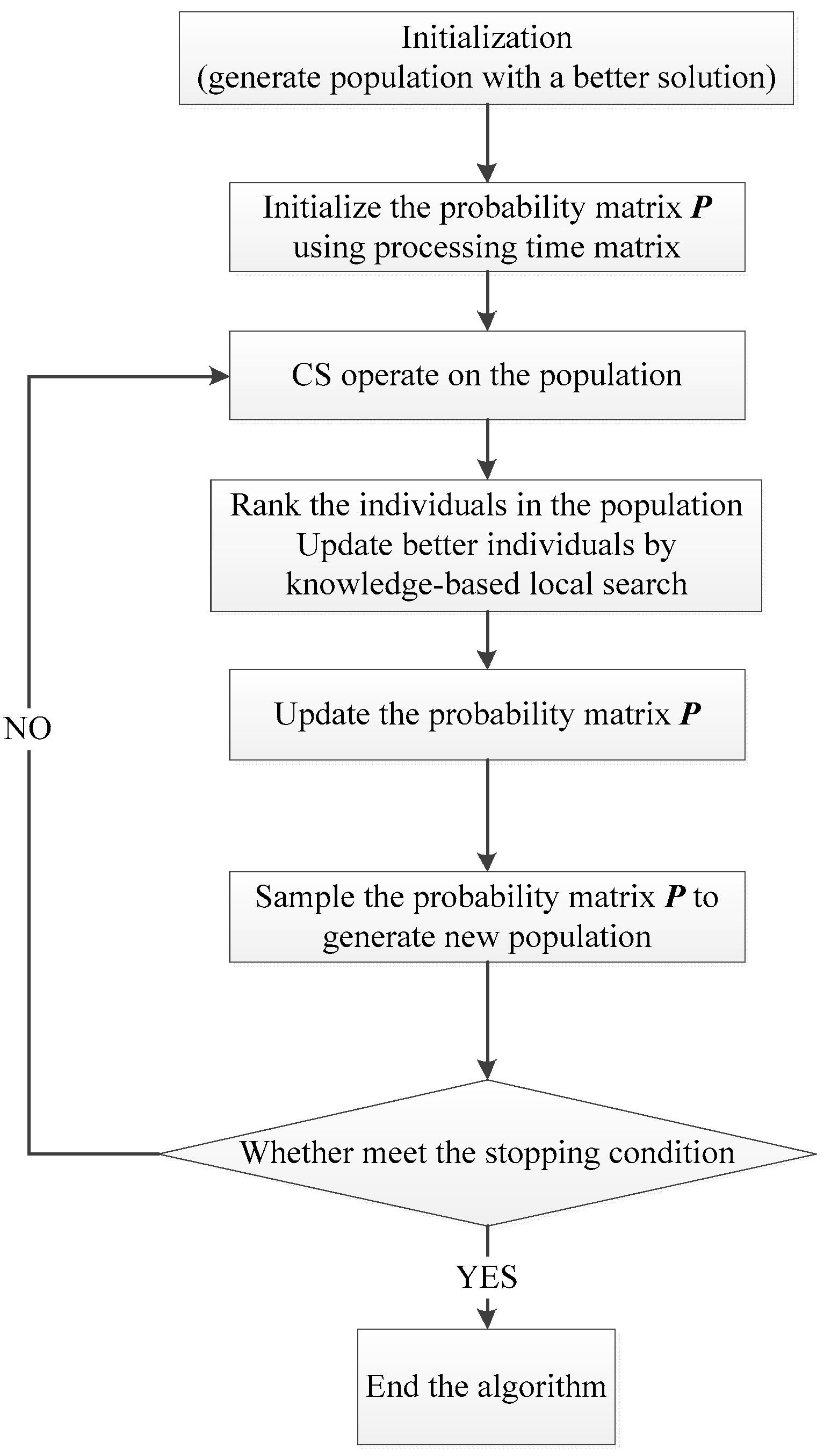
3.6. Overall Implementation
4. Results and Analysis
4.1. Parameter Setting
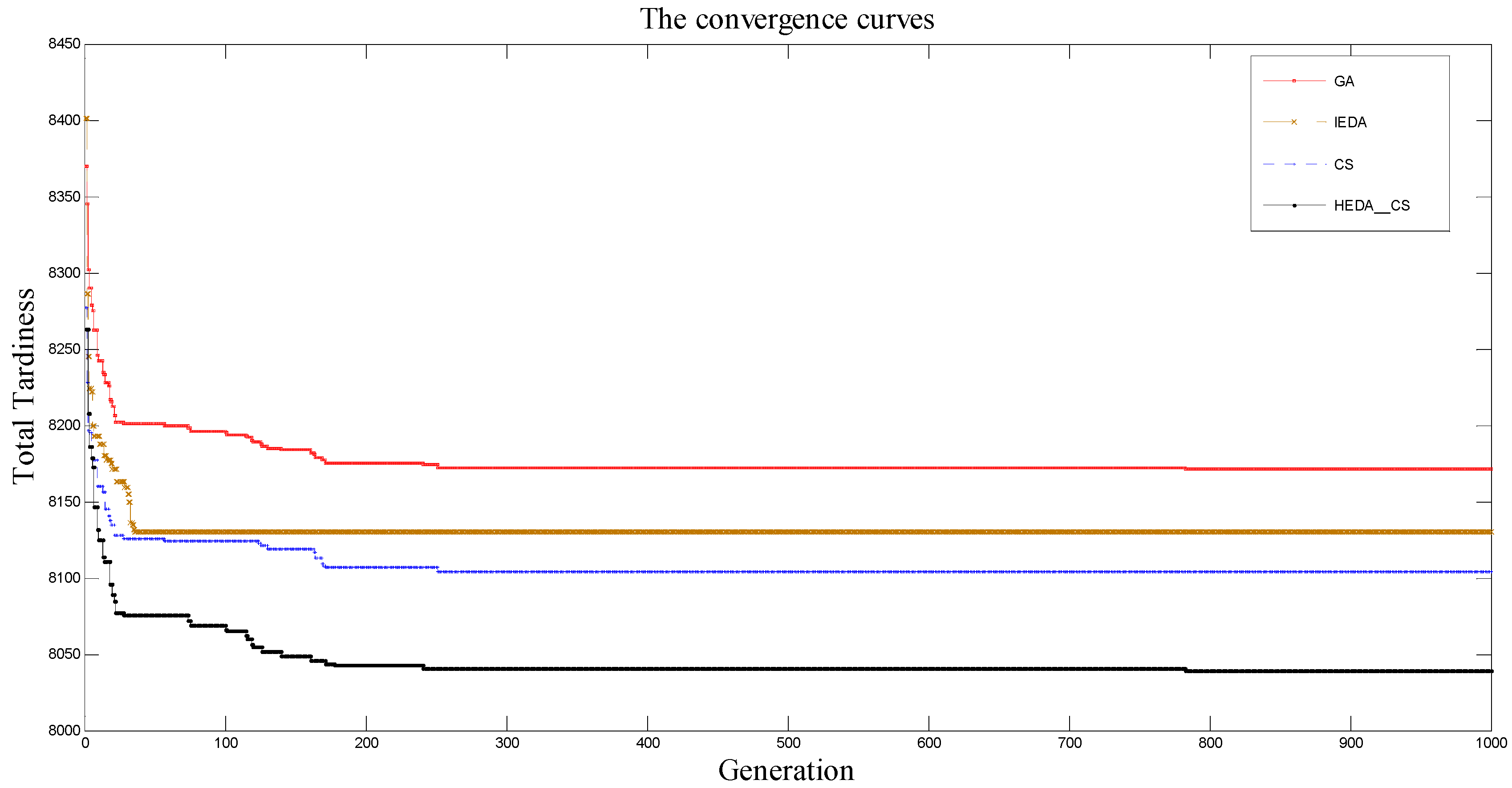
4.2. Results and Comparison of the Instances
4.3. Discussion of Experimental Results
5. Conclusions and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cepek, O.; Okada, M.; Vlach, M. Note: On the two-machine no-idle flowshop problem. Nav. Res. Log. 2000, 47, 353–358. [Google Scholar] [CrossRef]
- Ruiz, R.; Maroto, C. A comprehensive review and evaluation of permutation flowshop heuristics. Eur. J. Oper. Res. 2005, 165, 479–494. [Google Scholar] [CrossRef]
- Adiri, I.; Pohoryles, D. Flowshop/no-idle or no-wait scheduling to minimize the sum of completion times. Nav. Res. Log. Q. 1982, 29, 495–504. [Google Scholar] [CrossRef]
- Woollam, C.R. Flowshop with no idle machine time allowed. Comput. Ind. Eng. 1986, 10, 69–76. [Google Scholar] [CrossRef]
- Saadani, N.E.; Guinet, A.; Moalla, M. Three stage no-idle flow-shops. Comput. Ind. Eng. 2003, 44, 425–434. [Google Scholar] [CrossRef]
- Bozorgirad, M.A.; Logendran, R. A comparison of local search algorithms with population-based algorithms in hybrid flow shop scheduling problems with realistic characteristics. Int. J. Adv. Manuf. Technol. 2015, 83, 1135–1151. [Google Scholar] [CrossRef]
- Ramezani, P.; Rabiee, M.; Jolai, F. No-wait flexible flowshop with uniform parallel machines and sequence-dependent setup time: A hybrid meta-heuristic approach. J. Intell. Manuf. 2013, 26, 731–744. [Google Scholar] [CrossRef]
- Samarghandi, H. Studying the effect of server side-constraints on the makespan of the no-wait flow-shop problem with sequence-dependent set-up times. Int. J. Prod. Res. 2014, 53, 2652–2673. [Google Scholar] [CrossRef]
- Vasile, M.-A.; Pop, F.; Tutueanu, R.-I.; Cristea, V.; Kołodziej, J. Resource-aware hybrid scheduling algorithm in heterogeneous distributed computing. Future Gener. Comput. Syst. 2015, 51, 61–71. [Google Scholar] [CrossRef]
- Zhu, X.; Li, X. Iterative search method for total flowtime minimization no-wait flowshop problem. Int. J. Mach. Learn Cybern. 2014, 6, 747–761. [Google Scholar] [CrossRef]
- Dong, X.; Huang, H.; Chen, P. An improved neh-based heuristic for the permutation flowshop problem. Comput. Oper. Res. 2008, 35, 3962–3968. [Google Scholar] [CrossRef]
- Baraz, D.; Mosheiov, G. A note on a greedy heuristic for flow-shop makespan minimization with no machine idle-time. Eur. J. Oper. Res. 2008, 184, 810–813. [Google Scholar] [CrossRef]
- Kalczynski, P.J.; Kamburowski, J. A heuristic for minimizing the makespan in no-idle permutation flow shops. Comput. Ind. Eng. 2005, 49, 146–154. [Google Scholar] [CrossRef]
- Pan, Q.K.; Wang, L. A novel differential evolution algorithm for no-idle permutation flow-shop scheduling problems. Eur. J. Ind. Eng. 2008, 2, 279–297. [Google Scholar] [CrossRef]
- Pan, Q.-K.; Tasgetiren, M.F.; Liang, Y.-C. A discrete differential evolution algorithm for the permutation flowshop scheduling problem. Comput. Ind. Eng. 2008, 55, 795–816. [Google Scholar] [CrossRef]
- Tasgetiren, M.F.; Pan, Q.-K.; Liang, Y.-C. A discrete differential evolution algorithm for the single machine total weighted tardiness problem with sequence dependent setup times. Comput. Oper. Res. 2009, 36, 1900–1915. [Google Scholar] [CrossRef]
- He, Q.; Wang, L. A hybrid particle swarm optimization with a feasibility-based rule for constrained optimization. Appl. Math. Comput. 2007, 186, 1407–1422. [Google Scholar] [CrossRef]
- Li, B.B.; Wang, L. A hybrid quantum-inspired genetic algorithm for multiobjective flow shop scheduling. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2007, 37, 576–591. [Google Scholar] [CrossRef]
- Deng, G.; Gu, X. A hybrid discrete differential evolution algorithm for the no-idle permutation flow shop scheduling problem with makespan criterion. Comput. Oper. Res. 2012, 39, 2152–2160. [Google Scholar] [CrossRef]
- Tasgetiren, M.F.; Pan, Q.-K.; Suganthan, P.N.; Jin Chua, T. A differential evolution algorithm for the no-idle flowshop scheduling problem with total tardiness criterion. Int. J. Prod. Res. 2011, 49, 5033–5050. [Google Scholar] [CrossRef]
- Tasgetiren, M.F.; Pan, Q.-K.; Suganthan, P.N.; Buyukdagli, O. A variable iterated greedy algorithm with differential evolution for the no-idle permutation flowshop scheduling problem. Comput. Oper. Res. 2013, 40, 1729–1743. [Google Scholar] [CrossRef]
- Pan, Q.-K.; Ruiz, R. An effective iterated greedy algorithm for the mixed no-idle permutation flowshop scheduling problem. Omega 2014, 44, 41–50. [Google Scholar] [CrossRef]
- Yang, X.-S.; Deb, S. Cuckoo search via levy flights. In Proceedings of the 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC 2009), Coimbatore, India, 9–11 December 2009; pp. 210–214. [Google Scholar] [CrossRef]
- Dubey, H.M.; Pandit, M.; Panigrahi, B.K. Cuckoo search algorithm for short term hydrothermal scheduling. In Power Electronics and Renewable Energy Systems: Proceedings of Icperes 2014; Kamalakannan, C., Suresh, L.P., Dash, S.S., Panigrahi, B.K., Eds.; Springer: New Delhi, India, 2015; pp. 573–589. [Google Scholar]
- Lim, W.C.E.; Kanagaraj, G.; Ponnambalam, S.G. A hybrid cuckoo search-genetic algorithm for hole-making sequence optimization. J. Intell. Manuf. 2014, 27, 417–429. [Google Scholar] [CrossRef]
- Majumder, A.; Laha, D. A new cuckoo search algorithm for 2-machine robotic cell scheduling problem with sequence-dependent setup times. Swarm Evolut. Comput. 2016, 28, 131–143. [Google Scholar] [CrossRef]
- Marichelvam, M.K.; Prabaharan, T.; Yang, X.S. Improved cuckoo search algorithm for hybrid flow shop scheduling problems to minimize makespan. Appl. Soft Comput. 2014, 19, 93–101. [Google Scholar] [CrossRef]
- Dasgupta, P.; Das, S. A discrete inter-species cuckoo search for flowshop scheduling problems. Comput. Oper. Res. 2015, 60, 111–120. [Google Scholar] [CrossRef]
- Niknam, T.; Azizipanah-Abarghooee, R.; Aghaei, J. A new modified teaching-learning algorithm for reserve constrained dynamic economic dispatch. IEEE Trans. Power Syst. 2013, 28, 749–763. [Google Scholar] [CrossRef]
- Vallada, E.; Ruiz, R.; Framinan, J.M. New hard benchmark for flowshop scheduling problems minimising makespan. Eur. J. Oper. Res. 2015, 240, 666–677. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, L.; Wang, S.-Y.; Liu, M. An effective teaching–learning-based optimization algorithm for the flexible job-shop scheduling problem with fuzzy processing time. Neurocomputing 2015, 148, 260–268. [Google Scholar] [CrossRef]
- Wang, L.; Wang, S.; Xu, Y.; Zhou, G.; Liu, M. A bi-population based estimation of distribution algorithm for the flexible job-shop scheduling problem. Comput. Ind. Eng. 2012, 62, 917–926. [Google Scholar] [CrossRef]
- Viswanathan, G.M.; Afanasyev, V.; Buldyrev, S.V.; Murphy, E.J.; Prince, P.A.; Stanley, H.E. Levy flight search patterns of wandering albatrosses. Nature (London) 1996, 381, 413–415. [Google Scholar] [CrossRef]
- Grabowski, J.; Wodecki, M. A very fast tabu search algorithm for the permutation flow shop problem with makespan criterion. Comput. Oper. Res. 2004, 31, 1891–1909. [Google Scholar] [CrossRef]
- Dong, X.; Nowak, M.; Chen, P.; Lin, Y. Self-adaptive perturbation and multi-neighborhood search for iterated local search on the permutation flow shop problem. Comput. Ind. Eng. 2015, 87, 176–185. [Google Scholar] [CrossRef]
- Tasgetiren, M.F.; Pan, Q.-K.; Suganthan, P.N.; Oner, A. A discrete artificial bee colony algorithm for the no-idle permutation flowshop scheduling problem with the total tardiness criterion. Appl. Math. Model. 2013, 37, 6758–6779. [Google Scholar] [CrossRef]
- Wang, S.-Y.; Wang, L. An estimation of distribution algorithm-based memetic algorithm for the distributed assembly permutation flow-shop scheduling problem. IEEE. Trans. Syst. Man Cybern. Syst. 2016, 46, 139–149. [Google Scholar] [CrossRef]
- Masselink, G.; Ruju, A.; Conley, D.; Turner, I.; Ruessink, G.; Matias, A.; Thompson, C.; Castelle, B.; Puleo, J.; Citerone, V.; et al. Large-scale barrier dynamics experiment II (bardex II): Experimental design, instrumentation, test program, and data set. Coast. Eng. 2016, 113, 3–18. [Google Scholar] [CrossRef]
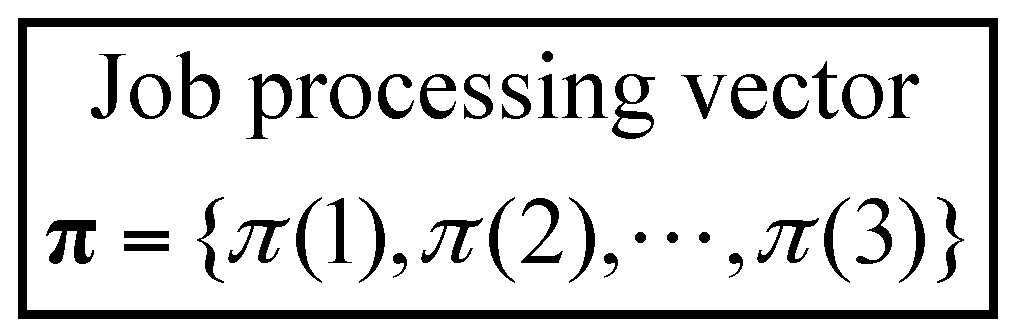
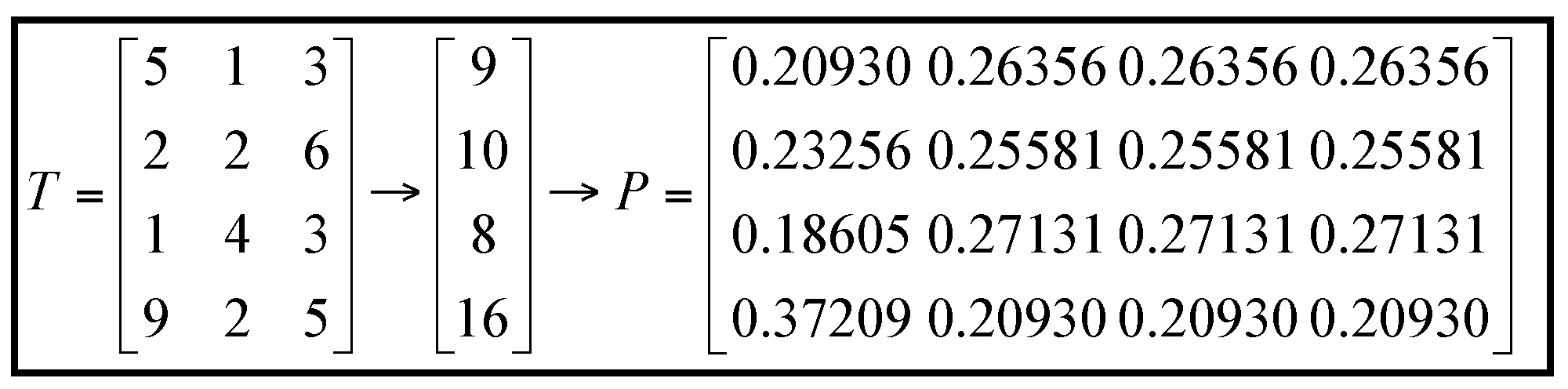
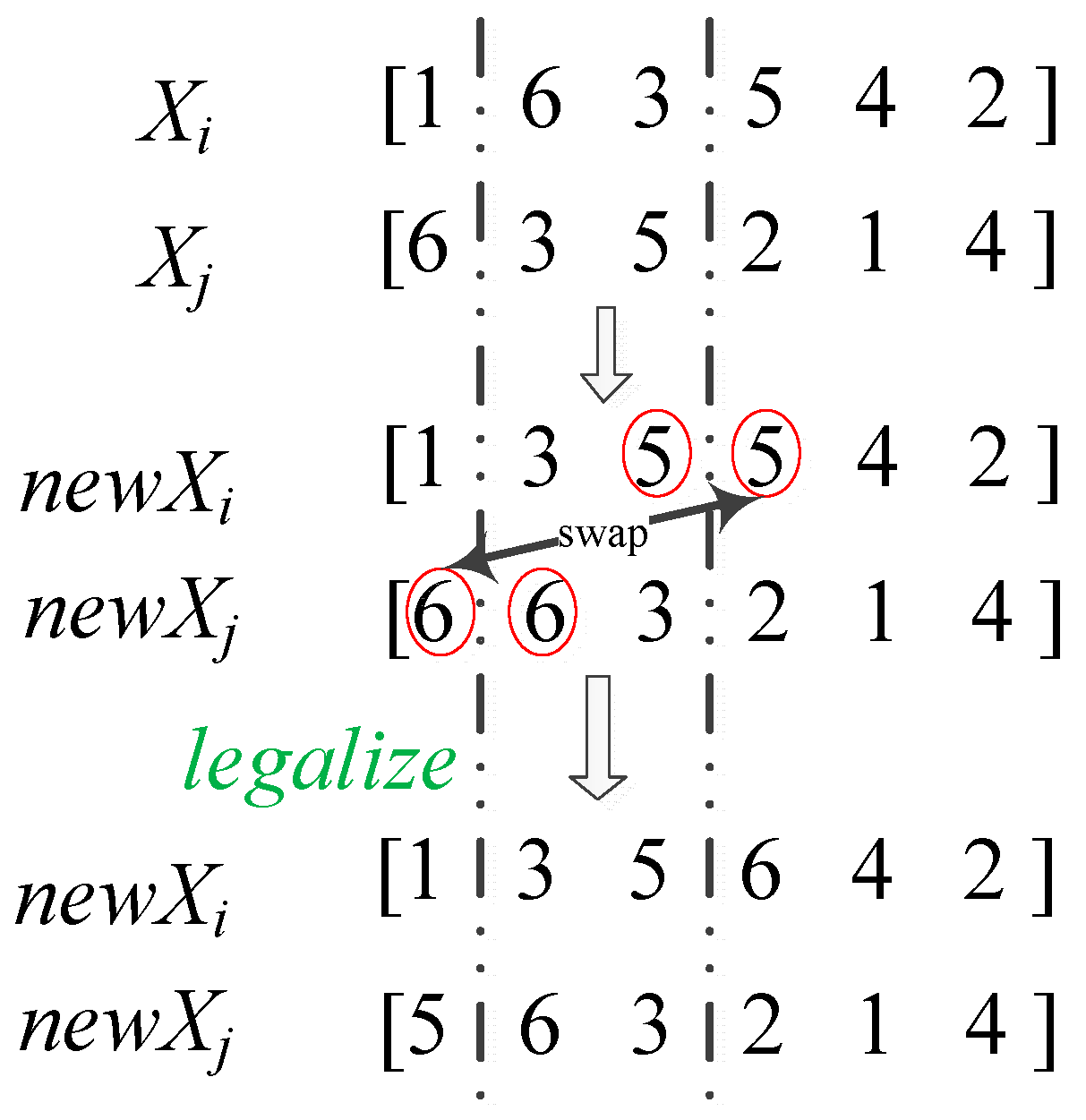

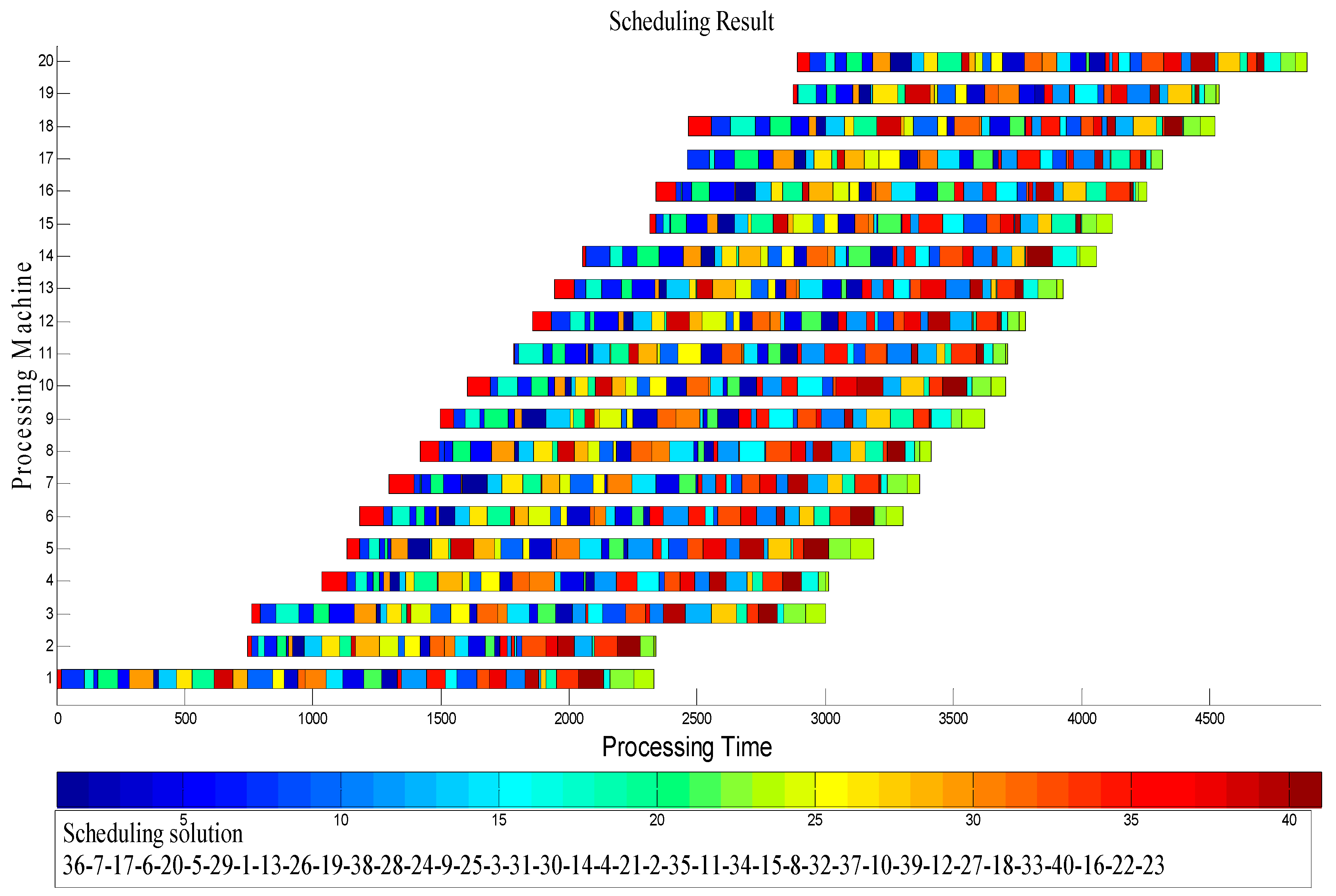
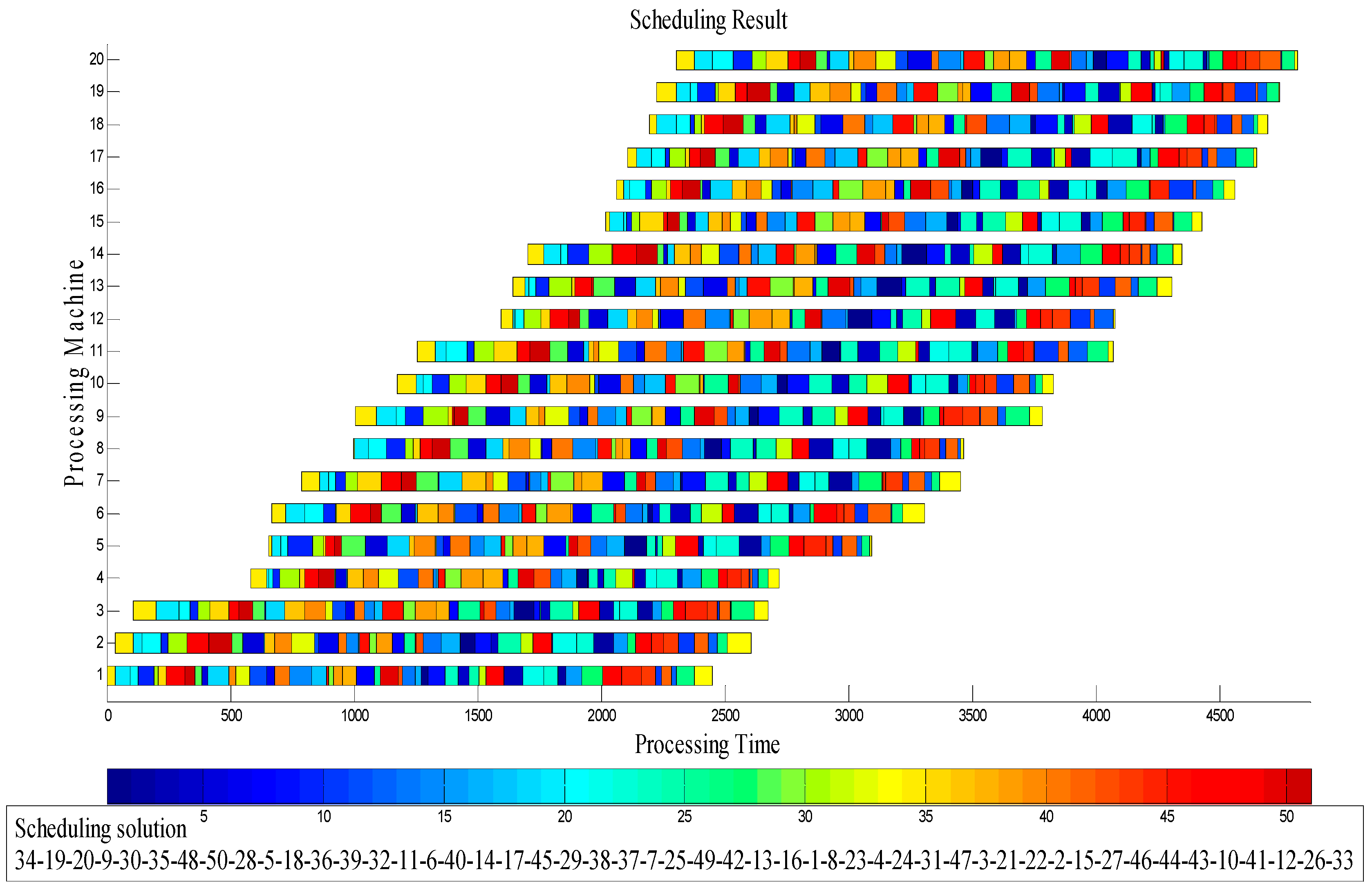
| Tightness Factor | Main Parameters | Factor Levels |
|---|---|---|
| 1, 2, 3 | Maxgeneration | 100(1), 500(2), 1000(3) |
| 1, 2, 3 | PopSize | 10(1), 50(2), 100(3) |
| 1, 2, 3 | SP | 5(1), 8(2), 10(3) |
| Experiment Number | Tightness Factor | Main Parameters | ARV | ||
|---|---|---|---|---|---|
| Maxgeneration | PopSize | SP | |||
| 1 | 1 | 100(1) | 10(1) | 5(1) | 0.3664 |
| 2 | 1 | 500(2) | 50(2) | 8(2) | 0.1719 |
| 3 | 1 | 100(1) | 100(3) | 10(3) | 0.2064 |
| 4 | 2 | 100(1) | 50(2) | 10(3) | 0.2021 |
| 5 | 2 | 500(2) | 100(3) | 5(1) | 0.2449 |
| 6 | 2 | 1000(3) | 10(1) | 8(2) | 0.1749 |
| 7 | 3 | 100(1) | 100(3) | 8(2) | 0.2686 |
| 8 | 3 | 500(2) | 10(1) | 10(3) | 0.1571 |
| 9 | 3 | 1000(3) | 50(2) | 5(1) | 0.0728 |
| Factor Level | Main Parameters | ||
|---|---|---|---|
| Maxgeneration | PopSize | SP | |
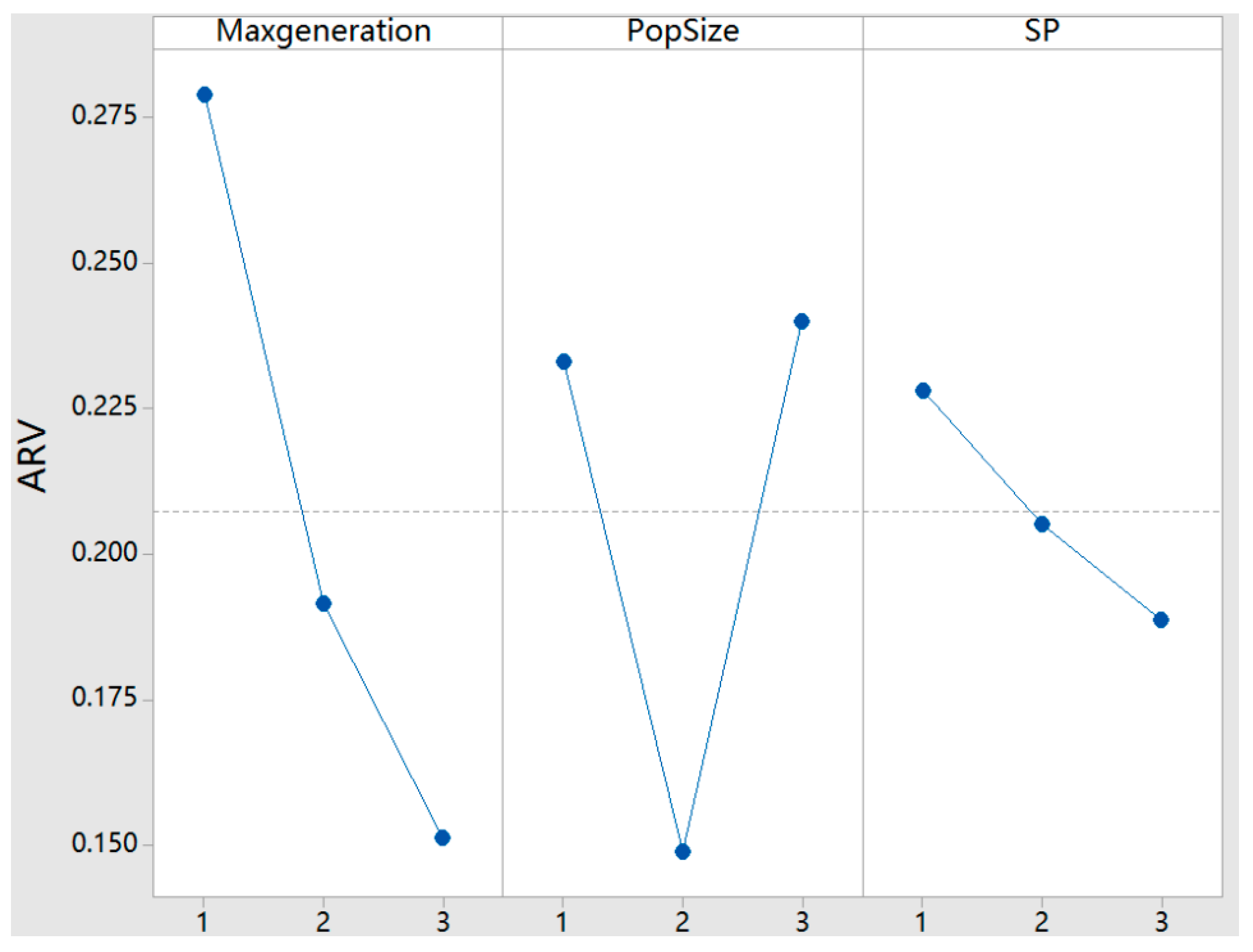
| 1 | 0.2790 | 0.2330 | 0.2280 |
| 2 | 0.1915 | 0.1489 | 0.2051 |
| 3 | 0.1514 | 0.2400 | 0.1887 |
| Range | 0.1277 | 0.0910 | 0.0393 |
| Rank | 1 | 2 | 3 |
| Factors | Levels |
|---|---|
| Number of jobs | 40, 50, 60, 100 |
| Number of machines | 20, 40, 60 |
| Processing time on each machine | U(1, 100) |
| Problem | GA | IEDA | CS | HEDA_CS | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AVE | MIN | MAX | AVE | MIN | MAX | AVE | MIN | MAX | AVE | MIN | MAX | |
| n = 40, m = 20 | 1.13 | 0.33 | 1.98 | 0.86 | 0.03 | 1.89 | 0.85 | 0.09 | 1.79 | 0.83 | 0.00 | 1.82 |
| n = 50, m = 20 | 1.31 | 0.45 | 2.05 | 0.94 | 0.23 | 1.87 | 0.89 | 0.10 | 1.77 | 0.77 | 0.00 | 1.70 |
| n = 60, m = 20 | 1.93 | 1.03 | 4.26 | 1.31 | 0.35 | 3.06 | 1.38 | 0.21 | 2.89 | 0.73 | 0.00 | 1.52 |
| n = 100, m = 20 | 2.36 | 1.31 | 5.18 | 1.53 | 0.36 | 3.86 | 1.21 | 0.18 | 3.41 | 0.43 | 0.00 | 0.93 |
| n = 100, m = 40 | 2.53 | 2.13 | 6.31 | 1.43 | 0.61 | 4.19 | 1.10 | 0.53 | 1.95 | 0.85 | 0.00 | 1.76 |
| n = 100, m = 60 | 3.76 | 3.35 | 7.51 | 1.51 | 1.03 | 4.51 | 1.43 | 0.99 | 2.97 | 0.94 | 0.00 | 1.92 |
| Average | 2.17 | 1.43 | 4.55 | 1.26 | 0.44 | 3.23 | 1.14 | 0.35 | 2.46 | 0.76 | 0.00 | 1.61 |
| Problem | GA | IEDA | CS | HEDA_CS | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AVE | MIN | MAX | AVE | MIN | MAX | AVE | MIN | MAX | AVE | MIN | MAX | |
| n = 40, m = 20 | 1.14 | 0.29 | 2.07 | 0.89 | 0.01 | 2.13 | 0.91 | 0.06 | 1.93 | 0.89 | 0.00 | 1.84 |
| n = 50, m = 20 | 1.19 | 0.36 | 2.84 | 1.18 | 0.17 | 2.52 | 1.09 | 0.15 | 2.21 | 0.75 | 0.00 | 1.88 |
| n = 60, m = 20 | 1.67 | 1.07 | 2.65 | 1.51 | 0.68 | 3.15 | 1.38 | 0.23 | 2.97 | 0.62 | 0.00 | 1.42 |
| n = 100, m = 20 | 2.13 | 1.79 | 3.09 | 1.87 | 1.01 | 3.24 | 1.57 | 0.29 | 3.31 | 0.41 | 0.00 | 0.92 |
| n =100, m = 40 | 2.31 | 1.93 | 4.35 | 2.01 | 0.97 | 4.13 | 1.51 | 0.35 | 3.15 | 0.93 | 0.00 | 1.99 |
| n = 100, m = 60 | 2.60 | 2.01 | 4.32 | 1.97 | 1.13 | 5.01 | 1.89 | 0.51 | 3.68 | 1.16 | 0.00 | 2.07 |
| Average | 1.84 | 1.24 | 3.22 | 1.57 | 0.66 | 3.36 | 1.39 | 0.27 | 2.88 | 0.79 | 0.00 | 1.69 |
| Problem | GA | IEDA | CS | HEDA_CS | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AVE | MIN | MAX | AVE | MIN | MAX | AVE | MIN | MAX | AVE | MIN | MAX | |
| n =40, m = 20 | 0.83 | 0.13 | 2.11 | 0.79 | 0.09 | 1.99 | 0.81 | 0.05 | 1.81 | 0.78 | 0.00 | 1.93 |
| n = 50, m = 20 | 0.99 | 0.27 | 2.25 | 0.86 | 0.14 | 2.07 | 0.82 | 0.01 | 1.83 | 0.78 | 0.00 | 1.62 |
| n = 60, m = 20 | 1.46 | 1.12 | 2.69 | 0.97 | 0.31 | 2.21 | 0.95 | 0.16 | 2.12 | 0.67 | 0.00 | 1.52 |
| n = 100, m = 20 | 1.68 | 1.53 | 2.86 | 1.31 | 0.46 | 2.56 | 1.16 | 0.25 | 2.51 | 0.42 | 0.00 | 0.93 |
| n = 100, m = 40 | 1.79 | 1.67 | 2.90 | 1.46 | 0.51 | 2.73 | 1.31 | 0.29 | 2.75 | 1.02 | 0.00 | 1.85 |
| n = 100, m = 60 | 2.14 | 1.89 | 2.98 | 1.58 | 0.59 | 2.64 | 1.62 | 0.36 | 2.81 | 1.28 | 0.00 | 2.12 |
| Average | 1.48 | 1.10 | 2.63 | 1.16 | 0.35 | 2.37 | 1.11 | 0.19 | 2.03 | 0.83 | 0.00 | 1.66 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Z.; Gu, X. Hybrid Algorithm Based on an Estimation of Distribution Algorithm and Cuckoo Search for the No Idle Permutation Flow Shop Scheduling Problem with the Total Tardiness Criterion Minimization. Sustainability 2017, 9, 953. https://doi.org/10.3390/su9060953
Sun Z, Gu X. Hybrid Algorithm Based on an Estimation of Distribution Algorithm and Cuckoo Search for the No Idle Permutation Flow Shop Scheduling Problem with the Total Tardiness Criterion Minimization. Sustainability. 2017; 9(6):953. https://doi.org/10.3390/su9060953
Chicago/Turabian StyleSun, Zewen, and Xingsheng Gu. 2017. "Hybrid Algorithm Based on an Estimation of Distribution Algorithm and Cuckoo Search for the No Idle Permutation Flow Shop Scheduling Problem with the Total Tardiness Criterion Minimization" Sustainability 9, no. 6: 953. https://doi.org/10.3390/su9060953
APA StyleSun, Z., & Gu, X. (2017). Hybrid Algorithm Based on an Estimation of Distribution Algorithm and Cuckoo Search for the No Idle Permutation Flow Shop Scheduling Problem with the Total Tardiness Criterion Minimization. Sustainability, 9(6), 953. https://doi.org/10.3390/su9060953





