1. Introduction
The Maldives, an island nation in the Indian Ocean, are largely recognized as one of the most beautiful countries in the world and an example of a natural paradise. However, a paradise with a particular issue: it is one of the most exposed countries in the world to the volatility and the rising of oil prices and it is extremely vulnerable to the effects of the climate change. The reason is twofold: country’s strong dependency on fossil fuel, which is essentially the only exploitable source of energy, and the natural conformation of the Archipelago. The Maldives are composed exclusively of corals and sand, without surface bodies of fresh waters and with no point higher than 2.3 m above mean sea level. Moreover, much of the groundwater is polluted and cannot be used, which makes the Maldives an easy prey of emergency situations and speculations [
1].
Several recent studies indicate a profound reorganization of the energy market and environmental policy in the Maldives, aiming to convert the island nation as the world’s first carbon neutral country. Solar photovoltaic, wind energy and biomass represent the key renewable resources according to the
Scaling up Renewable Energy Program (SREP) under the Climate Investment Funds [
2]. Energy from waste is under consideration. As for tidal and marine currents, a study conducted by the Robert Gordon University of Scotland in 2011 concluded that current technologies are not yet relevant [
3]. However, the SREP investment plan does not include in its study neither onshore/offshore wind source nor wave energy. Recently, the Government of the Maldives has recognized the need to improve the information available on solar and wind potential as it requested the support of the World Bank and ESMAP’s Renewable Energy Mapping Initiative to help carry out a resource assessment and mapping [
4], showing some preliminary results. With respect to traditional wind resource, offshore wind farms present benefits that include (a) lower visual and noise impact through distance from the shoreline and (b) higher wind resource (larger wind velocities) with lower turbulence levels than adjacent land sites. Furthermore, since industry is seeking economically viable devices for commercial deployment, the economic feasibility and regularity in the power output of offshore wind farms could be enhanced combining two forms of energy production, i.e., wind and wave, in one platform. Cases of integration of wave and wind power have been studied by [
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19,
20,
21,
22,
23], demonstrating as the joint exploitation of offshore wind and wave energy resources can have a number of advantages, including:
higher quality of produced power when mixing the power from wind and wave energy;
higher regularity of power delivered to the grid when swells continue after the wind declines;
reducing risk and cost through sharing components, infrastructure, submarine electric cables and maintenance activities;
less area and environmental impact for combined farms through the sharing of space.
Over the last two decades several efforts have been made to map the offshore wind and wave energy resource. Maps of the global offshore wind energy resources have earlier been published in [
24], and wind resource assessment was analysed by, e.g., [
25,
26,
27,
28,
29,
30,
31,
32,
33,
34,
35,
36,
37,
38,
39,
40,
41,
42].
Considerable works have been undertaken on wave energy assessment in several areas worldwide (e.g., [
43,
44,
45,
46,
47,
48,
49,
50,
51,
52,
53,
54,
55,
56,
57,
58,
59,
60,
61,
62,
63,
64,
65,
66,
67]). A global synthesis has been published in the review book by Cruz (2008), based on the WorldWaves data.
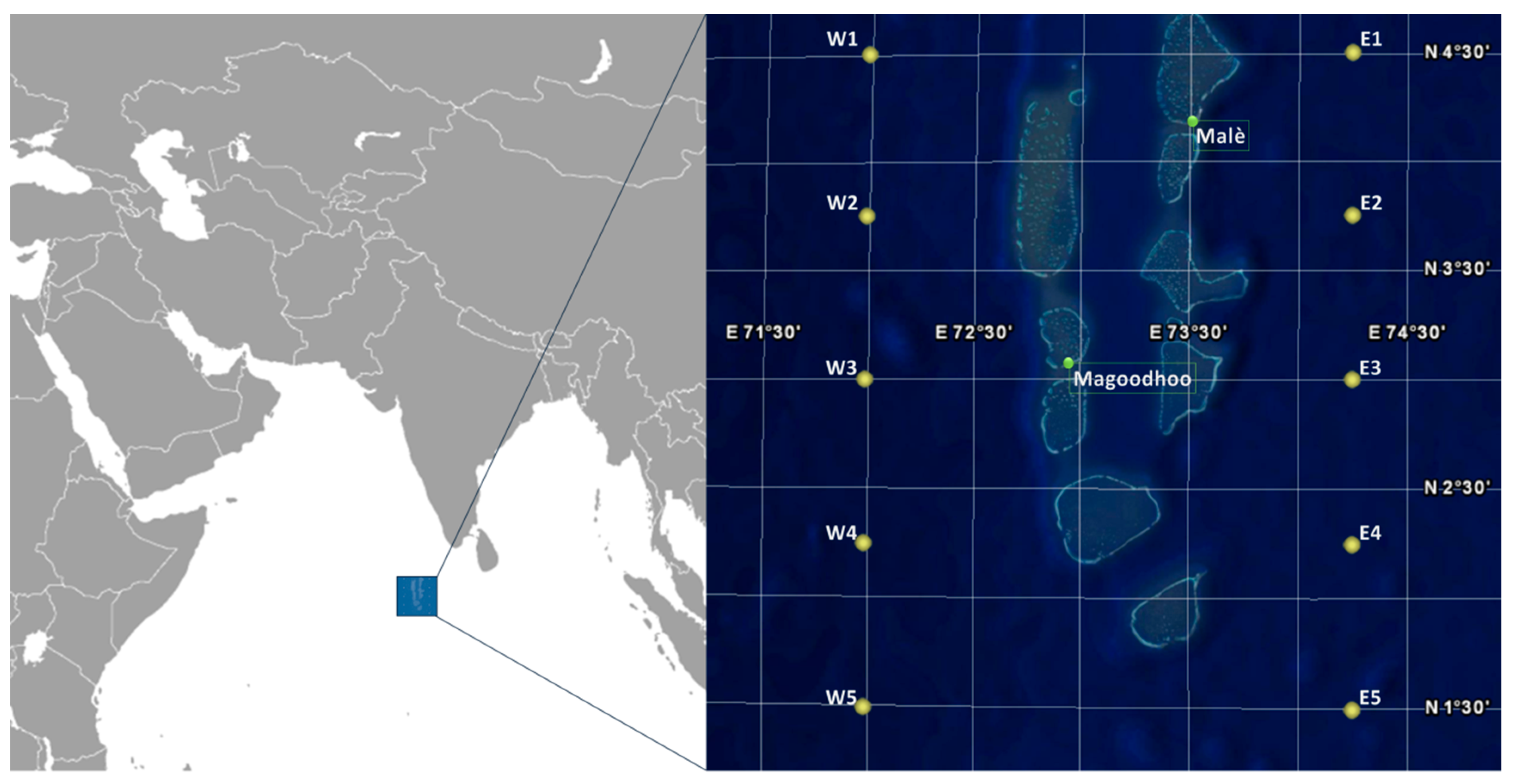
The present work analyses the blue energy resources along the Maldives coastline, using a 10-years data series provided by the European Centre for Medium-Range Weather Forecasts (ECMWF) dataset [
68]. The spatial distribution of both energy sources is analysed using data from 10 points along the coast. The approach used in the present study follows a widely validated methodology in literature for both the wind and the wave energy assessment undertaken for several locations worldwide [
25,
26,
27,
28,
29,
30,
31,
32,
33,
34,
35,
36,
37,
38,
39,
40,
41,
42,
43,
44,
45,
46,
47,
48,
49,
50,
51,
52,
53,
54,
55,
56,
57,
58,
59,
60,
61,
62,
63,
64,
65,
66,
67], but the two assessments have been concurrently compared and innovative applications of hybrid technologies have been considered.
In particular, the objectives of this work are:
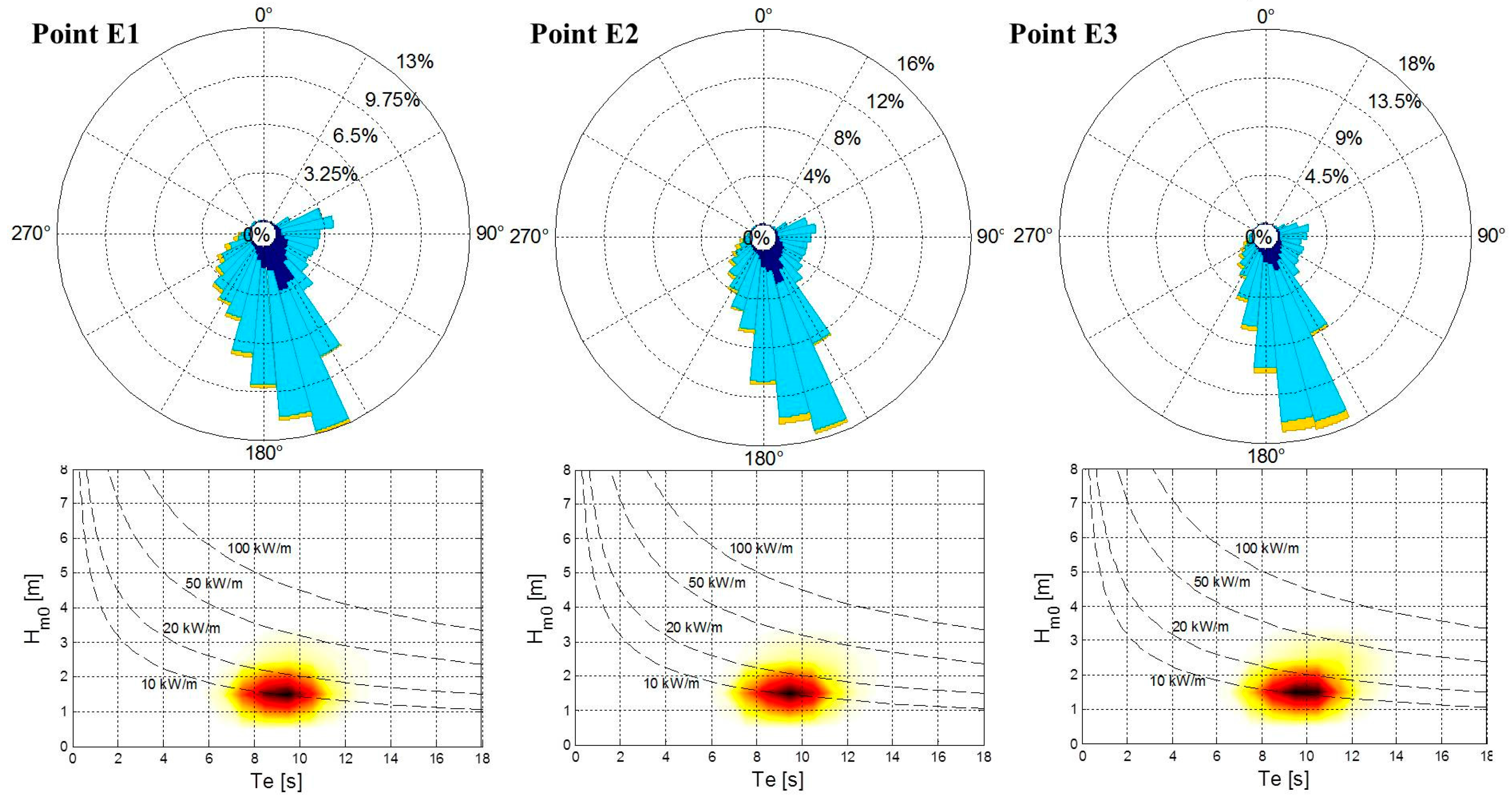
to characterize the wave climate around the study area, emphasizing wave power assessment and the involvement of different sea states (e.g., monthly variability and long period swell influence);
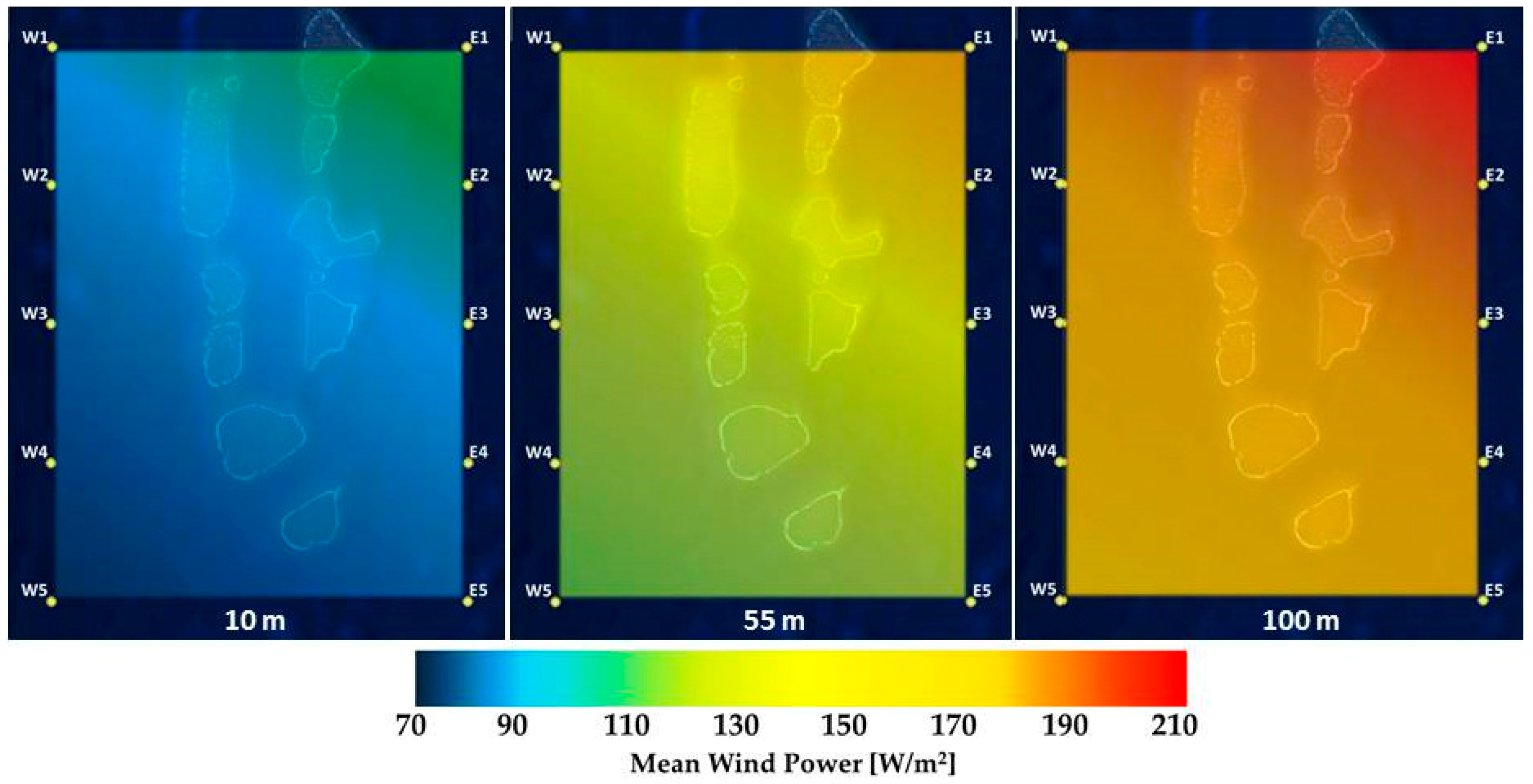
to provide a comprehensive study of offshore wind resource, provided at a height of 10, 25, 55, 80 and 100 m and referring to three practical utility-scale wind turbines;
to draw a preliminary discussion about the realistic perspectives of blue farm installations around the Maldives coastline, also through practical case studies of these innovative technologies.
For the last point, a special attention has been paid to enhance the environmental and socio-economical sustainability of blue energy technologies, identifying the possible “cost saving synergies” between wave energy and other sea uses. Two case scenarios will be presented to illustrate the approach: both of them include a hybrid platform of wave and wind and another (non-energy) sea use. Two representative islands are analyzed:
Malé, the capital, one of the most densely populated cities in the world, with approximately 23,000 people per km
2 and an electricity demand of over 220 GWh/year in 2012 [
69];
Magoodhoo, a remote small island on the Faafu Atoll, at a distance of 134 km from the capital, with a population of 683 inhabitants distributed on a surface of less than 0.36 km2.
The paper is structured as follows.
Section 2 briefly describes the study area, presents the available data and introduces the methodology. In
Section 3 the offshore wind energy and the wave energy resource along the Maldivian coasts are assessed. In
Section 4 the results are discussed and the best-case scenarios for the two sites are specifically investigated, showing the combined maritime uses that can be more feasible. Conclusions are finally drawn in
Section 5.
4. Additional Considerations and Discussion
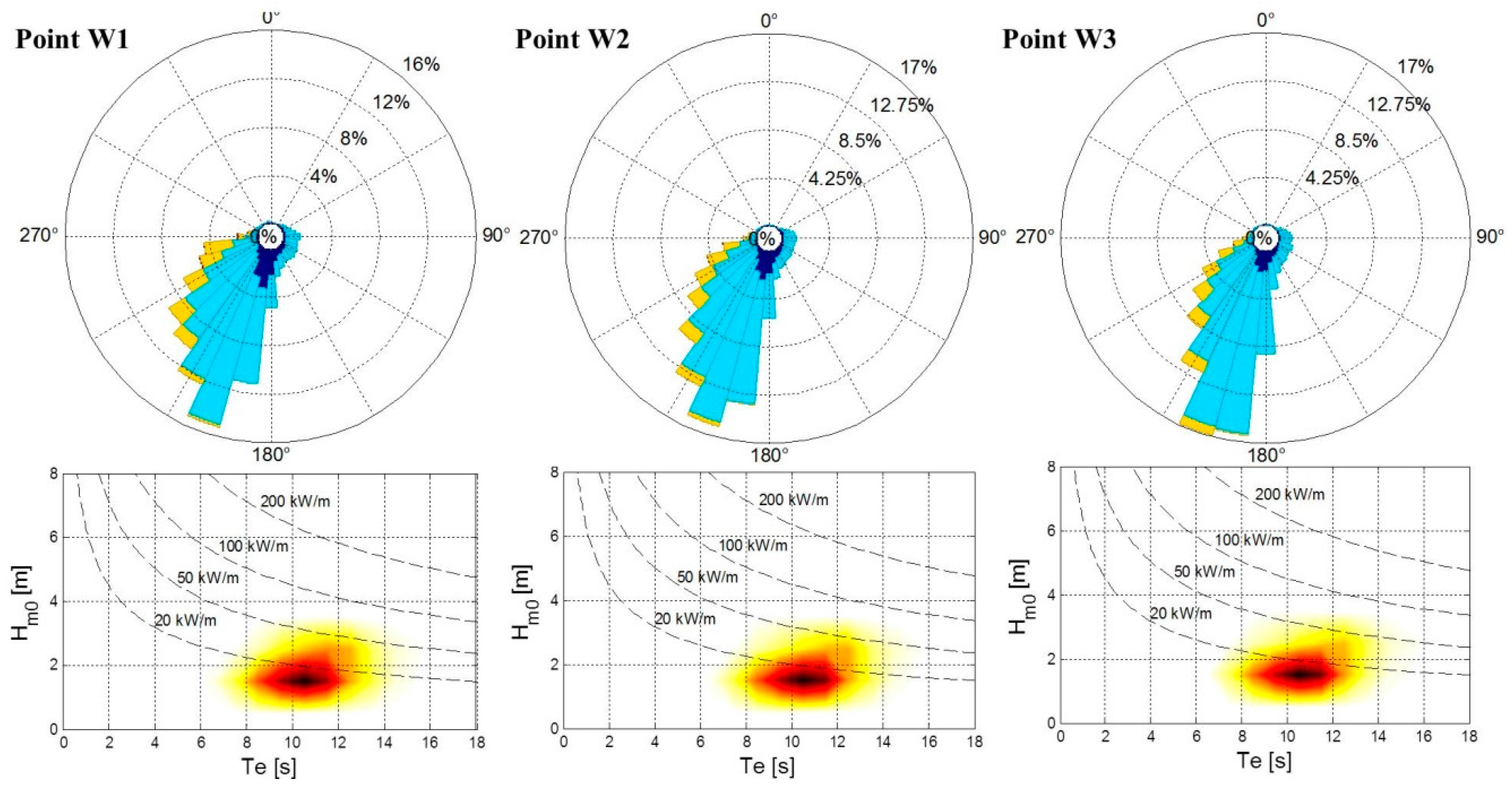
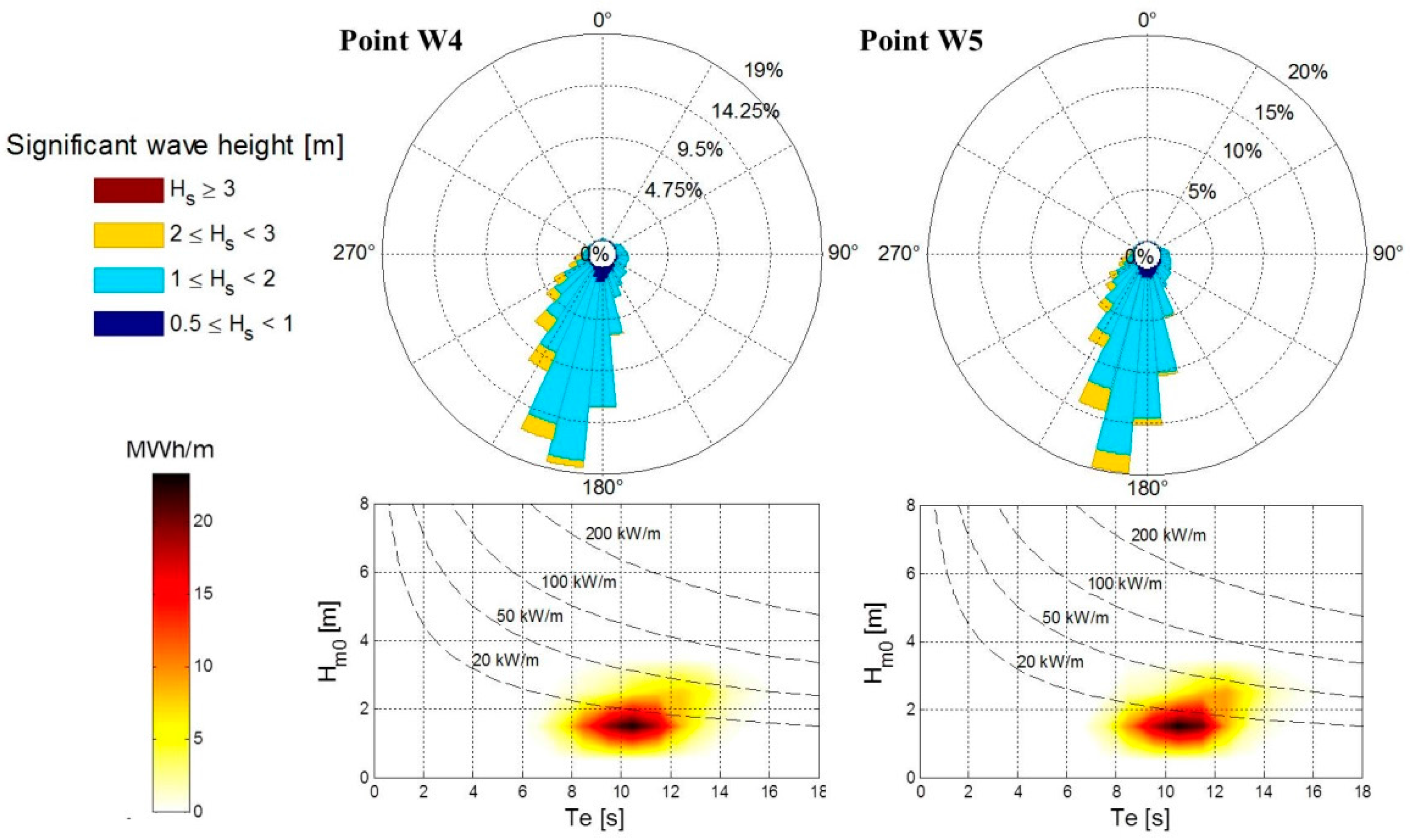
As showed in previous chapter, the area is characterized by a significant seasonality of wave regimes and a poor monthly variability of wind conditions. An heuristic explanation could be provided considering that the Maldives wave sea state is comprised of multiple wave fields, i.e., sea waves generated by local winds plus very long-period swells approaching from several distant sources and different directions. In support of this argument, it is possible to note as the highest values of wave power are measured from May to October, which correspond to the period when the southwest monsoon is in full swing [
72]. On the basis of the above considerations, it is reasonable to also explain the poor relationship between the main directions of waves and local winds. As demonstrate by [
73], the time scale of the directional response appears to be equal to the time scale of wave energy growth only for young sea states, hence in absence of swell. Therefore, the energy patterns suggest that wind and waves are generally uncorrelated, especially during the period of southwest monsoon. These conditions are very interesting in the perspective of reducing the overall variability of the produced power. Indeed, the correlation of ocean waves to wind is a very important aspect for both forecasting models of energy production and for design of mooring/substructure/structure of wind/wave energy devices.
In order to boost blue growth and make wind and wave energies environmentally and socio-economically sustainable, a role of preference could be addressed bringing together the energy demand with other local issues. Indeed, the need for fresh water is at the top of the Government agenda for critical problems. Malé, the capital of the Maldives, declared a state of emergency in 2014 due to the lack of potable water, when the majority of the inhabitants were left without access to potable water. Today, rainwater is more widely used than groundwater for drinking purpose and about 88% of the population in Malè intercepts rainwater via tanks [
1]. Furthermore, it is expected that population growth and the increase of the number of tourists will result in ever-increasing demands for clean water. Generally, the potable water demand in coastal areas is met by means of large-scale desalination systems. However, also the modern systems require very high energy consumption, which still represents a crucial drawback for this technology. Furthermore, numerous low-density population islands lack not only fresh water availability, but also the electrical grid connection or any other energy source. The real challenge, consequently, is to ensure adequate fresh water supplies at the minimum possible cost. For these reasons, wind and wave energy coupled with desalination systems appear as a promising opportunity for small islands and developing countries to meet their water supply needs. Providing for these crucial needs via renewable natural resources, resulting in a broad social acceptance.
The water supply is not the only problem for Maldivian islands: the result of a study [
74] shows that around 64% of all the islands reported severe beach erosion. Beach replenishment may only be a temporary remedy and traditional hard solutions, such as groynes, revetments or breakwaters, are often unpopular for aesthetic reasons and they reduce the recreational values. An interesting alternative may be represented by the beach drainage system, which has the great advantage to eliminate the visual impact. Additionally, its installation is not as costly as the traditional hard coastal structures and it does not suffer from wear rates as beach nourishments. This innovative system has been proven to stabilize the beachface when low incident wave energy conditions are ensured [
75,
76,
77], like the ones inside a coral reef. In the context of the promotion of hybrid systems, it is remarkable that the drained water flows may be considered as a water pre-treatment for desalination, with both drainage and desalination plants powered by inshore/offshore blue energy technologies, pursuing a very high ethics perspective.
In order to boost blue growth, the paper investigates the uses of multifunctional structures combining power generation, desalinization and coastal defence. As aforementioned, two representative islands are analysed: Malé, and Magoodhoo. The selection of these sites provides two good case studies for different reasons. The first one is the opposite demographic conditions between the two islands. Then, the difference in the waterfront and coastal line, since Magoodhoo is a natural environment without any sign of significant human activity, while the Male Island is almost entirely protected by six-kilometers circumference of sea walls. Furthermore, the electricity demand in the capital island increases at a yearly rate of 11% [
69] but, at the same time, there is not enough land to expand power plants. Therefore, it is crucial to find alternative options to supply electricity. Finally, Magoodhoo hosts the Marine Research and High Education Center born by the collaboration of Maldivian Government and the University of Milan-Bicocca. In particular, within the program “
Benefits of using renewable energy for Maldivian communities and marine ecosystems” promoted with the support of the Italian Caritas, a photovoltaic system has been donated to the people of Magoodhoo [
78]. This system feeds power to the island grid, and it is helping to reset the electricity production, moving from a small diesel sets configuration. Moreover, the cooperative agreement between Italy and the Maldives has also supported a new project termed “
Installation of a water desalination plant on the island of Magoodhoo—Faafu Atoll” [
79]. The desalination plant, through the use of solar thermal and photovoltaic panels, will provide clean water to the island’s population, who currently does not have drinking water, and so to the MaRHE Center.
Nowadays, over 1000 wave energy converters (WECs) [
80] have been patented over the last twenty years in order to transform wave energy into electrical energy. Several of these technologies are still in an early stage of technical development, and only few of them are ready for a pre-commercial stage (e.g., Aquabuoy, Aws II, Dexa wave, Limpet, Mutriku, OBREC, Oyster, Rewec III, Seabased, Pelamis, PowerBuoy, Wave Dragon, Wavestar, etc.) The selection of the best leading technologies or the tuning study of a specific WEC is out of the scope of this paper. Regarding the wave-to-wire efficiency of these technologies, from previous extensive literature [
81,
82,
83,
84,
85,
86,
87,
88,
89,
90,
91,
92,
93,
94,
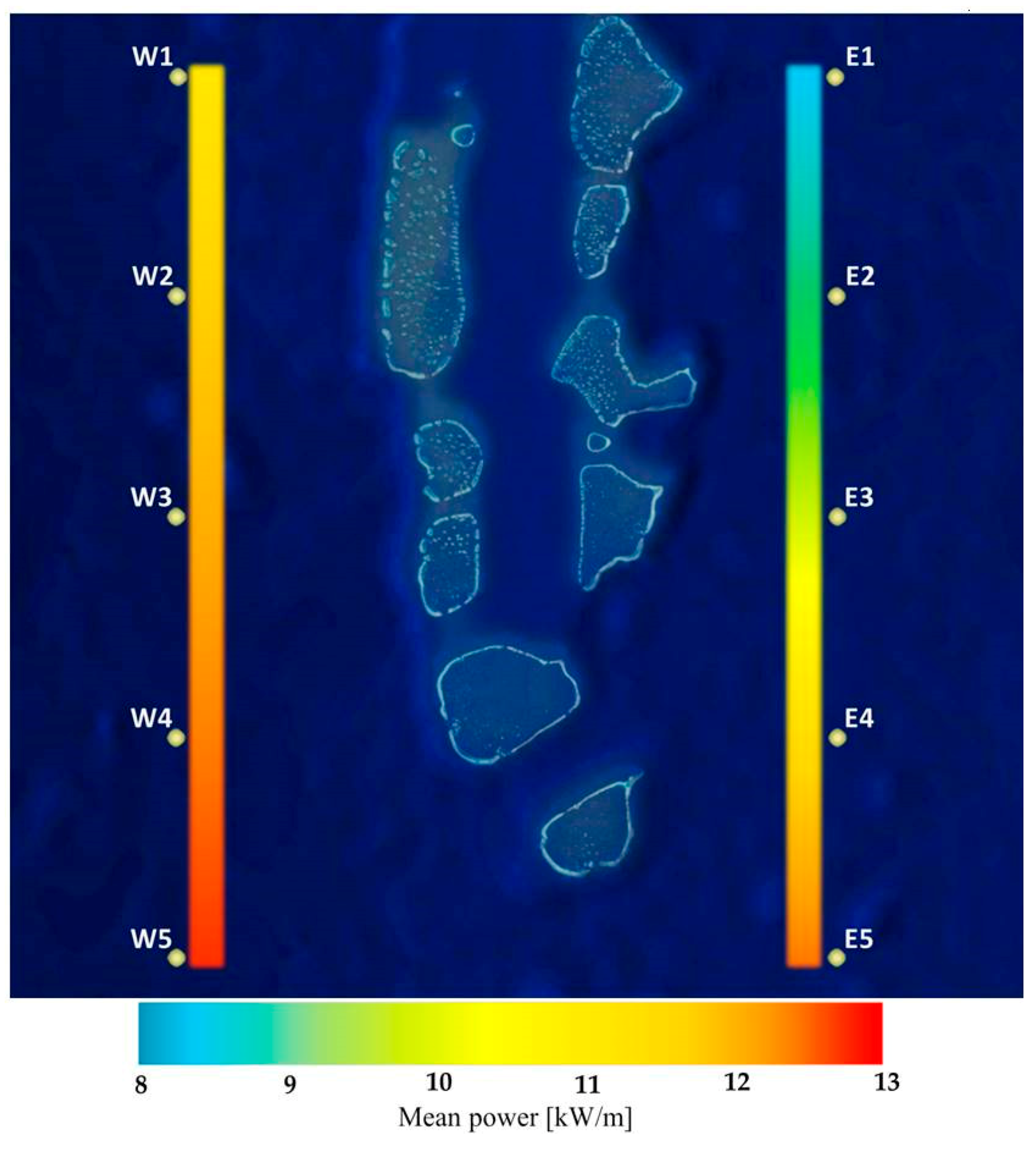
95] it is possible to assume, for a generic WEC, an overall averaged efficiency of 16.5%. In order to cover the Malé electricity demand of 300 GWh/year, a theoretical wave harvester over 20 km long should be required (8.8 kW/m are considered). Hence, wave energy seems more promising in supply energy in conjunction with other renewable sources. In particular, WECs have specific advantage for smaller islands, in order to maximize diesel savings in the short term and minimize the energy storage costs in the longer term. For instance, for Magoodhoo (where about 11.6 kW/m are computed), just a ten meters wide WEC is able to supply the whole island electricity demand (approximately 150 MWh).
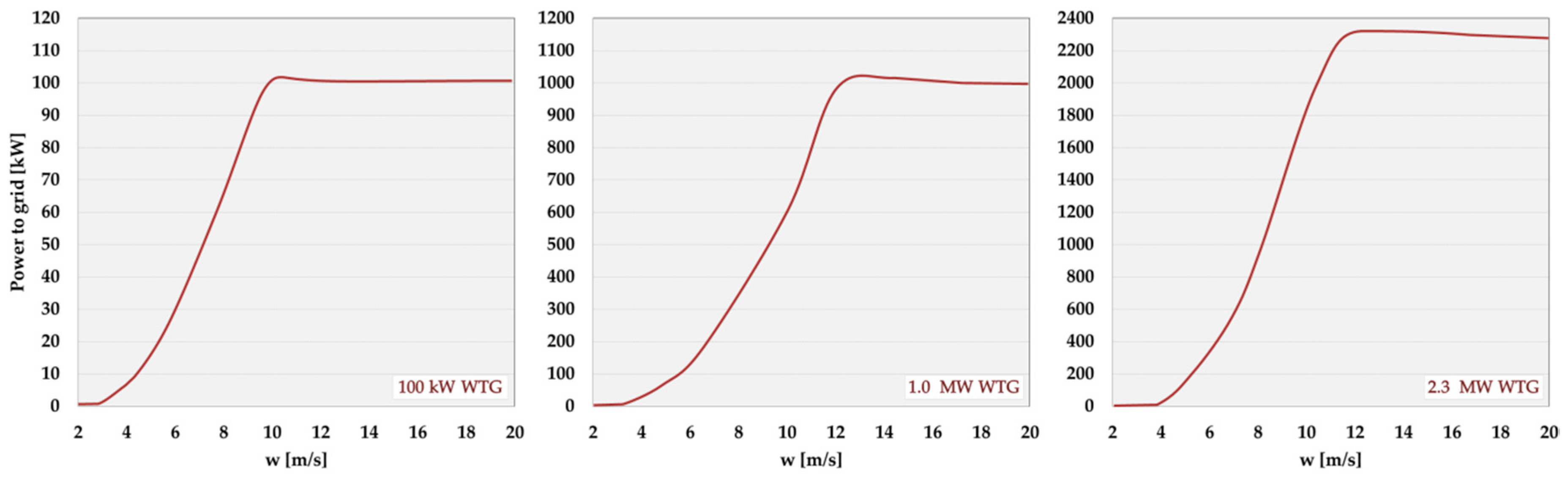
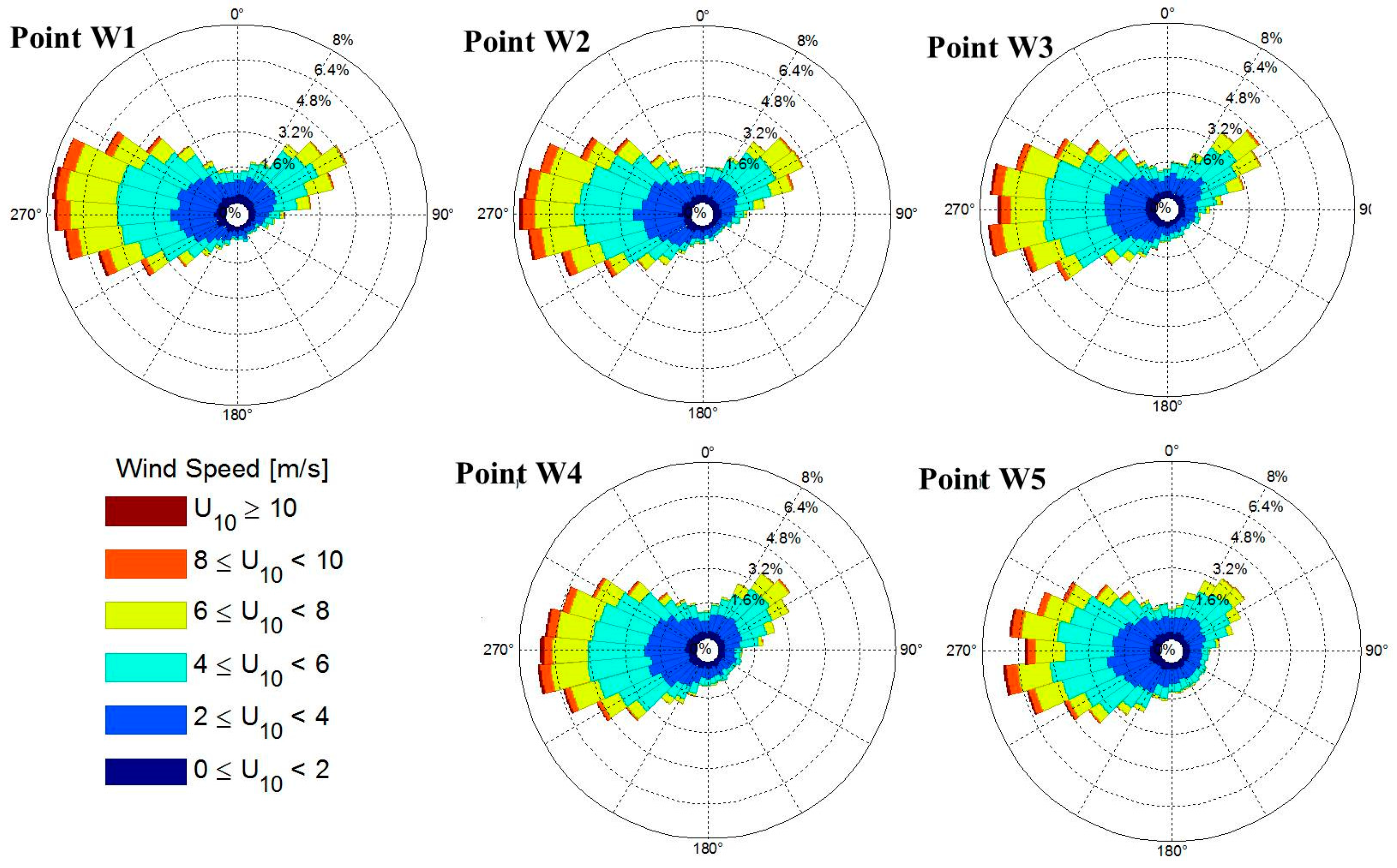
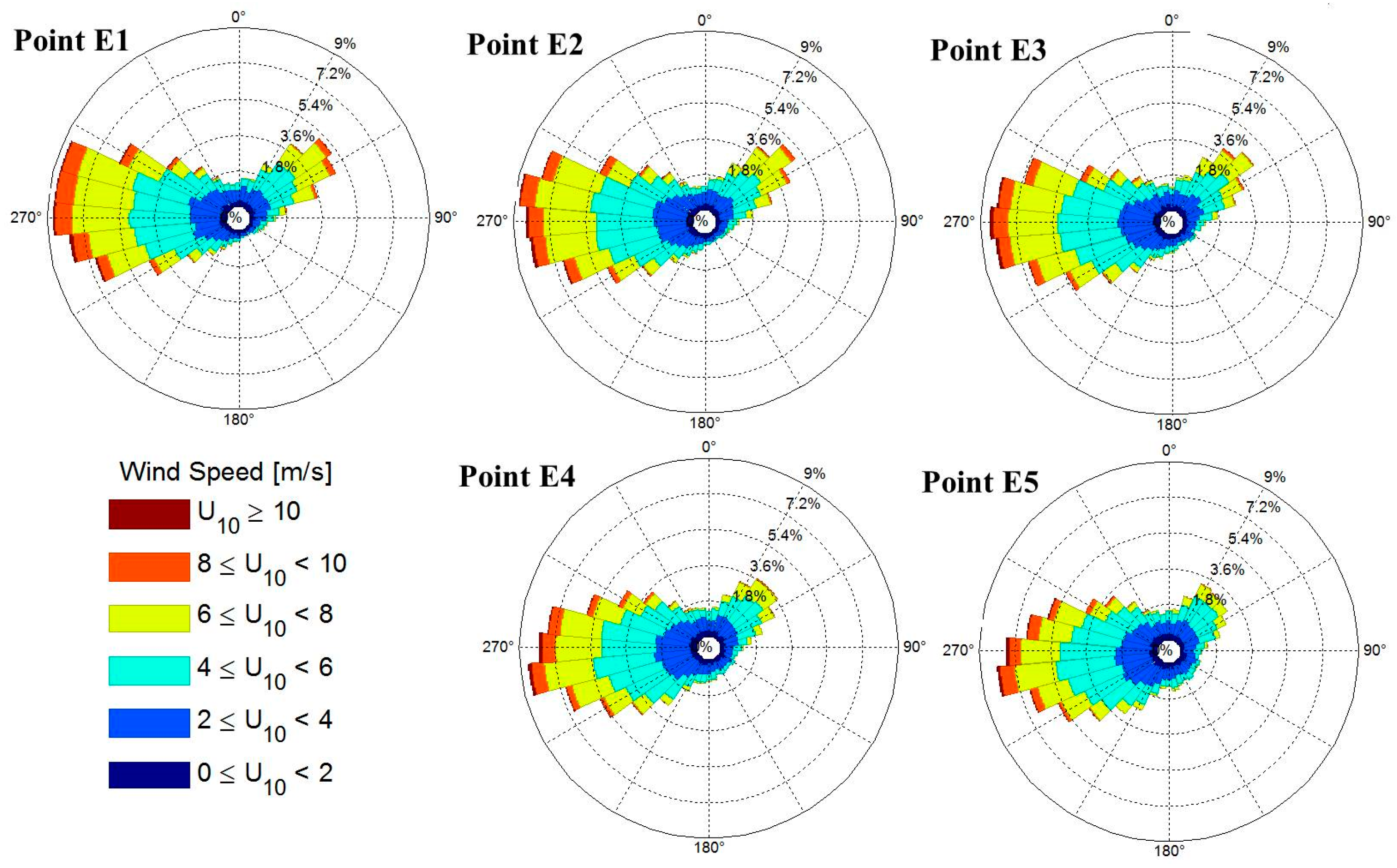
Wind resource in the Maldives is high in comparison to the energy demand.
Table 12 and
Table 13 compare the theoretical wind power, P
wind, the wind-to-wire power, P
tur, and the annual averaged energy, E
yearly,mean, produced by the three aforementioned idealized WTGs at each Western and Eastern grid points. From an economic point of view, results show that larger turbines are more efficient. In fact, regarding the energy production, for one 2.3 MW WTG, three 1.0 MW WTGs and about 21 small 100 kW WTGs are needed. For a large turbine, the yearly energy could arise in average 4.33 GWh on the west side and 5.11 GWh on the eastern part of the archipelago. This represents an important result because about 100 wind generator of 2.3 MW could provide the approximately 480 GWh of the whole electricity sector, moving the Maldives towards energy self-sufficiency using offshore wind power.
However, such a high level of wind energy potential does not come without difficulties. First of all, the use of a single source of energy does not fit with energy security strategies, addressed to ensure the uninterrupted physical availability of energy products and to balance and diversify the various sources of supply. Secondly, visual impacts of onshore and nearshore wind facilities represent one on the major concern considering the high value of Maldive’s natural seascapes. The environmental and socio-economic impact visual assets at highest risk from coastal and marine landscape change are directly linked to the height of wind towers and to the distance from the coastline [
96]. Both the social acceptance of an offshore WTG and the economic appeal for investors and utility providers remain heavily dependent on costs vs. payback analysis, that means competitively priced electricity supplies and reliability.
A solution to significantly decrease the production costs of blue energies would be to develop hybrid technologies, i.e., co-locating floating/fixed WTGs and WECs at offshore locations, possibly by promoting multi-use platforms [
13,
14,
15,
16,
17,
18,
19,
20,
21,
22,
23]. The combination of wind and wave energy resources reduce the overall dimensions per unit of power, the operational requirement for reserve and regulating power [
97,
98,
99,
100,
101] as well as the requirement for generation capacity to maintain the power system reliability [
102,
103,
104]. By the co-location of wind and wave generators, also the nearshore or shoreline devices are further promoted. Especially for the last case, devices embedded within coastal [
93,
105,
106,
107,
108,
109] or offshore infrastructures could be also combined with desalination plants. That solution has been recently considered in depth from many Authors (e.g., [
110,
111,
112,
113]). Numerous low-density population areas lack not only fresh water availability, but in most of the cases electrical grid connection or any other energy source as well [
114]. Most of the countries experiencing “water stress” have enough water, but lack the means to provide it in an accessible manner [
115]. For Magoodhoo, based on a specific energy consumption of 2.0 kWh/m
3 [
116] and water requirements of 1100 m
3 per person per year (included domestic, drinking and food production purposes according to [
117]), a 90 m wide WEC could ensure the total freshwater demand.
Moreover, this island has been recognized as one of the 86 islands that have reported severe beach erosion since 1990 [
118]. In order to provide stabilization to the 2.3 km of Magoodhoo coastline with a beach drainage system (considered a low impact soft-engineering solution by coastal managers), a preliminary configuration has been assessed. For such a configuration, constituted by 4 parallel pipelines surrounding the island and pumping stations characterized by 12 pumps of 6.5 kW (adapted from [
75] and [
119]), an average annual electricity demand of about 200 MWh €/year can be computed. Hence, a WEC 115 m wide could provide the total requests of energy, freshwater and beach stabilization purposes of the whole island. This proves the high benefits provided by WECs for small islands, according to [
56,
120].
On the other hands, due to the lower wave resource in the eastern region, the about 114 million m3/year of potable water for Malè requires large wind farms. A preliminary analysis using data for the 2.3 MW WTG, indicates as a number of 42 turbines are needed. Obviously, that number can reasonably be reduced if wind and wave harvesters are co-located.