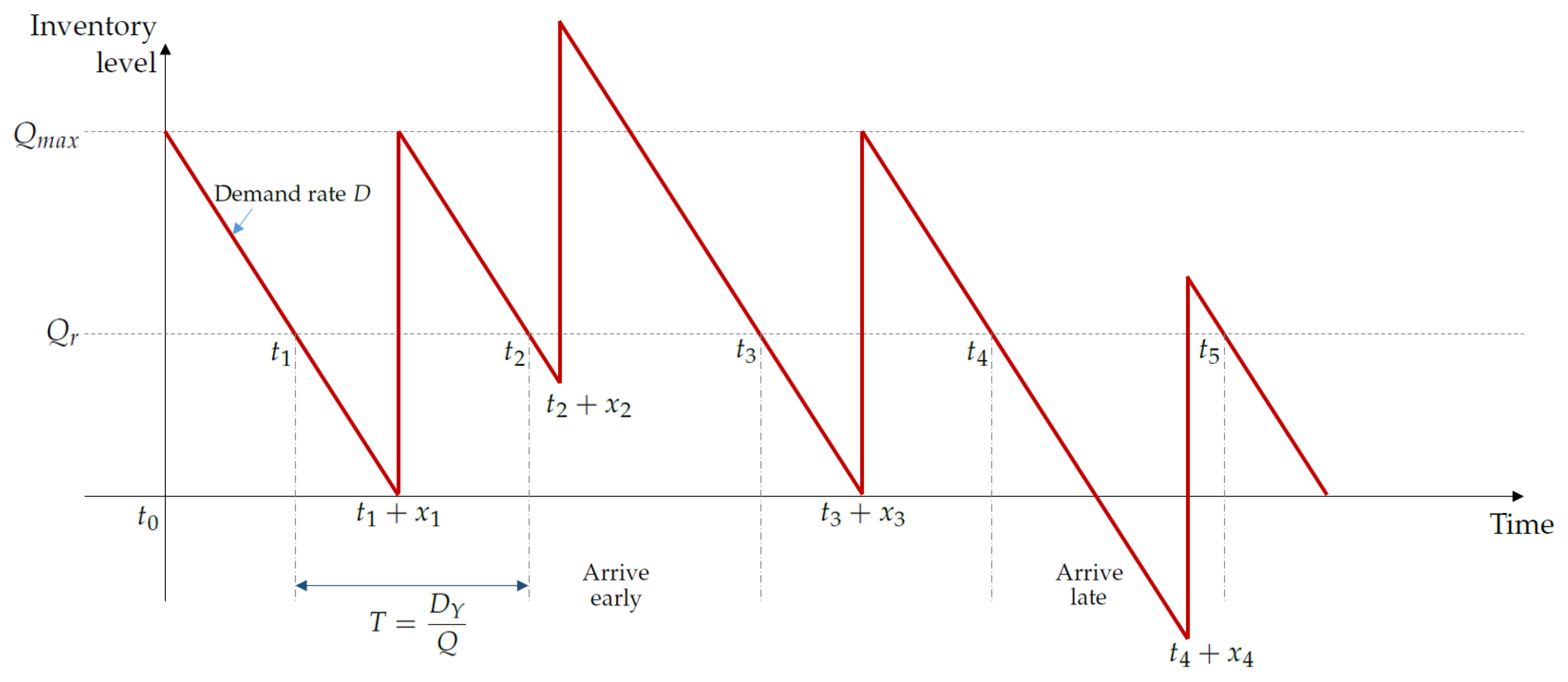1. Introduction
According to the World Trade Report 2015 [
1], international trade has been growing at a modest pace in recent years, and the exports of developing and emerging countries in particular have been growing faster than those of developed ones. Effective international trading and sourcing have become essential for competing on price in commodity markets. As the amount of international trade grows, transportation is regarded as a major driver of the globalization of supply chains, and subsequently, the distances managed by logistics have become much longer than before. Furthermore, because of the centralization of production, many companies use long-distance sourcing so that they can gain a competitive advantage on price.
However, growing international trade has exposed the now globalized supply chains to many types of risks, and the risks associated with long-distance sourcing have further increased due to longer and, therefore, more variable lead-times. Furthermore, the increase in transportation due to international trade causes much pollution. According to Sources of Greenhouse Gas Emissions [
2] by the EPA (U.S. Environmental Protection Agency) in 2014, 26 percent of total U.S. greenhouse gas emissions by the economic sector derived from the transportation area. The IPCC report [
3] also states that the greenhouse gas emissions caused by transportation are mainly from the burning of fossil fuels in cars, trucks, ships, trains and planes. Over 90 percent of the fuel used for transportation is petroleum-based, including gasoline and diesel. Recently, external emission costs [
4,
5] have become an important issue for supply chain management because of several environment conservation agreements, such as the Kyoto Protocol and the Paris Agreement. Due to increasing concerns about the environment and sustainability, managing transportation costs in inventory and supply chain management has become more important than ever.
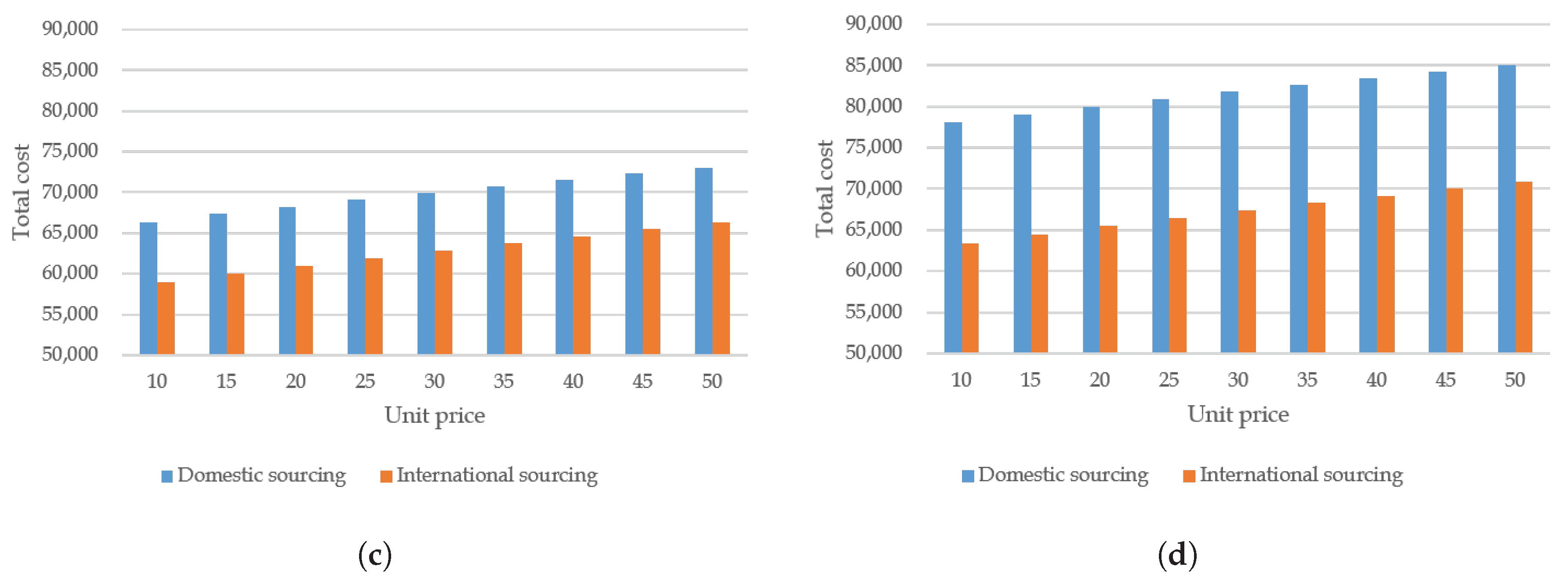
In this paper, we examine a single-product replenishment problem, which takes both lead-time uncertainty and multi-modal transports into account. We note that lead-time uncertainty and multi-modal transportation are two major characteristics of international trades and global supply chains. Specifically, we are interested in developing a mathematical model of the replenishment problem incorporating sustainability considerations, which has become essential as international trading and sourcing have grown, to reflect the growing recognition of the external effects of transport and subsequently more sustainable use of transport modes. Through the replenishment decision models, we intend to address the effects of sustainability considerations on operational decisions, such as replenishment decisions, choices of transportation modalities and sourcing decisions (specifically, domestic sourcing vs. international sourcing).
The remainder of the paper is as follows.
Section 2 reviews the previous studies relevant to the problem under consideration.
Section 3 provides a description of the sustainable EOQ (S-EOQ) problem with lead-time uncertainty and multi-modal transportation options and proposes its mathematical programming model. In
Section 4, we perform numerical experiments and a sensitivity analysis and discuss the managerial insights gained. Finally, we conclude the discussions in
Section 5.
2. Literature Review
In this section, we mainly review EOQ models incorporating environmental and sustainability factors and their extensions considering either uncertain lead-times or transportation mode selections. Turkay [
6] extends the conventional EOQ model to one incorporating sustainability considerations by adding environmental criteria and evaluates five different approaches including direct accounting, carbon taxes, direct caps, cap and trades and carbon offsets. Hua et al. [
7] consider a sustainable EOQ model using cap-and-trade approaches and examine the relation between the order size of carbon cap and carbon price. Their model, unlike ours, does not include transportation mode choices in the decision model. Bonney and Jaber [
8] also develop a model that extends the EOQ to include some environmental factors. However, their model has some shortcomings, including no calculation of the social costs of vehicle emissions and no examination of the effect of transportation mode selection. Wahab et al. [
9] partly examine the impact of considering the environment on the optimal production-shipment policy for items of imperfect quality in a two-level supply chain. In the model, they divide
emission costs into fixed and variable costs. They compare the case with and without environmental effects and evaluate how the total expected costs and optimal number of shipments change depending on the environmental considerations applied. However, they ignore the selection of transportation mode in the two-level international supply chain. Bouchery et al. [
10] reformulate the conventional EOQ model as a multi-objective problem because of the difficulty of developing a single objective problem that considers all aspects of sustainable issues. Moon et al. [
11] present a bi-objective mixed-integer linear programming model in a multi-period planning horizon with inaccurate information on raw material resources under a carbon emission constraint. However, the model does not consider combination of transport modes and the length of transportation routes, which are different from ours. Lastly, Battini et al. [
12] recently proposed a sustainable EOQ model, from which we extend in this paper. They investigate the environmental impact of inventory and transportation in the traditional EOQ model by additionally incorporating the sustainability factors into the replenishment model. For further information, we refer readers to a survey paper [
13], which comprehensively explores the evolution of EOQ models, including lot-sizing research on environmental sustainability.
None of the works reviewed above incorporate lead-time uncertainty, which is one of the primary sources of uncertainty, especially in international supply chains. There is limited research on EOQ models, including both lead-time uncertainty and sustainability considerations. Digiesi et al. [
14] develop a sustainable EOQ model, which, like ours, incorporates lead-time uncertainty. They identify the optimal order quantity and modal selection with respect to the loss factor of modals with different coefficients of variance. However, the paper compares only mono-modal transportation options.
When it comes to multi-modal transportation options, Winebrake et al. [
15] propose an intermodal network model called GIFTto help evaluate the costs, the delivery times and the environmental and energy impacts associated with mono-modal and intermodal freight transport. In the paper, they perform some numerical experiments with the same source and destination, but different routes. They show that the decision made varies depending on which decision criterion, such as the minimization of carbon dioxide, cost or time, is important to the decision maker. In this paper, we examine multi-modal freight transport with lead-time uncertainty.
3. Sustainable EOQ Model with Lead-Time Uncertainty and Multi-Modality
To understand the effects of lead-time uncertainty with multi-modal shipment options on S-EOQ decisions under the policy, we present the mathematical formulation of the concomitant S-EOQ problem. Before introducing the model formulation, all of the parameters and decision variables used in this paper are given as follows.
Decision variables:
| Q | order quantity |
| reorder point |
Sets and parameters:
| set of modals (1: air; 2: ship; 3: train) |
| X | random variable for lead-time, with pdf of and cdf of |
| H | planned time horizon |
| h | holding cost per unit item per unit time |
| s | shortage cost per unit item |
| D | demand per unit time |
| annual demand (constant) |
| T | length of cycle time |
| inventory level at time t |
| maximum inventory level |
| transport distance by modal k |
| n | number of orders () |
| j-th ordering time () |
| a | weight of an obsolete unit stored in the warehouse (ton/unit) |
| p | unit purchase price |
| unitary scrap price |
| o | ordering cost |
| average carbon emission cost coefficient of inventory waste for collection and disposal ($/ton) |
| b | space occupied by a product unit (/unit) |
| average carbon emission cost coefficient of a warehouse ($/) |
| total holding cost with carbon emission generated by warehousing per unit item per unit time |
| fixed internal cost coefficient for transportation mode k ($/km) |
| fixed external cost coefficient for transportation mode k ($/km) |
| variable internal cost coefficient for transportation mode k ($/km ) |
| variable external cost coefficient for transportation mode k ($/km ) |
In this paper, we assume that the annual demand is deterministic and constant as in the traditional EOQ model. Thus, it is assumed that
holds throughout the paper. We also assume that the initial inventory level
is equal to
as illustrated in
Figure 1. Given those assumptions, we now present the problem formulation for the S-EOQ model.
The total annual cost of the model (
) consists of the purchasing cost, ordering cost (
), holding cost (
), shortage cost (
) and transportation cost (
). Since the annual purchasing cost is independent of the decision variables, for simplicity, it is henceforth excluded from the total annual cost calculation as presented in Equation (
1).
From a sustainability point of view, the total annual cost
in this model includes economic costs associated with environmental and sustainability effects when we calculate holding cost
and transportation cost
due to the fact that storage and transportation of goods within supply chains are major causes of environmental damage in modern value-added processes. According to Dhooma and Baker [
16], carbon emission related to warehousing is a significant factor because of the considerable energy requirements for heating, cooling, materials handling equipment, and so on. Furthermore, transportation activities are responsible for around 25% of the world’s energy use and for almost 22% of global energy emissions [
4]. The incorporation of environmental costs in the calculation of both holding and transportation costs will be discussed with details in the following subsections.
We now take a look at the details of each cost component. For a better understanding of them, we first illustrate the structure of the inventory profile and its changes over time as shown in
Figure 1 and then explain the possible cases resulting from the lead-time uncertainty. According to the well-known
policy, an order of amount
Q is placed whenever the inventory level drops below the reorder point
and the order arrives after the lead-time
X, which is uncertain in this paper. As mentioned earlier, we assume that the inventory level drops by the constant rate of
D. Suppose that the lead-time of an order is
, and an order placed at
arrives at
. The lead-time uncertainty creates two possible cases. Consider the case of an order placed at
and with a lead-time
, which is less than the average lead-time. Assume it arrives at
before the inventory level drops below zero. This case obviously incurs a higher holding cost. Consider the contrasting case of an order placed at
and with a lead-time
, which is more than the average lead-time. Assume it arrives at
after the inventory level drops below zero. This can clearly incur higher stock-out costs. Thus, a supply chain with lead-time uncertainty may have higher total expected annual cost than the one with a deterministic lead-time. Based on the discussion above, the inventory level at time
t over a cycle
can be expressed as Equation (
2):
We remark that Equation (
2) is divided into two parts based on the time at which the order placed at
arrives.
We now examine each cost component in detail.
3.1. Ordering Cost
The annual ordering cost (
) is simply calculated as the number of orders multiplied by the (fixed) ordering cost per order, which is:
3.2. Holding Cost
Due to the lead-time uncertainty, the calculation of the annual holding costs () is not straightforward, and hence, we divide the calculation into two cases depending on the inventory level when a new order arrives.
- (a)
The case when the lead-time is less than the expected lead-time:
We let
be the holding cost per cycle when the order replenishment policy follows
. The lead-time
x is less than the expected lead-time. By referring to
Figure 1 and especially the interval between
and
, the holding cost per cycle can be expressed as in Equation (
4).
- (b)
The case when the lead-time is greater than the expected lead-time:
In this case, the lead-time
x is more than the expected lead-time. Refer to the interval between
and
. The corresponding holding cost
can be expressed in Equation (
5).
Based on the discussions above, the expected holding cost per cycle,
, is calculated as:
We remark that Equation (
6) is the expected holding cost per cycle, and we additionally need to take the residual part (i.e., inventory profiles over
and
in
Figure 1) into account to completely calculate the expected total holding costs completely. Then, the corresponding holding cost
for the residual part can be simply represented by:
Finally, we can calculate the total expected holding cost
by combining Equations (
6) and (
7) as below.
So far, we have derived the expected holding cost over the planning horizon for the conventional EOQ model under lead-time uncertainty. As mentioned earlier, the concomitant model under study incorporates the aspects of sustainability, and we now discuss how such aspects may influence the expected holding cost. In practice, carrying additional inventory incurs some emission cost due to factors such as the emissions for space, from maintenance facilities and by scrapped materials. Furthermore, the emission costs for holding inventory and for scrapped materials are separated into the one of the previous studies (for example, [
12]). However, they should have been included in a portion of the holding cost coefficient, as in Equation (
9).
For this reason, this paper will use , the holding cost with emission per item per unit time, in place of h.
3.3. Shortage Cost
Shortage cost is a sort of penalty cost due to the lack of product availability. According to Campo et al. [
17], the stock-out cost depends on many factors, such as the availability of acceptable alternatives, deal proneness, item loyalty, private label buyers, product importance, the regular package size and other package sizes. However, since most of the factors are qualitative, it is difficult to measure them. Moreover, the ways to obtain stock-out costs can differ depending on the types of items or their sectors. Thus, it is conventional to use a fraction of the unit price as the shortage cost, as is done in this paper.
Shortage occurs in the same situation for which we derived Equation (
5). In accordance with the discussion above, the shortage cost when the lead-time is
x is given in Equation (
10) below:
and hence, the expected shortage cost per cycle becomes:
Therefore, the annual shortage cost is as per the discussion on .
3.4. Transportation Cost
The transportation costs, in general, consist of two components: fixed and variable costs. Fixed costs include truck leasing cost, driver salaries, and so on, which are generally independent of order quantity. However, we assume that they depend on the travel distance. On the other hand, variable costs are additional costs that are proportional to the order quantity.
In this model, we consider multi-modal transportation options, and the travel distance depends on which shipment mode is used. When it comes to the transportation cost formulation, we take the multi-modal transportation options into account as presented in Equation (
12), which is similar to the transportation function given in Battini et al. [
12].
As shown in Equation (
12), both internal costs (e.g., vehicle rents, driver salaries, insurance and fuel fees) and external costs (e.g., air pollution from fuel, road congestion, traffic accidents and land use impacts) are considered as fixed, as well as variable transportation costs [
4]. We note that the transportation distance depends on the transportation mode used.
3.5. Total Annual Cost
So far, we have examined each cost component of the concomitant model under interest. We now present the mathematical formulation for the sustainable EOQ under lead-time uncertainty and multi-modal transportation options as follows.
We now examine the functional property of for determining the optimal order quantity and reorder point . By evaluating the Hessian matrix of with respect to Q and , it is straightforward to show that the Hessian matrix is positive semi-definite, and hence, we simply omit the proof. Based on the results, we can derive the following proposition.
Proposition 1. The total annual cost function is jointly convex in Q and .
We note that, according to Proposition 1, and simultaneously satisfy the system of linear equations and .