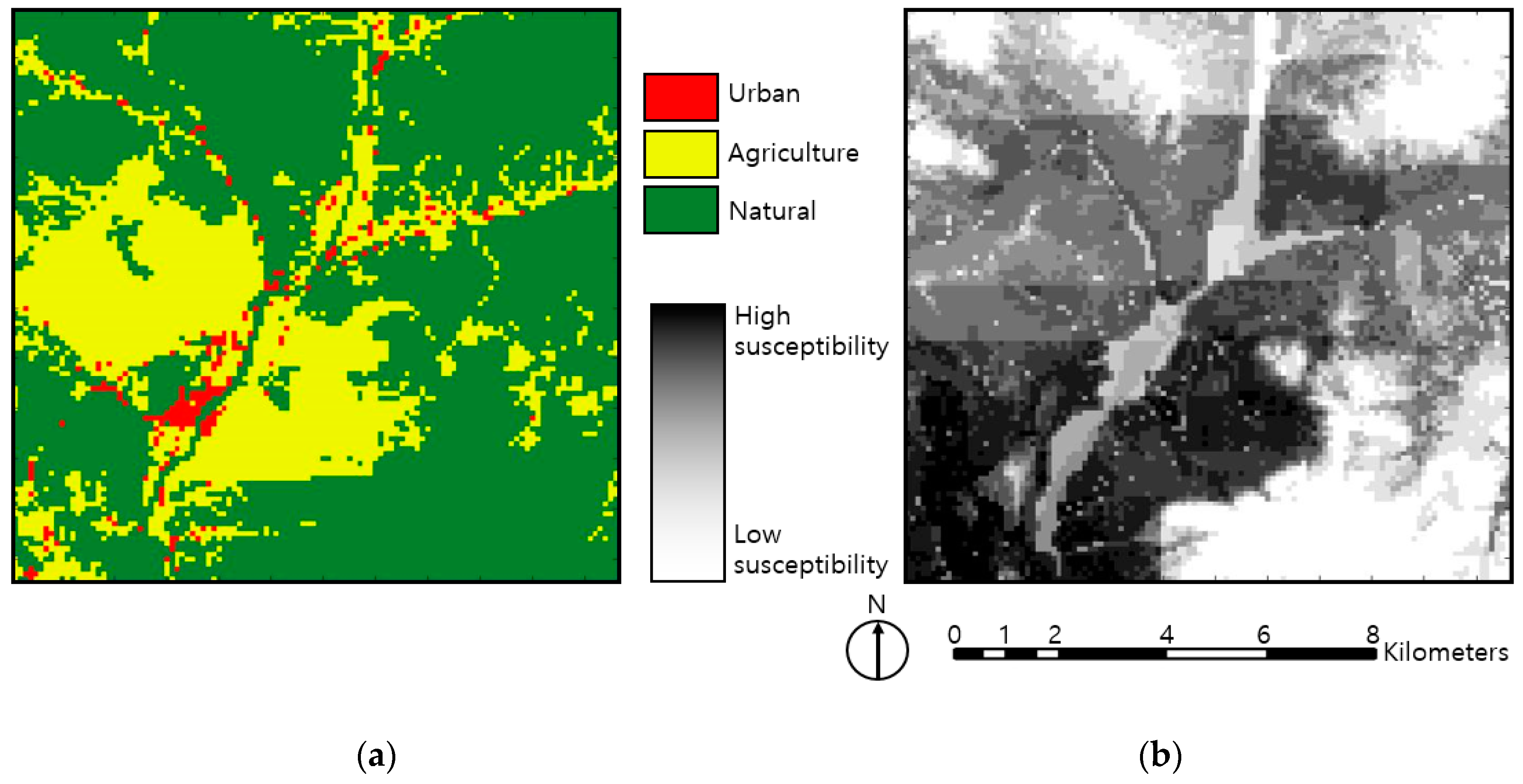
1. Introduction
In recent years, the increasing variability in precipitation patterns has triggered frequent extreme landslides [
1,
2]. Landslides are one of the critical natural phenomena that lead to serious problems in hilly regions on a global scale [
3]. In the case of Gangwon-do, a typical mountainous region in Korea, 44 casualties (including 19 missing persons) resulting from flooding and landslides were reported in 2006. The Baduella District of Sri Lanka, El Cambray Dos of Guatemala, Maharashtra of India, and the Sindhupachok District of Nepal have also experienced severe damage, with more than 100 casualties in the last three years. These cities are still at risk for potential landslide damage because the frequency and scale of landslides may further increase in the near future due to climate change. Therefore, we are concerned with where the landslides may occur and how we should respond to the risk of landslides in these cities.
Over the past two decades, numerous researchers have assessed landslide hazard under the present and future conditions influenced by climate change to estimate potential probabilities [
4,
5,
6,
7,
8,
9]. In those studies, the amount of overlapping urban and hazardous areas represents the regional risk level because landslide damage, such as property loss and casualties, is concentrated in urban areas. Even though the reduction of risk in advance is extremely important for mitigating large-scale disasters, only a few studies have addressed how to respond to potential landslide damage, i.e., landslide risk. For urban planning purposes, landslide risk can be reduced by placing urban areas in safe zones that have lower landslide hazard grades [
10,
11].
Land-use composition is driven by social, economic, and environmental factors and cannot be allocated based on the mitigation of landslide risk alone. In reality, numerous objectives, constraints, and stakeholders are involved in planning, which can be conflicting [
12]. Researchers have called this a “nonlinear problem,” which cannot be solved with qualitative knowledge or traditional linear modeling. In many cases, land-use planning systems have failed to balance different values, such as economic benefits, protection of natural resources, and social safety [
13]. Therefore, we require scientific and quantitative tools that can incorporate numerous factors and help us create comprehensive plans.
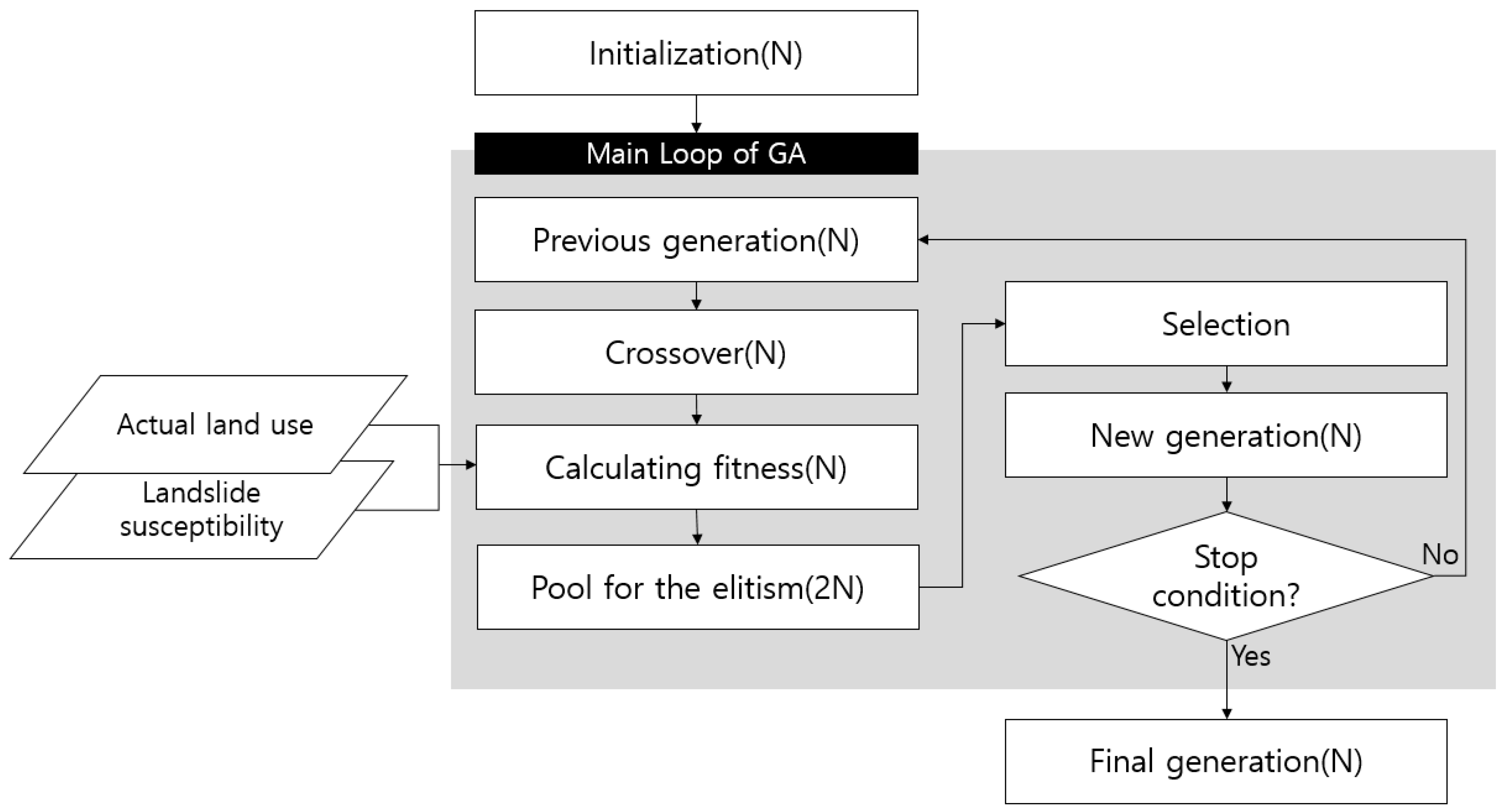
Genetic algorithms (GA) are the most popular optimization tools to address multi-objective problems in land-use planning [
14,
15,
16,
17,
18]. Unlike other heuristic approaches, the GA approach is a general-purpose search method, combining elements of directed and stochastic searches, which can create a superior balance between the exploitation and exploration of a search space [
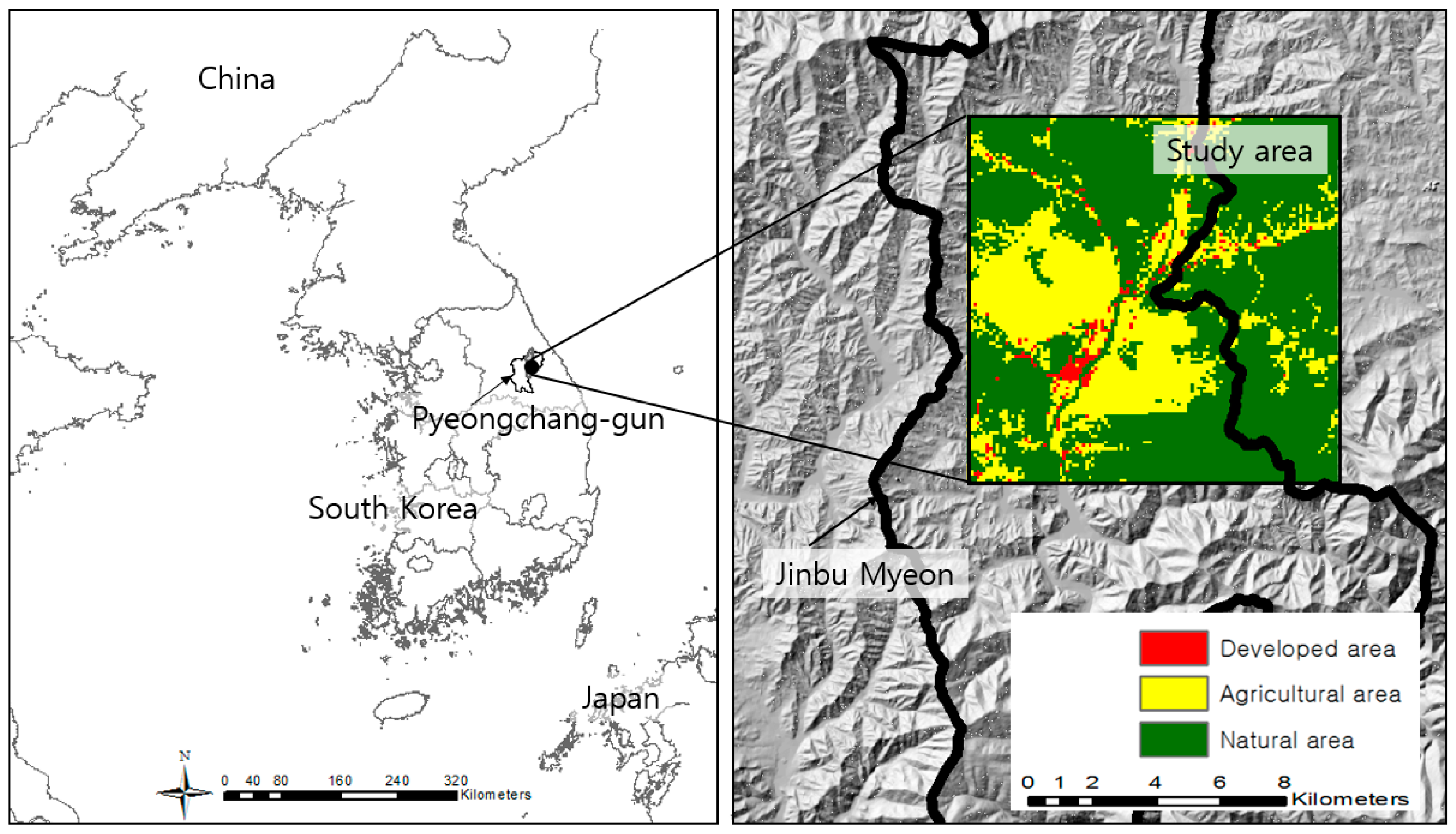
19]. Additionally, the application of a GA allows for immediate feedback to stakeholders because it can run a number of experiments with different parameter values. Therefore, we suggest a quantitative tool, the Multi-Objective Genetic Algorithm (MOGA), which can generate a comprehensive land-use allocation plan that considers landslides under climate change, and apply it to the Pyeongchang-gun area of Korea. Pyeongchang-gun, a typical mountainous city, is the fastest changing region in Korea due to its development for the 2018 Winter Olympics. Urban sprawl into natural areas in this city has caused an increase in potential disaster risk, especially with regard to landslides. We also considered the “minimization of land-use change” and the “maximization of compactness” as optimization objectives. Land-use change is associated with a certain amount of economic cost and compactness is an important factor for land management. The optimized land-use plans that we created can be used as guidelines or as basic data by regional stakeholders. They can also contribute to the spatial adaptation plans against climate change impacts. We are careful to note that the optimization results are not the only good alternatives; rather, they are meant to support further detailed design or analysis by stakeholders [
14,
20].
In
Section 2, we introduce the study areas and describe the datasets, the method of landslide hazard analysis, and optimization. The optimization objectives and constraints are also described in this section. In
Section 3, we present the changes in landslide hazards with climate change and related optimal land use patterns. In
Section 4, we present the implications and limitations of the optimization results and directions for future research.
4. Discussion
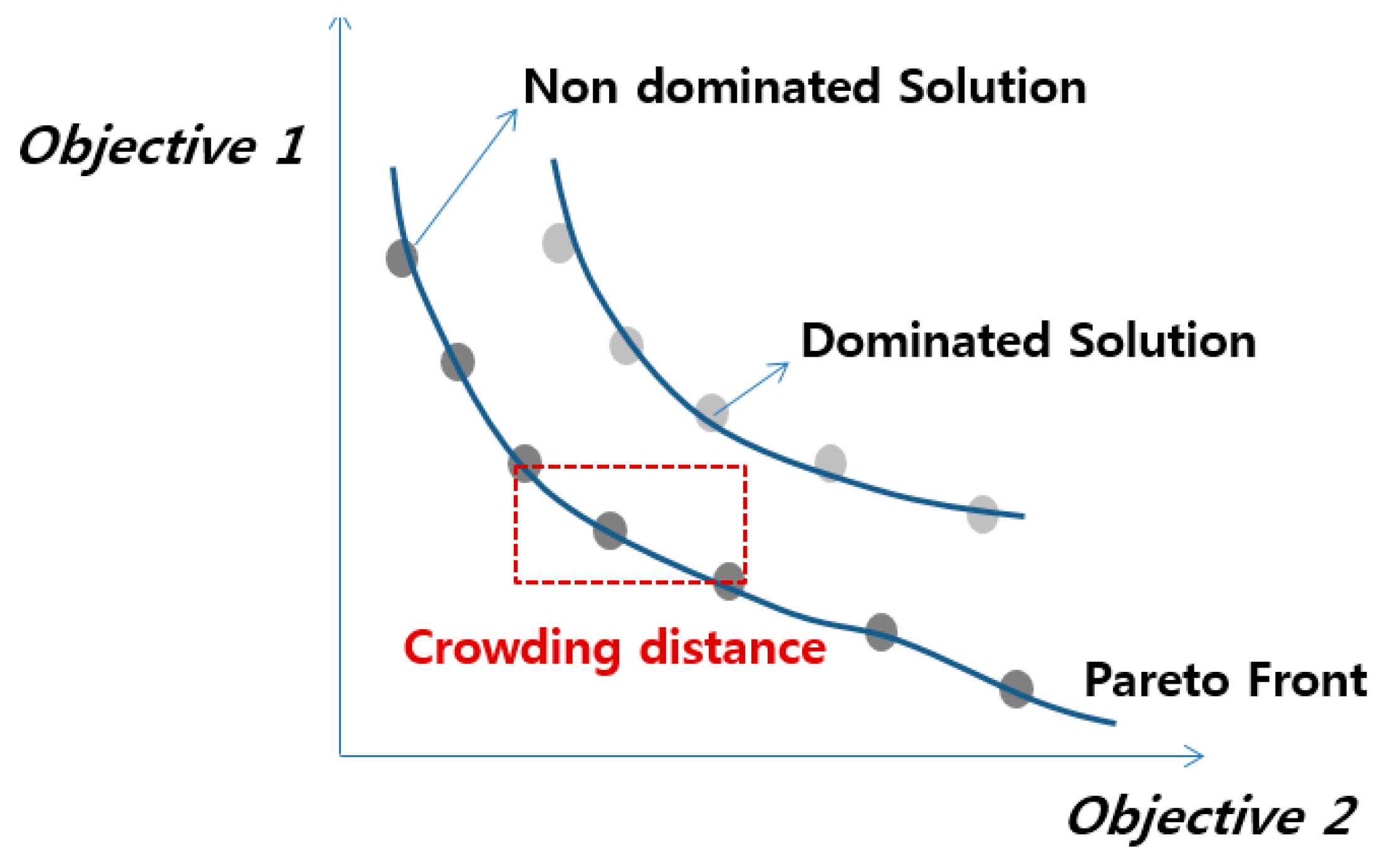
We generated a range of optimized plans for the multi-objective problems without the relative weighting factors. From the perspective of reducing the landslide risk, land-use plans optimized on one objective could be better than the other plans optimized on multi-objectives, but this can result in unacceptable plans for stakeholders with different interests. In multi-objective problems, however, defining the relative importance of each objective is very difficult. Additionally, the determined weights have difficulty in handling the changing environment; the most important objective under current conditions may not be the most important one in the future. The non-dominated land-use plans we suggested using NSGAII include all possible combinations of weighting factors [
29]. The planners or decision makers can choose one plan, depending on their knowledge or problem-related factors [
30] and use it to conduct detailed planning.
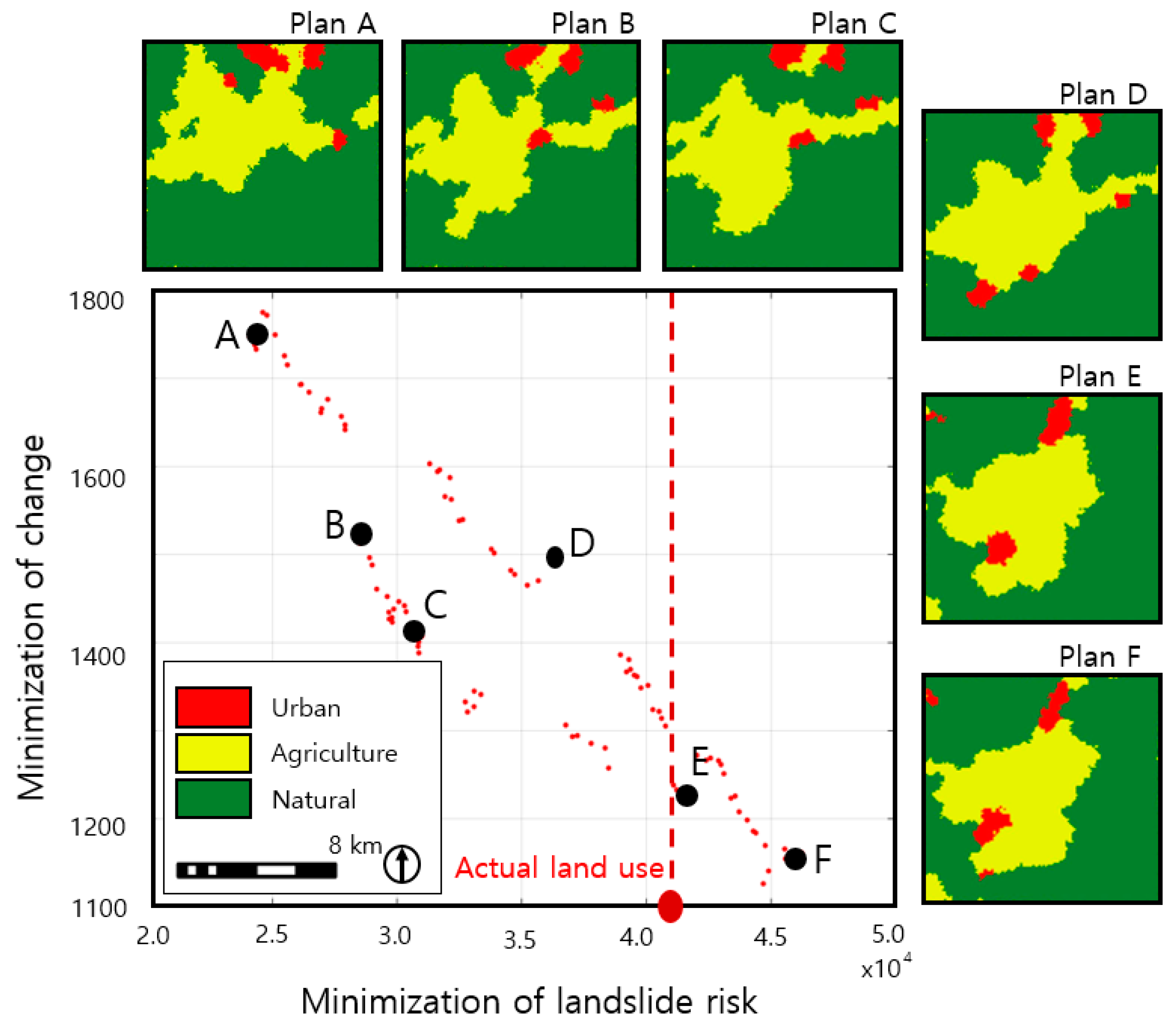
All the optimized plans are better than the actual land use for at least one objective: minimization of landslide risk or maximization of compactness. All plans showed a dramatic improvement—especially in compactness—by at least 60%. However, in case landslides become a major issue, plans E and F are difficult to select (
Figure 7) because of the landslide risk increase from the current level. Land conversion in these plans occurs only to improve compactness. Compactness is one of the most important objectives considered in most related studies [
17,
26,
27,
31,
32,
33,
34,
35,
36,
37], but landslide risk also needs to be reduced to some extent, because land use conversion is very costly. We have obtained 100 non-dominated plans of various weight combinations, but the range of plans that can actually be selected is narrow. If the Pareto front line is moved inward (southwestward), we can obtain more plans distributed on the left side of the red line (
Figure 7). We expect this can be done in future studies by incorporating the actual land use in the initial population or by establishing strict constraints such as the conversion ratio [
37,
38] and maximum cost [
39]. In this study, we employed some climate variables from the RCP scenario to reflect the long-term future of the study area in land-use planning. The spatial resolution of the RCP scenario can create some problems in generating land-use plans. The scenario data are produced at the resolution of 1 km by KMA and the resolution of other variables is 30 m. We considered a resolution of 100 m because further downscaling could decrease the reliability of the scenario data. However, the resolution of 100 m is too large to express linear land-use patterns such as rivers, railroads, and highways and subtle changes in soil and topography. In fact, the linear land-use types tend to disappear in all optimized plans. Therefore, we expect that the resolution problem of climate scenarios will be solved in future studies on land-use planning.
Our optimized results can also be considered spatial adaptation options or solutions for the potential landslide problem under climate change. Climate change research has so far focused on the assessment of the impacts of climate change on disasters, ecology, and industry. We now need to discuss spatial adaptation: how to change the actual space in response to climate change impacts because climate change is already happening [
23]. Adaptations to disasters such as landslides are a priority, as these events can lead to the loss of life and property. There are two ways to simulate land-use changes for adaptation: land-use predictions based on scenarios and land-use optimization to generate scenarios. Land-use prediction simulates land-use changes by a transition rule set based on the past trends and agent behavior. If we want to solve problems using land-use predictions, we have to establish related strategies first, then change the transition rule set, and finally simulate future land-use changes. It is not guaranteed, however, that simulated land-use change is appropriate for the problem at hand. Using the second approach, the land-use optimization, we can simulate appropriate land-use changes for the initial problem and then establish strategies to facilitate land-use optimization. GA is considered one of the most effective optimization tools. In some studies, these two approaches were applied in the coupled form to complement each other [
40,
41], but the optimization model was better than the prediction model in terms of problem-solving performance [
42].
To obtain more reasonable adaptation options, we plan to conduct future research that considers the positive possibilities together with the negative impacts of climate change [
43]. This study focused only on reducing the negative impacts of climate change by avoiding planning in urban areas where landslides are most likely to occur. However, by considering positive possibilities such as the expansion of suitable cultivation areas or habitats together, we can link the optimized results to sustainability in future climate change research, which will consider the balance among the social, environmental, and economic aspects.
5. Conclusions
In this study, we suggested tools to identify comprehensive land-use alternatives that could contribute to the reduction of the potential landslide risk in Pyeongchang-gun. This approach can provide guidance to municipal governments when allocating urban, agricultural, and natural areas and when establishing spatial adaptation plans that consider extreme meteorological disasters under climate change. The model developed based on GA is generally flexible and thus, can easily be applied to other similar problems. We only need to modify some part of the fitness function and dataset according to the objectives or adjust model parameters that suit the problem. For example, to consider the landslide hazard under different climate change scenarios, we could generate new optimized plans for that problem by replacing landslide hazard maps derived from new scenarios. Our model could also be used to generate land-use allocation plans for other cities suffering from landslides. A risk matrix for the land-use priority, objectives, and constraints, however, should be identified for any new cases.