Short Term Wind Power Prediction Based on Improved Kriging Interpolation, Empirical Mode Decomposition, and Closed-Loop Forecasting Engine
Abstract
1. Introduction
- (1)
- A new version of KIM, named Improved KIM (IKIM), is presented. The proposed IKIM includes the von Karman covariance model whose settings are optimized based on error variance minimization by an evolutionary algorithm.
- (2)
- An improved version of EMD is introduced. Cubic spline fitting of conventional EMD is replaced by IKIM in the proposed EMD. It is shown that the proposed EMD alleviates the problems of conventional EMD.
- (3)
- A new closed-loop forecasting engine is proposed for wind power prediction. This forecasting engine is based on NN trained by Levenberg–Marquardt learning algorithm.
- (4)
- A new wind power prediction approach is presented, which is composed of the proposed EMD, an information-theoretic feature selection method, and the proposed forecasting engine.
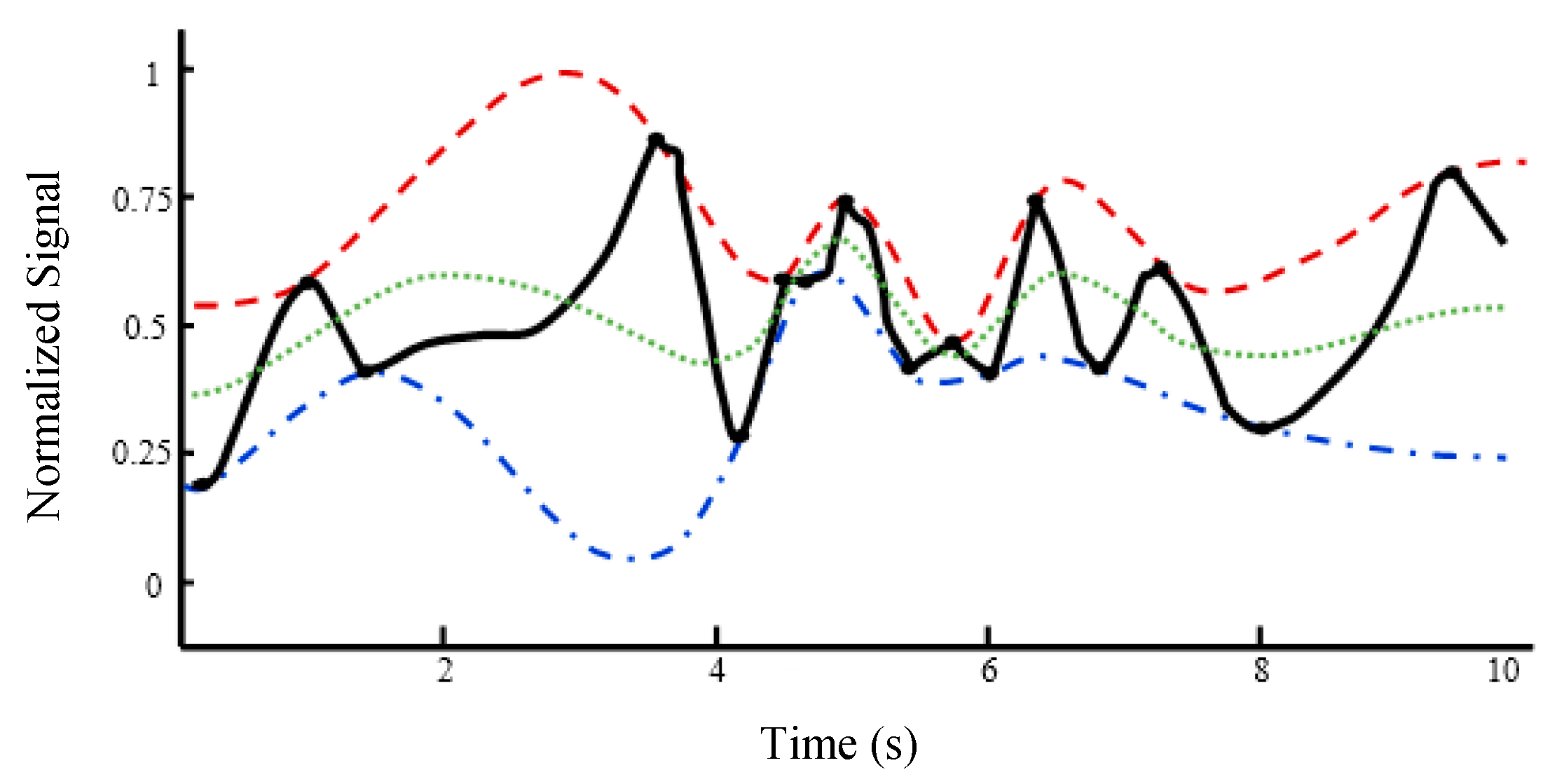
2. Empirical Mode Decomposition (EMD)
| EMD Algorithm: |
|
- Set x1(t) = x(t).
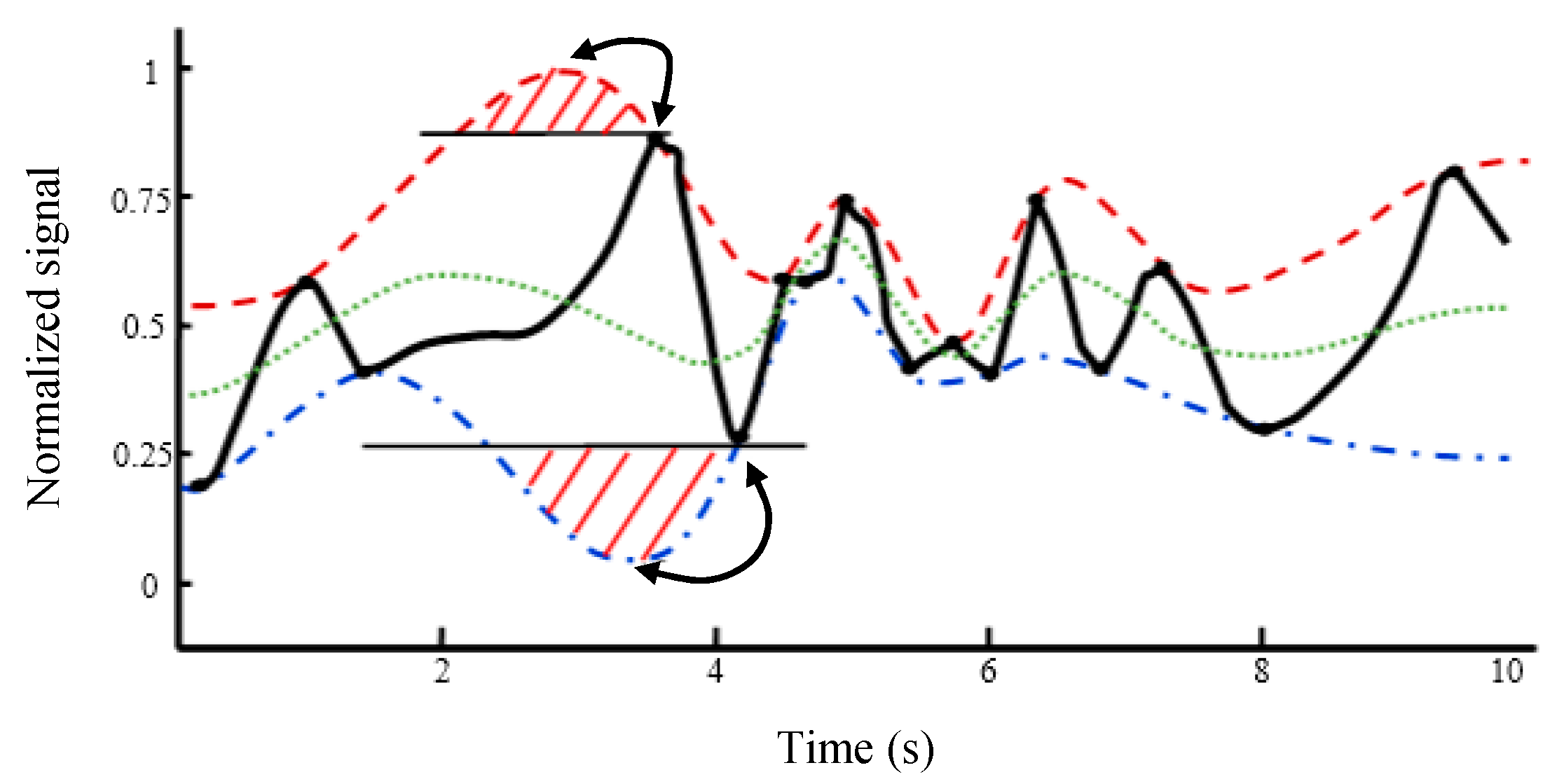
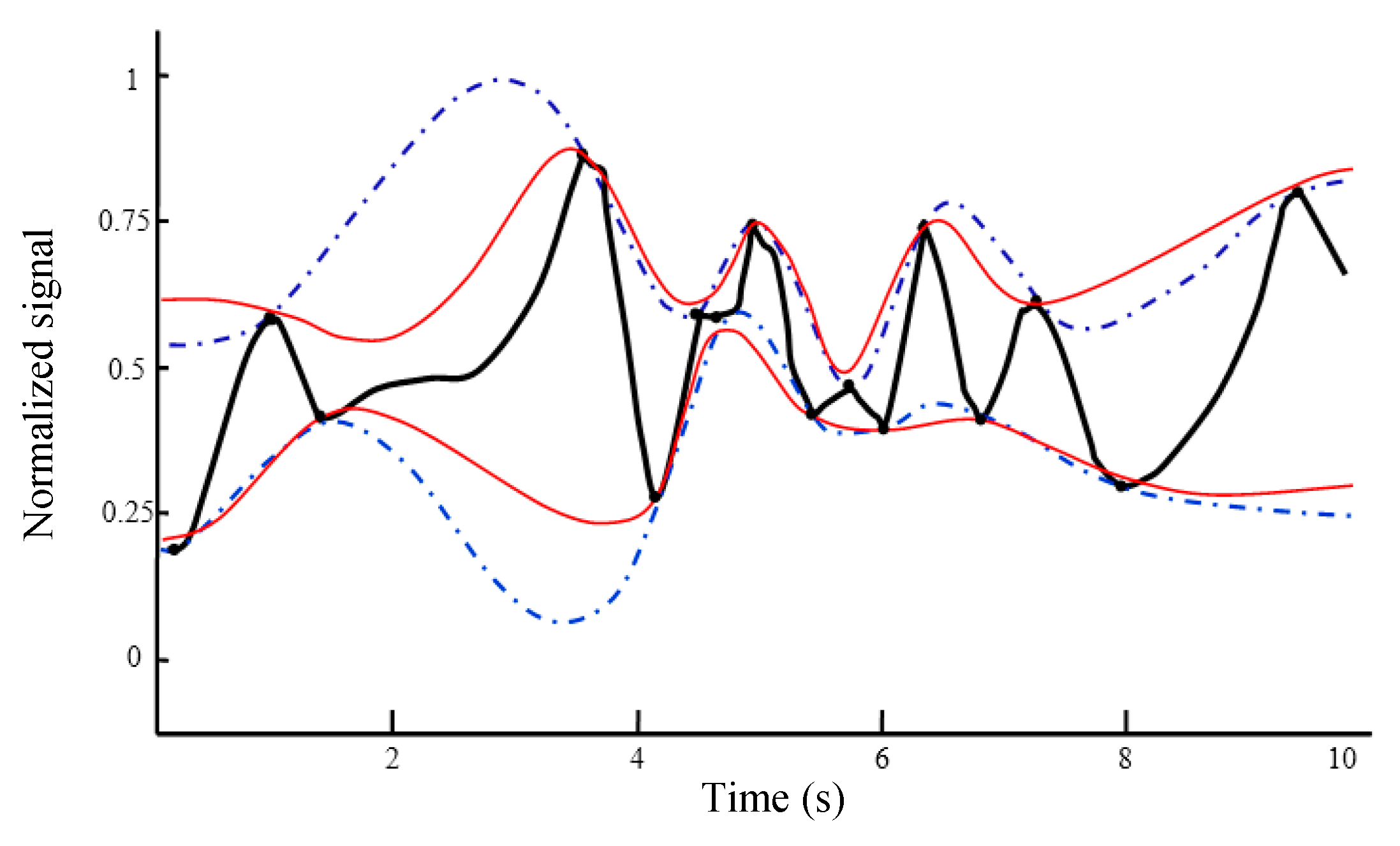
- Find the maxima of the signal x1(t) and obtain the upper envelope ue(t) using the proposed IKIM.
- Find the minima of the signal x1(t) and obtain the lower envelope le(t) using the proposed IKIM.
- Find the local mean m(t) = [ue(t) + le(t)]/2.
- Set x1(t) = x1(t) − m(t) and determine if x1(t) is an IMF or not by checking the properties of IMF. Repeat steps 2 to 5 until x1(t) becomes an IMF. Store the obtained IMF.
- Set x(t) = x(t) − x1(t).
- Repeat steps 1 to 6 until all IMFs and residual of signal x(t) are obtained.
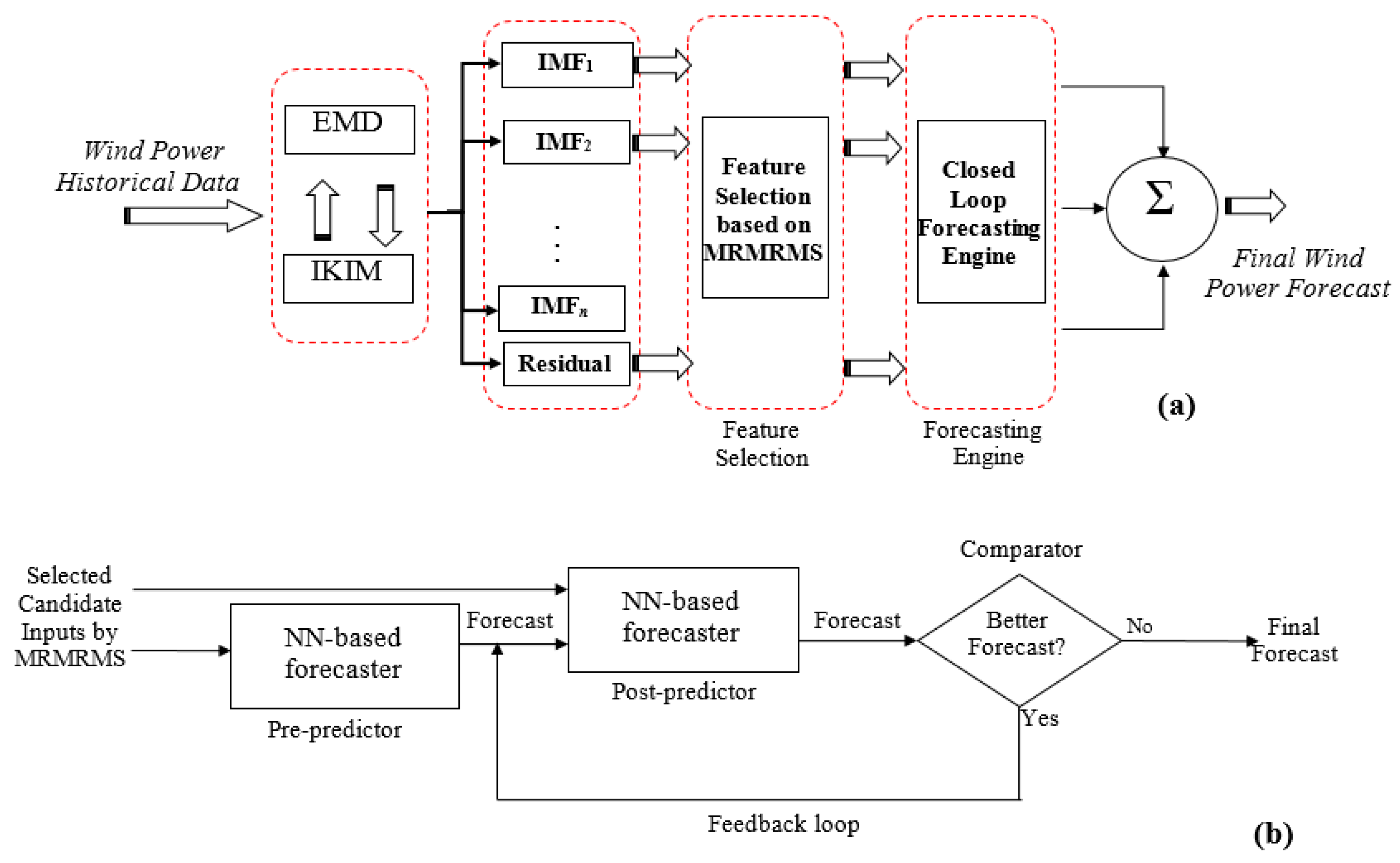
3. Proposed Wind Power Prediction Approach
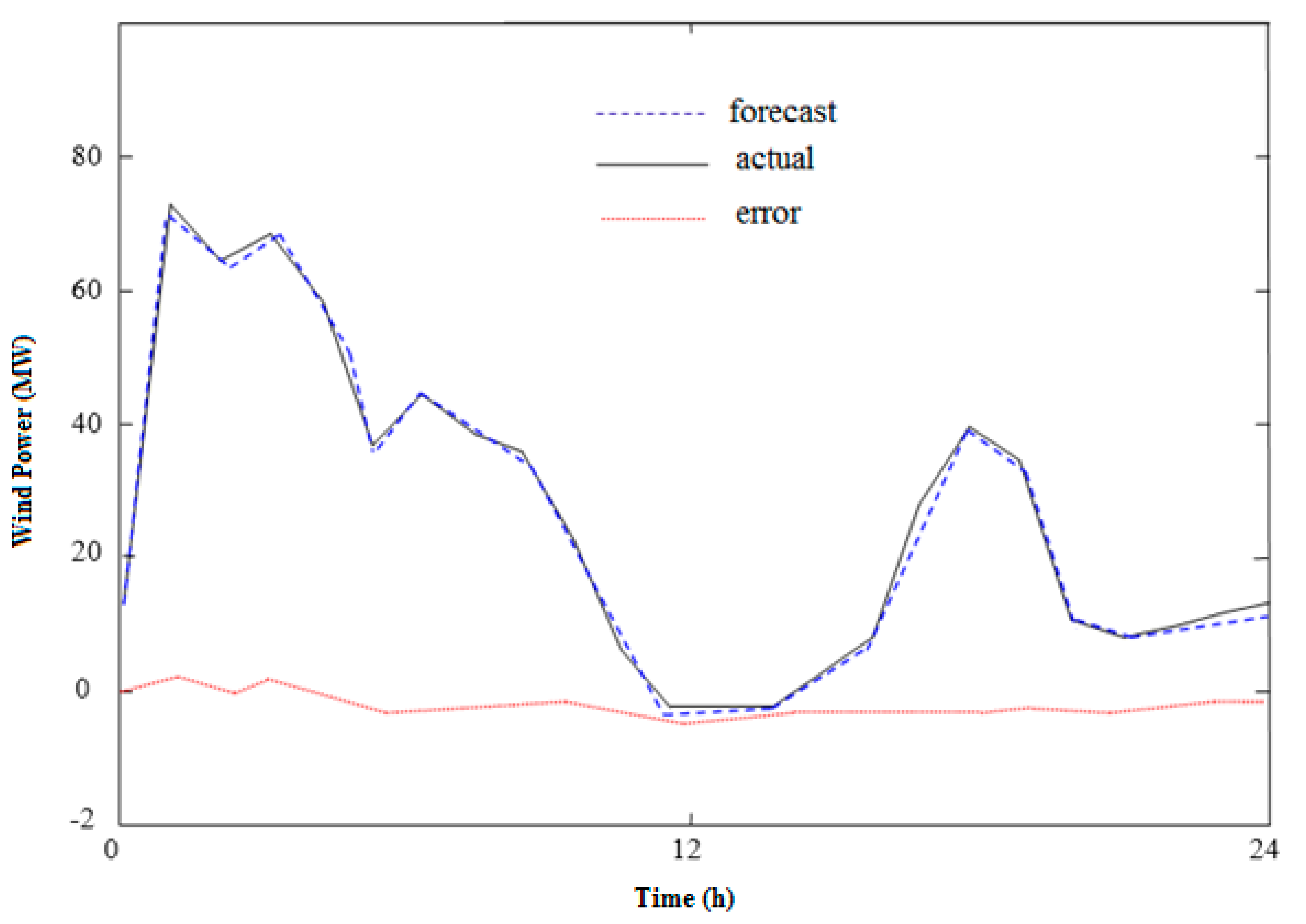
4. Numerical Results
4.1. Sotavento Wind Farm in Spain
4.2. Alberta Test Case
4.3. Blue Canyon Wind Farm
5. Discussion
6. Conclusions
Author Contributions
Conflicts of Interest
Abbreviations
| KIM | Kriging Interpolation Method |
| EMD | Empirical Mode Decomposition |
| IKIM | Improved KIM |
| CS | Cubic Spline |
| NN | Neural Network |
| HIFM | Hybrid Iterative Forecast Method |
| ARMA | Auto-Regressive Moving Average |
| RNN | Ridgelet Neural Network |
| DE | Differential Evolution |
| EPSO | Enhanced Particle Swarm Optimization |
| RBF | Radial Basis Function |
| LM | Levenberg-Marquardt |
| BFGS | Broyden, Fletcher, Goldfarb, Shannon |
| BR | Bayesian Regularization |
| FT | Fourier Transform |
| STFT | Short-Time FT |
| WT | Wavelet Transform |
| IMF | Intrinsic Mode Function |
| NWP | Numerical Weather Prediction |
| MRMRMS | Maximum Relevancy, Minimum Redundancy and Maximum Synergy |
| MLP | Multi-Layer Perceptron |
| RMSE | Root Mean Squared Error |
| BPNN | Back Propagation NN |
| RBFNN | Radial Basis Function NN |
| ANFIS | Adaptive Neuro-Fuzzy Inference System |
| NNPSO | NN based Particle Swarm Optimization |
| MI-IG | Mutual Information-Interaction Gain |
| SSO | Shark Smell Optimization |
| CSSO | Chaotic SSO |
| MAPE | Mean Absolute Percentage Error |
| NMAE | Normalized Mean Absolute Error |
| NRMSE | Normalized RMSE |
| WNN | Wavelet Neural Network |
| MSE | Mean Squared Error |
| MCC | Maximum Correntropy Criterion |
| CA | Correlation Analysis |
| BCD | Bayesian Clustering by Dynamics |
| SVR | Support Vector Regression |
| MHNN | Modified Hybrid Neural Network |
| Indexes | |
| i, j | Index of neighboring points in KIM |
| v | Index of order |
| t | Index of time |
| Superscripts | |
| T | Transpose sign |
| Variables | |
| KIM estimation of time series x(t) | |
| ti | Neighboring point i of time t |
| wi | Weight of neighboring point i in KIM |
| M | Number of neighboring points in KIM |
| e(.) | Error function of KIM |
| Variance function | |
| Cov(.,.) | Covariance function |
| λ | Lagrange multiplier |
| dij | Euclidean distance between ti and tj |
| C(.) | Covariogram function |
| Γ(.) | Gamma function |
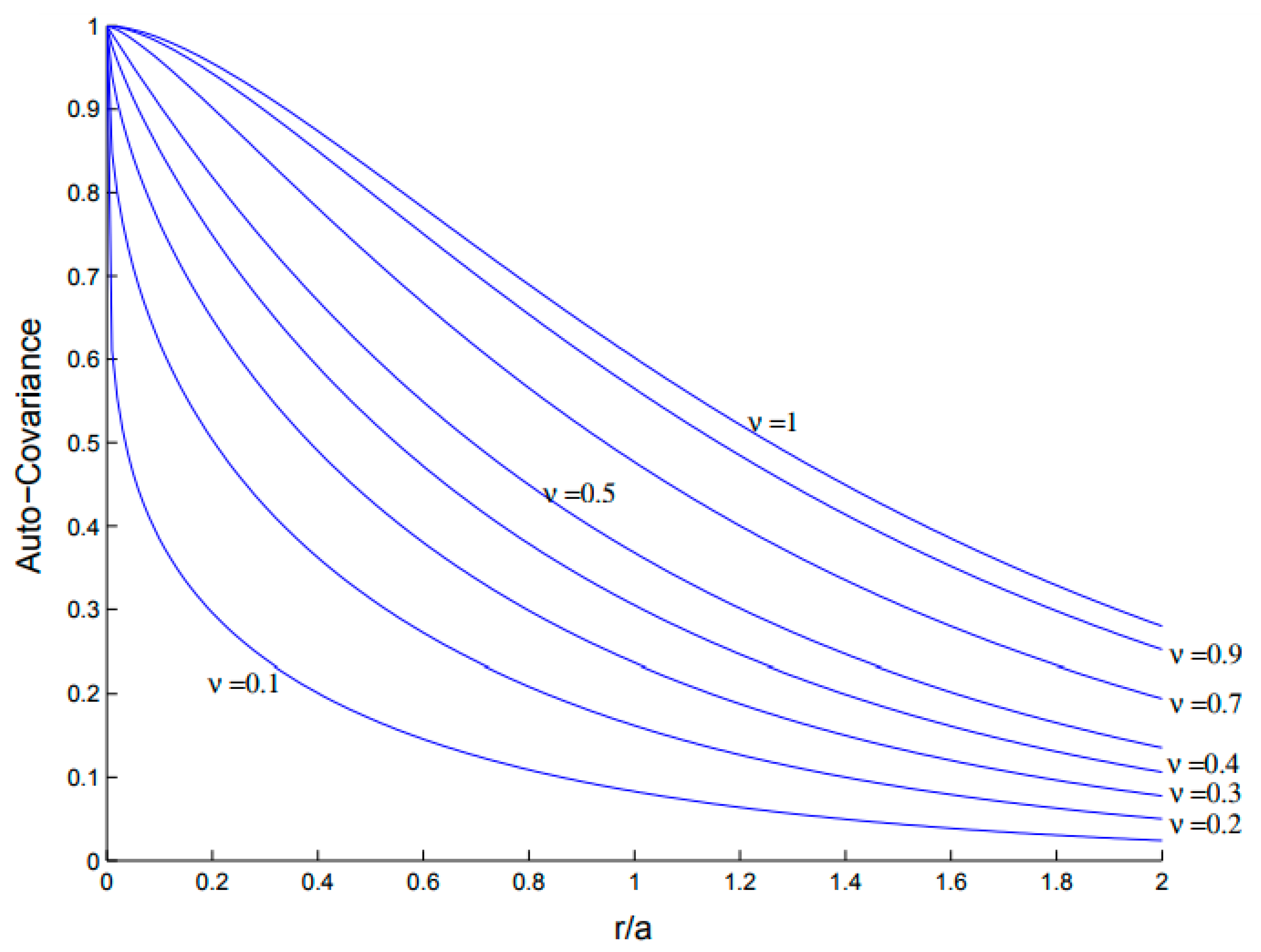
| Modified Bessel function of the second type of order v | |
| r | Lag in the anisotropic von Karman function |
| a | Correlation length in the anisotropic von Karman function |
| σ2 | Variance in the anisotropic von Karman function |
| XACT(t) | Actual values of the time series |
| XFOR(t) | Forecast values of the time series |
| N | Number of hours in the forecast horizon |
| Average of XACT(t) over the forecast horizon | |
| XN | Aggregated nameplate capacity of the wind farms |
References
- Manzano-Agugliaro, F.; Alcayde, A.; Montoya, F.G.; Zapata-Sierra, A.; Gil, C. Scientific production of renewable energies worldwide: An overview. Renew. Sustain. Energy Rev. 2013, 18, 134–143. [Google Scholar] [CrossRef]
- Hernández-Escobedo, Q.; Manzano-Agugliaro, F.; Zapata-Sierra, A. The wind power of Mexico. Renew. Sustain. Energy Rev. 2010, 14, 2830–2840. [Google Scholar] [CrossRef]
- Hernández-Escobedo, Q.; Manzano-Agugliaro, F.; Gazquez-Parra, J.A.; Zapata-Sierra, A. Is the wind a periodical phenomenon? The case of mexico. Renew. Sustain Energy Rev. 2011, 15, 721–728. [Google Scholar] [CrossRef]
- Montoya, F.G.; Manzano-Agugliaro, F.; López-Márquez, S.; Hernández-Escobedo, Q.; Gil, C. Wind turbine selection for wind farm layout using multi-objective evolutionary algorithms. Expert Syst. Appl. 2014, 41, 6585–6595. [Google Scholar] [CrossRef]
- Fan, S.; Liao, J.R.; Yokoyama, R.; Chen, L.; Lee, W.J. Forecasting the Wind Generation Using a Two-Stage Network Based on Meteorological Information. IEEE Trans. Energy Convers. 2009, 24, 474–482. [Google Scholar] [CrossRef]
- Khosravi, A.; Nahavandi, S.; Creighton, D. Prediction intervals for short-term wind farm power generation forecasts. IEEE Trans. Sustain. Energy 2013, 4, 602–610. [Google Scholar] [CrossRef]
- Jónsson, T.; Pinson, P.; Nielsen, H.A.; Madsen, H.K.; Nielsen, T.S. Forecasting Electricity Spot Prices Accounting for Wind Power Predictions. IEEE Trans. Sustain. Energy 2013, 4, 210–218. [Google Scholar] [CrossRef]
- Amjady, N.; Keynia, F.; Zareipour, H. A New Hybrid Iterative Method for Short Term Wind Speed Forecasting. Eur. Trans. Electr. Power 2011, 21, 581–595. [Google Scholar] [CrossRef]
- Amjady, N.; Keynia, F.; Zareipour, H. Short-term wind power forecasting using ridgelet neural network. Electr. Power Syst. Res. 2011, 81, 2099–2107. [Google Scholar] [CrossRef]
- Chang, W.Y. Short-Term Wind Power Forecasting Using the Enhanced Particle Swarm Optimization Based Hybrid Method. Energies 2013, 6, 4879–4896. [Google Scholar] [CrossRef]
- Amjady, N.; Keynia, F.; Zareipour, H. Wind Power Prediction by a New Forecast Engine Composed of Modified Hybrid Neural Network and Enhanced Particle Swarm Optimization. IEEE Trans. Sustain. Energy 2011, 2, 265–276. [Google Scholar] [CrossRef]
- Soman, S.S.; Zareipour, H.; Malik, O.; Mandal, P. A review of wind power and wind speed forecasting methods with different time horizons. In Proceedings of the North American Power Symposium (NAPS), Arlington, TX, USA, 26–28 September 2010; pp. 1–8. [Google Scholar]
- Wang, X.; Guo, P.; Huang, X. A Review of Wind Power Forecasting Models. Energy Procedia 2011, 12, 770–778. [Google Scholar] [CrossRef]
- Lei, M.; Shiyan, L.; Chuanwen, J.; Hongling, L.; Yan, Z. A review on the forecasting of wind speed and generated power. Renew. Sustain. Energy Rev. 2009, 13, 915–920. [Google Scholar] [CrossRef]
- Chang, W.Y. A Literature Review of Wind Forecasting Methods. J. Power Energy Eng. 2014, 2, 161–168. [Google Scholar] [CrossRef]
- Hassan, S.Z.; Li, H.; Kamal, T.; Arifoglu, U.; Mumtaz, S.; Khan, L. Neuro-Fuzzy Wavelet Based Adaptive MPPT Algorithm for Photovoltaic Systems. Energies 2017, 10, 394. [Google Scholar] [CrossRef]
- Ou, T.C.; Hong, C.M. Dynamic operation and control of microgrid hybrid power systems. Energy 2014, 66, 314–323. [Google Scholar] [CrossRef]
- Hong, C.M.; Ou, T.C.; Lu, K.H. Development of intelligent MPPT (maximum power point tracking) control for a grid-connected hybrid power generation system. Energy 2016, 50, 270–279. [Google Scholar] [CrossRef]
- Shiau, J.K.; Wei, Y.C.; Lee, M.Y. Fuzzy Controller for a Voltage-Regulated Solar-Powered MPPT System for Hybrid Power System Applications. Energies 2015, 8, 3292–3312. [Google Scholar] [CrossRef]
- Fumi, A.; Pepe, A.; Scarabotti, L.; Schiraldi, M.M. Fourier Analysis for Demand Forecasting in a Fashion Company. Int. J. Eng. Bus. Manag. 2013, 30, 10. [Google Scholar] [CrossRef]
- Amjady, N.; Keynia, F. Day ahead price forecasting of electricity markets by a mixed data model and hybrid forecast method. Int. J. Electr. Power Energy Syst. 2008, 30, 533–546. [Google Scholar] [CrossRef]
- Mishra, S.; Sharma, A.; Panda, G. Wind Power Forecasting Model using Complex Wavelet Theory. In Proceedings of the 2011 International Conference on Energy, Automation, and Signal (ICEAS), Bhubaneswar, India, 28–30 December 2011; pp. 1–4. [Google Scholar]
- Catalão, J.P.S.; Pousinho, H.M.I.; Mendes, V.M.F. Hybrid wavelet-PSO-NFIS approach for short-term wind power forecasting in Portugal. IEEE Trans. Sustain. Energy 2011, 2, 50–59. [Google Scholar]
- Wang, J. A Hybrid Wavelet Transform Based Short-Term Wind Speed Forecasting Approach. Sci. World J. 2014, 2014, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Mandal, P.; Zareipour, H.; Rosehart, W.D. Forecasting aggregated wind power production of multiple wind farms using hybrid wavelet-PSO-NNs. Int. J. Energy Res. 2014, 38, 1654–1666. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. A 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wang, D.; Yue, C.; Wei, S.; Lv, J. Performance Analysis of Four Decomposition-Ensemble Models for One-Day-Ahead Agricultural Commodity Futures Price Forecasting. Algorithms 2017, 10, 108. [Google Scholar] [CrossRef]
- Hong, Y.Y.; Yu, T.H.; Liu, C.Y. Hour-Ahead Wind Speed and Power Forecasting Using Empirical Mode Decomposition. Energies 2013, 6, 6137–6152. [Google Scholar] [CrossRef]
- Pegram, G.G.S.; Peel, M.C.; Mcmahon, T.A. Empirical mode decomposition using rational splines: An application to rainfall time series. Proc. R. Soc. A 2008, 464, 1483–1501. [Google Scholar] [CrossRef]
- Barnhart, B.L. The Hilbert-Huang Transform: Theory, Applications, Development. Ph.D. Thesis, The University of Iowa, Iowa City, IN, USA, 2011. [Google Scholar]
- Bohling, G. KRIGING. Available online: http://people.ku.edu/~gbohling/cpe940/Kriging.pdf (accessed on 9 November 2017).
- Li, J.; Heap, A.D. A Review of Spatial Interpolation Methods for Environmental Scientists; Geoscience Australia Record; Geoscience Australia: Canberra, Australia, 2008.
- Huang, Z.; Wang, H.; Zhang, R. An Improved Kriging Interpolation Technique Based on SVM and Its Recovery Experiment in Oceanic Missing Data. Am. J. Comput. Math. 2012, 2, 56–60. [Google Scholar] [CrossRef]
- Williams, C.K.I. Prediction with Gaussian Processes: From Linear Regression to Linear Prediction and Beyond. Available online: https://pdfs.semanticscholar.org/dcd0/a9b1921a34c37f082d03a4d240c9085351c7.pdf (accessed on 9 November 2017).
- Sidler, R.; Holliger, K. Kriging of Scale-Invariant Data: Optimal Parameterization of the Autocovariance Model. In Proceedings of the American Geophysical Union Spring Meeting, San Francisco, CA, USA, 13 December 2004. [Google Scholar]
- Goff, J.A.; Jennings, J.W. Improvement of Fourier-based unconditional and conditional simulations for band-limited fractal (von Kármán) statistical models. Math. Geol. 1999, 31, 627–649. [Google Scholar] [CrossRef]
- Abedinia, O.; Amjady, N.; Ghasemi, A. A New Meta-heuristic Algorithm Based on Shark Smell Optimization. Complexity 2016, 21, 97–116. [Google Scholar] [CrossRef]
- Abedinia, O.; Amjady, N.; Zareipour, H. A New Feature Selection Technique for Load and Price Forecast of Electrical Power Systems. IEEE Trans. Power Syst. 2017, 32, 62–74. [Google Scholar] [CrossRef]
- Amjady, N.; Keynia, F. Day-Ahead Price Forecasting of Electricity Markets by Mutual Information Technique and Cascaded Neuro-Evolutionary Algorithm. IEEE Trans. Power Syst. 2009, 24, 306–318. [Google Scholar] [CrossRef]
- Sotavento Wind Farm. Available online: www.sotaventogalicia.com (accessed on 26 June 2015).
- Alberta Wind Farms. Available online: http://canwea.ca/wind-energy/alberta/ (accessed on 28 June 2015).
- Abedinia, O.; Amjady, N. Short-Term Wind Power Prediction based on Hybrid Neural Network and Chaotic Shark Smell Optimization. Int. J. Precis. Eng. Manuf. Green Technol. 2015, 2, 245–254. [Google Scholar] [CrossRef]
- Chitsaz, H.; Amjady, N.; Zareipour, H. Wind power forecast using wavelet neural network trained by improved Clonal selection algorithm. Energy Convers. Manag. 2015, 89, 588–598. [Google Scholar] [CrossRef]
- Oklahoma Wind Farm. Available online: http://bluecanyonwindfarm.com (accessed on 5 July 2015).

| Test Week | Correlation Analysis + HIFM [8] | MI-MR Feature Selection + MLP [8] | MI-MR Feature Selection + HIFM [8] | EMD + Cubic Spline | KIM + Gaussian Model | KIM + Exponential Model | KIM + Linear Model | KIM + Spherical Model | Proposed |
|---|---|---|---|---|---|---|---|---|---|
| Feb. | 7.56 | 7.68 | 5.71 | 5.08 | 5.37 | 2.26 | 2 | 1.56 | 0.98 |
| May | 5.82 | 5.96 | 4.26 | 4.14 | 4.07 | 3.37 | 3.07 | 2.4 | 1.32 |
| Aug. | 6.93 | 7.01 | 5.92 | 4.37 | 4.08 | 2.03 | 1.9 | 1.28 | 0.87 |
| Nov. | 5.97 | 6.04 | 4.55 | 4.41 | 4.83 | 3.35 | 3.11 | 2.08 | 1.34 |
| Ave. | 6.57 | 6.68 | 5.11 | 4.5 | 4.59 | 2.75 | 2.52 | 1.83 | 1.13 |
| Test Day | Error Criterion | Persistence [25] | BPNN [25] | RBFNN [25] | ANFIS [25] | NN-PSO [25] | WT + BPNN [25] | WT + RBFNN [25] | WT + ANFIS [25] | WT + NNPSO [25] | MI-IG + NN + CSSO [42] | Proposed |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 December | MAPE | 10.03 | 13.62 | 10.41 | 14.81 | 9.54 | 11.26 | 8.26 | 11.08 | 7.28 | 7.12 | 4.18 |
| NMAE | 4.18 | 4.32 | 4.61 | 4.75 | 4.09 | 4.29 | 4.19 | 4.55 | 3.87 | 4.02 | 3.23 | |
| NRMSE | 5.41 | 5.73 | 5.84 | 6.13 | 5.38 | 5.44 | 5.43 | 5.91 | 5.07 | 4.86 | 3.32 | |
| 4 May | MAPE | 11.31 | 12.42 | 11.07 | 13.51 | 11.41 | 11.73 | 9.22 | 11.76 | 8.73 | 8.50 | 5.43 |
| NMAE | 4.58 | 4.88 | 4.61 | 4.71 | 4.51 | 4.67 | 4.18 | 4.39 | 4.11 | 4.12 | 3.12 | |
| NRMSE | 6.11 | 6.38 | 5.89 | 6.43 | 6.20 | 6.09 | 5.41 | 6.22 | 5.83 | 5.92 | 4.13 | |
| 7 July | MAPE | 21.58 | 17.44 | 16.72 | 19.30 | 12.26 | 14.11 | 12.39 | 16.38 | 11.27 | 10.12 | 7.32 |
| NMAE | 8.48 | 7.46 | 7.21 | 7.75 | 5.94 | 6.97 | 7.04 | 7.18 | 5.29 | 5.10 | 4.14 | |
| NRMSE | 11.25 | 9.23 | 8.88 | 10.16 | 7.33 | 8.96 | 8.36 | 9.63 | 7.02 | 6.76 | 5.44 | |
| 15 October | MAPE | 14.79 | 13.93 | 12.73 | 12.04 | 12.82 | 11.67 | 14.86 | 11.08 | 5.48 | 5.63 | 4.07 |
| NMAE | 7.48 | 7.26 | 7.31 | 7.76 | 6.85 | 7.14 | 7.08 | 7.32 | 6.17 | 6.08 | 5.21 | |
| NRMSE | 9.19 | 8.79 | 8.99 | 9.38 | 7.43 | 8.22 | 8.60 | 8.93 | 7.21 | 6.43 | 5.73 | |
| Average | MAPE | 14.43 | 14.35 | 12.73 | 14.91 | 11.51 | 12.19 | 11.18 | 12.57 | 8.19 | 7.84 | 5.25 |
| NMAE | 6.18 | 5.98 | 5.93 | 6.24 | 5.35 | 5.77 | 5.62 | 5.86 | 4.86 | 4.83 | 3.92 | |
| NRMSE | 7.99 | 7.53 | 7.4 | 8.02 | 6.58 | 7.18 | 6.95 | 7.67 | 6.28 | 5.99 | 4.65 |
| Methods | Error Criterion | March Test Week | June Test Week | September Test Week | December Test Week | Ave. |
|---|---|---|---|---|---|---|
| Persistence [43] | NRMSE | 13.71 | 15.14 | 18.44 | 12.49 | 14.95 |
| NMAE | 10.08 | 10.79 | 13.11 | 8.84 | 10.71 | |
| RBF [43] | NRMSE | 18.32 | 14.57 | 18.62 | 14.11 | 16.40 |
| NMAE | 13.32 | 10.45 | 13.77 | 10.24 | 11.95 | |
| MLP [43] | NRMSE | 15.36 | 15.62 | 19.80 | 12.32 | 15.78 |
| NMAE | 12.42 | 11.56 | 14.54 | 9.02 | 11.89 | |
| WNN with MSE [43] | NRMSE | 12.38 | 14.99 | 17.66 | 11.65 | 14.17 |
| NMAE | 9.36 | 10.64 | 12.49 | 8.53 | 10.26 | |
| WNN with MCC [43] | NRMSE | 12.23 | 12.48 | 16.68 | 11.58 | 13.24 |
| NMAE | 9.22 | 9.64 | 11.73 | 8.22 | 9.70 | |
| Proposed | NRMSE | 10.10 | 10.54 | 14.21 | 9.32 | 11.04 |
| NMAE | 7.32 | 7.47 | 9.14 | 6.36 | 7.57 |
| Test Conditions | Persistence Method [5] | CA+BCD + SVR [5] | MHNN + EPSO [11] | Proposed | |
|---|---|---|---|---|---|
| Forecast Horizon | Error | ||||
| 1-h. ahead | NMAE | 7.84 | 6.65 | 4.12 | 3.87 |
| 1-h ahead | NRMSE | 11.93 | 10.54 | 7.52 | 5.43 |
| 24-h ahead | NMAE | 21.24 | 14.38 | 7.90 | 6.64 |
| 24-h ahead | NRMSE | 29.84 | 19.74 | 12.60 | 10.29 |
| 48-h ahead | NMAE | 25.42 | 15.73 | 10.51 | 7.89 |
| 48-h ahead | NRMSE | 34.81 | 21.24 | 16.58 | 14.32 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amjady, N.; Abedinia, O. Short Term Wind Power Prediction Based on Improved Kriging Interpolation, Empirical Mode Decomposition, and Closed-Loop Forecasting Engine. Sustainability 2017, 9, 2104. https://doi.org/10.3390/su9112104
Amjady N, Abedinia O. Short Term Wind Power Prediction Based on Improved Kriging Interpolation, Empirical Mode Decomposition, and Closed-Loop Forecasting Engine. Sustainability. 2017; 9(11):2104. https://doi.org/10.3390/su9112104
Chicago/Turabian StyleAmjady, Nima, and Oveis Abedinia. 2017. "Short Term Wind Power Prediction Based on Improved Kriging Interpolation, Empirical Mode Decomposition, and Closed-Loop Forecasting Engine" Sustainability 9, no. 11: 2104. https://doi.org/10.3390/su9112104
APA StyleAmjady, N., & Abedinia, O. (2017). Short Term Wind Power Prediction Based on Improved Kriging Interpolation, Empirical Mode Decomposition, and Closed-Loop Forecasting Engine. Sustainability, 9(11), 2104. https://doi.org/10.3390/su9112104




