Low-Carbon Planning and Design in B&R Logistics Service: A Case Study of an E-Commerce Big Data Platform in China
Abstract
1. Introduction
- (i)
- Section 2 reviews the research literature on the supply chain model under the carbon constraint, including the research on the transportation and the retailer’s delivery, and the Bender’s decomposition method used in this paper to solve the mathematical model.
- (ii)
- The model construction of the retailer delivery strategy under the periodic carbon constraints is considered in Section 3. As the basic model of this paper, the periodic low-carbon constraints model (PLC) imposes a carbon emission constraint on the planning of each decision cycle because it is not a complicated design for the research approach to build and calculate a model.
- (iii)
- A study on the delivery strategy model of e-commerce retailers considering the relationship between early stage and supply and demand with three kinds of expansion carbon constraints. The low-carbon delivery strategy under the periodic local carbon policy restriction is a decision model with the highest intensity constraints from the point of view of the mathematical dynamic planning. In Section 4, the constraint intensity gradually relaxed, the paper obtains properties under different carbon constraint considering the lead time and delivery strategy model of supply and demand.
- (iv)
- Taking the JD.com global online shopping site as an example, the calculation experiment and simulation are carried out, and the feasibility and validity of the analytical method are illustrated by an example analysis, and some conclusions and relevant enlightenment are obtained according to the experimental results in the Section 5.
- (v)
- The conclusion and future prospects are shown in Section 6. This section summarizes the main research work and the conclusions of this paper, and points out the main contribution and the research work that needs to be carried out further.
2. Literature Review
2.1. Supply Chain Model with Carbon Emissions
2.2. Bender’s Decomposition
- Type I
- The main problem constraint model is intensified. From the solution of the decomposition algorithm, we can see that the purpose of the iterative process is to obtain more main problem constraints. If the results of each iteration can generate more compact and effective cutting plane, the efficiency of the algorithm is naturally improved (Fortz et al., 2009 [45]; Bektaş 2012 [46]; Saharidis et al., 2010 [47]; Wu et al., 2003 [48]).
- Type II
- A more feasible integer variable cutting plane. Some scholars put forward the idea of combining intelligent algorithms, which means that the more feasible solutions that exist, the more tangent planes. Naturally, the generation of a large number of cutting planes can greatly reduce the solution of the main problem (Rei et al., 2009 [49]; Poojari et al., 2009 [50]).
- Type III
- Effective cutting plane selection. Different from the previous two types, the method selects the tangent planes to obtain a more effective cutting plane. However, the method requires a significant amount of time to determine the effectiveness of the cutting plane (Yang et al., 2012 [51]).
3. Periodic Low-Carbon Constraints Model (PLC)
- : The average total value of ordering the product for the consumer;
- : The average price of the commodity on the e-commerce platform;
- : The average cost of the retailer’s product ;
- : The average time value of the consumer n;
- : The weighting index of the consumer’s time value for product p;
- : The average delay time of the product for consumers;
- : The average amount of orders placed by the consumer on the product during the period t;
- : Service cycle number;
- : Planning cycle;
- : The time window of the service cycle , ;
- : The average transit time for the retailer to deliver to the consumer, in the service cycle i;
- : The time of discharging for the goods after arrival at the consumer;
- : The lead time of the retailer delivery;
- : The average number of times a consumer receives a product within service period i;
- : The fixed cost of transportation mode k;
- : The variable cost of bulk product for transportation mode k;
- : The distance that the retailer needs to transport to the consumer n;
- : The minimum density of goods transported by mode can provide;
- : The carbon emission of transport mode delivers per kilometer of bulk products;
- : The average number of products delivered for the consumer n for mode within cycle ;
- : The largest unit of the carbon emission of product allowed by service cycle .
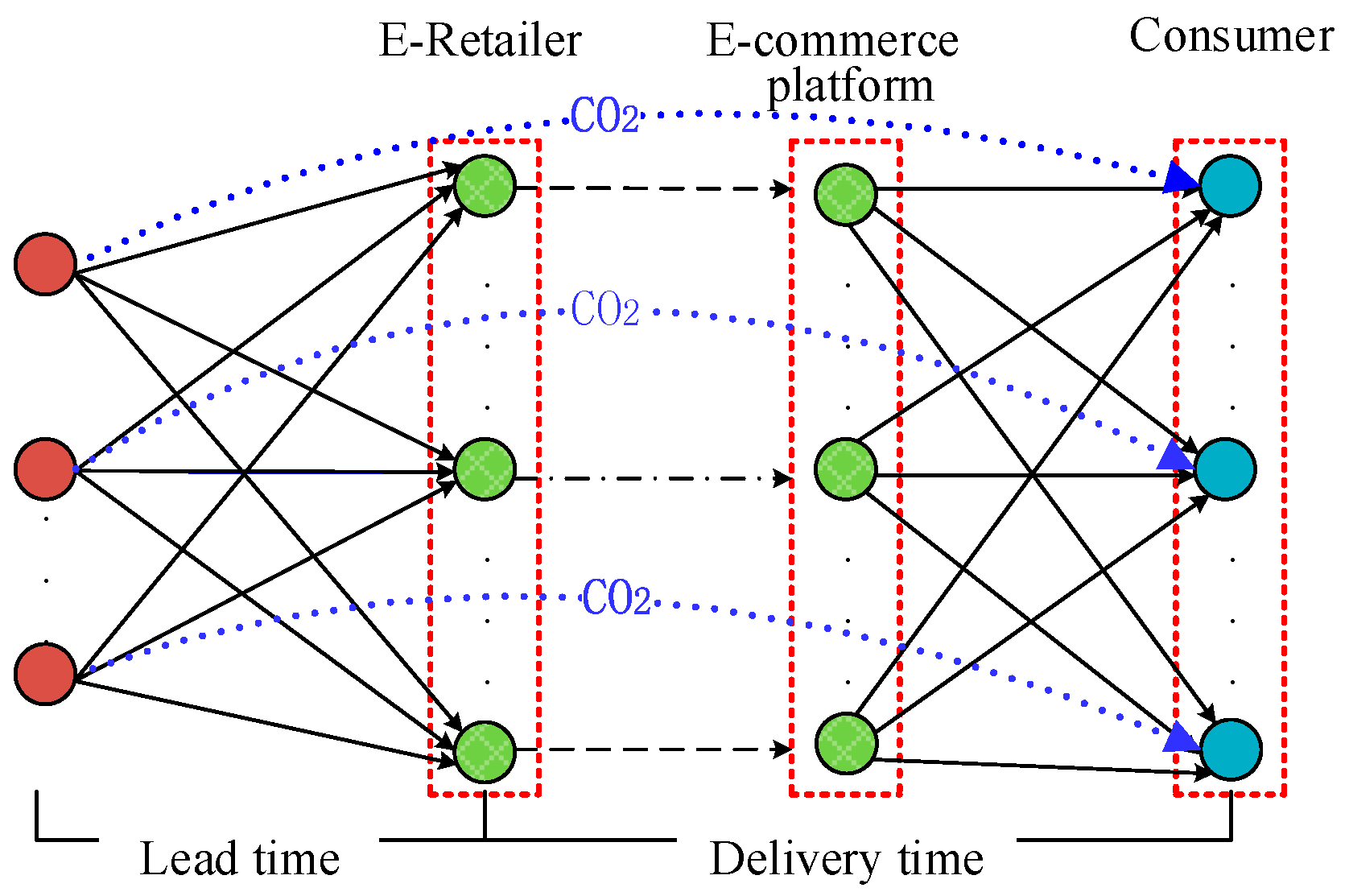
3.1. Descriptive Process Model: Consumers Choose E-Commerce Retailers
3.2. The Sustainable Profit Function of the E-Retailer from the E-Commerce Platform
3.3. The Delivery Model for Periodic Low-Carbon Constraints
4. Nonlinear Mixed Integer Programming Model with Three Kinds of Expansion Low-Carbon Constraints
4.1. The Environmental Delivery Model under Cumulative Low-Carbon Constraints (CLC)
4.2. The Delivery Model in Full Cycle Low-Carbon Constraints (FCLC)
4.3. The Distribution Model with the Constraint of Volatility Low-Carbon (VLC)
5. Computational Results
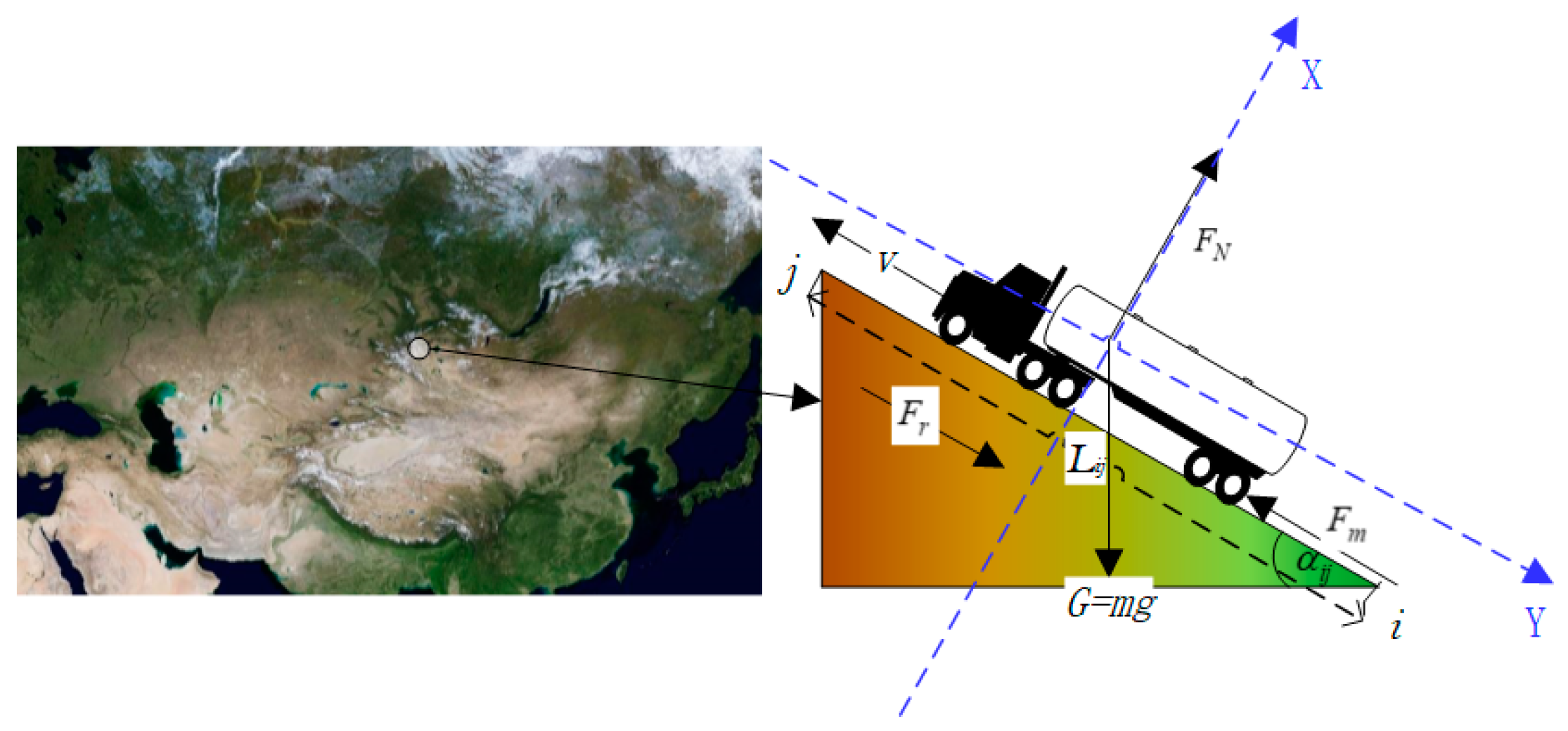
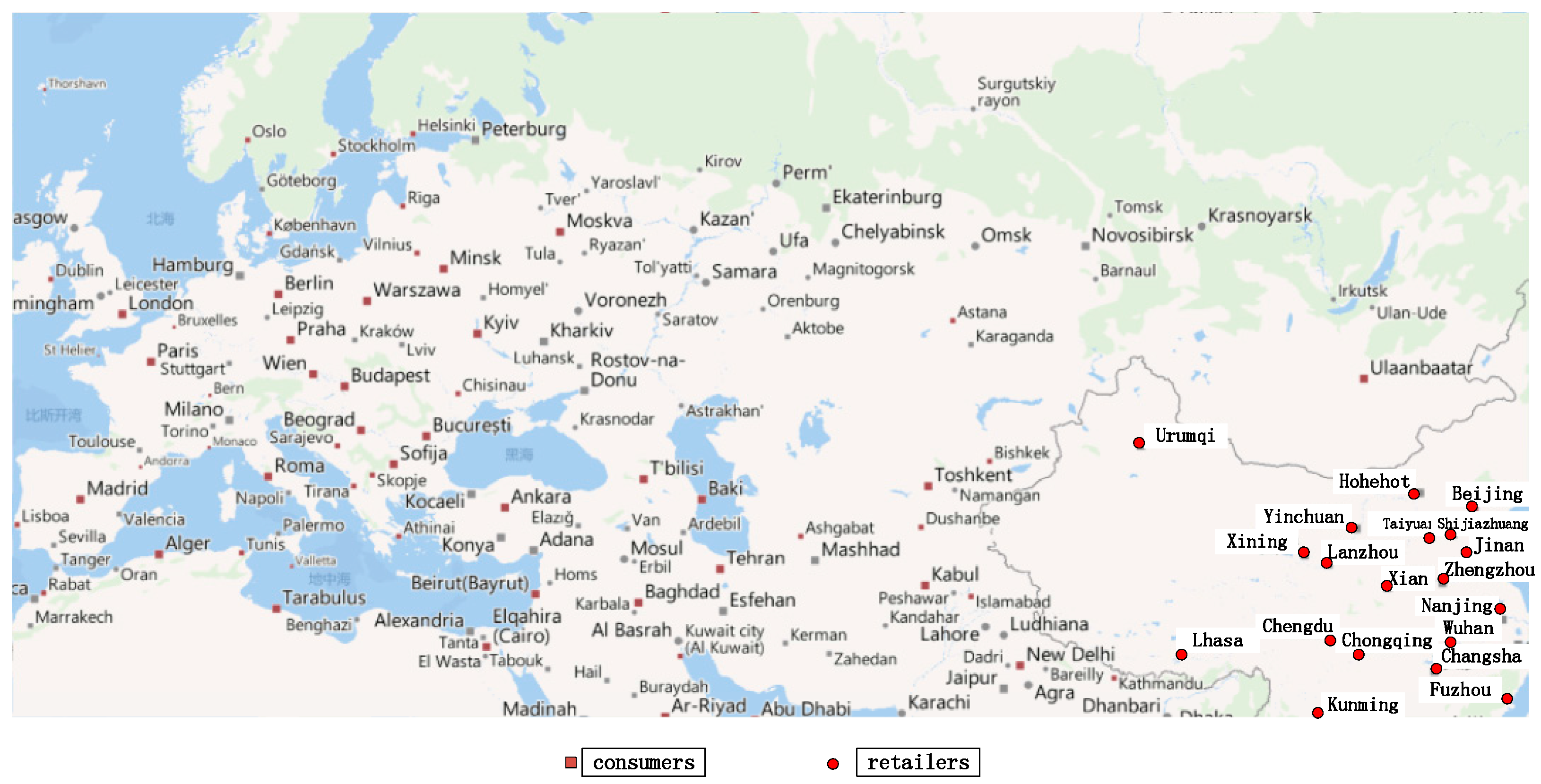
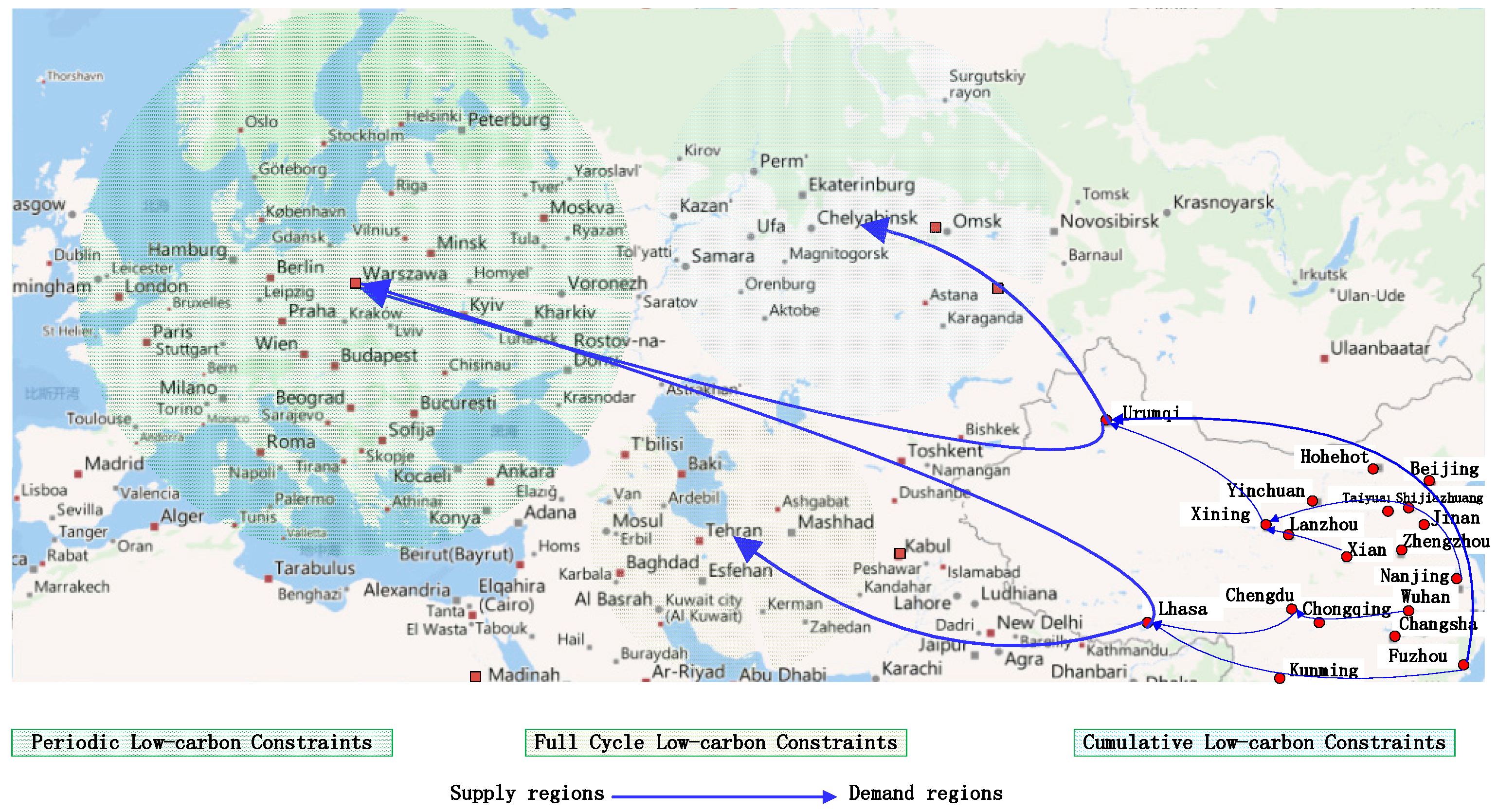
5.1. Initialization Data Analysis of JD.com Global Online Shopping Site
5.2. Object-Oriented Program Design: Tabu Search Algorithm and Bender’s Decomposition
| Algorithm 1. Public Framework |
| Step 1: Begin q iterations. Create a taboo table and record the operator through the disaster point. Create a taboo table to record the affected points of the operator. |
| Step 2: Initialize. Place the m operators in the first node of the delivery cycle before the operator completes a complete search, which is equivalent to a time window for the delivery model. Repeat the following steps until all the delivery cycle time windows are covered in the settings. |
| Step 3: Delivery time window selection. Each operator selects the next time window length that needs to be delivered according to the path selection rule. In the selection process, the operator is based on the probability that: |
| Step 4: Calculate the number of affected points that have been traversed during the simulation delivery. If it has exceeded the maximum number of traversals, cmax, then skip to Step 8; Otherwise continue to Step 6. |
| Step 5: Calculate the number of affected points that have been traversed during the simulation delivery, and jump to Step 8 with probability if the minimum traversal number, cmin, has been set; otherwise proceed to Step 6. |
| Step 6: Select the next time window to be delivered according to the probability . |
| Step 7: Check whether the delivery time window satisfies the constraint: if satisfied, add the result to the taboo table and return to Step 3; otherwise proceed to Step 8. |
| Step 8: Select the initial optimal solution of m delivery time windows, and perform a local search based on the variable domain search, and obtain the optimal solution of the q-th iteration after a partial search. |
| Step 9: Update the pheromone according to the optimal solution after a partial search, and clear the taboo table. |
| Step 10: Check the number of iterations: if q = q_max then exit the loop and output the results; otherwise return to Step 1 to continue operation. |
| Algorithm 2. Local Framework |
| Step 1: Initialization. Select the neighborhood structure set as the criterion to stop and give the initial solution s. |
| Step 2: Repeat the following steps until the stop criterion is met: |
| Step 2.1: Set ; |
| Step 2.2: If , then stop, and repeat the following steps: |
| Step 2.2.1: Local search: is the initial solution, the local optimal solution is obtained by the local search method, and the corresponding local optimal solution is |
| Step 2.2.2: Move or not: if the local optimal solution is better than the current optimal solution, and , set and , continue to search in the first neighborhood structure; otherwise set . |
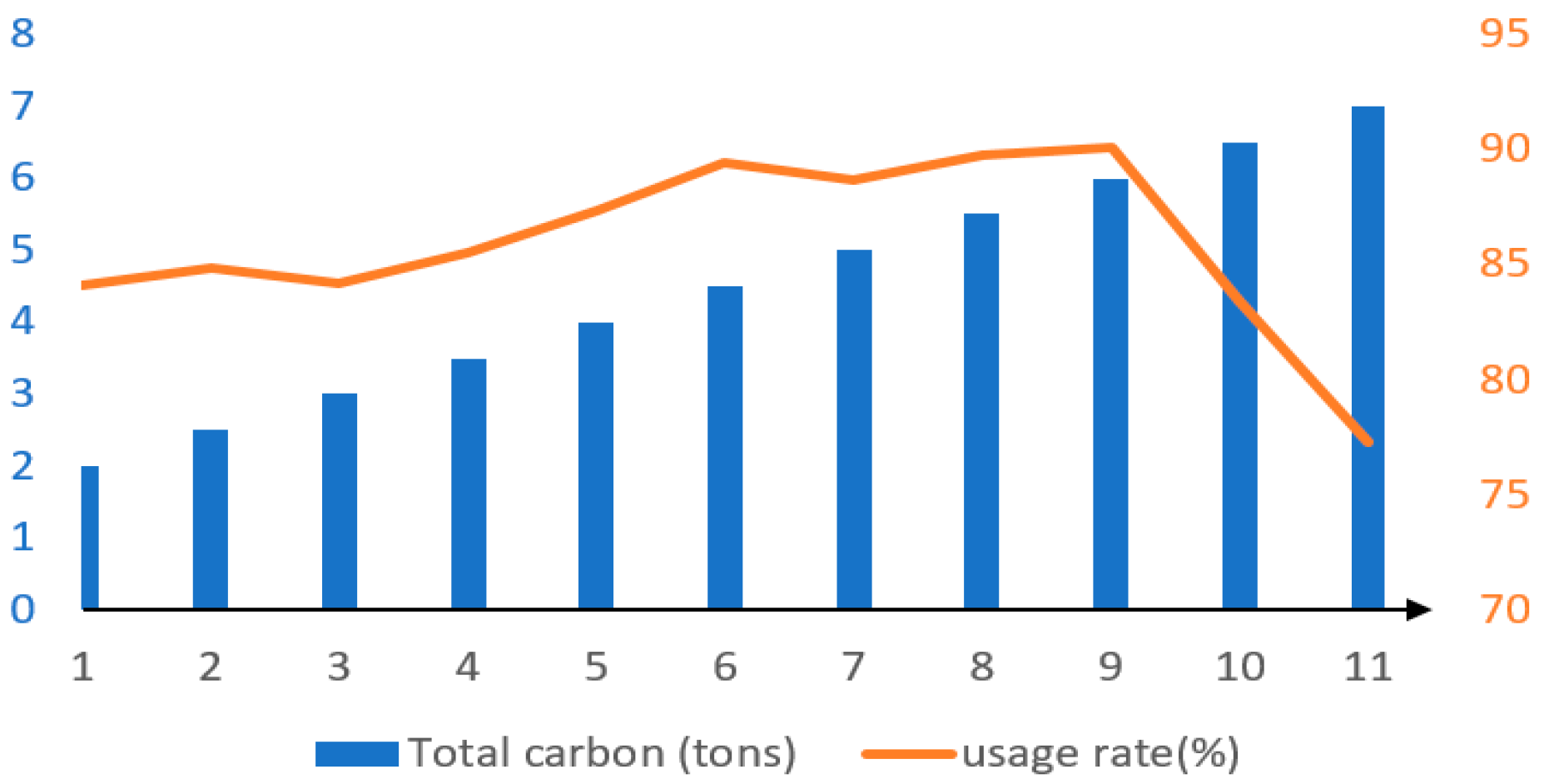
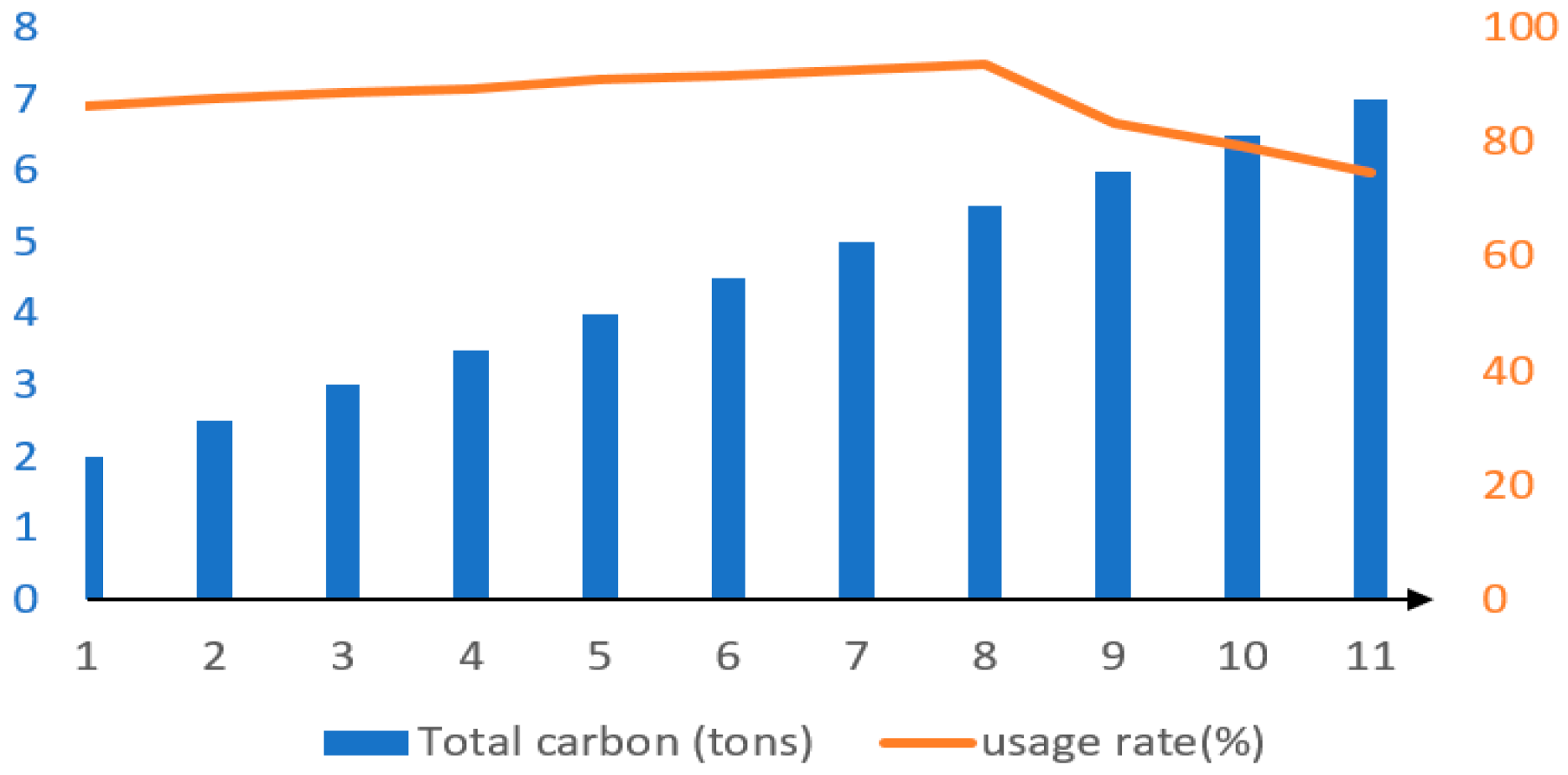
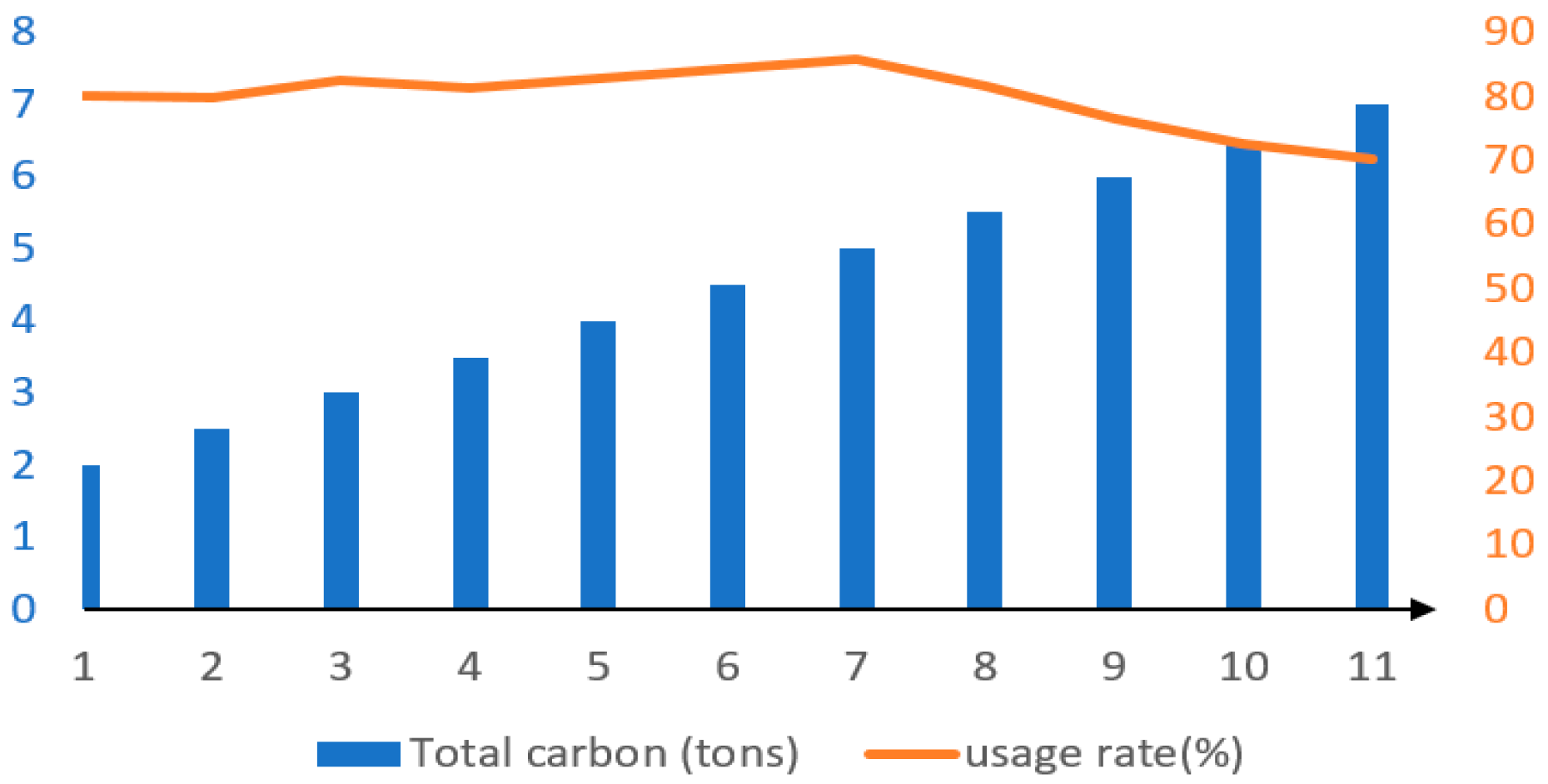
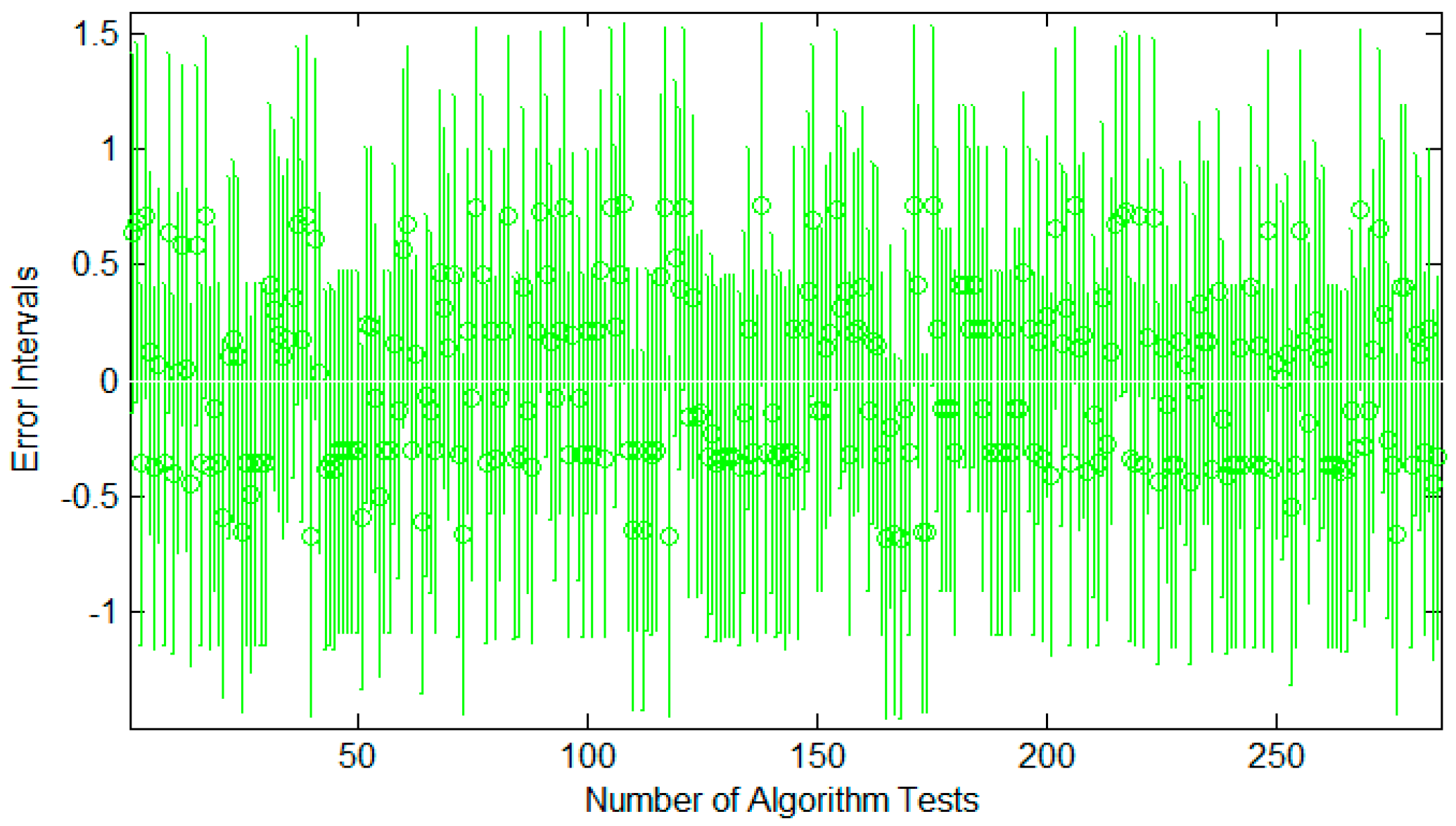
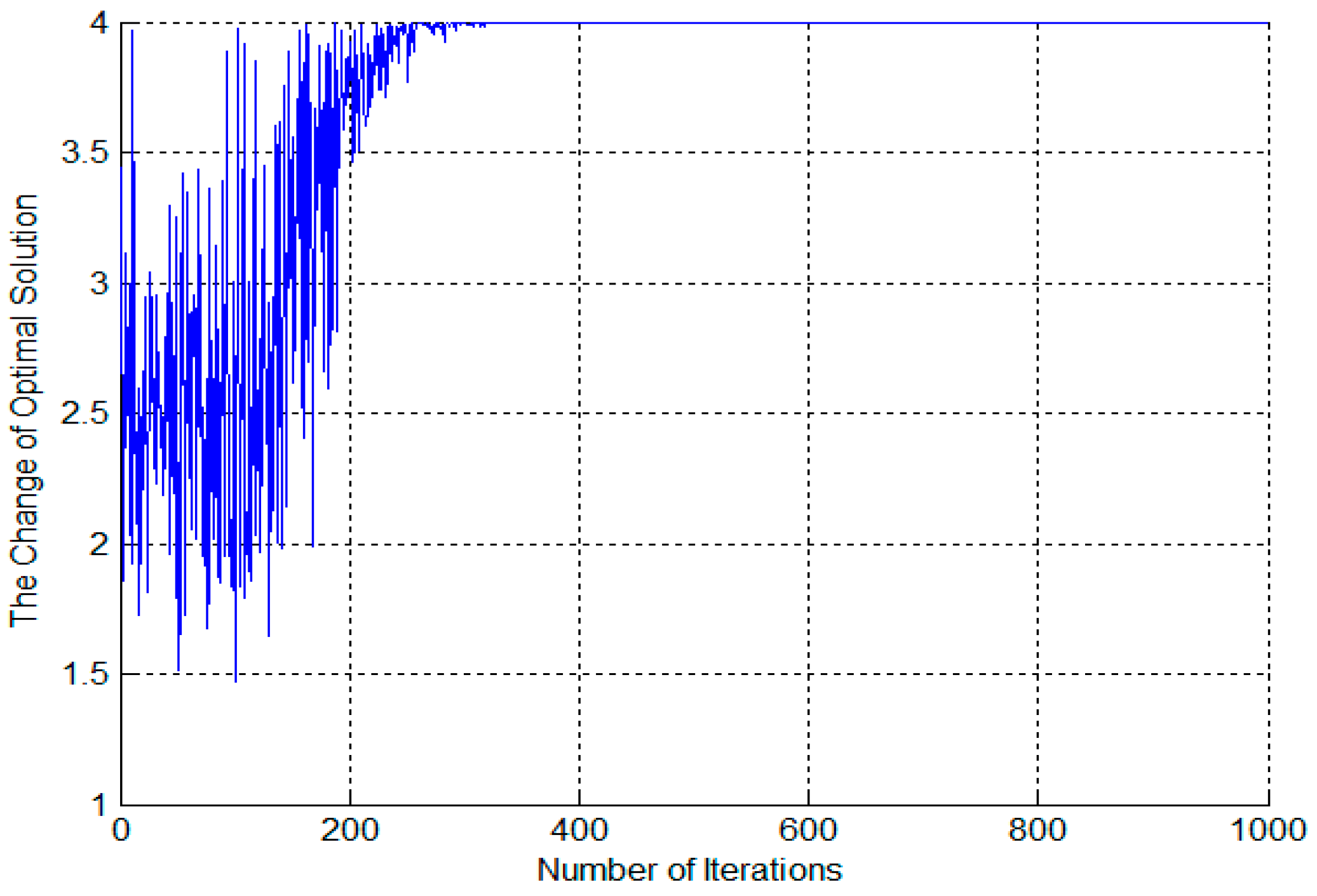
5.3. Results and Sensitivity Analysis
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Du, S.; Hu, L.; Song, M. Production optimization considering environmental performance and preference in the cap-and-trade system. J. Clean. Prod. 2016, 112, 1600–1607. [Google Scholar] [CrossRef]
- Mohammed, F.; Selim, S.Z.; Hassan, A.; Syed, M.N. Multi-period planning of closed-loop supply chain with carbon policies under uncertainty. Transp. Res. Part D Transp. Environ. 2017, 51, 146–172. [Google Scholar] [CrossRef]
- Krishnan, S.; Teo, T.S.H.; Lymm, J. Determinants of electronic participation and electronic government maturity: Insights from cross-country data. Int. J. Inf. Manag. 2017, 374, 297–312. [Google Scholar] [CrossRef]
- Lesk, C.; Rowhani, P.; Ramankutty, N. Influence of extreme weather disasters on global crop production. Nature 2016, 529, 84–87. [Google Scholar] [CrossRef] [PubMed]
- Moss, R.H.; Edmonds, J.A.; Hibbard, K.A.; Manning, M.R.; Rose, S.K.; van Vuuren, D.P.; Carter, T.R.; Emori, S.; Kainuma, M.; Kram, T.; et al. The next generation of scenarios for climate change research and assessment. Nature 2010, 463, 747–756. [Google Scholar] [CrossRef] [PubMed]
- Howarth, C.; Viner, D.; Dessai, S.; Rapley, C.; Jones, A. Enhancing the contribution and role of practitioner knowledge in the Intergovernmental Panel on Climate Change (IPCC) Working Group (WG) II process: Insights from UK workshops. Clim. Serv. 2017, 5, 3–10. [Google Scholar] [CrossRef]
- Geithner, T.F. Liquidity Risk and the Global Economy. Int. Financ. 2007, 102, 183–189. [Google Scholar] [CrossRef]
- Stern, N. The Stern review report on the economics of climate change. World Econ. 2006, 7, 1. [Google Scholar]
- Wang, R.; Liu, W.; Xiao, L.; Liu, J.; Kao, W. Path towards achieving of China’s 2020 carbon emission reduction target—A discussion of low-carbon energy policies at province level. Energy Policy 2011, 395, 2740–2747. [Google Scholar] [CrossRef]
- Gibbs, D.; Jonas, A.E.G.; While, A. The Implications of the Low-Carbon Economy for the Politics and Practice of Regional Development. In Territorial Policy and Governance: Alternative Paths; Routledge: Abingdon, UK, 2017; pp. 185–237. [Google Scholar]
- Chapman, L. Transport and climate change: A review. J. Transp. Geogr. 2007, 155, 354–367. [Google Scholar] [CrossRef]
- Kumar, A.; Jain, V.; Kumar, S. A comprehensive environment friendly approach for supplier selection. Omega 2014, 421, 109–123. [Google Scholar] [CrossRef]
- Dekker, R.; Bloemhof, J.; Mallidis, I. Operations Research for green logistics—An overview of aspects, issues, contributions and challenges. Eur. J. Oper. Res. 2012, 2193, 671–679. [Google Scholar] [CrossRef]
- Havinga, M.; Hoving, M.; Swagemakers, V. Alibaba: A Case Study on Building an International Imperium on Information and E-Commerce; Multinational Management; Springer International Publishing: Cham, Switzerland, 2016; pp. 13–32. [Google Scholar]
- Coase, R.H. The problem of social cost. J. Law Econ. 1960, 3, 1–44. [Google Scholar] [CrossRef]
- Robinson, J.; Brase, G.; Griswold, W.; Jackson, C.; Erickson, L. Business models for solar powered charging stations to develop infrastructure for electric vehicles. Sustainability 2014, 6, 7358–7387. [Google Scholar] [CrossRef]
- Burtraw, D.; Kahn, D.; Palmer, K. CO2 Allowance Allocation in the Regional Greenhouse Gas Initiative and the Effect on Electricity Investors. Electr. J. 2006, 19, 79–90. [Google Scholar] [CrossRef][Green Version]
- Sterner, T.; Muller, A. Output and abatement effects of allocation readjustment in permit trade. Clim. Chang. 2007, 86, 33–49. [Google Scholar] [CrossRef]
- Lee, D.H.; Kim, D.; Kim, S. Characteristics of forest carbon credit transactions in the voluntary carbon market. Clim. Policy 2017, 12, 1–11. [Google Scholar] [CrossRef]
- Baldwin, R. Regulation lite: The rise of emissions trading. Regul. Gov. 2008, 22, 193–215. [Google Scholar] [CrossRef]
- Dales, J. Pollution, Property, and Prices; University of Toronto Press: Toronto, ON, Canada, 1968. [Google Scholar]
- Bernard, A.; Haurie, A.; Vielle, M.; Viguier, L. A two-level dynamic game of carbon emission trading between Russia, China, and Annex B countries. J. Econ. Dyn. Control 2008, 32, 1830–1856. [Google Scholar] [CrossRef]
- Weikard, H.P.; Dellink, R. Sticks and carrots for the design of international climate agreements with renegotiations. Ann. Oper. Res. 2010, 220, 49–68. [Google Scholar] [CrossRef]
- Egenhofer, C. The Making of the EU Emissions Trading Scheme: Status, Prospects and Implications for Business. Eur. Manag. J. 2007, 25, 453–463. [Google Scholar] [CrossRef]
- Perdan, S.; Azapagic, A. Carbon trading: Current schemes and future developments. Energy Policy 2011, 39, 6040–6054. [Google Scholar] [CrossRef]
- Daskalakis, G.; Markellos, R.N. Are the European carbon markets efficient? Rev. Futur Mark. 2008, 17, 103–128. [Google Scholar]
- Chaabane, A.; Ramudhin, A.; Paquet, M. Design of sustainable supply chains under the emission trading scheme. Int. J. Prod. Econ. 2012, 135, 37–49. [Google Scholar] [CrossRef]
- Paltsev, S.; Reilly, J.M.; Jacoby, H.D.; Gurgel, A.C.; Metcalf, G.E.; Sokolov, A.P.; Holak, J.F. Assessment of US GHG cap-and-trade proposals. Clim. Policy 2008, 8, 395–420. [Google Scholar] [CrossRef]
- Ülkü, M.A. Daretocare: Shipment consolidation reduces not only costs, but also environmental damage. Int. J. Prod. Econ. 2012, 139, 438–446. [Google Scholar] [CrossRef]
- Choi, T.-M. Optimal apparel supplier selection with forecast updates under carbon emission taxation scheme. Comput. Oper. Res. 2013, 40, 2646–2655. [Google Scholar] [CrossRef]
- Liao, C.-H.; Tseng, P.-H.; Lu, C.-S. Comparing carbon dioxide emissions of trucking and intermodal container transport in Taiwan. Transp. Res. Part D Transp. Environ. 2009, 14, 493–496. [Google Scholar] [CrossRef]
- Jin, M.Z.; Nelson, A.; Ian Down, G.-M. The impact of carbon policies on supply chain design and logistics of a major retailer. J. Clean. Prod. 2014, 85, 453–461. [Google Scholar] [CrossRef]
- Kuo, T.C.; Chen, Y.H.; Wang, M.L.; Ming, W.H. Carbon footprint inventory route planning and selection of hot spot suppliers. Int. J. Prod. Econ. 2014, 150, 125–139. [Google Scholar] [CrossRef]
- Kim, N.S.; van Wee, B. Toward a Better Methodology for Assessing CO2 Emissions for Intermodal and Truck-only Freight Systems: A European Case Study. Int. J. Sustain. Transp. 2014, 8, 177–201. [Google Scholar] [CrossRef]
- Demir, E.; Bektas, T.; Laporte, G. A review of recent research on green road freight transportation. Eur. J. Oper. Res. 2014, 237, 775–793. [Google Scholar] [CrossRef]
- Soysal, M.; Bloemhof-Ruwaard, J.M.; vander Vorst, J.G.A.J. Modelling food logistics networks with emission considerations-The case of an international beef supply chain. Int. J. Prod. Econ. 2014, 152, 57–70. [Google Scholar] [CrossRef]
- Chen, W.T.; Hsu, C.I. Greenhouse gas emission estimation for temperature-controlled food distribution systems. J. Clean. Prod. 2015, 104, 139–147. [Google Scholar] [CrossRef]
- Soysal, M.; Bloemhof-Ruwaard, J.M.; Haijema, R.; vander Vorst, J.G.A.J. Modeling an Inventory Routing Problem for perishable products with environmental considerations and demand uncertainty. Int. J. Prod. Econ. 2015, 164, 118–133. [Google Scholar] [CrossRef]
- Demir, E.; Bektas, T.; Laporte, G. The bi-objective Pollution-Routing Problem. Eur. J. Oper. Res. 2014, 232, 464–478. [Google Scholar] [CrossRef]
- Konur, D. Carbon constrained integrated inventory control and truckload transportation with heterogeneous freight trucks. Int. J. Prod. Econ. 2014, 153, 268–279. [Google Scholar] [CrossRef]
- Tiwari, A.; Chang, P.C. A block recombination approach to solve green vehicle routing problem. Int. J. Prod. Econ. 2015, 164, 379–387. [Google Scholar] [CrossRef]
- Brandenburg, M. Low carbon supply chain configuration for a new product—A goal programming approach. Int. J. Prod. Res. 2015, 53, 6588–6610. [Google Scholar] [CrossRef]
- Jabir, E.; Vinay, V.; Sridharan, P.R. Multi-objective Optimization Model for a Green Vehicle Routing Problem. Procedia-Soc. Behav. Sci. 2015, 189, 33–39. [Google Scholar] [CrossRef]
- Benders, J.F. Partitioning procedures for solving mixed-variables programming problems. Numer. Math. 1962, 41, 238–252. [Google Scholar] [CrossRef]
- Fortz, B.; Poss, M. An improved benders decomposition applied to a multi-layer network design problem. Oper. Res. Lett. 2009, 37, 359–364. [Google Scholar] [CrossRef]
- Bektaş, T. Formulations and Benders decomposition algorithms for multidepot salesmen problems with load balancing. Eur. J. Oper. Res. 2012, 216, 83–93. [Google Scholar] [CrossRef]
- Saharidis, G.K.D.; Minoux, M.; Ierapetritou, M.G. Accelerating Benders method using covering cut bundle generation. Int. Trans. Oper. Res. 2010, 17, 221–237. [Google Scholar] [CrossRef]
- Wu, P.; Hartman, J.C.; Wilson, G.R. A demand-shifting feasibility algorithm for Benders decomposition. Eur. J. Oper. Res. 2003, 148, 570–583. [Google Scholar] [CrossRef]
- Rei, W.; Cordeau, J.F.; Gendreau, M.; Soriano, P. Accelerating Benders decomposition by local branching. Inf. J. 2009, 21, 333–345. [Google Scholar] [CrossRef]
- Poojari, C.A.; Beasley, J.E. Improving benders decomposition using a genetic algorithm. Eur. J. Oper. Res. 2009, 199, 89–97. [Google Scholar] [CrossRef]
- Yang, Y.; Lee, J.M. A tighter cut generation strategy for acceleration of benders decomposition. Comput. Chem. Eng. 2012, 44, 84–93. [Google Scholar] [CrossRef]
- Geoffrion, A.M. Generalized benders decomposition. J. Optim. Theory Appl. 1972, 10, 237–260. [Google Scholar] [CrossRef]
- Lasdon, L.S. Optimization Theory for Large Systems; Courier Corporation: North Chelmsford, MA, USA, 1970. [Google Scholar]
- Floudas, C.A. Nonlinear and Mixed-Integer Optimization: Fundamentals and Applications; Oxford University Press: New York, NY, USA, 1995. [Google Scholar]
- Hoen, K.M.R.; Tan, T.; Fransoo, J.C.; van Houtum, G.J. Effect of carbon emission regulations on transport mode selection under stochastic demand. Flex. Serv. Manuf. J. 2012, 26, 170–195. [Google Scholar] [CrossRef]
- Toro, E.M.; Franco, J.F.; Echeverri, M.G.; Guimarães, F.G. A multi-objective model for the green capacitated location-routing problem considering environmental impact. Comput. Ind. Eng. 2017, 110, 114–125. [Google Scholar] [CrossRef]
- Eswaramurthy, V.P.; Tamilarasi, A. Hybridizing tabu search with ant colony optimization for solving job shop scheduling problems. Int. J. Adv. Manuf. Technol. 2008, 40, 1004–1015. [Google Scholar] [CrossRef]
- Talbi, E.G.; Roux, O.; Fonlupt, C.; Robillard, D. Parallel ant colonies for the quadratic assignment problem. Future Gener. Comput. Syst. 2001, 17, 441–449. [Google Scholar] [CrossRef]


| The Type of Carbon Trading | Items | Shortened Form | The Connotation of Trading Products |
|---|---|---|---|
| Mandatory emission reduction transaction | Quota transaction [19,22] | CERs [21,23] | Certified emission reduction |
| EUAs [24,25,26,27] | European Union emission quota | ||
| AAUs [28] | Assigned amount units | ||
| Program trading | ERUs [29] | Emission reduction units | |
| RMUs | Carbon sink mitigation units | ||
| Voluntary emission reduction transaction | Quota transaction [20] | CFI | Carbon financial instrument |
| Odd-lot trading | Carbon Offsets | Carbon offsets | |
| Program trading [30] | VERs [31,32,33,34,35] | Voluntary emission reduction | |
| VCS [36,37,38] | Voluntary carbon standard |
| Center Warehouse (ID) | Product Category | ||||||
|---|---|---|---|---|---|---|---|
| Mobile | Computer | Electronic Accessory | Household Item | Food | Book | Clothing | |
| Urumqi (01) | 2000 | 1500 | 1000 | 700 | 3500 | 500 | 1000 |
| Hohehot (02) | 2100 | 1100 | 100 | 750 | 4000 | 500 | 1500 |
| Beijing (03) | 2000 | 1050 | 900 | 720 | 6500 | 3000 | 3200 |
| Yinchuan (04) | 2250 | 1200 | 850 | 660 | 3000 | 300 | 600 |
| Taiyuan (05) | 2300 | 600 | 880 | 640 | 1200 | 600 | 500 |
| Shijiazhuang (06) | 2200 | 540 | 860 | 600 | 500 | 2000 | 800 |
| Xining (07) | 2000 | 200 | 900 | 700 | 2000 | 350 | 500 |
| Lanzhou (08) | 2150 | 800 | 920 | 660 | 2300 | 400 | 900 |
| Jinan (09) | 2250 | 1250 | 950 | 680 | 3500 | 2000 | 2800 |
| Zhengzhou (10) | 2000 | 1200 | 850 | 620 | 2600 | 2200 | 3500 |
| Xian (11) | 2100 | 1100 | 840 | 600 | 1000 | 3000 | 4000 |
| Nanjing (12) | 2100 | 2150 | 850 | 640 | 2000 | 2800 | 3000 |
| Lhasa (13) | 2200 | 200 | 900 | 660 | 1500 | 300 | 1500 |
| Chengdu (14) | 2250 | 1000 | 860 | 700 | 3000 | 3000 | 2500 |
| Chongqing (15) | 2300 | 1500 | 920 | 680 | 4000 | 4200 | 2000 |
| Wuhan (16) | 2000 | 2100 | 900 | 700 | 3800 | 3000 | 3000 |
| Changsha (17) | 1500 | 900 | 800 | 600 | 3000 | 2000 | 1500 |
| Fuzhou (18) | 600 | 2200 | 600 | 300 | 3500 | 1000 | 4000 |
| Kunming (19) | 200 | 500 | 500 | 600 | 3000 | 500 | 2000 |
| Parameters | Mode of Transport | ||
|---|---|---|---|
| Highway | Railway | Aviation | |
| 1350 | 5500 | 8600 | |
| 2700 | 3500 | 6000 | |
| 5.2 | 6.4 | 20.0 | |
| 379 | 627 | 2250 | |
| Parameters | Commodity | ||||||
|---|---|---|---|---|---|---|---|
| Mobile | Computer | Electronic Accessory | Household Item | Food | Book | Clothing | |
| (/dozen) | 1280 | 11,500 | 4250 | 36,000 | 40 | 60 | 120 |
| (/dozen) | 624 | 1200 | 2320 | 28,800 | 15 | 30 | 60 |
| 1.20 | 1.10 | 1.35 | 1.65 | 1.15 | 1.00 | 1.25 | |
| (g/) | 0.5 | 1.3 | 1.2 | 5.0 | 2.9 | 10.4 | 1.5 |
| (kg) | 2.0 | 1.8 | 6.0 | 2.7 | 1.5 | 3.0 | 0.2 |
| 0.65 | 0.45 | 0.15 | 0.05 | 1.00 | 0.25 | 0.50 | |
| PLC | CLC | FCLC | VLC | |
|---|---|---|---|---|
| Time Window | (1,3) (3,5) (5,6) (6,7) (7,2) (2,4) (4,5) (5,6) (6,7) | (1,3) (3,5) (5,7) (7,1) (1,3) (3,5) (5,6) (6,7) | (1,4) (4,6) (6,1) (1,4) (4,6) (6,7) | (1,4) (4,7) (7,2) (2,5) (5,7) |
| Delivery Scheme | (H→GH,H→GH,H,R→H→GH,R→H→GH,H→GH,R→H→GH,GH,H→GH) (GH,A→GH,A→H→GH,A→H→GH,GH,H→GH,GH,H→GH,H→GH) (H→GH,A→GH,H,R→H→GH,R→H→GH,H→GH,R→H→GH,GH,H→GH) (H→GH,R→GH,H,R→H→GH,A→H→GH,H→GH,R→H→GH,GH,H→GH) (H→GH,R→GH,H,R→H→GH,H→GH,H→GH,R→H→GH,GH,H→GH) | (R→H,H,R→H,R→H,H→GH,A→H→GH,GH,H→GH) (R→H,A→H,R→H,R→H,A→H,GH,GH,H→GH) (R→H,R→H,R→H,R→H,H→GH,H→GH,GH,H→GH) (R→H,H,R→H,R→H,H→GH,A→H→GH,GH,H→GH) | (R→H,A→GH,R→H→GH,A→H→GH,H→GH,R→H→GH) (R→H,R→H,R→H,A→H→GH,R→H→GH,H→GH) (R→H→GH,H→GH,H→GH,R→H→GH,GH,H→GH) | (R→H→GH,R→H,R→H→GH,A→H→GH,H→GH) (H→GH,R→H,R→H→GH,R→H→GH,H→GH) |
| Average loading (%) | 82.27% | 81.36% | 80.41% | 79.82% |
| Allowable Emission (%) | 86.36% | 87.51% | 89.17% | 92.05% |
| Delivery Costs ($) | 115,724.8 | 109,619.1 | 100,503.9 | 98,400.3 |
| E-retailer Profit ($) | 288,600.2 | 285,392.4 | 284,846.7 | 283,015.6 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, S.; Sun, Q. Low-Carbon Planning and Design in B&R Logistics Service: A Case Study of an E-Commerce Big Data Platform in China. Sustainability 2017, 9, 2052. https://doi.org/10.3390/su9112052
Ji S, Sun Q. Low-Carbon Planning and Design in B&R Logistics Service: A Case Study of an E-Commerce Big Data Platform in China. Sustainability. 2017; 9(11):2052. https://doi.org/10.3390/su9112052
Chicago/Turabian StyleJi, Shoufeng, and Qi Sun. 2017. "Low-Carbon Planning and Design in B&R Logistics Service: A Case Study of an E-Commerce Big Data Platform in China" Sustainability 9, no. 11: 2052. https://doi.org/10.3390/su9112052
APA StyleJi, S., & Sun, Q. (2017). Low-Carbon Planning and Design in B&R Logistics Service: A Case Study of an E-Commerce Big Data Platform in China. Sustainability, 9(11), 2052. https://doi.org/10.3390/su9112052




