Abstract
Supply shortages and competitive disadvantages are the main problems faced by China’s hog sector. The non-essential import of pork products, triggered by competitive disadvantages, poses great challenges to hog farms. Structural changes are an important policy concern in China and elsewhere. Previous literature has ignored whether the ongoing structural changes from backyard to large farms can contribute to sustainable development. This study adopts the micro-level data of hog farms collected from Jiangsu Province, and uses a two-step metafrontier model and a primal system approach. The empirical results reveal that the ongoing structural changes are capable of boosting the growth in output in China’s hog sector, since the stronger increase in comparable technical efficiency compensates for the inappropriate technology. Furthermore, the ongoing structural changes are also beneficial in the reduction of production costs and in improving competitiveness in China’s hog sector. The decline in technical and allocative inefficiency costs, particularly for technical inefficiency costs, contributes to the cost advantage with the increasing farm size.
1. Introduction
As one of the world’s largest hog producers, China slaughters more than half the world’s hog numbers. China’s pork output increased from 39.7 million metric tons in 2000 to 54.9 million metric tons in 2015, with an annual growth rate of 2.2%. However, along with rising living standards, China has undergone a rapid dietary transition from a traditional diet dominated by fiber foods to western-style food with more meat products. As the main meat consumed by the Chinese, pork consumption increased from 39.6 million metric tons in 2000 to 55.7 million metric tons in 2015, with a rapid annual growth rate of 2.3%. Consequently, China has failed to balance its domestic pork supply and demand [1].
Importation is a feasible way to make up for the supply shortage. Before 2007, China was a self-sufficient net exporter of pork products and imported modest amounts of pork offal. However, in 2007, China’s pork and pork offal imports nearly quadrupled and doubled, to 0.09 and 0.4 million metric tons, respectively, and surged to 0.37 and 0.5 million metric tons, respectively, in 2008. Following a period of fall, China’s pork and pork offal imports rebounded to 0.47 and 0.88 million metric tons, respectively, in 2011 and rose to new heights in subsequent years. In fact, China’s pork importation greatly exceeds the level of domestic shortage. This non-essential importation may be attributed to a competitive disadvantage caused by soaring pork production costs in China [2]. In 2014, the average price of imported pork was 12 yuan per kilogram; this represented only 40% of the price of domestically produced pork. The two-fold-higher Chinese domestic market price, relative to the ceiling price of the world market, resulted in some of the domestic market share being inevitably replaced by imported pork, which makes some domestic outputs more difficult to sell. Hayes [3] holds the view that the potential for further Chinese importation of pork is enormous, due to the growing production costs within China. Hog producers around the world, especially in the USA, are applying themselves wholeheartedly to take full advantage of the potential opportunity presented by China’s emergence as a new source of demand for imported pork [2].
Fortunately, China’s hog sector has experienced structural changes, developing from backyard operations to specialized farms in the past decade [1,4,5,6], and a new operational structure is forming. More specifically, in 2002, hog farms with fewer than 50 animals (or heads) made up 99% of all China’s hog farms and slaughtered 72.8% of the total hog numbers. By 2010, while backyard farms still accounted for 95.7% of hog farms, the remaining 4.3% of hog farms were specialized operators with more than 50 heads per farm, and slaughtered approximately two-thirds of the total hog numbers. This implies that China’s hog industry is dominated by specialized operators. Compared with the operators with hog numbers between 50 and 499 heads, operators with more than 500 heads experienced more rapid development, and supplied more than one-third of the total hog numbers from only 0.4% of hog farms (shown in Figure 1). The growth in farmer wealth and the development of the non-farm labor market may also contribute to the structural changes from backyard to specialized farms [5,7]. In addition, the drastically fluctuating pork prices and the continual increase in feed prices have prompted extensive government intervention, and increasing private investment may have also accelerated structural changes since 2007 [2]. The ongoing structural changes in the hog industry are creating a situation whereby backyard farms dominate the farm count, but specialized farms account for the bulk of hog production.

Figure 1.
The share of hogs slaughtered in China across farm size.
Structural changes may cause negative impacts on environmental aspects, such as the increased risk of livestock diseases, the prevalence of antibiotic usage, and the local pollution of water bodies [4]. However, this study will mainly address the societal and economic aspects of these changes. What is the impact of ongoing structural changes on technical progress and efficiency? Furthermore, can the ongoing structural changes in the hog production sector balance out Chinese domestic pork supply and demand? Even if the ongoing structural changes can balance the Chinese domestic pork supply and demand through improved technical progress and increased technical efficiency in the hog sector, the gains may still be insufficient when the increasing hog production costs are taken into consideration. This gives rise to the question of whether the ongoing structural changes in the hog sector can alleviate the cost disadvantage and improve competitiveness.
Many agricultural economists have become increasingly concerned about the impacts of structural changes on productivity because the further growth of China’s livestock sector may have to rely on improvements in technical efficiency and progress, given less productive sow and resource constraints [1,8]. The Ministry of Agriculture of the People’s Republic of China (MOA) [9] has projected potential sources for further growth in the hog industry as specialized hog farms which may have higher levels of technical progress and efficiency than backyard farms. Agapi et al. [10] revealed that large-scale farms were more efficient than medium and backyard farms in China’s hog sector. Yu [11] argued that backyard dairy farms were less productive than specialized farms because their higher technical efficiency could not compensate for the low technology. Xiao et al. [1] found that technical progress and increasing technical efficiency [4] of hog farms accompanied ongoing structural changes. Rae et al. [8] revealed that when compared with specialized and commercial farms, backyard farms achieved lower total factor productivity and technical progress, but had a higher technical efficiency through the use of new panel data. These results indicated that structural changes from backyard to specialized farms might increase China’s pork outputs. Tian et al. [12] demonstrated that the technical efficiency of hog farmers showed a decreasing trend as the farm size increased, which may negatively impact further output growth of the hog sector.
Although the impacts of structural changes on the production costs of the livestock sector have been widely investigated in developed countries, this has unfortunately been ignored in China. Production costs can be broken down into frontier costs and inefficiency costs [13]. Based on 89 Utah dairy farms, Kumbhakar [14] found that a farm’s costs in relation to inefficiencies decreased with farm size. Tauer and Mishra [13] revealed that the frontier costs and inefficiency costs of US dairy farms decreased significantly as farm sizes increased. The inefficiency costs can be further broken down into technical inefficiency costs and allocative inefficiency costs. There have been studies that focused on the relationships between farm size and these two inefficiency costs, as these differences are of great importance to policy-makers. By using the panel data of Italian dairy farms, Maietta [15] revealed that technical inefficiency costs increased, whereas allocative inefficiency costs decreased for larger-scale farms. Mosheim and Lovell [16] found that both technical inefficiency costs and allocative inefficiency costs showed a statistically significant reduction as farm size increased.
This brief literature review illustrates the extensive studies evaluating the effects of structural changes on the productivity and the production costs of the livestock sector. However, to some extent, there are at least three shortcomings. First, most of the studies focus mainly on evaluating the potential room for future growth in productivity in China’s hog sector. However, even though improvements in productivity can greatly increase pork outputs, domestic pork may be difficult to sell because of cost disadvantages. The impact of structural changes on production costs in China’s hog sector, which has important policy implications, has unfortunately been ignored in the existing literature. Second, almost all of the research that has been done assumes that farms of different scales have homogenous technology [17,18] and that variation in productivity is attributed to differences in efficiency. However, feeding and management practice may differ significantly across farm types [8], and large-scale operators may employ relatively advanced technology in comparison with backyard farms [1]. Therefore, the heterogeneity of technology across farm types, which may result in differentiated production frontiers, should be taken into consideration. Third, the current studies (excluding Tian et al. [12]) mainly use macro data to estimate productivity where the data may be subject to over-reporting in production, and the underestimation of inputs [12,19,20].
The goal of this study, therefore, is to shed some light on the impact of structural changes on hog productivity and production costs. First, we will adopt the metafrontier model, developed by Battese et al. [21], O’Donnell et al. [22], and Huang et al. [23], to distinguish the heterogeneous technology among hog farms operating at different scales. Second, production costs will be broken down into its components, including frontier costs, technical inefficiency costs, and allocative inefficiency costs, by using the primal system approach developed by Kumbhakar and Wang [24], as well as household survey data. The results reveal that the ongoing structural changes are capable of boosting the growth of output in China’s hog sector and are also beneficial to the reduction of production costs and improving competitiveness in the Chinese hog sector.
The rest of this paper is organized as follows: in Section 2, we describe the primal system approach and the metafrontier model. The data are shown in Section 3. Section 4 presents the results and the discussion. The final section presents our conclusions based on the results and reflects on the corresponding policy implications.
2. Materials and Methods
2.1. A Primal System Approach to Break down Production Costs
The primal system approach proposed by Schmidt and Lovell [25] and extended by Kumbhakar and Wang [24], is more efficient than the cost system approach at breaking down cost inefficiency into technical and allocative inefficiency [24]. This approach allowed us to estimate the impacts of both observation-specific technical and allocative inefficiency on costs. The primal system approach includes the production function and the first-order conditions of cost minimization, and the use of the Cobb-Douglas (C-D) production function was algebraically equivalent to the cost system. Although translog production function is widely used in productivity analysis due to its flexible attributes such as variable returns to scale and variable elasticity of substitution [1,4], it is not possible to derive the algebraic expressions for the input demand function, with or without inefficiency in the primal system approach, which are used to break down the production costs into technical and allocative inefficiency costs [24]. The primal system approach can be described as consisting of the following steps:
Step 1: A C-D production function is used to calculate the technical inefficiency. The C-D production function, in conjunction with its first-order conditions for cost minimization, is used to measure the parameter , which is used to calculate the allocative inefficiency. The C-D production function is written as:
where refers to the output quantity of hog farms; is a vector of inputs, including piglet, feed, labor, and intermediate input quantity; is a technology parametric vector to be estimated and also refers to elasticity with respect to output for the C-D production function; is a random error term, which captures events (such as climatic factors) beyond the control of farmers, independently and identically distributed as ; refers to technical inefficiency and is independently and identically distributed as .
The first-order conditions of C-D production function for cost minimization are written as:
Taking logs for Equation (2) yields:
where represents the first derivative of C-D production function for input , and is the price of input . The parameter can be interpreted as allocative inefficiency for the input relative to input one, which acts as the numeraire input due to linear homogeneity in prices. The choice of numeraire input is usually arbitrary. The sign of can be used to identify the use condition of input , relative to numeraire input . A positive sign of indicates the underuse of input , relative to the numeraire input , while the negative sign means the overuse. is independently and identically distributed as , and independent of , and . is the cost share of input . Based on Equations (1)–(3), we can derive the input demand functions, with or without technical and allocative efficiencies, and further calculate the extent of overuse or underuse of each input, relative to numeraire input .
Step 2: The derived algebraic expressions for the input demand functions in logarithmic form are as follows:
where is returns to scale, and . The input demand function can be broken down into four parts: The first part, , is the function of input prices, the output of hogs, and the value of returns to scale. The second part, , depends on input allocative inefficiency, , and the value of returns to scale. The demand function of is different from numeraire input one. Based on the input demand function, we can derive the impact of allocative inefficiency on input demand for ; for example, if allocative inefficiency is removed, the actual demand for is changed by percent, while it is changed by percent for numeraire input . The third part, , depends on technical inefficiency , and the value of returns to scale. From this part, we can also derive the impact of technical inefficiency on the demand for input ; for example, if technical inefficiency is removed, the actual demand for is increased by . The fourth part, , depends on and the value of returns to scale.
Step 3: Break down the observation-specific production costs into frontier costs and technical and allocative inefficiency costs. Based on Equations (4) and (5), we can calculate the input demand, , under the condition of technical and allocative inefficiency by assuming and . We can also calculate the input demand , under the condition of only technical inefficiency by assuming , but . Similarly, we can calculate the input demand under the condition of only allocative inefficiency by assuming , but . Then, the corresponding costs , , and can be calculated by the price of each input multiplied by these three input demands under different inefficiency conditions.
2.2. Metafrontier Analysis
Rae et al. [8] claim that backyard farms may adopt feeding and management practices that differ from those adopted by specialized farms in China’s hog sector. Xiao et al. [1] further point out that large-scale operators may employ more advanced technology. The variation in technology and management practice may contribute to different production frontiers across production structures. It may also lead to a biased estimation of technical efficiency and make it impossible to identify the technology gaps across different size farms, if a single frontier is assumed for all farms. Fortunately, Battese et al. [21] and O’Donnell et al. [22] have developed a metafrontier model to envelop the group frontiers, which are estimated for farms in the same technology set groups, as well as to calculate the technology gaps and comparable technical efficiency across different size farms. The metafrontier model is estimated as follows:
The hog farms can be divided into groups. Based on the C-D production function in Equation (1), we are able to estimate differentiated frontiers for each group and calculate the observation-specific technical efficiency within groups. However, the technical efficiency levels in Group A cannot be compared with the technical efficiency levels in Group B [22]. The technical efficiency levels for th farm in th group show as:
where and denote the th farm in the th group. For simplicity, the C-D production function is written as in the metafrontier model. Then, the metafrontier production function for all farmers is defined as:
where denotes the vector of parameters for the metafrontier function and satisfies the following assumption
Equation (8) indicates that the metafrontier is a smooth deterministic parametric function, but is not a segmented envelop of the frontier for the group frontiers because its values are no smaller than the deterministic part [21,22]. Figure 2 presents the relationship between the group frontiers and the metafrontier.
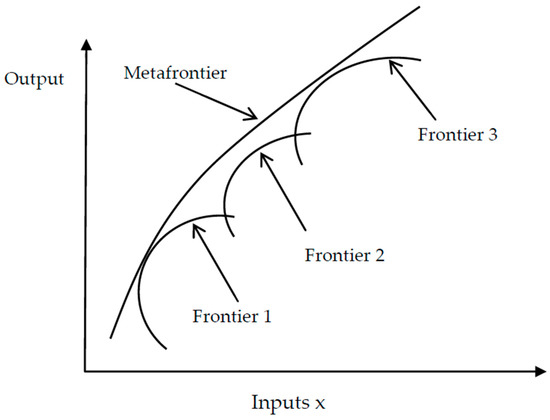
Figure 2.
Metafrontier function model [22,23].
A mathematical optimization programming approach, which aims to minimize the sum of the absolute deviations or the squared deviations of the distances between the group frontiers and the metafrontier, is proposed by Battese et al. [21] and O’Donnell et al. [22] to estimate the metafrontier function. For example, the optimization equation for minimizing the squared deviations is expressed by:
where are the group frontiers, estimated using maximum likelihood estimation (MLE). However, Huang et al. [23] argue that an error exists between the separated frontier and the estimated frontier , and the omitted error can result in problems when , instead of , is used to estimate the metafrontier . Therefore, the statistical interpretation and the statistical properties of the estimated metafrontier function are meaningless and unknown, respectively. Consequently, they propose an alternative two-step stochastic frontier method to estimate the metafrontier. Given the estimated group frontiers , the estimation error of the group frontier can be written as:
Due to the metafrontier enveloping all of the group frontiers , the metafrontier can also be expressed as the following equation [23]:
where refers to the non-negative technology gap ratio and is assumed to be distributed as truncated-normal [23]. Defining the estimation error in Equation (10) as , the metafrontier in Equation (11) can be rewritten as a new stochastic frontier function form:
Equation (12) is similar to the stochastic frontier function. However, the in Equation (12) is distinguished from the error in the stochastic frontier function [23]. More specifically, is important in formulating Equation (9) as a stochastic function, and it is reasonable to assume it to be asymptotically normally distributed with zero mean, dependently and identically distributed [23]. The average technology gap ratios (MTR) are expressed as follows:
The value of MTR is between zero and one and captures technology differences by using the ratio of group frontiers to metafrontier. A lower value represents an increase in the technology gap and vice versa. Hence, a value of one is the optimum. The comparable technical efficiency is expressed as follows:
The method developed by Huang et al. [23] will be employed in this study.
2.3. Hotelling’s T2 Generalized Mean Test
Hotelling’s T2 generalized mean test is an appropriate method in which to determinate whether a set of means is equal between two groups [16]. For two groups, the test of equality is:
where and are matrix of the means, refers to the number of variables. is the estimated covariance matrix.
This study uses it to identify the significant level of input quantity, input price, marginal values and inefficiency costs across farm sizes.
2.4. Marginal Product Value
The marginal product value, or shadow price, is calculated by the marginal products of each input multiplied by the average selling price of slaughtered hogs. By comparing the marginal product value with the corresponding input price, we can identify the extent of distortion, which is critically important for the choice of numeraire input [26]. This study used the 2012–2014 average prices of piglets, feed and labor. Input prices were deflated by using the corresponding input price indexes.
2.5. Local Polynomial Smooth Curve
Local polynomial smooth curves are based on the idea of making no assumptions about the function form for two variables. It involves fitting the variables to a polynomial form of the regressor via locally weighted least squares. Local polynomial smooth curves can be made by using lpolyci order in Stata. We will use local polynomial smooth curves to illustrate the relationships between farm sizes and production costs.
3. Data
The micro-level data of hog farmers in this study were periodically collected by the Jiangsu Provincial Price Bureau from 2012 to 2014. Jiangsu Province, as the 13th largest hog producer in China, produced 2.3 million metric tons of pork and slaughtered 30.7 million pigs in 2014. However, due to the rapid development in rural labor and the grain market [7], the share of both pork production and slaughtered pigs contracted in the past decade declined from 5% and 5.2%, respectively, in 2002 to 4.1% and 4.2% respectively, in 2014. Jiangsu Province, located in the eastern coastal area, has trained many experienced survey team members at the village, township, county, prefectural, and provincial levels to record the data of inputs and outputs for each commodity [27]. To increase the sample representativeness, a three-stage stratified sampling procedure was adopted to determine sample county, township, and, finally, individual farms. The surveyed hog farms were divided into four groups by size in our sample. Backyard farms refer to households producing a small number of hogs, usually fewer than 30 heads; small-scale farms are classified as having hog numbers between 30 and 100 heads; medium-scale farms are classified as having hog numbers between 100 and 1000 heads; and farms having more than 1000 heads are defined as large-scale. This classification criteria, which are different from the classification criteria in the China Livestock Yearbook, were adopted by the National Development and Reform Commission of China (NDRC) for cost-benefit analysis [28].
A total of 275 hog farms were surveyed from 2012 to 2014, and the numbers of backyard, small-scale, medium-scale, and large-scale farms were determined as being 96, 112, 36, and 31, respectively. Table 1 presents the summary statistics of hog farms’ outputs and inputs over groups. From the bottom half of Table 1, it can be seen that the average weight of each slaughtered hog is 103 kg, and a significant inverted quasi-U-shaped relationship appears as the farm size increases. Similarly, the relationship between feed inputs and farm size is also a similar inverted U-shape, with a mean quantity of 259 kilograms. The other intermedia inputs increase significantly with the farm size. In contrast, the labor inputs decrease as the farm size increases, implying that some other labor-saving inputs substitute for labor. The average weight of piglets is 22.65 kg, and there is no significant difference across the groups.

Table 1.
Summary statistics of variables.
4. Results and Discussion
Given resource constraints, the further output growth of China’s hog sector may have to rely on continuing improvements in productivity such as technical efficiency and technology, rather than the increase in input uses. Estimating a single frontier for all hog farmers cannot identify the differences in technology across groups and may lead to biased productivity estimates. Following the method developed by Battese et al. [21], O’Donnell et al. [22], and Huang et al. [23], this study adopted a two-step stochastic frontier approach to estimate group frontiers and the metafrontier, and to calculate comparable technical efficiency and technology gaps across groups.
Table 2 presents the results of the group frontiers and the metafrontier based on Equation (1) and Equation (12). The estimated group frontiers show that all the inputs have significant positive impacts on hog outputs for all groups, excluding labor in the middle-scale and large-scale frontiers and other intermediate inputs in the backyard frontier. The estimated variance of technical inefficiency (Sigma_u) is significantly different from zero and is larger than that of the random error term for most of the group frontiers, indicating that deviations from the frontier are primarily caused by technical inefficiency [29]. Thus, using a stochastic frontier model in this study was necessary and reasonable, because inefficiency is an important determinant of productivity. In addition, the output elasticities with respect to each input showed that feeds were the most efficient input with regard to increasing hog production. At the mean, a 1% increase in feed input will result in a 0.7% increase in hog production. Similarly, the hypothesis of technical efficiency for the metafrontier was also rejected at a 1% significance level, indicating that technical inefficiency plays an important role in the metafrontier.

Table 2.
The estimation results of group frontiers and the metafrontier.
The estimated technical efficiencies, which also refer to the rates of catching up to best practices with respect to each group frontier, are shown in Table 3. The mean technical efficiency level is around 90% or more for hog farmers across groups, implying that there is still some room left for improving the hog sector’s outputs by improving farmers’ technical efficiencies, which is in line with the results presented by Zhou et al. [4]. Unfortunately, the technical efficiency, with respect to each group cannot be compared because of differentiated frontiers across groups.

Table 3.
Technical efficiencies and technology gaps across groups.
The average value of comparable technical efficiencies is 0.916, implying that there is a possible 8.4% increase in hog production if the technical inefficiency is completely removed. One of the most important findings of our empirical study was that comparable technical efficiencies show a significantly increasing trend as farm sizes increase, which is in line with the results estimated by using livestock data from developed countries [13,14,16]. Although most studies focusing on China’s livestock sector reveal that backyard farms are more technically efficient than larger-scale farms [8,11,12] as backyard farms can make full use of their labor resources and monitor their production activities more closely, larger-scale farms may become more efficient if cheap modern inputs are provided and labor constraints are relaxed [30]. Similarly, Uddin et al. [31] used metafrontier productivity analysis and pointed out that the intensive production system had the closest distance to the technological frontier than extensive and traditional production systems.
The results of technology gaps across groups are in contrast to our expectations. The technology gaps relative to the metafrontier initially exhibit a slight increase as the farm size expands, but then narrow partially as hog numbers exceed 1000 heads. Vulnerability to disease, which is affected by the density of animal populations, facilities, technical knowledge among farm personnel [2] and biosecurity practices such as sharing boars, may contribute to underperformance in adopting the best available technology for small-scale and medium-scale farms. This is because small-scale and medium-scale farms do not build large and advanced facilities and mainly rely on their own labor [10]. Consequently, the density of their animal populations is higher and their farm personnel may lack technical knowledge. However, both facilities and the technical knowledge of farm personnel may be improved for large-scale farms. In addition, this finding suggests that the results estimated by using macro-level data may overestimate the technology of large-scale farms. In all, while a quasi-U-shaped relationship is found between technology gaps and farm size, there is a stronger increasing trend in the comparable technical efficiency, suggesting that ongoing structural changes from backyard to large-scale can boost the output growth in China’s hog sector.
However, the growth in output is not enough to solve the dilemma faced by China’s hog sector. Even though China can produce the pork products needed by consumers, the products may be hard to sell due to cost disadvantages. Reducing the production costs plays a core role in China’s hog sector. Therefore, there is a need to further evaluate the impact of ongoing structural changes, from backyard to large-scale, on the farmers’ production costs. Production costs can be broken down into frontier costs, technical inefficiency costs, and allocative inefficiency costs. To achieve the goal of evaluating the impact of ongoing structural changes, we adopted the primal system approach developed by Schmidt and Lovell [25] and Kumbhakar and Wang [24].
The analysis began by calculating the marginal product values in order to identify the actual distortion of each input. Table 4 presents the marginal product values and price of each input. The results show that the piglet input has lower distortion and, thus, acts as numeraire input in this study. The other findings are as follows: we found that the calculated marginal product values with respect to piglet, feed, and labor are higher than zero and different from the corresponding input price at the 5% significance level. The average marginal product value of a piglet is 11.86 yuan, which is significantly less than its price, suggesting a strong signal of overuse. The application of Hotelling’s T2 generalized mean test shows that compared with backyard farms, small-scale farms had a significantly lower marginal product value of piglets, whereas there was no significant difference among small-scale, medium-scale and large-scale farms. In contrast, at the mean, the marginal product values of feed and labor were higher than the corresponding input prices, indicating that increasing feed and labor can still produce additional output. Feed is underused for all four farm types. However, the increasing feed prices may have a negative impact on maintaining stable feed inputs [1]. Although the average value indicated underuse of labor input, the labor inputs for backyard farms and small-scale farms were saturated, consistent with Yu’s findings [11].

Table 4.
Marginal product values and price of each input.
Table 5 reports the production cost (P cost) and its components, including the frontier cost (F cost), technical inefficiency cost (TI cost), and allocative inefficiency cost (AI cost). The average production cost per kilogram of slaughtered hog is 14.39 yuan. The production cost for backyard farms is 15.51 yuan, which is higher than the mean level. In comparison with backyard farms, small-scale farms have a significantly lower production cost. However, there were no differences among small-scale, medium-scale and large-scale farms. At the mean, the frontier cost is 11.73 yuan per kilogram of slaughtered hog, accounting for 81.51% of the production cost. Similarly, the frontier cost initially shows a significant downward trend, and then remains stable among small-scale, medium-scale, and large-scale farms.

Table 5.
Average cost for per kilogram slaughtered hog under different inefficiency restrictions.
The average inefficiency cost is 2.66 yuan per kilogram of slaughtered hog, accounting for 18.49% of the production cost. This suggests that hog production costs may be underestimated if inefficiency costs are not taken into consideration. Small-scale farms have a lower inefficiency cost relative to backyard farms, and the inefficiency cost has an insignificant decrease as the farm size increases. Thus, higher production costs for small-scale farmers are caused by inefficiency rather than by technology.
In addition, both technical and allocative inefficiency costs are different from zero at a 1% significance level, with a mean value of 1.11 yuan and 1.56 yuan, respectively. Of the two components, allocative inefficiency cost plays a more important role in the overall inefficiency cost. Moreover, technical inefficiency costs show a significant and continuous downward trend as farm sizes increase. However, a quasi-U-shaped relationship is found between the allocative inefficiency cost and farm size. Therefore, the share of allocative inefficiency costs also increases with the farm size, and accounts for 89.19% of inefficiency costs for large-scale farms.
In summation, these results suggest that the ongoing structural changes from backyard to large-scale can reduce the production cost and improve competitiveness in China’s hog sector. The declining costs as hog farms change from backyard to large-scale are mainly attributed to the decline in inefficiency costs. In addition, in contrast to allocative inefficiency costs, technical inefficiency costs undergo a more remarkable decrease trend. There appears to be some room to achieve higher productivity and competitiveness by improving the allocative efficiency and adopting appropriate technology.
Table 5 shows that the relationships between average unit costs under different inefficiency restrictions and different farm sizes are nonlinear. Thus, we present the local polynomial smooth curves for these relationships in Figure 3. It is worth mentioning that production costs and frontier costs will show an upward trend when the farm size exceeds 3000 heads, while allocative inefficiency costs still show a downward trend.
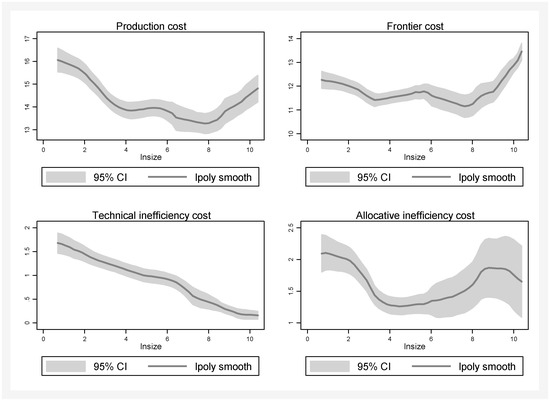
Figure 3.
Local polynomial smooth curves for the relationship between farm size and unit costs.
5. Conclusions and Policy Implications
China has undergone remarkable structural changes from backyard farms to large-scale farms, and the hog sector has been reformed in the past decade. Nowadays, backyard farms dominate the farm count, but specialized farms account for the bulk of hog production. The impacts of ongoing structural changes on technical progress and efficiency have been widely analyzed by agricultural economists. However, most studies assume a single frontier, which may lead to a biased estimation of technical efficiency and render it impossible to identify the technology gaps among farms of different sizes. In addition, the existing literature ignores the impact of ongoing structural change on production costs, which is unfortunate in the case of China’s hog sector because the cost disadvantages make it difficult to sell pork products. These gaps have been filled in this study. Based on the micro-level data of a 2012–2014 survey of hog farms in Jiangsu Province, this study illustrates the relationships between productivity, production cost, and farm size in China’s hog sector. Productivity is represented by technical efficiency and technology gaps, and the production costs are further broken down into three components: frontier cost, technical inefficiency cost, and allocative inefficiency cost. By adopting a two-step metafrontier model and a primal system approach, we found that comparable technical efficiencies show a significant increasing trend as the farm sizes increase, while a quasi-U-shaped relationship is found between technology gaps and farm size. In all, ongoing structural changes from backyard to large-scale can boost the output growth in China’s hog sector because there is a stronger increasing trend in the comparable technical efficiency. Furthermore, the ongoing structural changes reduce production costs and improve competitiveness in China’s hog sector. The declines in technical and allocative inefficiency costs, particularly for technical inefficiency costs, contribute to cost advantages as farm sizes increase.
Our results indicate that the ongoing structural changes may help solve both the short supply problem and the cost disadvantage problem. However, if policy-makers formulate policies and programs targeted at optimizing the allocation of resources and helping hog farms adopt the best appropriate technology, China’s hog sector may benefit further from the structural changes.
Acknowledgments
This work was funded by the Key Program of the National Natural Science Foundation of China (71333008; 71573126); the Key Program of the National Planning Office of Philosophy and Social Science of China (14ZDA037; 13&ZD160); the PHC Cai Yuanpei Program (34644SB), the Dissertation Scholarship of China Institute for Rural Studies, Tsinghua University (2016013); as well as the A Project Funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD). All remaining errors are ours.
Author Contributions
Xiaoheng Zhang and Yingheng Zhou proposed the research framework, wrote the protocol and the first draft together with Feng Chu and Jinyang Yang. Xiaohua Yu and Xu Tian surveyed the literature, carried out proofreading and restructured the paper. All of the research was guided and supervised by Yingheng Zhou. All of the authors read and approved the final manuscript.
Conflicts of Interest
The authors have declared no conflicts of interest in this paper.
References
- Xiao, H.; Wang, J.; Oxley, L.; Wang, H. The Evolution of hog production and potential source for future growth in China. Food Policy 2012, 37, 366–377. [Google Scholar] [CrossRef]
- Gale, F.; Marti, D.; Hu, D. China’s Volatile Pork Industry; A Report from the Economic Research Service LDP-M-211-01; USDA (U.S. Department of Agriculture): Washington, DC, USA, 2012.
- Hayes, D.J. The Potential Market for U.S. Pork Exports in China; Iowa State University Working Paper; Iowa State University: Ames, IA, USA, 2010. [Google Scholar]
- Zhou, Y.; Zhang, X.; Tian, X.; Geng, X.; Zhang, P.; Yan, B. Technical and environmental efficiency of hog production in China-A stochastic frontier production function analysis. J. Integr. Agric. 2015, 14, 1069–1080. [Google Scholar] [CrossRef]
- Qiao, F.; Huang, J.; Wang, D.; Liu, H.; Lohmar, B. China’s hog production: From backyard to large-scale. China Econ. Rev. 2016, 38, 199–208. [Google Scholar] [CrossRef]
- Huang, W.; Qiao, F.; Liu, H.; Jia, X.; Lohmar, B. From backyard to commercial hog production. China Agric. Econ. Rev. 2016, 8, 22–36. [Google Scholar] [CrossRef]
- Chen, J.; Rozelle, S. Market emergence and the rise and fall of backyard hog production in China. In Proceedings of the American Agricultural Economics Association Annual Meeting, Montreal, QC, Canada, 27–30 July 2003.
- Rae, A.N.; Ma, H.; Huang, J.; Rozelle, S. Livestock in China: Commodity-specific total factor productivity and decomposition using new panel data. Am. J. Agric. Econ. 2006, 88, 680–695. [Google Scholar] [CrossRef]
- MOA (Ministry of Agriculture of the People’s Republic of China). National Livestock Husbandry Development Plan during the 11th Five-Year (2006–2011); China Agriculture Press: Beijing, China, 2006.
- Agapi, S.; Zhang, X.; Tuan, F. China’s hog production structure and efficiency. In Proceedings of the American Agricultural Economics Association Annual Meeting, Montreal, QC, Canada, 27–30 July 2003.
- Yu, X. Productivity, Efficiency and structural problems in Chinese dairy farms. China Agric. Econ. Rev. 2012, 4, 168–175. [Google Scholar] [CrossRef]
- Tian, X.; Sun, F.; Zhou, Y. Technical efficiency and its determinants in China’s hog production. J. Integr. Agric. 2015, 14, 1057–1068. [Google Scholar] [CrossRef]
- Tauer, L.W.; Mishra, A.K. Can the small dairy farm remain competitive in US agriculture? Food Policy 2006, 31, 458–468. [Google Scholar] [CrossRef]
- Kumbhakar, S.C. Short-Run returns to scale, farm-size, and economic efficiency. Rev. Econ. Stat. 1993, 75, 336–341. [Google Scholar] [CrossRef]
- Maietta, O.W. The decomposition of cost inefficiency into technical and allocative components with panel data of Italian dairy farms. Eur. Rev. Agric. Econ. 2000, 27, 473–495. [Google Scholar] [CrossRef]
- Mosheim, R.; Lovell, C.A.K. Scale economies and inefficiency of U.S. dairy farms. Am. J. Agric. Econ. 2009, 91, 777–794. [Google Scholar] [CrossRef]
- Key, N.; McBride, W. Production contracts and productivity in the U.S. hog sector. Am. J. Agric. Econ. 2003, 85, 121–133. [Google Scholar] [CrossRef]
- Key, N.; McBride, W.D. Do production contracts raise farm productivity? An Instrumental Variables Approach. Agric. Resour. Econ. Rev. 2008, 37, 176–187. [Google Scholar] [CrossRef]
- Yu, X.; Abler, D. Where have all the pigs gone? Inconsistencies in pork statistics in China. China Econ. Rev. 2014, 30, 469–484. [Google Scholar] [CrossRef]
- Yu, X.; Abler, D. Matching food with mouths: A statistical explanation to the abnormal decline of per capital food consumption in rural China. Food Policy 2016, 63, 36–43. [Google Scholar] [CrossRef]
- Battese, G.E.; Rao, D.S.P.; O’Donnell, C.J. A metafrontier production function for estimation of technical efficiencies and technology gaps for firms operating under different technologies. J. Prod. Anal. 2004, 21, 91–103. [Google Scholar] [CrossRef]
- O’Donnell, C.J.; Rao, D.S.P.; Battese, G.E. Metafrontier frameworks for the study of firm-level efficiencies and technology ratios. Empir. Econ. 2008, 34, 231–255. [Google Scholar] [CrossRef]
- Huang, C.J.; Huang, T.; Liu, N. A new approach to estimating the metafrontier production function based on a stochastic frontier framework. J. Prod. Anal. 2014, 42, 241–254. [Google Scholar] [CrossRef]
- Kumbhakar, S.C.; Wang, H. Estimation of technical and allocative inefficiency: A primal system approach. J. Econ. 2006, 134, 419–440. [Google Scholar] [CrossRef]
- Schmidt, P.; Lovell, C.A.K. Estimating technical and allocative inefficiency relative to stochastic production and cost frontier. J. Econ. 1979, 9, 343–366. [Google Scholar] [CrossRef]
- Atkinson, S.E.; Dorfman, J.H. Chasing absolute cost and profit savings in a world of relative inefficiency. In Proceedings of the AAEA Annual Meeting, Long Beach, CA, USA, 26 July 2006.
- Fan, S. Technological change, technical and allocative efficiency in Chinese agriculture: The case of rice production in Jiangsu. J. Int. Dev. 2000, 12, 1–12. [Google Scholar] [CrossRef]
- NDRC (National Development and Reform Commission of China). China Agricultural Product Cost-Benefit Compilation; China’s Statistical Press: Beijing, China, 2014.
- Coelli, T.L. Estimators and hypothesis tests for a stochastic frontier function: A Monte Carlo Analysis. J. Prod. Anal. 1995, 6, 247–268. [Google Scholar] [CrossRef]
- Fan, S.; Chan-Kang, C. Is small beautiful? Farm size, productivity, and poverty in Asian agriculture. Agric. Econ. 2005, 32, 135–146. [Google Scholar] [CrossRef]
- Uddin, J.M.; Brümmer, B.; Peters, J.K. Technical efficiency and meta technology ratios under varying resource endowment in different production systems: A stochastic metafrontier model in Bangladesh dairy farms. China Agric. Econ. Rev. 2014, 6, 485–505. [Google Scholar] [CrossRef]
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).