Hesitant Trapezoidal Fuzzy QUALIFLEX Method and Its Application in the Evaluation of Green Supply Chain Initiatives
Abstract
:1. Introduction
2. Preliminaries
2.1. Some Useful Concepts
2.2. New Concept of Hesitant Trapezoidal Fuzzy Sets
- (1)
- ;
- (2)
- ;
- (3)
- ;
- (4)
- .
- (1)
- ;
- (2)
- ;
- (3)
- ;
- (4)
- ;
- (5)
- ;
- (6)
- .
- (1)
- if , then ;
- (2)
- if , then ;
- (3)
- if , then .
3. Hesitant Trapezoidal Fuzzy QUALIFLEX Analysis Method
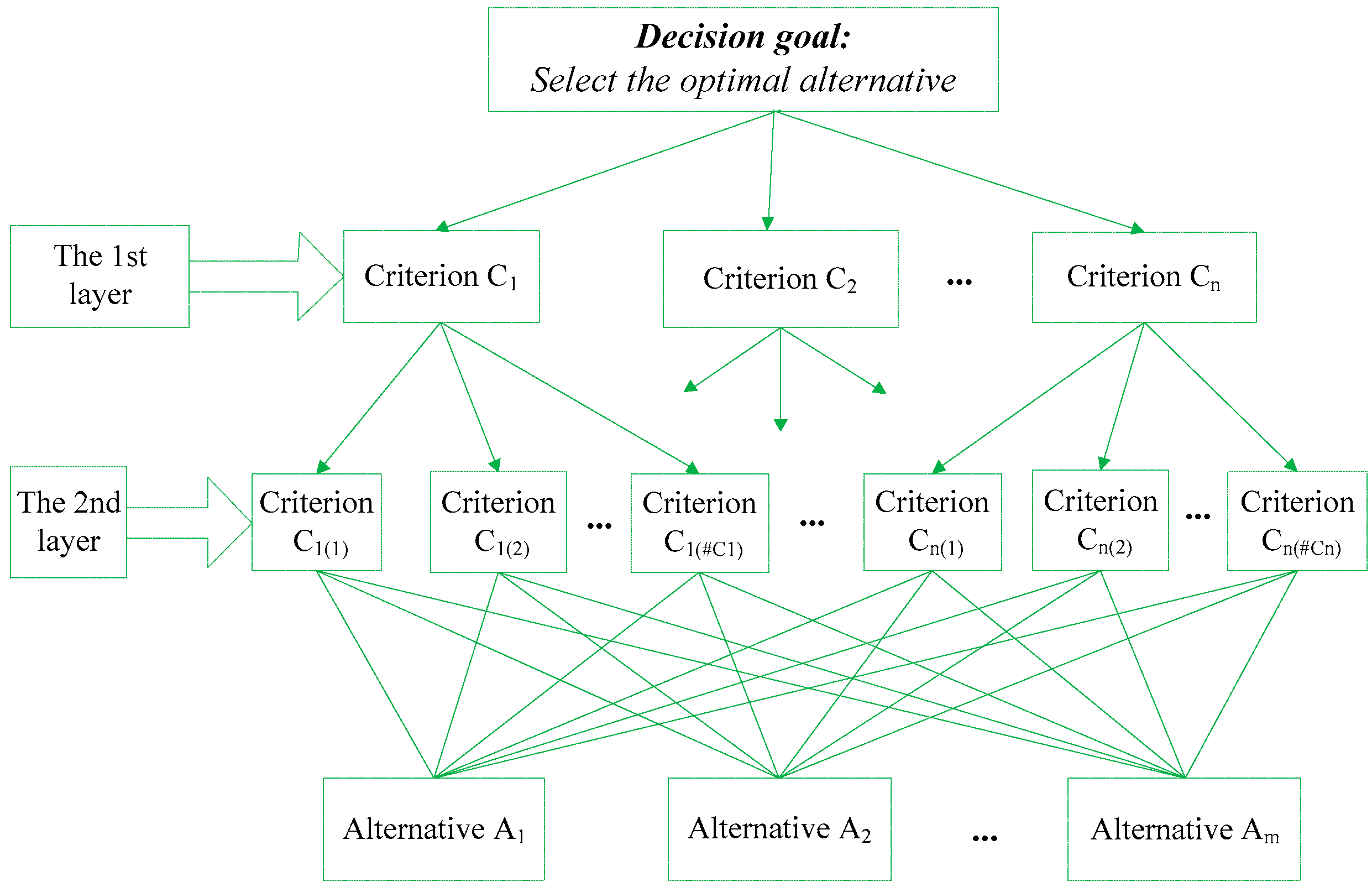
3.1. Description of the Hierarchical MCDM Problem with HTrFNs
3.2. The Proposed Method
3.3. The Proposed Algorithm
4. A Case Study for the Evaluation of Green Supply Chain Initiatives
4.1. Decision Context and the Analysis Process
4.2. Comparative Analysis
4.2.1. Comparative Analysis with the TOPSIS
4.2.2. Comparative Analysis with the ELECTRE
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wang, X.J.; Chan, H.K. A hierarchical fuzzy TOPSIS approach to assess improvement areas when implementing green supply chain initiatives. Int. J. Prod. Res. 2013, 51, 3117–3130. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning-I. Inf. Sci. 1975, 8, 199–249. [Google Scholar] [CrossRef]
- Herrera, F.; Martínez, L. A 2-tuple fuzzy linguistic representation model for computing with words. IEEE Trans. Fuzzy Syst. 2000, 8, 746–752. [Google Scholar]
- Martínez, L.; Herrera, F. An overview on the 2-tuple linguistic model for computing with words in decision making: Extensions, applications and challenges. Inf. Sci. 2012, 207, 1–18. [Google Scholar] [CrossRef]
- Rodríguez, R.M.; Martínez, L. An analysis of symbolic linguistic computing models in decision making. Int. J. Gen. Syst. 2013, 42, 121–136. [Google Scholar] [CrossRef]
- Xu, Z.S. Uncertain Multiple Attribute Decision Making: Methods and Applications; Tsinghua University Press: Beijing, China, 2004. [Google Scholar]
- Yager, R.R. An approach to ordinal decision making. Int. J. Approx. Reason. 1995, 12, 237–261. [Google Scholar] [CrossRef]
- Türkşen, I.B. Type 2 representation and reasoning for CWW. Fuzzy Set. Syst. 2002, 127, 17–36. [Google Scholar] [CrossRef]
- Wang, J.-H.; Hao, J.J. A new version of 2-tuple fuzzy linguistic representation model for computing with words. IEEE Trans. Fuzzy Syst. 2006, 14, 435–445. [Google Scholar] [CrossRef]
- Rodríguez, R.M.; Martínez, L.; Herrera, F. Hesitant fuzzy linguistic term sets for decision making. IEEE Trans. Fuzzy Syst. 2012, 20, 109–119. [Google Scholar] [CrossRef]
- Rodríguez, R.M.; Martínez, L.; Herrera, F. A group decision making model dealing with comparative linguistic expressions based on hesitant fuzzy linguistic term sets. Inf. Sci. 2013, 241, 28–42. [Google Scholar] [CrossRef]
- Beg, I.; Rashid, T. TOPSIS for hesitant fuzzy linguistic term sets. Int. J. Intell. Syst. 2013, 28, 1162–1171. [Google Scholar] [CrossRef]
- Liu, H.B.; Rodríguez, R.M. A fuzzy envelope for hesitant fuzzy linguistic term set and its application to multicriteria decision making. Inf. Sci. 2014, 258, 220–238. [Google Scholar] [CrossRef]
- Herrera, F.; Alonso, S.; Chiclana, F.; Herrera-Viedma, E. Computing with words in decision making: Foundations, trends and prospects. Fuzzy Opt. Decis. Mak. 2009, 8, 337–364. [Google Scholar] [CrossRef]
- Pedrycz, W. Granular Computing: Analysis and Design of Intelligent Systems; CRC Press, Francis Taylor: Boca Raton, FL, USA, 2013. [Google Scholar]
- Paelinck, J.H.P. Qualiflex: A flexible multiple-criteria method. Econ. Lett. 1978, 1, 193–197. [Google Scholar] [CrossRef]
- Chen, T.-Y.; Chang, C.-H.; Lu, J.-F.R. The extended QUALIFLEX method for multiple criteria decision analysis based on interval type-2 fuzzy sets and applications to medical decision making. Eur. J. Oper. Res. 2013, 226, 615–625. [Google Scholar] [CrossRef]
- Wang, J.-C.; Tsao, C.-Y.; Chen, T.-Y. A likelihood-based QUALIFLEX method with interval type-2 fuzzy sets for multiple criteria decision analysis. Soft Comput. 2015, 19, 2225–2243. [Google Scholar] [CrossRef]
- Zhang, X.L.; Xu, Z.S. Hesitant fuzzy QUALIFLEX approach with a signed distance-based comparison method for multiple criteria decision analysis. Expert Syst. Appl. 2015, 42, 873–884. [Google Scholar] [CrossRef]
- Chen, T.-Y.; Tsui, C.-W. Intuitionistic fuzzy QUALIFLEX method for optimistic and pessimistic decision making. Adv. Inf. Sci. Serv. Sci. 2012, 4, 219–226. [Google Scholar]
- Chen, T.-Y. Data construction process and qualiflex-based method for multiple-criteria group decision making with interval-valued intuitionistic fuzzy sets. Int. J. Inf. Technol. Decis. Mak. 2013, 12, 425–467. [Google Scholar] [CrossRef]
- Chen, T.-Y. Interval-valued intuitionistic fuzzy QUALIFLEX method with a likelihood-based comparison approach for multiple criteria decision analysis. Inform. Sci. 2014, 261, 149–169. [Google Scholar] [CrossRef]
- Torra, V. Hesitant fuzzy sets. Int. J. Intell. Syst. 2010, 25, 529–539. [Google Scholar] [CrossRef]
- Xia, M.M.; Xu, Z.S. Hesitant fuzzy information aggregation in decision making. Int. J. Approx. Reason. 2011, 52, 395–407. [Google Scholar] [CrossRef]
- Zhao, X.F.; Lin, R.; Wei, G.W. Hesitant triangular fuzzy information aggregation based on Einstein operations and their application to multiple attribute decision making. Expert Syst. Appl. 2014, 41, 1086–1094. [Google Scholar] [CrossRef]
- Liu, H.-W.; Wang, G.-J. Multi-criteria decision-making methods based on intuitionistic fuzzy sets. Eur. J. Oper. Res. 2007, 179, 220–233. [Google Scholar] [CrossRef]
- Xu, Z.S.; Xia, M.M. Distance and similarity measures for hesitant fuzzy sets. Inf. Sci. 2011, 181, 2128–2138. [Google Scholar] [CrossRef]
- Xu, Z.S.; Zhang, X.L. Hesitant fuzzy multi-attribute decision making based on TOPSIS with incomplete weight information. Knowl. Based Syst. 2013, 52, 53–64. [Google Scholar] [CrossRef]
- Abbasbandy, S.; Asady, B. Ranking of fuzzy numbers by sign distance. Inf. Sci. 2006, 176, 2405–2416. [Google Scholar] [CrossRef]
- Bao, Q.; Ruan, D.; Shen, Y.J.; Hermans, E.; Janssens, D. Improved hierarchical fuzzy TOPSIS for road safety performance evaluation. Knowl. Based Syst. 2012, 32, 84–90. [Google Scholar] [CrossRef]
- Hatami-Marbini, A.; Tavana, M. An extension of the Electre I method for group decision-making under a fuzzy environment. Omega 2011, 39, 373–386. [Google Scholar] [CrossRef]
- Pedrycz, W.; Chen, S.M. Granular Computing and Decision-Making; Springer: Heidelberg, Germany, 2015. [Google Scholar]
- Peters, G.; Weber, R. DCC: A framework for dynamic granular clustering. Granul. Comput. 2016, 1, 1–11. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Bridging gaps between several forms of granular computing. Granul. Comput. 2016, 1, 115–126. [Google Scholar] [CrossRef]
- Ahmad, S.S.S.; Pedrycz, W. The development of granular rule-based systems: A study in structural model compression. Granul. Comput. 2017. [Google Scholar] [CrossRef]
- Wilke, G.; Portmann, E. Granular computing as a basis of human–data interaction: A cognitive cities use case. Granul. Comput. 2016, 1, 181–197. [Google Scholar] [CrossRef]

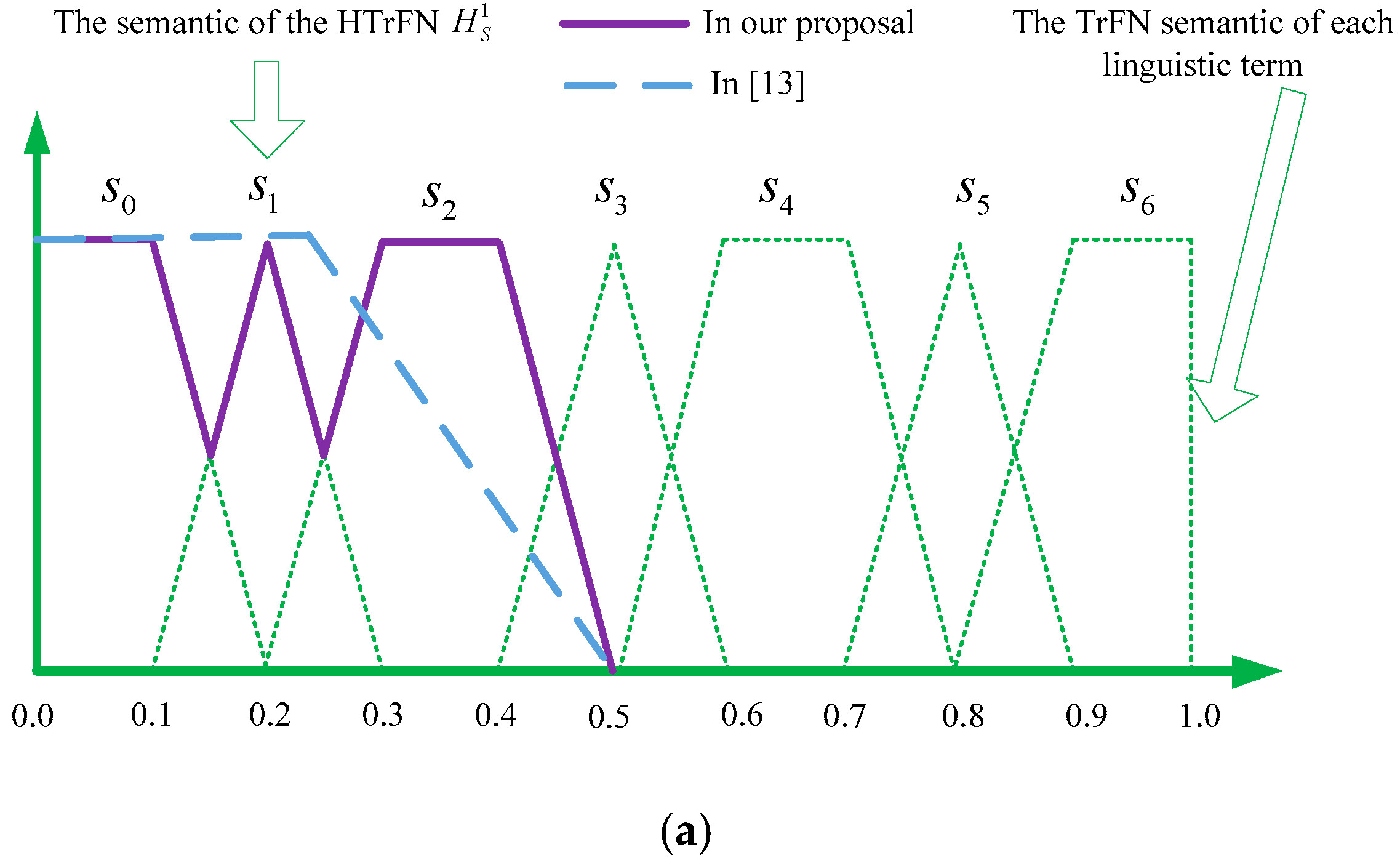
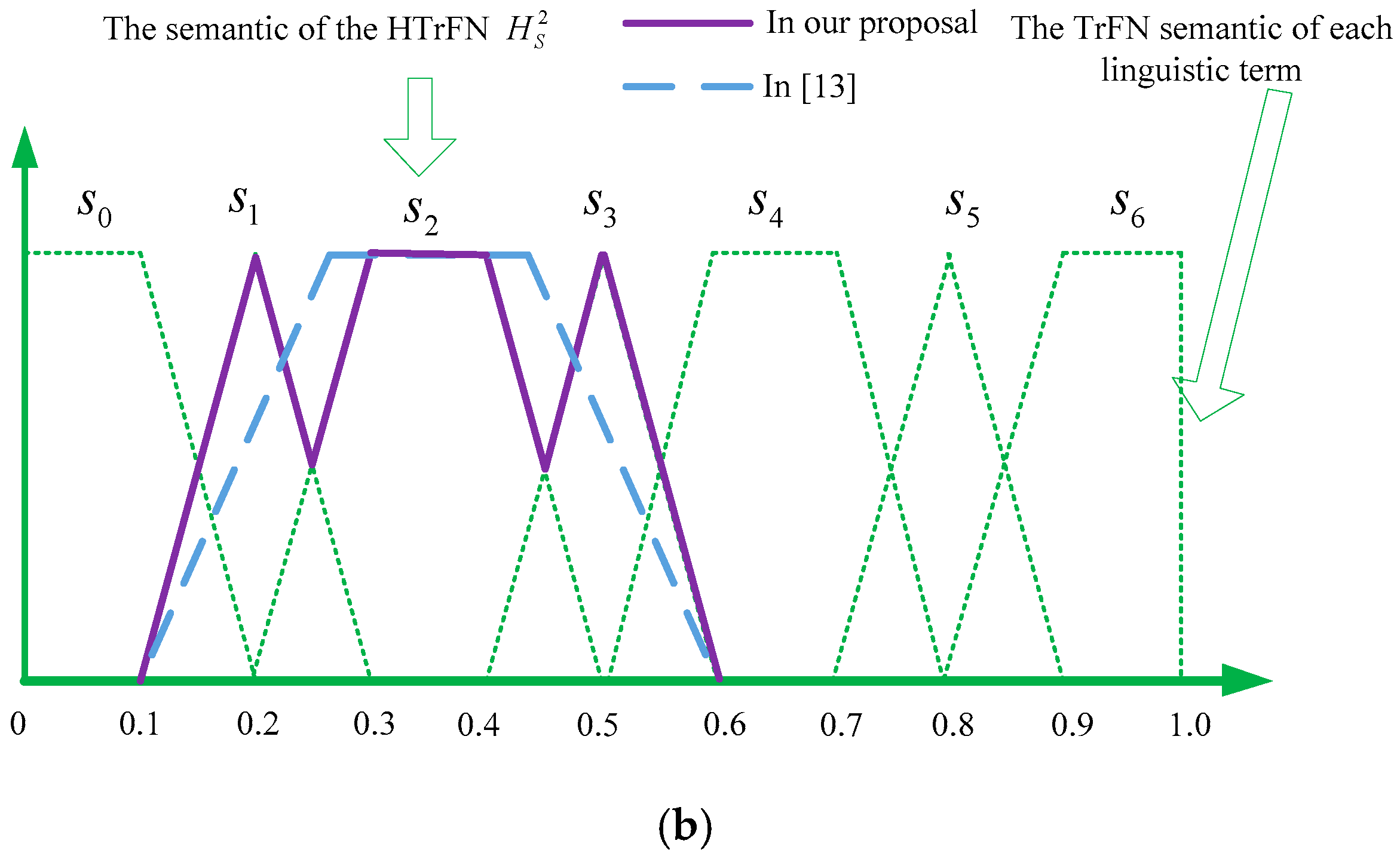
| Ratings | Abbreviation | TrFNs |
|---|---|---|
| s0: Very poor | VP | T (0.0, 0.0, 0.1, 0.2) |
| s1: Poor | P | T (0.1, 0.2, 0.2, 0.3) |
| s2: Medium poor | MP | T (0.2, 0.3, 0.4, 0.5) |
| s3: Fair | F | T (0.4, 0.5, 0.5, 0.6) |
| s4: Medium good | MG | T (0.5, 0.6, 0.7, 0.8) |
| s5: Good | G | T (0.7, 0.8, 0.8, 0.9) |
| s6: Very good | VG | T (0.8, 0.9,1.0, 1.0) |
| Main Criteria | Weights of Main Criteria | Sub-Criteria | Weights of Sub-Criteria | Alternative Initiatives |
|---|---|---|---|---|
| C1 Manufacturing | 0.285 | C1(1) Processes | 0.269 | A1 Implement Now |
| C1(2) Technical capability | 0.121 | |||
| C1(3) Innovation capability | 0.193 | |||
| C1(4) Production capacity | 0.417 | |||
| C2 Purchasing | 0.163 | C2(1) Raw material availability | 0.423 | A2 Implement in 6 months |
| C2(2) Suppliers | 0.227 | |||
| C2(3) Inventory level | 0.123 | |||
| C2(4) Assurance of supply | 0.227 | |||
| C3 Logistics | 0.184 | C3(1) Inbound logistics | 0.110 | A3 Implement in 12 months |
| C3(2) Outbound logistics | 0.230 | |||
| C3(3) Packaging | 0.302 | |||
| C3(4) Shipment accuracy | 0.358 | |||
| C4 Marketing | 0.368 | C4(1) Salability | 0.372 | |
| C4(2) Growth | 0.237 | |||
| C4(3) Marketability | 0.278 | |||
| C4(4) Customer service | 0.113 |
| Sub-Criteria | Alternatives | ||
|---|---|---|---|
| A1 | A2 | A3 | |
| C1(1) | MP | Between P and MP | At most MP |
| C1(2) | Between MG and G | MG | At least G |
| C1(3) | MP | Between MP and F | MP |
| C1(4) | At least MG | G | MG |
| C2(1) | Between P and MP | MG | P |
| C2(2) | G | Between MP and F | At least G |
| C2(3) | P | Between P and MP | Between MP and F |
| C2(4) | F | G | MG |
| C3(1) | MP | F | MP |
| C3(2) | P | MP | At most P |
| C3(3) | F | At least MG | F |
| C3(4) | At most MP | MP | Between P and MP |
| C4(1) | MG | MG | At least MG |
| C4(2) | MG | G | At least G |
| C4(3) | MP | F | F |
| C4(4) | Between F and G | At least MG | F |
| Sub-Criteria | Alternatives | ||
|---|---|---|---|
| A1 | A2 | A3 | |
| C1(1) | {T (0.2, 0.3, 0.4, 0.5), T (0.2, 0.3, 0.4, 0.5), T (0.2, 0.3, 0.4, 0.5)} | {T (0.1, 0.2, 0.2, 0.3), T (0.1, 0.2, 0.2, 0.3), T (0.2, 0.3, 0.4, 0.5)} | {T (0.0, 0.0, 0.1, 0.2), T (0.1, 0.2, 0.2, 0.3), T (0.2, 0.3, 0.4, 0.5)} |
| C1(2) | {T (0.5, 0.6, 0.7, 0.8), T (0.5, 0.6, 0.7, 0.8), T (0.7, 0.8, 0.8, 0.9)} | {T (0.5, 0.6, 0.7, 0.8), T (0.5, 0.6, 0.7, 0.8), T (0.5, 0.6, 0.7, 0.8)} | {T (0.7, 0.8, 0.8, 0.9), T (0.7, 0.8, 0.8, 0.9), T (0.8, 0.9, 1.0, 1.0)} |
| C1(3) | {T (0.2, 0.3, 0.4, 0.5), T (0.2, 0.3, 0.4, 0.5), T (0.2, 0.3, 0.4, 0.5)} | {T (0.2, 0.3, 0.4, 0.5), T (0.2, 0.3, 0.4, 0.5), T (0.4, 0.5, 0.5, 0.6)} | {T (0.2, 0.3, 0.4, 0.5), T (0.2, 0.3, 0.4, 0.5), T (0.2, 0.3, 0.4, 0.5)} |
| C1(4) | {T (0.5, 0.6, 0.7, 0.8), T (0.7, 0.8, 0.8, 0.9), T (0.8, 0.9, 1.0, 1.0)} | {T (0.7, 0.8, 0.8, 0.9), T (0.7, 0.8, 0.8, 0.9), T (0.7, 0.8, 0.8, 0.9)} | {T (0.5, 0.6, 0.7, 0.8), T (0.5, 0.6, 0.7, 0.8), T (0.5, 0.6, 0.7, 0.8)} |
| C2(1) | {T (0.1, 0.2, 0.2, 0.3), T (0.1, 0.2, 0.2, 0.3), T (0.2, 0.3, 0.4, 0.5)} | {T (0.5, 0.6, 0.7, 0.8), T (0.5, 0.6, 0.7, 0.8), T (0.5, 0.6, 0.7, 0.8)} | {T (0.1, 0.2, 0.2, 0.3), T (0.1, 0.2, 0.2, 0.3), T (0.1, 0.2, 0.2, 0.3)} |
| C2(2) | {T (0.7, 0.8, 0.8, 0.9), T (0.7, 0.8, 0.8, 0.9), T (0.7, 0.8, 0.8, 0.9)} | {T (0.2, 0.3, 0.4, 0.5), T (0.2, 0.3, 0.4, 0.5), T (0.4, 0.5, 0.5, 0.6)} | {T (0.7, 0.8, 0.8, 0.9), T (0.7, 0.8, 0.8, 0.9), T (0.8, 0.9, 1.0, 1.0)} |
| C2(3) | {T (0.1, 0.2, 0.2, 0.3), T (0.1, 0.2, 0.2, 0.3), T (0.1, 0.2, 0.2, 0.3)} | {T (0.1, 0.2, 0.2, 0.3), T (0.1, 0.2, 0.2, 0.3), T (0.2, 0.3, 0.4, 0.5)} | {T (0.2, 0.3, 0.4, 0.5), T (0.2, 0.3, 0.4, 0.5), T (0.4, 0.5, 0.5, 0.6)} |
| C2(4) | {T (0.4, 0.5, 0.5, 0.6), T (0.4, 0.5, 0.5, 0.6), T (0.4, 0.5, 0.5, 0.6)} | {T (0.7, 0.8, 0.8, 0.9), T (0.7, 0.8, 0.8, 0.9), T (0.7, 0.8, 0.8, 0.9)} | {T (0.5, 0.6, 0.7, 0.8), T (0.5, 0.6, 0.7, 0.8), T (0.5, 0.6, 0.7, 0.8)} |
| C3(1) | {T (0.2, 0.3, 0.4, 0.5), T (0.2, 0.3, 0.4, 0.5), T (0.2, 0.3, 0.4, 0.5)} | {T (0.4, 0.5, 0.5, 0.6), T (0.4, 0.5, 0.5, 0.6), T (0.4, 0.5, 0.5, 0.6)} | {T (0.2, 0.3, 0.4, 0.5), T (0.2, 0.3, 0.4, 0.5), T (0.2, 0.3, 0.4, 0.5)} |
| C3(2) | {T (0.1, 0.2, 0.2, 0.3), T (0.1, 0.2, 0.2, 0.3), T (0.1, 0.2, 0.2, 0.3)} | {T (0.2, 0.3, 0.4, 0.5), T (0.2, 0.3, 0.4, 0.5), T (0.2, 0.3, 0.4, 0.5)} | {T (0.0, 0.0, 0.1, 0.2), T (0.0, 0.0, 0.1, 0.2), T (0.1, 0.2, 0.2, 0.3)} |
| C3(3) | {T (0.4, 0.5, 0.5, 0.6), T (0.4, 0.5, 0.5, 0.6), T (0.4, 0.5, 0.5, 0.6)} | {T (0.5, 0.6, 0.7, 0.8), T (0.7, 0.8, 0.8, 0.9), T (0.8, 0.9, 1.0, 1.0)} | {T (0.4, 0.5, 0.5, 0.6), T (0.4, 0.5, 0.5, 0.6), T (0.4, 0.5, 0.5, 0.6)} |
| C3(4) | {T (0.0, 0.0, 0.1, 0.2), T (0.1, 0.2, 0.2, 0.3), T (0.2, 0.3, 0.4, 0.5)} | {T (0.2, 0.3, 0.4, 0.5), T (0.2, 0.3, 0.4, 0.5), T (0.2, 0.3, 0.4, 0.5)} | {T (0.1, 0.2, 0.2, 0.3), T (0.1, 0.2, 0.2, 0.3), T (0.2, 0.3, 0.4, 0.5)} |
| C4(1) | {T (0.5, 0.6, 0.7, 0.8), T (0.5, 0.6, 0.7, 0.8), T (0.5, 0.6, 0.7, 0.8)} | {T (0.5, 0.6, 0.7, 0.8), T (0.5, 0.6, 0.7, 0.8), T (0.5, 0.6, 0.7, 0.8)} | {T (0.5, 0.6, 0.7, 0.8), T (0.7, 0.8, 0.8, 0.9), T (0.8, 0.9, 1.0, 1.0)} |
| C4(2) | {T (0.5, 0.6, 0.7, 0.8), T (0.5, 0.6, 0.7, 0.8), T (0.5, 0.6, 0.7, 0.8)} | {T (0.7, 0.8, 0.8, 0.9), T (0.7, 0.8, 0.8, 0.9), T (0.7, 0.8, 0.8, 0.9)} | {T (0.7, 0.8, 0.8, 0.9), T (0.7, 0.8, 0.8, 0.9), T (0.8, 0.9, 1.0, 1.0)} |
| C4(3) | {T (0.2, 0.3, 0.4, 0.5), T (0.2, 0.3, 0.4, 0.5), T (0.2, 0.3, 0.4, 0.5)} | {T (0.4, 0.5, 0.5, 0.6), T (0.4, 0.5, 0.5, 0.6), T (0.4, 0.5, 0.5, 0.6)} | {T (0.4, 0.5, 0.5, 0.6), T (0.4, 0.5, 0.5, 0.6), T (0.4, 0.5, 0.5, 0.6)} |
| C4(4) | {T (0.4, 0.5, 0.5, 0.6), T (0.5, 0.6, 0.7, 0.8), T (0.7, 0.8, 0.8, 0.9)} | {T (0.5, 0.6, 0.7, 0.8), T (0.7, 0.8, 0.8, 0.9), T (0.8, 0.9, 1.0, 1.0)} | {T (0.4, 0.5, 0.5, 0.6), T (0.4, 0.5, 0.5, 0.6), T (0.4, 0.5, 0.5, 0.6)} |
| C1(1) | 0.05 | 0.1444 | 0.0694 | C1(1) | 0.1444 | 0.05 | −0.0694 |
| C1(2) | 0.0833 | −0.1333 | −0.2167 | C1(2) | −0.1333 | 0.0833 | 0.2167 |
| C1(3) | −0.075 | 0 | −0.075 | C1(3) | 0 | −0.075 | 0.075 |
| C1(4) | −0.0056 | 0.1445 | 0.15 | C1(4) | 0.1445 | −0.0056 | −0.15 |
| C2(1) | −0.375 | 0.075 | 0.45 | C2(1) | 0.075 | −0.375 | −0.45 |
| C2(2) | 0.375 | −0.0667 | −0.4417 | C2(2) | −0.0667 | 0.375 | 0.4417 |
| C2(3) | −0.075 | −0.225 | −0.15 | C2(3) | −0.225 | −0.075 | 0.15 |
| C2(4) | −0.3 | −0.15 | 0.15 | C2(4) | −0.15 | −0.3 | −0.15 |
| C3(1) | −0.15 | 0 | 0.15 | C3(1) | 0 | −0.15 | −0.15 |
| C3(2) | −0.15 | 0.067 | 0.2167 | C3(2) | 0.067 | −0.15 | −0.2167 |
| C3(3) | −0.2945 | 0 | 0.2945 | C3(3) | 0 | −0.2945 | −0.2945 |
| C3(4) | −0.14445 | −0.06945 | 0.075 | C3(4) | −0.06945 | −0.14445 | −0.075 |
| C4(1) | 0 | −0.1444 | −0.1444 | C4(1) | −0.1444 | 0 | 0.1444 |
| C4(2) | −0.15 | −0.2167 | −0.0667 | C4(2) | −0.2167 | −0.15 | 0.0667 |
| C4(3) | −0.15 | −0.15 | 0 | C4(3) | −0.15 | −0.15 | 0 |
| C4(4) | −0.1444 | 0.15 | 0.2945 | C4(4) | 0.15 | −0.1444 | −0.2945 |
| C1(1) | −0.05 | 0.0694 | 0.1444 | C1(1) | 0.0694 | −0.05 | −0.1444 |
| C1(2) | −0.0833 | −0.2167 | −0.1333 | C1(2) | −0.2167 | −0.0833 | 0.1333 |
| C1(3) | 0.075 | −0.075 | 0 | C1(3) | −0.075 | 0.075 | 0 |
| C1(4) | 0.0056 | 0.15 | 0.1445 | C1(4) | 0.15 | 0.0056 | −0.1445 |
| C2(1) | 0.375 | 0.45 | 0.075 | C2(1) | 0.45 | 0.375 | −0.075 |
| C2(2) | −0.375 | −0.4417 | −0.0667 | C2(2) | −0.4417 | −0.375 | 0.0667 |
| C2(3) | 0.075 | −0.15 | −0.225 | C2(3) | −0.15 | 0.075 | 0.225 |
| C2(4) | 0.3 | 0.15 | −0.15 | C2(4) | 0.15 | 0.3 | 0.15 |
| C3(1) | 0.15 | 0.15 | 0 | C3(1) | 0.15 | 0.15 | 0 |
| C3(2) | 0.15 | 0.2167 | 0.067 | C3(2) | 0.2167 | 0.15 | −0.067 |
| C3(3) | 0.2945 | 0.2945 | 0 | C3(3) | 0.2945 | 0.2945 | 0 |
| C3(4) | 0.14445 | 0.075 | −0.06945 | C3(4) | 0.075 | 0.14445 | 0.06945 |
| C4(1) | 0 | −0.1444 | −0.1444 | C4(1) | −0.1444 | 0 | 0.1444 |
| C4(2) | 0.15 | −0.0667 | −0.2167 | C4(2) | −0.0667 | 0.15 | 0.2167 |
| C4(3) | 0.15 | 0 | −0.15 | C4(3) | 0 | 0.15 | 0.15 |
| C4(4) | 0.1444 | 0.2945 | 0.15 | C4(4) | 0.2945 | 0.1444 | −0.15 |
| C1(1) | −0.1444 | −0.0694 | 0.05 | C1(1) | −0.0694 | −0.1444 | −0.05 |
| C1(2) | 0.1333 | 0.2167 | 0.0833 | C1(2) | 0.2167 | 0.1333 | −0.0833 |
| C1(3) | 0 | 0.075 | −0.075 | C1(3) | 0.075 | 0 | 0.075 |
| C1(4) | −0.1445 | −0.15 | −0.0056 | C1(4) | −0.15 | −0.1445 | 0.0056 |
| C2(1) | −0.075 | −0.45 | −0.375 | C2(1) | −0.45 | −0.075 | 0.375 |
| C2(2) | 0.0667 | 0.4417 | 0.375 | C2(2) | 0.4417 | 0.0667 | −0.375 |
| C2(3) | 0.225 | 0.15 | −0.075 | C2(3) | 0.15 | 0.225 | 0.075 |
| C2(4) | 0.15 | −0.15 | −0.3 | C2(4) | −0.15 | 0.15 | 0.3 |
| C3(1) | 0 | −0.15 | −0.15 | C3(1) | −0.15 | 0 | 0.15 |
| C3(2) | −0.067 | −0.2167 | −0.15 | C3(2) | −0.2167 | −0.067 | 0.15 |
| C3(3) | 0 | −0.2945 | −0.2945 | C3(3) | −0.2945 | 0 | 0.2945 |
| C3(4) | 0.06945 | −0.075 | −0.14445 | C3(4) | −0.075 | 0.06945 | 0.14445 |
| C4(1) | 0.1444 | 0.1444 | 0 | C4(1) | 0.1444 | 0.1444 | 0 |
| C4(2) | 0.2167 | 0.0667 | −0.15 | C4(2) | 0.0667 | 0.2167 | 0.15 |
| C4(3) | 0.15 | 0 | −0.15 | C4(3) | 0 | 0.15 | 0.15 |
| C4(4) | −0.15 | −0.2945 | −0.1444 | C4(4) | −0.2945 | −0.15 | 0.1444 |
| Ranking | ||||
|---|---|---|---|---|
| A1 | 0.5222 | 0.5324 | 0.5048 | 3 |
| A2 | 0.4794 | 0.5709 | 0.5436 | 1 |
| A3 | 0.4902 | 0.5655 | 0.5357 | 2 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Xu, Z.; Liu, M. Hesitant Trapezoidal Fuzzy QUALIFLEX Method and Its Application in the Evaluation of Green Supply Chain Initiatives. Sustainability 2016, 8, 952. https://doi.org/10.3390/su8090952
Zhang X, Xu Z, Liu M. Hesitant Trapezoidal Fuzzy QUALIFLEX Method and Its Application in the Evaluation of Green Supply Chain Initiatives. Sustainability. 2016; 8(9):952. https://doi.org/10.3390/su8090952
Chicago/Turabian StyleZhang, Xiaolu, Zeshui Xu, and Manfeng Liu. 2016. "Hesitant Trapezoidal Fuzzy QUALIFLEX Method and Its Application in the Evaluation of Green Supply Chain Initiatives" Sustainability 8, no. 9: 952. https://doi.org/10.3390/su8090952
APA StyleZhang, X., Xu, Z., & Liu, M. (2016). Hesitant Trapezoidal Fuzzy QUALIFLEX Method and Its Application in the Evaluation of Green Supply Chain Initiatives. Sustainability, 8(9), 952. https://doi.org/10.3390/su8090952







