Forested Land Use Efficiency in China: Spatiotemporal Patterns and Influencing Factors from 1999 to 2010
Abstract
:1. Introduction
2. Literature Review
3. Methods and Data
3.1. Non-Radial Directional Distance Function (NDDF)
3.2. Global Malmquist Index for Measuring Forested Land Productivity Growth
3.3. Data
4. Empirical Results
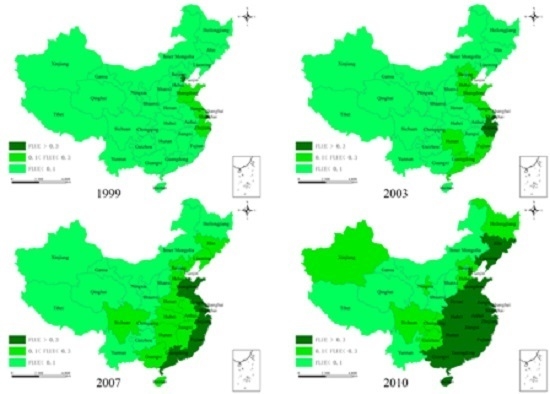
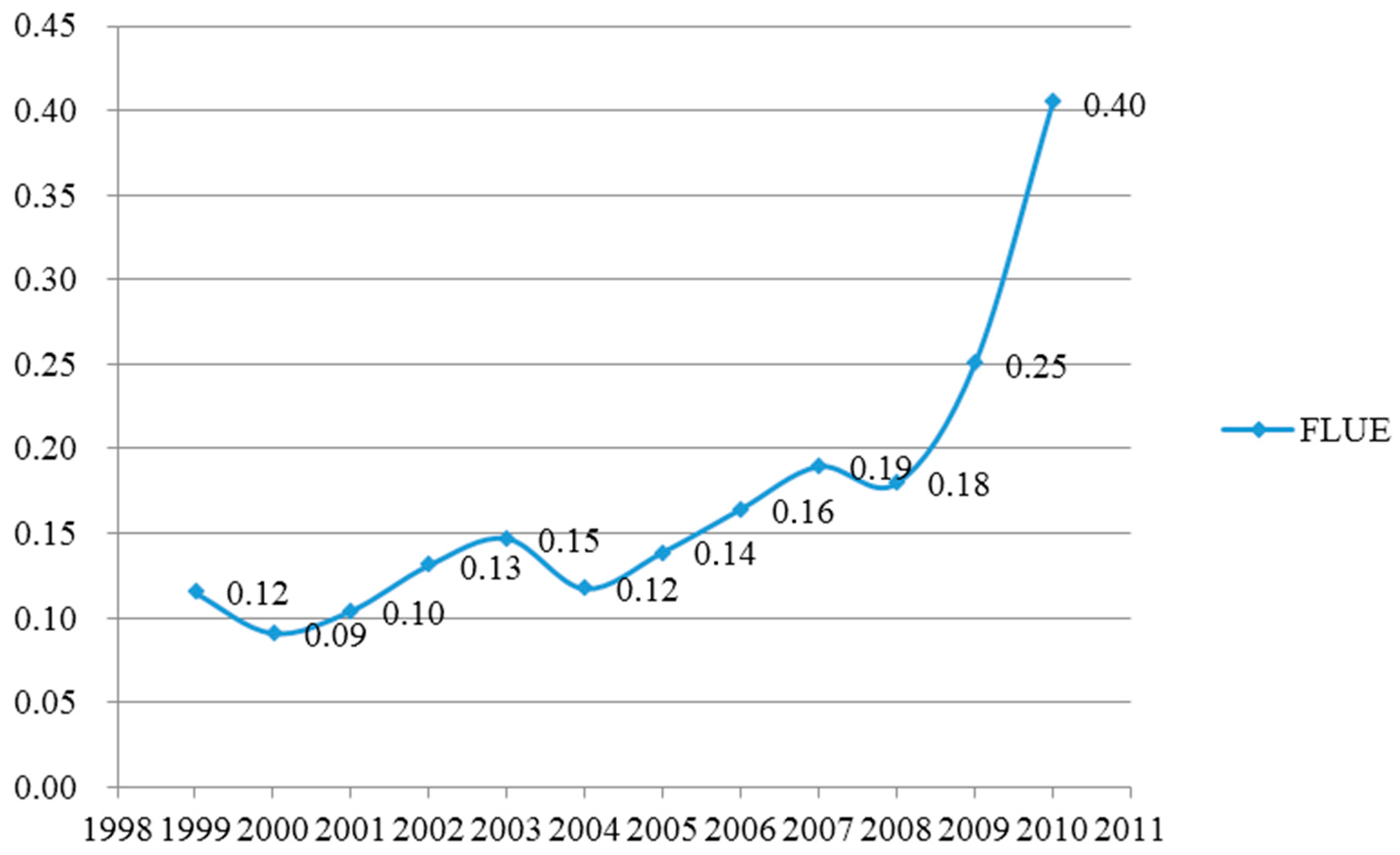
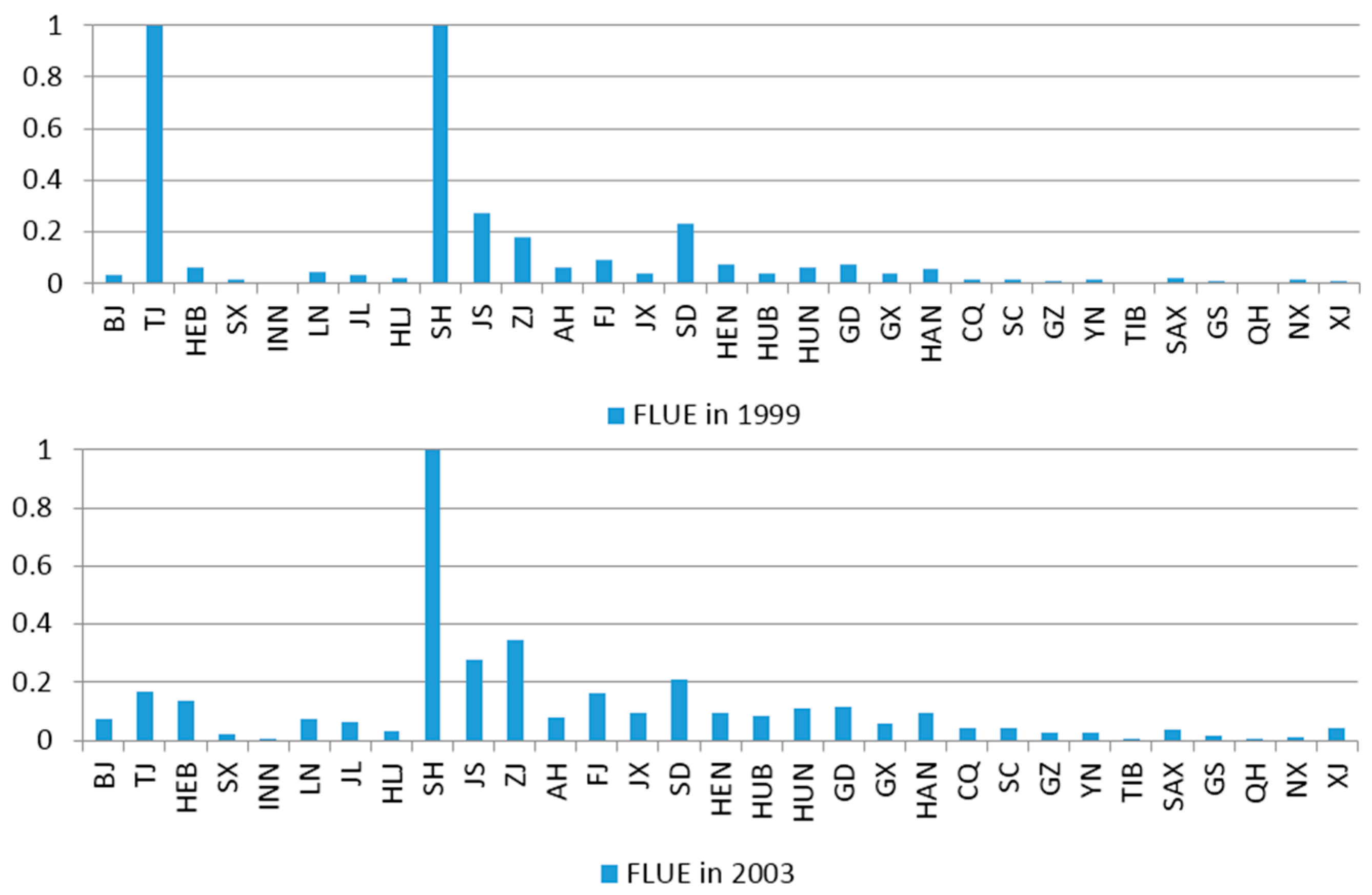
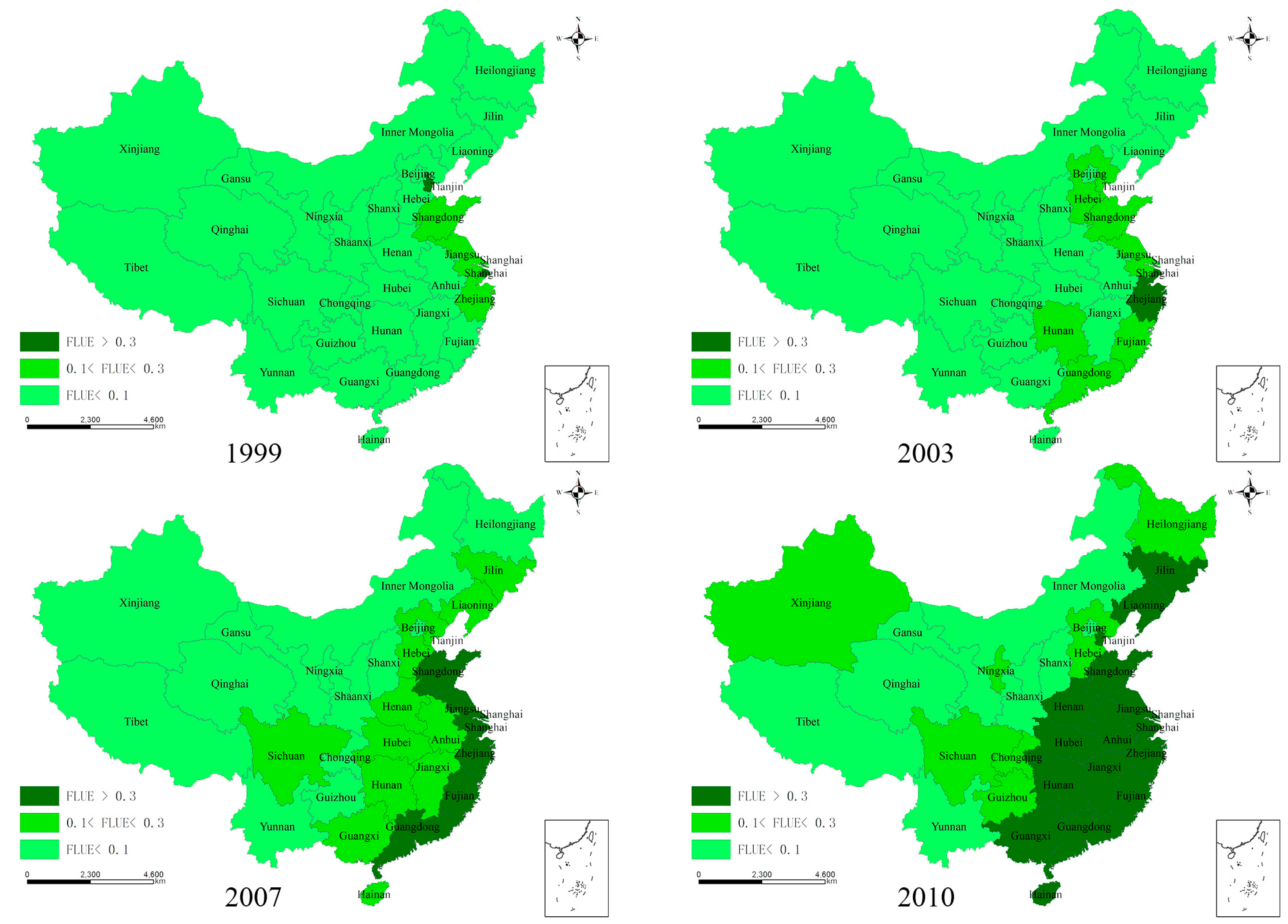
4.1. FLUE
4.2. Influential Factors in Regional FLUE Differences
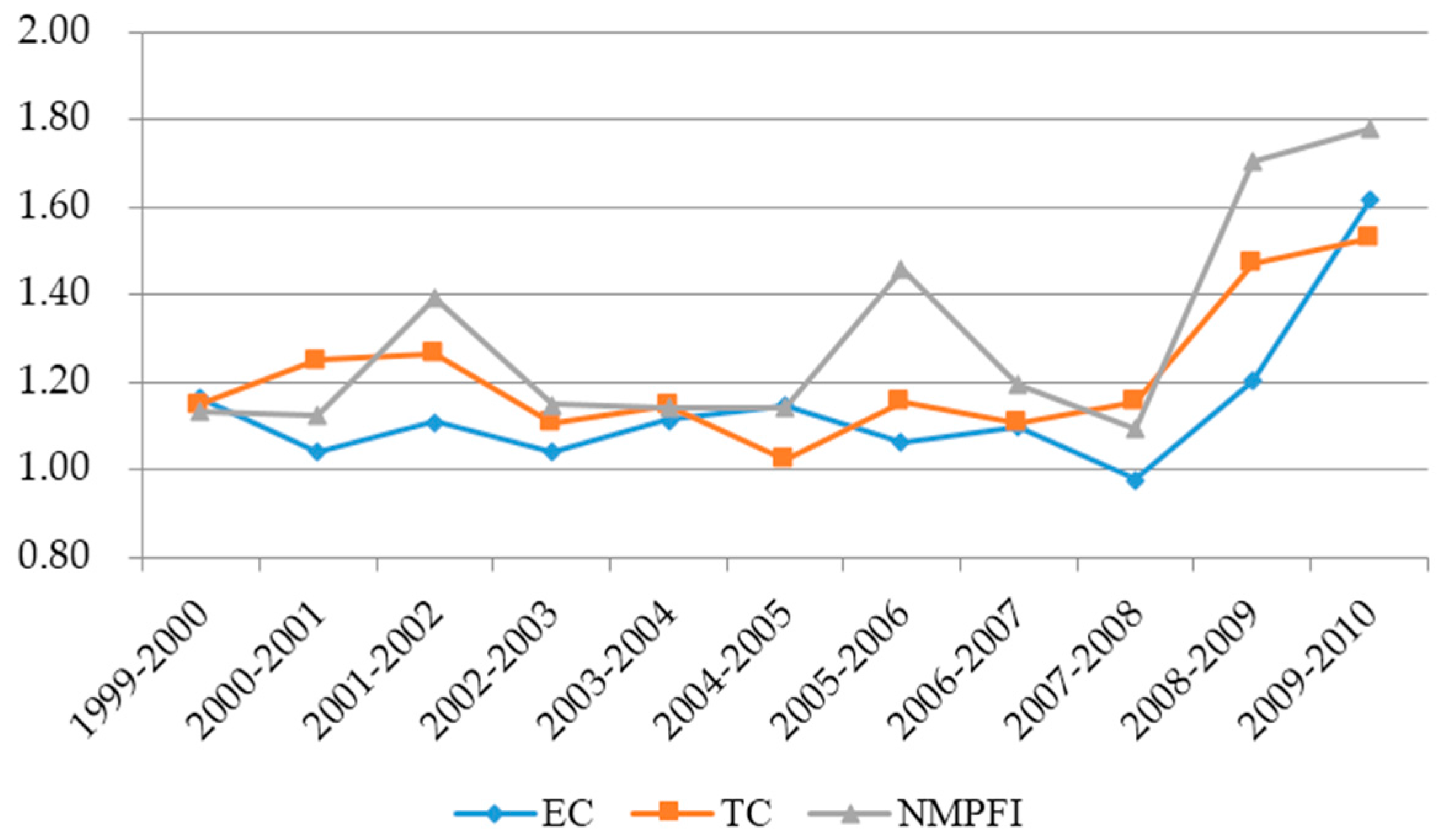
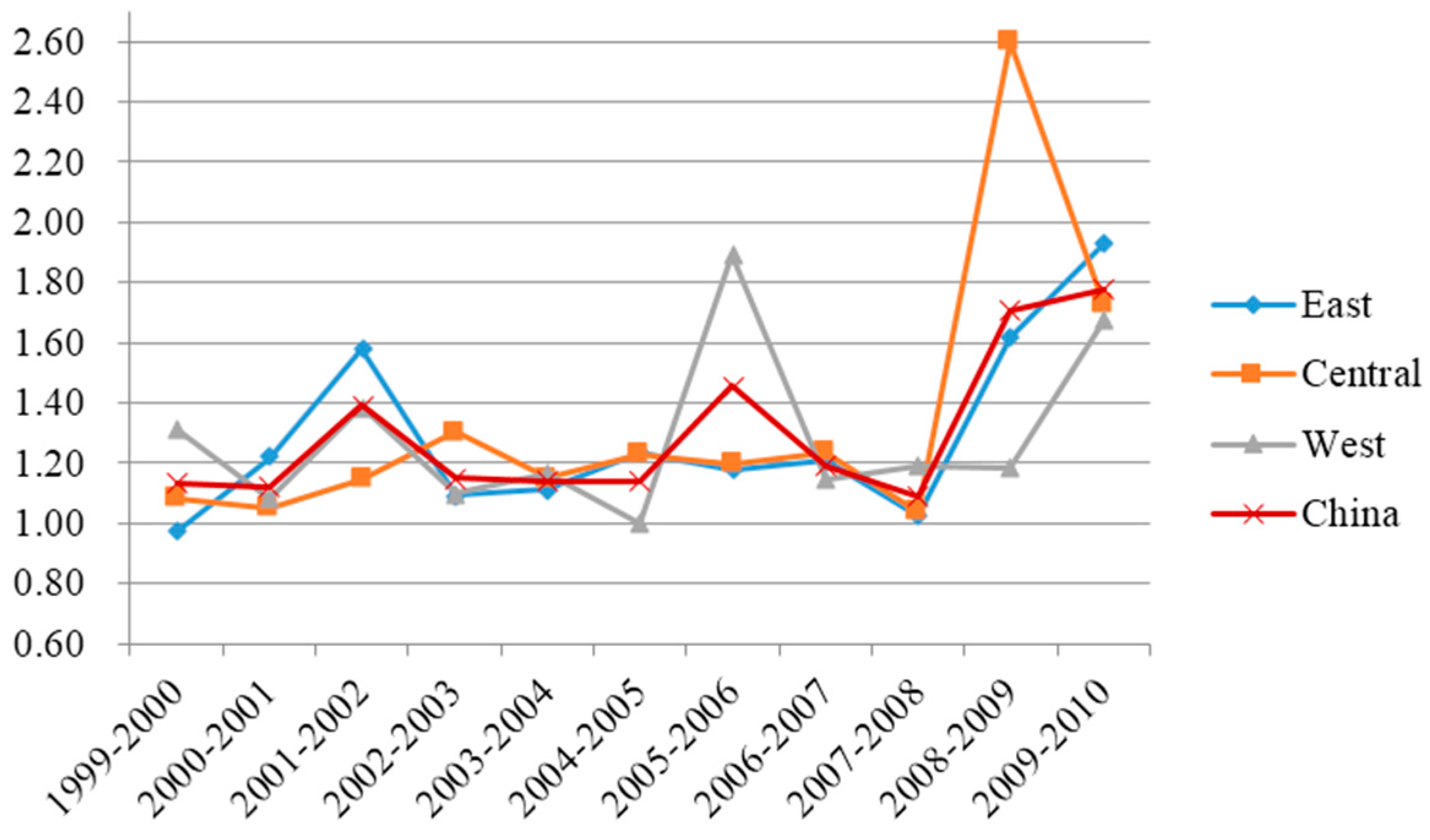
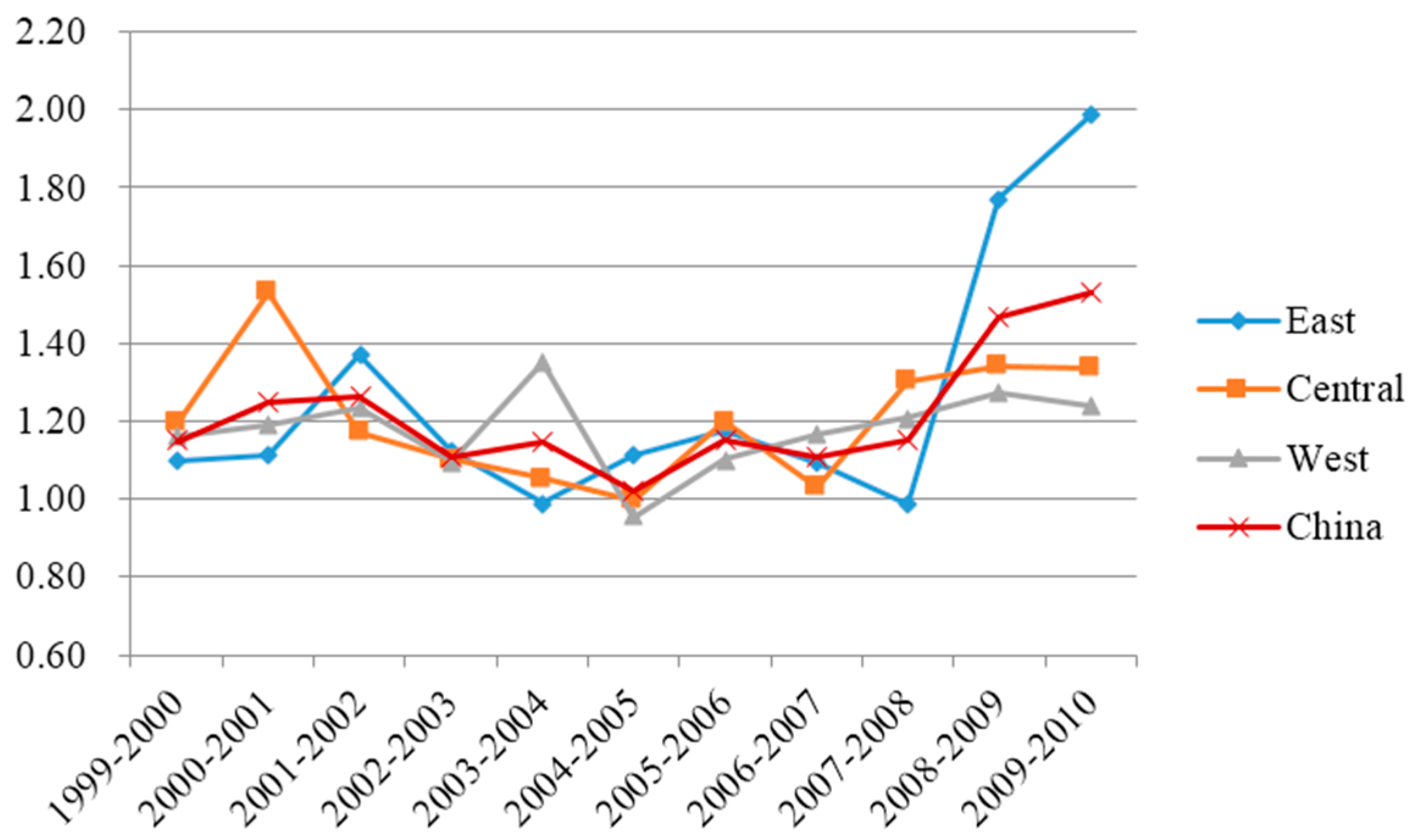
4.3. NMPFI and Its Decompositions
4.4. Convergences
- σ-convergence:
- absolute β-convergence:
- conditional β-convergence:
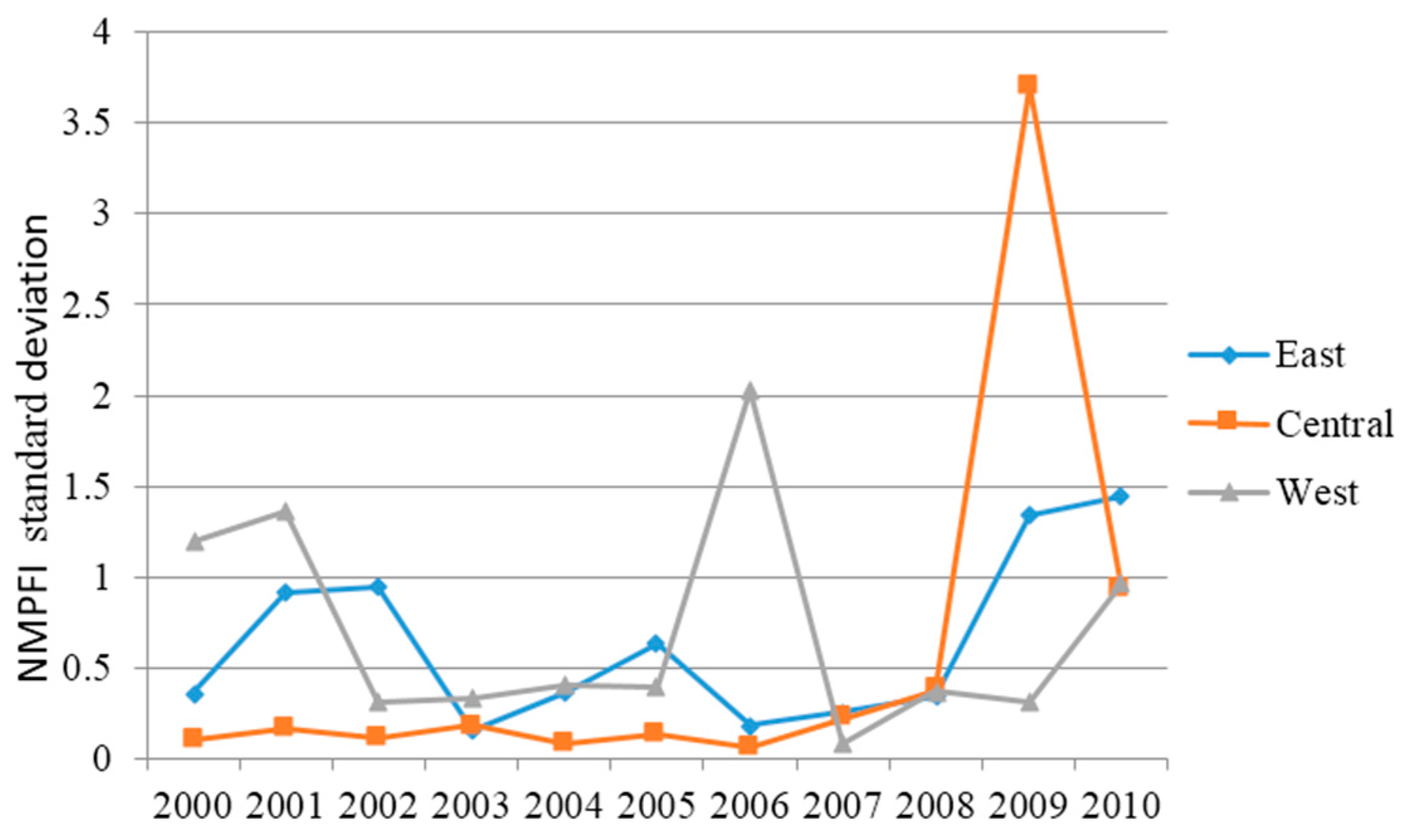
4.4.1. σ-Convergence
4.4.2. Absolute β-Convergence
4.4.3. Conditional β-Convergence
5. Discussion and Conclusions
5.1. Conclusions
5.2. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- State Forest Administration (SFA). The National Forest Resources Statistics—The Seventh National Forest Resources Inventory; State Forest Adminstration: Beijing, China.
- Su, S.; Wang, Y.; Luo, F.; Mai, G.; Pu, J. Peri-urban vegetated landscape pattern changes in relation to socioeconomic development. Ecol. Indic. 2014, 46, 477–486. [Google Scholar] [CrossRef]
- Xie, X.; Xie, H.; Fan, Y. Spatiotemporal Patterns and Drivers of Forest Change from 1985–2000 in the Beijing–Tianjin–Hebei Region of China. J. Resour. Ecol. 2016, 7, 301–308. [Google Scholar] [CrossRef]
- Hoek, J.; Ozdogan, M.; Burnicki, A.; Zhu, A. Evaluating forest policy implementation effectiveness with a cross-scale remote sensing analysis in a priority conservation area of Southwest China. Appl. Geogr. 2014, 47, 177–189. [Google Scholar] [CrossRef]
- Sharma, S.; Pandey, D.; Agrawal, M. Global warning potential and sustainable management of three land uses in Varanasi. Manag. Environ. Qual. 2016, 27, 364–373. [Google Scholar] [CrossRef]
- Li, M.; Mao, L.; Zhou, C.; Vogelmann, J.; Zhu, Z. Comparing forest fragmentation and its drivers in China and the USA with Globcover v2.2. J. Environ. Manag. 2010, 91, 2572–2580. [Google Scholar] [CrossRef] [PubMed]
- LeBel, G.; Stuart, W.B. Technical Efficiency Evaluation of Logging Contractors Using a Nonparametric Model. Int. J. For. Eng. 1998, 9, 15–24. [Google Scholar]
- Viitala, E.J.; Hänninen, H. Measuring the Efficiency of Public Forestry Organizations. For. Sci. 1998, 44, 298–307. [Google Scholar]
- Lee, J.Y. Using DEA to measure efficiency in forest and paper companies. For. Prod. Soc. 2005, 55, 58–66. [Google Scholar]
- Salehirad, N.; Sowlati, T. Productivity and efficiency assessment of the wood industry: A review with a focus on Canada. For. Prod. Soc. 2006, 56, 25–32. [Google Scholar]
- Lai, Z.; Zhang, Z. The DEA analysis of Guangdong forestry input-output efficiency. Issues For. Econ. 2008, 28, 323–326. (In Chinese) [Google Scholar]
- Lai, Z.; Zhang, Z. The super-efficiency DEA analysis of Guangdong forestry input-output. J. South China Agric. Univ. 2008, 7, 43–48. (In Chinese) [Google Scholar]
- Shi, L.; Zhang, C. Management efficiency analysis of farmer’s forest land based on the DEA method. Issues For. Econ. 2012, 32, 235–326. (In Chinese) [Google Scholar]
- Li, C.; Li, N.; Luo, H.; Wang, B. The efficiency analysis and path optimization of forestry input-output in China based on data envelopment analysis. Chin. Agric. Sci. Bull. 2011, 27, 55–59. (In Chinese) [Google Scholar]
- Tian, S.; Xu, W. Evaluation of China’s forestry input-output efficiency based on DEA modeling. Resour. Sci. 2012, 34, 1944–1950. (In Chinese) [Google Scholar]
- Lambin, E.F.; Baulies, X.; Bockstael, N. Land-Use and Land-Cover Change (LUCC): Implementation Strategy; A Core Project of the International Geospere-Biosphere Programme and the International Human Dimensions Programme on Global Environmental Change; IGBP Report 48, IHdp. Report 10; IGBP: Stockbolm, Sweden, 1995; p. 125. [Google Scholar]
- Ojima, D.; Lavorel, S.; Graumlich, L. Terrestrial Human-Environment Systems: The Future of Land Research in IGBP II. IGBP Glob. Chang. Newslett. 2005, 50, 31–34. [Google Scholar]
- Turner, B.L.; Skole, D.; Sanderson, S. Land Cover Change Science/Research Plan; IGBP Report No.35, HDP Report 7; IGBP of the ICSU: Stockholm, Sweden; HDP of the ISSC: Geneva, Switzerland, 1995. [Google Scholar]
- IGBP Secretariat. GLP Science Plan and Implementation Strategy; IGBP Report No. 53, IHDP Report No. 19; IGBP: Stockholm, Sweden, 2005; p. 64. [Google Scholar]
- Turner, B.L., II; Lambin, E.F.; Reenberg, A. The emergence of land change science for environmental change and sustainability. Proc. Natl. Acad. Sci. USA 2007, 104, 20666–20671. [Google Scholar]
- Xie, H.; Wang, W. Spatiotemporal differences and convergence of urban industrial land use efficiency for China’s major economic zones. J. Geogr. Sci. 2015, 25, 1183–1198. [Google Scholar] [CrossRef]
- Wang, W.; Xie, H.; Jiang, T.; Zhang, D.; Xie, X. Measuring the Total-Factor Carbon Emission Performance of Industrial Land Use in China Based on the Global Directional Distance Function and Non-Radial Luenberger Productivity Index. Sustainability 2016, 8, 336. [Google Scholar] [CrossRef]
- Tone, K. A slacks-based measure of efficiency in data envelopment analysis. Eur. J. Oper. Res. 2001, 130, 498–509. [Google Scholar] [CrossRef]
- Yang, L.; Wu, W.; Su, Q.; Jiang, X.; Wei, Y. Evaluation of road transport efficiency in China during 1997–2010 based on SBM-Undesirable model. Prog. Geogr. 2013, 32, 1602–1611. [Google Scholar]
- Pan, D.; Ying, R. Agricultural eco-efficiency evaluation in China based on SBM model. Acta Ecol. Sin. 2013, 33, 3837–3845. [Google Scholar] [CrossRef]
- Yang, Q.; Duan, X.; Ye, L.; Zhang, W. Efficiency evaluation of city land utilization in the Yangtze River Delta using a SBM-Undesirable model. Resour. Sci. 2014, 36, 712–721. [Google Scholar]
- Zhang, Y.; Jin, P.; Feng, D. Does civil environmental protection force the growth of China’s industrial green productivity? Evid. Perspect. Rent-Seek. 2015, 51, 215–227. [Google Scholar]
- Xie, H.; Wang, W.; Yang, Z.; Choi, Y. Measuring the sustainable performance of industrial land utilization in major industrial zones of China. Technol. Forecast. Soc. Chang. 2016. [Google Scholar] [CrossRef]
- Zhang, N.; Choi, Y. Total-factor carbon emission performance of fossil fuel power plants in China: A meta frontier non-radial Malmquist index analysis. Energy Econ. 2013, 40, 549–559. [Google Scholar] [CrossRef]
- Colinoa, A.; Benito-Osoriob, D.; Rueda-Armengotc, C. Entrepreneurship culture, total factor productivity growth and technical progress: Patterns of convergence towards the technological frontier. Technol. Forecast. Soc. Chang. 2014, 88, 349–359. [Google Scholar] [CrossRef]
- Xiong, Q.; Guo, G. Study on the efficiency difference of city industrial land production across provinces in China. Resour. Sci. 2013, 35, 910–917. (In Chinese) [Google Scholar]
- Wang, Z.; Feng, C. A performance evaluation of the energy, environmental, and economic efficiency and productivity in China: An application of global data envelopment analysis. Appl. Energy 2015, 147, 617–626. [Google Scholar] [CrossRef]
- Zhang, N.; Kong, F.; Choi, Y. Measuring sustainability performance for China: A sequential generalized directional distance function approach. Econ. Model. 2014, 41, 392–397. [Google Scholar] [CrossRef]
- Zhang, N.; Choi, Y. A note on the history on the evolution of directional distance function and its development in energy and environmental studies 1997–2013. Renew. Sustain. Energy Rev. 2014, 33, 50–59. [Google Scholar] [CrossRef]
- Oh, D. A global Malmquist-Luenberger productivity index. J. Product. Anal. 2010, 34, 184–197. [Google Scholar] [CrossRef]
- National Bureau of Statistics of China (NBSC). China Forestry Statistical Yearbook. Available online: http://www.stats.gov.cn/tjsj/ndsj/ (accessed on 23 May 2012). (In Chinese)
- Kong, F.; Wu, X.; Liao, W. Factors decomposition and calculation of contribution ratio of forestry science and technology advancement in 31 provinces (cities, autonomous regions) from 2002–2011. J. Agro-For. Econ. Manag. 2014, 13, 420–428. (In Chinese) [Google Scholar]
- The Central People’s Government of the People’s Republic of China (CPGPRC). Available online: http://www.gov.cn/jrzg/2008-07/14/content_1044403.htm (accessed on 14 June 2008).
- Su, S.; Zhou, X.; Wan, C.; Li, Y.; Kong, W. Land use changes to cash crop plantations: crop types, multilevel determinants and policy implications. Land Use Policy 2016, 50, 379–389. [Google Scholar] [CrossRef]
- Liu, Y.; Feng, Y.; Zhao, Z.; Zhang, Q.; Su, S. Socioeconomic drivers of forest loss and fragmentation: A comparison between different land use planning schemes and policy implications. Land Use Policy 2016, 54, 58–68. [Google Scholar] [CrossRef]
- Deng, X.; Huang, J.; Uchida, E.; Rozelle, S.; Gibson, J. Pressure cookers or pressure valves: Do roads lead to deforestation in China? J. Environ. Econ. Manag. 2011, 61, 79–94. [Google Scholar] [CrossRef]
- Moran, P. The interpretation of statistical maps. J. R. Stat. Soc. Ser. B 1948, 10, 243–251. [Google Scholar]
- Solow, R. A contribution to the theory of economic growth. Q. J. Econ. 1956, 70, 65–94. [Google Scholar] [CrossRef]
- Sala-i-Martin, X. Regional cohesion: Evidence and theories of regional growth and convergence. Eur. Econ. Rev. 1996, 40, 1325–1352. [Google Scholar] [CrossRef]



| Coefficient | p Value | |
|---|---|---|
| Ln IFA | −0.0419841 | 0.399 |
| Ln TFO | 0.0338353 | 0.477 |
| PGDP | 0.0021411 | 0.092 * |
| Ln PD | 0.3525266 | 0.041 ** |
| AR | 0.368872 | 0.141 |
| AAT | 0.0235676 | 0.251 |
| RM | −0.61059 | 0.426 |
| PNAP | 0.024445 | 0.014 ** |
| LUR | 0.0303061 | 0.000 *** |
| adjusted R-squared = 0.6768 |
| Eastern Region | Central Region | Western Region | |
|---|---|---|---|
| constant | 0.046 * | 0.043 * | 0.039 * |
| (2.862) | (2.492) | (3.434) | |
| −0.078 * | −0.096 | −0.113 ** | |
| (−2.72) | (−0.679) | (−4.869) | |
| Adjusted R-squared | 0.451 | 0.071 | 0.703 |
| Eastern Region | Central Region | Western Region | |
|---|---|---|---|
| constant | 0.016 * | 0.021 *** | 0.017 * |
| (3.791) | (4.610) | (2.391) | |
| −0.109 *** | −0.108 *** | −0.091 *** | |
| (−12.603) | (−10.060) | (−10.870) | |
| Adjusted R-squared | 0.595 | 0.564 | 0.500 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Y.; Xie, H.; Fan, Y.; Wang, W.; Xie, X. Forested Land Use Efficiency in China: Spatiotemporal Patterns and Influencing Factors from 1999 to 2010. Sustainability 2016, 8, 772. https://doi.org/10.3390/su8080772
He Y, Xie H, Fan Y, Wang W, Xie X. Forested Land Use Efficiency in China: Spatiotemporal Patterns and Influencing Factors from 1999 to 2010. Sustainability. 2016; 8(8):772. https://doi.org/10.3390/su8080772
Chicago/Turabian StyleHe, Yafen, Hualin Xie, Yuanhua Fan, Wei Wang, and Xue Xie. 2016. "Forested Land Use Efficiency in China: Spatiotemporal Patterns and Influencing Factors from 1999 to 2010" Sustainability 8, no. 8: 772. https://doi.org/10.3390/su8080772
APA StyleHe, Y., Xie, H., Fan, Y., Wang, W., & Xie, X. (2016). Forested Land Use Efficiency in China: Spatiotemporal Patterns and Influencing Factors from 1999 to 2010. Sustainability, 8(8), 772. https://doi.org/10.3390/su8080772