A Hybrid Multi-Step Rolling Forecasting Model Based on SSA and Simulated Annealing—Adaptive Particle Swarm Optimization for Wind Speed

Abstract

With the limitations of conventional energy becoming increasing distinct, wind energy is emerging as a promising renewable energy source that plays a critical role in the modern electric and economic fields. However, how to select optimization algorithms to forecast wind speed series and improve prediction performance is still a highly challenging problem. Traditional single algorithms are widely utilized to select and optimize parameters of neural network algorithms, but these algorithms usually ignore the significance of parameter optimization, precise searching, and the application of accurate data, which results in poor forecasting performance. With the aim of overcoming the weaknesses of individual algorithms, a novel hybrid algorithm was created, which can not only easily obtain the real and effective wind speed series by using singular spectrum analysis, but also possesses stronger adaptive search and optimization capabilities than the other algorithms: it is faster, has fewer parameters, and is less expensive. For the purpose of estimating the forecasting ability of the proposed combined model, 10-min wind speed series from three wind farms in Shandong Province, eastern China, are employed as a case study. The experimental results were considerably more accurately predicted by the presented algorithm than the comparison algorithms.

1. Introduction

Energy plays a vital part in modern social and economic development. Along with the rapid development of technology in the last few decades, energy demands continue to increase rapidly [1]. In accordance with the IEA World Energy Outlook 2010, China and India will be responsible for approximately 50% of the growth in global energy demand by 2050. The consumption of energy in China will be close to 70% greater than the energy consumed by the United States today. Second only to America, China will become the second leading energy-consuming country in the world. Nevertheless, China’s per capita energy consumption will remain lower than 50% of that of the USA [2]. Since conventional energy sources such as coal, natural gas, and oil for electricity generation are being quickly depleted, sufficient energy reserves and sustainable energy problems are garnering increased attention. Additionally, using traditional resources produces large amounts of carbon dioxide, which may lead to global warming, and is considered an international security threat. Therefore, it not only affects the environment, it also threatens the safety of individuals and the planet [3].

Consequently, to alleviate the pressure of this energy shortage, renewable energy sources are being explored and the sustainable development of green energy has become a significant measure of global energy development success [4]. Obviously, it has become necessary to seek and develop new environmentally friendly sources of renewable energy. Wind energy, the most significant new type of green renewable energy [5], is steady, abundantly available, reliable, inexhaustible, widespread, pollution-free, and economical. It contains enormous power and its usage does not harm the environment by creating greenhouse gas emissions. Furthermore, it has been considered or applied in the production and development for energy in a host of countries. In modern times, wind energy has become the most indispensable and vital renewable energy source globally. The fast growth of the power system enables the absorption of large amounts of wind power. However, in consideration of stochastic factors such as temperature, atmospheric pressure, elevation, and terrain, it is still difficult to make an accurate forecast, which can also give rise to trouble in terms of the energy transmission and the balance of the power grid. Hence, developing an effective approach to overcome these challenges is necessary.

In order to reduce time series prediction errors, thousands of methods have already been studied. First, many effective data denoising tools, including the Wavelet Transform (WT), the Empirical Mode Decomposition (EMD) [6,7,8], the Wavelet Packet Transform (WPT), the Singular Spectrum Analysis (SSA) [9], and the Fast Ensemble Empirical Mode Decomposition (FEEMD) algorithm [10], have been applied to process the original data to achieve a relatively higher forecasting accuracy. For instance, SSA, as a novel analytical method, is especially suitable for research into periodic oscillation, which has proven to be an effective tool for time series analysis in diverse applications; the results indicate that it can effectively remove the noise of the wind speed data to improve forecasting performance. Secondly, different prediction approaches are applied to time series forecasting, including SVM, ARMA, ANNS, etc. According to various researchers, these methods can be categorized into four classes [11]: (i) purely physical arithmetic [12,13,14]; (ii) mathematical and statistical arithmetic [15,16,17,18,19,20,21]; (iii) spatial correlation arithmetic; and (iv) artificial intelligence arithmetic [22].

Purely physical arithmetic not only utilizes physical data such as temperature, density, speed, and topography information, but also physical methods, including observation, experiment, analogy, and analysis, to forecast the future wind speed. However, these approaches do not possess unique advantages for short-term prediction. Mathematical and statistical methods, such as the famous stochastic time series models, typically make use of historical data to forecast the wind speed, which can be easy to employ and simple to realize. Therefore, some categories of time series models are often used in wind speed forecasting. Some examples that can be utilized to obtain excellent results include the exponential smoothing model, the autoregressive moving average (ARMA) model [18], filtering methods, and the autoregressive integrated moving average (ARIMA) model [23,24]. Distinct from other methods, spatial correlation arithmetic may achieve better prediction performance. Nevertheless, it is extremely difficult to obtain a perfect application due to the abundant amount of information that must be considered and collected. In recent years, as artificial intelligence technology has developed and become widely used, many researchers have utilized intelligence algorithms in their papers, including artificial neural networks (ANNs) [25,26,27,28,29], Support Vector Machine (SVM) [30,31], and fuzzy logic (FL) methods [32,33], which can be applied to combine new algorithms for enhancing wind speed forecasting ability.

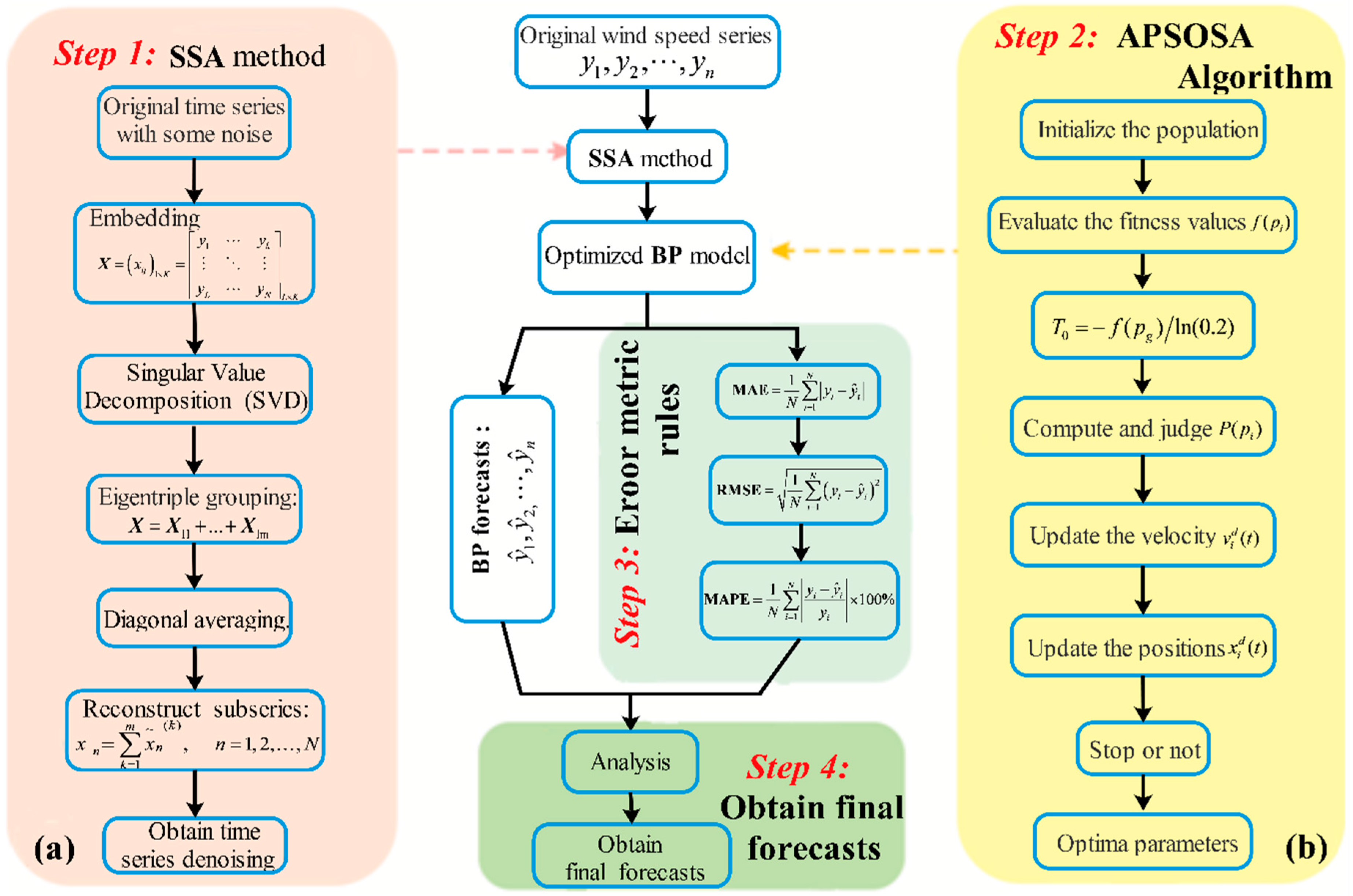
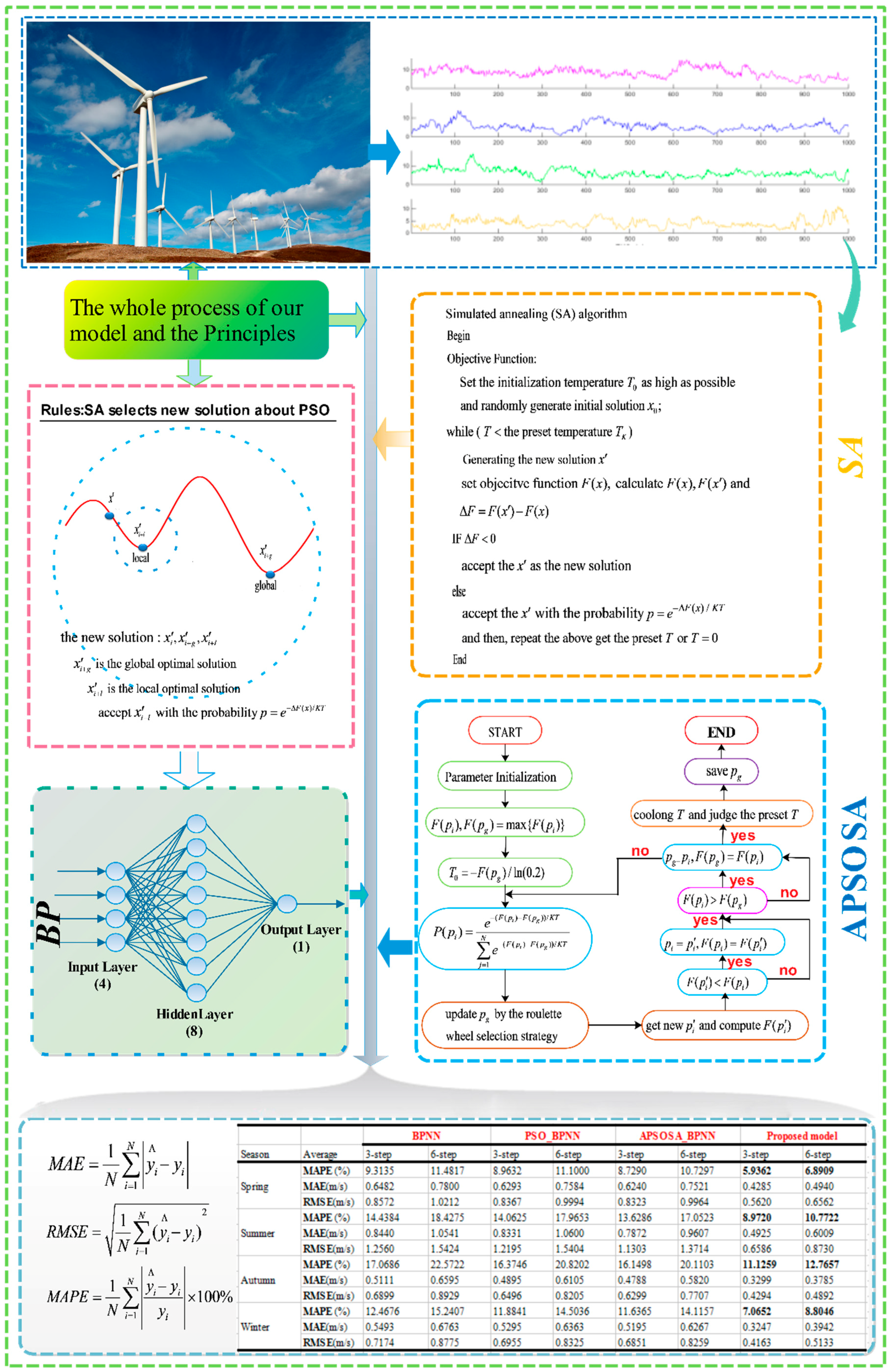
In this research, a hybrid algorithm was proposed with the goal of achieving better forecasting performance. Firstly, in comparison with other methods, including WNN (Wavelet Neural Network) and GRNN (generalized regression neural network), BPNN provides the best prediction performance for both half-hour and one-hour time frames. Therefore, BPNN was selected for use in our models. Next, as a different analytical method, SSA is employed to construct, decompose, and reconstruct the trajectory matrix. SSA can extract different components of the original signal, such as the long-term trend of the signal, a periodic signal, and noise signals, and is capable of removing the noise from the original signal. Next, the optimization algorithm APSOSA, combining APSO [34,35,36,37,38] and SA [39,40,41,42], can enhance the prediction accuracy and convergence of the basic PSO algorithm. Moreover, APSOSA is able to avoid falling into local extreme points so that the parameters of the Back Propagation neural network (BPNN) can be better optimized. Finally, to achieve better forecasting performances, the wind speed data after noise elimination are input into the BPNN. In addition, four commonly used error criteria (AE, MAE, MAPE, and MSE) are applied to assess the performance of the raised hybrid algorithm. The main aspects of the model are introduced as follows: (1) data preprocessing; (2) the best forecasting method, BPNN, is selected and its parameters are tuned by an artificial intelligence (APSOSA) model; (3) forecasting; and (4) comparison and analysis.

The main contributions of this paper are summarized as follows:

(1)

With the aim of reducing the randomness and instability of wind speed, the Singular Spectrum Analysis technique is applied to decompose the wind series data, revealing real and useful signals from the wind series.

(2)

The best prediction system, BPNN, is selected from the different methods, including WNN, GRNN, and BPNN.

(3)

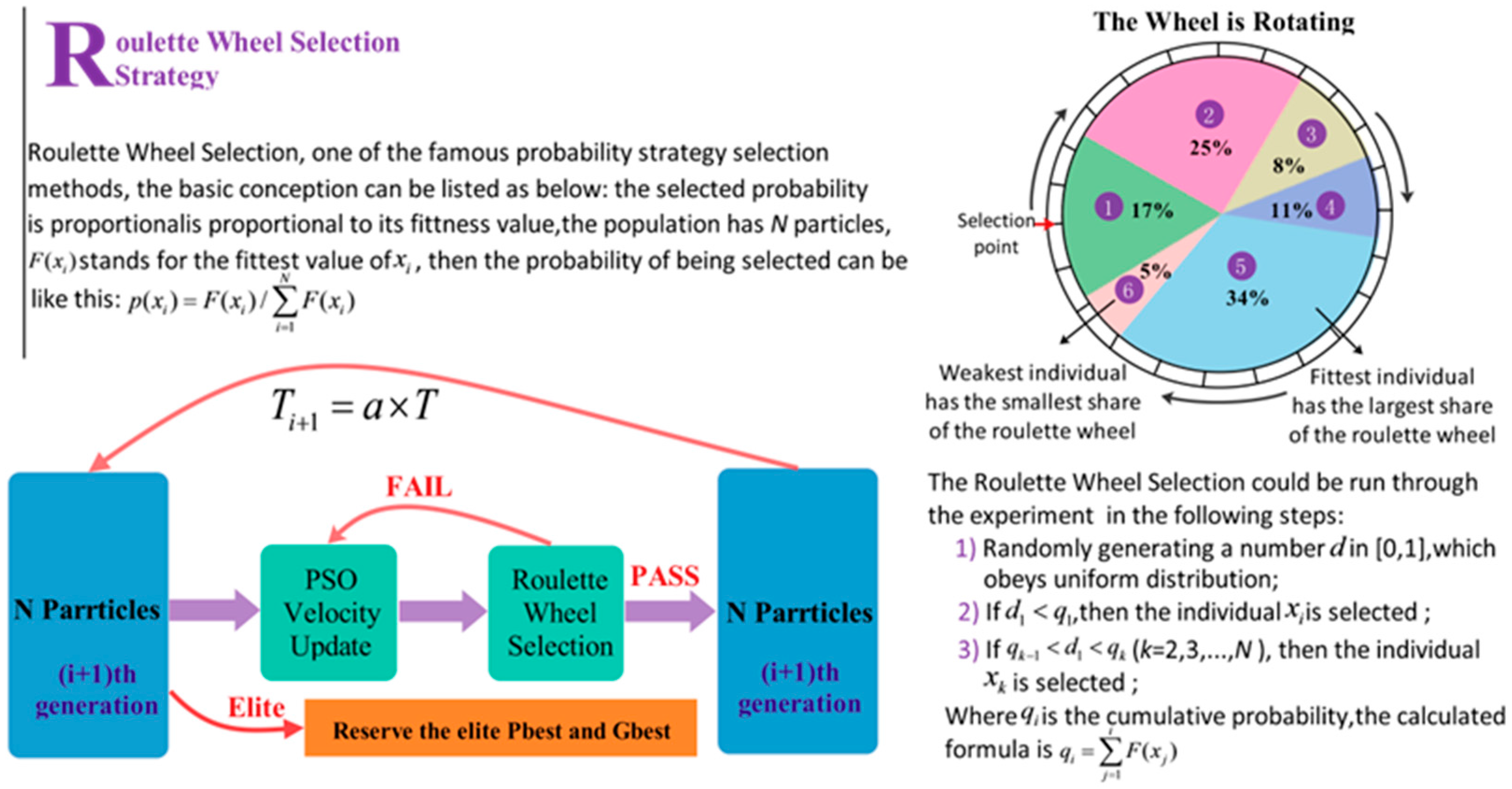
In view of the shortcomings of the PSO algorithm, APSOSA is developed to optimize parameters, which can assist the individual PSO in jumping out of the local optimum. Ultimately, parameters are selected and optimized by combining their respective advantages.

(4)

To examine the stability and accuracy of the new combined forecasting algorithm, 10-min wind speed series from three different stations are used in the experimental simulations. The experimental results indicate that the novel hybrid algorithm has a higher performance, significantly outperforming the other forecasting algorithms.

(5)

Giving full consideration to the other influential factors in the experiments, such as the seasonal factors, the geographical factors, etc., according to the results, this action proves that the new combined algorithm has a powerful adaptive capacity, which can be widely applied to the prediction field.

(6)

The Bias-Variance Framework and statistical hypothesis testing are employed to further illustrate the stability and performance of the proposed algorithm.

The remainder of this paper is designed as follows. The methodology is described specifically in Section 2. To verify the prediction accuracy of the raised algorithm, a case study is examined in Section 3. Next, the wind farms area and datasets are introduced in Section 3.1, whereas Section 3.2 displays the performance criteria of the forecast results. In Section 3.3, the results of the different algorithms are listed and compared with the proposed algorithm. In order to further illustrate the stability and performance of the proposed algorithm, in Section 4, the Bias-Variance Framework and statistical hypothesis testing are employed. Finally, the conclusions are provided in Section 5.

2. Methodology

In this section, all of the algorithms involved in this work are described. The full list of algorithms to be discussed in this section is as follows: the singular spectrum analysis algorithm, an efficient technology for time series analysis; the particle swarm optimization algorithm; the simulated annealing algorithm, which overcomes PSO falling into the local minima, and the back propagation neural network. The hybrid algorithm-APSOSA, raised to search for the optimal parameters of BPNN, will also be introduced in detail.

2.1. Singular Spectrum Analysis

Compared with other nonparametric approaches, such as EMD, which exhibits a potential mode-mixing problem, and EEMD, which does not completely neutralize the added white noise, singular spectrum analysis (SSA), which overcomes the traditional analysis methods’ (such as Fourier analysis) shortcomings, has been proven to be one of the most effective and powerful methods in time series analysis. It was developed by Broomhead and King in 1986 [43]. Figure 1 shows the decomposed series of wind speed by SSA. The details are shown in Appendix A.1.

2.2. Intelligent Optimization Algorithms

In this section, several optimization algorithms will be introduced.

2.2.1. Particle Swarm Optimization

Inspired by imitating the social behavior of flocks of bird and schools of fish, an effective approach for optimization, Particle swarm optimization (PSO), was first developed by Dr. Eberharts and Dr. Kennedy in 1995 [44]. It is a stochastic, population-based evolutionary algorithm, which involves searching for solutions [39] (details in Appendix B.1).

2.2.2. Back Propagation Neural Network

First proposed by Rumelhart and McCelland (1986) [45], the Back Propagation Neural Network (BPNN) is one of the most widely employed artificial neural network (ANN) models (details in Appendix B.2). It is not only capable of learning and storing a large amount of input–output mode mappings without needing to reveal the mathematical equations of the mapping relationship, but can also apply the steepest descent method, by back propagation, to constantly adjust the network weights and thresholds, resulting in the minimum square error. In addition, BPNN [46] consists of three layers: the input layer, the hidden layer, and the output layer. The experimental parameters are listed in

Table 1. The experimental parameters of BPNN.

Experimental Parameters	Default Value
neuron number in the input layer	4
neuron number in the hidden layer	8
neuron number in the hidden layer	1
the learning velocity	0.1
the maximum number of trainings	1500
training requirements precision	0.0001

.

2.2.3. Simulated Annealing

The concept of Simulated Annealing was first introduced by N. Metropolis et al. in 1953. In 1983, Kirkpatrick et al. succeeded in introducing SA in the field of combinatorial optimization [47]. Based on the Monte-Carlo iteration solving method, currently the SA algorithm has become one of the most popular heuristic random search methods. Unlike the PSO algorithm, SA can jump out of the trap of local minima in a timely manner to update the solutions and obtain the global optimum (details in Appendix B.3).

2.2.4. The Proposed Optimization Algorithm, APSOSA

This paper proposes a hybrid APSO algorithm by employing the SA algorithm to prevent the PSO from falling into local minima (the algorithm of SA-APSO is shown in

Table 2. A rudimentary SA-APSO algorithm is outlined as follows.

Algorithm: SA-APSO

Input:

${\mathit{x}}_s^{\left(0\right)}=\left({\mathit{x}}^{\left(0\right)}\left(1\right),{\mathit{x}}^{\left(0\right)}\left(2\right),\dots ,{\mathit{x}}^{\left(0\right)}\left(l\right)\right)–asequenceoftrainingdata.$

${\mathit{x}}_p^{\left(0\right)}=\left({\mathit{x}}^{\left(0\right)}\left(l+1\right),{\mathit{x}}^{\left(0\right)}\left(l+2\right),\dots ,{\mathit{x}}^{\left(0\right)}\left(l+n\right)\right)–asequenceofverifyingdata.$

Output:

Pg—the value of x with the best fitness value in population of particles

Parameters:

Itermax—the maximum number of iterations

n—the number of particles

Fi—the fitness function of particle i

xi—particle i

g—the current iteration number

d—the number of dimension

1: /* Set the parameters of PSO and SA. */

2: /* Initialize population of n particle xi (i = 1, 2,..., n) randomly */

3: FOR EACH i: 1 ≤ i ≤ n DO

4: Evaluate the corresponding fitness function Fi

5: END FOR

6: /* Determine the global best position */

7: FOR EACH i: 1 ≤ i ≤ n DO

8: Determine the global best position Pg by using F(xi).

9: {F(Pg), g}=max{(F(P1), …, F (PN)}

10: END FOR

11: WHILE (g < Itermax) DO

12: /* Determine the initial temperature. */

13: FOR EACH i: 1 ≤ i ≤ n DO

14: T0=−F(Pi)/ln(0.2)

15: END FOR

16: FOR EACH i = 1:n DO

17: FOR EACH j = 1:n DO

18: /* Calculate the probability P(Pi) */

19: /* Judge the relationship of the probability P(Pi) and rand () */

20: IF (P(Pi) > rand()) THEN

21: Pg = P′g = Pi

22: END IF

23: /* Update the velocity and position of each particle */

24: FOR EACH i: 1 ≤ i ≤ n DO

25: vi(t + 1) = w(t)vi(t) + c1r1(pi − xi(t)) + c2r2(pg − xi(t));

26: xi(t + 1)= xi(t) + vi(t + 1);

27: END FOR

28: /* Evaluate the new position P′i and fitness function F(P′i). */

29: FOR EACH i: 1 ≤ i ≤ n DO

30: Evaluate the corresponding fitness function F(P′i)

31: END FOR

32: /* Judge the relationship of fitness function F(P′i) and F (Pi). */

33: IF (F(P′i) > F (Pi)) THEN

34: Pi = P′i and F (Pi) = F(P′i)

35: END IF

36: /* Judge the relationship of fitness function F(Pi) and F(Pg). */

37: IF (F (Pi) > F (Pg)) THEN

38: Pg = Pi and F (Pg) = F(Pi)

39: END IF

40: /* Cooling the temperature */

41: FOR EACH i: 1 ≤ i ≤ n DO

42: Ti + 1 = a × Ti

43: END FOR

44: END FOR

45: END FOR

46: END WHILE

47: RETURN Pg

). The major steps of the hybrid optimization algorithm are as follows. First, enhance the accuracy and convergence rate of the basic PSO algorithm by applying a compression factor and selecting suitable parameters. Next, by combining the Simulated Annealing characteristics, PSO can more easily and quickly obtain the optimal solution in a larger search space. SA can also cancel the restrictions on speed border. Moreover, the Roulette Wheel Selection Strategy is chosen, shown in Figure 2, in this algorithm.

PSO can obtain better results in a faster setting with fewer parameters and is cheaper than other methods. It is also currently being widely used for promising results in continuous problems. However, the movement directionality of the particles is not certain, and particles are likely to jump out to obtain near-optimal solutions and their local search ability is relatively weak and easily trapped by the local optimum. Therefore, PSO is combined with the simulated annealing algorithm. The annealing algorithm is used when poor quality is probable to temporarily accept some solution features to construct a particle swarm algorithm, based on simulated annealing. A multitude of papers have verified that the improved particle swarm optimization algorithm obtains better results and have documented the effectiveness of the method through experimental simulation results. The velocity and position updating formula are as follows:

$${\mathit{v}}_{i,j}(k+1)=\mathbf{\chi }[{\mathit{v}}_{i,j}(k)+c_1{r}_1(p_{i,j}(k)-{\mathit{x}}_{i,j}(k))+c_2{r}_2(p_{g,j}(k)-{\mathit{x}}_{i,j}(k))]$$

(1)

$${\mathit{x}}_{i,j}(k+1)={\mathit{x}}_{i,j}(k)+{\mathit{v}}_{i,j}(k+1),j=1,\mathrm{...},n$$

(2)

where $r_1$ and $r_2$ are set randomly between 0 and 1, and the learning factors $c_1$ and $c_2$ are positive numbers, where $\mathbf{\chi }$ is computed by the following formula:

$$\mathbf{\chi }=\frac{2}{\left|2-C-\sqrt{C^2-4C}\right|}, C=c_1+c_2, C>4$$

(3)

In Equation (3), applying the best group positions, all particles fly to the best group positions, and then tend to the local minima solution if the best group positions are in the local minimum. Accordingly, this situation will cause the search dispersability and ability to become worse. To overcome this weakness, a new position $p_g^{\prime }$ will be selected from among the $p_i$ to replace $p_g$. Finally, in this paper, the Equation (1) is rewritten as the following formula, Equation (4):

$${\mathit{v}}_{i,j}(k+1)=\mathbf{\chi }[{\mathit{v}}_{i,j}(k)+c_1{r}_1(p_{i,j}(k)-{\mathit{x}}_{i,j}(k))+c_2{r}_2(p_{i,j}^{\prime }(k)-{\mathit{x}}_{i,j}(k))]$$

(4)

However, how to address the suitable position $p_i$ is one of the most critical steps of the combined algorithm. Clearly, better performance of $p_i$ shall be considered a higher priority. Under the characteristics of the SA algorithm, the best solutions of every particle $p_i$ should be taken as the special one, which may be worse than the global optimal solution $p_g$. Therefore, in the case of temperature T, we can calculate the leap probability using Equation (5):

$$P_{lp}(p_i)=e^{-(F(p_i)-F(p_g))/KT}$$

(5)

where F is the objective function value of the particle position.

The leap probability can be computed by the following formula, Equation (6):

$$P(p_i)=\frac{e^{-(F(p_i)-F(p_g))/KT}}{{\displaystyle \sum _{j=1}^N{e}^{-(F(p_i)-F(p_g))/KT}}}$$

(6)

where N is the population, on the side; considering the Roulette Wheel Selection strategy, we can randomly choose the $p_i$, which will be regarded as $p_g^{\prime }$.

The chief steps of the APSOSA algorithm are as follows, and a flowchart is depicted in Figure 2.

• Step 1: Set the initial temperature, and initialize the population along with every particle velocity and position.
• Step 2: Compute $\mathit{F}(p_i)(i=1,\mathrm{..},N)$, where N is the updated population.
• Step 3: Update the present position and fitness value of each particle by using $p_i$, $\mathit{F}(p_i)$ and $p_g$, $\mathit{F}(p_g)$, respectively.
• Step 4: Compute the initial temperature using Equation (7):

  $${\mathit{T}}_0=\mathbf{-}\mathit{F}(p_g)/\ln \left(0.2\right)$$

  (7)
• Step 5: Update the particle position and velocity and compute $\mathit{P}(p_i)$.
• Step 6: Through the roulette wheel selection strategy, the new global optimal solution $p_g^{\prime }$ is not regarded as $p_g$ until $\mathit{P}(p_i)>\text{rand} ()$.
• Step 7: Update every particle velocity and position by the pre-set update formula.
• Step 8: Compute every particle $\mathit{F}(p_i^{\prime })$, and then do not apply $p_i$ $\mathit{F}(p_i)$ to update the current global position $p_g$ and optimal fitness value $\mathit{F}(p_g)$, respectively, until $\mathit{F}(p_i)>\mathit{F}(p_g)$.
• Step 9: By applying the pre-set rules, the temperature reduces slowly.
• Step 10: Analyze whether the pre-set conditions are met; if they have been met, output the information of $p_g$ and then end running. Otherwise, repeat the above steps, beginning with Step 5.

2.2.5. SSA–APSOSA–BPNN Algorithm

In this section, we will introduce the hybrid model (SSA–APSOSA–BPNN) more clearly. The flowchart of the model is described in Figure 3. And the experimental parameters of APSOSA are given in

Table 3. The experimental parameters of APSOSA.

Experimental Parameters	Default Value
The population size: N	30
maximum initial velocity	2
minimum initial velocity	−2
the learning factor: C1	2.2
the learning factor: C2	1.8
The evolution number: M	200

. The hybrid algorithm contains four main stages.

• Stage I: Data prepossessing. Utilize the SSA method to process the original wind speed signals; as a result, the noise signals are removed, and the real and effective signals, which are shown in Figure 1, can be preserved. Lastly, the useful processed signal will be fed into the abovementioned hybrid model.
• Stage II: Data selection. The processed valid data from Stage I is classified into three parts: the training set, the validation set, and the test set for model training, validation, and testing, respectively.
• Stage III: Algorithm training and validation. Here, the SSA–APSOSA–BPNN algorithm is utilized for wind speed forecasting. Additionally, the detailed rules are given as below:

  • Step 1: Determine and initialize the parameters of APSOSA.
  • Step 2: Set the fitness function; the mean absolute error (MAE) of validation is taken as the fitness of the particles:

    $$fitness=MAE=\frac{1}{N}{\displaystyle \sum _{i=1}^N\left|y_i-{\widehat{y}}_i\right|}$$

    (8)

    where N is the number of validation sets and ${\widehat{y}}_i$ and $y_i$ stand for the predictive value and the observed value, respectively.
  • Step 3: Update the historical extremum $p_j$ of every particle and the global extremum $p_g$ and then repeat the above rules for the next particles.
  • Step 4: Set the conditions and judge whether the fitness value meets the conditions; if it does, save the corresponding optimal parameters and then stop running. Otherwise, run Step 3 again and continue to run.
• Stage IV: Forecasting. In this stage, the optimal parameters from Step 4 of Stage III will be applied into the BPNN model to forecast. Finally, the wind speed forecasting data will be obtained by completing all of the above steps.

3. Case Study

To examine the accuracy of the novel combined algorithm, four different multi-step forecasting algorithms are compared by analyzing the three-step-ahead-prediction (half–1-h-ahead) and the six-step-ahead-prediction (1-h-ahead) of a 10-min wind speed series at three different wind power stations.

3.1. Study Area and Datasets

Shandong, located on the east coast of China, is not only one of the provinces with the largest economy, but also one of the biggest energy consumers. However, 99% of the electrical energy comes from coal power generation. As a result, Shandong faces enormous energy pressures.

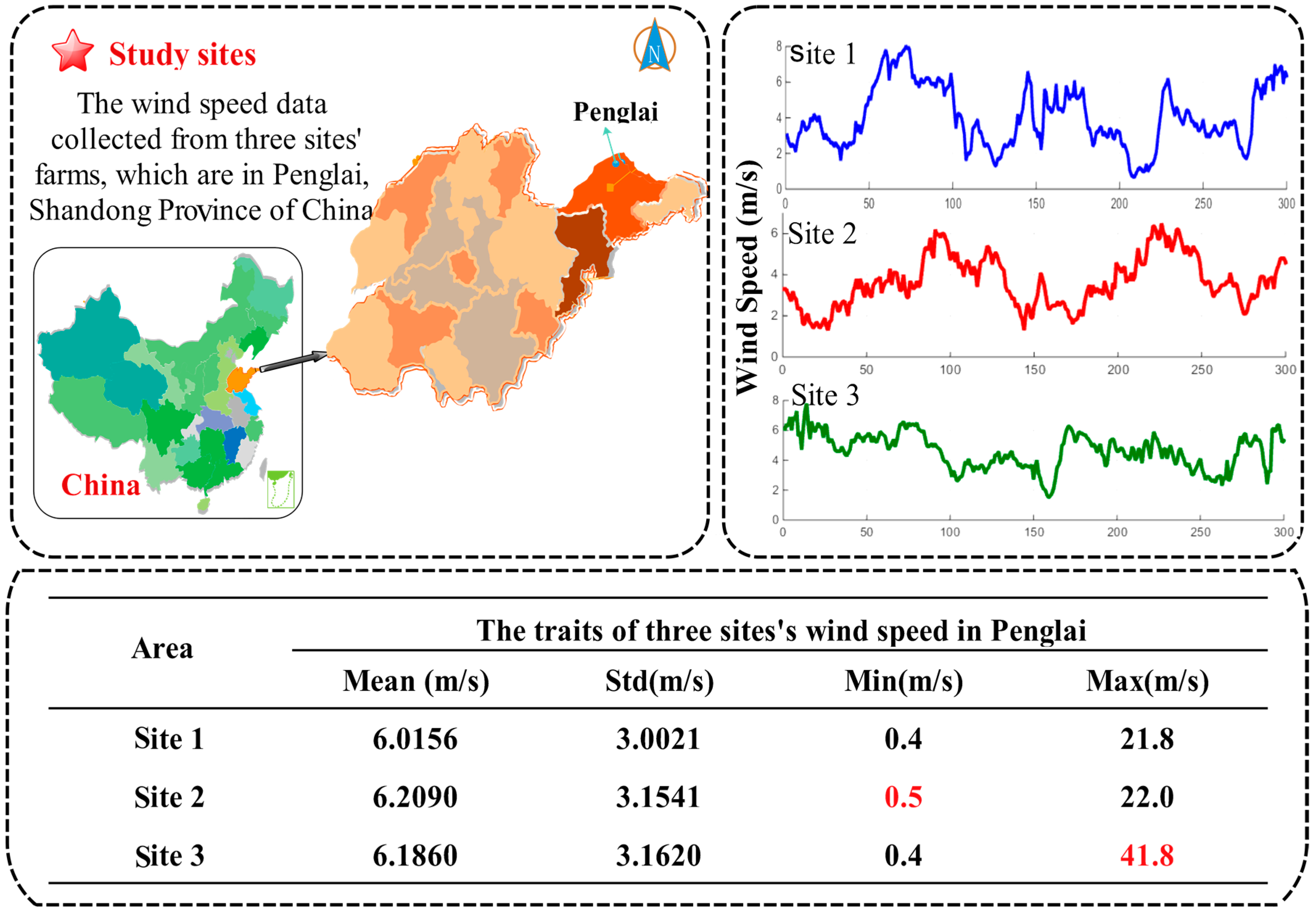
However, as a coastal province, Shandong possesses one of China’s largest wind farms, with an installed capacity of 58 million kilowatts. A simple map of the research area is depicted in Figure 4. With the aim of satisfying social development, achieving energy conservation, and protecting the environment, Shandong has begun developing wind power stations. Due to the area’s unique geographical advantages, capacity reached 260 billion KWH in 2007. In addition, the Shandong Province Bureau of Meteorology assessment notes that the entire output of wind energy resources in Shandong province is 67 million kilowatts, which is equivalent to the installed capacity of 3.68 times the capacity of the Three Gorges Hydro-power Station (18.20 million kilowatts), which ranks in the top three. To actively build wind power green energy bases, promote wind energy development, and protect the environment, Shandong has been focusing on building large-scale wind farms in Weihai, Yantai, Dongying, Weifang, Qingdao, and other coastal areas, and is gradually developing offshore wind power projects.

In this work, Penglai, which is located north of Shandong and lies north of the Yellow Sea and the Bohai Sea, was chosen as the area of study. It has tremendous, potentially valuable wind resources. The specific advantages are as follows: (i) higher elevation but relatively flat hilltops, ridges, and a special terrain that has much potential as an air strip; (ii) longer cycle of efficient power generation; (iii) suitable climatic conditions that are conducive to the normal operation of wind turbines; and (iv) small diurnal and seasonal variations of wind speed, which can reduce the impact on power.

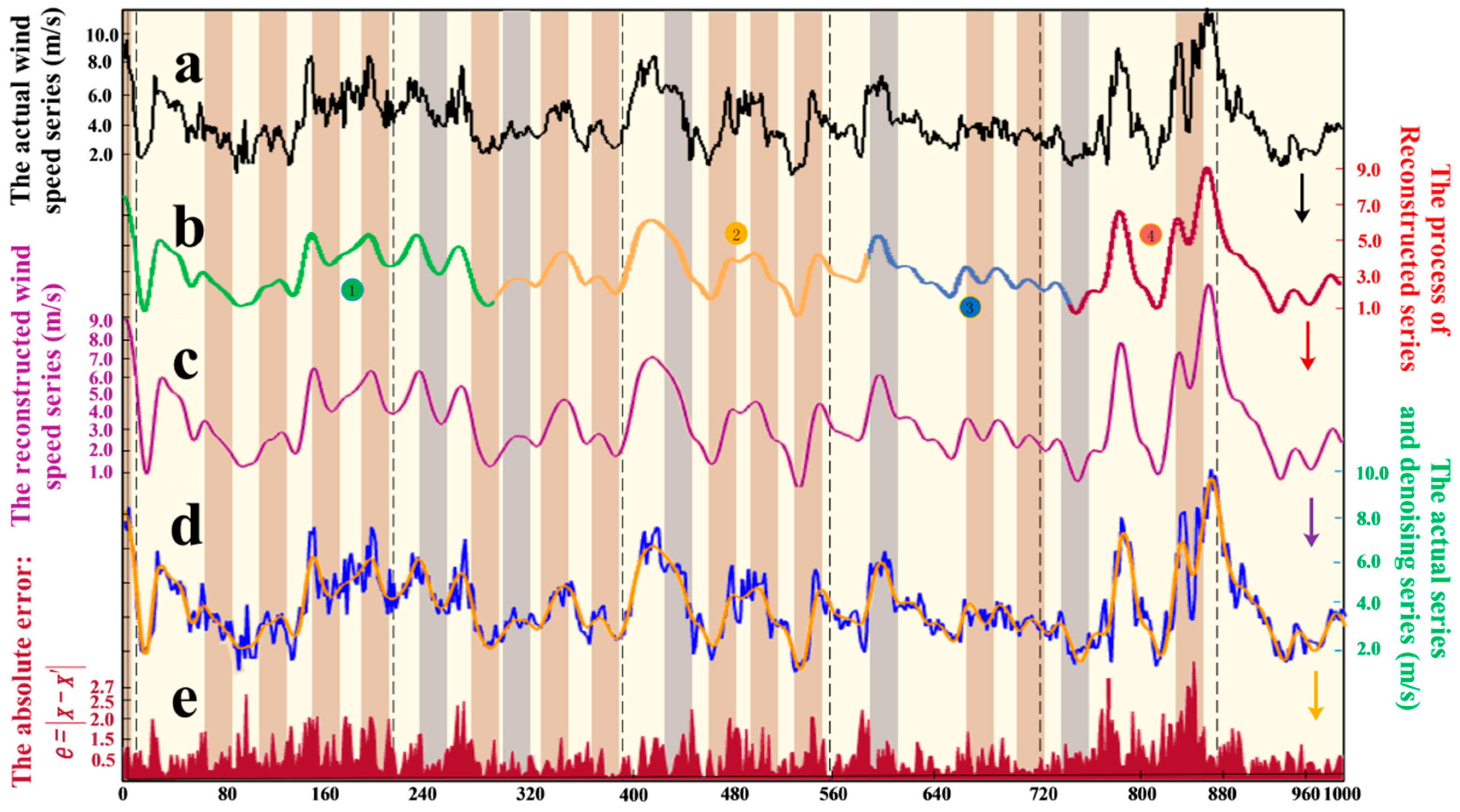
In this study, the 10-min wind speed data from Penglai wind farms are used to obtain a detailed example for evaluating the performance of the proposed model. First, the wind speed data are divided into four parts according to the seasons, so that the impact of seasonal variations can be considered to increase the stability of the proposed model. Next, every seasonal wind speed dataset is divided into three parts: a training set, a validation set, and a testing set. Additionally, the noise is removed from the data by using SSA. Finally, the processed data are entered into the model and, judging from the forecasting results, we determine whether the raised algorithm can be widely employed for real-world farm use. In this study, the experiment is applied to three different sites (Site 1, 2, and 3). The above-described experiment is scientific and is used to validate the performance of the proposed model.

3.2. Performance Criteria of Forecast Accuracy

To evaluate the prediction accuracy of the raised hybrid algorithm, four indexes are applied to measure the quality of the forecasting methods: absolute error (AE), mean absolute error (MAE), root mean square error (RMSE), and mean absolute percent error (MAPE), shown in

Table 4. Four metric rules.

Metric	Definition	Equation
AE	The average forecast error of i times forecast results	$\mathbf{\text{AE}}=\frac{1}{N}{\displaystyle \sum _{i=1}^N\left(y_i-{\widehat{y}}_i\right)}$
MAE	The average absolute forecast error of i times forecast results	$\mathbf{\text{MAE}}=\frac{1}{N}{\displaystyle \sum _{i=1}^N\left|y_i-{\widehat{y}}_i\right|}$
RMSE	The root average of the prediction error squares	$\mathbf{\text{RMSE}}=\sqrt{\frac{1}{N}{\displaystyle \sum _{i=1}^N{\left(y_i-{\widehat{y}}_i\right)}^2}}$
MAPE	The average of absolute error	$\mathbf{\text{MAPE}}=\frac{1}{N}{\displaystyle \sum _{i=1}^N\left|\frac{y_i-{\widehat{y}}_i}{y_i}\right|}\times 100\%$

(here N is the number of test samples, and ${\widehat{y}}_i$ and $y_i$ represent the real and forecast values, respectively). Here, the absolute error (AE) and the mean absolute error (MAE) are both selected so that the level of error can be more clearly reflected. RMSE is chosen because it can easily reflect the degree of changes between the actual and forecasted value. Additionally, MAPE is chosen because of its ability to reveal the credibility of the forecasting model. Wind speed forecasting errors are related to not only the forecasting models but the selected samples. Consequently, the forecasting errors within a certain scientific range can be accepted. Moreover, in order to better evaluate performance, four percentage error criterions are also applied in this study, listed in

Table 5. Four metric rules.

Metric	Definition	Equation
${\mathit{Q}}_{\mathbf{\text{AE}}}$	The percentage error of AE	${\mathit{Q}}_{\mathbf{\text{AE}}}=\left|\frac{{\mathbf{\text{AE}}}_1-{\mathbf{\text{AE}}}_2}{{\mathbf{\text{AE}}}_1}\right|$
${\mathit{Q}}_{\mathbf{\text{MAE}}}$	The percentage error of MAE	${\mathit{Q}}_{\mathbf{\text{MAE}}}=\left|\frac{{\mathbf{\text{MAE}}}_1-{\mathbf{\text{MAE}}}_2}{{\mathbf{\text{MAE}}}_1}\right|$
${\mathit{Q}}_{\mathbf{\text{RMSE}}}$	The percentage error of RMSE	${\mathit{Q}}_{\mathbf{\text{RMSE}}}=\left|\frac{{\mathbf{\text{RMSE}}}_1-{\mathbf{\text{RMSE}}}_2}{{\mathbf{\text{RMSE}}}_1}\right|$
${\mathit{Q}}_{\mathbf{\text{MAPE}}}$	The percentage error of MAPE	${\mathit{Q}}_{\mathbf{\text{MAPE}}}=\left|\frac{{\mathbf{\text{MAPE}}}_1-{\mathbf{\text{MAPE}}}_2}{{\mathbf{\text{MAPE}}}_1}\right|$

.

3.3. Experimental Simulations

In this subsection, three single models, WNN, GRNN, and BPNN, are compared to obtain the best prediction approach. As a result, whether for half-hour (rolling three-step) or one-hour (rolling six-step) predictions, BPNN gives the best prediction accuracy (see

Table 6. Comparison of errors of rolling three-step (half an hour ahead) forecasts.

Indexes	Site 1				Site 2				Site 3
	Spring	Summer	Autumn	Winter	Spring	Summer	Autumn	Winter	Spring	Summer	Autumn	Winter
					AE
WNN	−0.0538	0.2344	−0.0193	0.0733	0.1236	0.2813	0.0000	−0.0225	0.0654	0.2584	0.0863	0.0065
GRNN	−0.2328	−0.1134	0.0624	−0.1384	−0.3321	0.6803	−0.1214	0.1004	0.1447	0.2302	0.2108	−0.0541
BPNN	−0.1562	0.1230	0.0414	0.1203	0.0431	0.4185	−0.2744	−0.0795	−0.1986	0.0094	−0.0927	0.0843
PSO–BP	−0.1106	0.3070	−0.1049	−0.0652	0.0242	0.3804	−0.1223	−0.0294	−0.0670	−0.0296	−0.0619	0.0137
APSOSA–BP	−0.1181	0.0890	−0.0571	0.0024	0.103	0.3321	−0.1111	0.0022	−0.0396	0.0774	−0.0779	0.0099
Proposed model	−0.0132	0.0223	−0.0014	−0.0112	0.0136	0.0343	−0.0415	−0.0007	−0.0125	0.0078	−0.0198	0.0012
					MAE
WNN	0.8690	0.8388	0.7417	0.7927	0.8135	1.1342	0.5676	0.7151	0.7487	1.1515	0.5629	0.6335
GRNN	0.7394	0.6962	0.6873	0.6305	0.7157	1.0850	0.4713	0.5811	0.6138	0.9031	0.4673	0.5075
BPNN	0.7233	0.7007	0.5990	0.6311	0.6388	1.0317	0.5050	0.5335	0.5825	0.7996	0.4293	0.4833
PSO–BP	0.7011	0.7612	0.5777	0.5884	0.6233	0.9436	0.4664	0.5276	0.5634	0.7945	0.4245	0.4726
APSOSA–BP	0.6975	0.6545	0.5549	0.5761	0.6230	0.9133	0.4571	0.5143	0.5514	0.7938	0.4243	0.4681
Proposed model	0.4493	0.4151	0.3437	0.3489	0.4211	0.5312	0.3289	0.3351	0.4152	0.5312	0.3171	0.2900
					RMSE
WNN	1.1530	1.1683	0.9791	1.0244	1.0591	1.5757	0.7316	0.9383	0.9778	1.5987	0.7564	0.8070
GRNN	0.9784	0.9479	0.9999	0.8147	0.9165	1.6059	0.6052	0.7680	0.8038	1.2759	0.6333	0.6539
BPNN	0.9624	0.9478	0.8343	0.8145	0.8454	1.6364	0.6543	0.7169	0.7637	1.1838	0.5812	0.6207
PSO–BP	0.9381	1.1005	0.7735	0.7628	0.8267	1.3967	0.6005	0.6995	0.7453	1.1612	0.5747	0.6242
APSOSA–BP	0.9317	0.9134	0.7268	0.7472	0.8308	1.3191	0.5885	0.6927	0.7345	1.1585	0.5745	0.6155
Proposed model	0.5918	0.5454	0.4637	0.4466	0.5531	0.7008	0.4177	0.4336	0.5411	0.7297	0.4068	0.3688
					MAPE
WNN	12.8299	19.2123	24.2180	16.2978	9.4978	15.1054	20.8225	16.5005	11.6877	19.4706	16.7789	14.4603
GRNN	11.4804	17.6432	21.5985	13.5994	8.5776	12.8413	18.5481	13.0970	9.6661	15.0889	13.3686	12.5040
BPNN	11.0930	16.8607	18.5380	13.5335	7.4083	12.6158	19.6453	12.4060	9.4392	13.8388	13.0224	11.4632
PSO–BP	10.614	16.485	18.3886	12.3106	7.2490	11.9383	17.8111	12.1286	9.0266	13.7641	12.9241	11.2132
APSOSA–BP	10.5341	15.7025	18.2165	12.2418	7.1397	11.6154	17.4022	11.6352	8.5133	13.5678	12.8307	11.0325
Proposed model	6.6397	10.6659	11.3723	7.1128	4.7589	7.2473	12.2559	7.3750	6.4101	9.0027	9.7494	6.7077

and

Table 7. Comparison of errors of rolling six-step (one hour ahead) forecasts.

Indexes	Site 1				Site 2				Site 3
	Spring	Summer	Autumn	Winter	Spring	Summer	Autumn	Winter	Spring	Summer	Autumn	Winter
					AE
WNN	−0.1612	0.3295	0.2508	−0.0631	0.1107	0.1754	−0.0188	−0.0603	−0.0458	0.0132	−0.2371	0.0187
GRNN	−0.2724	−0.1850	0.0224	−0.1431	−0.4668	0.8426	−0.1809	0.1734	0.4493	0.3922	−0.1192	0.0486
BPNN	0.1676	−0.3026	−0.0800	−0.2177	−0.1111	−0.4045	0.4497	0.1120	0.2548	0.0088	0.1565	−0.1241
PSO–BP	0.1473	−0.5359	0.1845	0.0699	−0.0914	−0.4642	0.2082	0.0088	0.0262	0.0737	0.1042	0.0238
APSOSA–BP	0.1399	−0.1435	0.0799	−0.0624	−0.2008	−0.3763	0.1782	−0.0185	0.0301	−0.1283	0.1222	0.0253
Proposed model	0.0595	−0.0926	0.0235	0.0484	−0.0067	−0.1530	0.0557	0.0154	0.0285	−0.0040	0.0179	0.0175
					MAE
WNN	0.9833	0.9770	0.8332	0.8760	0.9599	1.2853	0.6176	0.7797	0.8332	1.2598	0.6525	0.7299
GRNN	0.8536	0.8151	0.8137	0.7500	0.8960	1.2891	0.5554	0.6993	0.8127	1.0877	0.5414	0.6148
BPNN	0.8325	0.958	0.7776	0.7954	0.7912	1.1887	0.6559	0.6417	0.7162	1.0157	0.5450	0.5919
PSO–BP	0.8327	1.0344	0.7430	0.7376	0.7576	1.1411	0.5542	0.6172	0.6848	1.0046	0.5343	0.5540
APSOSA–BP	0.8185	0.7955	0.6777	0.7117	0.7688	1.0920	0.5373	0.6143	0.6691	0.9946	0.5311	0.5542
Proposed model	0.5653	0.5078	0.4241	0.4086	0.4582	0.6306	0.3611	0.4061	0.4584	0.6643	0.3502	0.3678
					RMSE
WNN	1.2823	1.3406	1.1123	1.1349	1.2184	1.7978	0.7893	1.0301	1.0823	1.7689	0.8557	0.9242
GRNN	1.1125	1.1131	1.1222	0.9838	1.1428	1.8827	0.7175	0.9207	1.0658	1.5277	0.7282	0.7770
BPNN	1.0941	1.3032	1.1154	1.0336	1.0326	1.8427	0.8288	0.8449	0.9369	1.4813	0.7345	0.7541
PSO–BP	1.1012	1.4900	1.0244	0.9608	0.9898	1.6665	0.7132	0.8172	0.9073	1.4648	0.7238	0.7195
APSOSA–BP	1.0828	1.1063	0.8987	0.9423	1.0126	1.5784	0.6941	0.8151	0.8939	1.4294	0.7193	0.7202
Proposed model	0.7603	0.7360	0.5539	0.5295	0.6067	0.9561	0.4579	0.5322	0.6016	0.9269	0.4559	0.4783
					MAPE
WNN	15.6774	22.1542	26.5838	18.1273	11.4313	17.4636	22.7555	18.3793	13.9774	21.4955	21.0411	16.5445
GRNN	13.5174	22.0269	25.5008	16.4622	11.0234	15.7856	22.4828	15.6796	12.1603	17.6853	17.4406	14.5046
BPNN	13.2144	22.3227	23.5108	16.7841	9.3530	15.5730	26.6649	15.1189	11.8778	17.3869	17.5410	13.8192
PSO–BP	13.1579	21.6265	23.1254	15.5045	9.0061	14.8893	22.2483	14.5565	11.1359	17.3802	17.0869	13.4498
APSOSA–BP	12.7057	19.6883	22.3076	15.0001	8.9472	14.6322	21.2674	14.2413	10.5363	16.8365	16.756	13.1057
Proposed model	8.2895	12.4004	13.7975	8.8285	5.2338	8.2761	13.5699	9.2167	7.1493	11.6401	10.9296	8.3685

) of the four proposed models. Next, the APSOSA-BPNN is selected from BPNN, PSO-BPNN as the best prediction algorithm. Finally, the hybrid SSA–APSOSA–BP algorithm was proposed as our best prediction model.

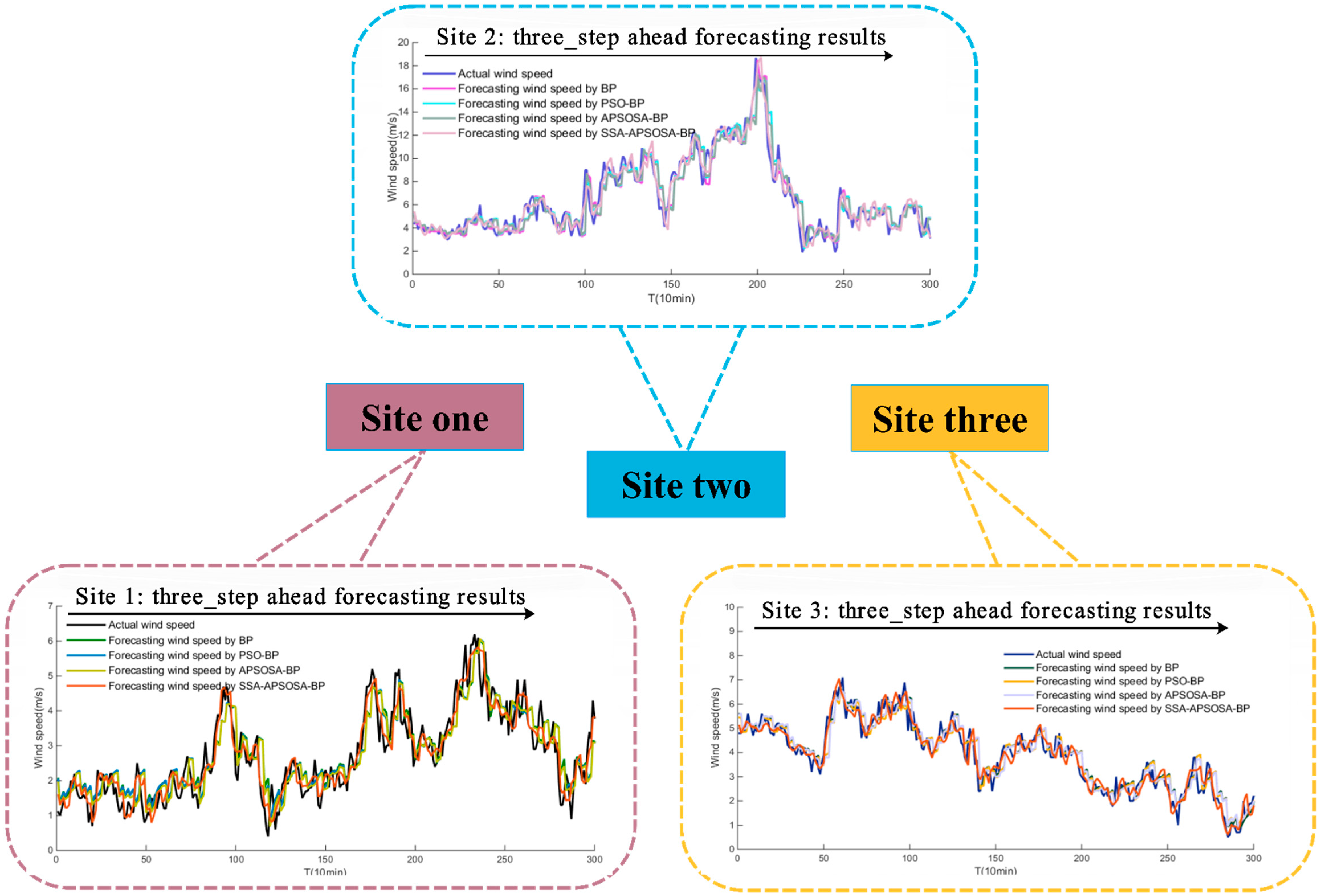
The BPNN, PSO-BPNN, and APSOSA–BPNN hybrid algorithms were selected to compare the forecasting results. Three sites from the Shandong–Penglai wind farms were selected, and then a sample (the 10-min wind speed series) of every season from each site was selected and entered into the above algorithms. Next, the multi-step predicted results were displayed. The specific results of the three sites are shown in Table 6 and Table 7, respectively. Additionally, the results from Site 1 are displayed in Figure 5 and the absolute errors of the three sites are shown in Table 6 and Table 7. Using the four percentage error criteria, the improvement percentages between each set of algorithms are shown in

Table 8. Improvement percentages among different forecasting models of rolling three-step (half an hour ahead) forecasts.

Indexes	Site 1				Site 2				Site 3
	Spring	Summer	Autumn	Winter	Spring	Summer	Autumn	Winter	Spring	Summer	Autumn	Winter
					QAE
BP vs. Proposed model	91.5470	81.8408	103.3182	109.3035	68.3453	91.7930	84.8808	99.1144	32.0906	34.9459	25.1336	41.4849
PSO vs. Proposed model	88.0618	92.7230	98.6902	82.8185	43.6765	90.9706	66.0777	97.6089	28.9866	34.5929	24.5642	40.1803
APSOSA vs. Proposed model	88.8219	74.9061	97.5929	564.8312	86.7541	89.6562	62.6562	131.4576	24.7049	33.6466	24.0151	39.2005
					QMAE
BP vs. Proposed model	37.8819	40.7592	42.6210	44.7156	34.0795	48.5122	34.8713	37.1884	28.7210	33.5668	26.1356	39.9959
PSO vs. Proposed model	35.9150	45.4677	40.5055	40.7036	32.4402	43.7050	29.4811	36.4860	26.3046	33.1403	25.3004	38.6373
APSOSA vs. Proposed model	35.5842	36.5775	38.0609	39.4376	32.4077	41.8373	28.0464	34.8435	24.7008	33.0814	25.2651	38.0474
					QRMSE
BP vs. Proposed model	38.5079	42.4562	44.4205	45.1688	34.5753	57.1743	36.1608	39.5174	29.1476	38.3595	30.0069	40.5832
PSO vs. Proposed model	36.9150	50.4407	40.0517	41.4525	33.0954	49.8246	30.4413	38.0129	27.3984	37.1598	29.2152	40.9164
APSOSA vs. Proposed model	36.4817	40.2890	36.1998	40.2302	33.4256	46.8729	29.0229	37.4044	26.3308	37.0134	29.1906	40.0812
					QMAPE
BP vs. Proposed model	40.1451	36.7411	38.6541	47.4430	35.7626	42.5538	37.6141	40.5530	32.0906	34.9459	25.1336	41.4849
PSO vs. Proposed model	37.4439	35.2994	38.1557	42.2222	34.3509	39.2937	31.1895	39.1933	28.9866	34.5929	24.5642	40.1803
APSOSA vs. Proposed model	36.9695	32.0751	37.5714	41.8974	33.3459	37.6061	29.5727	36.6148	24.7049	33.6466	24.0151	39.2005

and

Table 9. Improvement percentages among different forecasting models of rolling six-step (one hour ahead) forecasts.

Indexes	Site 1				Site 2				Site 3
	Spring	Summer	Autumn	Winter	Spring	Summer	Autumn	Winter	Spring	Summer	Autumn	Winter
					QAE
BP vs. Proposed model	64.5124	69.3882	129.3627	122.2531	93.9478	62.1808	87.6194	86.2288	39.8096	33.0525	37.6911	39.4429
PSO vs. Proposed model	59.5977	82.7136	87.2727	30.7280	92.6464	67.0416	73.2619	74.6921	35.7995	33.0267	36.0352	37.7797
APSOSA vs. Proposed model	57.4865	35.4692	70.6258	177.6135	96.6529	59.3472	68.7603	183.3262	32.1460	30.8639	34.7720	36.1461
					QMAE
BP vs. Proposed model	32.0961	46.9937	45.4604	48.6296	42.0880	46.9505	44.9459	36.7150	35.9955	34.5968	35.7431	37.8611
PSO vs. Proposed model	32.1124	50.9087	42.9206	44.6041	39.5195	44.7375	34.8430	34.2029	33.0607	33.8742	34.4563	33.6101
APSOSA vs. Proposed model	30.9346	36.1659	37.4207	42.5882	40.4006	42.2527	32.7936	33.8922	31.4901	33.2093	34.0614	33.6341
					QRMSE
BP vs. Proposed model	30.5091	43.5236	50.3407	48.7713	41.2454	48.1142	44.7514	37.0103	35.7882	37.4266	37.9306	36.5734
PSO vs. Proposed model	30.9571	50.6040	45.9293	44.8897	38.7048	42.6283	35.7964	34.8752	33.6934	36.7217	37.0130	33.5233
APSOSA vs. Proposed model	29.7839	33.4719	38.3665	43.8077	40.0849	39.4260	34.0297	34.7074	32.6994	35.1546	36.6189	33.5879
					QMAPE
BP vs. Proposed model	37.2692	44.4494	41.3142	47.3996	44.0415	46.8561	49.1095	39.0386	39.8096	33.0525	37.6911	39.4429
PSO vs. Proposed model	36.9998	42.6611	40.3362	43.0585	41.8861	44.4158	39.0070	36.6833	35.7995	33.0267	36.0352	37.7797
APSOSA vs. Proposed model	34.7576	37.0164	38.1489	41.1437	41.5035	43.4391	36.1939	35.2819	32.1460	30.8639	34.7720	36.1461

.

From Table 6 and Table 7, we can see following:

(a)

Different forecasting algorithms have different forecasting results;

(b)

All the algorithms’ forecasting results from the three sites are effective. Examples are included in Figure 5;

(c)

For different seasons at the same site, the hybrid algorithms show strong forecasting stability;

(d)

Among the algorithms studied, the hybrid SSA–PSOSA–BP algorithm (see in Figure 6) obtained better accuracy than the others. Moreover, to further illustrate the quality of the proposed hybrid algorithm, four percentage error criterions are used in Table 5.

It can be analyzed in detail that:

(a)

When comparing the hybrid PSO–BP algorithm with the single BP algorithm, we can make a conclusion that the PSO selects excellent parameters to run BP model, but the prediction accuracy of PSO–BP is increased only slightly. From Table 6 and Table 7, in the spring, the three-step MAPE results of the PSO–BP and the BP are 7.2490% and 7.4083%, respectively. For the six-step, they are 9.0061% and 9.3530%, respectively.

(b)

When comparing the hybrid PSOSA–BP algorithm with the combined PSO–BP algorithm, the former combines the advantages of simulated annealing, and further optimizes the parameters; as a result, with respect to (a), the predicted quality rises again, but not particularly clearly. The specific upgrade percentages are provided in Table 8 and Table 9.

(c)

When comparing the hybrid SSA–APSOSA–BP algorithm with the hybrid PSOSA–BP algorithm, the former MAPE results are better than the latter. In other words, the forecasting quality of the new combined algorithm is better because of the higher accuracy when comparing it with the BP, PSO–BP, and PSOSA–BP algorithms.

(d)

The forecasting quality of the hybrid SSA–APSOSA–BP algorithm is better than that of the hybrid PSO–BP algorithm. The decreases in MAPE results in comparison with the PSO–BP and SSA–APSOSA–BP algorithm of three-step and six-step forecasts are 37.4439% and 36.9998% in Table 8 and Table 9 for the spring season, respectively.

(e)

When comparing the hybrid SSA–APSOSA–BP algorithm with the single BP algorithm, the accuracy of the wind speed forecasting, is improved more obviously. As an example, in Table 6, the three-step forecasting MAPE results for the latter are 9.4392%, 13.8388%, 13.0224%, and 11.4632%, respectively. However, for the former, the three-step forecasting MAPE results are 6.4101%, 9.0027%, 9.7494%, and 6.7077%, respectively.

(f)

From (a) to (e), the reasons include:

(1)

The combination of the SA algorithm and the PSO algorithm has increased the forecasting ability and accuracy of the single BP algorithm effectively.

(2)

The SSA algorithm removes the noise signal from the original wind speed data and, due to the APSOSA algorithm, the best initial weights and thresholds are given to optimize the BP algorithm, which can lead to high-precision forecasting results.

(3)

The scientific and rational data selection used in this paper is also one of the paramount reasons for the outstanding performance achieved.

In different seasons at the same site, the proposed algorithms’ forecasting qualities can also be different. This phenomenon indicates that wind speed can be affected by seasonal factors. In this paper, we also consider this factor, and the different seasons’ forecasting results are listed in Table 6 and Table 7.

Table 10. Average errors of the different rolling forecasting models at the three sites.

		BP		PSO–BP		APSOSA–BP		SSA–APSOSA–BP
Area	Average	3-Step	6-Step	3-Step	6-Step	3-Step	6-Step	3-Step	6-Step
Site 1	AE (m/s)	−0.0321	−0.1082	−0.0066	−0.0336	0.0210	0.0035	0.0009	0.0097
	MAE (m/s)	0.6635	0.8409	0.6571	0.8369	0.6208	0.7509	0.3893	0.4765
	RMSE (m/s)	0.8898	1.1366	0.8937	1.1441	0.8298	1.0075	0.5119	0.6449
	MAPE (%)	15.0063	18.9580	14.4496	18.3536	14.1737	17.4254	8.9477	10.8290
Site 2	AE (m/s)	−0.0269	0.0115	−0.0632	−0.0847	−0.0816	−0.1044	−0.0014	−0.0222
	MAE (m/s)	0.6773	0.8194	0.6402	0.7675	0.6269	0.7531	0.4041	0.4640
	RMSE (m/s)	0.9633	1.1373	0.8809	1.0467	0.8578	1.0251	0.5263	0.6382
	MAPE (%)	13.0189	16.6775	12.2818	15.1751	11.9481	14.7720	7.9093	9.0741
Site 3	AE (m/s)	0.0494	0.0740	0.0362	0.0570	0.0076	0.0123	0.0058	0.0150
	MAE (m/s)	0.5737	0.7172	0.5638	0.6944	0.5594	0.6873	0.3884	0.4602
	RMSE (m/s)	0.7874	0.9767	0.7764	0.9539	0.7708	0.9407	0.5116	0.6157
	MAPE (%)	11.9409	15.1562	11.7320	14.7632	11.4861	14.3086	7.9675	9.5219

and

Table 11. Average errors of the different rolling forecasting models in different seasons.

		BP		PSO–BP		APSOSA–BP		SSA–APSOSA–BP
Season	Average	3-Step	6-Step	3-Step	6-Step	3-Step	6-Step	3-Step	6-Step
Spring	AE (m/s)	0.1039	0.1038	0.0511	0.0274	0.0182	−0.010	0.0040	0.0271
	MAE (m/s)	0.6482	0.7800	0.6293	0.7584	0.6240	0.7521	0.4285	0.4940
	RMSE (m/s)	0.8572	1.0212	0.8367	0.9994	0.8323	0.9964	0.5620	0.6562
	MAPE (%)	9.3135	11.4817	8.9632	11.100	8.7290	10.729	5.9362	6.8909
Summer	AE (m/s)	−0.1836	−0.2328	−0.2193	−0.3088	−0.166	−0.2160	−0.021	−0.083
	MAE (m/s)	0.8440	1.0541	0.8331	1.0600	0.7872	0.9607	0.4925	0.6009
	RMSE (m/s)	1.2560	1.5424	1.2195	1.5404	1.1303	1.3714	0.6586	0.8730
	MAPE (%)	14.4384	18.4275	14.0625	17.965	13.628	17.0523	8.9720	10.772
Autumn	AE (m/s)	0.1086	0.1754	0.0964	0.1656	0.0820	0.1268	0.0209	0.0324
	MAE (m/s)	0.5111	0.6595	0.4895	0.6105	0.4788	0.5820	0.3299	0.3785
	RMSE (m/s)	0.6899	0.8929	0.6496	0.8205	0.6299	0.7707	0.4294	0.4892
	MAPE (%)	17.0686	22.5722	16.3746	20.8202	16.1498	20.1103	11.1259	12.7657
Winter	AE (m/s)	−0.0417	−0.0766	0.0270	0.0342	−0.0048	−0.0185	0.0036	0.0271
	MAE (m/s)	0.5493	0.6763	0.5295	0.6363	0.5195	0.6267	0.3247	0.3942
	RMSE (m/s)	0.7174	0.8775	0.6955	0.8325	0.6851	0.8259	0.4163	0.5133
	MAPE (%)	12.4676	15.2407	11.8841	14.5036	11.6365	14.1157	7.0652	8.8046

are chosen as examples, and the detailed descriptions of this phenomenon are as follows:

(a)

Different sites can give different results. In Table 10, for the hybrid SSA–PSOSA–BP algorithm, the MAPE results of the three-step and six-step are 8.9477% and 10.8290%, respectively, at Site 1. However, for Sites 2 and 3, they are 7.9093% and 7.0741% vs. 7.9675% and 9.5219%, respectively.

(b)

In Table 11, for the hybrid SSA–APSOSA–BP algorithm in spring and winter, the MAPE of the three-step and six-step are 5.9362% and 6.8909% vs. 7.0652% and 8.8046%, respectively. However, in summer and autumn, they are 8.9720% and 10.7722% vs. 11.1259% and 12.7657%, respectively. Obviously, in spring and winter, the MAPE results are less than 9%, but in summer and autumn, the wind speed forecasting errors are all more than 10%, especially in autumn when they are close to 12%.

(c)

As can be clearly observed from the circumstances described above, geographical and seasonal factors must be considered in the wind speed prediction. From (b), it can be concluded that the prediction accuracy in spring and winter is better than that in summer and autumn. However, comparing with the other proposed algorithms, the forecasting errors of the hybrid algorithm are still effectively less.

4. Discussion

In this section, the bias–variance framework and the Diebold–Mariano (DM) are used to examine the accuracy, the stability, and the forecasting performance of the forecast models.

4.1. Bias–Variance Framework

In order to evaluate the different models’ accuracy and stability, in this subsection, we utilize the bias–variance framework, which includes bias and variance. The bias-variance framework can be shown as follows:

$$\mathrm{var}=E{[(\widehat{y}-y)-E(\widehat{y}-y)]}^2$$

(9)

$$Bia{s}^2=E{[\widehat{y}-y]}^2-E[\widehat{y}-E{(\widehat{y})}^2]$$

(10)

where $y$ and $\widehat{y}$ are the observed values and the forecasting values respectively.

The higher the bias, the lower the forecasting accuracy. Similarly, the bigger the variance, the worse the prediction performance. The results of the models are shown in

Table 12. Bias–variance and Diebold–Mariano test of different models (half an-hour ahead).

Different Models	Bias–Variance Framework		Diebold–Mariano Statistic
	Bias2	Var
WNN	0.019750	1.186340	15.016983 *
GRNN	0.067441	0.849879	12.978130 *
BPNN	0.030799	0.820297	13.903475 *
PSO–BP	0.024353	0.758024	13.244862 **
APSOSA–BP	0.014342	0.706074	12.841336 **
Proposed model	0.000375	0.278953	—

* is the 1% significance level; ** is the 5% significance level.

and

Table 13. Bias–variance and Diebold–Mariano test of different models (one hour ahead).

Different Models	Bias–Variance Framework		Diebold–Mariano Statistic
	Bias2	Var
WNN	0.025612	1.497107	16.081645 *
GRNN	0.124355	1.170295	13.999003 *
BPNN	0.055763	1.211757	12.749358 *
PSO–BP	0.052717	1.144234	12.080501 **
APSOSA–BP	0.024791	1.029058	12.739267 **
Proposed model	0.003605	0.424805	—

* is the 1% significance level; ** is the 5% significance level.

. Obviously, the bias and variance of the proposed hybrid model are smaller than the comparison models (GRNN, WNN, APSOSA–BPNN, etc.). In other words, the developed model possesses a higher accuracy and stability in wind-speed forecasting and performs much better than the comparison models in forecasting.

4.2. Statistical Hypothesis Testing

Hypothesis testing is a basic method of statistical inference, also called confirmatory data analysis. Its basic principle can be described as below: firstly, making some assumptions, then statistical reasoning, and lastly determining whether to reject or accept the hypothesis under a level of significance that is defined beforehand [4]. There are many commonly used methods of hypothesis testing such as T-test, F-test, rank and inspection, etc.

In this subsection, another hypothesis testing approach is employed to assess the models’ efficiency, called the Diebold–Mariano test [10]. The concrete content is described as follows:

$$H_0:E[(\mathit{L}(e_t^1)]=E[(\mathit{L}(e_t^2)]$$

$$H_1:E[(\mathit{L}(e_t^1)]\ne E[(\mathit{L}(e_t^2)]$$

where the Loss function L is the function of the prediction error, $e_t^1$ and $e_t^2$ are the forecasting errors of the two comparison models.

Establishing the DM Statistics:

$$DM=\frac{\overline{d}}{\sqrt{\frac{2\pi {\widehat{f}}_d(0)}{N}}}\stackrel{d}{\to }N(0,1)$$

(11)

$$\overline{d}=\frac{1}{N}{\displaystyle \sum _{t=1}^N[L(e_t^1)-L(e_t^2)]}$$

(12)

where $2\pi {\widehat{f}}_d(0)$ represents a consistent estimator of the asymptotic variance, ${\widehat{f}}_d(0)$ is the zero spectral density, and N is the length of forecasting results.

Comparing the calculated DM with the $Z_{\alpha /2}$, which can be found in the normal distribution table, the null hypothesis will be rejected if $\left|DM\right|>\left|Z_{\alpha /2}\right|$; this means that under the significance level α, there is a significant difference between the two models (the proposed model and the compared models including WNN, GRNN, BPNN, etc.) in terms of their prediction performance. The concrete results are shown in Table 12 and Table 13.

4.3. Analysis

From Table 12 and Table 13, we can see that:

(a)

No matter the bias or the variance, the values of the proposed model are far smaller than those of the other five models, which means that the hybrid model has a higher accuracy and stability than the other five models.

(b)

The smallest value of the $\left|DM\right|$ in both tables is 12.080501, which is much larger than the $Z_{\alpha /2}$ ($Z_{0.005}=2.58$, $Z_{0.025}=1.96$); as a consequence, the null hypothesis can be rejected and the hybrid model observably outperforms the other five models.

5. Conclusions

With the conventional energy for electricity generation being quickly depleted, wind energy has become the most significant new type of green renewable energy available, and contains enormous power. However, due to the uncertainty of meteorological factors, it is still an extremely challenging task to forecast wind speed. In this paper, we put forward a novel hybrid SSA–APSOSA–BP model based on SSA and simulated annealing—adaptive particle swarm optimization algorithm (the specific process is given in Figure 6). From the above discussion and analysis, the conclusions are expressed as follows:

(1)

Among the three single prediction methods (WNN, GRNN, and BPNN), the best one is BPNN, which possesses a stronger prediction performance than the others (see Table 6 and Table 7).

(2)

In summer and autumn, wind speed forecasting errors are larger than in another two seasons because of the more complex features of wind speed in Penglai.

(3)

The experimental simulations indicate that the hybrid SSA–APSOSA–BP algorithm can perform better than the other five algorithms. There is no difference between the means of the forecasting series and the real series, and the accuracy of the wind speed forecasting results can be acceptable and credible within a reasonable range. The detailed reasons are provided in the above experimental simulations Section 3.3.

Overall, the proposed hybrid model adds a new viable option for wind speed forecasting, and the excellent performance and reasonable prediction accuracy reveal that they can be employed for time series forecasting, especially for wind-speed forecasting in some cases.